Introduction

Artificial Intelligence (AI) is advancing at a rapid pace, and as a result there have been many attempts to harness AI based models in the field of medicine to improve upon pre-existing clinical tools. In fact, predictive AI models have demonstrated competitive, or in certain context, superior performance compared to traditional logistic regression models in various healthcare applications1,2,3. However, one obstacle that AI faces in its integration into the medical field is its inherent “Black Box” nature, which is when internal workings of a machine learning (ML) model are unclear where only inputs and outputs are known, thus reducing trust among physicians and patients in this technology4. In contrast, logistic regression models offer inherent explainability through features such as odds ratios and the Wald’s statistic values, which help quantify the importance of variables and their influence on outcomes5. One way of addressing this issue is by adopting explainable AI models, which are models capable of explaining how a particular conclusion is reached, increasing transparency6.

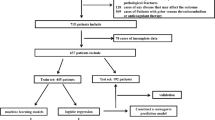
In fields like orthopedic surgery, where timely and accurate risk stratification is vital, AI-driven predictive tools have the potential to improve clinical decision-making. Hip fractures are common among the elderly population, and carry a high risk of mortality, 20 to 30% within the first year, and substantial morbidity7,8. Surgical intervention within 48 h of a hip fracture is the main therapy today. It has been shown to be superior to conservative management in terms of complications and mortality rates9. Few calculators have been developed using ML models to predict the 30-day risk of mortality for hip fracture patients10,11,12. However, few of them prioritized preserving explainability and parsimony, which are essential to clinical application. Our group has developed risk score calculator for hip fracture mortality upon admission or discharge from hip fracture surgery using the American College of Surgeons (ACS) National Surgical Quality Improvement Program (NSQIP) database13. In this study, we investigated the performance of several machine learning (ML) models for predicting 30-day hip fracture mortality, on admission, and on discharge, using the same dataset. Additionally, we implemented an explainability analysis to ensure that the patterns learned by the models are clinically robust. A summary of the full process can be found in Fig. 1.

Fig. 1
figure 1

Overview of the main steps in the pipeline used to develop risk score models.

Full size image

Materials and methods

Study design and patient population

This is a retrospective study based on NSQIP database, a robust multicenter database which collects data from elective and emergency surgical procedures from over 700 hospitals, both academic centers and community hospitals, across the United States and abroad14. Captured data includes demographic information such as age and race, preoperative variables such as comorbidities and pre-operative labs, and post-operative variables such as complications for up to 30 days after the relevant procedure14. It is worth noting that socioeconomic status, geographic location and the type of institute where a specific procedure was performed are not captured by the dataset. We merged the yearly NSQIP orthopedic databases from 2011–2017.We did not include data from 2005 till 2010 since the number of surgeries during these years was low compared to that after 2010. We then selected for the following specific 5 CPT codes for hip surgeries: CPT 27,125: partial hip hemiarthroplasty; CPT 27,236: open reduction and internal fixation of a femoral neck fracture; CPT 27,244: open reduction and internal fixation of an intertrochanteric, peritrochanetric, or subtrochanteric femoral fracture; CTP 27,245: intramedullary fixation of an intertrochanteric, peritrochanteric, or subtrochanteric femoral fracture; and CPT 27,130: total hip arthroplasty.

We selected the appropriate ICD codes for hip fractures at the femoral neck, intertrochanteric, subtrochanteric and peritrochanteric. For those who have ICD 10, we selected age related osteoporosis (M80.051A, M80.051G, M80.051K, M80.051P, M80.052A, M80.052G, M80.052K, M80.052P, M80.059A, M80.059G, M80.059K, M80.059P), S72.0 × for femoral neck, S72.1 × for intertrochanteric, and S72.2 × for subtrochanteric fractures. For those who have ICD 9, we selected the following cases: ICD 820 and 820.xx. We excluded atypical femoral, pathologic, and stress fractures.

  • Inclusion criteria:

    1. o

      Men and women aged 65 years or above who underwent surgery for a hip fracture (either femoral neck fracture via ORIF or total hip hemiarthroplasty or inter / peri / subtrochanteric femoral fracture via ORIF or intramedullary fixation), as per above defined CPT and ICD codes.

  • Exclusion criteria:

    1. o

      Cancer patients.

    2. o

      Patients with atypical femoral, pathologic, and stress fractures.

Data collection and preparation

We based our models on the same database that was used for the development of the predictive risk score using classic logistic regression modeling13. This dataset originally consisted of 181 features (predictors) and 84,825 rows. This large number of features, as well as the presence of some empty cells in the data, required preprocessing and feature selection before starting with the model training. The following steps were adopted:

  1. 1-

    Removing features with more than 30% missing data: In order to minimize potential bias introduced by missing values without resorting to imputation, we developed a Python script to identify missing values (empty cells or cells marked as ‘N/A’) in each column, and excluded any column with more than 30% missing data. We selected the 30% threshold after careful consideration of the trade-offs between retaining valuable information and preserving data integrity. Retaining variables with a higher proportion of missing values would have necessitated removing a significant number of rows, which could have substantially reduced our dataset of 84,825 rows and compromised the robustness of our analysis. Thus, the 30% cutoff represents a balanced approach that preserves as much data as possible while ensuring that the remaining dataset is sufficiently complete to support reliable modeling. This criterion ultimately resulted in the removal of 49 columns from the analysis.

  2. 2-

    Feature to Output correlation: We computed the correlation of each predictor feature with the output column (‘Dead’) and excluded features exhibiting very low correlation relative to the others. A threshold for the absolute value of the correlation was set at 0.015, based on the observed distribution of correlations and in accordance with Haldun Akoglu’s criteria for very weak or poor correlation15. This relatively low threshold was intentionally chosen to avoid prematurely discarding potentially meaningful information, especially since further feature selection based on feature importance will be conducted in later stages. This process led to the removal of 52 additional columns. Six other columns, that could represent pre-op or post-op features (for example, airway trauma, neurologic deficit), exhibited no correlation with our target variable of ‘Dead’. This was due to the absence of these complications in these six columns. We therefore decided to drop them.

  3. 3-

    Feature-to-feature correlation: We derived feature-to-feature correlation and set an absolute threshold of 0.65 to eliminate highly correlated features, based on the pattern of distribution of correlations. This reduces multicollinearity and simplifies the model, while aligning with Halgun Akoglu’s15 and Sapra’s criteria16 for strong correlation. This process led to the removal of 28 features in total. Our correlation analysis in steps 2 and 3 included three types of correlations each tailored to the nature of the variables under investigation:

  4. •

    Categorical, Categorical: For correlations between two categorical features, we used Cramer’s V correlation16.

  5. •

    Continuous, Categorical: For correlations between a continuous variable and a categorical variable, we used the Point-biserial correlation17.

  6. •

    Continuous, Continuous: For correlations between two continuous features, we used the Pearson correlation coefficient15, which measures the linear relationship between the variables.

  7. 4-

    Eliminating data leakage: The dataset included a feature indicating the discharge destination of each patient. It contains multiple categories one of which is “Expired”, which was included amongst the features and was deleted. We ended up with 45 features, 28 depicting pre-operative features and 17 additional post-operative features. The meanings of these features are explained in Appendix Table 1. Namely, the abbreviations for these features in NSQIP are: WORKRVU, Female, Age, Weight_kg, Height_meter, PRSODM, PRBUN, PRWBC, PRHCT, PRPLATE, PRINR, smoke, DNR, VENTILAT, HXCOPD, ASCITES, HXCHF, RENAFAIL, DIALYSIS, WNDINF, WTLOSS, BLEEDDIS, TRANSFUS, EMERGNCY, dyspnea, FNSTATUS2, PRSEPIS, ASACLAS, OUPNEUMO, REINTUB, PULEMBOL, FAILWEAN, RENAINSF, OPRENAFL, CNSCVA, CNSCOMA, CDARREST, CDMI, OTHSYSEP, CPTnew, OTHSESHOCK, readmission, OPTIME, DOptoDis, NOTHBLEED.

  8. 5-

    Feature Encoding: one of the remaining features, “CPTnew” (stands for CPT codes), had string values. We used one-hot encoding due to the 4 distinct implications of these string values. This encoding method transforms the 4 categories into binary vectors and preserves the uniqueness of each. Additionally, it avoids introducing ordinal relationships and ensures compatibility with a broad range of machine learning models, as each of the 4 unique CPT code represents a different surgical approach to hip fracture treatment.

  9. 6-

    Removing rows with missing values: After completing the above processing steps, rows containing missing values were removed, reducing the dataset to 62,492 rows, including 4,068 rows representing deceased patients. No imputation techniques were applied; however, given the large initial dataset size and that the retained data preserved the most valuable information, this removal did not adversely affect model performance.

  10. 7-

    Data division: We divide the processed dataset at hand between 95% training (59,367 samples, including 3,865 deaths) and 5% testing (3,125 samples, including 203 deaths) using a stratified random sampling approach to maintain the original distribution of the data. Given the substantial size of our dataset, dedicating the majority to training allows us to thoroughly teach the model the less common patterns associated with mortality, which are crucial for making accurate predictions. To further enhance the training effectiveness, we implemented tenfold cross-validation, where 10% of the training data (5,937 samples, including 387 deaths) is used for validation in each fold, cycling through all data in order to perform hyperparameter tuning. The patient baseline demographics of the training set, testing set, and the full set can be found in Table 1. It is clear that the characteristics of patients are aligned across the three sets, indicating a consistent representation.

Table 1 Baseline characteristics of patients overall, and in the training and testing datasets, divided by continuous variables (A) and categorical variables (B).
Full size table

Pre-operative model training

After data processing, we selected a set of training models with varying complexities and designs. These include:

  • LightGBM18: A gradient boosting framework that uses tree-based learning algorithms, efficient for large data sets due to its fast processing speeds.

  • Random Forest19: An ensemble learning method that constructs multiple decision trees during training and outputs the class that is the mode of the classes of individual trees, providing high accuracy and robustness against overfitting.

  • Logistic Regression20: A statistical model that predicts the probability of a binary outcome, commonly used for binary classification tasks such as disease/no disease.

  • Naive Bayes20: A group of simple probabilistic classifiers based on applying Bayes’ theorem with strong independence assumptions between the features.

  • Gradient Boosting20: A method that builds an ensemble of decision tree models in a sequential manner, focusing on correcting the errors of the previous trees in the sequence.

  • XGBoost20: An implementation of gradient boosted decision trees designed for speed and performance, widely used in winning many machine learning competitions.

  • CatBoost21: An algorithm for gradient boosting on decision trees, developed to handle categorical variables very efficiently.

  • AdaBoost20: A boosting algorithm that combines multiple weak learners to create a strong learner, typically increasing the accuracy of simple models.

We then applied tenfold cross-validation with randomized search to identify the optimal hyperparameters for these ML models using the training set. Subsequently, we evaluated the models on the test set, computed the Area Under the Receiver Operating Characteristic Curve (AUC) along with its 99% confidence interval, and conducted DeLong’s test to assess the statistical significance of performance differences between models. Based on these analyses, we selected the best-performing model for the next experiments. We apply this to the 28 pre-operative features defined in Table 1-Appendix.

Feature selection

We aimed to streamline the application of the highest-performing model by minimizing the number of required input features without substantially sacrificing performance. Our approach involved leveraging the feature importance scores generated by the best model to identify the most impactful predictors. We incrementally changed the number of features starting with one feature and incrementing them one by one until we reached 28 features. For each feature set, we reported the AUC on the test set.

Post-operative model training

In this part, we repeated the same modeling process that was done with the 28 features, but this time using all the 45 variables. We select the same models as before: LightGBM, Random Forest, Logistic Regression, Naive Bayes, XGBoost, CatBoost, AdaBoost, and Gradient Boosting. We then applied tenfold cross-validation with randomized search to identify the optimal hyperparameters for these ML models using the training set. Subsequently, we evaluated the models on the test set, computed the AUC along with its 99% confidence interval, and performed DeLong’s test to assess the statistical significance of performance differences between models. Based on these analyses, we selected the best-performing model.

Feature selection

The same process of feature selection that was applied to the best pre-operative model was applied to the post-operative model. First, we derived the feature importance for this model and ranked the features. Then, we repeated the training process by varying the number of features, —specifically, 1 to 10, then 15, 20, 25, 30, 35, 40, and the complete set of 45 post-operative features, prioritizing features with the highest importance scores, and each time deriving AUC on the test set.

Model explainability

Our approach leverages SHAP22 (SHapley Additive exPlanations) values to uncover and quantify the impact of individual features on the predictions made by the best post-operative model. SHAP values, based on cooperative game theory, assign a numerical value to each feature in each sample, quantifying its impact on the prediction. This value not only indicates the strength of the impact but also shows whether this feature value increases or decreases the prediction. This method ensures that the influence of each feature on the prediction is fairly and consistently attributed. These values illuminate how each feature contributes, either positively or negatively, to the model’s output, thereby ensuring that the model’s operations are transparent and comprehensible for clinical end-users. To do that, we use a SHAP beeswarm plot, which organizes individual SHAP values for each feature across all data points. This plot not only shows the impact but also the variability and direction of each feature’s effect on model behavior. Features with higher variability in their SHAP values have greater influence on model behavior.

Results

Patient population

We included a total of 62,492 patients for years 2011–2017: 28.6% were males and 71.4% were females (Table 1). The mean (SD) age of the population was 82.51 (7.2) years. The race of 79.9% of our patients was classified as “white”, 3.1% as black, 3.1% as ”Other”, and the race of the remaining 13.8% was classified as “unknown”. Most of the study patients were functionally independent (78.4%). Approximately half of the patients had a normal BMI (48.9%), 9.1% were underweight, 28% were overweight, and 14% were obese. 38.7% of the study population underwent intramedullary fixation of femoral fracture, followed by 29.3% undergoing open reduction internal fixation (ORIF) of the femoral neck. The mean duration of the surgery was 66.2 min. The clinical characteristics of patients in the training, testing and full datasets were comparable (Table 1).

Pre-operative model performance

Figure 2a illustrates the ROC curves and the corresponding AUC values for the eight models. The AUCs achieved are around 0.78, including logistic regression, and with the exception of for Naive Bayes, which attained an AUC of 0.734. The highest-performing model is AdaBoost, with an AUC of 0.792 and a 99% confidence interval of (0.752, 0.828). Notably, AdaBoost exhibits the highest lower bound (0.752) and upper bound (0.828) among all models, further reinforcing its superior and more stable performance. To further assess the significance of performance differences, we conducted DeLong’s test, comparing each model against AdaBoost. The results indicate that LightGBM, Random Forest, Naïve Bayes, and XGBoost exhibit statistically significant differences (p < 0.05) when compared to AdaBoost, suggesting that their performance is significantly lower. In contrast, Logistic Regression, CatBoost, and Gradient Boosting did not show a statistically significant difference from AdaBoost (p > 0.05), indicating that their performance is comparable. Given that AdaBoost achieved the highest AUC, the best confidence interval bounds, and no model significantly outperformed it, we selected AdaBoost as the best-performing model for pre-operative prediction.

Fig. 2
figure 2

(a). ROC curves comparing performance of pre-operative models on the test set ROC: Receiver Operating Characteristic (b). Absolute feature importance for the trained pre-operative AdaBoost model (c). AUC score vs. incremental feature set size for the pre-operative AdaBoost model on the test set AUC: Area Under the Curve.

Full size image

The most important features for the AdaBoost model are shown in Fig. 2b where features like Weight, Age, and Height stand out as the most significant. Figure 2c depicts the AUC for each subset of features selected based on their importance. Initially, as features are added, the AUC score increases significantly. For example, adding the first nine features (Weight, Age until reaching ASA classification) raised the AUC score from 0.520 to 0.771. The model’s performance improves steadily up to around 17 features, reaching an AUC of approximately 0.792. Beyond this point, the addition of more features shows no significant benefit, with the AUC score stabilizing.

Post-operative model performance

Figure 3a illustrates the Receiver Operating Characteristic Curve (ROC) curves and the corresponding AUC values for the eight models. All models performed well, achieving AUCs around 0.88, except for Naive Bayes, which attained an AUC of 0.836, and Logistic Regression, which achieved an AUC of 0.873. The highest-performing model was CatBoost, with an AUC of 0.885 and a 99% confidence interval of (0.855, 0.913). Importantly, CatBoost exhibited both the highest lower bound (0.855) and upper bound (0.913) among all models, further highlighting its strong and stable performance. To evaluate the statistical significance of performance differences, we applied DeLong’s test, comparing each model against CatBoost. The results indicate that only Logistic Regression and Naïve Bayes exhibited a statistically significant difference (p < 0.05) when compared to CatBoost, suggesting that their performance was significantly lower. In contrast, LightGBM, Random Forest, XGBoost, AdaBoost, and Gradient Boosting did not show a statistically significant difference (p > 0.05), meaning their performance was comparable to CatBoost. Since CatBoost achieved the highest AUC, the most favorable confidence interval bounds, and no model significantly outperformed it, we selected CatBoost as the best-performing model for post-operative prediction. Additionally, CatBoost is known to handle categorical variables effectively, and since the dataset contains a majority of categorical variables, as shown in Table 1, this made CatBoost an even more suitable choice for the task.

Fig. 3
figure 3

(a). ROC Curves comparing performance of Post-operative models on the test set ROC: Receiver Operating Characteristic (b). Absolute feature importance for the trained post-operative CatBoost model (c). AUC score vs. incremental feature set size for the post-operative CatBoost model on the test set AUC: Area Under the Curve.

Full size image

The most important features for the CatBoost model are shown in Fig. 3b, with Age, ASA classification, and functional health status prior to surgery identified as the most influential variables. Figure 3c depicts the AUC for each subset of features selected based on their importance. Initially, the AUC jumps from 0.653 to 0.793 with the top four features, reaching 0.854 after including the top nine features. The AUC stabilizes at 0.885 when 35 features are included, indicating that adding more features beyond this point offers minimal improvement to the model’s performance.

The SHAP beeswarm plot, as shown in Fig. 4, visually represents the impact of various features on the best model’s output. Each point corresponds to a feature value from a patient’s data, with the color indicating its magnitude—red for higher values and blue for lower values in continuous variables, and red for a ‘yes’ response (presence of a feature) and blue for a ‘no’ response in binary variables. The horizontal position of each point reflects how the feature value affects the model’s prediction, with points to the right contributing to an increased predicted risk and points to the left contributing to a decreased risk. Notably, the features positioned at the top of the plot are the most influential, as they exhibit the highest absolute SHAP values, indicating a strong contribution to the model’s decision-making process. As one moves down the plot, the features demonstrate progressively lower SHAP values, suggesting a lesser impact on the model’s predictions.

Fig. 4
figure 4

SHAP Feature Explainability for the post-operative CatBoost model on the full set Each dot represents the impact of a specific feature value from an individual patient’s data on the model’s prediction. For continuous variables, shades leaning towards red indicate higher values of the variable, while shades leaning towards blue represent lower values. In the case of binary variables, solid red dots signify an affirmative response (‘yes’), and solid blue dots indicate a negative response (‘no’). The vertical distribution of dots for each feature shows the density and variability of the SHAP values among different patients. Positive SHAP values (dots to the right) signify an increase in the risk score, whereas negative SHAP values (dots to the left) indicate a decreased risk. The features shown include various clinical metrics and patient characteristics, highlighting their respective influences on the model’s output.

Full size image

For instance, according to SHAP, the most important features are Age and Functional Status (FNSTATUS), while features like Coma > 24 h (CNSCOMA_m) and Ventilator Dependent (VENTILAT_m) have a limited impact.

For the ‘Age’ variable, which is continuous, the plot clearly shows that higher values (indicated by red points) significantly increase the model’s output, as they are located to the right. This suggests an increased risk or poorer prognosis. Conversely, for the ‘Weight’ variable, despite higher values also being indicated by red points, they decrease the model’s output, as evidenced by their positioning to the left. This indicates a lower mortality risk prediction associated with higher body weight. These findings align with the literature, as will be expanded in the Discussion.

Additionally, the plot illustrates mixed colors on both the positive and negative sides of SHAP values for certain features, such as ‘Days from Operation to Discharge’. This indicates a complex interaction pattern where patients with similar values for this feature may exhibit either positive or negative SHAP values, depending on other associated features. This demonstrates how interactions between different features can significantly influence the model’s predictions, highlighting the dynamics that must be considered when interpreting the model’s output, as detailed in the Discussion.

Model validation

We also acquired access to the 2018–2020 orthopedic NSQIP dataset (N = 47,322). Baseline demographics of that dataset were broadly similar to those in our original dataset (2011–2017). We applied our models from the 2011–2017 model to the new dataset. The AUCs expressing predicted versus actual mortality were slightly lower in the new dataset compared to the original dataset, which is expected for the validation of a model. For example, the pre-operative model reached a maximum AUC of 0.792 in the original dataset, whereas it reached a lower AUC of 0.771 in the validation dataset. Similarly, the post-operative model achieved a maximum AUC of 0.885 in the original dataset, whereas it achieved a lower AUC of 0.864 in the validation dataset.

Deploying the models in a calculator

Based on the remarkable results, we deployed the pre-operative and post-operative models in a web app accessible for medical professionals. The application was designed to be intuitive, requiring users to input patient-specific values into clearly labeled fields, after which the pre-operative and post-operative risk scores are instantly generated, as shown in Appendix Fig. 1(a, b, c). To enhance usability, built-in validation checks ensure that numerical values fall within reasonable clinical ranges and that categorical inputs are correctly formatted, reducing the likelihood of errors. The model used for pre-operative risk prediction is AdaBoost, utilizing the top 15 pre-operative features as indicated in Fig. 2b. For post-operative risk prediction, the model is CatBoost, leveraging the top 15 post-operative features according to Fig. 3b. This app will be deployed for public usage soon, with ongoing improvements based on user feedback to optimize its clinical utility.

Discussion

We developed a risk predictive model for 30-day mortality for patients admitted for hip fracture surgery, one to be used upon admission and the other upon discharge, through exploration of 8 different established machine learning models, including logistic regression. Our data set illustrates the typical profile of patients admitted with hip fractures in terms of age, gender, BMI, and co-morbidities. The final selected models are parsimonious and display high performance. The AUC for the risk score on admission using AdaBoost is 0.725 with 8 predictors, 0.785 with 12 predictors, and it saturates at 0.792 with 19 predictors. Similarly, the AUC for the calculator on discharge using CatBoost is 0.851 with 6 predictors, 0.860 with 10 predictors, 0.872 with 15 predictors, and saturating at 0.885 with 35 predictors. The predictors of highest importance are clinically relevant and easily obtainable, rendering the risk score calculator practical and easily applicable to guide patient management in clinical care settings.

The top 8 strongest predictors for the preop model were: weight, age, height, preoperative WBC, functional health status, pre-operative platelets, pre-operative hematocrit, and pre-operative sodium; and the top 12, would in addition include ASA classification, pre-operative INR, gender and pre-operative BUN. The top 6 strongest predictors for the post-op model were age, ASA classification, functional health status, cardiac arrest requiring CPR, postoperative pneumonia, and hospital length of stay; and the top 10 would in addition include preoperative BUN, weight, unplanned re-intubation, and pre-operative INR. When examining the patterns from the SHAP plot in Fig. 4, we see that the predictors identified and their incurred risk prediction on 30-day mortality are consistent with clinical observations and are biologically plausible. For instance, low hematocrit count is a predictor of mortality whereas low ASA classification (better functional status) was protective. In addition, high weight is protective against hip fracture mortality, consistent with the “obesity paradox” observed in the literature23. Moreover, high age is a well-known predictor of mortality, which is commonly included in widely used hip fracture mortality calculators such as the Nottingham Hip Fracture Score (NHFS) and the Hip Fracture Estimator of Mortality Amsterdam (HEMA)24,25,26. Likewise, for days from operation to discharge, short stays (blue color) may indicate efficient, complication-free recoveries (negative SHAP values) or premature discharges leading to readmission or death (positive SHAP values). Conversely, long stays (red color) might reflect necessary extended care for recovery (negative SHAP values) or a complicated hospital stay leading to death (positive SHAP values). Such dual interpretations underline how the impact of one feature can vary significantly based on interactions with other patient-specific data, demonstrating the complexity of model predictions in healthcare.

Few studies have investigated a variety of ML based techniques to develop hip fracture mortality calculators using the NSQIP dataset (Table 2). Harris et al., developed a model base spanning admissions from 2011–2017, and including 82,168 subjects using a ML based Least Absolute Shrinkage and Selection Operator (LASSO) logistic regression model. They achieved an AUC of 0.76, with 15 pre-operative variables10. Our model performed better, with a higher AUC of 0.771 with only 9 variables, and that reached 0.789 with 15 variables. This improvement is due to our use of more powerful machine learning models, such as CatBoost, XGBoost, and Random Forest, as well as advanced hyperparameter tuning, rigorous data preprocessing, and feature selection strategies. These methodological enhancements allowed our model to extract more predictive insights from the data while maintaining efficiency with fewer variables. In contrast, DeBaun et al., with a sample of 19,835 patients admitted between 2016 and 2017, developed multiple models using 47 pre- and postoperative predictors. The model with the highest performance used the artificial neural network (ANN) and achieved a remarkable AUC of 0.9211, that is excellent, but however at the cost of numerous predictors, which would increase the clinical workload on clinicians in real life application11. Moreover, their study used a much smaller dataset than ours and lacked hyperparameter tuning and data pre-processing11. Furthermore, while the neural network model used achieved a higher AUC than our model, it lacked inherent interpretability, a crucial feature in building trust with clinicians and patients11. These drawbacks may hinder the clinical application of their model. In contrast, our approach leverages boosting techniques such as CatBoost and AdaBoot, which provide a strong balance between performance and interpretability, enabling feature importance analysis. By optimizing our models with hyperparameter tuning and a streamlined set of predictors, we achieve a practical and explainable solution without sacrificing accuracy. These advantages make our model more suitable for real-world clinical applications. Lin et al. used a LASSO logistic regression model, with a sample size of 107,660 hip fracture patients admitted between 2016 and 2020, to develop two models. The first used 68 pre-operative predictors and the second a total of 84 pre and postoperative predictors12. Their pre-operative and post-operative models reached AUCs of 0.68 and 0.83 respectively12. While the LASSO coefficient allows for interpretability of the magnitude and direction of influence each predictor, their study did not implement hyperparameter tuning and data preprocessing which may explain their lower performance despite a using larger sample. Importantly, while a larger dataset can improve model performance, simple models like LASSO logistic regression do not necessarily benefit as much from increased data as more complex machine learning models. In contrast, our study employed more sophisticated models which are better equipped to capture complex patterns in the data. Combined with hyperparameter tuning and robust preprocessing, these techniques allowed us to achieve superior performance with fewer predictors, demonstrating the advantages of a more refined modeling approach. DeBaun et al. and Lin et al. did not explore performance under parsimonious conditions11,12.

Table 2 Performance of various models to predict 30-day mortality post-hip fracture surgery using ACS NSQIP in our study and in the literature.
Full size table

Rhayem et al. developed classic logistic regression models with backward selection to identify significant pre-operative and post-operative predictors13. Their models achieved a pre-operative AUC of 0.742 with 16 predictors, and a post-operative AUC of 0.813 with 27 predictors13. In contrast, when matching the number of predictors, our models outperform theirs, achieving a pre-operative AUC of 0.789 with 16 predictors and a post-operative AUC of 0.878 with 27 predictors. Moreover, when comparing performance, our approach can achieve similar or better results with fewer predictors. Specifically, our pre-operative model can reach an AUC of 0.771 with only 9 variables, and our post-operative model can attain an AUC of 0.829 with just 5 variables. This efficiency in predictor usage without sacrificing accuracy stems from a combination of data processing, correlation analysis, modern ML techniques with hyperparameter tuning, and feature selection based on importance—strategies that other studies did not fully exploit. We identified 2 other studies that developed predictive models for 30-day hip fracture mortality using traditional logistic regression models based on pre-operative predictors25,26. The Nottingham Hip Fracture Score (NHFS, UK) (7 predictors) and the Hip Fracture Estimator of Mortality Amsterdam (HEMA, Netherlands) (9 predictors) we found the following: When matching for number of predictors, our pre-operative model performed as well as the NHFS score (0.717 vs 0.719) but slightly less than the HEMA score (0.771 vs 0.790)25,26. However, it is worth mentioning that the datasets used to train and evaluate the 3 models were from different countries, with slightly different gender distributions (Table 3). When comparing the 10 most impactful predictors of our model to the predictors used in the aforementioned calculators, we only found age as the common predictor between our model and the HEMA score25. However, it is worth noting that 3 of the 9 predictors used by the HEMA score were not available in our patient population in the NSQIP database (in-hospital fracture, malnutrition) or because of our study’s exclusion criteria (recent history of malignancy)25.

Table 3 Performance of various Logistic Regression Based Calculators as compared to our study’s model.
Full size table

As for the NHFS, of the 7 variables they used, 3 were not available in our dataset, and 3 out of the 4 common remaining ones were selected amongst our top 7 strongest predictors (order rank 2, 5 and 7)26. They were age for both, functional health status in ours mirroring institutionalization in their study, pre-op Hct in our study, and pre-op hemoglobin in theirs26. Of the variables applicable to our population, only gender was not among the 10 most impactful predictors in our model, which may explain their equivalent performance26.

Overall, our study not only achieves superior predictive performance but also does so with greater efficiency, requiring fewer predictors than previous models while maintaining or exceeding their performance. This balance between performance and practicality enhances real-world applicability, making our approach more adaptable for clinical use. Furthermore, the methodology and pipeline we developed can be readily adapted to different datasets and patient populations, ensuring flexibility for future applications.

This study has few limitations. We did not have access to periods beyond 2017 to validate our findings in a more current period. We, however, plan to do so. The ultimate litmus test would be in an independent population altogether. The NSQIP database contains a disproportionately high contribution stems from large academic centers, limiting its generalizability in the community setting27. However, it has robust data, from a diverse patient population, from centers across the United States. Moreover, the model could be readily applied and adapted to community hospitals and other healthcare settings. This study has other several strengths. It does not include race among the 45 pre and post-operative predictors. While this was not intentional, this may prove to be an advantage in the long term as many medical societies are considering to retrospectively remove race as a characteristic from their calculators due to historic bias28,29. Our model is parsimonious, and we know that it performs well with few variables, most of which are routinely obtained during pre-operative assessment, which is extremely beneficial in clinical scenarios. Finally, the additional layer of interpretability provided by the SHAP analysis ensures model transparency, making it easier to identify and correct potential model bias.

In conclusion, by implementing a combination of data preprocessing and post-modeling feature selection, our ML models predicted 30-day hip fracture mortality with robust performance, a low number of readily available clinical predictors, while maintaining transparency and interpretability. Further clinical validation is required via the use of additional datasets, or conducting prospective studies in real-world clinical scenarios for testing accuracy.