Introduction

The Bel Canto vocal performance is a complex and multidimensional art form, encompassing various features such as pitch, timbre, technique, emotion, language, and aesthetic expression1. However, in actual vocal evaluation scenarios, due to differences in background, aesthetic preferences, and professional knowledge among judges, different judges may have different feelings about the same performance, resulting in high subjectivity and variability in their comments. Given this, we aim to explore an objective and accurate vocal technique evaluation method to effectively reduce the influence of subjective factors on the scoring results and provide a new solution for the standardization of vocal technique evaluation.

In recent years, there has been increasing research interest in pattern recognition of audio and sound. These studies involve multiple tasks, including music genres classification2,3,4, environmental sound classification5,6, sound event detection7,8,9 and so on. However, with the deeper integration of artificial intelligence (AI) and music, the focus of research has shifted from pattern recognition to more sophisticated and expressive tasks, such as vocal technique assessment10,11. Vocal technique assessment aims to quantify and assess singing quality by analyzing pitch, timbre, rhythm, and affective expression features. This task holds excellent significance for vocal teaching and performance evaluation. Compared to simple audio and sound, vocal performance involves richer artistic expression and multidimensional vocal features, which puts higher demands on the ability to understand deep learning models. In prior works, Convolutional Neural Networks (CNNs) were widely used in audio pattern recognition due to their powerful capability to capture spatial hierarchical information8,9,12,13,14. At the same time, Transformer-based networks15,16,17,18 for audio spectrum outperform traditional CNNs by performing pretraining on large datasets and fine-tuning them for small datasets applied to downstream tasks. However, Transformers based on self-attention19 have high computational costs in training and inference and overly rely on well-labeled large-scale datasets. Consequently, CNNs remain the preferred choice under resource constraints and efficiency requirements.

However, 2D convolution in CNNs still has limitations in handling audio pattern recognition tasks. Specifically, it includes the following three aspects:

  1. 1.

    Fixed convolution kernel parameters. Standard convolution uses a fixed convolution kernel on the entire input data and applies the same parameters to all samples, lacking dynamic adaptability. This static nature makes it impossible to adjust the feature extraction mechanism for diverse input data, especially when dealing with complex audio and image data, with limited performance13,20,21,22,23.

  2. 2.

    Lack of ability to capture dynamic features. The neat convolution kernel assumes that the input data features are translation equivariant, but this does not hold true in the dimensions of audio data, such as frequency and time axes, resulting in the model being unable to effectively capture complex changing time-frequency features20,24,25.

  3. 3.

    Lack of adaptability to multidimensional data. 2D convolution uses a single convolution operation for different dimensions (such as time, frequency, space, and channel), which fails to fully consider the interactivity and heterogeneity of multidimensional data, making it difficult to accurately capture the complex correlations between high-dimensional data25.

Recent studies8,9,15,16,18,26 have shown that pretraining CNNs on large-scale datasets such as ImageNet27and Audioset7, followed by transfer learning to specialized datasets using techniques like knowledge distillation (KD)28,29,30, an substantially enhance classification accuracy. However, for the model itself, there is still much room for improvement in its capability to mine spectral features. To process the audio data of complex vocal performances and better serve the needs of objective vocal evaluation. We urgently need to improve CNN to enhance its ability to learn features.

Although scaling CNNs by width and depth usually improves performance, it dramatically increases the complexity of the model and may even backfire. So, we have introduced Omni Dimensional Dynamic Convolution (ODConv)25 to mine more feature information. Unlike standard convolutions, ODConv’s convolution kernel supports multidimensional dynamics (time, frequency, space, and channel) and can dynamically adjust the weights of the convolution kernel based on the distribution of input features. This dynamism breaks the limitations of traditional convolution kernels with fixed parameters to explore more implicit features.

At the same time, to effectively utilize the multi-scale contextual information in the network, we adopt dense connections31 to cascade different convolutional layers to utilize the multi-scale spectral features repeatedly. To verify the effectiveness of the proposed method, we conducted extensive experiments on audio pattern recognition tasks such as vocal technique assessment, environmental sound classification, music genre classification, and sound event detection. The experimental results show that our method outperforms traditional CNNs and Transformer-based models in performance. In summary, the main contributions of our work are as follows:

  1. 1.

    We introduce Omni Dimensional Dynamic Convolution (ODConv) to replace ordinary convolution as the main module and construct a Dense Dynamic Convolutional Network (DDNet) with a dense connection structure.

  2. 2.

    We have studied the performance of various CNNs and spectral transformers in vocal technique assessment tasks, achieving a SOTA of 90.11% (Top-1_Acc).

  3. 3.

    We have demonstrated that DDNet can be employed for other audio pattern recognition tasks, including music genre classification, environmental sound classification, and sound event detection, beyond classical CNNs and Transformer-based models. They reached 73.95%, 89.31% (Top-1_Acc), and 41.89% (mAP).

Releated works

CNN architectures

In recent years, Convolutional Neural Networks (CNNs) have shone in the field of audio pattern recognition due to their powerful ability to capture spatial hierarchical information. Yeshwant Singh and Anupam Biswas proposed a method called MGA-CNN32, aimed at automatically finding the optimal lightweight CNN architecture for music genre classification tasks. Ashraf et al.33 proposed a hybrid architecture combining CNN and recurrent neural network (RNN) variants (such as LSTM, Bi LSTM, GRU, and Bi-GRU) for music genre classification, aiming to overcome the limitations of a single model. Gao et al.34 proposed an innovative multimodal information fusion evaluation method, which combines sound information and motion data to extract action features by CNNs, achieving a comprehensive evaluation of student instrumental performance. Its effect is significantly better than traditional classroom evaluation.

Currently, with the continuous emergence of efficient CNN networks, the performance of models is constantly improving. For example, GhostNet35, MobileNetV2 36, DenseNet31 and other methods. MobileNetV2 introduces inverse residual blocks with linear bottlenecks, combining deep convolution and \(\:1\times\:1\) point-by-point convolution to improve accuracy and computational efficiency. DenseNet and GhostNet introduce dense connections to cascade convolutional layers, in order to repeatedly utilize the multi-scale features of each layer. It optimizes the network structure from the perspectives of depth and width, and reduces the inherent information loss of network downsampling.

Transformer architectures

The Transformer-based models15,16,18,36 have recently refreshed the ranking of audio pattern recognition. Gong et al.16further applied ViT37 to audio spectrograms and improved the audio classification performance of AudioSet and ESC-5026 by fine-tuning using pre-trained models of computer vision. The Transformer architecture consists of a series of self-attention layers19 that can learn the dependency relationships between different elements in a sequence, regardless of the position or spacing of the sequence. Compared to CNNs, the main drawback of AST16 is its high computational cost. Self-attention computation and memory complexity increase exponentially with sequence length. Therefore, researchers have done a lot of work18,38,39 in optimizing computational costs, but often at the cost of reducing predictive performance. At the same time, when Transformers are applied for fine-tuning downstream tasks, they rely too much on a large-scale dataset and pretraining to achieve good performance.

Pre-trained audio models

In the past few years, pre-trained deep neural networks have become an essential paradigm in machine learning. By utilizing transfer learning techniques, pre-trained models can significantly improve the performance of downstream tasks, especially when there is insufficient training data. Many transfer learning works9,15,16,17,18 utilize supervised models pre-trained on the ImageNet image dataset to initialize the weights of audio models. Nevertheless, it may not be the best choice because there are significant differences between the spectrogram of audio content and the actual image, except for similar low-level semantics (the image’s shape). J. F. Gemmeke et al.16 proposed the Audioset dataset to fill the gap in large audio datasets. Subsequently, an increasing number of tasks8,9,16,17,26,36,39 are using Audioset’s pre-trained weights to fine-tune models for different downstream tasks, rapidly advancing audio pattern recognition technology development. However, in the transfer learning process, label bias between different datasets will inevitably transfer to the model, affecting performance. In addition, transfer learning has not improved the feature-mining ability of the model itself.

Exploration of dynamic convolution

Many publications21,22,23,25 have improved standard convolutions to dynamically and adaptively extract features efficiently. Unlike standard convolution, dynamic convolution can adaptively adjust kernel weights based on input features. CondConv22 linearly combines a set of K kernels to weight attention based on input features to maintain efficient inference. However, it only focuses on the dynamic characteristics given to convolutional kernels by multiple kernels (number of convolutional kernels) in a single dimension while ignoring other multidimensional information (spatial information and feature channel information of each convolutional kernel). Similar to CondConv, DyNet21 proposes using global average pooling in CNN blocks to extract shared context from the input and parameterize all dynamic convolutions in the block. The Omni-Dimensional Dynamic Convolution (ODConv)25 utilizes multidimensional attention mechanisms and parallel strategies to learn the complementary attention of convolutional kernels in the kernel space, space, and channel dimensions of any convolutional layer. Its more efficient multidimensional attention structure enables it to mine multi-level spatial information more effectively.

In audio, variations of dynamic convolution include Time Dynamic Convolution (TDY)24 and Frequency Dynamic Convolution (FDY)20. TDY focuses on the time-varying characteristics of speech and designs a dynamic filter that adjusts along the time axis. FDY improves sound event detection by adjusting the dynamic filter along the frequency axis, while maintaining the shift in the frequency dimension unchanged. However, like CondConv, TDY and FDY perform K parallel convolutions repeatedly, resulting in significant computational overhead. DyMN13 effectively extracts shared context from the feature maps input by integrating dynamic convolution23 into residual inversion block40.

Proposed methods

Omni-Dimensional Dynamic Conv

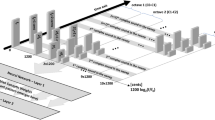
Different from the dynamic convolution in previous work, Omni- Dimensional Dynamic Conv (ODConv)25 introduces a parallel multidimensional attention mechanism that learns the features of different attentions along the kernel-space, spatial, input-channel and output-channel dimensions of the convolution kernel, the formulation of ODConv in Eq. 1:

$$\:y=\left({\alpha\:}_{w1}\odot\:{\alpha\:}_{f1}\odot\:{\alpha\:}_{c1}\odot\:{\alpha\:}_{s1}\odot\:{W}_{1}+...+{\alpha\:}_{wn}\odot\:{\alpha\:}_{fn}\odot\:{\alpha\:}_{cn}\odot\:{\alpha\:}_{sn}\odot\:{W}_{n}\right)\text{*}x,\:\:\:\:\:\:$$
(1)

where \(\:{\alpha}_{wi}\in\:\mathbb{R}\) denotes the attention scalar for the convolutional kernel \(\:{W}_{i}\), and \(\:{\alpha}_{si}\in\:{\mathbb{R}}^{k\times\:k},{\alpha}_{ci}\in\:{\mathbb{R}}^{{\text{C}}_{in}}\) and \(\:{\alpha}_{fi}\in\:{\mathbb{R}}^{{\text{C}}_{out}}\) denote three newly introduced attentions, which are computed along the spatial dimension, the input channel dimension and the output channel dimension of the kernel space for \(\:{W}_{i}\). \(\:\odot\:\) denotes the multiplication operations along different dimensions of the kernel space.

In contrast to standard convolution, the dynamic convolution in previous publications21,22 applies a linear combination of \(\:n\) kernels, which increases plenty of parameters by a factor of n. In addition, they only focus on features in the spatial dimension of a single kernel, but ignore the multidimensional information in the spatial dimension, the input channel dimension, and the output channel dimension of the convolutional kernel. It also results in the loss of multidimensional feature information.

However, the parallel multi-attention mechanism of ODConv can gradually learn corresponding attention scalars from the dimensions of spatial position, channel, and kernel space in parallel, and then multiply them by the convolution kernel \(\:{W}_{i\in{n}}\) to capture rich multidimensional context, with a good balance between module performance and size. Figure 1 shows the process of multiplying these four types of attention by \(\:n\) convolutional kernels.

Fig. 1
figure 1

The process of multiplying four types of attention by convolutional kernels.

Full size image

In ODConv, for each convolution \(\:{W}_{i\in{n}}\): (1) \(\:{\alpha}_{si}\) assigns spatial attention scalars to each convolution (each filter); (2) \(\:{\alpha}_{ci}\) assigns different attention scalars to the \(\:{c}_{in}\) channels of each convolutional filter; (3) \(\:{\alpha}_{fi}\) assigns different attention scalars to the \(\:{c}_{out}\) channels convolutional filter; (4) Assign different attention scalars of kernel-space to the convolutional kernels as \(\:{\alpha}_{wi}\).

Regarding to spatial dimensions \(\:{\alpha}_{si}\), input channel \(\:{\alpha}_{ci}\), output channel \(\:{\alpha}_{fi}\) and the kernel-space \(\:{\alpha}_{wi}\), dimensions, we design independent attention modules to capture the information characteristics of each dimension and adaptively generate attention weights for each dimension. Finally, these weights are dynamically weighted with the convolution kernel to generate attention convolution kernels for different dimensions.

The calculation of attention weights for all dimensions is performed in parallel, rather than sequentially. Our goal is to simultaneously consider the correlation between multiple dimensions and avoid overly relying on the features of one dimension. It is particularly effective for audio with complex time-frequency characteristics or images with rich multi-level information25.

Despite introducing parallel attention mechanisms, the parallel structure of ODConv effectively controls computational overhead. We assume that the time complexity of standard convolution is:

$$\:O\left(n\right)=O({C}_{in}\cdot\:H\cdot\:W\cdot\:{K}^{2})$$
(2)

where \(\:{C}_{in}\) is the number of input channels in the feature map, \(\:{C}_{out}\) is the number of output channels, \(\:H\) and \(\:W\) are the height and width of the feature map, and \(\:{K}^{2}\) is the size of the convolution kernel.

We introduces dynamic convolution kernel generation and parallel multi-attention mechanism on the basis of standard convolution for ODConv, so its total time complexity can be expressed as:

$$\:{O}^{{\prime\:}}\left(n\right)=O\left(Standard\:Conv\right)+O\left(Parallel\:Attention\right)+O\left(Dynamic\:Weighting\right)$$
(3)

The time complexity of dynamic convolution kernel generation and parallel multi attention is:

$$\:O\left(Parallel\:Attention\right)=O(M\cdot\:({C}_{in}\cdot\:r+r\cdot\:{C}_{out}\left)\right)$$
(4)
$$\:O\left(Dynamic\:Weighting\right)=O({C}_{in}\cdot\:H\cdot\:W\cdot\:\text{B})$$
(5)

where \(\:r\) is the coefficient that reduces the dimensionality in the attention module. Where \(\:M\) is the number of parallel attention modules. \(\:B\) is the number of convolution kernels. So the final Eq. 2 can be simplified as:

$$\:{O}^{{\prime\:}}\left(n\right)=O({C}_{in}\cdot\:H\cdot\:W\cdot\:{(K}^{2}+B))+O(M\cdot\:({C}_{in}\cdot\:r+r\cdot\:{C}_{out}))$$
(6)

where \(\:B\) and \(\:r\) are designed to be small, for example, \(\:B=4,\:r=\frac{1}{4}\). Although the time complexity of ODConv is slightly higher than that of standard convolution (\(\:{O}^{{\prime\:}}\left(n\right)=O\left(n\right)+kO\left(n\right)\)), its additional cost is controllable. Table 1 reports the data in detail in the experiment.

Table 1 Detailed parameters for each dataset.
Full size table

Dense Omni-Dimensional dynamic Conv

In the classic CNN structure, the network can learn a hierarchical representation by a low-level representation in a shallow layer and a high-level representation in a deeper layer. However, a major drawback is that shallow features are difficult to spread to deep convolutional layers, and they are easily lost during the process. Meanwhile, multi-level semantic information in the middle layer is graduately lost. Thus, all layers can only capture less semantic feature from the input spectrogram.

We assume that the spectrogram \(\:{F}^{0}\) is fed into a CNN network consisting of \(\:L\) layers, where the \(\ell\) layer performs the non-linear transformation \(\:\mathcal{H}(\cdot\:)\). The \(\ell\) standard convolutional layer can then be learned from the output of its predecessor layer \(\:{F}^{\ell-1}\) as follows:

$$\:{F}^{\ell}={{H}}^{\ell}\left({F}^{\ell-1}\right),\:$$
(7)

To overcome the above problems, we introduce dense connections to optimize the structure. Specifically, for each standard convolutional layer, the output of all previous layers is used as its input, and its own output is used as the input of all subsequent layers. The \(\:{F}^{\ell}\) in Eq. 7 becomes:

$$\:{F}^{\ell}={{H}}^{\ell}\left(\right[{F}^{0},{F}^{1},\dots\:,{F}^{\ell-1}\left]\right),$$
(8)

where \(\:\left[\cdot\:\right]\) represents the concatenation of outputs from all previous layers. \(\:{F}^{\ell}\) learns from multi-level representations, which helps to aggregate multi-level shape semantics and multi-scale information. In this way, each layer in the network can capture a certain scale of context, and as the network deepens, multi-scale information can gradually increase.

Due to the fact that the input of each layer contains all the outputs of the previous layers, the model can effectively reuse the previous features instead of repeating calculations. This mechanism reduces the computation of redundant features, and deep networks can easily obtain both shallow low-level features and deeper high-level features, forming cross level feature combinations. Moreover, the dense connection structure provides short shortcuts for each layer, making it easier for gradients to propagate from deep to shallow layers. Therefore, it is easier to train in deep networks and helps overcome the problem of gradient vanishing.

On this basis, we propose an improved version of ODConv, namely Dense Omni-Dimensional Dynamic Conv (DODConv). Similar to DenseNet31, it adopts dense connections, that is, the layers are directly connected in a feedforward manner. So, Eqs. 7 and 8 can be concluded that:

$$\:S=\mathcal{\:}\mathcal{H}\left(y\cdot\:\varvec{W}\right),$$
(9)
$$\:{S}^{\ell}={{H}}^{\ell}(\left[{S}^{0},{S}^{1},\dots\:,{S}^{\ell-1}\right],$$
(10)

where \(\:y\) represents the output of ODConv, \(\:\varvec{W}\) is the learnable parameter, and \(\:S\) is the output feature of a DODConv layer. Compared to ODConv, DODConv is capable of learning multi-scale spectral representations. In addition, the dense context obtained in deep layers can enrich the content of advanced semantics (texture features), making the learning process of the entire network closely integrated. Finally, the wealthy local to global semantic information in the input \(\:{S}^{0},{S}^{1},\dots\:,{S}^{\ell-1}\) can be gradually aggregated to form a dense contextual representation of spectral features. Therefore, DODConv can significantly enhance the feature extraction capability of CNN.

Dense dynamic convolutional network

The architecture of Dense Dynamic Convolutional Network (DDNet) is shown in Fig. 2.

Fig. 2
figure 2

An illustration of the structure of Dense Dynamic Convolutional Network.

Full size image

Figure 2 illustrates the structure of Dense Dynamic Convolutional Network. The left side of the diagram shows the main structure of the network, and the right side shows the details of its modules.

In DDCNet, DODConv is applied to each stage of the network to learn dense contextual representations of spectrograms. Finally, three fully connected layers (FC) are used as classifiers. When the network deepens, DDCNet will face high complexity because taking all the previous layers as input will result in significant convolution overhead in the deep layers. Therefore, we conducted extensive experiments on DDCNet to further determine the most suitable structure (as shown in Table 2). We increase the depth of the DDCNet network while reducing the channel size of each filter layer to control the complexity of the network. Specifically, we set small constants (C = 32, 64, 128) as the number of channels.

Table 2 Accuracy of deep learning models in vocal technique assessment on MVSet dataset (vaildation and 10-fold cross-vaildation). All models are trained and tested under the same conditions (hardware) without using pre trained models.
Full size table

Experimental setup

Dataset

The datasets used in this study—The MVSet11, The Urbansound8k41, The GTZAN2, and FSD50 K8—were chosen to comprehensively evaluate the proposed method across diverse audio processing tasks. MVSet targets vocal performance analysis and technique assessment, making it ideal for domain-specific tasks. UrbanSound8k simulates real-world urban environments, testing the model’s robustness in noisy and complex soundscapes. GTZAN focuses on music genre classification, assessing the method’s ability to learn semantic audio features. Finally, FSD50 K provides a large-scale platform for sound event detection, validating the model’s scalability and generalization capabilities. This combination ensures a thorough evaluation across different audio domains and task types. We have detailed the parameters of the four datasets in Table 3.

Table 3 Accuracy of deep learning models in audio evaluation on Urbansound8k dataset. All models are trained and tested under the same conditions (hardware) without using pre trained models.
Full size table
  1. 1.

    The MVSet dataset focuses on Mezzo-sopranos, which collects recordings of several professional singers in vocal singing and obtains 1212 high-quality audio segments of mezzo-sopranos. Each segment lasts for three to five minutes, sampled at 48,000 Hz. MVS aims to comprehensively characterize and evaluate the critical technical features of mezzo-soprano singing. The audio segments in MVS are labeled under ten vocal techniques: Vibrato, Throat, Position, Open, Clean, Resonate, Unify, Falsetto, Chest, and Nasal. Each technique is rated on a scale of 1 (highest) to 5 (lowest).

  2. 2.

    The Urbansound8k datasetis is a classic audio dataset containing 8732 detailed annotated urban sound clips, covering 27 h of audio recording, all stored in WAV format at a sampling rate of 44,100 Hz. This dataset covers ten categories of urban sounds, such as air-conditioning, car horns, and children playing.

  3. 3.

    The GTZAN is a widely used dataset for music classification. It was developed by George Tzanetakis and Perry Cook. The dataset contains 1000 audio clips, including ten music genres, each containing 100 clips. The types include Blues, classical, Country, Disco, Hip hop, Jazz, Metal, Pop, Reggae, and Rock.

  4. 4.

    The FSD50 K dataset is a large-scale, open audio dataset that can be used for sound event detection tasks. It contains approximately 51,000 audio clips covering various daily sound events. The dataset is labeled according to the structure of AudioSet and contains 200 categories.

Baseline

We selected five CNN-based networks (CRNN8, MobileNetV236, CAM + +12, ResNet8, and GhostNet35) and two Transformer based methods (AST16 and PETL_AST15). During the testing process, the predicted results are the average accuracy of three separate training sessions of these models. At the same time, we designed three variants (M, L and XL), DDNet-M without dense connection structure and ODConv, DDNet-L without ODConv, and the full version (XL) for comparative experiments. We use hyperparameter settings and training programs similar to other baseline models.

Training and evaluation

All of our models are implemented and trained on PyTorch42. We use Adam as the optimizer, with an initial learning rate of 0.0001, and train our model using the Cross-Entropy loss function. During the training process, the batch size is 64. In addition, when precision does not improve after more than ten verifications, we adopted an early stopping strategy to halt the training process. The random seeds are fixed to avoid biased results. We standardize the input data and convert it to a size of 224 × 224 to facilitate subsequent transfer learning. All models were trained and tested on a single Nvidia RTX 3090 GPU and Intel Core i9-14900 K CPU. Meanwhile, no models have undergone any pre-training to initialize their weights. We believe that this can better reflect the actual performance of the model.

Metric

We use Top-1 accuracy on the validation set of MVSet, Urbansound8k, and GTZAN to evaluate. Top-1 accuracy is a commonly used metric for evaluating the performance of classification models. Specifically, the model outputs a set of predicted scores or probabilities for each test sample. At the same time, Top-1 accuracy measures whether the category predicted by the model with the highest score (i.e., the category considered most likely by the model) is consistent with the actual category. The formula for accuracy is defined as follows:

$${\text{Top - 1\_Acc}} = \frac{{TS}}{{TS + FS}},$$
(11)

where \(\:TS\) (True Sample) is the number of correctly predicted samples, and \(\:FP\) (False Sample) is the number of incorrectly predicted samples. \(\:TS+FS\) is the number of total predicted samples.

For sound event detection (FSD50 K), we use mAP as an objective metric. We calculate the \(\:AP\) for each target category in the entire dataset. Take the average of all categories of \(\:AP\) to obtain the \(\:mAP\) value:

$$\:mAP=\frac{1}{n}\mathop\sum\limits_{i=1}^{n}\:{AP}_{i},$$
(12)

where \(\:n\) is the total number of categories, and \(\:{AP}_{i}\) is the average precision of the i-th category. So \(\:AP\) is defined by the following equation:

$$\:\text{AP}=\frac{1}{11}\mathop\sum\limits_{\text{r}\in\:\left\{\text{0.0,0.1},\dots\:,1.0\right\}}\:{P}_{\text{interp}}\left(R\right),$$
(13)
$$\:P=\frac{TP}{TP+FP},$$
(14)
$$\:R=\frac{TP}{TP+FN}.$$
(15)

where \(\:P\) is accuracy, \(\:R\) is recall, \(\:TP\) is the number of positive samples judged as positive, \(\:FP\) is negative samples judged as positive, \(\:FN\) is positive samples judged as negative, \(\:TN\) is negative samples judged as negative. \(\:mAP\) integrates \(\:P\) and \(\:R\) to more accurately measure the performance of the model.

Results

Vocal technique assessment results

In Table 4, we present the vocal technique assessment performance of different deep learning models on the MVSet. We have listed the evaluation results of various models, including CRNN, MobileNet v2, CAM++, AST, PETL-AST, ResNet, GhostNet, and several proposed model variants (M, L and XL). We use three key metrics: Top-1_Acc (%), Paramters (M), and FLOPs (G). From the results, it can be seen that the DDNet-XL performs the best in Top-1 accuracy, reaching 90.11%. At the same time, its parameter count (Paramters) and computational complexity (FLOPs) are only 12.74M and 12.33G. At the same time, we found that each of our design choices (dense connections and ODConv) improved the performance of CNN, with a 4.95% Top-1_Acc improvement compared to the baseline DDNet-M. These results highlight that proposed DODConv can improve the efficiency and performance of CNN spectral feature mining.

Table 4 Accuracy of deep learning models in audio evaluation on GTZAN dataset. All models are trained and tested under the same conditions (hardware) without using pre trained models.
Full size table

Environmental sound classification results

Environmental sound classification is an essential field of audio pattern recognition that classifies captured nonverbal audio segments into specific sound categories. It has a wide variety of categories and is difficult to determine. Environmental sounds are often mixed in with background noise, increasing classification difficulty. Table 5 shows the accuracy of various deep-learning models for audio classification on the Urbansound8k dataset. Among all models, DDNet XL achieved the highest Top-1 accuracy, at 89.31%, outperforming other models. The DDNet-L model also showed a high accuracy of 87.71%. In contrast, the accuracy of AST and PETL-AST, which were not pre-trained, was behind our method and had high computational costs (FLOPs).

Table 5 Accuracy of deep learning models in audio evaluation on FSD50 K dataset. All models are trained and tested under the same conditions (hardware) without using pre trained models.
Full size table

Music genre classification results

In addition, we also use DDNet for music genre classification tasks, where the goal is to classify music into specific categories based on its different features, such as music genres. Table 6 reports the accuracy of various deep-learning models on the GTZAN dataset. DDNet XL also achieved excellent performance, with a Top1_Acc of 73.95%.

Table 6 The ablation experiment of various components in the network.
Full size table

Sound event detection results

Finally, we apply DDNet to the most challenging sound event detection task. The data for sound event detection often contain overlapping sounds, which may confuse event recognition with noise and unrelated sounds, thus increasing the complexity of detection. Sound characteristics vary greatly in different environments, requiring the model to have good generalization ability.

We report the performance of various deep learning models on the FSD50 K dataset in Table 7. All models were evaluated under the same conditions without using pre-trained models. This setting ensures a fair comparison of their performance.

Table 7 The impact of selecting the number of convolutional layers in a network on performance.
Full size table

DDNet-XL achieved optimal performance, with a 41.89% mAP. In summary, our model has demonstrated excellent performance in various audio pattern recognition tasks, with high efficiency and accuracy.

Ablation

We conducted ablation experiments on each component of DDNet to verify their effectiveness. Table 2 lists the ablation experiment results on the MVSet test set. We used the full version of DDNet as the baseline, with step-by-step dismantling of critical components to control variables. We dismantled the dense structure and found that it relatively reduced by 1.78%, resulting in a 25% decrease in parameters. Next, we removed the ODConv but only used the dense structure, resulting in a significant decrease of 3.67%. These results indicate that the fusion of ODConv and Dense structures can significantly improve performance. Meanwhile, ODConv contributes the most to performance, intuitively reflecting enhancement of dynamic convolution.

Table 8 evaluates the impact of the number of convolutional layers in DDNet on performance. The results indicate that as the dynamic convolutional layers are stacked, the model’s performance continues to improve. When the number of convolutional layers is 4, the model’s accuracy reaches its highest level. However, further increasing the convolutional layers afterward has the opposite effect. On the one hand, appropriate network depth can make performance better. On the other hand, excessive modules can lead to many redundant parameters interfering with each other, reducing network performance.

Table 8 Model parameters for different audio pattern recognition tasks.
Full size table

Our DDNet adopts four dynamic convolutional layers, and then we present the parameters (dimension, stride, kernel size, and group) of each dynamic convolutional layer in the network in Table 9, where each convolutional layer consists of two convolutional blocks. Dimension is the number of output channels of the convolutional layer, the Stride is the stride setting of all convolutional layers, Kernel Size is the size of the convolutional kernel, and Group is the number of convolutional groups. These convolutional layer parameter configurations ensure the model’s effectiveness on different datasets, supporting efficient feature extraction and audio recognition.

Table 9 The impact of pre training on network performance.
Full size table

Using pre-trained models with large-scale datasets to initialize model weights is a standard method for improving the model. Inspired by this, we use ImageNet and Audioset, respectively, as well as joint pre-trained DDNet, to break through the boundaries of existing accuracy. Table 1 reports the effectiveness of each pre-training strategy. Especially after pre-training with ImageNet and Audioset, DDNet achieved the new highest Top1_Acc, 91.88%.

Table 10 shows the results of integrating different popular dynamic convolutions (CondConv22, DyConv23, and ODConv25) into DDNet-M. Although several different dynamic convolution methods can substantially improve over the standard 2DConv, ODConv has the most significant improvement margin (+ 2.33%), making it the preferred choice for our proposed Dense convolution module. In addition, the FLOPs overhead caused by ODConv is also relatively small (11.78G). Compared to ODConv, we can intuitively observe that DODConv only increases the computational overhead slightly (12.33G) but significantly improves the accuracy of vocal technique assessment (+ 4.95%).

Table 10 Comparison of different dynamic convolutions.
Full size table

Discussion

Despite achieving significant experimental results, our method still has some limitations. Firstly, DDNet introduces additional computational overhead during the dynamic convolution kernel generation process, which may limit its application on resource constrained devices. In addition, although we have achieved good results in tasks such as vocal technique evaluation, the performance of the model may be limited by the size and quality of the training data.

Future research directions can revolve around the following aspects:

  1. 1.

    Optimizing dynamic Convolution for greater efficiency and Real-Time applications: We aim to explore lighter and more efficient dynamic convolution techniques. For instance, reducing the computational complexity of dynamic weight generation could significantly improve the efficiency of the model, making it more suitable for resource-constrained devices and real-time applications. Moreover, we plan to integrate DDNet with a real-time processing framework to enable low-latency operations.

  2. 2.

    Evaluating Cross-Task generalization with multimodal datasets: To assess the generalization capabilities of our model across various tasks, we will test its performance on larger multimodal datasets. These datasets, which may include combinations of audio, video, and textual information, will help determine how well the model adapts to diverse applications such as multimedia analysis, multimodal sentiment analysis, and cross-domain audio tasks. This line of research could also uncover new ways to leverage complementary information from different modalities to enhance the accuracy and robustness of vocal performance assessment.

  3. 3.

    Investigating environmental noise and acoustic variability: We will specifically study the impact of environmental noise and acoustic variability on vocal performance assessment. Controlled experiments will be designed to simulate various noise levels, types of interference (e.g., urban noise, household sounds, and industrial noise), and diverse recording conditions. This will allow us to evaluate the robustness and adaptability of the model under real-world conditions. These enhancements will ensure that the model performs consistently in dynamic and noisy environments, thereby increasing its applicability in remote vocal education and other real-world scenarios. 

By addressing the aforementioned limitations and exploring new research directions, our approach has the potential to further promote the development of vocal education, sound classification, and related fields, providing more comprehensive support for intelligent and universal educational solutions.

Conclusion

In this paper, we introduce Omni-Dimensional Dynamic Convolution (ODConv) into Convolutional Neural Networks (CNN) to significantly enhance the feature extraction capability of convolution operations. At the same time, we use dense connections to optimize the network structure, fully utilizing the multi-scale feature information between multi-level dynamic convolutional layers and reducing the information loss during the downsampling process of the network. On this basis, we propose the Dense Dynamic Convolutional Network (DDNet). To verify the effectiveness of the proposed method, we conducted experiments on tasks such as vocal technique evaluation, environmental sound classification, music classification, and sound event detection. The experimental results show that our DDNet outperforms traditional CNN and Transformer models in terms of performance, especially in vocal technology evaluation tasks, achieving the SOTA effect.