Intelligent diagnosis of gearbox in data heterogeneous environments based on federated supervised contrastive learning framework

Abstract

To address the model training bottleneck caused by the coupling of data silos and heterogeneity in intelligent fault diagnosis, this study proposes a Federated Supervised Contrastive Learning (FSCL) framework. Traditional methods face dual challenges: on one hand, the scarcity of fault samples in industrial scenarios and the privacy barriers to cross-institutional data sharing result in insufficient data for individual entities; on the other hand, the data heterogeneity caused by differences in equipment operating conditions significantly diminishes the model aggregation effectiveness in federated learning. To tackle these issues, FSCL integrates the federated learning paradigm with a supervised contrastive mechanism: firstly, it overcomes the limitations of data silos through distributed collaborative training, enabling multiple participants to jointly develop diagnostic models without disclosing raw data; secondly, to address the feature space mismatch induced by heterogeneous data, a hybrid contrastive loss function is designed, which constrains the similarity between local models and the global model through supervised loss, thereby enhancing the feature representation capability of the global model. Experiments on two gearbox datasets demonstrate that the FSCL framework effectively resolves the issues of data insufficiency and heterogeneity, providing a novel approach for intelligent maintenance of industrial equipment that optimizes both data efficiency and privacy protection.

Introduction

The persistent operation under harsh working conditions often leads to a variety of faults in gearboxes, which result in equipment shutdowns, production delays, and additional maintenance costs¹. Consequently, the timely and accurate diagnosis of gearbox faults is particularly crucial. Conventional fault diagnosis methods primarily depend on manual feature selection and expert knowledge, utilizing feature extraction and pattern recognition techniques such as Fourier transform², spectral analysis³, wavelet transform⁴, and support vector machines⁵. These methods are highly reliant on the prior knowledge and experience of specialists and become time-consuming and prone to errors in complex systems.

In recent years, the development of intelligent fault diagnosis technologies is gradually reducing the reliance on expert knowledge and enhancing the automation level of diagnostics⁶. These intelligent methods, such as Convolutional Neural Networks⁷, Recurrent Neural Networks⁸, and Generative Adversarial Networks⁹, overcome some limitations of traditional methods by automatically learning to recognize faults through feature extraction. These deep learning-based fault diagnosis methods can effectively diagnose minute and complex fault patterns by capturing intricate structures and patterns in data. Despite the great potential of deep learning in fault diagnosis, it often requires extensive computational resources and data to train complex network structures, posing a high demand for some practical application environments. The performance of deep learning models largely depends on the quality and diversity of training data; inaccurate or biased data may lead to decreased model performance.

However, in actual industrial scenarios, while different enterprises might have similar types of operating machinery, due to issues such as data security, legal restrictions, and conflicts of interest, data owners can only utilize their small-scale datasets for training and cannot integrate these data into large-scale datasets suitable for deep learning training¹⁰.

The emergence of federated learning offers an effective solution to this problem. Federated learning consists of a central server with a global fault diagnosis model and multiple clients holding private data¹¹. In the federated learning framework, the central server distributes the global model to clients, each of which trains and updates the local model using their own data, then uploads the model weights back to the server. The server aggregates the weights from all clients to form a new model with global weights. Thus, the federated learning framework enables data holders to integrate data into large-scale datasets suitable for deep learning training. However, in a real federated learning scenario, there is a severe issue of data heterogeneity among clients, leading to significant differences in datasets¹². For fault diagnosis, due to variations in sensors and data collection points, there are disparities between various types of faults and the data samples that each client can provide, resulting in substantial differences between local models during training¹³. This causes the global model to lose adaptability to the specific distributions present in each client, and under these circumstances, the performance of the global model may even be inferior to that of a single client’s local model, making it challenging to train an effective model. Based on the above issues, there is now a need for a fault diagnosis model based on federated learning to address the adverse effects brought about by data heterogeneity.

This paper proposes a method that combines federated learning with supervised contrastive learning to address the above issues, termed Federated Supervised Contrastive Learning. Contrastive learning primarily enhances the representation learning capability of the model by comparing the similarities and dissimilarities between different samples¹⁴. The proposed method introduces supervised contrastive learning, enabling the federated learning framework not only to extract feature information from local models of each client during global model aggregation but also allowing local models at the client-side to be aggregated with the global model from the previous round during training. Thus, as federated learning training progresses, the local models at each client gradually approach the global model, while also being able to capture data features provided by other clients.

To ascertain the efficacy of the approach, empirical evaluations were executed utilising two distinct gearbox datasets. The outcomes indicate that, in the preponderance of instances, the performance metrics associated with FSCL surpass those of alternative federated learning methodologies, thereby corroborating the pertinence and competence of our proposed technique within the ambit of gearbox fault diagnosis. The main contributions of this paper are as follows:

• (1) We embed supervised contrastive learning within federated learning, reducing the distributional divergence between client local models and the server global model using two contrastive loss functions, which enhances the model’s generalization.

• (2) Addressing the data heterogeneity present in real industrial scenarios, experiments were conducted on two gearbox fault diagnosis datasets partitioned into three non-independent and identically distributed subsets. The results demonstrate that our method exhibits good performance and generalization capabilities even under data heterogeneity.

Related work

Federated learning in fault diagnosis

Federated learning is a distributed machine learning framework that enables multiple participants to collaboratively train models while protecting data privacy and complying with legal regulations, by exchanging model parameters or update information to jointly cultivate a global model¹⁵. McMahan et al.¹⁶ proposed a FedAvg algorithm, which uploads model parameters from each client to the server, where the server computes the weighted average of all model parameters and distributes this average back to all clients. Li et al.¹⁷ introduced the FedProx algorithm, which builds upon FedAvg and specifically targets issues of device heterogeneity and data heterogeneity. FedProx incorporates a proximal term to prevent the model from deviating too far from its original state after updates based on new data, preventing overfitting. Wang et al.¹⁸ put forward the FedMA algorithm for multi-task federated learning scenarios. This algorithm allows each client to focus on its local task by adaptively decomposing tasks, while still learning shared knowledge from other clients.

Due to its unique advantages in data privacy protection, federated learning has attracted increasing interest from scholars in the field of fault diagnosis, offering a novel possibility for cross-organizational collaboration. Wang et al.¹⁹ proposed a federated adversarial generalization network that learns features across different clients using generative adversarial networks, addressing the distributional divergence among various client populations within a federation. Yu et al.²⁰ introduced an edge-cloud collaborative framework for machinery fault diagnosis via federated learning, where each client is equipped with a convolutional autoencoder and the server-side adaptively weights the selection mechanism to aggregate a global convolutional autoencoder for diagnosing mechanical failures, providing a secure decentralized solution. Mehta et al.²¹ constructed a dual classifier, decomposing the mixed fault classification task into parallel networks, with each network responsible for one component, and diagnosed mixed failures from multiple clients using the federated learning framework.

Contrastive learning in fault diagnosis

Recently, in the field of self-supervised learning, contrastive learning has emerged as a promising research area and garnered widespread attention²². Contrastive learning generates positive and negative sample pairs through data augmentation, training the model to maximize the similarity between positive sample pairs while minimizing that between negative sample pairs. Supervised contrastive learning is a branch within the contrastive learning domain; it is a method that combines the advantages of self-supervised contrastive learning with traditional supervised learning²³. Differing from conventional self-supervised contrastive learning , supervised contrastive learning utilizes label information during the training process, which can guide the model to better distinguish between different categories of data, thereby enhancing learning efficiency and performance.

Contrastive learning has demonstrated remarkable capabilities in leveraging unlabeled data, handling few-shot learning, and enhancing model comprehension, making it an increasingly popular research direction in the field of fault diagnosis. Wang et al.²⁴ proposed a self-supervised contrastive learning-based momentum encoder to capture distinguishable features between sample pairs, enabling direct cross-domain fault diagnosis and identification of new faults in labeled samples from the target domain. Peng et al.²⁵ employed supervised contrastive learning to learn the discriminative features between known normal and fault conditions, classifying unknown faults from open datasets. Zhang et al.²⁶ designed an improved dual-view wavelet feature fusion with an embedded contrastive network, which enhanced the diagnostic knowledge extraction capability of the contrastive learning network and utilized the available fault information contained within a large amount of unlabeled dataset. In summary, contrastive learning has been widely applied in the field of fault diagnosis, whether under the umbrella of unsupervised or supervised learning.

Method

In this section, we first elucidate the federated learning scheme. Subsequently, we introduce methods related to signal preprocessing. Afterward, we elaborate on the methods of federated learning and its network framework structure. Following that, we conduct an in-depth analysis of the mixed contrastive loss function in contrastive learning. Finally, we provide a detailed description of the complete algorithm presented in this paper.

Concept definition

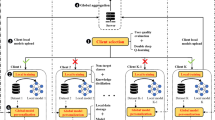
In the context of federated learning, where K clients collaborate to train a global model, each client is denoted by $S = \left\{ {S_1 ,S_2 , \ldots ,S_K } \right\}$ and possesses private data represented by $D = \left\{ {D_1 ,D_2 , \ldots ,D_K } \right\}$. To cultivate an effective model without direct data sharing, a center server is employed to aggregate the parameters of local models. The framework of federated learning, as depicted in Fig. 1, involves four primary steps, which are detailed as follows.

• (1) Local model training: Each client $S_K$ trains a local model using its private data $D_K$.

• (2) Local model uploading: The client $S_K$ uploads the local model parameters $w_k$ to the center server.

• (3) Global model aggregating: The center server aggregates the local model parameters ${w}_{glob}\leftarrow \sum_{k}\frac{{n}_{k}}{n}{w}_{k}$ from all clients to update the global model, where $n = \sum_k {n_k }$ is the total number of data used in the federated learning setup.

• (4) Global model downloading: The center server distributes the updated global model back to each client.

Fig. 1

Illustration of The Federated Learning Scheme.

The core privacy protection of federated learning stems from its data localization characteristic. As shown in Fig. 1, all raw data is always retained locally on the client side, and only desensitized model update parameters are allowed to be transmitted to the central server through an encrypted channel. This mechanism fundamentally avoids the risk of data leakage inherent in traditional centralized learning.

Signal preprocessing

To extract features from the raw signal prior to local training at the client side, it is necessary for the raw signal to undergo preprocessing via a feature extractor. In this paper, we employ the Gramian Angular Field (GAF) for feature extraction from signals, which is a method of signal encoding that effectively preserves the temporal dependencies and dynamic variations inherent in the original signal²⁷. The process begins by applying piecewise aggregate approximation to smooth the time series of the given signal $X = \left\{ {X_1 ,X_2 , \ldots ,X_{\text{n}} } \right\}$, consisting of n values, and rescaling X so that all signal values fall within the interval [0, 1], resulting in a new time series $\widetilde{x.}$ Subsequently, $\widetilde{x}$ is transformed into polar coordinates through the use of angles $\phi =\mathit{arccos}(\widetilde{\widetilde{x}})$ and radii $r=t/N$. Finally, considering the temporal correlation between adjacent points in the signal, each value $GAF=[cos({\phi }_{i}+{\phi }_{j})]$ within the GAF is obtained, mapping the relationships among all neighboring points in the signal to construct a two-dimensional feature space that forms the GAF.

Initially, the client segmented the original signal into a series of sub-signals, each with a length of n. Each sub-signal was then fed into the feature extractor, which generated GAF feature maps that were subsequently used as training samples for the local model training process at the client. This approach enables clients to extract local time-structural features from each sub-signal, which are then utilized to construct and refine a highly discriminative training model.

Federated supervised contrastive learning framework

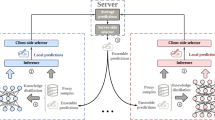
The primary principle of FSCL lies in the reduction of feature representation distances between positive sample pairs while increasing the distances between negative sample pairs. In FSCL, to enable the global model of the same round to learn better feature representations than the local models, it is crucial to ensure that the feature representations of the local models are closer to those of the previous round’s global model and distant from those of the previous round’s local models. This approach enhances the global model’s capability to represent features.

The overall framework of FSCL for fault diagnosis is depicted in Fig. 2. The raw signals collected are processed by a feature extractor before entering the FSCL network. During each training round, the neural network model consists of three main components: a backbone network for feature extraction, a linear projection layer to adjust the feature dimensions, and a fully connected layer that outputs the predicted probabilities for each class. Specifically, the backbone network is responsible for extracting useful feature information from the input samples; the linear projection layer transforms the extracted features into a specific dimensional space (the backbone network employs the DenseNet121 architecture²⁸, and the linear projection layer consists of two fully connected layers that map the feature vector to a 256-dimensional space); the fully connected layer generates diagnostic results for each type of fault based on these features. The local model of round t and the global model of round t-1 are jointly trained using the FSCL method, and the mixed loss function used will be detailed in subsequent sections.

Fig. 2

Overall Framework of The FSCL for Fault Diagnosis.

Optimization objective

The objective optimization in this study involves two loss functions: the cross-entropy loss ${L}_{CE}$ and the supervised contrastive loss ${L}_{SC}$ used for contrastive learning. During the local training phase at client ${S}_{i}$ in round t, the local model is characterized by ${w}_{i}^{t}$, while the global model is represented by ${w}_{glob}^{t}$. Assuming ${F}_{w}\left(x\right)$ is the feature vector obtained after data $x$ passes through the linear projection layer of the neural network model, then the global model ${w}_{glob}^{t-1}$ extracts a feature vector representation ${v}_{glob}^{t-1}\left({v}_{glob}^{t-1}={F}_{{w}_{glob}^{t-1}}\left(x\right)\right)$ from data $x,$ and the local model ${w}_{i}^{t}$ extracts a feature vector representation ${v}_{i}^{t}\left({v}_{i}^{t}\right.={F}_{{w}_{i}^{t}}\left(x\right))$. The contrastive learning method employs a supervised loss function to reinforce proximity constraints between samples, referring to the NT-Xent loss function²⁹, the supervised contrastive loss is defined as in Eq. 1.

$${L}_{SC}=-log\frac{exp\left(sim\left({v}_{i}^{t},{v}_{glob}^{t-1}\right)/\tau \right)}{exp\left(sim\left({v}_{i}^{t},{v}_{glob}^{t-1}\right)/\tau \right)+exp\left(sim\left({v}_{i}^{t},{v}_{i}^{t-1}\right)/\tau \right)}$$

(1)

Here, $sim\left(\cdot \right)$ denotes the function that measures the similarity between vectors, and $\tau$ represents the temperature coefficient. In this paper, two different similarity functions will be utilized to measure the supervised contrastive loss, with specific details to be elaborated in the following sections. The mixed loss function is defined as in Eq. 2.

$${L}_{mix}={L}_{CE}\left({w}_{i}^{t},x\right)+\mu {L}_{SC}\left({w}_{i}^{t},{w}_{i}^{t-1},{w}_{glob}^{t-1},x\right)$$

(2)

In the Eq. 2, μ is a hyperparameter used to control the weight of the supervised contrastive loss. Consequently, the expression for the global model optimization objective can be derived as in Eq. 3.

$$\underset{{w}_{glob}}{argmin}L\left({w}_{glob}\right)=\sum_{k=1}^{K}\frac{{n}_{k}}{n}{L}_{mix}^{k}\left({w}_{glob}\right)$$

(3)

Here, ${L}_{mix}^{k}\left(\cdot \right)$ denotes the mixed loss at the client ${S}_{k}$.

Algorithm

Algorithm 1. presents the training process of FSCL. During the global training phase of each round, the server receives local models from all clients and generates a new global model by taking a weighted average of these local models. Subsequently, the server distributes this global model to each client. The clients then update the global model received from the server using their local data via gradient descent, and the updated model serves as the new local model to continue training. During the local training process at the client side, the supervised contrastive loss function is employed to enhance the training efficacy.

In Algorithm 1, T represents the total number of communication rounds between all client sides and the server side, K represents the number of participating clients, E represents the number of local training rounds each client performs, η is the learning rate used by the clients for local deep learning model training, μ is the hyperparameter used for calculating the mixed supervised contrastive loss, and D represents the private data on the client side.

Algorithm 1 Training process of FSCL

Experiments

Datasets

We assess the performance of the FSCL framework using two gearbox fault datasets: the Drivetrain Dynamic Simulator (DDS) dataset³⁰, and our laboratory’s Wind Turbine Drivetrain Simulator (WTDS) dataset.

The DDS gearbox dataset includes a total of five conditions: Crack occurs in the gear feet (Chipped/C), Healthy (H), Missing one of the gear feet (Miss/M), Crack occurs in the root of gear feet (Root/R), and Wear occurs on the surface of the gear (Surface/S). Each condition corresponds to two different scenarios, namely different rotational speeds and load conditions. One scenario involves data collected at a rotational speed of 20 Hz (1,200 rpm) and a load of 0 V (0Nm), while the other is at 30 Hz (1,800 rpm) with a load of 2 V (7.32Nm). These two scenarios, combined with the four fault types and healthy state, make up nine different condition categories. The DDS test rig is equipped with seven Model 608A11 vibration sensors to collect vibration data from the planetary gearbox and reduction gearbox in the x, y, z axes, as well as the motor’s z-axis direction, with a sampling frequency of 5,120 Hz. The faulty gear is installed inside the reduction gearbox, and we will use the data collected from the x, y, z-axis position sensors of the reduction gearbox for our experiments. Each sub-signal consists of 1,000 time points.

The WTDS gearbox dataset was collected from the test rig illustrated in Fig. 2. The test rig consists of a drive motor, bearing pedestal, parallel gearbox, planetary gearbox, and magnetic powder brake. The WTDS gearbox dataset includes a total of five conditions: Broken tooth (BT), Eccentric gear (EG), Gear crack (GC), Normal (N), and Tooth surface wear (TSW). Each condition corresponds to two different scenarios, one at a rotational speed of 1,500 rpm with a load of 0.8hp, and the other at 2,000 rpm with a load of 1.2hp. Similarly to the DDS gearbox dataset, the WTDS gearbox dataset encompasses nine condition categories. The test rig employs Model PCB333B40 accelerometers to collect data from three channels—radial horizontal, radial vertical, and axial—at both the output and drive ends for the experiments. With a sampling frequency of 20,480 Hz, each sub-signal is composed of 1,500 time points due to the higher sampling rate. Subsequent experiments utilize data collected from the output speed sensor across the three channels.

The two datasets are partitioned into training, test and validation sets according to a ratio of 3:1:1, with details about datasets provided in Table 1.

Table 1 Experimental Datasets Information.

Experiment scheme

To validate the performance of the proposed method, this study designed four experimental schemes to simulate real-world industrial scenarios where federated learning is employed for equipment fault diagnosis.

• (1) Independently and identically distributed (IID): This adopts the most fundamental distributed learning model, where the dataset possessed by each participating client complies with the IID assumption. That is, the data collected by each client originates from sensors at the same location on the same experimental equipment, ensuring uniformity in data sampling; all clients hold an equal number of samples; and the amount of data collected for each state category remains balanced across all clients. Although such a scenario is unlikely to occur in a real-world industrial setting, it provides a reference standard.

• (2) Non-IID-Class: In a real-world industrial environment, subject to various factors such as equipment usage, environmental conditions, and maintenance strategies, samples of different types of faults often exhibit an uneven distribution. To recreate this phenomenon in experiments, we ensure that each participating client possesses a unique collection of samples for the various fault states.

• (3) Non-IID-Client: In federated learning, due to the distinctive environments and equipment usage of participating entities, there is often a disparity in their data volume distributions. To reflect the complexity of this realistic scenario in an experimental setting, we designed for each client to have a different total number of samples to simulate this imbalance in data distribution.

• (4) Non-IID-Domain: Considering that participants may collect fault data in different ways based on factors such as their equipment configuration, monitoring strategies, and other aspects. To align the experimental design with this reality, we arrange for each client to use fault signals collected from sensors at various different locations during the training process, thereby reflecting the data collection disparities in the actual environment.

In the experiments, we require each client to use its feature extractor to generate GAF two-dimensional feature maps of size 224 × 224. These feature maps will be used as input to the neural network model for federated learning. During the local training process of the clients, we set the batch size to 8 and employ the Adam optimizer with a learning rate of 1e-3. The range of the momentum coefficient is between 0.9 and 0.99. Additionally, in the mixed loss function, the weight of the supervised contrastive loss is set to 1, and the temperature coefficient is set to 0.5. Following subsequent experimental comparisons, we decide to use cosine similarity to measure the similarity between different vectors. To evaluate the performance of the proposed method, we will use five common diagnostic indicators: accuracy, specificity, sensitivity, AUC, and F1 score. Due to the high communication cost between devices in federated learning, we adopted the delayed update strategy from the FedCM³¹ mechanism in our experiments to reduce this cost. Specifically, clients train locally for 5 epochs before uploading the model parameters to the server for global model updating.

Similarity function

In the context mentioned above, the supervised contrastive loss requires the computation of similarity between vectors. In this subsection, we will conduct comparative experiments to select the similarity function between vectors. Cosine similarity and Euclidean distance are two commonly used methods to measure the relationship between vectors. Cosine similarity is primarily used to measure the directional similarity of two vectors, and it is determined by calculating the cosine of the angle between the two vectors. The range of cosine similarity is [-1, 1], where a value of 1 indicates that the vectors are in the same direction, and a value of -1 indicates they are in opposite directions. Euclidean distance is used to measure the absolute difference in feature vectors; it calculates the straight-line distance between two vectors in space. The magnitude of the Euclidean distance directly reflects the degree of difference between vectors—larger distances indicate greater dissimilarity. Cosine similarity is represented by Eq. 4, and Euclidean distance by Eq. 5, where $X = \left\{ {X_1 ,X_2 , \ldots ,X_{\text{n}} } \right\}$ and $Y = \left\{ {Y_1 ,Y_2 , \ldots ,Y_{\text{n}} } \right\}$.

$$cos\left(X,Y\right)=\frac{\sum_{i=1}^{n}\left({x}_{i}\cdot {y}_{i}\right)}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}}\cdot \sqrt{\sum_{i=1}^{n}{y}_{i}^{2}}}$$

(4)

$$dist\left(X,Y\right)=\sqrt{\sum_{i=1}^{n}{\left({x}_{i}-{y}_{i}\right)}^{2}}$$

(5)

To filter out a more appropriate method for measuring vector relationships and to prepare for experiments in the Non-IID environment, we first conducted a series of experiments in the IID environment and took the average of multiple experimental results. Table 2. presents the experimental results under the IID condition for two datasets.

Table 2 Performance Metrics of Two Similarity Functions.

Experimental results demonstrate that on the DDS dataset, cosine similarity outperformed Euclidean distance in all five performance evaluation metrics. For the WTDS dataset, cosine similarity also showed superior performance to Euclidean distance in most cases. Based on these findings, we decided to use cosine similarity as the function to calculate the supervised contrastive loss under Non-IID conditions in subsequent experiments. The table data reveals that the DDS dataset surpasses the WTDS dataset in performance across all indicators. This discrepancy may be attributed to the distant installation of sensors from the faulty gearbox on the WTDS test rig, resulting in signal interference from the vibrations of other mechanical components.

Impact on the number of clients

In this section, we further analyze the impact on the generalization ability of FSCL when a varying number of clients participate in federated learning. In the experiments under the Non-IID-Class scenario, for the DDS dataset, the ratio distribution of the nine different state categories is 716:582:404:517:634:420:447:519:261; whereas for the WTDS dataset, the ratio distribution of these nine state categories is 434:393:386:458:628:268:592:638:703. In the Non-IID-Client setting, each client holds an unequal number of samples. Additionally, in the Non-IID-Domain setting, the DDS dataset uses data from sensors at three axial positions x, y, and z of the reduction gearbox, with a data volume ratio of 1:2:1; whereas the WTDS dataset employs data from the output speed sensor in the radial horizontal, radial vertical, and axial directions, also with a data volume ratio of 1:2:1.

Table 3 Comparison of the Impact of Different Numbers of Clients on the Model

Based on the data analysis from Table 3. and Fig. 3, it can be observed that as the number of clients participating in federated learning increases, the learning effect tends to decline. This phenomenon is relatively mild under IID data conditions but becomes more pronounced in Non-IID scenarios. This may be due to the fact that with an increasing number of clients, the heterogeneity among data intensifies, and federated learning requires more communication resources to synchronize model updates, both of which adversely affect the training process and consequently impact the performance of the global model.

Fig. 3

The Impact of the Number of Clients on Model Performance.

Under the Non-IID-Class scenario, due to the different ratio distributions of state categories in the two datasets, they are affected to varying degrees by data imbalance. The results show that in the Non-IID-Client scenario, the impact on model performance is more severe. This may be because the uneven distribution of client data participating in federated learning makes it difficult for the global model to balance category information during the aggregation process, usually favoring the dominant classes and resulting in insufficient learning of minority class features, thereby affecting overall performance. In contrast, the impact on model performance in the Non-IID-Domain scenario is smaller. This could be because, although differences in sensor location may affect signal strength or quality, each client still maintains its unique data characteristics. The influence of these unique characteristics on model performance is less than that caused by the imbalance in data volume among clients.

To obtain more ideal experimental results, subsequent experiments comparing other methods will use 4 clients as the standard experimental setup.

Compare other methods

To demonstrate the superior performance of FSCL, we compared it with three experimental methods, including FedAvg, FedProx, and Central training. Under Non-IID-Client conditions, the data sample ratio held by 4 clients during local training is 1,354:406:677:270, while the other two Non-IID data settings are the same as mentioned above. It is important to note that under Non-IID-Client conditions, the central training method cannot be implemented.

Based on Fig. 4 and Table. 4, the federated learning strategies have demonstrated superior performance compared to centralized training methods. This advantage can be attributed to federated learning’s ability to update models in a timely manner at the client-side, quickly adapting to changes in new data and environments. In contrast, centralized training often requires periodic retraining of the model, which can sometimes lead to suboptimal performance when dealing with new data. Faced with Non-IID data environments, federated learning can handle data heterogeneity more effectively by allowing participants to train models using local data, thereby capturing unique knowledge and features of specific environments. Centralized training might overlook these local features because it mixes all data together for model training, potentially reducing the model’s predictive capabilities for certain subgroups. On both datasets, the two federated learning algorithms, FedAvg and FedProx, achieved good results. However, the FSCL method proposed in this paper has achieved better results compared to these algorithms, proving the superiority of the FSCL method.

Fig. 4

Average Test Accuracy of Different Method Strategies.

Table 4 Comparison of FSCL with Different Schemes.

According to Fig. 5, although the test accuracy under the Non-IID setting is lower than that under the IID setting, both datasets ultimately achieved favorable results. For the DDS dataset, the impact of the Non-IID data environment is less pronounced compared to the WTDS dataset. In contrast to Non-IID data, IID data can achieve higher effectiveness in a shorter period. However, as the number of communication rounds increases, the test accuracy of Non-IID data also gradually improves, indicating that even in a data-heterogeneous environment, FSCL can demonstrate excellent performance.

Fig. 5

Test Accuracy of FSCL under Different Experimental Schemes.

As demonstrated in the confusion matrix results depicted in Fig. 6, the FSCL method has achieved high accuracy of common fault types in gearboxes across four experimental conditions on two datasets. Notably, for healthy gears without any faults, FSCL has attained a 100% recognition accuracy rate. This outcome is instrumental in enhancing the monitoring and predictive performance of equipment health, bearing significant practical implications for industrial applications.

Figure. 6

Confusion Matrix of Different FSCL Experimental Schemes.

Training efficiency analysis

In the IID scenario of the DDS dataset, by applying FSCL and setting up three control groups, Fig. 7 showing the accuracy changes over training epochs was plotted. From the chart, it is evident that both the convergence epoch and accuracy of FSCL are lower than those of the three control groups. Table 5 compares the efficiency of various frameworks. Since FSCL requires additional transmission operations and supervised comparative training, the time it takes to complete one training stage is relatively long. However, the faster convergence of FSCL compensates for its longer training time. Overall, when analyzing from the perspective of the total training time consumed, the efficiency of FSCL is satisfactory.

Figure. 7

Test accuracy of different methods of DDS dataset in IID scenario.

Table 5 DDS-IID Efficiency Comparison of All Methods.

Anti-noise performance analysis

To evaluate the noise robustness of the proposed model, we conducted experiments by adding Gaussian white noise with a signal-to-noise ratio (SNR) of -6 dB to the gear fault signals in both datasets. The experimental setup remained consistent with the IID scenario described earlier. As shown in Table 6 and Fig. 8., the diagnostic accuracy of FSCL experienced a slight decline after the introduction of Gaussian white noise. Specifically, the accuracy decreased by 0.47% for the DDS dataset and 1.18% for the WTDS dataset. Despite these minor reductions, FSCL maintained a high level of diagnostic performance, demonstrating its robustness in noisy environments. These results indicate that the proposed FSCL framework is capable of effectively handling noise interference, making it suitable for real-world industrial applications where signal noise is often unavoidable.

Figure. 8

Confusion Matrix of FSCL under Gaussian White Noise.

Table 6 Performance Measurement of FSCL after Adding Noise.

Conclusion

This study introduces a framework termed FSCL, designed to optimize the fault detection process in gearboxes. The framework specifically addresses the challenges faced by data owners in accessing sufficient large-scale datasets for deep learning training within the realm of intelligent fault diagnosis, as well as the discrepancies due to data heterogeneity among participants in real-world federated learning environments.

Within the FSCL framework, initially, each client participating in federated learning is required to preprocess their raw signal data through a feature extractor, generating high-dimensional data with enhanced feature representation capabilities. Subsequently, to augment the feature representation of the global model, FSCL integrates a supervised contrastive loss function during the training process of federated learning. The objective of this loss function is to bring the current local model features of each client closer to the feature representation of the previous global model and to distance them from the feature representation of the previous round’s local models, thereby improving the global model’s ability to represent features. To validate the effectiveness and practicality of the framework, the study designed four sets of experiments to simulate real-world scenarios that may be encountered when using federated learning technology for equipment fault diagnosis. These experiments utilized two different datasets. The results indicated that, without considering communication costs, the FSCL framework demonstrated robust resilience to data heterogeneity and showed promising application potential. FSCL has shown significant effectiveness in addressing the challenges of data scarcity and heterogeneity. Its applications are not limited to multi-factory equipment failure prediction but also extend to joint training for cross-hospital disease prediction, accurate traffic flow prediction and intelligent traffic light optimization, and efficient training of anti-fraud models across banks. Additionally, the FSCL framework can be integrated with technologies such as blockchain and edge computing to enhance the security of the FSCL framework, reduce data transmission delays, and minimize bandwidth consumption.

In our future work, we plan to further optimize the algorithm to bolster privacy protection for all participants. This will be achieved by employing more secure aggregation techniques to prevent inference attacks and potential data leakage risks. At the same time, we will collect real fault data from wind turbine gearboxes for experiments and deploy the FSCL framework on different types of wind turbines to collect data. This will help alleviate the problem of data scarcity in a single device and data heterogeneity across devices.