Empirical validation of size effects in sub-sized tensile specimens for nuclear structural materials

Abstract

Advancing the understanding of material behavior and phenomena related to size effects in small-scale components is critical for settings where limited quantities of material samples can be tested. Established guidelines for sub-sized specimen testing encompass best practices for specimen preparation, testing equipment, test procedures, and data analysis methods. However, prior investigations of specimen size effects in the literature typically involved a relatively small number of tests performed and analyzed. To address this limitation, our team created a large database of 1,050 tensile test records for nuclear structural materials collected from peer-reviewed articles. In this study, we introduced a machine learning-based approach for predicting the tensile properties of sub-sized specimens, and we developed methods for uncertainty quantification of predicted properties. Furthermore, we conducted an experimental validation of the reported critical values for the dimensions and geometry of sub-sized specimens, and we validated existing analytical models for correlating total elongation between sub-sized and standard-sized specimens. Our findings demonstrate the potential of machine learning techniques to enhance understanding of specimen size-dependent material behavior and highlight the need for coordinated efforts in developing large, open-source databases of mechanical testing data to support future research.

Introduction

The current trend toward product miniaturization across scientific and engineering disciplines is likely to continue in the foreseeable future, due to an increasing demand for micro-sized parts and components in various applications. Notable examples include micro components in electronic systems, thin films, multilayer materials, and components in micromechanical and biomedical devices. The reduction in physical dimensions of small-scale components causes distinct mechanical, electrical, and thermal behaviors in comparison to bulk materials^1,2,3,4. Namely, the dimensional constraints at smaller scales and the increase in surface-to-volume ratio contribute to changes in microstructural characteristics—such as grain size, second-phase particle precipitation, or dislocation motion—thereby altering material properties. Similarly, the validity of established contemporary theories of deformation mechanics and fracture behavior breaks down as the physical size of components decreases below certain critical thresholds⁵. These changes in material behavior of small-scale components stemming from reduced dimensions are commonly referred to as “size effects.” Understanding the pertinent phenomena deriving from size effects and elucidating their impact on the performance of small-scale components has potential for innovative applications in advanced materials and devices^6,7,8.

Accordingly, small specimen testing techniques have been actively pursued by both industry and academia for several decades^9,10,11,12. Mechanical testing methods using small specimens including tensile testing, creep testing, impact testing, and other tests enabled researchers to investigate strength, ductility, creep resistance, impact toughness, and other properties^13,14,15. In addition to advancing the understanding of material behavior and phenomena related to size effects in small-scale components, small specimen testing has also been important for evaluating the mechanical properties of materials in situations where only limited quantities of material are available. For instance, sub-sized specimen tests have been extensively conducted in the nuclear industry, where the space limitations for irradiation within nuclear reactors pose constraints on specimen size^{16,17,18,−19}. Other applications of sub-sized specimen testing include assessing the residual life of in-service components by extracting small volumes of material¹⁶, facilitating rapid alloy prototyping processes where the fabrication of miniature specimens allows for accelerated material development^17,18, and measuring local properties of welded parts¹⁹.

To ensure the consistency, reliability, and reproducibility of measured material properties using sub-sized specimen testing techniques, several recommendations and guidelines have been established through sustained research and collaboration efforts by the research community and industry stakeholders. For tensile testing, Miniaturized Tensile Test (MTT)^13,20 is outlined in a series of scientific papers that provide guidelines for evaluating the properties of materials using specimens with dimensions ranging from hundreds of microns to several millimeters. MTT includes recommendations for sub-sized specimen geometry and critical threshold values for specimen dimensions relative to the characteristic length of the material microstructure (i.e., the grain size in metal alloys²¹). Additionally, MTT recommendations encompass best practices for specimen preparation, testing equipment, test procedures, and data analysis.

Data analysis methods are crucial for the interpretation and calculation of mechanical properties of materials in sub-sized specimen tests. Data analysis in tensile tests can include conventional techniques for stress-strain curve analysis, methods for determination of tensile properties, imaging methods for strain measurement, computational methods, and statistical analyses^{12,13,14,15,16,17,18,21,22,23,24}. To correlate the total elongation of sub-sized specimens to standard-size specimens, Barba’s equation²⁵ and Bertella-Oliver equation²⁶ are widely used. Furthermore, the inverse Finite Element Method^27,28 is often employed for predicting the true stress-strain relationship from engineering strain-stress values by minimizing the deviations in contact-type strain measurements. Similarly, the Hall-Petch relationship^1,2,9 is adopted for analyzing the influence of grain size on the mechanical properties of materials. To correlate the fatigue life between sub-sized and standard-sized specimens, Tomaszewski¹² employed the traditional Basquin fatigue model. A major limitation of current analytical models and conversion methods for sub-sized specimen tests is that they are developed under specific assumptions regarding the used test method or material. Consequently, the assumptions may not be reliably generalized to different testing conditions or materials, and may result in inaccurate calculations of material properties. In addition, most analytical models require extensive material-specific measurements for determining the values of coefficients or constants, and some models do not provide means for quantifying the importance of test conditions or other factors on specimen size effects.

The approach proposed in this work employs Machine Learning (ML) models for addressing specimen size effects in mechanical testing. Despite the demonstrated ability of ML models to capture complex patterns in high-dimensional data, we are not aware of existing efforts for applying ML models to estimating tensile properties using sub-sized specimens. One potential reason is the lack of curated databases for model training, as most related works conducted analyses using a relatively small number of data points. Our team recently created the first large public database of tensile test records from sub-sized specimens of nuclear structural material^29,30. The data was collected from peer-reviewed publications and consists of 1,050 tensile test records with 55 parameters. We used the database to train a set of ML models for predicting the yield strength, ultimate tensile strength, uniform elongation, and total elongation of sub-sized specimens from stainless steel 316. Additionally, we implemented uncertainty-aware ML models to provide confidence intervals for the predicted values of tensile properties. We studied specimen size effects and assessed the validity of recommended critical values for sub-sized specimen dimensions and geometry. Finally, we leveraged the available database to evaluate existing analytical models for correlating total elongation in tensile testing between sub-sized and standard-sized specimens.

Several related works in the published literature have applied ML approaches for predicting the mechanical properties measured on sub-sized specimens. The research team of Luo, Hu, et al.^31,32 investigated the application of ML models for predicting the fatigue life of additively manufactured sub-sized specimens of Inconel 718. In another work, Wan et al.³³ outlined a roadmap for employing data-driven ML methods for estimating the fatigue life of sub-sized specimens fabricated by additive manufacturing. Pan et al.³⁴ employed ML techniques for establishing correlations between force-displacement curves in small punch tests and strain-stress curves of sub-sized tensile specimens for pressure vessel steels. Prior works have also focused on developing ML models for predicting tensile properties of standard-sized specimens^35,36. These related works demonstrate the potential of ML-based approaches for addressing specimen size effects in materials science. On the other hand, most previous works employed small databases of mechanical test results and focused on predicting properties related to fatigue tests or small punch tests, rather than on tensile properties of sub-sized specimens.

Uncertainty Quantification (UQ) has become increasingly important in materials science modeling^37,38,39, as all models and experimental measurements inherently exhibit variability, arising from random noise (aleatory uncertainty) or from assumptions and simplifications in the modeling process (epistemic uncertainty)⁴⁰. Addressing uncertainties is hence essential for risk assessment and informed decision-making, as it provides insights into the reliability of predicted material properties. Applying UQ to modeling tensile properties of sub-sized specimens yields not only a single estimated value but also a confidence interval around the prediction, which is critical in assessing reliability and safety margins³⁸. Furthermore, for the task of predicting tensile properties of sub-sized specimens UQ is particularly important, because the measured properties of sub-sized specimens exhibit greater scatter than standard-sized specimens.

The following are the main contributions of this work:

• Investigating specimen size effects using a large database of tensile properties measured from sub-sized specimens and conducting an experimental validation of the reported critical values for size effects.

• Validating current analytical models for correlating total elongation between sub-sized and standard-sized specimens.

• Developing Machine Learning models for predicting tensile properties from sub-sized specimens. To the best of our knowledge, these are the first ML models for this task.

• Implementing ML models for the uncertainty quantification of predicted tensile properties.

Preliminary matters

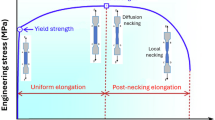
Specimen size effects in tensile tests

The impact of specimen size effects on tensile properties is commonly considered for two levels of size reduction. The first level considers a reduction in specimen dimensions for which the measured tensile properties may differ from the corresponding properties of standard-sized specimens, however the bulk properties of the material described by continuum mechanics are preserved. I.e., if the differences in the results between sub-sized and standard-sized specimens are within an acceptable range (e.g., ± 15%¹⁸), the test results are considered adequate for assessing the mechanical properties. The second level pertains to scenarios where the specimen dimensions are reduced beyond critical thresholds, and the bulk material properties are no longer preserved. For this level of size reduction, the measured tensile properties cannot be correlated to standard-sized specimens or converted by using data processing techniques or analytical conversion methods.

Prior studies have recommended critical values for several important dimensions of sub-sized specimens, such as thickness, width-to-thickness ratio, diameter-to-grain-size ratio, and length-to-square-root-of-area ratio. Accordingly, Table 1 lists the critical values for sub-sized specimens with flat (rectangular) and round (cylindrical) geometry and the impacted tensile properties^13,21,24.

Table 1 Critical values for sub-sized specimen dimensions and affected tensile properties, including yield strength (YS), ultimate tensile strength (UTS), uniform elongation (UE), and total elongation (TE).

Analytical models for correlating tensile properties

When the specimen dimensions are above the critical thresholds listed in Table 1, prior studies reported no significant impact of the specimen size and geometry on yield strength, ultimate tensile strength, and uniform elongation. On the other hand, it has been universally acknowledged that the total elongation is affected by the specimen’s geometry when the dimensions are above the critical thresholds^41,42. To account for the influence of specimen geometry on total elongation, several different analytical methods have been proposed in the literature. These methods are based on observations that the total elongation is inversely proportional to the length-to-square-root-area ($\:L/\sqrt{A}$) ratio (i.e., slenderness ratio). The two most widely employed conversion methods for total elongation are Barba’s Law²⁵ and the Bertella-Oliver formula²⁶.

Barba’s law is based on previous studies with aluminum, mild steel, copper alloys, and other materials, which proposed a linear relationship between total elongation and slenderness ratio. Accordingly, the total elongation, $\:{e}_{t}$, is expressed as:

$$\:{e}_{t}=\:c+d(\sqrt{A}/L),$$

(1)

where $\:c$ and $\:d$ are material-dependent constants, and $\:\sqrt{A}/L$ is the inverse of the slenderness ratio. The constants $\:c$ and $\:d$ are obtained by fitting a linear regression model to the available data, and correspond to the intercept and slope of the fitting line. Mathew et al.²⁵ investigated the validity of Barba’s law for stainless steel 316 alloys, and reported that the relationship can be reliably used for converting total elongation between specimens of different dimensions.

The Bertella-Oliver formula for total elongation is based on another observation that the linear relationship between total elongation and slenderness ratio, as reported by Barba, does not hold over a broad range of experimental values²⁶. Thus, the authors proposed the following power law equation:

$$\:{{e}_{t}=m\left(\frac{\sqrt{A}}{L}\right)}^{n},$$

(2)

where $\:m$ and $\:n$ are material constants that are determined analytically from experimental data.

To convert total elongation between specimens with different geometries using Barba’s law, the following equation is commonly employed⁴³:

$$\:{e}_{tc}=\:{e}_{u}+\frac{L}{\sqrt{A}}\frac{\sqrt{{A}_{c}}}{{L}_{c}}\left({e}_{t}-{e}_{u}\right),$$

(3)

where $\:{e}_{t}$, $\:{e}_{u}$, $\:L$, and $\:A$ denote the measured total elongation, uniform elongation, gauge length, and cross-section area for a specimen (e.g., standard-size specimen), and $\:{e}_{tc}$ is the converted total elongation for a specimen with gauge length $\:{L}_{c}$ and area $\:{A}_{c}$ (e.g., sub-size specimen).

Similarly, the conversion of total elongation following the Bertella-Oliver formula⁴⁴ is based on:

$$\:{e}_{tc}=\:{\left(\frac{L}{\sqrt{A}}\right)}^{n}{\left(\frac{\sqrt{{A}_{c}}}{{L}_{c}}\right)}^{n}{e}_{t}.$$

(4)

For calculating the total elongation using Eqs. 3 and 4, the approach proposed by Zhang et al.⁴⁴ uses specimens with a specific geometry as a reference, and calculates the average value of the total elongation for other specimens that have the same slenderness ratio.

Gap in current understanding of the specimen size effect

The gap in the current understanding of size effects in sub-sized specimens addressed in this study is related to the shortcomings of existing computational methods and guidelines. Specifically, the conversion methods by Barba and Bertella-Oliver introduce several assumptions and constraints, and these methods are also sensitive to various test factors and conditions. Namely, the Bertella-Oliver formula may produce unreliable conversion results for specimens with a slenderness ratio greater than 25, and with a width-to-thickness ratio greater than 20^13,44. Also, ultimate tensile strength should be below 700 MPa to obtain reliable results⁴⁵. In addition, the exponent $\:n$ in Eq. (2) is sensitive to specimen thickness, and increases with decreasing specimen thickness. Moreover, the formula requires to be modified for thinner specimens¹³. Additionally, the validity of Barba’s law and Bertella-Oliver formula may break when converting between flat and round specimens, due to the variations in strains in the width and thickness directions²⁵. In addition, these models do not integrate important information regarding the specimen manufacturing process, irradiation conditions, or other important factors, which otherwise can have a significant impact on the tensile properties of sub-sized specimens. Advanced computational methods developed based on comprehensive information about test conditions and specimen preparation can improve the reliability and accuracy of existing methods for correlating tensile properties.

Additionally, the critical values for measuring the tensile properties of bulk materials presented in Table 1 are experimentally derived in prior studies using small-scale tensile test studies that typically include several tens of test records. Future validations involving a larger number of tensile test records can further validate and refine the recommended threshold values and serve as valuable guidelines for material selection and design.

Experimental results

Validation of analytical models for correlating tensile properties

This section presents an experimental validation of the analytical models based on Barba’s law and Bertella-Oliver formula for correlating tensile properties using the sub-sized specimens database created by our team. Figure 1 shows the fitted models for correlating total elongation to the length-to-square-root-area ($\:L/\sqrt{A}$) ratio (slenderness ratio) based on Barba’s law given in Eq. (1) and the Bertella-Oliver formula given in Eq. (2). The resulting analytical equations for our database are similar to the models fitted by Mathew et al.²⁵, which were obtained based on approximately 30 to 40 tensile tests of SS316 with different specimen dimensions (the exact number of specimens was not specified in²⁵). Specifically, the reported model based on Barba’s law in²⁵ is $\:{e}_{t}=62+89(\sqrt{A}/L$), and in comparison, the obtained model obtained from our compiled data and depicted in Fig. 1(a) has a regression equation $\:{e}_{t}=34.07+234.41(\sqrt{A}/L)$. For the model based on the Bertella-Oliver formula given in Eq. (2), the reported formula in²⁵ is $\:{{e}_{t}=111\left(\sqrt{A}/L\right)}^{0.20}$, whereas the corresponding model obtained by our team is $\:{{e}_{t}=136.34\left(\sqrt{A}/L\right)}^{0.38}$. Conclusively, although both the models fitted on the database created by our team and the models reported in²⁵ are based on tensile tests from SS316 specimens, the specific tensile test conditions and other factors from the obtained values of the parameters in the fitted models.

Fig. 1

Analytical models for correlating total elongation to slenderness ratio ($\:L/\sqrt{A}$) based on: (a) Barba’s law given in Eq. (1), and (b) Bertella-Oliver formula given in Eq. (2).

The values of the coefficient of determination $\:{R}^{2}$, Pearson correlation coefficient (r), and root-mean-square error (RMSE) based on the fitted Barba’s law and Bertella-Oliver formula in Eqs. (1) and (2) using our database are shown in the first two rows of Table 2. The same parameters for the conversion models in Eqs. (3) and (4) based on Barba’s law and Bertella-Oliver formula are given in the last two rows of Table 2. In both cases, the Bertella-Oliver model shows a better correlation compared to Barba’s law. The results are consistent with Mathew et al.²⁵, who reported a slightly higher correlation for the Bertella-Oliver model based on their available data.

Table 2 Performance metrics for the analytical correlation models based on Barba’s law and Bertella-Oliver formula.

Machine learning models for tensile properties prediction

Single-point prediction machine learning models

This section presents the experimental evaluation of ML methods for single-point prediction of tensile properties from sub-sized specimens. For a given tensile test record in the database with information about material composition, manufacturing and treatment information, specimen dimensions, and tensile test conditions, the objective is to predict the following tensile properties: yield strength (YS), ultimate tensile strength (UTS), uniform elongation (UE), or total elongation (TE). The performance of the following regression ML models is evaluated for this task: k-Nearest Neighbors (kNN), Support Vector Machine, Decision Trees, Random Forest, Extreme Gradient Boosting (XGBoost), Gaussian Process Regression, and Artificial Neural Network. For evaluating the performance of the ML models for single-point predictions, we used the following performance metrics which are common for regression tasks: R² (coefficient of determination), R (Pearson correlation coefficient), and RMSE (root-mean-squared error). Better-performing models are characterized by high values of R² and R, and low values of MSE, respectively.

The obtained values of the performance metrics for predicting the yield strength and ultimate tensile strength are provided in Table 3, and the corresponding values for predicting the uniform elongation and total elongation are provided in Table 4. After the initial step of data cleaning, the total number of available records for yield strength and ultimate tensile strength is 204, for uniform elongation is 86, and for total elongation is 190. The number of input features, related to experimentally collected parameters for each training record is 36. For training and testing the models, we employed five-fold cross-validation using four folds (80%) of the available data for training and the remaining fold (20%) for testing the models. Each model was run five times, with each run containing four different folds for training the models, and one set-aside fold for testing the models. To maintain consistency and guarantee that all models are evaluated using the same data points, we applied the same random seed for training and testing all models.

Table 3 Performance metrics for predicting yield strength and ultimate tensile strength, given as average value ± standard deviation (in subscript). Best performance metrics are highlighted in bold.

Table 4 Performance metrics for predicting uniform elongation and total elongation, given as average value ± standard deviation (in subscript). Best performance metrics are highlighted in bold.

The performance of the ML models for the tensile properties in Tables 3 and 4 indicates a high correlation between predicted tensile properties and the ground-truth values (i.e., the actual, experimentally measured values of the tensile properties), as most models achieved r values higher than 0.9 for all tensile properties. The trees-ensemble ML models Random Forest and Extreme Gradient Boosting are generally among the best performing for this task, with Random Forest achieving the best values for ultimate tensile strength for all metrics (R² = 0.975), and Extreme Gradient Boosting having the best predictive performance for ultimate tensile strength and total elongation (R² = 0.867 and 0.870, respectively). Similarly, Decision Trees achieved the highest performance for uniform elongation (R² = 0.966). In addition, Gaussian Process Regression produces highly accurate results, and it is competitive with the tree-ensemble models for all tensile properties. The performance of the Neural Network models is competitive, but lower than the best-performing models. Similarly, kNN and Support Vector Machines exhibited a lower overall predictive performance in comparison to the other ML models. Generally, there is a correlation between the values of the performance metrics, where the model with the highest R² typically has also the highest r and the lowest RMSE values.

Parity plots depicting the ground-truth values of the tensile properties of sub-sized specimens and the predicted values by the best-performing model for each property are presented in Fig. 2. The shaded areas in the figure indicate the 95% confidence intervals for the predicted values. Several outliers are also noticeable, where a possible reason for the presence of outliers is the heterogeneity of the database, since the tensile records were collected from different works based on differing test conditions and protocols.

Fig. 2

Parity plots of the best-performing ML model for: (a) yield strength—Random Forest model, (b) ultimate tensile strength—Extreme Gradient Boosting model, (c) uniform elongation—Decision Trees model, and (d) total elongation—Extreme Gradient Boosting model.

The predicted values of total elongation by the ML models presented in Table 4 are more consistent with the measured values and yield R² = 0.966, which is a significant improvement in comparison to the estimated values by Barba’s law and Bertella-Oliver formula presented in Table 2, where the highest value is R² = 0.542. The main reason for the enhanced performance is that, unlike the analytical correlation models, ML models account for the differences in test conditions and other important factors.

Uncertainty quantification models

The experimental results for the evaluation of the ML for the uncertainty quantification (UQ) of yield strength and ultimate tensile strength are presented in Table 5, and for uniform elongation and total elongation in Table 6. As performance metrics for assessment of the predictive accuracy of the models, we employ R² (coefficient of determination) and RMSE (root-mean-squared error), similar to the previous section. We omit here the values for r to reduce clutter in the presented results, since this metric strongly correlates with the values of R² and RMSE. For assessing uncertainty estimates we use coverage as a metric, which refers to the proportion of ground-truth values that fall within the predicted uncertainty interval by the model. The best performing models are characterized by high coverage values. However, one should be cautious in assessing UQ solely based on coverage, because a coverage of 100% may indicate that the model overestimates the prediction interval.

Table 5 Performance metrics for UQ models for yield strength and ultimate tensile strength, given as average value ± standard deviation (in subscript). Best performance metrics are highlighted in bold.

Table 6 Performance metrics for UQ models for uniform elongation and total elongation, given as average value ± standard deviation (in subscript).

The best-performing models are Bayesian Neural Network-MCMC and Natural Gradient Boosting. Also, the performance of Gaussian Process Regression is competitive in most cases for both point and uncertainty estimates. The results indicate that the Quantile Regression models perform well for properties prediction, but underestimate the coverage in most cases. Similarly, Deep Ensemble and MC Dropout achieve high predictive accuracy, but consistently underestimate the confidence interval. Bayesian NNs with Variational Inference achieve lower predictive accuracy for all properties.

Plots of the predicted tensile properties and confidence intervals for the best-performing models for one of the five folds that are set aside for model testing are presented in Fig. 3. In the figure, each data point represents a tensile test record; the horizontal axis displays the identifier numbers assigned to each tensile test record, while the vertical axis shows the experimental and predicted values of the tensile properties.

Fig. 3

Uncertainty quantification plots with confidence intervals for: (a) yield strength—Natural Gradient Boosting model, (b) ultimate tensile strength—Gaussian Process Regression model (c) uniform elongation—Natural Gradient Boosting model, and (d) total elongation—BNNs-MCMC model.

Test factors attribution to tensile properties of sub-sized specimens

To quantify the importance of different test factors for tensile properties of sub-sized specimens, we employ explainable ML methods and statistical analysis. First, the SHapley Additive exPlanations (SHAP) technique⁴⁶ is used for identifying test factors that have the greatest influence on the predicted tensile properties by the ML models. Next, statistical analysis is applied to study the relationships between the most important features and yield strength, ultimate tensile strength, uniform elongation, and total elongation.

Feature importance via explainable machine learning

Multiple post-hoc explainability methods in ML have been developed to provide insights into the decision-making process of the models. Such methods are essential for interpreting the outputs of ML models, and are especially important for understanding the internal working of ensemble models and deep neural networks. Among post-hoc explainability methods, SHAP⁴⁷ and Local Interpretable Model-agnostic Explanations (LIME)⁴⁸ are the most popular. The SHAP approach provides advantages in terms of robustness, consistency, and flexibility in explaining ML models. SHAP is based on the concept of Shapley values from cooperative game theory that allocates the payoff of a cooperative game among multiple players in a team based on their contributions⁴⁹. In ML, Shapley values are employed to quantify the contributions of individual input features to the output of a model. A Shapley value for an input feature is calculated by averaging the change in the model output when that feature is included in all possible subsets of features⁴⁷.

Figure 4 shows bar charts of the eight most important SHAP features with respect to the predicted values for Random Forest, Extreme Gradient Boosting (XGBoost), and Gaussian Process Regression. The graphs indicate that for all four tensile properties, specimen treatment is the most significant input feature, followed by test temperature. Other important input features that impact the predictive performance of the models include features based on specimen dimensions and geometry, such as thickness, width, thickness-to-width ratio, and, to a lesser extent, length and length-to-width ratio. Additionally, grain size understandably carries some importance, because it is associated with the treatment procedure. The rest of the input features are omitted in Fig. 4 for clarity of presentation, and include post-treatment temperature, post-treatment time, cooling method, irradiation dose, irradiation temperature, irradiation time, strain rate, chemical composition (with several exceptions), specimen length, and fillet radius.

Fig. 4

SHAP feature importance for the top eight features for Random Forest, XGBoost, and Gaussian Process Regression models in predicting: (a) yield strength, (b) ultimate tensile strength, (c) uniform elongation, and (d) total elongation.

Statistical data analysis

This section presents a statistical analysis of the collected tensile data to further investigate the key test factors that affect tensile properties.

The specimen treatment is investigated first, as the most important input feature in the analysis from the previous sub-section. Figure 5 shows the yield strength and ultimate tensile strength of sub-sized and standard-sized specimens for three groups of treatments: 20% cold-worked, solution annealed (post treatment temperature over 1000 °C), and stress-relieved (post treatment temperature below 1000 °C). The number of tensile records for sub-sized SS316 specimens is 556, and for comparison, we collected 420 tensile records for standard-sized SS316 specimens⁵⁰. In addition, each subplot in Fig. 5 shows box plots color-grouped by gauge length, ranging from 5 mm to 50.8 mm. In general, most sub-sized specimens have gauge lengths shorter than 20 mm, and most standard-sized specimens have gauge lengths longer than 25 mm. However, there is no distinct threshold for the gauge length to separate sub-sized from standard-sized specimens, as there are differences between different standards, such as ASTM (American Society for Testing and Materials) International, ISO (International Organization for Standardization), JIS (Japanese Industrial Standards), DIN (German Institute for Standardization), etc. From the plots in Fig. 5, it is noticeable that the type of treatment has a significant influence on yield strength and ultimate tensile strength, as expected, where 20% cold-worked specimens have higher yield strength and ultimate tensile strength compared to solution-annealed and stress-relieved specimens. While yield strength is independent of specimen gauge length, for ultimate tensile strength the specimens with 50.8 mm gauge lengths show decreased strength in comparison to the shorter specimens.

Fig. 5

Box plots of the influence of treatment and specimen gauge length on (a) yield strength and (b) ultimate tensile strength.

Figure 6 shows the corresponding plots for uniform elongation and total elongation of sub-sized and standard-sized specimens. For the plot of uniform elongation in Fig. 6(a), there are no data points for stress-relieved specimens. Similar to Figs. 5 and 6 shows a noticeable difference in ductility for the different treatment groups. Regarding the influence of specimen gauge length, Fig. 6(a) indicates that it does not have a significant influence on uniform elongation. Conversely, for solution-annealed specimens, total elongation is not independent of the specimen gauge length, as in Fig. 6(b) there is a clear decrease in elongation for specimens with 50.8 mm gauge length. This observation is consistent with reports of the sensitivity of total elongation to specimen size and geometry^13,25,26.

Fig. 6

Box plots of the influence of treatment group and specimen gauge length on (a) uniform elongation, and (b) total elongation.

Next, we studied test temperature as the second most important factor for the developed ML models⁵¹. The effect of test temperature and treatment group in the range from room temperature to 704 °C is presented in Figs. 7 and 8. The plots in Figs. 7 and 8(b) show a decrease in yield strength, ultimate tensile strength, and uniform elongation as the test temperature is increased for both 20% cold-worked and solution-annealed treatment groups. For total elongation In Fig. 8(b), the impact of test temperature is not as evident as for yield strength, ultimate tensile strength, and uniform elongation.

Fig. 7

Box plots showing the influence of test temperature and treatment on (a) yield strength, (b) ultimate tensile strength.

Fig. 8

Box plots of the influence of test temperature and treatment on (a) uniform elongation, and (b) total elongation.

The influence of tensile test parameters related to specimen size and geometry, as well as grain size, is presented in the following section, dedicated specifically to specimen size effects.

Investigation of specimen size effects

This section presents the empirical study of the four hypotheses regarding specimen dimensions and geometry, critical values, and affected tensile properties.

Hypothesis 1

Specimen thickness affects YS, UTS, UE, PE, and TE.

Figure 9 depicts the influence of specimen thickness on yield strength, ultimate tensile strength, and total elongation based on tensile data from Kohno et al.²⁴. The recommended critical value of 0.12 mm is shown with a green dashed line in the graphs. The figure supports the hypothesis that tensile properties are independent of specimen thickness above a critical value, while below the critical value, tensile properties decrease with decreasing specimen thickness. Nevertheless, Fig. 9 does not corroborate the critical thickness value of 0.12 mm as suggested, as the inflection point is approximately at 0.2 mm for all three tensile properties. The gray shaded areas in the subfigures represent 95% confidence interval range for the data points.

Fig. 9

Influence of specimen thickness on: (a) yield strength, (b) ultimate tensile strength, and (c) total elongation.

Figure 10(a) shows the effect of low-dose irradiation on yield strength at a temperature of 157 °C. The plots indicate that increasing the irradiation dose to 12 dpa and 24 dpa caused irradiation hardening. On the other hand, the critical thickness value is close to 0.12 mm in this case. In conclusion, the increase in yield strength at higher irradiation doses is due to matrix hardening, and not due to grain boundary hardening²⁴. Figure 10(b) and (c) present the influence of increased irradiation dose and irradiation temperature on yield strength for specimen thicknesses above the critical value. The subplots (b) and (c) correspond to irradiation temperatures of 420 °C and 520 °C. The graphs reveal that yield strength saturates when irradiation dose increases. For the temperature of 420 °C in Fig. 10(b), the yield strength does not increase for irradiation values above 44 dpa, and similarly, for the temperature of 520 °C in Fig. 10(c), saturation occurs at 35 dpa. Furthermore, as expected, yield strength remains approximately constant with an increase in specimen thickness.

Fig. 10

(a) Influence of low-dose irradiation and specimen thickness on yield strength. Influence of high-dose irradiation and specimen thickness on yield strength for (b) irradiation temperature = 420 °C, and (c) irradiation temperature = 520 °C.

Figure 11 shows the influence of specimen thickness on yield strength for all available sub-sized tensile records, grouped by specimen treatment. Specifically, subfigures (a), (b), and (c) present the graphs for specimens subjected to 20% cold-worked, solution-annealed, and stress-relieved, respectively. The data points for stress-relieved specimens are from Kohno et al.²⁴, and are presented in Fig. 9a and discussed above. For 20% cold-worked specimens, there are no available data to establish a critical value of specimen thickness, although the critical value may be higher due to increased grain size. For solution-annealed specimens in Fig. 11(b), the data is fairly scattered and does not show a clear pattern. However, there is a decrease in yield strength below a critical value of approximately 0.12 mm, and the yield strength is not constant for values above the critical value.

Fig. 11

Influence of specimen thickness on yield strength based on treatment procedure: (a) 20% cold-worked, (b) solution annealed, and (c) stress relieved.

A similar figure that depicts the relationship between specimen thickness and total elongation based on treatment is shown in Fig. 12. Similar to the previous figure, there are no available data for specimens with 20% cold-working below the critical thickness. For solution-annealed specimens in Fig. 12(b), the critical thickness is approximately 0.18 mm, and above the critical value the total elongation increases.

Fig. 12

Influence of specimen thickness on total elongation based on treatment: (a) 20% cold-worked, and (b) solution-annealed.

Hypothesis 2

Specimen width-to-thickness ratio affects UTS, PE, and TE.

Figure 13 shows the relationship between ultimate tensile strength and the inverse of $\:W/T$ ratio, confirming the hypothesis that for $\:W/T$ > 5 (i.e.,$\:\:T/W<\:0.2)$, ultimate tensile strength decreases. Above the critical value, ultimate tensile strength remains approximately constant.

Fig. 13

Influence on ultimate tensile strength of thickness-to-width (T/W) ratio.

Figure 14 shows the relationship between the thickness-to-width ($\:T/W$) ratio and yield strength. The plot supports the hypothesis that yield strength is independent of the width-to-thickness ratio.

Fig. 14

Influence of thickness-to-width (T/W) ratio on yield strength.

Figure 15 illustrates the influence of irradiation dose and thickness-to-width ($\:T/W$) ratio on total elongation. A critical value of approximately $\:0.2$ ($\:W/T$ $\:=5$) seems appropriate when the irradiation dose is increased to 12 dpa, whereas for irradiation dose of 24 dpa the trend is not clear (probably due to the limited available data).

Fig. 15

Influence of irradiation dose and thickness-to-width (T/W) ratio on total elongation.

Figure 16 presents similar plots to Fig. 15 regarding the dependence of total elongation on the thickness-to-width ($\:T/W$) ratio and includes all available data points from sub-sized specimens that were not exposed to irradiation. Figure 16(a) relates to 20% cold-working, and Figure 16(b) pertains to solution-annealing. The available data in these graphs show significant scatter. Yet, the graphs support a general trend of increasing total elongation with increasing thickness-to-width ratio. The increase in total elongation is due to variations in the necking behavior, which changes from localized to diffuse necking¹⁸.

Fig. 16

Influence of thickness-to-width (T/W) ratio on total elongation based on treatment: (a) 20% cold-working, and (b) solution-annealing.

Hypothesis 3

Specimen thickness-to-grain-size ratio affects YS, UTS, UE, and TE.

Figure 17 shows the dependence of tensile properties on the thickness-to-grain-size ratio, based on data from Miyahara et al.⁵². Figure 16(a) and (b) show that ultimate tensile strength and total elongation increase with increasing thickness-to-grain-size ratio, and above a critical value the fitted curves flatten. The critical value of the thickness-to-grain-size ratio for ultimate tensile strength is between 10 and 20, and for total elongation is around 15.

Fig. 17

Influence of thickness-to-grain-size (T/GS) ratio on: (a) ultimate tensile strength, and (b) total elongation.

Figure 18 includes plots of the influence of thickness-to-grain-size ratio and irradiation conditions on the strength of the material, based on data from Kohno et al.²⁴. The relationship for low irradiation dose in Fig. 18(a) follows the hypothesis that the critical value is approximately 6. The plots with higher irradiation dose in Fig. 18(b) and (c) show no dependence of ultimate tensile stress on thickness-to-grain-size ratio, and also indicate saturation of strength with increasing irradiation dose.

Fig. 18

(a) Influence of low-dose irradiation and specimen thickness-to-grain size (T/GS) ratio on yield strength. Impact of high-dose irradiation and specimen thickness on ultimate tensile strength for (b) irradiation temperature = 420 °C, and (c) irradiation temperature = 520 °C.

Figure 19 presents plots of the dependence of total elongation on grain size for different specimen thickness values from Miyahara et al.⁵² for three different heats of SS316. As specimen thickness increases from 0.15 mm to 1 mm, total elongation is no longer affected by grain size, while for smaller thickness values, total elongation decreases for increasing grain size.

Fig. 19

Influence of grain size and specimen thickness on total elongation for: (a) heat 1, (b) heat 2, and (c) heat 3.

Hypothesis 4

Specimen length-to-square-root-area ratio affects PE and TE.

Figure 20 presents plots that investigate the relationship between the length-to-square-root-area ($\:L/\sqrt{A}$) ratio and the tensile properties of sub-sized specimens. The graphs illustrate the relationship for specimens subjected to solution-annealing, as this treatment has the most available data points. In Figure 20(a) it can be noted that yield strength remains approximately constant with the slenderness ratio. A similar pattern is observed for ultimate tensile strength in Figure 20(b), whereas for uniform elongation in Figure 20(c) there is a decreasing trend as the slenderness ratio increases. On the other hand, scatter in the data is significant. The dashed line in the figure represents the recommended critical value for length-to-square-root-area ($\:L/\sqrt{A}$) of 5.65.

Fig. 20

Influence of slenderness (length-to-square-root-area, $\:L/\sqrt{A}$) ratio on: (a) yield strength, (b) ultimate tensile strength, and (c) uniform elongation.

Figure 21 shows plots of the dependence of total elongation on the length-to-square-root-area ($\:L/\sqrt{A}$) ratio for sub-sized specimens. The graphs depict data for all three treatment groups, due to the significance of the slenderness ratio for total elongation. Figures 21(a), (b), and (c) indicate a decrease in total elongation with increasing slenderness ratio, which is consistent with the literature^13,18,44. The color of the data points for stress-relieved specimens in Fig. 21(c) is based on the irradiation dose.

Fig. 21

Influence of slenderness (length-to-square-root-area, $\:L/\sqrt{A}$) ratio on total elongation for: (a) 20% cold-working, (b) solution-annealing, and (c) stress-relief.

The recommended critical value for the length-to-square-root-area ($\:L/\sqrt{A}$) ratio is 5.65, according to ISO 6892e1:2016 standard. DIN EN ISO 6892-1 standard recommends a critical value of 11, and in other studies the recommended value varies from 4 to 11.3¹⁸. In Figs. 19 and 20, the critical threshold of 5.65 is displayed with the green dashed line. However, it can be noticed that only 4 data points in the database have a slenderness ratio below 5.65. Consequently, the analysis does not provide enough evidence to derive a conclusion regarding the critical value of the slenderness ratio.

Discussion

The experimental results obtained by implementing ML models for single-point prediction of tensile properties presented in the Results section indicate that Ensemble models based on Extreme Gradient Boosting and Random Forest achieve the best performance. In addition, Gaussian Process Regression provides accurate predictions that are competitive with Ensemble models. Among the models for uncertainty quantification of tensile properties, Natural Gradient Boosting and Bayesian NNs with MCMC approximation are the best-performing models. Gaussian Process Regression also achieves competitive performance for uncertainty quantification. The trustworthiness and reliability of ML models in materials science can be enhanced by incorporating UQ into the predicted values. For example, engineers may adopt a different design approach if the predicted tensile strength of a material is characterized by a high level of variability, in comparison to a case where the predicted tensile strength for that material has a low level of variability. In addition, the provision of uncertainty estimates by an ML model can serve as an indicator of the confidence of the model in its prediction for given input features, and hence can reflect the degree to which the outputs of the model can be trusted.

Based on the applied techniques for explainable ML and statistical analysis to quantify the contribution of the test parameters to the predictive capabilities of ML models, the most important parameters are specimen treatment and test temperature, followed by specimen dimensions, geometry, and grain size. The identification of key factors was useful for studying specimen size effects in our study, and in general, it can be helpful to guide test matrix design and establish conditions for tensile tests on novel materials.

To investigate specimen size effects, we tested four hypotheses based on recommendations from previous studies. In most cases, our findings are consistent with the published literature. However, our experimental results show that a critical value of the specimen thickness of 0.2 mm is recommended for SS316, as opposed to the generally recommended value of 0.12 mm. Similarly, our data analysis shows that specimen thickness should contain at least 10 grains, although other studies recommended between 6 and 10 grains. Furthermore, while it has been reported that uniform elongation is independent of the slenderness ratio, we observed decreasing uniform elongation with increasing slenderness ratio.

In our assessment of the analytical methods for the estimation of total elongation, we report similar trends for Barba’s law and Bertella-Oliver formulas with respect to the literature. We assessed the sensitivity of the analytical models to test factors and conditions. In practice, the validity of derived models is adequate only for a limited range of conditions, and separate models are required for specimens with the same composition subjected to different treatments, test temperatures, irradiation conditions, or other factors.

The summary of our findings is as follows:

• Employing ML models capable of uncertainty quantification is necessary for predicting tensile properties of sub-sized specimens, due to the greater scatter of measured properties caused by inconsistency in manufacturing processes, higher surface-to-volume ratio, sensitivity to dimensional deviations, specimen alignment, measurement errors, and other sources of variability.

• Ensemble ML models achieve high predictive accuracy for single-point predictions (Random Forest, XGBoost) and for uncertainty estimation (NGBoost). Bayesian NN-MCMC models are promising models for this task and provide reliable and accurate predictions for tensile property prediction. Gaussian Process Regression models achieve competitive results with respect to the best-performing models and should also be considered as potential candidates.

• Specimen treatment and tensile test temperature are the most important factors affecting tensile properties. Secondary contributing factors are specimen dimensions and grain size.

• Yield strength and uniform deformation are independent of specimen gauge length, for a given treatment. Although it has been reported that ultimate tensile strength is also independent of gauge length, we observed lower ultimate tensile strength in specimens with shorter gauge lengths. Total elongation decreases with increasing gauge length, which is consistent with previously published studies.

• Increasing test temperature causes a decrease in yield strength and ultimate tensile strength. For uniform deformation, there is a small increase with increasing test temperature, although similar studies reported no trend. Total elongation is independent of test temperature.

• The threshold critical value for specimen thickness below which size effects are observed is 0.2 mm, different than the value of 0.12 mm suggested for SS316 in²⁴.

• Related to the previous items, the observed threshold value for specimen thickness-to-grain-size is 10 or above 10, although other studies recommend a critical value between 6 and 10.

• Yield strength and ultimate tensile strength are independent of the slenderness ratio, whereas total elongation is not independent, as reported in prior studies. Differently from published studies, uniform elongation appears to be inversely proportional to the slenderness ratio.

• Existing analytical methods for estimating total elongation are valid under specific testing conditions, and require developing different models based on specimen treatment, test temperature, and other factors, as we have presented here.

A limitation of our study is that although it is the largest experimental study of this type, the compiled database is still relatively small. In addition, the database was created by collecting tensile test records from articles that used different testing procedures and studied different aspects of sub-sized tensile testing. This leads to heterogeneity of the data, which may violate the ML assumption that the data-generating process is fixed, and data is independent and uniformly distributed. Consequently, having access to larger databases and collecting data from large test studies performed under standard testing conditions can improve the quality of the data, mitigate the presence of outliers, improve the predictive capacity of ML models, and result in improved statistical analysis.

Furthermore, the reported information on specimen manufacturing and preparation in the original sources was inconsistent, with specific details often omitted. Specifically, the form factors of the original stock material from which specimens were manufactured and the orientation of specimens relative to the stock can influence tensile properties. Since this information was generally not reported, we treated the material as isotropic in our analysis. We acknowledge that unreported material anisotropy could contribute to scatter and variability in tensile properties. Future studies would benefit from consistently reporting specimen orientation and grain anisotropy to clarify the subtle influences on tensile behavior.

Materials and methods

Database of tensile properties from sub-sized specimens

To investigate size effects and develop computational methods to correlate the tensile properties obtained from sub-sized specimens and standard-sized specimens, our team created an open database of tensile properties from sub-sized specimens from nuclear structural materials. The database is available at the open-access repository for research data in materials science, Materials Cloud²⁹, and the corresponding article that describes the database is available at arXiv³⁰. We constructed the database through an extensive literature review of relevant publications for the following nuclear structural materials: stainless steel 316, reactor pressure vessel steels, and fuel cladding Zirconium alloys. The database contains 1,050 tensile test records comprising 55 parameters that include material type and composition, manufacturing information, irradiation conditions, specimen dimensions, and tensile properties.

From the articles that provide structured tabular data of tensile test results, specimen size, and other relevant data in the form of tables, spreadsheets, or databases, we manually extracted the data. For the articles that present the data in graphical form, we employed the plot digitization software WebPlotDigitizer⁴⁶ to manually extract the coordinates for each point in the graphs. Data post-processing included conversion of the measurement units to ensure consistency in the data records (e.g., temperature conversion from Fahrenheit to Celsius), and calculating the composition for elements containing the term “balance” to have the weight% of all elements add up to 100%. Technical validation of the database involved a thorough review of the retrieved data from the literature by materials science experts. This step included verifying the accuracy of material types, chemical composition of the materials, and ensuring the use of standardized material names. Statistical analyses and data visualization techniques were applied to identify and address data outliers.

The information for each tensile test record in the database consists of 55 columns, divided into the categories Reference, Material Type and Composition, Manufacturing and Treatment Information, Irradiation Conditions, Specimen Dimensions, Tensile Test Conditions, and Tensile Properties. The Reference category lists the article from which the data were extracted. The Material Type and Composition columns record the material type of the sub-sized specimens and their chemical composition, listing the elements given in weight%. The category Manufacturing and Treatment Information includes the type of treatment, post-treatment temperature (ºC) and time (hours), microstructure, morphology, grain size (µm), and similar information. The Irradiation Conditions columns, if applicable to the tensile test record, provide information regarding the irradiation dose (milli-displacement per atom), temperature (ºC), and time (hours). Specimen Dimensions are provided in millimeters and provide information regarding the gauge length, width, thickness, fillet radius, and aspect ratios of the dimensions of sub-sized specimens. Tensile Test Conditions provide information regarding the temperature of the tensile test (ºC), and the strain rate (1⁄s) of the test. Finally, Tensile Properties include data on yield strength (MPa), ultimate tensile strength (MPa), uniform elongation (%), and total elongation (%).

Machine learning models for tensile property prediction

Recent advancements in ML offer unique potential to advance materials science and address challenges associated with modeling the multi-physics and multi-scale mechanisms that drive material behavior. The demonstrated advantages of ML models for extracting complex patterns in high-dimensional data can be effectively used for the challenges of size effect in materials science as well. Our proposed approach employs ML methods for predicting the tensile properties from sub-sized specimens for a given tensile test record. Input features for training the ML models include material type and composition, manufacturing and treatment information, specimen dimensions, and tensile test conditions. The output variable of the ML models is one of the four tensile properties: yield strength (YS), ultimate tensile strength (UTS), uniform elongation (UE), or total elongation (TE). This learning problem represents a regression task since the outputs of the ML models are continuous values.

Our focus in this study is on ML models that extend beyond single-point predictions for the target variable and encompass uncertainty quantification (UQ)^37,40 of the predicted values. Particularly in material science, using an ML model to provide an estimate of the tensile strength, creep fracture life, or other properties of a material without indicating the range of probable values for that property may not be sufficient for informed decision-making^38,39. The inherently stochastic structure of materials at micro- and nano-scales introduces several sources of uncertainties, leading to variability in the macro-scale properties of the material. To address variability in material properties, mechanical tests are typically performed on multiple specimens of the same material. Consequently, in the design of engineering components and products, the variability of material properties is taken into consideration, typically by adopting lower bound values for the material properties to guarantee safety.

For predicting tensile properties from sub-sized specimens, the quantification of uncertainty is particularly important, and we argue that it is necessary, because the measured properties of sub-sized specimens exhibit greater scatter than standard-sized specimens. The sources of variability include inconsistencies in manufacturing processes, higher surface-to-volume ratio (sensitivity to surface imperfections), increased variability in grain orientations and sizes (due to smaller volume), sensitivity to local material inhomogeneity, and increased sensitivity of sub-sized test results to dimensional deviations, specimen alignment and handling, and measurement errors^13,16. Reducing these variations typically involves implementing strict guidelines for specimen preparation, controlling testing conditions, and employing advanced measurement techniques specifically designed for sub-sized specimens.

Whereas the majority of supervised ML models for classification by default output the probabilities of class predictions, most regression ML models typically output single-point predictions. Several conventional regression ML models do provide UQ in their predictions, including Quantile Regression, Natural Gradient Boosting, and Gaussian Process Regression. Another important category of deep learning models that has recently emerged as a promising framework for UQ is Bayesian Neural Networks (BNNs)^39,53. BNNs represent the network parameters with probability distributions. This property allows BNNs to generate probabilistic outputs and quantify the uncertainties of predicted values. Despite that the calculation of the posterior distribution of the network parameters for given input data in BNNs is theoretically intractable, approximation methods such as Variational Inference (VarInf) and Markov Chain Monte Carlo (MCMC) allow training and performing inference with BNNs in practice^39,53. Additionally, deep learning-based approaches for UQ have been developed that utilize standard Neural Networks with deterministic network parameters. Representatives of these methods are Deep Ensemble⁵⁴ and Monte Carlo (MC) Dropout⁵⁵.

Implementation details

Conventional single-point ML prediction models were implemented using the scikit-learn Python library⁵⁶. For the kNN model, the number of neighbors was set to 2. For the Support Vector Machine model, a linear kernel was applied with default hyperparameters. For Decision Trees, the default DecisionTreeRegressor was used. For Random Forest, the default RandomForestRegressor setting was used, and the number of estimators was set to 10,000. For XGBoost, the learning objective was set to ‘linear’, the number of estimators was set to 10, and the xgboost Python library was used. For Gaussian Process Regression, a customed kernel was applied consisting of matern, dot product, and white noise kernels, and the number of times the optimizer restarts was set to 8. For standard NN with deterministic parameters, three fully-connected layers were used with 1000, 200, and 40 neurons respectively, with ReLU activation function.

For the ML models for uncertainty quantification, a CatBoost base model was used in Quantile Regression, and the number of boost rounds was set to 5,000. For NGboost, the distribution was set to ‘LogNormal’, the number of estimates was set to 1,000, and the learning rate was 0.005. For Gaussian Process Regression, the same model hyperparameters as for single-point prediction were used. Model training and evaluation were performed using the scikit-learn, ngboost, and catboost Python libraries.

For the Deep Ensemble model, 5 base learners were used each comprising a standard NN with two fully-connected layers containing 400 neurons followed by dropout layers with a rate of 0.5 and ReLU activation. For the MC Dropout model, a standard NN architecture with three fully-connected layers containing 300 neurons followed by dropout layers with a rate of 0.5 and ReLU activation. For model training, MSE loss and Adam optimizer with a learning rate of 0.01 were adopted. The experimental results were computed as the mean and ± 3 standard deviations of the estimates by the base learners for Deep Ensemble, and based on generated 1,000 outputs for MC Dropout. The PyTorch library was employed for implementing Deep Ensemble, MC Dropout, and standard NNs.

For BNN-VI, the architecture comprised two fully-connected layers with 100 neurons and ReLU activation functions. A normal distribution with a mean of 0 and a standard deviation of 0.06 was employed as the prior distribution for network parameters. For training, Stochastic Gradient Descent (SGD) with Nesterov Momentum and a learning rate of 0.001 was adopted. Inference involved generating 1,000 samples from the variational distribution to calculate point estimates and uncertainty estimates. For BNN-MCMC, the architecture has two fully-connected layers containing 10 neurons. Network parameter priors followed a normal distribution with a mean of 0 and a standard deviation of 1. For an approximation of the posterior distribution, the No-U-Turn Sampling (NUTS) algorithm was used. Inference involved drawing 100 samples with point and uncertainty estimates. The torchbnn library for BNN-VI and the Pyro library was used for implementing BNN-MCMC.

Investigation of specimen size effects

To evaluate the recommended critical values for sub-sized tensile specimens in Table 1, our proposed approach was organized around four hypotheses regarding specimen dimensions and geometry, critical values, and affected tensile properties.

Hypothesis 1

Specimen thickness affects YS, UTS, UE, and TE. The hypothesis is based on previous studies contending that the strength and ductility of sub-sized specimens are affected when the thickness is below a critical threshold. Since thickness is typically the smallest dimension, it should contain a sufficient number of grains to reflect the bulk material properties. For most structural steels, the suggested critical thickness is about 0.2 mm, and for SS316 the recommended critical value is 0.12 mm²⁴. The values are based on an assumed average grain size of 20 micrometers, and the recommendation that the specimen thickness contain at least 6 to 10 grains.

Hypothesis 2

Specimen width-to-thickness ratio affects UTS, and TE. Specimen width also influences the test results for ultimate tensile strength, and total elongation in flat sub-sized specimens, even when the thickness is sufficient to reflect bulk material properties. The specimen width is typically accounted for through the width-to-thickness ($\:W/T$) ratio, also referred to as aspect ratio. Above the recommended critical value of 5, the affected tensile properties (ultimate tensile strength and total elongation) decrease with increasing ratio. Yield strength and uniform elongation are independent of the width-to-thickness ($\:W/T$) ratio. Some studies also consider the thickness-to-width ($\:T/W$) ratio for the assessment of specimen size effects, instead of the width-to-thickness ($\:W/T$) ratio.

Hypothesis 3

Specimen thickness-to-grain size ratio affects YS, UTS, UE, and TE. This hypothesis is related to Hypothesis 1, as the thickness of sub-sized specimens is typically the smallest dimension, and therefore, it should contain at least 6 to 10 grains for the tensile test results to reflect bulk material properties. Particularly, when the thickness-to-grain size ($\:T/GS)$ ratio is below the critical value, the increase in surface layer grains causes increased dislocation density that cannot maintain the strain hardening rate of the bulk material, and results in decreased flow stress and ductility. Above the critical value, the tensile properties are independent of the thickness-to-grain size ($\:T/GS)$ ratio. The critical value of the thickness-to-grain size ratio is typically between 6 and 10 for structural steels, while for SS316 the recommended critical value is 6¹⁸. For Aluminum alloys the critical value is between 3 and 5, while it is 18 for fine-grained Cu¹³.

Hypothesis 4

Specimen length-to-square-root-area ratio affects TE. Previous studies on specimen size effects reported that yield strength, ultimate tensile strength, and uniform elongation are independent of gauge length. On the other hand, total elongation (TE) is impacted by gauge length, namely shorter gauge lengths lead to an increase in total elongation. These claims are supported by our analysis, presented in Figs. 5 and 6. In addition, numerous studies investigated the tensile properties of geometrically similar specimens, and reported that for specimens having identical length-to-square-root-area ($\:L/\sqrt{A}$) ratio, yield strength, ultimate tensile strength, and uniform elongation are unaffected by gauge length. Conversely, total elongation is impacted by the length-to-square-root-area ($\:L/\sqrt{A}$) ratio and decreases with increasing ratio. The length-to-square-root-area ratio is also referred to as slenderness ratio or slimness ratio¹⁸.

The presented study employs the curated database of tensile records from sub-sized specimens to test the hypotheses. The objective of this study is to conduct and present the most comprehensive study of specimen size effects in tensile specimens.

Conclusions

This paper provides an experimental evaluation of specimen size effects in tensile testing, with a focus on stainless steel 316. The study uses a large, curated database of tensile test records of sub-sized specimens that our team recently compiled from peer-reviewed articles in the published literature. We applied ML models to predict the tensile properties measured from sub-sized specimens, and we developed ML models for estimating the uncertainties of the predicted values. The experimental results indicate that Ensemble models based on Gradient Boosting, Gaussian Process Regression, and Bayesian Neural Networks achieved the most accurate and reliable predictions. By employing explainable ML methods and statistical analyses, we identified specimen treatment, test temperature, and specimen size and geometry, as the most important features that affect the predictive capabilities of the models. Furthermore, we investigated the existing guidelines for the influence of critical values of specimen dimensions and geometries on specimen size effects. Additionally, we explored the validity of analytical methods for estimating total elongation in tensile testing. The findings of this study confirm the potential of ML methods and techniques for understanding the material behavior and phenomena related to specimen size effects.