Introduction

Breast cancer is the most common cancer among females in the United States, with estimated over 3,00,000 of new cases in 20241. It accounts for 31% of the new cases of all types of cancer diagnoses and is the second leading cause of cancer related death in the United States1. Ultrasonography is becoming increasingly important in diagnosing breast cancer, especially in low-resource settings where mammography is less feasible2. Ultrasound imaging increased the diagnostic sensitivity, but reduced the specificity, which necessitates the integration of computer-aided detection (CAD) systems to improve the diagnostic performance3,4. The effectiveness of ultrasound can be substantially influenced by the radiologist’s experience, however, CAD systems are shown to be effective in augmenting the diagnostic performance of less experienced radiologists5,6. Although, these systems require additional research to be considered fully reliable7.

Recently, deep learning (DL) has shown significant advancements in breast cancer detection using mammograms8,9,10,11. With the increasing demand of resource-aware settings, researchers have integrated artificial intelligence-based techniques12, including DL with ultrasound systems, and shown promising results5,13,14,15. DL models perform automated feature extraction from the raw data, unlike the traditional CAD approaches16,17,18,19. The diagnostic accuracy of the DL models is demonstrated to be comparable with that of the ultrasound experts, which shows their clinical usefulness in minimizing the number of biopsies due to false positive outcomes20. Further, DL is useful in improving the evaluation standards between experienced and less experienced clinicians20,21. It has substantially augmented the capabilities of B-mode ultrasound by providing a sophisticated method of image classification and feature extraction, outperforming the traditional CAD systems16. The integration of DL-based radiomics with B-mode ultrasound has shown improvement in the classification of breast masses22. Recent DL networks such as, convolutional neural networks have demonstrated remarkable performance in breast lesion classification showing comparable performance to radiologists23,24,25.

Related works

Based on the recent research works for breast cancer detection using DL, we categorize them into two groups, with each group having its own distinct methodologies and distinctions. The first category uses DL models trained from scratch, based on mostly, convolutional neural network (CNN) architectures. For example, in Refs.26–30, different combinations of VGGNet, DenseNet, and ResNet, AlexNet, GoogleNet, and MobileNetv2 were used for classifying benign and malignant breast lesions. The study using ResNet50 was applied to a private dataset29, and the method used in Ref.30 concatenated deep features extracted from AlexNet, MobileNetV2, and ResNet50 to feed to a support vector machine classifier using a public dataset. Another work in Ref.31 explored InceptionV3 and Xception along with MobileNet and DenseNet121 models to categorize the malignant and benign lesions in a private dataset, and demonstrated superior performance as compared to MobileNet. The performance was further improved by using a modified VGG-like architecture, RepVGG on a large private dataset32. Huang et al. proposed a multi-class categorization of breast tumors by developing ROI-CNN based on VGGNet for tumor localization and graded CNN based on encoding and concatentation scheme for tumor classification using two public datasets33. However, the overall method was complex in terms of model parameters. Researchers proposed two cascaded CNNs based on Inceptionv3 architectures, i.e., Mt-Net to detect malignant lesions, and Sn-Net to identify the solid masses using a private dataset and demonstrated the robustness with respect to variations in shapes and sizes of breast lesions34. Recently, Ragab et al. employed an ensemble of VGG-16, 19, and SqueezeNet for diagnostic feature extraction and multi-layer perceptron for classification of benign and malignant lesions with a high accuracy on a public dataset35. However, the performance is subject to the effectiveness of image segmentation technique, which was used prior to classification in this work35.

The second category of DL models is increasingly emerging for breast cancer classification, i.e. transfer learning-based or pre-trained models with or without modifications. For example, literary works utilize the pre-trained ResNet-101, AlexNet, VGG16, VGG19, and DarkNet-53 models directly in Ref.36–39 for different cases of breast cancer classification. Kaplan et al. in Ref.37 proposed pyramid triple deep feature generator for image decomposition prior to feature extraction using pre-trained models, and applied it to a private dataset for identifying the benign and malignant lesions. Other research studies introduced different spatial attention mechanisms in the pre-trained ResNet-18 and VGG16 models40,41, and achieved comparable performances. Further, Sin et al. proposed a joint weakly and semi-supervised model based on R-CNN and ImageNet pretrained VGG-16 for localizing and classifying breast masses using a private and a public dataset42. The research works show that transfer learning can offer efficiency and a good starting point for learning domain-specific features. However, they may not always capture nuanced characteristics of images obtained from ultrasonography as effectively as models that are trained specifically on such data43.

Objectives

The aforementioned scholarly studies utilize the standard CNN-based models for image classification-based feature extraction and their alterations for breast lesion classification. These studies establish effective discrimination between benign and malignant breast lesions in different datasets by extracting the corresponding pertinent features. However, these studies lack in terms of sufficient elucidation, need for segmenting the lesions prior, and monitoring the overall computational complexity involved in detecting breast cancer, which is crucial for timely diagnosis along with a reduction in the number of biopsies for benign lesions. In view of these aspects, we propose a novel variational mode directed low-complex deep learning framework to classify lesions in breast ultrasound images without segmenting them prior to classification. The proposed framework is built in two stages. The first stage includes elucidatory low level textural and boundary-based feature extraction using two-dimensional variational mode decomposition (2D-VMD) of the B-mode images of the scanned area, and the second stage includes high level feature extraction and classification of the images using a simplified sequential CNN-based deep learning network. To the best of our knowledge, this is the first work which uses 2D-VMD for deriving the discriminatory modes for feature extraction to assist a straightforward deep learning architecture towards breast cancer classification. The proposed DL architecture is guided by the 2D-VMD modes along with the input B-mode images and uses depth-wise separable convolutions along with mixed pooling and squeeze-and-excite-attention mechanisms for the first time to effectively classify the breast lesions with low computational complexity. The mixed-pooling and squeeze-and-excite-attention mechanisms help to improve the accuracy of breast lesion classification by focusing on the relevant features of the input images without having to extract the lesions or the regions of interest manually as done in many of the existing works which first segment the lesions and then classify them. Furthermore, the classification performance is evaluated using two publicly available datasets, and an in-hospital recorded dataset. The key contributions of this work are outlined as follows.

  • Introduction of 2D-VMD for extracting discriminatory low level features of breast lesions to feed a deep learning network.

  • Utilization of a computationally efficient deep learning network with depth-wise separable convolutions for extracting high level features to classify the lesions.

  • An extensive performance evaluation and comparison of the proposed framework using two public datasets and an in-clinic dataset.

  • Comparison of the computational complexity of the proposed framework with respect to existing methods for establishing its utility in real-time detection of breast lesion malignancy.

  • An analysis of interpretability of the layers of the proposed deep learning network for discriminating benign and malignant breast lesions.

This work is presented and organized as follows. Section Methods describes the methods utilized in this work to build the proposed framework. Section Results presents the datasets used in this work and performance assessment results along with the comparison studies. Section Discussion discusses the results and future directions of the proposed work. Finally, section Conclusion concludes the work.

Methods

In this section, we present the proposed framework which uses two-dimensional variational mode decomposition and a sequential CNN-based deep learning model for breast cancer classification, as shown in Fig. 1.

Fig. 1
figure 1

Proposed framework for breast cancer classification.

Full size image

Two-dimensional variational mode decomposition for ultrasound images

Zosso et al. in45 proposed a two-dimensional (2D) extension of the non-recursive and fully adaptive one dimensional variational mode decomposition (VMD) technique, following the same analogy. 2D-VMD decomposes an ultrasound image in a sparse manner, into constituent sub-images or modes with each mode having a very limited bandwidth around a distinctive center frequency. 2D-VMD composes the image decomposition process into a constrained variational problem of minimizing an objective function derived from the definition of 2D analytical signal with one sided spectrum, shifted to baseband by combining with a complex exponential of the current center frequency estimate45. The corresponding function is represented as:

$$\begin{aligned} \begin{aligned} \min _{m_n, \varvec{\omega }_n}\left\{ \sum _n \alpha _n\left\| \nabla \left[ m_{A S, n}(\varvec{z}) e^{-j\left( \varvec{\omega }_n, \varvec{z}\right) }\right] \right\| _2^2\right\} \quad \text{ s.t. } \\ \quad \forall \varvec{z}: \sum _n m_n(\varvec{z})=I(\varvec{z}), \end{aligned} \end{aligned}$$
(1)

where an \(n^{th}\) 2D band-limited mode/sub-image of an ultrasound image \(I({\textbf {z}})\) to be decomposed is denoted as \(m_n(\textbf{z})\) with the center frequency \(\varvec{\omega }_n\), \(\nabla\) and \(\alpha _n\) denote the gradient with respect to \({\textbf {z}}\) and data fidelity constant respectively, and \(m_{A S, n}({\textbf {z}})\) denotes the 2D analytical image obtained after Hilbert transformation45. Further explanation of above constrained minimization problem and its unconstrained formulation by adding a quadratic penalty term and Lagrangian multiplier along with optimization using alternate direct method of multipliers (ADMM) can be found in45. The solution to this minimization problem is obtained in iterations which produces a number of decomposed modes in frequency domain with distinctive center frequencies. The complete iterations-based process of 2D-VMD can be summarized in three steps as follows45.

  1. 1.

    Minimization with respect to modes \({m}_n\) : The frequency domain of modes is updated using Weiner filter with the center as the current center frequency, and the corresponding mode update is obtained as:

    $$\begin{aligned} \begin{aligned} \hat{m}_n^{j+1}(\varvec{\omega })=\left( \hat{I}(\varvec{\omega })-\sum _{i \ne n} \hat{m}_i(\varvec{\omega })+\frac{\hat{\lambda }(\varvec{\omega })}{2}\right) \frac{1}{1+2 \alpha _n\left| \varvec{\omega }-\varvec{\omega }_n\right| ^2} \\ \forall \varvec{\omega } \in \Omega _n: \Omega _n=\left\{ \varvec{\omega } \mid \left\langle \varvec{\omega }, \varvec{\omega }_n\right\rangle \ge 0\right\} , \end{aligned} \end{aligned}$$
    (2)

    Here, \(\hat{m}_n(\varvec{\omega })\) represents the frequency domain sub-image/mode, \(\hat{I}(\varvec{\omega })\) represents image in frequency domain, \(\alpha\) is data fidelity constant, \(\lambda\) denotes Lagrangian multiplier, and j is the iteration number. The first few modes are updated with lower frequencies capturing the overall structure and outline of the ultrasound B-mode image with slow changes in intensity and texture. While the higher order modes are updated with higher frequencies that represent the finer details with rapid fluctuations in intensity and texture. In the context of breast lesions, the first few modes provide softer boundaries of the lesion and the higher order modes provide the sharp edges and details of the area surrounding the lesion.

  2. 2.

    Minimization with respect to center frequencies \(\omega _n\) : Center frequencies are obtained based on the first moment of the corresponding mode’s power spectrum \(\left| \hat{m}_n(\varvec{\omega })\right| ^2\) on the spectral half plane \(\Omega _n\) as:

    $$\begin{aligned} \varvec{\omega }_n^{j+1}=\frac{\int _{\Omega _n} \varvec{\omega }\left| \hat{m}_n(\varvec{\omega })\right| ^2 d \varvec{\omega }}{\int _{\Omega _n}\left| \hat{m}_n(\varvec{\omega })\right| ^2 d \varvec{\omega }} \end{aligned}$$
    (3)

    The center frequencies of the sub-images vary from low to high values as the number of sub-images increase.

  3. 3.

    Maximization with respect to the Lagrangian Multiplier \(\lambda\): Lagrangian multiplier in the unconstrained formulation is updated using a conventional gradient ascent with fixed time step \(\tau\) as:

    $$\begin{aligned} \lambda ^{j+1}(\varvec{z})=\lambda ^j(\varvec{z})+\tau \left( f(\varvec{z})-\sum _n m_n^{j+1}(\varvec{z})\right) , \end{aligned}$$
    (4)

    where the term in the parentheses denotes the data residual.

The all-inclusive algorithm is provided as the ADMM optimization of 2D-VMD in algorithm 145.

Algorithm 1
figure a

Pseudocode for 2D-VMD.

Full size image

Decomposition of breast ultrasound images using 2D-VMD

In this section, we introduce the use of 2D-VMD with selective design parameters for the decomposition of ultrasound images with breast lesions such that the distinctive features are captured in one or more modes. Let I(z) denote an input B-mode image to be decomposed. The decomposed modes using 2D-VMD can be expressed as:

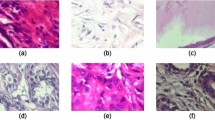
$$\begin{aligned} m_n\{z, f, \omega \}= V M D\{I(z)\} \end{aligned}$$
(5)

The two method parameters i.e, data fidelity constant (\(\alpha\)) and number of modes (N) need to be selected exhaustively for obtaining the required features in the decomposed modes. \(\alpha\) determines the admissible bandwidth in each mode, and the adequate number of modes helps in maintaining the appropriate distribution of energy of the image. Based on an extensive experimental evaluation, \(\alpha\) and N are selected as 500 and 4 respectively for capturing the distinctive features of benign and malignant lesions in breast ultrasound images. Figure 2a and b illustrate the decomposed modes of two example images with benign and malignant lesions respectively, with these method parameters. It can be observed from the figure that for both images, the first mode is able to capture the complete structure of image with lesion. Further, for the benign lesion, modes 2 and 4 display the definite lesion boundaries, whereas, the malignant lesion is captured in the third mode with improper boundary. This aligns with the fact that benign lesions have more definite boundaries as compared to malignant lesions. Further, the textural differences between the modes in benign and malignant lesions are notable. Therefore, it can be demonstrated that 2D-VMD modes are discriminatory for benign and malignant lesions. Further, it can also be observed that there are modes which have regular texture throughout the image, and thereby, do not contain relevant information, such as, mode 3 for benign, and modes 2 and 4 for malignant case. We discard these modes from the analysis for smooth learning process of the proposed deep learning network. For this purpose, we propose an entropy-based exclusion criteria, which first estimates the entropy of each mode of an image, and then rejects the mode with minimum entropy value. The selection of entropy is based on the fact that the mode which captures lesion, will have irregularities in the overall textural structure, while the one with uniform texture does not contain relevant features of the lesion area. The mathematical description of this criteria is provided as follows.

  • Firstly, Entropy estimation is performed for each mode of the mode/ sub-image, as:

    $$\begin{aligned} E t_{m_{n i}(z)}=-\operatorname {sum}\left( h_{m_{n i}(z)}^p \cdot * \log 2\left( h_{m_{n i}(z)}^p\right) \right) \end{aligned}$$
    (6)

    where \(h_{m_{n i}(z)}^p\) denotes the histogram counts representing the distribution of pixel values of the \(n^{th}\) mode of \(i^{th}\) image, i.e., \(m_{ni}\).

  • Reject the mode \(m_{n i}(z)\) , if:

    $$\begin{aligned} \begin{aligned}&E t_{m_{n i}(z)}=\min \left( \varvec{E} \varvec{t}_{\varvec{m}_{\varvec{i}}(\textbf{z})}\right) \text{; }&\\ \text{ where, } \varvec{E} \varvec{t}_{\varvec{m}_{\varvec{i}}(\textbf{z})}=&{\left[ E t_{m_{n i}(\textrm{z})} \forall n\right] } \end{aligned} \end{aligned}$$
    (7)

    where [] denotes set.

Fig. 2
figure 2

Illustration of 2D-VMD modes of example images with benign and malignant lesions in (a) and (b) respectively taken from BUSI database: (i) Original image, (ii)-(v) Decomposed modes.

Full size image

In this work, the images and the corresponding selected 2D-VMD modes based on above criteria are used as the inputs to train the proposed deep learning model, as shown in Fig. 1. The proposed model is described in the next sub-section.

Proposed deep learning model

The proposed deep learning model for breast lesion classification is shown in Fig. 1. The layered structure comprises majorly three two-dimensional (2D) depth-wise separable convolutional layers and a 2D convolutional layer along with batch normalization, dropout, and 2D mixed pooling layers with and without weighted sum, a squeeze and excite block, flatten layer, and an output dense layer for classification, as illustrated in Fig. 1. In this sub-section, we describe the functioning of the proposed model layers for classification.

  • The input data, consisting of B-mode images and the corresponding selected 2D-VMD modes are fed to the first layer of the proposed model, i.e., depth-wise separable convolutional layer with 64 filters. This layer performs a two-step convolution operation unlike the standard convolution48,49. Supplementary Fig. S1 illustrates the operation of both standard and depth-wise separable convolutional layers, for an N channel input image with dimensions \(I \times I\) and P \(k \times k\) filters48. It can be observed that for the standard convolution, for each input channel is convolved with a particular filter, and all channels are convolved at the same time. For P filters, the corresponding output dimension is \(I \times I \times P\). While, for the depth-wise separable convolution, it can be observed that the first step involves convolution operation with each channel at a time by dividing each of the prior filters into N \(k\times \times 1\) filters. The second step involves the point-wise convolution operation which is the standard convolution using 1 \(\times\) 1 filters, as shown in the figure. As a result, the overall operation of depth-wise separable convolution helps in reducing the total number of weights and parameters as required by the standard convolution. More details can be found in50. Batch normalization and dropout with a factor of 0.3 is used after this layer to reduce over-fitting.

  • This work proposes the use of mixed pooling operation for down-sampling in the context of breast cancer classification, as shown in the figure. It is a combination of max-pooling and average pooling operation as shown by the dotted block in Supplementary Fig. 2. Mixed pooling helps in capturing the spatial information by adding the average pooling (Avg()) after max-pooling (Max()) and can reduce over-fitting. The feature map after using this operation is denoted as:

    $$l'_{i}=Max(l_{i-1})+Avg(l_{i-1})$$

    where \(l_{i-1}\) represents the output feature map of the preceding layer \(i-1\). The feature map is more localized as compared to that obtained by using only the max-pooling operation. This further helps in extracting more discriminant features between the benign and malignant lesions. Previous related works utilized the conventional max-pooling mechanisms for down-sampling the convolved outputs, while we introduce the use of mixed-pooling for downsampling, which provides more robust and accurate features capturing the global as well as local information for enhancing the breast lesions discrimination. The output of this layer is again fed to a similar block as described previously. Further, it can be observed from Fig. 1 that the corresponding output is fed to a third block, including depth-wise separable convolution2D with 256 filters, batch normalization, convolution2D with 256 filters, batch normalization and dropout followed by a mixed-pooling2D layer with weighted sum. It uses an attention mechanism with sigmoid activation for assigning the weights to the max-pooling and average pooling outputs before adding them together, as shown in Supplementary Fig. 2. The corresponding output is obtained as:

    $$l_{i}=z \times Max(l_{i-1})+(1-z) \times Avg(l_{i-1})$$

    It helps in regulating the outputs of both the down-sampling layers by using the weighted attention mechanism, which further helps in keeping the relevant amount of local and global information about the lesions51. Further, it provides an attention mechanism to select an appropriate combination of max-pooling and average pooling mechanisms for down-sampling the deeper features.

  • The attention-based mixed pooling output is further fed to a second attention mechanism, which uses a squeeze-and-excite-block. This block consists of initial global average pooling layer for squeezing each input feature map to a single scalar value52. These single valued feature maps are further presented as inputs to two dense/fully connected layers with ReLu and sigmoid activation respectively, to estimate the learned weights in the excite phase. Finally, these learned weights are used to scale/multiply the corresponding original input feature maps from the preceding mixed pooling layer, which adds the second attention mechanism and further enhances the relevant features for classification. It boosts the attention mechanism by recalibrating the channel-level features. Finally, it can be observed from Fig. 1 that the output is flattened for converting to a suitable shape, i.e., a vector of dimension 262144 (\(512 \times 512\)) to be given as input to the output dense layer with sigmoid activation for binary classification of breast lesions, i.e., benign (assigned as ’0’) or malignant (assigned as ’1’).

The aforementioned layers are used to build the proposed network in TensorFlow Keras 2.2.1 deep learning framework in Python. Keras Tuner is utilized to select the optimal number of layers and combinations based on the optimal performance. The data is split into 80% training, 10% for validation, and 10% for testing. The training hyper-parameters such as batch size, epochs, steps per epoch, learning rate and algorithm, are discussed in the later section.

Results

This section discusses about the performance assessment of the proposed framework for classification of breast lesions in ultrasound images. Firstly, we describe the different datasets used in this work. Secondly, we present the different learning parameters and classification metrics for analysis of the proposed model. Thirdly, we analyze the proposed framework without using 2D-VMD for demonstrating the effectiveness of 2D-VMD. Finally, we compare the framework with some of the commonly used recent methods for breast lesion classification.

Datasets

This section provides a description of the two public datasets and an in-clinic dataset utilized in this study.

UDIAT dataset

This is the first public breast ultrasound dataset used in this work. It consists of 163 B-mode images with 110 benign and 53 malignant lesions, and only one lesion per image53. The data was acquired using Siemens ACUSON Sequoia C512 system 17L5 HD linear array transducer with a frequency of 8.5 MHz, at the UDIAT Diagnostic Centre of the Parc Taul’ı Corporation, Sabadell (Spain). All images were \(760 \times 570\) pixels in size and pre-processed for noise removal. The ground truth segmented masks were obtained from the manually segmented lesions by experienced radiologists in this dataset53. This data is available for research purposes only after request from the authors in53.

Breast ultrasound images (BUSI) dataset

The second public breast ultrasound dataset consists of 780 B-mode images including 437 benign and 237 malignant lesions, and 133 normal cases54. The data was acquired from 600 female volunteers with ages ranged between 25 and 75 years, using LOGIQ E9 and LOGIQ E9 Agile ultrasound system with \(1-5\) MHz transducers on ML6-15-D matrix linear probe, at Baheya hospital, Cairo, Egypt54. It is available at https://scholar.cu.edu.eg/?=afahmy/pages/dataset. All images were \(500 \times 500\) pxels in size, and pre-processed for artifact removal. For maintaining uniformity across all datasets used in this work, we analyzed the images containing only one lesion per image, and discarded the ones with multiple lesions. Therefore, the number of images was 421 for benign and 209 for malignant cases, leading to total 630 images.

In-hospital recorded (IHR) dataset

The third dataset is a private breast ultrasound imaging dataset consisting of 2205 B-mode images with 1315 malignant and 890 benign lesions. The data was acquired from 655 female volunteers on multiple days, with each volunteer having a pre-biopsy scan, and three post-biopsy scans. The data was collected using the Supersonic Imagine Aixplorer (SSI, Aix-en-Provence, France) system with a 4-15 MHz array transducer, at Mayo Clinic, USA. The institutional review board approval (IRB:12-003329 and IRB: 19-003028)) was received in compliance with the Health Insurance Portability and Accountability Act along with signed written informed consent with permission for publication from each enrollee prior to this study. Four B-mode image acquisitions were performed with two each in the longitudinal and transverse orientations. Some images were duplicated, and thereby needed to be removed from the analysis, resulting in 2066 images in total. All images were stored in PNG format. Each image was \(1400 \times 1050\) in size, and were kept without prior processing for any type of artifact removal, for the purpose of analyzing the robustness of the proposed framework with respect to artifacts.

Training hyper-parameters

For adequate training of the proposed network, different learning hyper-parameters and number of layers are used in this work. For this purpose, Keras tuner is used to automatically select the parameters based on optimal performance. These include dropout rate of 0.3, filter width of \(3 \times 3\), stride of 1, batch sizes of 8 and 16, epochs between \(150-250\), and squeeze-and-excite ratio of 2. Besides these, Adam is used for optimization of the network, with a learning rate of 0.00001.

Classification performance metrics

For analyzing the performance of the proposed framework, a train-validation-test split of 80%-10%-10% respectively is utilized for all the datasets in this work. To deal with the the class-imbalance in the datasets, binary focal cross entropy loss function is used during the training process for performance evaluation of classification task55. Further, it enhances the performance by focusing more on hard training samples55. For assessment of the proposed model, different standard classification metrics are used, such as, Accuracy (Ac), Precision (Pr), sensitivity/recall (Se), specificity (Sp), area under receiver operating characteristics (ROC) curve (AUROC). Further, we examine the area under precision recall curve (AUPRC) for analyzing the performance with respect to false positives and class imbalance. Description of these metrics is provided in56,57. Further, the confusion matrices are also presented for analyzing the class-wise performance of all datasets used in this work.

Table 1 Performance metrics of the proposed framework.
Full size table

Performance analysis

Table 1 and Fig. 3 show the performance metrics and confusion matrices of the proposed framework respectively for breast lesion classification in all the three datasets used in this work. It can be observed from the table that for the public dataset UDIAT, the overall classification performance is highest, with an accuracy of 0.98, indicating that the proposed method is able to classify most of the breast lesions correctly. Further, it can be observed that the specificity, AUROC and AUPRC are all 1, which demonstrates that all benign lesions are predicted correctly. Further, the confusion matrix in Fig. 3 (a) for this dataset shows that there are no false positives and only one false negative, which demonstrates the outstanding classification performance of the proposed framework for this dataset. For the BUSI dataset, the overall classification accuracy is 0.93 and the areas under both curves are above 0.95, which indicates that the capability of the proposed framework in classifying the lesions with high performance for this dataset. However, it can be observed from the confusion matrix Fig. 3 (a) that the overall false positives are higher than the false negatives, however, the balance between the sensitivity and precision is still better, as indicated by AUPRC value of 0.98. Finally, for the IHR data, the performance is slightly low, however, it can be observed from the Table 1 and confusion matrix in Fig. 3 that the number of falsely detected malignant cases are lower, indicating a fair specificity, although the sensitivity is quite low. This may attribute to the presence of non pre-processed images in this dataset. However, the overall fair performance indicates the noise robustness capability of the proposed framework.

Fig. 3
figure 3

Confusion matrices for (a) UDIAT, (b) BUSI, and (c) IHR datasets. Here, False denotes Benign class, and True denotes malignant class.

Full size image

We analyze the variability of different parameters and classification performance metrics across the three datasets in Supplementary Table 1. We estimated the statistical parameters such as the standard deviation (SD) and the inter-quartile range (IQR) of the total number of images, number of benign and malignant images, and the classification performance metrics across the datasets. Substantial variations were observed in the number of images with a SD of 804.16 and IQR of 951.5. Similar variations can be noted for the number of benign and malignant images across the datasets. Further, the classification performance variability demonstrates higher SD (0.08 and 0.06) and IQR (0.09 and 0.08) for Se and F1 respectively, while lower values (SD: 0.02, IQR: 0.03) for AUROC.

Effectiveness of 2D-VMD

In this sub-section, we analyze the performance of the proposed framework without using the 2D-VMD prior to the deep learning network training. Figure 4 shows the AUROC curves obtained with and without 2D-VMD for all datasets used in this work. We also show the AUPRC curves in Supplementary Fig. 3. It can be observed that there is a considerable decrease in the areas under these curves when the proposed framework is built without 2D-VMD. Since, the proposed network trains from the raw B-mode images which makes it slightly difficult for the model to extract more effective high level features, the dip in the performance is expected. These results further demonstrate that 2D-VMD can extract more representative discriminatory feature modes which can guide the deep learning network for obtaining enhanced feature maps, resulting in improved classification performance.

Fig. 4
figure 4

AUROC curves for: (a) and (b) UDIAT dataset with and without using 2D-VMD respectively, (c) and (d) BUSI dataset with and without using 2D-VMD respectively, (e) and (f) IHR dataset with and without using 2D-VMD respectively.

Full size image

Comparison with state-of-the-art methods

The proposed framework was analyzed with respect to some of the commonly existing methods for breast lesion classification in this sub-section. We present the comparative evaluation results for the two public datasets followed by that for the in clinic data. Table 2 shows the lesion classification accuracies and other metrics reported by some of the existing works for the two public datasets used in this work. It can be observed that for the UDIAT dataset, the proposed framework outperformed the existing methods in terms of classifying the lesions, with a considerable increase in all metrics. For the BUSI data, the proposed framework performed comparable classification with respect to a few existing methods and outperformed rest of the methods. Since most of the methods reported accuracy, we further estimated the improvement in accuracy of the proposed method with respect to these methods. For the existing dataset UDIAT, the proposed method achieved improvements in the range of \(4-32\%\) relative to these existing state-of-the-art methods, with a mean improvement (standard deviation) of \(14.37\% (8.42\%)\). While for BUSI, the proposed method was comparable to two existing state-of-the-art methods based on hybrid of Alexnet, MobilenetV2, Resnet5030 and spatial attention with Resnet1840, and achieved improvements in the range of \(2-13\%\) relative to the remaining existing state-of-the-art methods, with a mean improvement (standard deviation) of \(5.75\% (4.52\%)\).

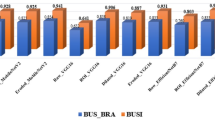
Table 2 Comparative analysis of state-of-the-art methods with respect to the proposed method for breast lesion classification.
Full size table

For the in-clinic data, we implemented some of the commonly used deep learning models in27,28,29,36,39 among others to assess the proposed framework, and the corresponding accuracies obtained are presented in Fig. 5. These models are selected based on their wide usage and ease of implementation. It is clearly observable from the figure that the proposed framework outperforms these existing models for the IHR data. We further estimate the total number of model parameters and the floating point operations (FLOPS) required by each model for analyzing the corresponding computational complexities. Figure 6 presents these values for all implemented models and the proposed model. It is evident from the figure that the proposed model achieves the classification with a considerable reduction in the parameters and FLOPS with respect to existing methods. We further estimated that the proposed method achieved a reduction of \(44-99\%\) in parameters and \(18-97\%\) in FLOPS as compared to existing methods. These results demonstrate the superiority of the proposed framework with respect to the existing deep learning networks in terms of performance as well as computational complexity.

Fig. 5
figure 5

Comparison results of the proposed framework with some common methods for breast lesion classification for IHR data. Note: P denotes pre-trained.

Full size image
Fig. 6
figure 6

Computational complexities of the proposed framework and some common methods for breast lesion classification for IHR data: (a) Total number of model parameters, (b) FLOPS. Note: P denotes pre-trained.

Full size image

Interpretability of the proposed network

To further analyze the proposed network, we extract the feature maps of the intermediate and final layers for two example cases of benign and malignant lesions. Supplementary Fig. 4 demonstrates these maps for some intermediate layers and the final layer. It can be observed that the average pooling focuses on the general features of the depth-wise separable convolution output while max pooling focuses on the localised features as indicated by slightly higher contrast and activations (darker areas). Mixed-pooling output has a contrast between the average and max pooling outputs. The fourth depth-wise separable convolution output has lower activations (lighter areas) for the lesion area and some background pixels. It shows the differences at pixel-level for lesion and the surrounding areas. Further, the weighted sum mixed pooling output demonstrates a higher contrast and activations for lesion area and some surroundings. It can also be observed that the preceding max pooling output is weighted more as as indicated by higher activations with respect to the average pooling output. The activations for benign lesion are observed to be lower as compared to malignant lesion. The squeeze-and-excite output slightly refines the activations which are flattened to a vector. Finally it can be observed that the amplitudes of the samples of the flattened vector are small for benign and higher for malignant cases. This output is converted to probability values of “(\(1.22 \times 10^{-33}\))” for benign and “1” for malignant, by the sigmoid activation. This demonstrates the explicability of the proposed network layers to classify the lesions.

Discussion

The proposed framework is rigorously evaluated by using two different public datasets and a private dataset without any prior processing. The corresponding performance metrics highlight its effectiveness across all three datasets. While performance on the IHR dataset is marginally lower compared to the other two datasets, it remains robust. This indicates that our framework maintains a reliable performance, even on the data without any prior pre-processing. It can be observed that the framework is able to achieve a high specificity with a minimal trade-off in the sensitivity, as indicated by the AUPRC values. This shows promising results of using deep learning with variational modes that can potentially guide radiologists in identifying pathologies with more accuracy. We also demonstrated the confusion matrices for all datasets for a thorough analysis and performance visualization of the proposed framework. The indication of low false positives for UDIAT and IHR data from these matrices demonstrates the capability of the framework toward reducing benign biopsies. Further, since the benign lesions are high in number as compared to malignant lesions, the trade off between the false positives and false negatives is justifiable. The high variability in sensitivity and F1 score across the datasets attributes to the corresponding high variability in the number of benign and malignant lesions as well as total images across the datasets. Alternatively, since the number of images were highly dispersed across the datasets along with some inconsistencies such as noisy images in IHR versus the public datasets, there were performance fluctuations across the datasets. However, the AUROC values were consistent across the datasets.

This study presents another exhaustive analysis of the proposed deep learning network with and without using 2D-VMD in Fig. 4 and Supplementary Fig. 3. A higher steepness is observed in the ascent towards the left upper corner in Fig. 4 for all datasets in the presence of 2D-VMD as compared to that in its absence, which affirms an excellent trade-off between sensitivity and specificity with 2D-VMD. This is essential in clinical practice, where missing a diagnosis is much more unacceptable than false positive. Supplementary Fig. 3 shows the AURPC, which is a more informative parameter in situations of class imbalance compared to the AUROC curve, and thereby it could further assert the model’s precision in identifying true positive cases. It can be observed that it also showed a high precision across a range of real levels with 2D-VMD as compared that without it, which is another important factor in a clinical context where a false positive may lead to unnecessary invasive or expensive procedures. Thereby, the effectiveness of 2D-VMD in improving the performance of deep learning model is clearly evident from these results. Finally, we compared our proposed framework with some of the common DL networks reported in recent studies. Firstly, we selected the corresponding existing studies utilizing the two public datasets UDIAT and BUSI, and presented the classification accuracies reported by these works in Table 2. It is assertive that the proposed framework performs significantly better on UDIAT data, and marginally closer to that for the BUSI data. Further, we implemented some of the common DL models for IHR after experimentally selecting them based on their adaptations in literary works. The corresponding results in Fig. 2 and 6 exhibit the capability of our framework in surpassing the existing models in terms of classification performance and computational complexity.

The integration of 2D-VMD with DL for breast lesion classification can be a unique contribution to the field of ultrasound image classification, unlike most of the recent related studies. For example, the ensemble convolutional neural network (CNN) employed in the study of W. K. Moon et al. in27, has demonstrated the effectiveness of image fusion in classification tasks, however, the image decomposition techniques still remain unexplored. Furthermore, the weakly supervised approach in the model developed by J. Kim et al. in26, leverages class activation mapping to alleviate the need for detailed annotations, however, it failed to address the potential of signal processing methods to further refine the discriminatory features. The multi-scale kernel approach in the model developed by X. Qi et al. in34, highlighted the potential benefits of architectural innovation in complementary neural networks, however, our study demonstrates on the other hand that the decomposition-based feature enhancement can simplify the architecture of the DL models. Further, in comparison with the the multi-view learning strategy introduced in42, our study underscores the substantial impact of pre-processing strategies on model performance. The utilization of 2D-VMD has led to a perceptible increase in both AUROC and AUPRC values, which suggests that the approach utilized in the proposed study, successfully captures nuanced features in ultrasound images unlike the traditional DL models. The methodical divergence illustrates the multifaceted approaches for the collective goal of advancing diagnostic accuracy in medical imaging, where each study might contribute to a gathered understanding and improvement of ML application in clinical settings.

The proposed DL model is less complex with respect to the existing traditional models in terms of the total number of layers, parameters, and operations. An expected outcome is that it can facilitate a quicker training process, and moreover, enhance the model’s feasibility for real-time applications. A potential clinical impact of this outcome is that it prioritizes timely diagnosis of malignant lesions. Further, our dual-stage approach, which starts with discriminative low-level feature extraction using 2D-VMD, followed by a high-level feature extraction and classification, demonstrates the ability of the proposed framework to process breast ultrasound images efficiently and with lower computational demands. This can deliver high performance without extensive computational and time complexity, which are typically associated with DL models. Another expected outcome of our approach is that it can detect the benign lesions more precisely with a potential clinical impact of minimizing the unnecessary biopsies for benign lesions. Finally, the activation maps demonstrate the interpretability of the proposed network unlike the existing networks which lack in explainability, towards classification outcomes. In the future direction, we plan to incorporate a larger private dataset for validating our proposed framework. In addition to that, we plan to test the proposed framework in real time to test its efficacy in clinical settings. Further, the proposed method can be adapted to other imaging modalities, such as, 2D magnetic resonance imaging (MRI), computed tomography (CT), and mammography. For these adaptations, slight parameter modifications may need to be done for the VMD and the deep learning network depending upon the initial experimental assessment.

Conclusion

In this study, a novel variational mode directed deep learning framework is proposed for ultrasound-based breast lesion classification. An exhaustive evaluation using two public datasets and an in-clinic dataset demonstrates the proficiency of the proposed framework in classification of breast lesions. The utilization of 2D-VMD with a low complex deep learning model demonstrates a considerable improvement in the overall classification performance by enhancing the discriminatory features obtained in the variational modes. The comparative evaluation of the proposed framework with respect to some of the reported networks for public datasets indicate the supremacy of the proposed framework. Further implementations of the recently used networks on the in-clinic data demonstrate the superiority of the proposed framework. Finally, the low complexity of the DL model with only a few convolutional layers demonstrates its suitability for real-time breast lesion classification.