Introduction

The fracture behavior of quasi-brittle materials such as concrete plays a crucial role in structural engineering, as crack propagation significantly affects durability and safety. Unlike purely brittle materials, concrete exhibits a fracture process zone (FPZ), where micro-cracks develop before failure, leading to nonlinear fracture behavior that differs from classical linear elastic fracture mechanics1,2,3,4,5. Several analytical and computational models have been developed, such as the Cohesive Zone Model, which effectively simulates FPZ development and nonlinear crack propagation, and Bazant’s size effect law, which explains the dependence of fracture toughness on specimen size1,2,3,4,5. Furthermore, finite element methods (FEM) and extended finite element methods (XFEM) provide detailed numerical simulations of crack propagation under complex loading conditions1. On the other hand, Zhang et al.2 examined the phase-field model for numerical simulation of mixed-mode fracture behavior of concrete beams with zigzag notches. They2 concluded that some discrepancies between the simulation and experimental results were observed due to the simplifications in the model. Fallahnejad et al.3 evaluated the fracture behavior of recycled aggregate concrete under varying water-to-cement ratios using work-of-fracture and size effect methods, highlighting that lower water-to-cement ratios increase fracture energy and reduce brittleness. The tensile and shear fracture behaviors of slag-based geopolymer mortars with recycled fine aggregates revealed that greater recycled aggregate content and notch-to-depth ratios increased brittleness and reduced fracture energy, particularly in Mode II loading4. De La Rosa et al.5 demonstrated in their experimental study that incorporating steel fibers into self-compacting concrete with longitudinal reinforcement improved ductility, delayed brittle failure, and enhanced energy absorption under mixed-mode fracture conditions.

Various experimental, analytical, and numerical methods have been developed to investigate the fracture of quasi-brittle materials, each offering unique insights into crack initiation, energy dissipation, and failure mechanisms6,7,8,9,10. It has been found that modified maximum tangential stress (MMTS) and generalized maximum tangential strain (GMTSN) criteria refine fracture analysis by incorporating higher-order stress terms and mode mixity effects6,7. Salehi et al.8 agreed well between the fracture toughness behavior measured from SCB specimens and the theoretical predictions of the MMTS criterion. Bahrami et al.9 found that optimizing the equivalent material concept with the GMTS criterion improves failure predictions in 3D-printed components. These findings contribute to ongoing advancements in additive manufacturing, particularly improving mechanical integrity for structural applications. They also found that9 while annealing minimally affected the yield strength, it significantly enhanced fracture toughness, energy absorption capacity, and reduced anisotropy. Among experimental techniques, the single-edge notched, cracked Brazilian disc, and semi-circular bend (SCB) specimens are widely adopted to evaluate fracture toughness, crack growth, and mode mixity effects (Mode I, Mode II, and Mixed-mode I/II). On the other hand, digital image correlation, scanning electron microscopy, and acoustic emission analysis provide real-time imaging and microstructural insights into crack evolution10. Machine learning-based predictive models have emerged as innovative tools for data-driven fracture behavior analysis8. Beyond laboratory testing, full-scale structural tests on large concrete beams and slabs are valuable for assessing fracture behavior in real-world applications11.

Many researchers use SCB specimens to investigate the Mixed mode I/II crack growth behavior12,13,14,15,16,17,18,19,20. Song et al.12 analyzed the size effect on the Mode I fracture behavior of hot mix asphalt using SCB tests. The study demonstrated that larger specimens exhibit higher fracture toughness, supporting the size effect law. Ayatollahi et al.13 introduced an improved SCB test method for evaluating brittle fracture under mixed-mode conditions. Aliha et al.17 and Lim et al.19 used SCB specimens to investigate the mixed-mode fracture toughness of asphalt mixtures and rock materials, respectively. Aliha et al.14 used edge-cracked and uncracked SCB specimens subjected to three-point bending to evaluate Mode I fracture toughness, KIc, and the tensile strength, σt, for chopped strand glass fiber reinforced polymer concrete. They found that cracked and uncracked SCB specimens are suitable for measuring KIc and σt in polymer concrete. Lim et al.19 utilized the SCB specimen under three-point bending to determine the rocks’ Mixed-mode (I and II) fracture toughness envelope. They concluded that the mode II loading increased when the span length decreased or the length and crack angle increased. Adamson et al.21 used the weight function method to obtain the stress intensity factor (SIF) and crack opening displacement (COD) expressions for single-edge cracks in SCB specimens.

The development of cracks in concrete structures can significantly impact their strength and durability. One effective method employed to resist and minimize crack propagation during various loading conditions is to add different types of fibers into the concrete mixture during the manufacturing process of these structural elements. Over recent decades, Fiber-reinforced concrete (FRC) has emerged as a focal point of interest within the construction industry, as it integrates fibers to enhance crack resistance. FRC composites have been employed to enhance the effectiveness of conventional concrete materials22. FRC has attracted considerable attention for its ability to improve the fracture toughness and ductility of high-strength concrete (HSC)22,23. These fibers, available in various materials, shapes, and sizes, serve multiple purposes. They primarily reinforce the concrete and help prevent cracking, particularly during the initial setting and drying phases, while also reducing water permeability and bleeding. Notably, large steel or synthetic fibers can replace traditional steel reinforcement bars23. Adding fibers to concrete was expected to have a positive effect, similar to how aggregates help decrease bridge cracks24. The effectiveness of these fibers within the concrete mix depends on factors such as their material composition, geometric properties (including shape, length, longitudinal profile, and diameter), and the quantity added.

Recently, Shaaban et al.25 introduced a method aimed at refining the management of multi-level cracking in reinforced concrete beams to enhance their ductility, toughness, and failure modes through the application of fiber hybridization. A crucial aspect in this area involves calculating the SIF to simulate concrete fracture behavior, serving as the primary method26,27. Over time, numerous studies have led to the development of various concrete fracture models, facilitating the assessment of concrete cracking resistance using fracture mechanics techniques26,27. The initiation of concrete cracking occurs when the SIF approaches the fracture toughness value, prompting extensive study to assess concrete’s fracture toughness under differing constituent mixing ratios27,28. Fracture mechanics has evolved significantly, with applications extending to concrete beams for determining fracture toughness29. Various research groups have proposed numerous fracture models to examine the nonlinear behavior of concrete27,30,31. Notably, through statistical analysis, Ding32 established a correlation between mid-span deflection and crack mouth opening displacement (CMOD) in cracked FRC beams, revealing a linear relationship. On a different front, Zhang and Li33 used a fracture mechanics approach to numerically solve a model based on a partial differential equation describing bridged cracks that were proposed by Cox and Marshall34 to simulate the propagation of Mode I fracture in FRC uncracked beams. They suggested that the CMOD, which includes both CMOD and elastic deformation inside the extensometer’s gauge length, may be indirectly measured by the extensometer positioned in the middle portion of the beam’s tensile side. Their results showed that, in terms of load-CMOD curves, there was excellent agreement between model predictions and experimental outcomes.

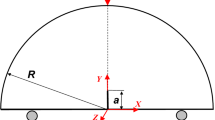
The present work aims to investigate the Mixed mode I/II fracture behavior of high-strength concrete (HSC) and polypropylene fiber reinforcement concrete (PPFRC) experimentally and numerically using the SCB specimen with various diameters (2R) and thicknesses (t). The mode of mixity can be obtained in the SCB specimen by changing the position of the right support (S2/S1), as shown in Fig. 1. In the case of pure Mode 1, i.e., Mode II = 0, (S2/S1) = 1, while Mode II increased with decreasing (S2/S1). The flexural and fracture toughness tests were conducted in the present work to obtain the flexural and fracture behavior of the HSC and PPFRC. Furthermore, the effect of geometry and sizes of SCB specimens on the flexural behavior of smooth (uncracked) specimens, and fracture energy and fracture toughness of HSC and PPFRC under pure Mode I and mixed mode loading using the AASHTO (TP 105–13 (2015) standard test35 were investigated experimentally and numerically.

Fig. 1
figure 1

Geometry of SCB specimen.

Full size image

Experimental work

Materials

Ordinary Portland cement (OPC), which satisfies the specified requirements of Type I Portland cement according to the ASTM C15036, was used in this research to produce two types of concrete: HSC and PPFRC.15% silica fume with a specific gravity of 2.3 and 1.5% type F superplasticizer (SP) were used. Natural sand and coarse aggregate, with a specific gravity of 2.6 and 2.68, respectively, were used in the concrete mixture. The maximum size of the coarse aggregate was 9.5 mm. The mix proportion of concrete is shown in Table 1.

Table 1 Mix proportion of concrete for 1m3.
Full size table

Specimen preparation

Cubes with dimensions of 100 × 100 × 100 mm and cylinders of 100 mm in diameter and 200 mm in height were prepared to be tested by a static compression test according to ASTM C3937. Cylinders of 100 mm diameter and 200 mm height were cast and tested to determine the indirect tensile strength according to the ASTM D3967-95a38. Beams with dimensions of 10 × 10x300 mm were cast and tested under flexural load to determine the flexural strength according to ASTM C 293–0239. The mechanical properties test setups are shown in Fig. 2.

Fig. 2
figure 2

Mechanical properties test setup: (a) compression test for cylinders, (b) indirect tension test, and (c) three-point bending test.

Full size image

To study the size effect on the flexural and fracture behavior of HSC and PPFRC, smooth (uncracked) and cracked SCB specimens with three different radii (R) and three different thickness-to-radius ratios (t/R) for each radius were cast. It is worth noting that the SCB specimen suggested by AASHTO (TP 105–13 (2015) standard test35, i.e., R = 75 mm, t/R = 0.33, and the crack-to-radius a/R = 0.2, was adopted in the present study. Accordingly, the three values of R were 50, 75, and 100 mm, and the three values of t/R were 0.33, 0.66, and 1 for each R for both uncracked (a/R = 0) and cracked (a/R = 0.2) SCB specimens. At least four specimens were cast for each test to ensure the reliability of the results. The specimens were left 24 h in the molds after cast, then removed from the molds and cured in a water tank for 28 days, as shown in Fig. 3. The specimens were tested using a universal testing machine with 2000 kN maximum capacity calibrated annually.

Fig. 3
figure 3

Test specimens:(a) flexural test specimens, (b) indirect tensile test specimens, (c) SCB specimens, and (d) curing of SCB specimens.

Full size image

Test variables

The SCB specimen was chosen due to its simple geometry and ease of loading with different modes of mixites, providing several advantages for experimental investigation. Figure 4 illustrates the loading conditions of the SCB specimens. Different modes of mixites can be achieved by varying the loading span ratio (S2/S1). The S1/R ratio was preserved as a constant and equal to 0.8 for all SCB specimens, and the span ratio (S2/S1) varied within values of 0.18, 0.34, and 1. When S2 equals S1 (S2/S1 = 1), pure Mode I (opening mode) is obtained, while Mode II appears when S2 is less than S1, as described in references40,41. In the case of pure Mode I SIF (KI), KI is defined according to AASHTO TP10535 as:

Fig. 4
figure 4

Geometry and loading conditions of SCB specimens.

Full size image
(1)

Where YI is defined as the normalized mode I SIF or the geometry correction factor:

(2)

where,

\({\sigma }_{ap}=applied stress \frac{P}{2Rt}\) , P = applied load, R = specimen radius, t = specimen thickness, and a = crack length.

In the case of mixed mode SIF (KI and KII), Eq. (1) can be generalized as follows13:

(3)

It is clear from Eq. (3) that Yi, i.e., YI and YII, is assumed to be a function of only a/R and S2/S1. Then, the effective SIF (Keff) can be calculated by the following equation:

$${K}_{eff}=\sqrt{{K}_{I}^{2}+{K}_{II}^{2}}$$
(4)

Marsavina et al.42 predicted the geometry correlation factors (YI and YII) numerically based on the given data (R = 40 mm, a/R = 0.5, S1/R = 0.8, S2/S1 = 1, 0.4, 0.267, 0.2, 0.133, and 0.09) through the following equations:

$${\text{Y}}_{{\text{I}}} = { 6}.{2347}({\text{S}}_{{2}} /{\text{R}})^{{3}} - { 15}.0{69}({\text{S}}_{{2}} /{\text{R}})^{{2}} + { 17}.{229}({\text{S}}_{{2}} /{\text{R}}) \, - { 1}.0{618}$$
(5)
$${\text{Y}}_{{{\text{II}}}} = { 1}.{884}({\text{S}}_{{2}} /{\text{R}})^{{5}} - { 7}.{3}0{88}({\text{S}}_{{2}} /{\text{R}})^{{4}} + { 5}.0{375}({\text{S}}_{{2}} /{\text{R}})^{{3}} + { 2}.{7796}({\text{S}}_{{2}} /{\text{R}})^{{2}} - { 5}.0{751}({\text{S}}_{{2}} /{\text{R}}) \, + {1}.{9831}$$
(6)

Table 2 summarizes the configuration of SCB specimens. The identifications of SCB specimens were as follows: SCBR-N-T/M where R refers to SCB radius (5, 7.5, and 10 cm), N refers to a/R ratio (0 and 0.2), T refers to t/R ratio (0.33, 0.66, and 1), and M refers to S2/S1 different modes of mixites (0.18, 0.34, and 1).

Table 2 Specimen configuration to simulate Mode I and Mixed mode I/II.
Full size table

Numerical work

The fracture behavior of HSC and PPFRC was investigated using ABAQUS/Explicit and ABAQUS/Standard three-dimensional finite element codes43. The main objective of the present numerical analysis is to assist in determining the mixed mode fracture toughness of HSC and PPFRC, i.e., the effective SIF Keff, using the ultimate load obtained from the experimental test and the geometry correlation factors (YI and YII) obtained numerically. The concrete material was assumed to be homogeneous and elastic with isotropic behavior. The mechanical properties of HSC and PPFRC, which are needed as input data in the numerical analysis, such as modulus of elasticity, E, and Poisson’s ratio, are taken from the experimental results. The meshes were constructed with hexagonal structural mesh and C3D8 (8-node linear brick) elements. Approximately 30,000 elements were used in the current model. The size of the elements decreased gradually with decreasing the distance from the tip of the notch, as shown in Fig. 5.

Fig. 5
figure 5

Typical finite elements mesh idealization of the SCB specimen.

Full size image

XFEM was used to simulate the fracture crack propagation in different mixed modes. The crack growth path for different SCB specimen sizes was predicted using the extended FEM (XFEM) method, and then it was compared with the experimental crack path to validate the present model. XFEM describes the crack initiation and propagation according to the maximum principal stress criterion of inelastic-brittle material. The XFEM technique relies on phantom nodes to represent the discontinuity of cracked elements once the fracture criterion is met. These phantom nodes become detached when the equivalent strain energy release rate surpasses the critical strain energy release rate at the crack tip44.

Furthermore, the contour integral method, which can involve blocking each node along the crack path from the crack face to the opposite crack face for the material neighboring, was used in the present work to obtain the Mode I and mixed mode stress intensity factors. In linear elastic fracture mechanics, SIFs identify the local crack-tip/crack-line stress and displacement fields. J-integral values can be obtained from ABAQUS/Standard, and then the SIF can be calculated through the following Equation: \(J=\frac{{K}^{2}}{E}\), where E is the modulus of elasticity.

Validation of the numerical results

Firstly, the accuracy of the present model in predicting the Mode I fracture toughness (KIc) was made by comparing its results with the corresponding values measured experimentally according to AASHTO TP10535, i.e., based on Eq. (1), as shown in Fig. 6. It can be observed that there is a good agreement between the numerical and experimental results for both HSC and PPFRC. This indicates that the numerical results are reliable, and the present model can be further used to predict the mixed mode fracture toughness. The KIc results generally showed that PPFRC has a higher fracture resistance than HSC.

Fig. 6
figure 6

Comparison between experimental and numerical KIc for HSC and PPFRC.

Full size image

Secondly, to verify the present model in predicting the values YI and YII in different geometries of SCB specimen and mixity modes, a comparison between the predictions obtained from the present numerical model and those suggested by Marsavina et al.42, i.e., Eqs. (5) and (6), at the same circumstances. Figure 7 confirms a good agreement between the present numerical results and the values obtained through Eqs. (5) and (6) 42 as evidence of the accuracy of the present model.

Fig. 7
figure 7

A comparison between the present numerical results of YI and YII and the values obtained from Eqs. (5) and (6).

Full size image

Thirdly, the fracture crack path predicted using the XFEM has been checked for correctness by comparing it with the corresponding present experimental results. Figure 8 shows typical fracture paths on the outer surface of the cracked SCB specimens subjected to Mixed mode I/II loading, both experimentally observed and numerically predicted. Both the experimental and the numerical results showed that the fracture was initiated from the pre-crack tip in all SCB specimen geometries. When S2 equals S1 (mode I), the crack propagated parallel to the applied compressive load, as depicted in Fig. 8. However, when S2 is less than S1 (mode mixity), the crack follows a curvilinear trajectory path and eventually terminates at the location of the applied compressive load. It is clear that the numerical simulation agreed with the experimental results regarding the fracture paths for cracked SCB specimens subjected to Mixed mode I/II loading. These findings are consistent with previous references40,41.

Fig. 8
figure 8

Crack paths on the outer surface of the cracked SCB specimen subjected to mixed mode I/II loading: (a) experimental and (b) numerical.

Full size image

Based on the outcomes of the above three evaluations, the present numerical model can reliably predict the values YI and YII in different geometries. Subsequently, the effective fracture toughness (Keff-c) of HSC and PPFRC can be obtained by substituting the maximum load (measured experimentally) and the values of YI and YII (predicted numerically) in Eqs. (3) and (4). Furthermore, the X-FEM can be performed to show the evolution of the implemented to show the development of the crack front through the specimen thickness at different stages of the crack path for a deeper understanding of the size effect.

Numerical results

Figure 9 illustrates the values YI and YII (at the outer and the middle/inner surfaces) in different geometries (R = 50, 75, and 100 mm, and t/R = 0.33, 0.65, 1) of SCB specimens and different mixity modes (S2/S1 = 0.18, 0.34, and 1) for a/R = 0.2. The value of YI is approximately equal to zero when S2/S1 equals about 0.2 (approximately pure Mode II), while for S2/S1 equals 1 (pure Mode I), it reaches the peak value. On the other hand, YII shows the opposite trend to YI, where the value of YII has the peak value when S2/S1 equals about 0.2 and decreases gradually with the increase of S2/S1 reaching a value of zero in pure Mode I. It is worth noting that there is no difference between the values of YI and YII in the inner plane and those calculated in the outer plane. Furthermore, the values of YI and YII are marginally affected by the specimen size, i.e., the specimen’s thickness and diameter (t/R and R). This finding supports the assumption of Eq. (3), i.e., YI and YII are only functions of a/R and S2/S1. It is clear from the figure that YI and YII intersect at a value that equals unity, i.e., no geometry correction affects the SIFs (YI and YII = 1) at almost the same S2/S1, which equals about 0.25 for all values t/R and R.

Fig. 9
figure 9

Variations of the YI and YII for different R (R = 50, 75, and 100 mm) and t/R (t/R = 0.33, 0.65, 1) at (a) the inner and (b) the outer surfaces of the specimens.

Full size image

Figures 10, 11, 12 show the development of the crack front at different stages of crack paths for two different radii and two different thicknesses at S2/S1 = 0.34. As expected, all three figures show that the crack front development of the pre-crack, which has a straight crack front, commences at the mid-thickness of the specimen without any indication on the specimen surface. This may be due to the absence of ZZ on the surface of the specimen, while the value of ZZ keeps increasing toward the specimen thickness to reach its maximum value, i.e., the plane strain condition. This observation agrees with previous findings in the brittle materials17 and also in the ductile materials45. Once again, neither the crack path nor the crack front development was affected by the specimen size. It can be concluded that the development of the crack front commences at the mid-thickness of the SCB specimen, and then it spreads out along the thickness direction (like a thumb-nail shape) regardless of the specimen thickness and diameter. When the crack reaches the specimen’s surface, more growth happens in the forward direction, and so on.

Fig. 10
figure 10

(a) Crack front development and (b) crack path in SCB specimen by using XFEM for S2/S1 = 0.34, R = 100 mm, and t/R = 0.33.

Full size image
Fig. 11
figure 11

(a) Crack front development and (b) crack path in SCB specimen by using XFEM for S2/S1 = 0.34, R = 50 mm, and t/R = 0.33.

Full size image
Fig. 12
figure 12

(a) Crack front development and (b) crack path in SCB specimen by using XFEM for S2/S1 = 0.34, R = 50 mm, and t/R = 1.0.

Full size image

Results and discussion

Mechanical properties of HSC and PPFRC

The mechanical behavior results of HSC and PPFRC concrete, such as compressive strength, splitting tensile strength, and flexural strength, are listed in Table 3. As seen in the table, PPFRC enhanced the mechanical properties of the concrete compared to HSC, which can give the concrete the ability to withstand crack propagation. This finding is in agreement with the literature24,25.

Table 3 Mechanical Properties of HSC and PPFRC.
Full size table

Effect of SCB geometry and mode of mixity

Figure 13 presents the load versus displacement curves for SCB specimens with radii 50, 75, and 100 mm, considering different t/R ratios and modes of mixity, S2/S1. Several observations can be conducted regarding the behavior of the specimens by monitoring the performed tests. The relationship between the load and displacement is initially linear, indicating elastic deformation of the specimen. As the load increases, the crack propagates, causing a deviation from linearity in the load–displacement curve. This nonlinear behavior signifies the initiation of crack growth in the specimen. As the crack propagates, it becomes unstable and reaches a critical point, resulting in a peak load value. The curve starts to descend at this stage, and the applied load gradually decreases. The specimen approaches complete failure as the load decreases. The same observation was previously found for other quasi-brittle materials4,5,7,8,9,10.

Fig. 13
figure 13

Load–displacement curve of SCB specimen with different t/R and S2/S1 for radius equals (a) 50 mm, (b) 75 mm, and (c) 100 mm.

Full size image

At constant values of t/R, the peak load increases as the S2/S1 decreases, as shown in Fig. 14. This indicates that a higher mode mixity (lower S2/S1) leads to a greater peak load value. The fracture energy (GF) also increases with a decrease in the S2/S1 value, as depicted in the figure. On the other hand, when considering the same value of S2/S1, the maximum applied load value increases with increasing t/R. This means that a larger thickness ratio results in a higher peak load.

Fig. 14
figure 14

Effect of the radius R of SCB specimen on the load–displacement curve (a) t/R = 0.33 and S2/S1 = 0.34, and (b) t/R = 0.66 and S2/S1 = 0.18.

Full size image

Furthermore, the stiffness of the SCB specimen is influenced by both the specimen geometry and the mode of mixity. The stiffness increases with an increase in the t/R value at a constant mode of mixity. In other words, a larger thickness ratio leads to a higher stiffness. Additionally, the stiffness increased with the decrease of the mode mixity (an increase in the S2/S1 value). This indicates that a higher mode I loading component (lower mode mixity) increases stiffness.

On the other hand, the effect of the radius (R) on the maximum applied load for different t/R ratios and modes of mixity S2/S1 were studied. As seen in Fig. 14 for t/R = 0.33, S2/S1 = 0.34, and t/R = 0.66, S2/S1 = 0.18 as an example, it can be observed that the maximum applied load increased with the increases of the radius R for the different t/R and S2/S1 ratios. The same observation was obtained for the stiffness of different t/R and S2/S1 ratios; increasing the radius increased the stiffness of the tested SCB specimens.

Figure 15 illustrates the effect of the t/R ratio on the maximum applied load for smooth SCB specimens (a/R = 0) and cracked SCB specimens with a/R = 0.2 for different radii (R). It can be observed that the same observation of increasing the maximum applied load by increasing the t/R ratio can be used for both smooth specimens and cracked specimens. This implies that as the t/R ratio increases, it becomes more capable of withstanding higher loads before failure. Additionally, the maximum load increases with an increase in the radius R, as shown in the figure. This indicates that a larger thickness ratio relative to the radius leads to a higher maximum load.

Fig. 15
figure 15

Effect of t/R ratio on the maximum applied load with different R for (a) smooth SCB specimen and (b) SCB specimen with a/R = 0.2.

Full size image

Figure 16 shows the effect of radius R and the mode of mixity on the maximum applied load for SCB specimens with different t/R ratios. As mentioned in Fig. 13, the maximum applied load increases with increasing SCB geometries, implying that larger SCB specimens can withstand higher loads. Additionally, the maximum applied load decreases with the decrease of the mode of mixity (increase in the S2/S1 value), indicating that the resistance of the SCB specimens to fracture is lower in Mode I compared to Mode II or Mixed mode at a different mode mixity.

Fig. 16
figure 16

Relation between the maximum applied load and t/R of SCB specimen with a/R = 0.2 with different radius R and mode of mixity; (a) S2/S1 = 0.18, (b) S2/S1 = 0.34, and (c) S2/S1 = 1.

Full size image

Effect of PP fiber

This section discusses the effect of adding PP fiber to HSC on the applied load for SCB test specimens. A comparison between HSC and PPFRC using SCB specimens having a/R equal to 0.2 with different radius R and modes of mixity (S2/S1 = 0.18, 0.34, and 1) are illustrated in Figs. 17, 18, 19, respectively. As seen in the figures, it can be observed that adding PP fiber improves the resistance of the specimen to fracture. The maximum applied load of PPFRC is higher than that of HSC, regardless of the SCB geometry and mode of mixity. This suggests that incorporating PP fiber enhances the fracture resistance and overall mechanical behavior of the concrete, leading to higher applied loads before failure occurs. The same observation for S2/S1 equals 0.34 and 1. PP fiber enhances the fracture resistance of the concrete, leading to higher applied loads before failure occurs, as shown in Figs. 18 and 19.

Fig. 17
figure 17

Effect of concrete type HSC and PPFRC on the load–displacement relationship of SCB specimen with a/R = 0.2 with S2/S1 = 0.18 for (a) R = 50 mm, (b) R = 75 mm and (c) R = 100 mm.

Full size image
Fig. 18
figure 18

Effect of concrete type HSC and PPFRC on the load–displacement relationship of SCB specimen with a/R = 0.2 with S2/S1 = 0.34 for (a) R = 50 mm, (b) R = 75 mm and (c) R = 100 mm.

Full size image
Fig. 19
figure 19

Effect of concrete type HSC and PPFRC on the load–displacement relationship of SCB specimen with a/R = 0.2 with S2/S1 = 1 for (a) R = 50 mm, (b) R = 75 mm and (c) R = 100 mm.

Full size image

Effect of the SCB Geometry on the fracture toughness for different types of concrete

Figures 20, 21, 22, 23 provide the Mode I and Mode II stress intensity factors (KI and KII, respectively) for HSC and PPFRC SCB specimens. These values were obtained using a numerical method based on the contour integral method at the maximum applied load (Fmax) extracted from the experimental tests and the geometry correction factors from Fig. 9. Figure 20 illustrates the relationship between the Mode I stress intensity factor (KI) and the mode mixity (S2/S1) shown for different values of R and t/R ratios for HSC.

Fig. 20
figure 20

The relation between mode I SIF (KI) value at the average fracture load of SCB specimen and S2/S1 with different radius R for (a) t/R = 0.33, (b) t/R = 0.66 and (c) t/R = 1.

Full size image
Fig. 21
figure 21

The relation between mode II SIF (KII) value at the average fracture load of SCB specimen and S2/S1 with different radius R for (a) t/R = 0.33, (b) t/R = 0.66 and (c) t/R = 1.

Full size image
Fig. 22
figure 22

The relation between Mode I SIF (KI) value at the average fracture load of SCB specimen and S2/S1 with different radius R for (a) t/R = 0.33, (b) t/R = 0.66 and (c) t/R = 1.

Full size image
Fig. 23
figure 23

The relation between mode II SIF (KII) value at the average fracture load of SCB specimen and S2/S1 with different radius R for (a) t/R = 0.33, (b) t/R = 0.66 and (c) t/R = 1.

Full size image

As seen in the figure, it can be observed that the value of KI increases as the value of S2/S1 (mode mixity) increases; in other words, it increases as the loading becomes less shear-dominated. This indicates that as the shear component of loading decreases relative to the opening component, the Mode I stress intensity factor increases. The Mode I stress intensity factor reaches its peak value when S2/S1 equals 1, corresponding to the opening mode when the loading is purely tensile, see Fig. 20. On the other hand, the effect of t/R on the Mode I stress intensity factor (KI) does not exhibit a clear trend based on the information provided. This suggests that the thickness (t) ratio to the radius (R) does not significantly influence the Mode I stress intensity factor.

Unlike the values of KII, which increase as the value of S2/S1 (mode mixity) decreases, when the shear component of loading increases relative to the opening component, the Mode II stress intensity factor increases. The maximum values of the Mode II stress intensity factor were obtained when S2/S1 equals 0.18 for the different values of radius R, as seen in Fig. 21.

Figs.. 22 and 23 illustrate the relationship between Mode I (KI), Mode II (KII) stress intensity factor, and the mode mixity (S2/S1) for different values of R and t/R ratios for PPFRC, respectively.

The figures show that the fracture toughness value is higher for PPFRC than HSC. This implies that PPFRC exhibits a higher resistance to fracture than HSC, as the fracture toughness is a measure of a material’s ability to withstand crack propagation.

Fracture energy and work of fracture for HSC and PPFRC

Tables 4 and 5 present the fracture force Fmax, fracture energy Gf, and work of fracture Wf for HSC and PPFRC SCB specimens. These values were measured according to the AASHTO TP105 standard35. As described in AASHTO TP10535, the Mode I fracture toughness (stress intensity factor at critical load, KIC) at S2/S1 = 1 can obtained based on Ref. 1.

Table 4 Maximum applied load, fracture energy Gf, and work of fracture Wf of HSCSCB specimens according to AASHTO TP105.
Full size table
Table 5 Maximum applied load, fracture energy Gf, and work of fracture Wf of PPFRC SCB specimens according to AASHTO TP105.
Full size table

It is observed that the fracture force increases with an increase in the volume of the SCB specimen and the mode of mixity. This indicates that larger SCB specimens have a higher fracture force, and that a higher mode mixity (lower S2/S1 value) increases the fracture force. Additionally, it is noted that PPFRC exhibits a higher fracture force compared to HSC, suggesting that the incorporation of fibers enhances the resistance to fracture.

However, no clear trend is evident for the fracture energy and work of fracture for both SCB specimens made of HSC and PPFRC. The fracture energy and work of fracture may depend on various factors, such as the concrete mixture proportions, fiber content, and test conditions. Therefore, it is difficult to establish a specific trend based solely on the information provided in Tables 4 and 5. It is essential to consider additional factors and conduct further analysis to fully understand the relationship between fracture energy, work of fracture, and the properties of SCB specimens made of HSC and PPFRC.

Conclusion

This study investigated the fracture behavior of HSC and PPFRC under Mode I and mixed-mode loading conditions. The study also highlighted the influence of specimen geometry on fracture behavior. The numerical simulations and experimental investigations provided valuable insights into crack propagation, crack paths, load–displacement responses, and fracture toughness, and the findings revealed that:

  • - The crack path deviated from a straight line under mixed-mode loading and followed a curvilinear trajectory. The mode of mixity, characterized by the ratio of shear to tensile loading, influenced the fracture behavior significantly. Decreasing mode mixity resulted in higher peak loads and increased fracture energy. This indicates that shear loading is crucial in fracture initiation and propagation.

  • - Increasing the specimen size, represented by a larger radius, led to higher maximum loads. Incorporating polypropylene fibers in the concrete matrix improved fracture resistance, as evidenced by higher maximum loads and enhanced fracture toughness in the PPFRC specimens compared to the HSC specimens.

  • - Furthermore, calculating stress intensity factors provided insights into the severity of stress concentration near the crack tip. The Mode I stress intensity factor decreased with increasing mode mixity, while the Mode II stress intensity factor increased. This indicates that shear loading contributes to a reduction in tensile stress severity near the crack tip.

  • - The results of this study have practical implications for the design and analysis of concrete structures subjected to mixed-mode loading. Understanding the fracture behavior under complex loading conditions enables engineers to optimize structural designs and enhance their resilience and durability.