Abstract
Business engineering creates novel business solutions using a social and technological system. Business engineering is facing several challenges like (1) complexity management (2) rapid technological advancements (3) Resource constraints (4) Interdisciplinary collaboration etc., and there is a need to classify the solutions for these issues faced by the business community. To cover more advanced data and overcome the chance of data loss, in this article, we have developed the idea of a complex Pythagorean fuzzy rough set based on Tamir’s idea of a complex fuzzy set. We have developed basic operational laws for the proposed idea under the notion of Yager’s t-norm and t-conorm. Additionally, we have initiated the theory of complex Pythagorean fuzzy rough Yager weighted average and geometric aggregation operators. To discuss the utilization of the initiated work, we have introduced the WASPAS technique that can help us tackle the MADM problems. Moreover, we have provided an illustrative example for the classification of the solutions regarding the problems in business engineering. Also, a comparative analysis of the initiated theory shows the advantages of the introduced work.
Similar content being viewed by others
Introduction
The creation and application of business approaches, ranging from technology and data systems to business models, company procedures, and organizational frameworks, is known as business engineering. The goal of business engineering is to create novel business solutions using a social and technological systems perspective. Because an enterprise and an airline system or a manufacturing facility are similar in complexity, the social and technological system approach treats an enterprise as a whole system. Engineering, management, and business administration are all combined in the multidisciplinary discipline of business engineering. The objective is to enhance efficiency, effectiveness, and competitiveness through the design and optimization of business processes, structures, and strategies. For contemporary firms, business engineering is essential for several reasons:
-
Through the use of business engineering, firms can become more adaptable and successful in dynamic situations by being more sensitive to shifts in the market, technology, and client needs.
-
Business engineering helps companies minimize waste, cut expenses, and boost productivity through process optimization, which results in more effective operations.
-
By using business engineering concepts to continuously innovate and improve their procedures, goods, and amenities, firms can maintain their competitiveness.
-
To ensure that assets are deployed successfully and that efforts are concentrated on reaching long-term goals, business engineering assists in aligning business procedures and frameworks with the organization’s overarching strategic goals.
-
Business engineering fosters and controls invention within the company, assisting in the creation of novel goods, services, and business models that promote expansion and uniqueness.
-
Business engineering assists in identifying possible risks and developing ways to manage them, assuring company stability and resilience, by carefully examining business procedures and systems.
While business engineering offers numerous benefits, certain issues must be fixed if businesses are to be successful. It can be challenging to identify and create a workforce with specialized knowledge in both engineering and business, however, this is necessary for executing business engineering ideas. (2) Some firms may find it prohibitive to invest in business engineering projects due to the large initial costs associated with technology, training, and process transformation. (3) Gathering, organizing, and interpreting accurate and thorough data is essential for effective business engineering, but organizations may encounter difficulties in doing so. (4) All organizational levels must be committed to, and actively monitor, changes to make sure they are long-lasting. (5) Business engineering initiatives need to be in line with the organization’s overarching strategic objectives, which can be difficult to do if they face an abundance of leadership clarity or interaction. (6) The application of business engineering techniques may be impacted by differences in corporate culture, necessitating initiatives to promote an innovative and continually enhanced culture.
Researchers are working and producing their ideas in the field of business engineering. Hengst and Vreede1 discuss collaborative business process reengineering. The primary goal was to provide ten years of fieldwork related to collaborative business process reengineering. Following the implementation and thorough analysis of nine business process reengineering projects, 87 themes about the project’s efficacy and efficiency were found. A strategy-driven approach to business reengineering is proposed by Talwar2 where he/she has discussed the two primary methods for business re-engineering (1) Process re-engineering and (2) Business re-engineering. The business performance measuring techniques used by engineering organizations in construction were covered by Robinson et al.3. Legner et al.4 talked about the opportunities and challenges facing the field of business and information systems engineering. Buchananl5 talked about the advantages and disadvantages of business process re-engineering in a politically sensitive workplace environment in 1997. Childe et al.6 discussed the frameworks for understanding business process re-engineering. Here, Childe et al. talked about a specific method for small- and medium-sized manufacturing enterprises to use when re-engineering their business processes. The current challenges in business process re-engineering were covered by Maull et al.7. In their research, Maull et al. expressed dissatisfaction with the findings of empirical research regarding problems faced by 25 businesses undergoing business process re-engineering initiatives. Furthermore, Weerakkody et al.8 discussed the difficulties, issues, and concerns associated with using application service providers to re-engineer business processes. It is generally acknowledged that the absence of suitable alignment approaches makes maintaining business and information technology alignment a difficult undertaking. Based on this observation Ullah et al.9 have described a requirements elicitation method that is goal-oriented for the organization. Van Meel and Sol10 have defined business engineering as the integral design of both data systems and organizational frameworks.
Multiple criteria decision making (MCDM) is a field of decision theory that addresses decision-making when faced with several criteria. In many domains, including engineering, business, healthcare, and public policy, MADM methods are employed to assess and choose the optimal solution from a range of possibilities. Some key aspects of MADM are criteria, alternatives, weights, and decision matrix. MADM follows the following steps (1) Categorize the issues (2) Recognize the choices (3) Determine standards (4) Allocate weights (5) Apply MADM method (6) Make decision based on score values. Many MADM approaches have been made in literature based on fuzzy set theory. Kousar and Kausar11 utilized the notion of an integrated fuzzy rough set approach and proposed MCDM for sustainable agritourism. Baranidharan et al.12 utilized the new Fermatean fuzzy score function for assessing the impact of pre-pandemic impact. Jeon et al.13 proposed an MCDM perspective for selecting flexible packaging bags under the notion of a hesitant fuzzy set. Kumar and Pamucar14 proposed a comprehensive and systematic review of MCDM to solve decision-making problems.
Different generalized fuzzy structures have utilized MADM like Verma and Alvarez-Miranda15 used the CRITIC-WASPAS technique with power aggregation operators (AOs) to implement a MAGDM methodology under the environment of two-dimensional linguistic intuitionistic fuzzy sets (IFSs). Generalized Interval neutrosophic Schweizer-Sklar prioritized AOs are the foundation of the MADM that Khan et al.16 suggested. Extension of probability IF AOs in the fuzzy MADM approach has been developed by Sirbiladze and Sikharulidze17. In 1994 Yager18 proposed Yager t-norm and t-conorm and Dhankhar and Kumar19 MADM utilized these norms to establish q-rung orthopair fuzzy (q-ROF) Yager power weighted geometric AOs. Akram et al.20 have utilized complex Pythagorean fuzzy (CPyF) Yager structures and proposed an MCDM model. Akram and Shahzadi21 established the DM approach under the framework of PyF Yager weighted AOs. Based on q-ROFS, a hybrid DM approach has been produced by Shahzadi et al.22 based on Yager AOs. Chinram et al.23 introduced a decision support approach for spherical fuzzy (SF) Yager AOs and utilized it in a wind energy project site. Moreover, Naeem et al.24 introduced a novel DM method under the structure of spherical hesitant fuzzy Yager AOs. Also, Ali et al.25 proposed a MADM approach under the environment of q-ROF bipolar soft sets.
Pawlak26 developed the rough set theory (RST), a mathematical tool for managing ambiguity in data processing. It is employed to approximate sets that are challenging to define with exact bounds. Applications for rough set theory can be found in many domains, such as information discovery, algorithms for learning, and data analysis. Some key aspects of rough set theory are (1) information system (2) Indiscernibility relation (3) Lower and upper approximation (4) Boundary region. Different work is done on the application of RS like Wang et al.27 provided a survey on RST and application. Pieta and Szmuc28 gave an introduction and discussed the uses of RS in large-scale data processing. Using RS data explorer, RST was applied in data mining market evaluation by Jayasuruthi et al.29. The use of RST to predict the use of energy in houses experiencing heat modernization was created by Szul and Kokoszka30. The current hot issue is fuzzy set theory (FST) combined with RST. Recently much research all over the world has focused on the hybrid notions of FS and RS. Dubois and Prade31 introduced a hybrid structure of fuzzy rough sets (FRSs) by combining the FS and RS. Many other structures like IF rough set (IFRS)32, multi-granulation PyF rough set (PyFRS)33, PyF soft rough set (PyFSRS)34, q-ROF soft rough set (q-ROFSRS)35, SF soft rough set (SFSRS)36 and T-SF soft rough set (T-SFSRS)37 have been developed which are the evidence of the hybrid structure of RS and generalized fuzzy structures. Moreover, Khan et al.38 developed the idea of a complex fuzzy rough aggregation operator in polar form. Yi et al.39 developed the theory of complex fuzzy rough sets in Cartesian form and proposed its application in digital marketing for business growth. Moreover, Tamir et al.40 looked at a novel interpretation of complex membership grades. In 2016, Ali et al.41 discussed the complex IF classes. Labassi et al.42 developed the structure of complex PyF set (CPyFS) theory and its uses in visualization technology.
Notice that the notion of the complex fuzzy set (CFS) proposed by Tamir et al.40 is a limited structure because there is a possibility of data loss in this arrangement. This proposed structure can never discuss the rough structure that is the upper and lower approximations. The possibility of data loss exists in this structure. Furthermore, this structure is unable to address the non-membership grade (NG). The notion of complex IFS (CIFS) developed by Ali et al.41 can discuss the membership grade (MG) and NG in Cartesian form. But it is also limited structure because it can never discuss the roughness in its structure. The idea of CPyFS was recently developed by Labassi et al.42 in Cartesian form. Although this structure is more advanced than that of Ali et al.41 idea but it can still never discuss the upper and lower approximations. If we discuss the notion of FRS31, IFRS32, and multi-granulation PyFRS33, we can notice that these notions can discuss the roughness in their structures. But if the decision-makers discuss their data in complex form that is if fuzzy MG and NG are in Cartesian form. The above structure lacks these conditions.
As we can see there is a research gap in the literature that can be disused which could be helpful for many decision-making situations. There is a research gap in discussing the membership and non-membership grades in one structure in a Cartesian form that can discuss the upper and lower approximation. To cover this research gap of data loss and all limitation-based that occur in prevailing theories, we have developed the idea of complex Pythagorean fuzzy rough sets (CPyFRSs) in Cartesian form. Moreover, we have discussed Yager’s operational laws based on the initiated notion of CPyFRNs. After that, we discussed AOs like CPyFR Yager weighted average (CPyFRYWA) and CPyFR Yager weighted geometric (CPyFRWG) AOs in Cartesian form. To see the application perspectives of the proposed theory for the utilization of the developed theory, we have developed an algorithm for the WASPAS approach for MADM. We have developed an application for the classification of key aspects of business engineering based on the WASPAS technique. Moreover, we have a comparative analysis of the initiated theory to discuss its importance. In the end, we have a conclusion.
The arrangement of the article is given as follows: In Sect. 1 we have discussed the introduction of business engineering. Additionally, we have discussed the literature review and motivation of the initiated theory. Section 2, is devoted to discussing some useful definitions that can help in defining the notion of CPyFRSs. In Sect. 3, we have developed the basic notion of CPyFRS and Yager’s operational laws based on the developed notion. Section 4 is developed to discuss the idea of CPyFRYWA and CPyFRYWG AOs. In Sect. 5, we have defined a WASPAS algorithm for the developed theory and provided an application for the classification of possible solutions for business engineering. In Sect. 6, we have compared the initiated work with some existing theories to discuss the importance and superiority of the produced work. Section 7, is about the concluding remarks.
Preliminaries
The concepts of Yager t-norm and t-conorm, RS, and CFRS in Cartesian form are to be covered in this section.
Definition 1 18
For given two real numbers, \(\:p\) and \(\:q\), the definitions of Yager’s t-norm and t-conorm are respectively as follows:
Definition 2 26
Let \(\:\text{U}\) be a universal set and \(\:R\subseteq\:\text{U}\times\:\text{U}\) be an arbitrary relation on \(\:\text{U}.\) Let \(\:{R}^{*}\) be a set-valued map given by \(\:{R}^{*}:\:\text{U}\to\:P\left(\text{U}\right)\) and defined by \(\:{R}^{*}\left(u\right)=\left\{v\in\:\text{U}:\left(u,\:v\right)\in\:R\:and\:v\in\:\text{U}\right\},\:\)then the pair \(\:\left(\text{U},\:R\right)\) is crisp approximation space. The lower and upper approximations of \(\:A\) w.r.t \(\:\left(\text{U},\:R\right)\) are
The pair \(\:\left(\underline{R}\left(A\right),\:\overline{R}\left(A\right)\right)\) is a RS, where\(\:\:\underline{R}\left(A\right)\ne\:\overline{R}\left(A\right)\).
Definition 3 39
Let \(\:R\) be a complex fuzzy relation on \(\:\mathbb{U}\) and \(\:\left(\mathbb{U},\mathbb{\:}R\right)\) be a complex fuzzy approximation space. Now for any set \(\:A\in\:CFS\left(\mathbb{U}\right),\:A=\left\{\mathcal{M}\left(\begin{aligned} \rotatebox{90}{{\rm Q}} \end{aligned}\right)+\iota\:{\mathcal{M}}^{{\prime\:}}\left(\begin{aligned} \rotatebox{90}{{\rm Q}} \end{aligned}\right)\right\}.\) The upper and lower approximations are
Where
The pair \(\:\left(\overline{R}\left(A\right),\:\underline{R}\left(A\right)\right)\) is called CFRS if \(\:\overline{R}\left(A\right)\ne\:\underline{R}\left(A\right).\)
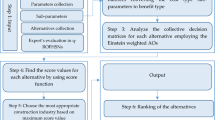
The main development of this article is given in (Table 1).
Moreover, the flow chart of the developed approach is given in (Fig. 1).
Complex Pythagorean fuzzy rough set (CPyFRS)
In this section, we initiate the notion of CPyFRS, and for this first, we define the CPyF relation. We denote the CPyF relation by "\({\mathcal{R}}\)" and the universal set by \(\:\mathbb{U}\).
Definition 4
Let \(\:\mathbb{U}\) be the universal set, then any CPyF subset \(\:\mathcal{R}\) is called CPyF relation on\(\:\:\mathbb{U}\) that is given as \(\:\:\mathcal{R}=\left\{\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right),\mathcal{\:}\mathcal{M}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)\mathcal{\:},\mathcal{N}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)|\mathcal{M}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)=a\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)+\iota\:b\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right),\mathcal{\:}\mathcal{\:}\mathcal{N}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)=c\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)+\iota\:d\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)\right\}\), where \(\:\mathcal{M}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)\) and \(\:\mathcal{N}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right)\) are called MG and NG respectively and M\(\:\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right):\mathbb{U}\times\:\mathbb{U}\to\:\left[0,\:1\right]+\iota\:\left[0,\:1\right]\) and\(\:\mathcal{\:}\mathcal{N}\left(\mathfrak{x}\mathfrak{\:},\mathfrak{\:}y\right):\mathbb{U}\times\:\mathbb{U}\to\:\left[0,\:1\right]+\iota\:\left[0,\:1\right]\) satisfying the following conditions:
Example 1
Let \(\:\mathbb{U}=\left\{{\mathfrak{x}}_{1},\:{\mathfrak{x}}_{2}\right\}\) then CPyF relation on \(\:\mathbb{U}\) is given by
Definition 5
Let \(\:\mathbb{U}\ne\:\mathbb{\varnothing\:}\mathbb{\:}\)finite universe of discourse and \(\:\mathcal{R}\mathcal{\:}\)be a CPyF relation on \(\:\mathbb{U},\:\)then \(\:\left(\mathbb{U},\mathcal{\:}\mathcal{R}\right)\) define the CPyF approximation space. Let \(\:A=\left\{\left(\mathfrak{x},\mathfrak{\:}{\mathcal{M}}_{A}\left(\mathfrak{x}\right)+\iota\:{\mathcal{M}^{{\prime}}}_{A}\left(\mathfrak{x}\right),\:\:{\mathcal{N}}_{A}\left(\mathfrak{x}\right)+\iota\:{\mathcal{N}^{{\prime}}}_{A}\left(\mathfrak{x}\right)\right)|\mathfrak{x}\in\:\mathbb{U}\right\}\:\)be a CPyFS over\(\:\mathbb{\:}\mathbb{U}\), where \(\:{\mathcal{M}}_{A}\left(\mathfrak{x}\right)\:and\:{\mathcal{N}}_{A}\left(\mathfrak{x}\right)\) are real parts of MG and NG, \({\mathcal{M}}^{\prime} _{A} \left( {\mathfrak{x}} \right)~and~{\mathcal{N}}^{\prime} _{A} \left( {\mathfrak{x}} \right)\) are imaginary parts of MG and NG. Now upper and lower approximation of a set \(\:A\:\)is defined and denoted as:
Where,
With the conditions of \(\:\:0\le\:{\left({\alpha\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}+\:{\left({\delta\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}\le\:1\)and \(\:0\le\:{\left({\beta\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}+\:{\left({\gamma\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}\le\:1.\)
With the conditions of \(\:\:0\le\:{\left({\alpha\:}_{\overline{\mathcal{R}\mathcal{\:}}\:}\right)}^{2}+\:{\left({\delta\:}_{\overline{\mathcal{R}\mathcal{\:}}\:}\right)}^{2}\le\:1\)and \(\:0\le\:{\left({\beta\:}_{\underline{R}}\right)}^{2}+\:{\left({\gamma\:}_{\underline{R}}\right)}^{2}\le\:1.\)
The pair \(\:\mathcal{R}\left(A\right)=\left(\overline{\mathcal{R}\mathcal{\:}}\left(A\right),\:\underline{R}\left(A\right)\right)=\left\{\left(\mathfrak{x},<{\text{{\rm\:M}}}_{\overline{\mathcal{R}\mathcal{\:}}}\left(\mathfrak{x}\right),{\text{N}}_{\overline{\mathcal{R}\mathcal{\:}}}\left(\mathfrak{x}\right)>,<{\text{{\rm\:M}}}_{\underline{R}}\left(\mathfrak{x}\right),{\text{N}}_{\underline{R}}\left(\mathfrak{x}\right)>\right)|\mathfrak{x}\in\:\mathbb{U}\right\}\) is called CPyFRS with respect \(\:\left(\mathbb{U},\mathcal{\:}\mathcal{R}\right).\) For the sake of simplicity, we can say \(\:\mathcal{R}\left(A\right)=\left(\overline{\mathcal{R}\mathcal{\:}}\left(A\right),\:\underline{R}\left(A\right)\right)=\left(\left({\alpha\:}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{\beta\:}_{\overline{\mathcal{R}\mathcal{\:}}},{\delta\:}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{\gamma\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right),\left({\alpha\:}_{\underline{R}}+\iota\:{\beta\:}_{\underline{R}},{\delta\:}_{\underline{R}}+\iota\:{\gamma\:}_{\underline{R}}\right)\right)\) represent the CPyFRN in Cartesian form.
Example 2
Let \(\:\mathbb{U}=\left\{{\mathfrak{x}}_{1},\:{\mathfrak{x}}_{2}\right\}\) be the universal set and \(\:\mathcal{R}=\left\{\begin{array}{c}\left(\left({\mathfrak{x}}_{1},\:{\mathfrak{x}}_{1}\right),\:\left(0.24+\iota\:0.21,\:0.31+\iota\:0.15\right)\right),\:\left(\left({\mathfrak{x}}_{1},\:{\mathfrak{x}}_{2}\right),\:\left(0.33+\iota\:0.43,\:0.27+\iota\:0.19\right)\right),\\\:\:\left(\left({\mathfrak{x}}_{2},\:{\mathfrak{x}}_{1}\right),\:\left(0.15+\iota\:0.12,\:0.13+\iota\:0.10\right)\right),\:\left(\left({\mathfrak{x}}_{2},\:{\mathfrak{x}}_{2}\right),\:\left(0.25+\iota\:0.32,\:0.31+\iota\:0.41\right)\right)\end{array}\right\}\) be the CPyFR on \(\:\mathbb{U}\) as given in example 1. Now assume that \(\:A=\left\{\left({\mathfrak{x}}_{1},\:0.23+\iota\:0.35,\:0.45+\iota\:0.39\right),\:\left({\mathfrak{x}}_{2},\:0.21+\iota\:0.17,\:0.16+\iota\:0.13\right)\right\}\) be CPyFS. Now the upper and lower approximations are given by
And
Hence.
\(\:\mathcal{R}\left(A\right)=\left(\overline{\mathcal{R}\mathcal{\:}}\left(A\right),\:\underline{R}\left(A\right)\right)=\left\{\begin{array}{c}\left(\begin{array}{c}{\mathfrak{x}}_{1},\:\left(0.33+\iota\:0.43,\:0.16+\iota\:0.13\right),\\\:\:\left(0.21+\iota\:0.17,\:0.45+\iota\:0.39\right)\end{array}\right),\:\\\:\left(\begin{array}{c}{\mathfrak{x}}_{2},\:\left(0.25+\iota\:0.35,\:0.13+\iota\:0.1\right),\:\\\:\left(0.15+\iota\:0.12,\:0.45+\iota\:0.41\right)\end{array}\right)\end{array}\right\}\) is a CPyFRS.
Definition 6
For the classification of CPyFRNs, there is a need to define the concept of score function and accuracy function. The defied notions are given by
For CPyFRN\(\:\:{CPyFR}_{1}=\left\{\left(\left({{\alpha\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\beta\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}},\:{{\delta\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\gamma\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}\right),\left({{\alpha\:}_{1}}_{\underline{R}}+\iota\:{{\beta\:}_{1}}_{\underline{R}},{{\delta\:}_{1}}_{\underline{R}}+\iota\:{{\gamma\:}_{1}}_{\underline{R}}\right)\right)\right\}\), the score function is defined by
Example 3
For any CPyFRNs\(\:\:{CPyFR}_{1}=\left\{\left(\begin{array}{c}\left(0.19+\iota\:0.34,\:0.13+\iota\:0.11\right),\\\:\left(0.12+\iota\:\text{0.22,0.34}+\iota\:0.17\right)\end{array}\right)\right\}\), the score value and accuracy values are calculated by
Aggregation theory based on CPyFRSs
Definition 7
Le \(\:{CPyFR}_{1}=\left\{\left(\left({{\alpha\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\beta\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}},\:{{\delta\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\gamma\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}\right),\left({{\alpha\:}_{1}}_{\underline{R}}+\iota\:{{\beta\:}_{1}}_{\underline{R}},{{\delta\:}_{1}}_{\underline{R}}+\iota\:{{\gamma\:}_{1}}_{\underline{R}}\right)\right)\right\}\) and \(\:{CPyFR}_{2}=\left\{\left(\left({{\alpha\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\beta\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}},\:{{\delta\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\gamma\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}}\right),\left({{\alpha\:}_{2}}_{\underline{R}}+\iota\:{{\beta\:}_{2}}_{\underline{R}},{{\delta\:}_{2}}_{\underline{R}}+\iota\:{{\gamma\:}_{2}}_{\underline{R}}\right)\right)\right\}\) be two CPyFRNs and \(\:\begin{aligned} \rotatebox{90}{{\rm Q}} \end{aligned}>0\) and\(q > 0\) The Yager t-norm and t-conorm operations are as follows
1)
2)
3)
4)
Theorem 1
Let \(\:{CPyFR}_{1}=\left\{\left(\left({{\alpha\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\beta\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}},\:{{\delta\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\gamma\:}_{1}}_{\overline{\mathcal{R}\mathcal{\:}}}\right),\left({{\alpha\:}_{1}}_{\underline{R}}+\iota\:{{\beta\:}_{1}}_{\underline{R}},{{\delta\:}_{1}}_{\underline{R}}+\iota\:{{\gamma\:}_{1}}_{\underline{R}}\right)\right)\right\}\) and \(\:{CPyFR}_{2}=\left\{\left(\left({{\alpha\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\beta\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}},\:{{\delta\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}}+\iota\:{{\gamma\:}_{2}}_{\overline{\mathcal{R}\mathcal{\:}}}\right),\left({{\alpha\:}_{2}}_{\underline{R}}+\iota\:{{\beta\:}_{2}}_{\underline{R}},{{\delta\:}_{2}}_{\underline{R}}+\iota\:{{\gamma\:}_{2}}_{\underline{R}}\right)\right)\right\}\) be two CPyFRNs, then the following properties hold in this case
1)
2)
3)
4)
5)
6)
Now utilizing the operational laws given in def. 7, we can define AOs under the environment of CPyFRNs as follows.
Definition 8
Let \(\begin{aligned} CPyFR & = \left\{ {\left( {\left( {\alpha _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \beta _{{i_{{{\overline{\mathcal{R}}}}} }} ,~\delta _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{i_{{{\overline{\mathcal{R}}}}} }} } \right),\left( {\alpha _{{i_{{{\underline{R} }}} }} + \iota \beta _{{i_{{{\underline{R} }}} }} ,\delta _{{i_{{{\underline{R} }}} }} + \iota \gamma _{{i_{{{\underline{R} }}} }} } \right)} \right)} \right\} \\ & \left( {i = 1,~2,~ \ldots ,~m} \right) \\ \end{aligned}\) be the collection of CPyFRNs. Then the notion of the CPyFRYWA operator is defined by a mapping \(\:F:{A}^{m}\to\:A\) such that
Where \(\:\gimel\:={\left({\gimel\:}_{1},\:{\gimel\:}_{2},\:{\gimel\:}_{3},\:\dots\:,\:{\gimel\:}_{m}\right)}^{\text{{\rm\:T}}}\) is the weight vector (WV) of \(\:CPyFRNs\) and \(\:{\sum\:}_{i=1}^{m}{\gimel\:}_{i}=1.\)
Theorem 2
Let \(\begin{aligned} CPyFR & = \left\{ {\left( {\left( {\alpha _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \beta _{{i_{{{\overline{\mathcal{R}}}}} }} ,~\delta _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{i_{{{\overline{\mathcal{R}}}}} }} } \right),\left( {\alpha _{{i_{{{\underline{R} }}} }} + \iota \beta _{{i_{{{\underline{R} }}} }} ,\delta _{{i_{{{\underline{R} }}} }} + \iota \gamma _{{i_{{{\underline{R} }}} }} } \right)} \right)} \right\} \\ & \left( {i = 1,~2,~ \ldots ,~m} \right) \\ \end{aligned}\) be the collection of CPyFRNs. The outcome obtained through the CPyFRYWA operator is again CPyFRN.
\(\:CPyFRYW{A}_{\gimel\:}\left({CPyFR}_{1},\:{CPyFR}_{2},\:{CPyFR}_{3},\dots\:,\:{CPyFR}_{m}\right)={\oplus\:}_{i=1}^{m}\left({\gimel\:}_{i}{CPyFR}_{i}\right)\)
Proof
Proof of Eq. (1) followed by the use of a mathematical induction technique.
Definition 9
Let \(\begin{aligned} CPyFR & = \left\{ {\left( {\left( {\alpha _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \beta _{{i_{{{\overline{\mathcal{R}}}}} }} ,~\delta _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{i_{{{\overline{\mathcal{R}}}}} }} } \right),\left( {\alpha _{{i_{{{\underline{R} }}} }} + \iota \beta _{{i_{{{\underline{R} }}} }} ,\delta _{{i_{{{\underline{R} }}} }} + \iota \gamma _{{i_{{{\underline{R} }}} }} } \right)} \right)} \right\} \\ & \left( {i = 1,~2,~ \ldots ,~m} \right) \\ \end{aligned}\) be the collection of CPyFRNs. Then the notion of CPyFRYWG AO is defined by
Where \(\:\gimel\:={\left({\gimel\:}_{1},\:{\gimel\:}_{2},\:{\gimel\:}_{3},\:\dots\:,\:{\gimel\:}_{m}\right)}^{\text{{\rm\:T}}}\) is the WVs of \(\:{CPyFR}_{i}\) with condition that \(\:{\sum\:}_{i=1}^{m}{\gimel\:}_{\mathfrak{i}}=1\) and \(\:{\gimel\:}_{\mathfrak{i}}>0.\)
Theorem 3
Let \(\begin{aligned} CPyFR & = \left\{ {\left( {\left( {\alpha _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \beta _{{i_{{{\overline{\mathcal{R}}}}} }} ,~\delta _{{i_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{i_{{{\overline{\mathcal{R}}}}} }} } \right),\left( {\alpha _{{i_{{{\underline{R} }}} }} + \iota \beta _{{i_{{{\underline{R} }}} }} ,\delta _{{i_{{{\underline{R} }}} }} + \iota \gamma _{{i_{{{\underline{R} }}} }} } \right)} \right)} \right\} \\ & \left( {i = 1,~2,~ \ldots ,~m} \right) \\ \end{aligned}\) be the collection of CPyFRNs. The outcome obtained through the CPyFRYWG operator is again CPyFRN.
\(\:CPyFRYW{G}_{\gimel\:}\left({CPyFR}_{1},\:{CPyFR}_{2},\:{CPyFR}_{3},\dots\:,\:{CPyFR}_{m}\right)={\otimes}_{i=1}^{m}\left({{CPyFR}_{i}}^{{\gimel\:}_{i}}\right)\)
Proof
Proof of Eq. (2) followed by the use of a mathematical induction technique.
Methods
The Weighted Aggregated Sum Product Assessment (WASPAS) method is a multi-criteria decision-making methodology that combines the advantages of the weighted product model and the weighted sum model.
Algorithm 1
To handle the multicriteria decision-making techniques, many decision-making tools have been developed. Here in this section, we have defined the WASPAS technique. Assume that \(\:{A}_{L}=\left\{{A}_{L1},\:{A}_{L2},\:{A}_{L3},\:\dots\:,\:{A}_{Lm}\right\}\) is the collection of \(^{'} m^{'}\) alternatives and \(\:{A}_{T}=\left\{{A}_{T1},\:{A}_{T2},\:{A}_{T3},\:\dots\:,\:{A}_{Tn}\right\}\) represents\(^{'} n^{'}\) attributes. Let \(\left\{ {{\text{e}}_{1} ,~{\text{e}}_{2} ,~{\text{e}}_{3} ,~ \ldots ,~{\text{e}}_{\hbar } } \right\}\) represents "\(\hslash\)" decision analyst for each alternative \(\:{A}_{L\mathfrak{i}}\left(i=1,\:2,\:3,\:\dots\:,\:m\right)\) against attributes \(\:{A}_{Tj}\left(j=1,\:2,\:3,\:.,\:n\right).\:\)Let \(\:{\gimel\:=\left({\gimel\:}_{1},\:{\gimel\:}_{2},\:{\gimel\:}_{3},\:\dots\:,\:{\gimel\:}_{n}\right)}^{\text{{\rm\:T}}}\) be the WVs for attributes \(\:{A}_{Tj}\) and \(\:\varpi\:={\left({\varpi\:}_{1},\:{\varpi\:}_{2},\:{\varpi\:}_{3},\:\dots\:,\:{\varpi\:}_{\hslash\:}\right)}^{\text{{\rm\:T}}}\) be the WVs for experts \({\text{e}}_{z} \left( {z = 1,~2,~3,~ \ldots ,~\hbar } \right)\) such that \(\:{\sum\:}_{j=1}^{n}{\gimel\:}_{j}=1\) and \(\:{\sum\:}_{z=1}^{\hslash\:}{\varpi\:}_{z}=1\). The algorithm of the WASPAS method is given by
Step 1
Assume decision analysts deliver their evaluation as CPyFRNs corresponding to each attribute. The decision matrix is given by.
Step 2
Afterward, normalize the provided decision-making matrix in Step 1 utilizing the formula as
Where \({\left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\alpha _{{ij_{{{\overline{\mathcal{R}}}}} }} + \beta _{{ij_{{{\overline{\mathcal{R}}}}} }} ,} \\ {\delta _{{ij_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{ij_{{{\overline{\mathcal{R}}}}} }} } \\ \end{array} } \right),} \\ {\left( {\begin{array}{*{20}c} {\alpha _{{ij_{{{\underline{R} }}} }} + \iota \beta _{{ij_{{{\underline{R} }}} }} ,} \\ {\delta _{{ij_{{{\underline{R} }}} }} + \iota \gamma _{{ij_{{{\underline{R} }}} }} } \\ \end{array} } \right)} \\ \end{array} } \right)}\) is the complement of \({\left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\delta _{{ij_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{ij_{{{\overline{\mathcal{R}}}}} }} ,} \\ {\alpha _{{ij_{{{\overline{\mathcal{R}}}}} }} + \beta _{{ij_{{{\overline{\mathcal{R}}}}} }} } \\ \end{array} } \right),} \\ {\left( {\begin{array}{*{20}c} {\delta _{{ij_{{{\underline{R} }}} }} + \iota \gamma _{{ij_{{{\underline{R} }}} }} ,} \\ {\alpha \delta _{{ij_{{{\underline{R} }}} }} + \iota \beta _{{ij_{{{\underline{R} }}} }} } \\ \end{array} } \right)} \\ \end{array} } \right)}\)
Step 3
Compute the relative importance of the alternative by using Eq. (1)
Step 4
Similarly, we have used Eq. (2) to find out the weighted product model given by.
Step 5
Lastly, using WASPAS methods to arrange alternatives, as provided by
Step 6
To obtain score values and access the optimal option, use def. 6.
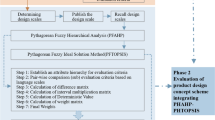
The flowchart of the proposed WASPAS technique is given in (Fig. 2).
Illustrative example
Discussion
Business engineering is an interdisciplinary profession that combines information technology, engineering concepts, and business administration to create, optimize, and apply creative solutions to problems in the real world. Its main goals are to increase organizational effectiveness, simplify intricate procedures, and improve decision-making by using data-driven approaches. In practice, business engineering uses systematic frameworks, mathematical modeling, and AI-powered technologies to handle issues including supply chain inefficiencies, digital transformation, and risk management. This strategy is especially helpful in sectors where increasing operational resilience and resource optimization are essential for competitive success, such as manufacturing, healthcare, and finance. A multifaceted strategy integrating expertise from administration, engineering, computer science, and business is necessary for business engineering. Experts in this domain typically possess an engineering or business background, together with supplementary instruction in data technology and operation management.
Some key aspects of business engineering are given in tabular form in (Table 2).
Here we have explained the possible solutions for handling the issues regarding business engineering.
Improve process efficiency through six sigma methods and robotic process automation (RPA)
Put lean principles into practice to save waste and boost workflow effectiveness. Utilize six sigma methods to lower process variance and raise quality. Businesses can improve the effectiveness of their internal processes by implementing the six sigma technique, which provides the necessary tools. This increase in efficiency and decrease in process variance leads to improvements in profits, employee morale, and the caliber of the products or services. Defects also reduce as a result. Often referred to as software robotics, RPA leverages intelligent automation technology to carry out data extraction and other tedious office duties that are performed by human workers. To improve efficiency and precision, automate repetitive operations with software solutions like RPA.
Figure 3 shows aspects of improving process efficiency.
Deploy enterprise resource planning (ERP), Implement customer relationship management system (CRMS) and data integration platform (DIP)
ERP is a platform that businesses use to handle and integrate the essential elements of their operations. Businesses need a variety of ERP software systems because they make asset planning easier to adopt by combining all operational processes into one system. To combine several business operations into a single system, the implementation of ERP is necessary for business engineering. Moreover, customer relationship management implementation entails configuring CRM software to gather accurate information that the sales and marketing team may use to direct advertising and boost revenue. CRMs let employees learn more about client interaction paths, identify potential, and expand their company. So the implementation of a CRM system is necessary to enhance customer interaction and data efficiency. IT specialists may combine data from several sources and give a full, precise, and current dataset for business intelligence (BI), data mining, and other applications and procedures by using a data integration platform. To guarantee smooth data transfer between various systems and programs, the deployment of data integration platforms is the best solution in business engineering to overcome issues regarding data analysis.
The graphical representation of ERP, CRMS, and DIP is given in (Fig. 4).
Decide the best quality management principle
In Table 3 below we have elaborated on different quality management principles that help to resolve the issues related to business engineering.
Enhance supply chain visibility
Implement technologies like loT (The network of physical items, or “things,” that are implanted across software, hardware, sensors, and other tools to communicate and exchange information with other gadgets and networks over the internet, is known as the Internet of Things) to enhance supply chain visibility. To minimize risks and lessen reliance on a single source, there is a need to diversify the supplier base. To maximize stock levels and guarantee rapid supply, sophisticated inventory management systems must be used in business engineering.
Now based on these alternatives, a team of experts is assigned a task to select the best solution for issues related to business engineering. The committee members provided a theory assessment under the following attributes given in (Table 4).
Results of Algorithm 1
Step 1
Assume that a team of three experts provide their assessment in the form of CPyFRNs in Cartesian form and the overall data against each alternative is given in (Tables 5, 6 and 7).
The combined matrix by utilizing the notion of CPyFRYWA aggregation operators and WVs of experts that \(\:\varpi\:={\left(0.42,\:\text{0,39},\:\text{0,19}\right)}^{\text{{\rm\:T}}}\:\)is given in Table 8 as follows.
Step 2
As all criteria are of benefit type, so we utilize the Eq. (3) to normalize the data given in (Table 8). We can observe that by utilizing the formula in Eq. (3), we get the same values as given in (Table 8). Hence Table 8 is a normalized matrix.
Step 3
Assume that the WVs for the attributes are \(\:\left(0.23,\:0.31,\:0.28,\:0.18\right).\) Use CPyFRYWA AOs to compute the relative importance of alternatives by using the formula
Hence Table 9 shows the relative importance of alternatives.
Step 4
Also compute \(\:{{\text{B}}_{i}}^{WP}\) by utilizing the formula
Hence \(\:{{\text{B}}_{i}}^{WP}\) values are given in (Table 10).
Step 5
Finally use WASPAS techniques for ordering alternatives as given by.
Table 11 for \(\:{\text{B}}_{i}\) values are given below
Step 6
Now we utilize the formula given in def. 6 to compute score values and score values are given by.
Hence ranking of the alternative is given by.
Algorithm 2
To handle the multicriteria decision-making techniques, many decision-making tools have been developed. Assume that \(\:{A}_{L}=\left\{{A}_{L1},\:{A}_{L2},\:{A}_{L3},\:\dots\:,\:{A}_{Lm}\right\}\) is the collection of \(^{'} m^{'}\) alternatives and \(\:{A}_{T}=\left\{{A}_{T1},\:{A}_{T2},\:{A}_{T3},\:\dots\:,\:{A}_{Tn}\right\}\) represents\(^{'} n^{'}\) attributes. Let \(\left\{ {{\text{e}}_{1} ,~{\text{e}}_{2} ,~{\text{e}}_{3} ,~ \ldots ,~{\text{e}}_{\hbar } } \right\}\) represents "\(\hslash\:\)" decision analyst for each alternative \(\:{A}_{L\mathfrak{i}}\left(i=1,\:2,\:3,\:\dots\:,\:m\right)\) against attributes \(\:{A}_{Tj}\left(j=1,\:2,\:3,\:.,\:n\right).\:\)Let \(\:{\gimel\:=\left({\gimel\:}_{1},\:{\gimel\:}_{2},\:{\gimel\:}_{3},\:\dots\:,\:{\gimel\:}_{n}\right)}^{\text{{\rm\:T}}}\) be the WVs for attributes \(\:{A}_{Tj}\) and \(\:\varpi\:={\left({\varpi\:}_{1},\:{\varpi\:}_{2},\:{\varpi\:}_{3},\:\dots\:,\:{\varpi\:}_{\hslash\:}\right)}^{\text{{\rm\:T}}}\) be the WVs for experts \({\text{e}}_{z} \left( {z = 1,~2,~3,~ \ldots ,~\hbar } \right)\) such that \(\:{\sum\:}_{j=1}^{n}{\gimel\:}_{j}=1\) and \(\:{\sum\:}_{z=1}^{\hslash\:}{\varpi\:}_{z}=1\). The step-wise algorithm is given by
Step 1
Assume decision analysts deliver their evaluation as CPyFRNs corresponding to each attribute. The decision matrix is given by.
Step 2
Assessment of combined matrix by using the notion of CPyFRYWA AOs.
Step 3
Normalize the decision-making matrix in Step 1 by using the formula as.
Where \({\left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\alpha _{{ij_{{{\overline{\mathcal{R}}}}} }} + \beta _{{ij_{{{\overline{\mathcal{R}}}}} }} ,} \\ {\delta _{{ij_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{ij_{{{\overline{\mathcal{R}}}}} }} } \\ \end{array} } \right),} \\ {\left( {\begin{array}{*{20}c} {\alpha _{{ij_{{{\underline{R} }}} }} + \iota \beta _{{ij_{{{\underline{R} }}} }} ,} \\ {\delta _{{ij_{{{\underline{R} }}} }} + \iota \gamma _{{ij_{{{\underline{R} }}} }} } \\ \end{array} } \right)} \\ \end{array} } \right)}\)is the complement of\({\left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\delta _{{ij_{{{\overline{\mathcal{R}}}}} }} + \iota \gamma _{{ij_{{{\overline{\mathcal{R}}}}} }} ,} \\ {\alpha _{{ij_{{{\overline{\mathcal{R}}}}} }} + \beta _{{ij_{{{\overline{\mathcal{R}}}}} }} } \\ \end{array} } \right),} \\ {\left( {\begin{array}{*{20}c} {\delta _{{ij_{{{\underline{R} }}} }} + \iota \gamma _{{ij_{{{\underline{R} }}} }} ,} \\ {\alpha \delta _{{ij_{{{\underline{R} }}} }} + \iota \beta _{{ij_{{{\underline{R} }}} }} } \\ \end{array} } \right)} \\ \end{array} } \right)}\)
Step 4
Utilization of CPyFRYWA or CPyFRYWG AOS and find out the aggregated result.
Step 5
Use the formula in def. (6) to get the score values.
Step 6
Rank the results and find out the best alternative.
Results of Algorithm 2
Utilization of CPyFRYWA AOs
Step 1
Here we use the data of (Tables 5, 6 and 7).
Step 2
Assessment of combined matric by using the notion of CPyFRYWA AOs is given in (Table 8).
Step 3
No need to normalize the combined matrix because all attributes are benefit types.
Step 4
Now we use the notion of CPyFRYWA AOS and find out the aggregated result. The obtained outcomes are given by.
Step 5
Now we compute the score values by using the def. (6). The score values are given by.
Step 6
According to score values the ranking results are given by.
Utilization of CPyFRYWG AOs
Step 1
Same as above.
Step 2
Same as above.
Step 3
Same as above.
Step 4
Now we use the notion of CPyFRYWG AOS and find out the outcomes. The obtained outcomes are given by.
Step 5
Now we compute the score values by using the def. (6). The score values are given by.
Step 6
According to score values the ranking results are given by.
Comparative analysis
Here in this section, we have to develop a comparative analysis of the proposed study to depict the advantages of the proposed theory. Moreover, we have to mention the limitations of the previous theories and determine that initiative approaches are more advanced and more suitable for handling complicated data. We will talk about the data in Tables 5, 6 and 7 now.
Tamir et al.40 presented the idea of a CFS, which has a limited structure due to the potential for data loss. The rough structure, which consists of the upper and lower approximations, cannot be discussed in this proposed framework40. It means this structure has some gaps in its structure to address the complete information. Furthermore, this structure is unable to address the non-membership grade as well. The concept of a CIFS, as introduced by Ali et al.41, allows for the Cartesian discussion of MG and NGs. However, because it is unable to address the roughness in its structure, we can notice that structure is also limited and it can discuss limited information. Labassi et al.42 recently established the idea of CPyFS in Cartesian form. Despite being a more advanced structure than the notion presented by Ali et al.42, it is unable to address the upper and lower approximations. The concepts of FRS31, IFRS32, and multi-granulation PyFRS33 can all be used to talk about the roughness of their respective structural formulations. However, if fuzzy MG and NGs are in Cartesian form, and the decision-makers argue their facts in a complex manner. Certain requirements are absent from the structure mentioned above. If we compare our work with the WASPAS technique based on previously limited notions of intuitionist fuzzy set43, Pythagorean fuzzy data44. The data of the proposed theory can never be handled by prevailing theories while introduced work can handle all limitations that exist in previous structures. In this regard, we may state that the current theory is dominated by progressed work. The analysis of the results given in (Table 12), shows that the data covered in Tables 5, 6 and 7 is based on CPyFR information and it can never be handled by all the above existing notions. Table 12 shows the overall results. Recently Mahmood et al.45 introduced the idea of a complex intuitionistic fuzzy rough set model and it is based on Tamir’s idea of CFS. We can notice that this approach uses the condition that the sum of the upper and lower approximation of MG and NMG must belong to [0, 1]. But we can note that if the decision maker provides their assessment in the form of data like \(\:\left(\left(\begin{array}{c}0.3+\iota\:0.5,\\\:0.5+\iota\:0.6\end{array}\right),\left(\begin{array}{c}0.2+\iota\:0.3,\\\:0.4+\iota\:0.5\end{array}\right)\:\right)\) then we can notice that the basic condition is violated because \(\:\left(0.5+0.6\right)\notin\:\left[0,\:1\right].\) Therefore, we can say that the devised form of CIFRS by Mahmood et al.45 is limited. The introduced idea can handle this limitation because of using a more advance condition that the sum of the square of upper and lower approximation values of MG and NMG must belong to [0, 1] and in this case, the condition is satisfied. Hence, we can say that the chance of data loss decreases. If we compare our work with hesitant FS13,14 we can see that the data covered in Tables 5, 6 and 7 can never be covered by idea in13,14. This idea can never discuss the upper and lower approximations that show the limitations of the existing work. The developed approach can handle such a situation. The initiated approach can assist in MCDM approaches to handle the more advance information. The developed approach helps in business engineering to handle the issues and it can provide assistance to prioritize the solutions.
Sensitivity analysis of the proposed work
In this subsection, we have analyzed the sensitivity analysis of the proposed work by using different values of parameters. The overall score values and ranking results are given in (Table 13).
From the results of Table 13 we can notice that in all of these cases, the best result in these cases is "\({A}_{L1}\)" that show the consistency and reliability of the introduced approach. As there is no change in ranking result, we can say that the introduced approach is more reliable and authentic.
Moreover, the characteristic analysis of the developed approach is given in (Table 14).
Conclusion
WASPAS approach is the MCDM approach that can combine the weighted sum and weighted product models to handle decision-making problems. Prioritization of possible solutions regarding business engineering is MADM problem. To discuss this issue, we have developed the idea of a CPyFR set based on Tamir’s idea of CFS. To discuss the utilization of this approach to aggregation theory, we have utilized Yager’s t-norm and t-conorm. We have developed the idea of CPyFRYWA and CPyFRYWG AOs. The developed approach can help to handle the chance of data loss in the form of upper and lower approximation and more accurate decisions can be made based on initiated work. In this way, the developed theory is superior to many other existing theories like CIFS in polar and Cartesian form, and CPyFS in Cartesian and polar form. Moreover, to discuss the utilization of the delivered approach we have developed the WASPAS approach and discussed the applicability of this approach to business engineering. The comparative analysis of the introduced work depicts the importance and feasibility of the developed theory. The sensitivity analysis for the introduced work shows the reliability of the delivered. We can notice for different values of parameters there is no change in the ranking result and the best alternative is the same in all cases which is evidence of the reliability of the introduced work.
The developed notions are limited because these notions used the condition that \(\:0\le\:{\left({\alpha\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}+\:{\left({\delta\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}\le\:1\) and \(\:0\le\:{\left({\beta\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}+\:{\left({\gamma\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}\le\:1\) and \(\:0\le\:{\left({\alpha\:}_{\overline{\mathcal{R}\mathcal{\:}}\:}\right)}^{2}+\:{\left({\delta\:}_{\overline{\mathcal{R}\mathcal{\:}}\:}\right)}^{2}\le\:1\) and \(\:0\le\:{\left({\beta\:}_{\underline{R}}\right)}^{2}+\:{\left({\gamma\:}_{\underline{R}}\right)}^{2}\le\:1.\) We can notice that whenever decision-makers provide theory assessment as \(\:\left(\begin{array}{c}0.5+\iota\:0.9,\:0.4+\iota\:0.8,\:\\\:0.3+\iota\:0.5,\:0.2+\iota\:0.7\end{array}\right)\)then we can notice that for this data the main condition fails to cover it because we can see that \(\:sum\:\left({0.9}^{2},\:{0.8}^{2}\right)=1.45\notin\:\left[0,\:1\right]\) and the main condition \(\:0\le\:{\left({\beta\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}+\:{\left({\gamma\:}_{\overline{\mathcal{R}\mathcal{\:}}}\right)}^{2}\le\:1\) is violated. Hence we can say that introduced notions are also limited.
These notions can be extended to complex q-rung orthopair fuzzy rough set theory. Moreover, some new developments can be made on this idea like distance measures as given in46. A new algorithm can be developed based on the initiated work as discussed in47. Some distance ranking methods can be formulated based on the developed approach as covered in48. Additionally, MCDM approach can be developed as proposed in49.
Moreover, the nomenclature Table is given in (Table 15).
Data availability
The data will be available on reasonable request to corresponding author or anyone can use the data by just citing the article.
References
Hengst, M. D. & Vreede, G. J. D. Collaborative business engineering: a decade of lessons from the field. J. Manage. Inform. Syst. 20 (4), 85–114 (2004).
Talwar, R. Business re-engineering—A strategy-driven approach. Long Range Plann. 26 (6), 22–40 (1993).
Robinson, H. S., Anumba, C. J., Carrillo, P. M. & Al-Ghassani, A. M. Business performance measurement practices in construction engineering organisations. Meas. Bus. Excell. 9 (1), 13–22 (2005).
Legner, C. et al. Digitalization: opportunity and challenge for the business and information systems engineering community. Bus. Inform. Syst. Eng. 59, 301–308 (2017).
Buchananl, D. A. The limitations and opportunities of business process re-engineering in a politicized organizational climate. Hum. Relat. 50 (1), 51–72 (1997).
Childe, S. J., Maull, R. S. & Bennett, J. Frameworks for understanding business process re-engineering. Int. J. Oper. Prod. Manag. 14 (12), 22–34 (1994).
Maull, R. S., Weaver, A. M., Childe, S. J., Smar, P. A. & Bennett, J. Current issues in business process re-engineering. Int. J. Oper. Prod. Manag. 15 (11), 37–52 (1995).
Weerakkody, V., Currie, W. L. & Ekanayake, Y. Re-engineering business processes through application service providers: Challenges, issues and complexities. Bus. Process. Manag. J. 9 (6), 776–794 (2003).
Ullah, A. & Lai, R. Modeling business goal for business/IT alignment using requirements engineering. J. Comput. Inform. Syst. 51 (3), 21–28 (2011).
Van Meel, J. W. & Sol, H. G. Business engineering: Dynanic modeling instruments for a dynamic world. Simul. Gaming 27 (4), 440–461 (1996).
Kousar, S. & Kausar, N. Multi-criteria decision-making for sustainable agritourism: An integrated fuzzy-rough approach. Spectr. Oper. Res. 2 (1), 134–150. https://doi.org/10.31181/sor21202515 (2025).
Baranidharan, B., Meidute-Kavaliauskiene, I., Mahapatra, G. S. & Cincikaite, R. Assessing the sustainability of the prepandemic impact on fuzzy traveling sellers problem with a new fermatean fuzzy scoring function. Sustainability 14 (24), 16560 (2022).
Jeon, J. et al. An innovative probabilistic hesitant fuzzy set MCDM perspective for selecting flexible packaging bags after the prohibition on single-use plastics. Sci. Rep. 13 (1), 10206 (2023).
Kumar, R. & Pamucar, D. A Comprehensive and systematic review of multi-criteria decision-making (MCDM) methods to solve decision-making problems: Two decades from 2004 to 2024. Spectr. Decis. Mak. Appl. 2 (1), 178–197. https://doi.org/10.31181/sdmap21202524 (2025).
Verma, R. & Alvarez-Miranda, E. Multiple-attribute group decision-making approach using power aggregation operators with CRITIC-WASPAS method under 2-dimensional linguistic intuitionistic fuzzy framework. Appl. Soft Comput. 157, 111466 (2024).
Khan, Q., Abdullah, L., Mahmood, T., Naeem, M. & Rashid, S. MADM based on generalized interval neutrosophic Schweizer-Sklar prioritized aggregation operators. Symmetry 11 (10), 1187 (2019).
Sirbiladze, G. & Sikharulidze, A. Extensions of probability intuitionistic fuzzy aggregation operators in fuzzy MCDM/MADM. Int. J. Inform. Technol. Decis. Mak. 17 (02), 621–655 (2018).
Yager, R. R. Aggregation operators and fuzzy systems modeling. Fuzzy Sets Syst. 67 (2), 129–145 (1994).
Dhankhar, C. & Kumar, K. Multi-attribute decision making based on the q-rung orthopair fuzzy Yager power weighted geometric aggregation operator of q-rung orthopair fuzzy values. Granul. Comput. 8 (5), 1013–1025 (2023).
Akram, M., Peng, X. & Sattar, A. Multi-criteria decision-making model using complex Pythagorean fuzzy Yager aggregation operators. Arab. J. Sci. Eng. 46, 1691–1717 (2021).
Akram, M. & Shahzadi, G. A hybrid decision-making model under q-rung orthopair fuzzy Yager aggregation operators. Granul. Comput. 6, 763–777 (2021).
Shahzadi, G., Akram, M. & Al-Kenani, A. N. Decision-making approach under Pythagorean fuzzy Yager weighted operators. Mathematics 8 (1), 70 (2020).
Chinram, R., Ashraf, S., Abdullah, S. & Petchkaew, P. Decision support technique based on spherical fuzzy Yager aggregation operators and their application in wind power plant locations: A case study of Jhimpir, Pakistan. J. Math. 2020 (1), 8824032 (2020).
Naeem, M. et al. A novel decision-making technique based on spherical hesitant fuzzy Yager aggregation information: application to treat Parkinson’s disease. AIMS Math. 7 (2), 1678–1706 (2022).
Ali, G., Alolaiyan, H., Pamucar, D., Asif, M. & Lateef, N. A novel MADM framework under q-rung orthopair fuzzy bipolar soft sets. Mathematics 9 (17), 2163 (2021).
Pawlak, Z. Rough sets. Int. J. Comput. Inform. Sci. 11 (5), 341–356 (1982).
Wang, G. Y., Yao, Y. Y. & Yu, H. A survey on rough set theory and applications. Chin. J. Comput. 32 (7), 1229–1246 (2009).
Pięta, P. & Szmuc, T. Applications of rough sets in big data analysis: an overview. Int. J. Appl. Math. Comput. Sci. 31 (4), 659–683 (2021).
Jayasuruthi, L., Shalini, A. & Kumar, V. V. Application of rough set theory in data mining market analysis using rough sets data explorer. J. Comput. Theor. Nanosci. 15 (6–7), 2126–2130 (2018).
Szul, T. & Kokoszka, S. Application of rough set theory (RST) to forecast energy consumption in buildings undergoing thermal modernization. Energies 13 (6), 1309 (2020).
Dubois, D. & Prade, H. Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 17 (2–3), 191–209 (1990).
Cornelis, C., De Cock, M. & Kerre, E. E. Intuitionistic fuzzy rough sets: at the crossroads of imperfect knowledge. Expert Syst. 20 (5), 260–270 (2003).
Sun, B., Tong, S., Ma, W., Wang, T. & Jiang, C. An approach to MCGDM based on multi-granulation Pythagorean fuzzy rough set over two universes and its application to medical decision problem. Artif. Intell. Rev. 55 (3), 1887–1913 (2022).
Hussain, A., Ali, M. I. & Mahmood, T. Pythagorean fuzzy soft rough sets and their applications in decision-making. J. Taibah. Univ. Sci. 14 (1), 101–113 (2020).
Wang, Y. et al. Decision-making based on q‐rung orthopair fuzzy soft rough sets. Math. Probl. Eng. 2020 (1), 6671001 (2020).
Zheng, L., Mahmood, T., Ahmmad, J., Rehman, U. U. & Zeng, S. Spherical fuzzy soft rough average aggregation operators and their applications to multi-criteria decision making. IEEE Access. 10, 27832–27852 (2022).
Akram, M. & Martino, A. Multi-attribute group decision making based on T-spherical fuzzy soft rough average aggregation operators. Granul. Comput. 8 (1), 171–207 (2023).
Khan, F. M., Bibi, N., Abdullah, S. & Ullah, A. Complex fuzzy rough aggregation operators and their applications in EDAS for multi-criteria group decision-making. Int. J. Fuzzy Log. Intell. Syst. 23 (3), 270–293 (2023).
Yi, J., Ahmmad, J., Mahmood, T., Ur Rehman, U. & Zeng, S. Complex fuzzy rough set: An application in digital marketing for business growth. IEEE Access 12, 66453–66465 (2024).
Tamir, D. E., Jin, L. & Kandel, A. A new interpretation of complex membership grade. Int. J. Intell. Syst. 26 (4), 285–312 (2011).
Ali, M., Tamir, D. E., Rishe, N. D. & Kandel, A. Systems complex intuitionistic fuzzy classes. In 2016 IEEE International Conference on Fuzzy (FUZZ-IEEE) 2027–2034 (IEEE, 2016).
Labassi, F., ur Rehman, U., Alsuraiheed, T., Mahmood, T. & Khan, M. A. A novel approach towards complex Pythagorean fuzzy sets and their applications in visualization technology (IEEE Access, 2024).
Stanujkic, D. & Karabasevic, D. An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: a case of website evaluation. Oper. Res. Eng. Sci. Theory Appl. 1 (1), 29–39 (2018).
Kahraman, C., Onar, S. C., Oztaysi, B. & Ilbahar, E. Selection among GSM operators using Pythagorean fuzzy WASPAS method. J. Mult. Valued Log. Soft Comput., 33. (2019).
Mahmood, T., Idrees, A., Hayat, K. & Ashiq, M. Selection of AI architecture for autonomous vehicles using complex intuitionistic fuzzy rough decision making. World Electr. Veh. J. 15 (9). (2024).
Baranidharan, B., Liu, J., Mahapatra, G. S., Mahapatra, B. S. & Srilalithambigai, R. Group decision on rationalizing disease analysis using novel distance measure on Pythagorean fuzziness. Complex. Intell. Syst. 10 (3), 4373–4395 (2024).
Changdar, C., Pal, R. K. & Mahapatra, G. S. A genetic ant colony optimization based algorithm for solid multiple travelling salesmen problem in fuzzy rough environment. Soft. Comput. 21, 4661–4675 (2017).
Kang, D., Suvitha, K. & Narayanamoorthy, S. Comprehensive distance-based ranking method for evaluating hydraulic converters in tidal stream turbines utilizing picture fermatean fuzzy set. Facta Univ. Ser. Mech. Eng. 1–21. https://doi.org/10.22190/FUME240730046K (2024).
Gul, R. An extension of VIKOR approach for MCDM using bipolar fuzzy preference δ-covering based bipolar fuzzy rough set model. Spectr. Oper. Res. 2 (1), 72–91. https://doi.org/10.31181/sor21202511 (2025).
Acknowledgements
The study was funded by Researchers Supporting Project Nmber (RSPD2025R749), King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
Muhammad Iftikhar and Jabbar Ahmmad prepared the original manuscript, Walid Emam and Dragan Pamucar revised the manuscript as per comments of the reviewers while Tahir Mahmood and Ubaid ur Rehman validate the results, proofread the manuscript and correct the mistakes, wherever necessary.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethics declaration statement
The authors state that this is their original work and it is neither submitted nor under consideration in any other journal simultaneously.
Human and animal participants
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Mahmood, T., Emam, W., Ahmmad, J. et al. Classification of possible solutions regarding business engineering problems by using complex Pythagorean fuzzy rough WASPAS approach. Sci Rep 15, 16538 (2025). https://doi.org/10.1038/s41598-025-99297-x
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-99297-x