Forecasting water quality indices using generalized ridge model, regularized weighted kernel ridge model, and optimized multivariate variational mode decomposition

Abstract

Permeability index (PI) and magnesium absorption ratio (MAR) are both primary irrigation water quality indicators (IWQI) used to evaluate the efficacy of agricultural water supplies. This is considered a complex environmental issue to reliably forecast IWQI parameters without its appropriate time series and limited input sequences. Hence, this research develops an innovative hybrid intelligence framework for the first time to forecast the PI and MAR indices at the Karun River, Iran. The proposed framework includes a new hybrid machine learning (ML) model based on generalized ridge regression and kernel ridge regression with a regularized locally weighted (GRKR) method. This research developed an optimized multivariate variational mode decomposition (OMVMD) technique, optimized by the Runge-Kutta algorithm (RUN), to decompose the input variables. The light gradient boosting machine model (LGBM) is also implemented to select the influential input variables. The main contribution of the intelligence framework lies in developing a new hybrid ML model based on GRKR coupled with OMVMD. Five water quality parameters from the Karun River at two stations (Ahvaz and Molasani) over 40 years are used to forecast the PI and MAR indices monthly. Statistical metrics confirmed that the proposed OMVMD-GRKR model, concerning the best efficiency in the Ahvaz (R = 0.987, RMSE = 0.761, and U95% = 2.108) and Molasani (R = 0.963, RMSE = 1.379, and U95% = 3.828) stations, outperformed the OMVMD and simple-based methods such as ridge regression (Ridge), least squares support vector machine (LSSVM), deep random vector functional link (DRVFL), and deep extreme learning machine (DELM). For this reason, the suggested OMVMD-GRKR model serves as a valuable framework for predicting IWQI parameters.

Introduction

Rivers are vital sources of water for human life, they are playing a crucial role in agriculture, electricity generation, domestic usage, and industry. However, their dynamic nature increases the risk of pollution due to variations in water flow and runoff from nearby areas. Additionally, poor waste disposal practices contribute to both physical and chemical contamination of river ecosystems. These factors exacerbate the susceptibility of rivers to ecological pollution^1,2. Historically, water quality (WQ) problems have often received less attention in research discussions because of abundant water resources³. Nonetheless, as global water availability is expected to decrease due to climate change⁴, there is an urgent need to address WQ to ensure a sufficient water supply for irrigation and other essential uses. Consequently, forecasting WQ facilitates the early identification of pollutants and supports cost-effective treatment strategies. forecasting WQ enables preventive measures to safeguard water supplies, ensuring compliance with health rules and mitigating public health hazards. Therefore, forecasting WQ enhances resource utilization, lowers treatment costs, and ensures access to clean water, particularly by identifying pollutants in river systems.

Reusing water from agricultural drainage systems shows promise as a means to increase the availability of irrigation water in the face of constraints⁵, including growing water shortages, runoff pollution, and conflicting demands from urban and industrial sectors. However, insufficient treatment of this drainage water have adverse effects on soil quality, agricultural growth, and irrigation infrastructure. There are questions about the efficacy of recycled water persist. Several metrics are employed to evaluate the quality of irrigation water. These metrics include residual sodium carbonate (RSC)⁶, the sodium adsorption ratio (SAR)⁷, permeability index (PI)^8,9, magnesium absorption ratio (MAR)¹⁰, and potential of salinity (PS)⁸. Accurate estimating of them can be helpful for use in agricultural purposes. Thus, ongoing attempts exist to create non-physical methods for predicting such indexes^11,12. Non-physical methods utilize computational models and algorithms, such as machine learning (ML) models, to analyze and predict phenomena without relying on direct physical measurements.

ML models offer several advantages, such as their ability to handle missing data, non-linear structure, big datasets of varying sizes, and complex events. ML techniques such as support vector machines (SVMs)¹³, artificial neural networks (ANNs)¹⁴, and least square SVMs (LSSVMs)¹⁵ are among the most reliable computational approaches for rapid and practical WQ modeling^16,17. Numerous studies have demonstrated the reliability and accuracy of these models. For example, the monthly sodium (Na⁺) levels were predicted by two different models, namely, hybrid wavelet-linear genetic programming (WLGP) and wavelet-ANN (W-ANN) in Turkey¹⁸. The computed outcomes proved that the LGP model offers more accuracy compared to the ANN model. In another study, the Karun River’s water quality index (WQI) was predicted by Ref.¹⁹. They employed advanced variable reduction methods, such as the forward selection M5 model tree (FS-M5), focusing on several WQ factors. Their finding showed that the river’s WQ parameters were “Relatively Bad,” with only a 19% chance of improvement. Nouraki et al. (2021) applied four ML models, namely, random forest (RF), multiple linear regression (MLR), support vector regression (SVR), and the M5P model tree to forecast total hardness (TH), total dissolved solids (TDS), and SAR in the Karun River from 1999 to 2019²⁰. The study’s results showed that, even with complicated pollution sources, such models could accurately predict WQ metrics.

In recent years, Ahmadianfar et al. (2022) proposed a new framework called the weighted exponential regression hybridized by gradient-based optimization (WER-GBO)²¹ with the purpose of monthly sodium (Na⁺) forecasts in Maroon River. When WER-GBO was compared to other methods, such as ANFIS, LSSVM, BLR, and RSR, WER-GBO showed better accuracy. Moreover, to forecast the irrigation WQI (IWQI) of Bahr El-Baqr, Egypt, the V-KELM-INFO model was created by Chen et al. (2024) to predict TDS²². They combined the weighted mean of vectors (INFO) algorithm, kernel extreme learning machine (KELM), and variational mode decomposition (VMD) with Boruta-XGBoost. This model greatly enhanced the accuracy of predictions made at the Iranian Idenak station compared to previous models based on metaheuristics.

The prediction of WQ indicators has been supported by a number of effective models in the work of prior scholars^19[,23,]24. However, there is an urgent need for a high-performance, sophisticated framework because of complicated and non-linear datasets. The complexity of WQ data also is a common challenge for traditional ML models. Hence, new advanced ML and artificial intelligence methods offer tremendous potential for solving these challenges^21,25,26. As an illustration, ridge regression, SVMs, hybrid models, deep learning methods, and others can better manage big datasets and non-linear connections. Optimization strategies also allow these models to maximize computing efficiency and forecast accuracy. Thus, to improve decision-making and long-term planning for water resources, it is essential to create and use these advanced models for WQ management.

The main shortcomings of the previous studies can be summarized as,

• Traditional ML models such as ANN, SVR, and MLR have been widely used; however, they exhibit limited effectiveness in capturing the complex, non-linear dynamics of water quality prediction.

• Decomposition methods like the VMD are highly sensitive to their control parameters. Most previous studies did not carefully optimize these settings, which could lead to less accurate results.

• Combining ML models and developing a robust and accurate framework is essential to solve complex forecasting problems. However, most previous water quality research relied on single machine learning models, which often limited the accuracy and comprehensiveness of predictions.

To address the above shortcomings, the main objective of this research is to develop a unique hybrid approach, namely the GRKR, for forecasting IWQI. The GRKR model is developed based on a combination of a generalized ridge regression, an efficient weighted least squares method with regularization, and kernel ridge regression with a wavelet kernel. The optimal control parameters for the proposed GRKR model are also determined using a mathematical optimization technique known as Runge-Kutta optimization (RUN). Decomposing the input variables through optimized multivariate variational mode decomposition (OMVMD) enhances prediction accuracy.

Consequently, the proposed intelligent framework significantly improves decision-making in WQ management by enabling water quality managers to take preventive actions through precise predictive insights. The framework integrates GRKR, OMVMD, LGBM, and RUN methods to provide reliable predictions, allowing decision-makers to make informed choices that lead to improved WQ outcomes. This research contributes to the academic understanding of ML applications in environmental science while also offering practical tools for professionals working in the field.

Material and method

Case study

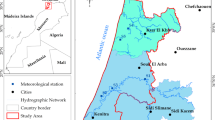
The Karun River’s watershed is situated in southwestern Iran. The Karun River with 950Km is the longest and most significant river in Iran. The Karun River’s longitudinal and latitudinal coordinates are 48° 15′ to 52° 30′ E and 30° 17′ to 33° 49′ N, respectively. Figure 1 depicts the Karun River within the Khuzestan Plain, as well as the specific locations of the WQ monitoring units situated along the river. In recent years, the WQ of the Karun River has significantly declined because of agricultural activities, human consumption, and industrial processes. The lack of sewage networks, non-compliance with environmental regulations by major industries, and the direct discharge of wastewater into the river are the primary factors affecting the WQ in this river. As a result, forecasting WQ has become essential for monitoring and managing the river’s environmental health, allowing for early problem detection, timely interventions, and informed decision-making to safeguard public health and preserve the ecosystem.

This study utilized monthly WQ data collected from two monitoring sites over a 40-year period. The time-series graph of WQ parameters is provided in Appendix A. The independent variables in this research include nine key WQ indicators: chloride (Cl), discharge (Q), sulfate (SO₄²⁻), sodium (Na), magnesium (Mg), bicarbonate (HCO₃), calcium (Ca), electrical conductivity (EC), and total dissolved solids (TDS). The dependent variables also include two IWQI, namely: the magnesium absorption ratio (MAR) and the permeability index (PI), which are measured at the Ahvaz and Molasani stations along the river.

Table 1 presents the dataset’s statistical summary, including the mean (Mean), maximum (Max), minimum (Min), and median (Med) values. It also reports skewness (Skew), standard deviation (SD), and kurtosis (Kur). Skewness and kurtosis are critical statistical measures for WQ evaluation, as they provide insights into data distribution. Skewness indicates the asymmetry of the data, showing whether pollutant concentrations tend to exceed or fall below the mean. Kurtosis quantifies the “tailedness” of the distribution, emphasizing the presence of outliers and the potential risks associated with extreme values. Therefore, these statistical factors enhance the understanding of data variability and trends, supporting informed decision-making and efficient WQ management strategies.

Concerning PI, the variable measures how water affects soil aeration and water infiltration, which are vital for plant growth. In fact, PI is used to evaluate the long-term impact of irrigation water on soil structure and permeability. High PI levels in water can hinder soil aeration and water penetration, negatively affecting plant development. When determining whether or not irrigation water is suitable for agricultural use, the MAR provides a useful metric to consider. An evaluation of the potential effects of magnesium content in water on soil and plant life is now part of the research process. To sustain fertile soil and achieve peak crop production, managing the MAR in irrigation water is critical. Here are the steps to compute the PI and MAR:

$$\:\text{P}\text{I}=\left(\frac{\left[\text{N}\text{a}\right]+\sqrt{\left[\text{H}\text{C}\text{O}3\right]}}{\left[\text{C}\text{a}\right]+\left[\text{M}\text{g}\right]+\left[\text{N}\text{a}\right]}\right)\times\:100$$

(1)

$$\:\text{M}\text{A}\text{R}=\left(\frac{\left[\text{M}\text{g}\right]}{\left[\text{C}\text{a}\right]+\left[\text{M}\text{g}\right]}\right)\times\:100$$

(2)

PI and MAR were determined using parameters Ca, Na, and Mg, HCO3, which were not suitable to be employed as input parameters in ML models. Consequently, $\:{\text{S}\text{O}}_{4}^{-2}$, TDS, Q, EC, and Cl were the factors that were used as inputs.

Table 1 Statistical characteristics of Ahvaz and Molasani stations.

Fig. 1

Karun River location and selected two stations (Ahvaz and Molasani)²⁷.

Generalized ridge regression

The proposed generalized ridge regression (GRM) method is designed to resolve issues associated with multicollinearity and overfitting. GRM integrates ridge regression with generalized linear models (GLM)²⁸ to yield a powerful and flexible model. This hybrid approach updates the model coefficients continually through an iteratively reweighted least squares (IRLS) procedure. The IRLS chooses the appropriate link function, its derivative, and a variance function to be used in any given distribution namely: normal, binomial, Poisson, or gamma. The link function is used to compute the mean response at each iteration and the linear predictor. Then, it makes a weight matrix and a pseudo-response variable. The main formulas in GLM can be defined as,

$$\:\eta\:=X\alpha\:$$

(3)

where $\:\eta\:$ represents the linear predictor for the observation in a GLM. $\:X$ indicates the matrix of explanatory variables and $\:\alpha\:$ denotes the vector of coefficients.

The link function connects the expected outcome of the dependent variable with its linear component. The aforementioned function transforms a mean value for the response variables into a linear combination, even if they are not directly related to the predictors²⁸. This transformation facilitates an efficient modeling using linear regression methods. The link function of GLM is expressed as,

$$\:f\left(\mu\:\right)=\eta\:$$

(4)

where $\:\mu\:$ represents the mean of the response variables. For different GLM distributions (such as normal, binomial, or Poisson), there are different link functions $\:f$ according to $\:\mu\:$ and $\:\eta\:$​ appropriately. Various link functions are used to connect the mean response ($\:\mu\:$) to the linear predictor ($\:\eta\:$) in a GLM method. Each distribution, such as normal, binomial, or Poisson, requires a specific link function to accurately represent the relationship between the response variable and the predictors.

Based on Eq. (3), the coefficient $\:\alpha\:$ is formulated by using GLM approach. Consequently, $\:\alpha\:$ is obtained by the standard weighted least squares method. In order to minimize the weighted sum of squared residuals, the mentioned method optimizes the coefficients $\:\alpha\:$. In this step, the residuals are weighted by the diagonal matrix $\:w$. This method is very helpful in the GLM because the distribution of response variable may not be normal and the variance might be non-constant across observations. Consequently, the weights $\:w$ are adjusted to align with these model features, which after accurate approximations of $\:\alpha\:$ are obtained. The coefficient $\:\alpha\:$ can be calculated as,

$$\:\alpha\:={({X}^{T}\times\:w\times\:X)}^{-1}\times\:({X}^{T}\times\:w\times\:z)$$

(5)

in which

$$\:w=diag\left(\frac{{f}^{{\prime\:}}\left(\mu\:\right))}{Var\left(Y\right)}\right)$$

(5.1)

and

$$\:z=\eta\:+\frac{y-\mu\:}{{f}^{{\prime\:}}\left(\mu\:\right))}$$

(5.2)

where $\:\left({f}^{{\prime\:}}\right(\mu\:\left)\right)$ expresses the derivative of the link function $\:f$ with respect to $\:\mu\:$. $\:Var\left(Y\right)$ represents the variance function associated with the distribution of the response variable $\:Y$ .

Based on the main formula for GLM (Eq. (3)), the GRM can be obtained by incorporating ridge regularization. We add the regularization term ($\:{\lambda\:}_{1}$) to the original equation (Eq. (4)). Therefore, the coefficient of GRM method is defined as,

$$\:\alpha\:={({X}^{T}\times\:w\times\:X+{\lambda\:}_{1}\times\:I)}^{-1}\times\:({X}^{T}\times\:w\times\:z)$$

(6)

where $\:{\lambda\:}_{1}$ indicates the regularization term. $\:I$ denotes the unit matrix. To calculate the predicted value based on the GRM model ($\:{\stackrel{\prime }{y}}_{GRM})$, Eq. (7) is employed.

$$\:{\stackrel{\prime }{y}}_{GRM}=X\alpha\:$$

(7)

Kernel ridge regression with regularized locally weighted method

Kernel ridge regression (KRidge) is built on ridge regression (Ridge) by enhancing its efficiency, particularly in modeling non-linear relationships through kernel methods²⁹. Ridge regression effectively addresses linear models and mitigates overfitting via a penalty term that shrinks coefficients; the KRidge enhances this approach by integrating kernel approaches, enabling the capturing of non-linear correlations in the data. This new feature allows the KRidge to model complicated datasets with comparability, in contrast to conventional ridge regression. Thus, the KRidge serves as a significant enhancement of the original methodology, especially for non-linear variables. Equation (8) is employed to achieve the predicted value ($\:{\stackrel{\prime }{y}}_{KRidge})$.

$$\:{\stackrel{\prime }{y}}_{KRidge}=X\beta\:$$

(8)

In which

$$\:\beta\:{=\left(KrF+{\lambda\:}_{2}I\right)}^{-1}{X}^{T}\text{y}$$

(9)

Where $\:\beta\:$ expresses the regression coefficient of the KRdige, and $\:{\lambda\:}_{2}$ indicates the regularization factor of the KRidge model. $\:KrF$ represents the kernel function. The wavelet kernel function was employed, formulated as,

$$\:{KrF}_{ik}=\text{cos}\left(\rho\:\times\:\frac{-\left({x}_{i}-{x}_{k}^{{\prime\:}}\right)}{\nu\:}\right)\times\:{exp}\left(\frac{-{\left|\left|{x}_{i}-{x}_{k}^{{\prime\:}}\right|\right|}^{2}}{4\times\:\delta\:}\right)$$

(10)

where $\:\rho\:$,$\:\:\nu\:$, and $\:\delta\:$ indicate the kernel function factors. The RUN optimization method was applied to derive optimal values for these factors.

This research used the regularized locally weighted (RLW) approach to compute new input variable coefficients, which improved the KRidge forecasting accuracy even more. The main formula of RLW can be formulated as,

$$\:\psi\:={({X}^{T}\times\:\omega\:\times\:X+{\lambda\:}_{3}\times\:I)}^{-1}\times\:({X}^{T}\times\:\omega\:\times\:y)$$

(11)

where $\:\omega\:$ denotes a kernel function based on the wavelet kernel. $\:{\lambda\:}_{3}$ indicates the regularization factor for the RLW method. The factor $\:\psi\:$ is used to create a new kernel function based on the following formulas,

$$\:{X}_{new}=\psi\:X$$

(12)

$$\:{KrF}_{new}=KrF\left({X}_{new},{X}_{new,k}\right)$$

(13)

where $\:{KrF}_{new}$ is a new version of $\:KrF$, which is calculated based on $\:{X}_{new}$.

Equation (9) can be reformulated as,

$$\:{\beta\:}_{new}{=\left({KrF}_{new}+{\lambda\:}_{2}I\right)}^{-1}{X}^{T}\text{y}$$

(14)

and

$$\:{\stackrel{\prime }{y}}_{KRidge}=X{\beta\:}_{new}$$

(15)

where $\:{\beta\:}_{new}$ is a new version of $\:\beta\:$, which is calculated based on $\:{KrF}_{new}$.

The proposed hybrid model

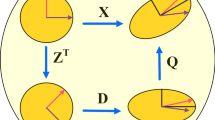
A new hybrid regression model for IWQI forecasting was created in this study. It is based on two successful regression models, the GRM (sometimes called the GRKR model) and the KRidge (described above). The following relationship was defined,

$$\:{\stackrel{\prime }{y}}_{GRKR}=a\times\:{\stackrel{\prime }{y}}_{KRidge}+\left(1-a\right)\times\:{\stackrel{\prime }{y}}_{GRM}$$

(16)

where $\:{\stackrel{\prime }{y}}_{GRKR}$ denotes the predicted value calculated based on $\:{\stackrel{\prime }{y}}_{KRidge}$ and $\:{\stackrel{\prime }{y}}_{GRM}$. $\:a$ indicates a number in the interval of [0, 1]. $\:a$ is achieved by optimization method (RUN). Figure 2 displays the schematic of the proposed GRKR model.

Fig. 2

Schematic of GRKR model.

Runge-Kutta optimization (RUN)

RUN algorithm with two main operators, namely the Runge-Kutta search (RKS) engine and the enhance solution mechanism (ESM), is a mathematics-based optimization method³⁰. The RUN algorithm was developed based on the Rung-Kutta method (RKM). The main components of the algorithm are described in the following sub-sections.

RKS operator

RUN algorithm uses the RKS operator to search globally and locally in the feasible space of each problem. The RKS’s solution is calculated as follows,

$$\:{x}_{RKS}=\left\{\begin{array}{c}\left({x}_{a}+{\sigma\:}_{1}.A.c.{x}_{a}\right)+A.RKS+\phi\:.randn\text{.(}{x}_{b}-{x}_{a})\:\:\:\:\:\:\:if\:rand<0.5\\\:\left({x}_{b}+{\sigma\:}_{1}.A.c.{x}_{b}\right)+A.RKS+\phi\:.\:randn.\left({x}_{e1}-{x}_{e2}\right)\:\:\:\:\:\:otherwise\:\:\:\end{array}\right.$$

(17)

where $\:{\sigma\:}_{1}$ indicates an integer number with the value of 1 or -1. $\:c$ expresses a random value within the interval of [0, 2]. $\:A$ is an adaptive factor. $\:{x}_{e1}$ and $\:{x}_{e2}$ express two random solutions ($\:e1\ne\:e2\ne\:n$), which are selected within the range of [1, Np]. Np indicates the number of populations and $\:\phi\:$ expresses a random number. $\:RKS$ is defined based on the Runge-Kutta method. The RKS is thoroughly formulated in³⁰.

ESM operator

In order to enhance the quality of solutions and escape from local optima solutions, the ESM operator is embedded in the RUN. The solution achieved by the ESM ($\:{x}_{ESM}$) is defined as,

$$\begin{gathered} {\varvec{i}}{\varvec{f}}~~rand<0.5 \hfill \\ \,\,\,\,\,\,\,{\varvec{i}}{\varvec{f}}~~\varvec{\upvarrho}<1 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_{ESM}}={x_{p1}}+{\sigma _2}{\text{.}}\varvec{\upvarrho}{\text{.|}}\left( {{x_p} - {x_m}} \right)+randn| \hfill \\ \,\,\,\,\,\,\,\,{\varvec{e}}{\varvec{l}}{\varvec{s}}{\varvec{e}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_{ESM}}=\left( {{x_{p2}} - {x_m}} \right)+{\sigma _2}{\text{.}}\varvec{\upvarrho}{\text{.|}}\left( {2.rand{\text{.}}{x_p} - {x_m}} \right)+randn| \hfill \\ \,\,\,\,\,\,\,\,\,{\varvec{e}}{\varvec{n}}{\varvec{d}} \hfill \\ {\varvec{e}}{\varvec{n}}{\varvec{d}} \hfill \\ \end{gathered}$$

(18)

$$\:\varrho\:=rand\left(0\text{,}\:2\right)\text{.}exp\left(-q.\left(\frac{Iter}{MIter}\right)\right)$$

(18.1)

$$\:{x}_{m}=\frac{{x}_{e1}+{x}_{e2}+{x}_{e3}}{3}$$

(18.2)

$$\:{x}_{p1}=\theta\:\times\:{x}_{m}+(1-\theta\:)\times\:{x}_{bst}$$

(18.3)

where $\:\theta\:$ indicates a random value within the range of [0, 1]. $\:q$ expresses a random value ($\:q=5\times\:rand$), and $\:{\sigma\:}_{2}$ denotes an integer number, equal to 1, 0, or -1.

$\:{x}_{ESM}$ may not exhibit a superior objective function compared to solution $\:{x}_{n}$ (a new solution). $\:{x}_{p2}$ is generated to explore the possibility of obtaining more promising solution. The formulation of $\:{x}_{p2}$ is as follows:

if rand<$\:\:\varrho\:$

$$\:{x}_{p2}=\left({x}_{ESM}-rand\text{.}{x}_{ESM}\right)+A\text{.(}rand\text{.}{x}_{RKS}+(2.rand\text{.}{x}_{bst}-{x}_{ESM}))\:$$

(19)

end.

Feature selection

Overloading ML models with excessive parameters weakens their overall performance. Many techniques are employed for input selection, mainly emphasizing linear connections. They include auto-correlation, correlation, principal component analysis, and so on³¹. This research used the LGBM data filtering technique for improving accuracy of the potential model. This technique is a nonlinear way to select parameters for input. LGBM also is a well-known gradient-boosting ML approach that consistently delivers top-notch results across several domains³². LGBM trains decision trees using a histogram-based approach, which divides continuous information into bins to speed up training. This approach reduces data complexity leading to faster computation and lower memory usage while maintaining high accuracy during training and testing. To promote instances with more considerable gradients, LGBM prioritizes these and incorporates an autonomous feature-selection technique. This study employed LGBM to identify the optimal variables for input, to enhance the overall effectiveness of the model and reduce the dimensionality of the forecasting problem (specifically, the number of input variables that can complicate the prediction process).

Optimized multivariate variational mode decomposition (OMVMD)

Decomposition techniques break down complicated data into separate high- and low-frequency components, enhancing clarity and streamlining analysis. A notable multivariate variant of the VMD method is the MVMD³³. The main parameters in MVMD are the total value of decomposition methods (K) and the quadratic penalty component ($\:\phi\:$). The value of IMF and the bandwidth of IMF is determined by K and $\:\phi\:$, respectively. When the K value is too high, mode aliasing occurs, and when it is too low, feature extraction is inadequate, and incomplete decomposition occurs. Therefore, the optimization of the K and $\:\phi\:$ variables was achieved in the current study by using the RUN optimization method. RUN mitigated the negative impacts of tuning parameter selection processes by making sure that the MVMD decomposition factors were adequately scaled.

Employing an adaptation function as the optimization criteria is necessary for optimizing the MVMD variables. Therefore, developing an adaptive function compatible with strain time series is of paramount importance. The envelope entropy quantifies the degree of sparsity in a signal, and its numerical value exhibits an inverse correlation with the periodic nature of the signal. To put it simply, as the signal’s periodicity increases, the envelope entropy decreases. Because of the mentioned conditions, the objective function chosen for optimization is the minimal envelope entropy. This function aims to enhance the extraction of periodic features from the input parameter and increase the decomposition performance by optimizing the K and $\:\phi\:$. Here is the formula for determining the envelope entropy³⁴:

$$\:Objective\:Function=\:\frac{1}{K}\sum\:_{k=1}^{K}EI\left(k\right)$$

(20)

in which

$$\:{EI}_{pd}\left(k\right)=-\sum\:_{j=1}^{m}\:\:{pd}_{i}{\text{l}\text{o}\text{g}}_{2}{pd}_{i}$$

(21)

$$\:{pd}_{i}=es\left(j\right)/\sum\:_{j=1}^{m}\:\:es\left(j\right)$$

(22)

$$\:es\left(j\right)=\sqrt{\left[x\right(j){]}^{2}+\{H\left[x\right(j\left)\right]{\}}^{2}}$$

(23)

The equation $\:{EI}_{pd}$ expresses the envelope entropy of an IMF signal $\:x$, where $\:m$ and $\:pd$ denote the length of the signal and probability distribution, respectively. $\:es$ and $\:H\left[\text{*}\right]$ define the series of envelope signals derived by Hilbert demodulation of the signal $\:x$ and the Hilbert transform, respectively.

The following represent the precise phases of the signal decomposing process based on RUN-OMVMD presented in this study, as illustrated in the flow diagram (Fig. 3):

• (1) Consider the input signal $\:x\left(t\right)$ and employ the OMVMD control variable pair [K, $\:\phi\:$] as the two-dimensional population of the RUN. Establish the value interval for the control factor pair, with K having a range of [2,10] and $\:\phi\:$ having a range of [200,5000] options. Put the RUN algorithm’s parameters, such as the population size Np and the maximum number of iterations $\:MIter$, into the initial state.

The limits for K [2, 10] in the MVMD decomposition method prevent excessive dimensionality, balancing complexity and manageability. The range for $\:\phi\:$ [200,5000] allows flexibility in capturing data characteristics while avoiding excessive smoothing. These parameters are informed by previous studies^35,36 to optimize performance and maintain interpretability.

• (2) Use the initialized two-dimensional population [K, $\:\phi\:$] as an input variable to decompose the input features in OMVMD. Compute the fitness value of each mode and choose the initial solution with the least fitness value.

• (3) Evaluate the present iteration’s fitness value in relation to the previous iteration. Make sure to update the answers by substituting the current iteration’s fitness value in the prior iteration if the current iteration’s value is low.

• (4) Use Eqs. (17–19) to revise the best solution and existing solution locations.

• (5) To achieve the ideal fitness value of RUN and the accompanying optimal parameters [K, $\:\phi\:$], repeat steps 3 through 4, and continue loop iterations until the maximum number of iterations $\:MIter$ is achieved.

• (6) Utilize OMVMD to decompose the input signal into many IMFs by setting an ideal value [K, $\:\phi\:$] as the control factor.

Fig. 3

Flowchart of optimized MVMD.

Statistical metrics

This study employs seven statistical criteria for selecting the most effective ML models in predicting IWQI. A lower result for RMSE (root-mean-square error), which may range from 0 to ∞, indicates a better match. The correlation coefficient (R) ranges from − 1 to 1, with 1 showing perfect correlation. The uncertainty coefficient (U_95%) at a 95% confidence level also ranges from 0 to ∞, signifying uncertainty levels. Vicis symmetric distance (VSD) ranges from 0 to ∞, where lower values suggest better similarity. The index of agreement (I_A) ranges from 0 to 1, with 1 indicating perfect agreement. Maximum absolute error (MaxAE) and mean absolute percentage error (MAPE) both range from 0 to ∞, with lower values showing better performance. Despite the fact that a few of these measures are associated with linear models, they are useful for evaluating non-linear models as well. They provide insight into the consistency and accuracy of predictions made using different methods. These metrics are formulated as,

$$\:R=\frac{\sum\:_{i=1}^{N}\left({IWQI}_{Ms,i}-\:{\stackrel{-}{IWQI}}_{Ms}\right)\times\:\left({IWQI}_{F,i}\:-{\stackrel{-}{IWQI}}_{F}\:\right)\:}{\sqrt{\sum\:_{i=1}^{N}({{IWQI}_{Ms,i}-\:{\stackrel{-}{IWQI}}_{Ms})}^{2}\times\:\:\sum\:_{\text{i}=1}^{\text{N}}({{IWQI}_{F,i}\:-\:{\stackrel{-}{IWQI}}_{F}\:)}^{2}\:\:\:\:\:}\:\:}$$

(24)

$$\:MAPE=\frac{1}{N}\:\sum\:_{i=1}^{N}\left|\frac{{IWQI}_{Ms,i}-\:{IWQI}_{F,i}}{{IWQI}_{Ms,i}}\right|\times\:100$$

(25)

$$\:MaxAE={max}_{i=1,\dots\:,N}\left|{IWQI}_{Ms,i}-{IWQI}_{F,i}\right|$$

(26)

$$\:RMSE=\sqrt{\frac{1}{N}\:\sum\:_{i=1}^{N}({IWQI}_{Ms,i}-\:{IWQI}_{F,i}{)}^{2}}$$

(27)

$$\:IA=1-\frac{\sum\:_{i=1}^{N}{\left({IWQI}_{F,i}-{IWQI}_{Ms,i}\right)}^{2}}{\sum\:_{i=1}^{N}{\left(\left|\left({IWQI}_{F,i}-\stackrel{-}{{IWQI}_{F}}\right)\right|+\left|\left({IWQI}_{Ms,i}-\stackrel{-}{{IWQI}_{Ms}}\right)\right|\right)}^{2}},\:0<IA\le\:1$$

(28)

$$\:VSD=\:\sum\:_{i=1}^{N}\frac{{({IWQI}_{Ms,i}-{IWQI}_{F,i})}^{2}}{\text{m}\text{i}\text{n}({IWQI}_{Ms,i},{IWQI}_{F,i})}$$

(29)

$$\:{U}_{95\%}=1.96\sqrt{{SD}^{2}+{RMSE}^{2}}$$

(30)

where $\:{IWQI}_{Ms,i}$ and $\:{IWQI}_{F,i}$ express the measured and forecasted IWIQ values, correspondingly. $\:{\stackrel{-}{IWQI}}_{Ms}$ and $\:{\stackrel{-}{IWQI}}_{F}$ are the average values of the measured and forecasted IWQIs, respectively. N indicates the size of the dataset, and SD expresses the standard deviation of dataset.

Model development

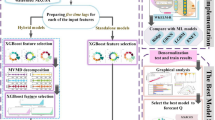
The IWQI at two Iranian stations were predicted using several ML models in this research. A total of five ML methods, namely deep random vector functional link (DRVFL)³⁷, GRKR, LSSVM, deep ELM (DELM)³⁸, Ridge, and a stacking technique based on the regression tree model and generalized linear regression (GLM), were integrated into the proposed framework. They also incorporated the OMVMD decomposition method and the LGBM feature selection technique. The architecture that was built to anticipate IWQI is shown in Fig. 4. A three-month advance forecast of IWQI values (t + 3) was the aim of this research. The two primary steps in developing the model were:

Decomposition and feature selection approach

The MAR and PI parameters represented the output elements, whereas Q, $\:{SO}_{4}^{-2}$, Cl, TDS, and EC constituted the key input variables, as stated in Sect. 2.8. A total of 50 input parameters (5 × 10 = 50) were employed with a 10-time lag applied to each of the 5 input factors. The 10 lag-time of PI and MAR were also used as the input variables. Therefore, there were a total of 65 variables for input. The 65 variables were first deconstructed by the OMVMD approach to simplify the signals to capture different frequency patterns, isolating noise and significant trends. Simplifying signals can also be accomplished through OMVMD aimed at reducing complexity and enhancing clarity.

The mode decomposition factor (k) and the penalty parameter $\:\phi\:$ were the main adjustment parameters for the MVMD approach. They also were crucial for achieving promising accuracy. This goal was achieved by optimizing the MVMD using the RUN algorithm to determine the optimal values of k and $\:\phi\:$ at all the stations. Table 2 reports the ideal values of k and $\:\phi\:$.

Table 2 Optimal values of MVMD parameters.

The OMVMD method used 65 input parameters to perform a simultaneous decomposition, resulting in the storage of IMFs that represented the independent variables’ constituent components. The parameters for input were the initial set of 65-time delays, which improved accuracy. In the case of PI-A forecasting, for example, 65 × 8 IMFs were applied as input variables (a total of 520 variables). Then, the optimal input variables were specified using the LGBM, as mentioned in Sect. 2.5. The step towards dimensionality reduction in the input variables was the selection of the most significant features (35% of the total) for further analysis. According to this process, the procedure yielded the following feature counts: 73 for PI-A, 128 for MAR-A, 129 for PI-M, and 128 for MAR-M. The features used for the PI-A and MAR-A are shown in Fig. 5. It is worth mentioning that the important features for the PI-M and MAR-M are found in Appendix (B).

Fig. 4

Developed framework to forecast IWQIs using ML models.

Fig. 5

Selected features for (a) PI-A and (b) MAR-A.

Model adjustment

Parameter tuning in ML algorithms is a significant part of model development for predicting. However, using solutions that are close to the optimal region during tuning decrease the precision of the method, which can lead to an inequitable evaluation of various prediction approaches. This occurs because models may appear less effective due to suboptimal parameter configurations. The RUN method was employed to optimize the main parameters of the GRKR method, ensuring a more thorough exploration of the parameter space and providing a fairer evaluation of forecasting techniques. The RUN method also helped to tune the tuning parameters for the other ML methods (DELM, LSSVM, Ridge, DRVFL, and Stacking). Tables 3 and 4 demonstrate the ideal values for the parameters relating to the simple-based and OMVMD-based ML methods, respectively.

Table 3 Control parameter values of simple-based ML models for four cases.

Table 4 Control parameter values of OMVMD-based ML models for four cases.

Results and discussion

Evaluate ML models using statistical metrics

Table 5 compares the performance of several models (simple-based and OMVMD-based) with R, RMSE, MAPE, IA, MaxAE, VSD, and U_95% to forecast the PI-A index. The study like previous studies are also evaluated over testing stages to better demonstrate the performance of ML models^21,22. Almost all criteria demonstrated that the OMVMD-GRKR model performed well. When the predicted amounts compared with the observed values of the PI-A parameter, OMVMD-GRKR achieved the highest R values (0.987), the lowest RMSE (0.761) and MAPE (0.990). The I_A value, which was near to 1, highlighted even more the strong predictive capacity of the OMVMD-GRKR model. To demonstrate minor prediction errors and variability, OMVMD-GRKR reported quite low MaxAE, VSD, and U_95% values compared to other models. The OMVMD-GRKR model’s low values suggest that the proposed model outperforms other models in accuracy and reliability. On the other hand, simple-based models like GRKR, Ridge, LSSVM, DELM, DRVFL, and Stacking showed much higher error metrics, such as RMSE, MAPE, MaxAE, U_95%, and VSD, along with lower R values. OMVMD-GRKR stood out among the OMVMD-based models as it successfully obtained the best outcomes for forecasting the PI-A index.

The statistical results for the simple and OMVMD-based MAR-A forecasting models are shown in Table 6. With an R-value of 0.981, an RMSE of 1.862, and a MAPE of 3.945, the OMVMD-GRKR retained its superior performance for the test data. These results demonstrated that the model maintained its reliability and accuracy even when faced with unknown data (the testing dataset). The I_A stayed high at 0.990, which supported the model’s accuracy even more. Simpler models such as GRKR, Ridge, LSSVM, DELM, DRVFL, and Stacking had far lower R values and much larger errors. Consequently, the OMVMD-GRKR model was the best option among the models assessed overall for predicting MAR-A because of minimal errors, strong correlation, and a reasonable agreement with accurate data.

Table 5 Statistical metrics achieved by ML models for PI-A case.

Table 6 Statistical metrics achieved by ML models for MAR-A case.

Table 7 shows PI-M forecasting outcomes with all ML models. The OMVMD-GRKR model displayed the highest performance in predicting PI-M, With high prediction accuracy (R = 0.963), low RMSE (1.379), and low MAPE and MaxAE values. It also preserved a strong I_A (0.980), reflecting high model stability. Other OMVMD-based models, such as GRKR, Ridge, LSSVM, DELM, DRVFL, and Stacking, performed better than simpler models that did not use OMVMD, but none of them were as effective as OMVMD-GRKR. This demonstrated how the OMVMD approach, combined with GRKR, improves reliability and the accuracy of forecasts.

Table 8 shows the detailed statistical findings for MAR-M forecasting. The OMVMD-GRKR model outperformed the others in predicting MAR-M. Its high R and IA values, low RMSE, and MAPE demonstrate good alignment between predicted and actual values, and lower MaxAE and VSD values show better handling of severe errors. Though they were not as successful as the OMVMD-GRKR model, other OMVMD-based models also outperformed their simpler equivalents. These analyses show that OMVMD-based methods, especially when coupled with the GRKR model, were the most successful in predicting the IWQI with high accuracy.

Table 7 Statistical metrics achieved by ML models for PI-M case.

Table 8 Statistical metrics achieved by ML models for MAR-M case.

Figure 6 presents the ARAS (additive ratio assessment (ARAS))³⁹ scores for all ML models. The ARAS method is a multi-criteria decision-making (MCDM) method, which is used to evaluate and prioritize several options based on multiple criteria⁴⁰. The ARAS technique evaluates and ranks OMVMD- and simple-based models with considering seven performance criteria (R, RMSE, MAPE, IA, MaxAE, VSD, and U_95%). The models’ relative efficacy is graphically shown in a cumulative bar graph that compares their overall performance. Each bar represents the entire ARAS score, and higher cumulative scores suggest better performance. The goal of this research is to identify the model type that performs best overall. The cumulative scores for OMVMD-GRKR, OMVMD-Ridge, OMVMD-LSSVM, OMVMD-DELM, and OMVMD-Stacking were 2.998, 1.977, 1.935, 1.198, 2.143, and 1.126, respectively. Consequently, the OMVMD-GRKR model achieved the best ARAS score to forecast the IWQI.

Fig. 6

ARAS score calculated for ML models.

Evaluate ML models using scatter plot

An essential tool for evaluating model performance in regression analysis is the scatterplot of predicted values compared to actual values. A well-fitting linear correlation model is represented by points along a diagonal line. large variations also refer to predicting trends or biases. This graph offers valuable insights for assessing the reliability and accuracy of the model. Figure 7 shows the scatter plot representing all models at the Ahvaz station. The best ML method in Fig. 7 is the one that exhibits the least disparity between the lower and upper bounds (UB-LB) of the data samples. It can be seen that the OMVMD-GRKR model for PI-A had the lowest (UB-LB) of 3.62, demonstrating its high precision in predicting compared to the other ML methods. The LSSVM and DRVFL methods had a (UB-LB) value of 4.92, which was somewhat lower than the DELM model’s (UB-LB) value of 5.83. The Ridge and Stacking models exhibited larger (UB-LB) values of 7.27 and 13.17, respectively, suggesting less accurate projections for the PI-A index. For MAR-A forecasting, the UB-LB values for OMVMD-GRKR, OMVMD-DELM, OMVMD-DERVFL, OMVMD-LSSVM, OMVMD-stacking, and OMVMD-Ridge were 12.38, 14.44, 14.93, 14.98, 18.11, and 21.32, respectively. These findings showed that the OMVMD-GRKR model could achieve the smallest UB-LB, resulting in the best model to forecast the MAR-A and PI-A index.

Scatter plots of PI-M and MAR-M is presented in Appendix C. In the case of PI-M and MAR-M forecasting, the proposed OMVMD-GRKR indicated the best performance compared with the other models. The OMVMD-GRKR was able to yield the smallest values of UB-LB for PI-M (6.41) and MAR-M (13.06), indicating high accuracy and reliability compared to the other models.

Fig. 7

Scatter plot achieved using ML models for (a) PI-A and (b) MAR-A.

Evaluate ML models using density plot

ML models’ relative error distribution for PI-A and MAR-A forecasting is shown in Fig. 8. A mix of box and strip graphs is used to display the relative error distribution of all the ML models. The figure illustrates that the relative errors of the OMVMD-GRKR model for PI-A forecasting were tightly distributed around zero, with the range of [-0.03, 0.03]. The predicted values of PI-A were quite accurate and consistent, as seen by the tightly packed data points around the zero-error line in the strip plot. For the OMVMD-Ridge, OMVMD-DRVFL, OMVMD-Stacking, OMVMD-DELM, and OMVMD-LSSVM models, the ranges of relative error were [-0.05, 0.07], [-0.05, 0.04], [-0.10, 0.14], [-0.15, 0.09], and [-0.04, 0.05], respectively, indicating a broader range of relative errors. The proposed OMVMD-GRKR model was able to achieve the smallest range of relative error ([-0.15, 0.23]) compared with the other models for the MAR-A forecasting.

Appendix D shows the relative error distribution of PI-M and MAR-M forecasting. The figure clearly indicates that the OMVMD-GRKR method outperformed the others, demonstrating the smallest range of relative error for PI-M ([-0.07, 0.04]) and MAR-M ([-0.28, 0.22]) compared to the other ML methods.

Fig. 8

Relative error distribution of ML models for (a) PI-A and (b) MAR-A.

Evaluate ML models using violin plot

The violin plot (in Fig. 9) shows the distribution of PI-A, MAR-A, PI-M, and MAR-M for all ML models. The mentioned plots present a comparison between a measured reference and six prediction models (GRKR, Ridge, dRVF1, Stacking, DELM, and LSSVM) for the distribution of all IWQI (PI-A, MAR-A, PI-M, and MAR-M) values. Each plot shows the IWQI range and density; the median and the interquartile range are shown by a white dot and box. The PI-A value distribution for the GRKR model showed a high degree of resemblance by being somewhat near to the measured values. For measured, GRKR, Ridge, DRVFL, Stacking, DELM, LSSVM, PI-A ranges were [46.91, 73.70], [46.80, 73.60], [46.77, 73.28], [49.13, 72.86], [48.57, 73.23], [53.34, 70.03], and [47.84, 72.84]. Both showed the lowest minimum PI-A values (Measured = 46.91 and GRKR = 46.80). In contrast, other models such as DELM had higher minimum values (53.34) and lower maximum values (70.03). The GRKR’s efficiency in accurately reproducing the measured data is shown by its general near match to the PI-A value distribution.

When it came to the other IWQI, such as MAR-A, PI-M, and MAR-M, the GRKR model consistently performed better. Predictions of IWQI made by the model showed remarkable agreement with the actual data. The ranges of suggested model (MAR-A (GRKR = [10.75, 63.33]), PI-M (GRKR = [47.16, 73.02]), and MAR-M (GRKR = [15.23, 67.83])) were somewhat comparable to the observed values (MAR-A = [11.29, 65.35], PI-M = [46.52, 72.77], and MAR-M = [13.74, 67.21]). This made the GRKR model a useful ML model for forecasting IWQI as it showed its accuracy and dependability in estimating these parameters.

Fig. 9

Violin plot the distribution of (a) PI-A, (b) MAR-A, (c) PI-M, and (d) MAR-M for ML models.

Evaluate ML models using residual density distribution

Figure 10 illustrates the residual density distribution across all IWQI (PI-A, MAR-A, PI-M, and MAR-M) for several predictive models (GRKR, Ridge, dRVFI, Stacking, DELM, and LSSVM). The colorful curves represent the residual distributions of the various models. Vertical dashes show all of the models’ 95% confidence intervals. The residuals are spread uniformly about the average with varying degrees of dispersion and concentration since the distributions often have a central tendency around zero. the figures showed that the GRKR model with the narrowest and tallest distributions exhibited a higher density of residuals near zero for all IWQI (namely: (a) PI-A, (b) MAR-A, (c) PI-M, and (d) MAR-M). This model was able to provide more accurate and error-free predictions of the IWQI. Conversely, models with broader distributions (e.g., DELM and LSSVM) exhibited a higher variability in their prediction errors.

Fig. 10

Residual density distribution of ML models for (a) PI-A, (b) MAR-A, (c) PI-M, and (d) MAR-M.

Evaluate ML models using Taylor plot

Figure 11 shows a comparison of six ML models’ Taylor diagrams with a reference model. These models are DELM, DRVFI, Stacking, Ridge, LSSVM, and GRKR. The position of each model on the plot was estimated by the standard deviation and correlation coefficient of its data. the horizontal axis shows the standard deviation, and the radial lines show the correlation coefficient. The GRKR model was closest to the reference point for all IWQI (PI-A, MAR-A, PI-M, and MAR-M) comparing the position of ML models in the Taylor diagram. The closeness level between GRKR and the reference point indicated that GRKR had the most similarity to it. The results proved that when it came to predicting the reference dataset, the GRKR model was the most effective.

Fig. 11

Taylor diagram of (a) PI-A, (b) MAR-A, (c) PI-M, and (d) MAR-M for all ML models.

Conclusion

A complementary hybrid intelligence framework was developed for the first time to forecast monthly PI and MAR indices in Ahvaz and Molasani stations, Khouzestan province, Iran. The framework comprised a new hybrid ML model based on generalized ridge regression and kernel ridge regression with the regularized locally weighted method called the GRKR model. Furthermore, an optimized MVMD method was developed to decompose the input variables. Finally, the LGBM model was considered to select the most important features. Two stations’ PI and MAR indices were predicted using the suggested framework: PI-A and MAR-A for the Ahvaz station and PI-M and MAR-M for the Molsani station. A novel hybrid ML model (GRKR) and an optimized MVMD based on the RUN optimization technique were developed as the key contributions of this study. Notably, the best control parameters for ML models were derived using the RUN optimization technique.

The decomposed input variables were utilized in the GRKR model to design OMVMD-GRKR to forecast monthly PI and MAR. In this work, OMVMD-Ridge, OMVMD-DRVFL, OMVMD-DELM, OMVMD-LSSVM, and OMVMD-Stacking models were developed to assess the forecasting precision versus the OMVMD-GRKR model utilizing seven statistical metrics (R, RMSE, MAPE, IA, MaxAE, VSD, and U95%). The findings showed that, when the suggested OMVMD-GRKR compared to other OMVMD-based models, it had better performance accuracy for both stations in predicting PI and MAR indices. The OMVMD-GRKR model could achieve the highest degree of accuracy in terms of (R = 0.987, RMSE = 0.761, IA = 0.994, VSD = 1.312, and U95% = 2.108) to forecast the PI index at the Ahvaz station and (R = 0.963, RMSE = 1.379, IA = 0.980, VSD = 4.314, and U95% = 3.828) to forecast the PI index at the Molasani station.

The results show that the OMVMD-GRKR and OMVMD-Stacking models were the most and least accurate for predicting PI and MAR at two stations, respectively. The simple GRKR, Ridge, LSSVM, DELM, and Stacking models also indicated lower accuracy as compared to the OMVMD-based methods. Therefore, the OMVMD-GRKR model could yield superior accuracy compared to other OMVMD-based models to forecast PI and MAR indices. The suggested hybrid intelligence framework OMVMD-GRKR can effectively be used in the future to address climate change, sustainable energy, environmental and agricultural fields, and renewable energy.