Abstract
This study presents a planning approach that considers the simultaneous expansion of generating and transmission systems, taking into account the location and sizing of generation units, AC transmission lines, and high-voltage direct-current (HVDC) systems. The HVDC system utilizes AC and DC substations equipped with AC/DC and DC/AC power electronic converters, respectively, to effectively regulate and control the reactive power of the transmission network. The problem aims to minimize the combined annual cost of constructing the specified parts and operating the generation units. This is subject to constraints such as the size and investment budget limits, an AC optimum power flow model, and the operational limits of both renewable and non-renewable generation units. The scheme incorporates a non-linear model. The Red Panda Optimization (RPO) is utilized to solve the provided model in order to attain a dependable and optimal solution. This research focuses on several advances, including the planning of the HVDC power system, the regulation of reactive power in HVDC substations, and the resolution of related issues using the RPO algorithm. The numerical findings collected from several case studies demonstrate the effectiveness of the suggested approach in enhancing the economic and technical aspects of the transmission network. Efficiently coordinating the generation units, AC transmission lines, and HVDC system leads to a significant enhancement in the economic performance of the network, resulting in a 10–40% improvement compared to the network power flow studies.
Similar content being viewed by others
Introduction
Motivation
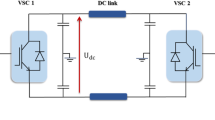
With the growth of the population, there will inevitably be a commensurate rise in the need for electrical energy in the future. Moreover, the rise of innovative technologies like electric vehicles in recent years, together with the expected increase in their numbers in the coming years, acts as an extra driving force for the growth of electric energy usage1. In order to meet the growing energy requirements and provide a reliable power grid, it is imperative to carry out power system expansion planning. By ensuring a balance between energy production and consumption, possible concerns can be prevented2. This plan encompasses three components: generation expansion planning (GEP), transmission expansion planning (TEP), and simultaneous generation and transmission expansion planning (GTEP)3. GEP/TEP is a process that determines the best location, size, and type of generating units (GUs) and transmission lines in a power system. GTEP is a composite of GEP and TEP3. This planning aligns with the economic and technological objectives of the planner and the network. In order to optimize the expansion planning of the network equipment, it is essential to not only minimize construction, maintenance, and operation costs, but also enhance economic indicators such as network operation costs, as well as technical indicators like voltage profile, voltage security, and reliability4. Furthermore, the development of power electronics technologies has led to the emergence of high-voltage direct-current (HVDC) systems as a prominent method for power transmission in the power system. This has garnered significant attention from numerous organizations in recent years5. This system comprises two alternating current (AC) and direct current (DC) substations, as well as DC transmission lines. An AC-DC converter is employed in the AC substation, while a DC-AC converter is utilized in the DC substation. This method utilizes a dual cable configuration (positive/negative) for power transmission, whereas AC transmission lines necessitate a minimum of three cables5. In HVDC systems, both AC and DC substations typically incorporate modern technologies like IGBT bridges5. As a result, they have the ability to regulate both the active and reactive power that flows through them at the same time. Therefore, it is anticipated that the power transmission through the HVDC system will be efficient and financially advantageous. It has the potential to significantly enhance the technical and economic condition of the network. By developing an optimization model for GTEP with HVDC that is in line with the goals of the planner and the transmission system operator (TSO), it is expected that it would be possible to successfully attain the economic objectives of the planner as well as the economic and technical objectives of the TSO.
Literature review
Multiple studies have been conducted in the domain of designing various equipment in the power system. Reference6 assesses the effects of repairing and maintaining power lines on the planning of expanding generating and transmission systems. This evaluation takes into account the reliability of both the transmission and generation components. The goal is to achieve equilibrium between the expansion and operational costs of transmission and generating, while also considering the expenses of repairing and maintaining power lines, as well as ensuring reliability. The reliability of the transmission system is measured by the loss of load (LOL) and load shedding resulting from line outages. Similarly, the reliability of the generation system is determined by the LOL and load shedding indices caused by transmission congestion and generator unit outages. In7, it examines the most effective ways for long-term robust expansion planning. The proposed expansion planning problem aims to optimize the supplied electricity to end-users while minimizing the risk of wildfire ignition, taking into account quantitative risk factors. The scheme provided offers utility decision-makers three categories of network expansion decisions: the addition of new lines, the modification of existing lines, and the installation of distributed energy resources (DERs). In the planning optimization process of Voltage Source Controlled-Multiterminal HVDC (VSC-MTDC) systems, FACTS devices, and Reactive Power Planning (RPP) are combined. This allows for a single formulation of AC-TEP. To attain an ideal transmission configuration, a non-linear mathematical programming technique and a metaheuristics based on differential evolution are selected. Reference8 presented a study that examined the effects of high Distributed Energy Resources penetrations on the transmission system. The study focused on various aspects including voltage management, methods of mitigation, availability and consumption of reactive power, optimal operation of generating units, and the switching actions of different equipment. The reference9 introduces a GEP model that focuses on enhancing the integration of renewable energy sources by prioritizing flexibility. The model integrates GEP with unit commitment, taking into account enhanced reserve requirements. The utilization of GEP and unit commitment involves the consideration of short-term operational constraints. Moreover, considering the rise in renewable portfolio standards (RPS) and the necessity for precise assessment of reserve requirements, it is crucial to take into account enhanced reserve requirements in the suggested model. The paper10 presents a stochastic model for coordinated generation and transmission expansion planning. The model considers the influence of demand response programs. The demand response model provides a detailed description of the operating parameters, including power, energy, reserve, response duration, and response number. A reliability-constrained TEP (RCTEP) is introduced in11. The net power demand forecasting technique (NPDFT) is based on both load forecasting and renewable sources generation. The NPDFT utilizes a logistic method based on time series analysis to predict load levels for future planning years. RES generation forecasting predicts the generation for the upcoming year using an anticipated coefficient. RCTEP aims to reduce the total cost of planning, operation, and reliability. This cost is constrained by the AC optimum power flow equations, planning constraints, and reliability limitations for N – 1 contingency.
Extensive research has been conducted in the domain of power system planning, specifically focusing on HVDC systems. Reference12 presents a planning strategy that focuses on dependability in order to create dependable topologies for meshed HVDC grids. The proposed steady-state model for HVDC grids serves as the basis for formulating a bi-level and multiobjective planning issue. The optimization approach considers both dependability as a separate target and the inclusion of power flow controls (PFCs). A dynamic hybrid model is introduced in13 for TEP that incorporates both high voltage AC (HVAC) system and multi-terminal Voltage Sourced Converter (VSC)-based HVDC options over many years. The suggested model takes into account the possibility of converting existing HVAC transmission lines to HVDC lines, in addition to the implementation of new HVAC and HVDC lines. Reference14 presents a novel paradigm for addressing the Transmission Network Expansion Planning (TNEP) problem in energy markets. This framework considers both HVAC and HVDC lines simultaneously, taking into account the unpredictability associated with wind generation. The suggested model is formulated as a stochastic bi-level optimization problem with risk constraints. At the upper level, the TSO makes optimal investment decisions. The lower-level concerns pertain to the optimization of social welfare through network-constrained market-clearing. Table 1 presents a summary of the work conducted in the research background.
Research gaps
According to the study background in Table 1, the field of power system planning has the following significant research gaps:
-
The majority of power system planning research has focused on GEP, TEP, or a mixture of both referred to as GTEP. The inclusion of HVDC system planning in the power system has been examined in a limited number of studies, such as those referenced as12,13,14. Within these systems, AC power is initially transformed into DC power by an AC-DC power electronic converter. Subsequently, the transmission of power is accomplished through DC lines. Ultimately, the DC power is transformed into AC power with the use of a DC-AC power electronic converter. In the HVDC system, the power transmission line consists of two conductors, one positive and one negative. This configuration requires less cables compared to the AC transmission method. Consequently, a decrease in the planning cost for the DC transmission system is anticipated. In this system, the voltage drop across the buses at the start and end of the transmission line is lower compared to AC transmission lines. This is because the lines in this system only possess resistance. However, in AC systems, the lines possess both resistance and reactance. Consequently, the implementation of HVDC in the transmission network is anticipated to play a significant role in enhancing the technical indicators of the network. However, this issue has only been addressed in a limited number of studies, including those referenced as12,13,14. However, these research studies do not include the GTEP variable. Furthermore, the analysis conducted in the time period between 6 and 15 focuses exclusively on the arrangement of lines, power generating units, and HVDC systems. Nevertheless, a crucial aspect of achieving optimal planning is the determination of element sizes, which has received limited attention in existing research.
-
In the HVDC system, the AC substation and DC substation must have the capability to transmit power bidirectionally, meaning power can flow from the AC substation to the DC substation and vice versa. Therefore, it is imperative to incorporate sophisticated power electronics, such as Insulated Gate Bipolar Transistor (IGBT) bridges, into the converter’s design. By appropriately controlling the IGBTs, a power electronic converter can generate or absorb reactive power. By using the HVDC system, it is possible to regulate the reactive power of the network as well. However, the matter of HVDCs has not been examined in the context of12,13,14. Put simply, a limited number of studies have examined the ability of HVDC systems to manage reactive power. Furthermore, it is important to acknowledge that the primary determinant for enhancing the voltage profile is the effective management of reactive power. Moreover, by regulating the reactive power, it is anticipated that several economic and technical metrics will enhance within the network. Reactive power control, for instance, results in the reduction of power losses, enhancement of voltage security, and decrease in the cost of energy losses. However, only a small number of studies have incorporated reactive power management of HVDC into the power system planning problem.
-
The aims of the planner, which might be a private corporation or a company managed by the TSO, have typically been included in most study, as indicated by references8,9,11,12,13,14,15. Typically, the objective of the planner involves economic goals, such as reducing the expenses associated with building and upkeep. Expansion planning in the electricity system should aim to enhance the economic and technical performance of the network, including operations and other associated indices. Put simply, the objectives of the TSO, which encompass both the economic and technical aspects of the network, should be incorporated into the electricity system’s planning process. However, this problem has received limited attention in the existing study, as indicated by references6–7,10.
Contributions
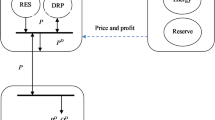
In order to address the initial research deficiency, this article presents the GTEP method using HVDC systems for power transmission. The method focuses on determining the optimal placement and size of DC and AC transmission lines, AC and DC substations in HVDC, and generating units (GUs), as illustrated in Fig. 1. In order to address the second discrepancy, it is presumed that AC and DC substations in HVDC systems have the ability to regulate their generation or consumption of reactive power. This problem is expressed as an optimization model. The target function is to minimize the combined yearly investment cost of elements and the overall annual running costs of GUs. The second term of the objective function addresses the third research gap and is directly related to the aims of the TSO. The restrictions of the listed elements include limitations on their size and investment budget, as well as the AC optimum power flow model and the performance limitations of both renewable and non-renewable generation units. The Red Panda Optimization (RPO) algorithm is employed to address the research gap and solve the proposed scheme. This method has the capability to acquire dependable ideal solutions for intricate engineering challenges. Upon comparing the proposed approach and research background, the following novelties, advantages, objectives and contributions can be identified for the proposed plan:
-
The placement and sizing of production units, AC transmission lines, and HVDC systems in the transmission network are done simultaneously. This is done in accordance with the economic goals of the planner and the economic and technical goals of the transmission system operator.
-
The objective is to enhance the economic and technical state of the transmission network by including reactive power management in the HVDC system through AC and DC substations.
-
Obtaining the reliable optimal solution for the GTEP problem incorporating HVDC planning by Red Panda Optimization at minimal computing time.
In general, there is a growth in electrical energy consumption in the coming years due to population growth, the entry of new consumers into the network, and other things. To increase social welfare in the coming years by preventing consumers from black out of power, there is a need to develop the generation and transmission sector in the power system. The proposed plan calculates the optimal location, type, and size for generation units and transmission lines. It develops the power system by considering the minimum cost. Since the development of the power system is generally carried out by a government agency, reducing costs can be an advantage for increasing social welfare. This plan also considers the presence of renewable resources. Therefore, this plan improves the environmental conditions. This is also one of the goals of improving social welfare conditions.
Paper organization
In the subsequent section, the development of GTEP incorporating HVDC is outlined. The problem model proposed in the third section is based on the RPO algorithm. The fourth section presents the numerical findings derived from various case studies. Ultimately, overall conclusions are deliberated upon in the fifth section.
Modelling of HVDC-based GTEP
This section presents the formulation of GTEP, taking into account the HVDC system. The model includes planning (siting and sizing) and operation models for GUs, AC transmission lines, and HVDC systems in the transmission network. The objective is to minimize the construction and operation costs. The specific details of the proposed plan are outlined below:
Subject to:
The objective function of the problem is to minimize the annual total investment cost (ATIC) of AC and DC transmission lines, GUs, and AC and DC substations in the HVDC system, as well as the annual total operation cost (ATOC) of all GUs. This objective function is similar to relation (1) and is based on references11,14, and6. It should be noted that the final line of Eq. (1) encompasses the operational expenses of all GUs. The primary objective of the TSO is to create ideal economic and technical circumstances inside the transmission network in order to decrease the operational expenses of GUs16. Hence, the objective function associated with TSO is presented in the final line of Eq. (1). Constraints (2)-(6) specify the maximum size of these components. Constraints (2) and (3) were used to represent the maximum size or capacity of AC and DC transmission lines, respectively. The maximum capacity of GUs is directly proportional to the Eq. (4). Constraints (5) and (6) define the maximum dimensions of AC and DC substations in the HVDC system, respectively. Restrictions (7)-(9) demonstrate the investment budget limitations17 for the building of AC lines, GUs, and HVDC systems. The term “po” denotes the duration of the planning horizon. The entire investment cost of the indicated elements is represented on the left side of Eqs. (7)-(9). The investment budget for HVDC, as determined by Eq. (9), encompasses the expenses associated with the construction of DC lines, as well as AC and DC substations. The logical rule utilized in constraints (10) and (11) states that the size of a transmission line between buses n and l is equivalent to the size of the line between buses l and n. The transmission line connecting buses n and l is identical to the transmission line connecting buses l and n.
The transmission network operation model is represented by equations (12) to (26)18,19,20,21,22,23. The power flow model is described in the AC and DC parts of the transmission network in restrictions (12)-(19)11,14. The Eqs. (12) and (13) provide the active and reactive power balance models for different buses11. The active power flowing via AC and DC substations in the HVDC system is determined using Eqs. (14) and (15) correspondingly. The HVDC system, seen in Fig. 1, consists of an AC substation at the start of the DC transmission line and a DC substation at the conclusion of the line. The AC substation is equipped with an AC to DC converter, whereas the DC substation has a DC to AC converter. Thus, the active power of each substation can be determined by utilizing the active power flowing over the DC transmission line, as expressed in Eqs. (14) and (15). These connections assume that power flows from the AC post side to the DC post side in the DC line. Thus, in the AC substation, the DC line’s power serves as the output power, while the substation’s power functions as the input power. Thus, the AC substation’s efficiency is represented in the denominator of Eq. (14). The DC substation receives power from the DC line and distributes it to the DC substation. Thus, the numerator in Eq. (15) represents the efficiency of the DC substation. The model for the flow of active and reactive power across an AC transmission line is described in restrictions (16) and (17)18,19,20,21,22,23. Equation (18) presents the model for the active power flowing through the DC transmission line. Equation (19) specifies the voltage angle at the slack bus, specifically at bus 1. The limits (20)-(25) illustrate the operational and technological limitations of the transmission network. The bus voltage magnitude limitation is indicated in constraint (20)17. The purpose of this relationship is to establish a maximum (minimum) threshold to protect equipment insulation from being compromised (network blackout) due to excessively high voltage (voltage drop). The apparent power flowing through the AC line is represented by the mathematical model described in relation (21)17, whereas the active power passing through the DC line is directly proportional to the expression (22). It is important to mention that active and reactive power flow across AC lines. Therefore, Eq. (21) considers the limit of apparent power in the AC line11. However, only the active power is transmitted in the DC line. Thus, Eq. (22) just incorporates the constraint of active power in the DC line. The maximum amount of apparent power that can flow via AC and DC substations in the HVDC system, as well as GUs, is described by Eqs. (23)-(25) in reference16. The paper considers the reactive power of AC and DC substations in the HVDC system as a decision-making or independent variable. However, their active power is a dependent variable determined by relations (14) and (15). The Eq. (25) is true for several types of production units16,17. However, in the context of renewable sources, the active power remains rather consistent as given by Eq. (26)24,25,26,27,28,29. The hourly production capacity of these resources is equal to the product of their capacity and the generation power rate (ϕG)17. The value of ϕG is found by the observation and study of natural occurrences30,31,32,33. For instance, in the case of wind systems, the determination is contingent upon the wind speed, whereas in solar systems, it relies on the quantity of solar radiation.
According to Fig. 1, generation units, AC and DC station in HVDC provide the reactive power (MVAr requirement) in the transmission network. The reactive power control by AC and DC posts in HVDC, and generation units is modelled in Eqs. (23)-(25). In this equations, the reactive power of these elements are the decision variables34–35. Hence, the optimal value of this variables are obtained by solver (RPO algorithm).
Solution process based on RPO
The Eqs. (1)-(26) exemplify a nonlinear optimization problem. This subsection elucidates the methodology for resolving the issue by employing the RPO36 to expedite the identification of a dependable solution. This approach, which relies on the findings of reference36, has already exhibited its robustness and efficiency in tackling optimization problems. Subsection 4.2 contains additional details concerning the potential of the RPO. To solve the problem described in Eqs. (1)-(26), a collection of N random values is created for the decision variables. These variables consist of SACL, SDCL, SG, SACP, SDCP, QACP, QDCP, QG and PG. The values are chosen according to the limitations stated in Eqs. (2)-(6), [-SACP SACP], [-SDCP SDCP], [-SG SG], and [0 SG] for ΩG - ΩRES, respectively. Afterwards, the values for the dependent variables ATC, PACL, QACL, PDCL, PACP, QACP, PDCP, QDCP, V, σ, and PG for ΩRES are calculated using the decision variables and equations. The numbers 12 to 19, inclusive, and 26. In this situation, the penalty function technique37 evaluates the constraints (7)-(9) and (20)-(25). The current approach depicts the penalty function for the constraint a ≤ b as as µ.max(0, a − b). In addition, the sign µ ≥ 0 is used to represent a Lagrangian multiplier, which acts as a variable for making decisions37. The fitness function (FF) is created by merging the objective function (1) with the sum of the penalty functions, as specified in Eq. (27). Subsequently, the RPO algorithm is employed to revise the decision variables. The method reaches convergence when the number of updating steps approaches its maximum value. Figure 2 illustrates the flowchart of the suggested approach using the RPO.
In this paper, the proposed design and solution is based on a mathematical model38,39,40,41,42. It involves an optimization problem43,44,45,46,47. The optimization formulation includes an objective function that has the task of minimizing or maximizing economic, environmental, and technical objectives48,49,50,51,52. This problem also includes various constraints, which are equal and unequal format53,54,55,56,57. To apply the optimization problem to the power system, an intelligent platform is needed. This platform is based on smart algorithms and telecommunication devices58,59,60,61,62.
Numerical results
This section examines and explores the numerical outcomes acquired from the suggested approach, (1)-(26), which is founded on the RPO, as depicted in Fig. 2. The presented problem model in Sect. 2 has no limitations for implementation on different network, resource and HVDC data. The analysis and investigation focus on the modified IEEE 6-bus and IEEE 118-bus transmission networks. The simulation is conducted within the MATLAB software environment. It is crucial to note that the population size for all solvers is 80, and the total number of convergence iterations for them is 4000.
Modified IEEE 6-bus transmission network
Data
The IEEE 6-bus transmission network has a single-line configuration, which may be seen in Fig. 363. The network has a fundamental power capacity of 100 MVA. The base voltage is 230 kV. Bus 1 is the designated reference bus. The voltage magnitude of the system is 1 per unit (p.u.), and the voltage angle is zero63. The allowable range of the voltage magnitude is equivalent to [0.95 1.05] p.u64,65,66,67,68,69. The network consists of four currently operational generating units, namely G1-G4, as seen in Fig. 3. The rated capacity of G1 is 12 MVA, G2 is 12 MVA, G3 is 7 MVA, and G4 is 7 MVA. The fuel price for G1 is $25/MWh, G2 is $25/MWh, G3 is $35/MWh, and G4 is $37/MWh17. The coincidence factor (CF) was assigned a value of 0.7, as reported in references11,17. It is expected in this network that either an AC line or an HVDC system can be added in parallel with each existing line (AT1-AT7). Tables 2 and 3 display the attributes of AC lines and HVDC systems, respectively. The parameters of AT1-AT7, including line resistance, reactance, and line capacity, are identical to those of A1-A7, as outlined in Table 263. The specifications of the production units that can be installed are provided in Table 463. Based on Fig. 3, buses 3–5 contribute 30%, 40%, and 30% of the total network load, respectively. The power factor, defined as the quotient of active power divided by apparent power70,71,72,73,74, is 0.9. The hourly load is calculated by multiplying the peak load by the load factor75,76,77,78,79. The daily load factor curve is depicted in80. The predicted daily curve of the power generation rate (ϕG) for wind farms (WF) and photovoltaic farms (PVF) is shown in16–17. This section assumes that the allocated funds for the building of AC lines, GUs, and HVDCs are $20 million, $40 million, and $20 million, respectively. The time frame for planning is 10 years.
Modified IEEE 6-bus transmission network63.
Investigating the status of transmission system planning
The planning findings of the 6-bus transmission network are presented in Table 5. The analysis considers the inclusion or exclusion of the HVDC system for various peak load levels, specifically 40 MW, 60 MW, and 80 MW. Based on the provided data, it can be observed that at a demand level of 40 MW, only the wind farms U14 and U15 are connected to the transmission system, utilizing their full capacity. In a scenario where HVDC installation is excluded, the network is expanded by adding AC transmission lines connecting buses 1 and 4 (A3) and 5 and 6 (A6), with capacities of 5 MVA and 6 MVA, respectively, according to Table 5. However, in the building of HVDC, H3 substitutes A3, which possesses a capacity of 4 MW for the DC line and 5 MVA for the substations. Based on the information provided in Table 2, it can be observed that the construction cost for A3 is rather expensive. However, H3 has the capability to construct the transmission line connecting buses 1 and 4 at a comparatively cheaper cost. Furthermore, the installation of AC and DC substations in buses 1 and 4, respectively, can effectively minimize the operating expenses of GUs through reactive power control. The examination of this topic can be found in Sect. 4.1.C. By increasing the demand level to 60 MW, the photovoltaic farms (U16 and U17) are operating at their maximum capacity in the network, without taking into account HVDC according to Table 5. U1 and U11 are connected to bus 1, which has a capacity of 5 MVA and 7 MVA, respectively. An AC transmission line with a capacity of 5 MVA is built between buses 3 and 6 (A7). Indeed, the capacity of both A3 and A7 lines will be augmented to 9 MVA. In the context of HVDC planning, H3 is substituted for A3. A DC transmission line with a capacity of 7 MW is necessary, while the AC and DC substations have a capacity of around 9 MVA. Under these circumstances, the photovoltaic farm (U16) is dismantled, and the capacity of U1 and U11 is decreased to 4 MVA and 7 MVA, respectively. The reduction in production unit capacity is a result of the regulation of reactive power in HVDC substations. When comparing the load levels of 80 MW and 60 MW, it is evident that all renewable sources (U14-U17) are operating at their maximum capacity in the network, without the presence of HVDC based on Table 5. The capacity of U1 remains constant, but the capacity of U11 is enhanced to 10 MVA. Furthermore, units U8 and U12 are allocated to buses 3 and 2, respectively, each having a maximum capacity of 7 MVA. In addition to the existing load level of 60 MW, a 5 MVA AC transmission line (A5) is installed between buses 4 and 5 in the transmission network. The inclusion of HVDC in the transmission system results in the continued replacement of A3 with H3. The DC line has a capacity of 7 MW, while the substations have a capacity of 9 MVA. Under these circumstances, the maximum power output of U1, U8, U11, and U12 is decreased to 4 MVA, 4 MVA, 8 MVA, and 5 MVA, respectively.
Figure 4 presents an analysis of the economic aspect of planning. According to Fig. 4(a), the yearly construction cost for load levels of 40 MW, 60 MW, and 80 MW, without HVDC, is 0.86 M$/year, 2.678 M$/year, and 3.808 M$/year, respectively. At the low load level, the number of constructed elements is reduced, resulting in a lower construction cost for the transmission network. Conversely, at the high load level, the number of constructed elements increases, leading to a higher construction cost for the transmission network. At a load level of 40 MW, the annual operating cost of the constructed GUs is zero, as only wind farms were constructed. However, when the network incorporates GUs with fuel costs at different load levels, the operating cost of new GUs is not equal to $0. For a load level of 60 (80) MW, the ATOC of the new GUs is 1.316 (3.512) million dollars. The total annual planning cost (ATPC) for load levels of 40 MW, 60 MW, and 80 MW is calculated by adding the ATIC and ATOC connected to new generation units. The ATPC values for these load levels are 0.86 M$/year, 3.994 M$/year, and 7.320 M$/year, respectively. When HVDC is present in the transmission network as shown in Fig. 4(b), the ATIC climbs to 1.032 million dollars per year for every 40 MW load level. ATOC remains the same for new GUs. The presence of HVDC did not alter the capacity of the established GUs in this scenario. Consequently, the load level of 40 MW resulted in a greater cost compared to the scenario without HVDC. Nevertheless, when the transmission system operates at different load levels, the inclusion of HVDC results in a decrease in the overall expenses for construction and operation over the course of a year. The ATPC values for load levels of 40 MW, 60 MW, and 80 MW are 1.032 M$/year, 3.667 M$/year, and 6.893 M$/year, respectively. Put simply, the introduction of HVDC at high load levels has resulted in a decrease in ATPC ranging from 5.8 to 8.2% when compared to the scenario where HVDC is not present.
C) Investigating the operation status of the transmission network: Fig. 5 displays the operational indicators of the transmission network, including ATOC of all GUs, energy loss (EL), maximum voltage drop (MVD), maximum overvoltage (MOV), and peak load carrying capacity (PLCC). The data is presented for various load levels, considering different scenarios: without HVDC, with HVDC with/without RPC. PLCC refers to the maximum peak load that a network can handle based on the load factor curve described in reference26, while still staying within the network’s operational boundaries. Based on the data presented in Fig. 5, it can be observed that as the load level increases, there is an increase in ATOC, EL, MVD, and PLCC. However, there is a drop in MOV. As the load level increases, the energy consumption of loads also increases. Consequently, ATOC, EL, and MVD, which are influenced by the energy consumption of loads, also increase. The magnitude of the MOV increases when there is a high power injection from the GUs. Nevertheless, as the load level increases, the energy consumption of loads also increases, resulting in the power of GUs being consumed at the location of consumption. Consequently, as the load level increases, the amount of power injected into the network busses is decreased, resulting in a drop in the MOV. Table 5 indicates that when the load level increases, the number of GUs in the transmission system also increases. Consequently, the quantity of PLCC likewise rises in proportion to the increase in the load level. Furthermore, the inclusion of HVDC in the transmission system has resulted in the enhancement of the aforementioned indicators, with the most significant improvement observed when utilizing RPC for HVDC. In this scenario, when HVDC is present at the high load level, ATOC, EL, MVD, MOV, and PLCC experience improvements of around 10%, 10.2%, 16.3%, 40%, and 3.1%, respectively, compared to the situation without HVDC. Additionally, based on Fig. 4, the inclusion of HVDC at the low load level results in an augmentation of ATIC. However, as indicated by Fig. 5, it has led to a reduction in ATOC for all GUs. Figure 4 shows that the inclusion of HVDC at a load level of 40 MW results in a 20% increase in ATIC compared to the scenario without HVDC. However, based on the information presented in Fig. 5, the ATOC is decreased by 16.5% when comparing the scenario with HVDC to the scenario without HVDC, at a load level of 40 MWh. Thus, it is evident that the implementation of HVDC with RPC is cost-effective and highly efficient in optimizing the functioning of the transmission network.
IEEE 118-bus transmission network
This section analyzes the current status of manufacturing, transmission, and HVDC plans in the IEEE 118-bus transmission network81. The data, specifications of generation units, and AC transmission lines are provided in reference81. This section assumes that a non-renewable GU with a maximum capacity of 50 MVA can be built at each bus. The cost of constructing each GU is $60 per kVA-year, while the price of their fuel is $30 per MWh. Within this network, it is possible to establish 5 Wind Farms (WF1-WF5) with a maximum capacity of 35 MVA, as well as 4 Photovoltaic Farms (PVF1-PVF4) with a maximum capacity of 30 MVA. The installation cost of renewable sources is indicated in Table 4. The location WF1-WF5 corresponds to busses 4, 21, 45, 78, and 106, respectively. The PVF1-PVF4 modules can be put in busses 15, 51, 94, and 115, respectively. It is presumed that an AC or HVDC transmission line can be positioned beside each existing transmission line. The specifications of the new AC lines are identical to those of the current lines. In HVDC systems, the capacity of the DC line is 20% lower than the capacity of the existing line. However, the capacity of the substation is equivalent to the capacity of the transmission line. The cost of establishing AC and DC transmission lines is 8 dollars per kilovolt-ampere per year and 5 dollars per kilovolt-ampere per year, respectively. The cost of installing substations in HVDC is equivalent to the cost specified in Table 3. The additional information utilized in the suggested strategy aligns with Sect. 4.1.A.
The findings of economic planning for load levels of 100% and 120% are presented in Table 6. Based on the information provided in Table 6, it can be observed that at a load level of 100%, only sustainable energy sources, specifically wind farms (WF1-WF5) and solar farms (PVF1-PVF4), have been implemented. The transmission system includes AC transmission lines such as A5, A7, A11, A23, A32, A67, A94, and A110 at the specified load level. When the load level is increased to 120%, the network includes G1, G4, G7, G45, and G95, which are not present at the 100% load level. Additional AC lines, specifically A39 and A53, are incorporated into the transmission system. H23, H32, and H110 are substitutes for A23, A32, and A110. In addition, H71 has been incorporated into the network. Table 6 indicates that the yearly cost for building and operation at a load level of 100% is approximately 66.7 million dollars per year and zero dollars, respectively. Hence, the annual planning cost amounts to 66.7 million dollars. At this particular level of demand, the operational expenses of the newly implemented units amount to $0, as the network exclusively incorporates renewable energy sources. However, its worth amounts to $59.4 million per year while operating at a load level of 120%. Non-renewable units were installed at this load level. The total yearly operating cost for all production units operating at maximum capacity is 72.3 million dollars per year. As the load level increases, the specified charges will also increase. Given the circumstances, it is imperative to construct additional resources and infrastructure.
The convergence status of the suggested design for a load level of 120% derived from several solvers is displayed in Table 7. The problem is solved using RPO, Ant Lion Optimizer (ALO)82, Crow Search Algorithm (CSA)83, Sine Cosine Algorithm (SCA)84, Gray Wolf Optimizer (GWO)85, Teaching Learning-based Optimization (TLBO)86, Artificial Bee Colony (ABC)87, Genetic Algorithm (GA)88, and particle swarm optimization (PSO)89 in this table. The population size and maximum convergence repetition for all algorithms are both set at 80 and 6000, respectively. In order to determine the standard deviation of the final result, each algorithm is executed 30 times to solve the given problem. Table 7 reveals that the proposed plan resulted in RPO achieving the lowest value, specifically 214.1 M$/year, for the objective function or ATC. However, alternative algorithms achieved a yearly revenue of over 219 million dollars for the objective function. The RPO algorithm has achieved ideal conditions after 2236 iterations of convergence, which translates to a computing time of 27.4 min. However, there are algorithms that require over 2890 iterations to achieve convergence, and their computation time exceeds 31 min. Furthermore, the RPO method exhibits a smaller standard deviation in its final output compared to other algorithms. Hence, the RPO method offers a superior and more precise solution with a faster convergence rate compared to ALO, ABC, CSA, SCA, GWO, TLBO, PSO, and GA.
The proposed problem is a nonlinear and non-convex optimization. In these problems, a solver is selected that has the most optimal value for the objective function. Because in this situation, it is expected that the distance of the obtained point from the global optimal point is the smallest compared to the results of other algorithms. According to Table 7, RPO has the minimum value for ATC. Therefore, RPO has found a solution that has a smaller distance from the global optimal point compared to other algorithms. To obtain the global optimum point, it is necessary to transform the non-convex problem into a convex problem in the first step. Since the constraints of the proposed problem (i.e., the power flow equations) are non-convex; therefore, to extract the convex problem, it is necessary to perform a linear approximation model for the proposed scheme. There are various techniques for linearizing the power flow equations. Although this method can obtain the absolute optimum point, significant computational errors arise for some variables. For example, according to16,17, the minimum computational error for power losses in the linearization technique for power flow equations is about 10%. Therefore, the obtained solution is not reliable. In addition, in linearizing the equations, different tuning parameters arise that have different values for different operating points. Therefore, if the problem volume changes, there is a need to change the tuning parameters.
Conclusions
This study explores generation and transmission expansion planning by optimizing the siting and sizing of HVDC systems, AC transmission cables, and renewable and non-renewable generation units. The proposed approach aims to minimize the total annual construction costs associated with these components, as well as the operational costs of generation units. Key constraints include size limitations, investment budgets limit, and adherence to the network’s optimal power flow model. To solve this formulation, the Red Panda Optimization algorithm was utilized. The numerical results reveal that renewable energy resources are integrated into the transmission system during periods of low demand, while both renewable and non-renewable resources are employed in network if demand increases. It was noted that the capacity of DC cables in HVDC systems is generally lower than that of AC lines. Additionally, HVDC systems with reactive power regulation can reduce the required capacity of generation units. At high load levels, HVDC demonstrates significant efficiency by simultaneously lowering construction and operational costs. Specifically, implementing HVDC reduces planning costs by approximately 5.8–8.2% compared to scenarios without HVDC. At lower load levels, the adoption of HVDC technology initially raises construction costs; however, it eventually leads to reductions in the operational costs of all generation units. The integration of reactive power control in HVDC enhances the network’s economic performance by 10% and improves the operational efficiency of the transmission system by 10–40%. Moreover, the Red Panda Optimization algorithm outperforms other evolutionary methods by delivering more accurate solutions with a faster convergence rate, making it a highly efficient approach for addressing such complex planning challenges.
Future works
In the proposed scheme, the load and power generation of renewable resources are associated with uncertainty. To extract a reliable solution, stochastic, robust or probabilistic modeling of the aforementioned parameters is required. Therefore, the proposed scheme by considering modeling the uncertainties of load and renewable power is considered as future work. In addition, the proposed scheme has a nonlinear model. Solving this problem in large-scale networks is time-consuming. To reduce the computational time, powerful computing systems can be used. This is also costly. To compensate for this, it is necessary to use powerful solvers such as hybrid evolutionary algorithms, decomposition methods (such as the Benders decomposition approach and the master and slave technique), and heuristic methods appropriate to the network structure. The proposed scheme is considered as future work by considering the aforementioned solution techniques. In this scheme, wind and solar renewable resources were used. However, different renewable resources can be constructed based on different geographical areas. For example, a tidal system can be constructed in coastal areas. In places where there is environmental waste, a renewable source of bio-waste can be established. Therefore, the proposed plan is considered as future work, taking into account different geographical areas.
Data availability
All data generated or analyzed during this study are included in this published article, Sect. 4.1. and 4.2. Also, the datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Abbreviations
- ATC :
-
Annual total investement and operation cost ($/year)
- P ACL , Q ACL :
-
Active (MW) and reactive (MVAr) power of an AC transmission line
- P ACP , Q ACP :
-
Active (MW) and reactive (MVAr) power of an AC substation in the HVDC system
- P DCL :
-
Active (MW) power of a DC transmission line
- P DCP , Q DCP :
-
Active (MW) and reactive (MVAr) power of a DC substation in the HVDC system
- P G , Q G :
-
Active (MW) and reactive (MVAr) power of a generation unit (GU)
- S ACL :
-
Capacity or size (MVA) of an AC transmission line
- S ACP :
-
Capacity or size (MVA) of an AC substation in the HVDC system
- S DCL :
-
Capacity or size (MW) of a DC transmission line
- S DCP :
-
Capacity or size (MVA) of a DC substation in the HVDC system
- S G :
-
Capacity or size (MVA) of a GU
- V :
-
Voltage magnitude (p.u.)
- σ :
-
Voltage angle (rad)
- A ACL :
-
Incidence matrices of buses and AC transmission lines
- A DCL :
-
Incidence matrices of buses and DC transmission lines
- A G :
-
Incidence matrices of buses and GUs
- B ACL , G ACL :
-
Susceptance and conductivity of an AC transmission line (p.u.)
- \({\overline{C} }^{ACL}\) :
-
Investment budget for construction of an AC transmission line ($)
- CF :
-
Coincidence factor
- \({\overline{C} }^{G}\) :
-
Investment budget for a GU ($)
- \({\overline{C} }^{HVDC}\) :
-
Investment budget for the HVDC system ($)
- G DCL :
-
Conductivity of a DC transmission line (p.u.)
- IC ACL :
-
Annual construction cost of an AC transmission line ($/MVA-year)
- IC DCL :
-
Annual construction cost of a DC transmission line ($/MW-year)
- IC ACP :
-
Annual construction cost of an AC substation in the HVDC system ($/MVA-year)
- IC DCP :
-
Annual construction cost of a DC substation in the HVDC system ($/MVA-year)
- IC G :
-
Annual construction cost of a GU ($/MVA-year)
- P C , Q C :
-
Active (MW) and reactive (MVAr) power of the load
- po :
-
Planning horizon (year)
- \({\overline{S} }^{ACL}\) :
-
Maximum size (MVA) of an AC transmission line
- \({\overline{S} }^{DCL}\) :
-
Maximum size (MW) of a DC transmission line
- \({\overline{S} }^{ACP}\) :
-
Maximum size (MVA) of an AC substation in the HVDC system
- \({\overline{S} }^{DCP}\) :
-
Maximum size (MVA) of a DC substation in the HVDC system
- \({\overline{S} }^{G}\) :
-
Maximum size (MVA) of a GU
- \(\underline{V}, \overline{V }\) :
-
Minimum and maximum voltage magnitude (p.u.)
- β G :
-
Operation (fuel) price of a GU ($/MWh)
- η AC , η DC :
-
Efficiency of AC and DC substations in the HVDC system
- φ G :
-
Power generation rate
- g :
-
GU
- l :
-
Bus
- n :
-
Bus
- (n, l) :
-
Transmission line between buses n and l
- t :
-
Operation hour
- Ω B :
-
Set of buses
- \({\Omega }_{CL}^{AC}\) :
-
Set of AC transmission lines proposed for construction
- \({\Omega }_{L}^{AC}\) :
-
Set of AC transmission lines
- \({\Omega }_{CL}^{DC}\) :
-
Set of DC transmission lines proposed for construction
- \({\Omega }_{L}^{DC}\) :
-
Set of DC transmission lines
- Ω CG :
-
Set of GUs proposed for construction
- Ω G :
-
Set of Gus
- Ω RES :
-
Set of renewable sources
References
Wu, Y., Gu, W., Huang, S., Wei, X. & Safaraliev, M. A four-layer business model for integration of electric vehicle charging stations and hydrogen fuelling stations into modern power systems. Appl. Energy. 377, 124630 (2025).
Hjelmeland, M., Nøland, J. K., Backe, S. & Korpås, M. The role of nuclear energy and Baseload demand in capacity expansion planning for low-carbon power systems. Appl. Energy. 377, 124366 (2025).
Quiroga, D., Sauma, E. & Pozo, D. Power system expansion planning under global and local emission mitigation policies. Appl. Energy. 239, 1250–1264 (2019).
Peker, M., Kocaman, A. S. & Kara, B. Y. A two-stage stochastic programming approach for reliability constrained power system expansion planning. Int. J. Electr. Power Energy Syst. 103, 458–469 (2018).
Sun, Q. et al. Operational reliability evaluation and risk mitigation of asynchronous grids coupled through flexible HVDC systems. J. Mod. Power Syst. Clean. Energy. 12, 1–12 (2025).
Mahdavi, M., Javadi, M. S. & Catalão, J. P. Integrated generation-transmission expansion planning considering power system reliability and optimal maintenance activities. Int. J. Electr. Power Energy Syst. 145, 108688 (2023).
Bayani, R. & Manshadi, S. D. Resilient expansion planning of electricity grid under prolonged wildfire risk. IEEE Trans. Smart Grid. 14 (5), 3719–3731 (2023).
Suprême, H., de Montigny, M., Dione, M. M., Ramos-Leaños, O. & Compas, N. A quasi-static time-series approach to assess the impact of high distributed energy resources penetration on transmission system expansion planning. Electr. Power Syst. Res. 235, 110635 (2024).
Choubineh, K., Yousefi, H. & Moeini-Aghtaie, M. Developing a new flexibility-oriented model for generation expansion planning studies of renewable-based energy systems. Energy Rep. 11, 706–719 (2024).
Yang, Q., Wang, J., Liang, J. & Wang, X. Chance-constrained coordinated generation and transmission expansion planning considering demand response and high penetration of renewable energy. Int. J. Electr. Power Energy Syst. 155, 109571 (2024).
Oboudi, M. H., Hamidpour, H., Zadehbagheri, M., Safaee, S. & Pirouzi, S. Reliability-constrained transmission expansion planning based on simultaneous forecasting method of loads and renewable generations. Electr. Eng., 1–21. (2025).
Xie, H., Bie, Z. & Li, G. Reliability-oriented networking planning for meshed VSC-HVDC grids. IEEE Trans. Power Syst. 34 (2), 1342–1351 (2018).
Moradi-Sepahvand, M. & Amraee, T. Hybrid AC/DC transmission expansion planning considering HVAC to HVDC conversion under renewable penetration. IEEE Trans. Power Syst. 36 (1), 579–591 (2020).
Heydari, R. & Barforoushi, T. HVDC/HVAC transmission network expansion planning in electricity markets in the presence of wind resources. Electr. Power Syst. Res. 229, 110182 (2024).
Araujo, R. A., Torres, S. P., Pissolato Filho, J., Castro, C. A. & Van Hertem, D. Unified AC transmission expansion planning formulation incorporating VSC-MTDC, FACTS devices, and reactive power compensation. Electr. Power Syst. Res. 216, 109017 (2023).
Baziar, A., Bo, R., Ghotbabadi, M. D., Veisi, M. & Rehman, W. U. Evolutionary algorithm-based adaptive robust optimization for AC security constrained unit commitment considering renewable energy sources and shunt FACTS devices. IEEE Access. 9, 123575–123587 (2021).
Hamidpour, H. et al. Coordinated expansion planning problem considering wind farms, energy storage systems and demand response. Energy 239, 122321 (2022).
Jiang, W. et al. Optimal economic scheduling of microgrids considering renewable energy sources based on energy hub model using demand response and improved water wave optimization algorithm. J. Energy Storage. 55, 105311 (2022).
Dehghani, M. et al. Blockchain-based securing of data exchange in a power transmission system considering congestion management and social welfare. Sustainability 13.1 : 90. (2020).
Yuan, Z. et al. Probabilistic decomposition-based security constrained transmission expansion planning incorporating distributed series reactor. IET generation. Transmission Distribution. 14 (17), 3478–3487 (2020).
Yu, D. & Ghadimi, N. Reliability constraint stochastic UC by considering the correlation of random variables with copula theory. IET renewable power generation 13.14 : 2587–2593. (2019).
Eslami, M. et al. A new formulation to reduce the number of variables and constraints to expedite SCUC in bulky power systems. Proceedings of the national academy of sciences, india section a: physical sciences 89 : 311–321. (2019).
Nejad, H. et al. Reliability based optimal allocation of distributed generations in transmission systems under demand response program. Electr. Power Syst. Res. 176, 105952 (2019).
Zhu, L. et al. Multi-criteria evaluation and optimization of a novel thermodynamic cycle based on a wind farm, Kalina cycle and storage system: an effort to improve efficiency and sustainability. Sustainable Cities Soc. 96, 104718 (2023).
Bo, G. et al. Optimum structure of a combined wind/photovoltaic/fuel cell-based on amended Dragon fly optimization algorithm: a case study. Energy sources, part A: recovery, utilization, and environmental effects 44.3 : 7109–7131. (2022).
Mir, M. et al. Application of hybrid forecast engine based intelligent algorithm and feature selection for wind signal prediction. Evol. Syst. 11 (4), 559–573 (2020).
Abedinia, O. et al. A new combinatory approach for wind power forecasting. IEEE Syst. J. 14 (3), 4614–4625 (2020).
Leng, H. et al. A new wind power prediction method based on ridgelet transforms, hybrid feature selection and closed-loop forecasting. Adv. Eng. Inform. 36, 20–30 (2018).
Abedinia, O. et al. Optimal offering and bidding strategies of renewable energy based large consumer using a novel hybrid robust-stochastic approach. J. Clean. Prod. 215, 878–889 (2019).
Cao, Y. et al. Optimal operation of CCHP and renewable generation-based energy hub considering environmental perspective: an epsilon constraint and fuzzy methods. Sustainable Energy Grids Networks. 20, 100274 (2019).
Meng, Q. et al. A single-phase transformer-less grid-tied inverter based on switched capacitor for PV application. J. Control Autom. Electr. Syst. 31, 257–270 (2020).
Mehrpooya, M. et al. Numerical investigation of a new combined energy system includes parabolic dish solar collector, Stirling engine and thermoelectric device. Int. J. Energy Res. 45 (11), 16436–16455 (2021).
Ghadimi, N. et al. An innovative technique for optimization and sensitivity analysis of a PV/DG/BESS based on converged Henry gas solubility optimizer: A case study. IET generation. Transmission Distribution. 17 (21), 4735–4749 (2023).
Bharti, D. & De, M. Framework for multipoint optimal reactive power compensation in radial distribution system with high distributed generation penetration. Int. Trans. Electr. Energy Syst., 29(7), e12007. (2019).
Bharti, D. & De, M. A centrality index based approach for selection of optimal location of static reactive power compensator. Electr. Power Compon. Syst. 46 (8), 886–899 (2018).
Givi, H., Dehghani, M. & Hubálovský, Š. Red panda optimization algorithm: an effective bio-inspired metaheuristic algorithm for solving engineering optimization problems. IEEE Access. 11, 57203–57227 (2023).
Khalafian, F., Iliaee, N., Diakina, E., Parsa, P., Alhaider, M. M., Masali, M. H.,… Zhu, M. (2024). Capabilities of compressed air energy storage in the economic design of renewable off-grid system to supply electricity and heat costumers and smart charging-based electric vehicles. Journal of Energy Storage, 78, 109888.
Li, S. et al. Evaluating the efficiency of CCHP systems in Xinjiang Uygur autonomous region: an optimal strategy based on improved mother optimization algorithm. Case Stud. Therm. Eng. 54, 104005 (2024).
Guo, X. & Ghadimi, N. Optimal design of the proton-exchange membrane fuel cell connected to the network utilizing an improved version of the metaheuristic algorithm. Sustainability 15, 13877 (2023).
Chang, L., Wu, Z. & Ghadimi, N. A new biomass-based hybrid energy system integrated with a flue gas condensation process and energy storage option: an effort to mitigate environmental hazards. Process Saf. Environ. Prot. 177, 959–975 (2023).
Yuan, K. et al. Optimal parameters Estimation of the proton exchange membrane fuel cell stacks using a combined Owl search algorithm. Energy Sour. Part A Recover. Utilization Environ. Eff. 45 (4), 11712–11732 (2023).
Han, E. & Ghadimi, N. Model identification of proton-exchange membrane fuel cells based on a hybrid convolutional neural network and extreme learning machine optimized by improved honey Badger algorithm. Sustain. Energy Technol. Assess. 52, 102005 (2022).
Liu, J. et al. An IGDT-based risk-involved optimal bidding strategy for hydrogen storage-based intelligent parking lot of electric vehicles. J. Energy Storage. 27, 101057 (2020).
Zhang, J., Khayatnezhad, M. & Ghadimi, N. Optimal model evaluation of the proton-exchange membrane fuel cells based on deep learning and modified African Vulture optimization algorithm. Energy sources, part A: recovery, utilization, and environmental effects 44.1 : 287–305. (2022).
Duan, F. et al. Model parameters identification of the PEMFCs using an improved design of crow search algorithm. Int. J. Hydrog. Energy. 47 (79), 33839–33849 (2022).
Ye, H. et al. High step-up interleaved Dc/dc converter with high efficiency. Energy sources, part A: recovery, utilization, and environmental effects : 1–20. (2020).
Chen, L. et al. Optimal modeling of combined cooling, heating, and power systems using developed African Vulture optimization: a case study in watersport complex. Energy sources, part A: recovery, utilization, and environmental effects 44.2 : 4296–4317B (2022).
Guo, H. et al. Parameter extraction of the SOFC mathematical model based on fractional order version of dragonfly algorithm. Int. J. Hydrog. Energy. 47 (57), 24059–24068 (2022).
Rezaie, M. et al. Model parameters Estimation of the proton exchange membrane fuel cell by a modified golden Jackal optimization. Sustain. Energy Technol. Assess. 53, 102657 (2022).
Mahdinia, S. et al. Optimization of PEMFC model parameters using meta-heuristics. Sustainability 13.22 : 12771. (2021).
Karamnejadi Azar et al. Developed design of battle Royale optimizer for the optimum identification of solid oxide fuel cell. Sustainability 14, 9882 (2022).
Saeedi, M. et al. Robust optimization based optimal chiller loading under cooling demand uncertainty. Appl. Therm. Eng. 148, 1081–1091 (2019).
Akbary, P. et al. Extracting appropriate nodal marginal prices for all types of committed reserve. Comput. Econ. 53, 1–26 (2019).
Hamian, M. et al. A framework to expedite joint energy-reserve payment cost minimization using a custom-designed method based on mixed integer genetic algorithm. Eng. Appl. Artif. Intell. 72, 203–212 (2018).
Cai, W. et al. Optimal bidding and offering strategies of compressed air energy storage: A hybrid robust-stochastic approach. Renew. Energy. 143, 1–8 (2019).
Khodaei, H. et al. Fuzzy-based heat and power hub models for cost-emission operation of an industrial consumer using compromise programming. Appl. Therm. Eng. 137, 395–405 (2018).
Mohammadi, M. et al. Small-scale Building load forecast based on hybrid forecast engine. Neural Process. Lett. 48, 329–351 (2018).
Zhang et al. A deep learning outline aimed at prompt skin cancer detection utilizing gated recurrent unit networks and improved orca predation algorithm. Biomed. Signal Process. Control. 90, 105858 (2024).
Liu, H. & Ghadimi, N. Hybrid convolutional neural network and flexible Dwarf mongoose optimization algorithm for strong kidney stone diagnosis. Biomed. Signal Process. Control. 91, 106024 (2024).
Han, M. et al. Timely detection of skin cancer: an AI-based approach on the basis of the integration of echo state network and adapted seasons optimization algorithm. Biomed. Signal Process. Control. 94, 106324 (2024).
Gong, Z., Li, L. & Ghadimi, N. SOFC stack modeling: a hybrid RBF-ANN and flexible Al-Biruni Earth radius optimization approach. Int. J. Low-Carbon Technol. 19, 1337–1350 (2024).
Ghiasi, M. et al. A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: past, present and future. Electr. Power Syst. Res. 215, 108975 (2023).
Hamidpour, H. et al. Flexible, reliable, and renewable power system resource expansion planning considering energy storage systems and demand response programs. IET Renew. Power Gener. 13 (11), 1862–1872 (2019).
Jordehi, A. R. et al.A risk-averse two-stage stochastic model for planning retailers including self-generation and storage system. J. Energy Storage 51, 104380 (2022).
Naghibi, A. F. et al. Stochastic economic sizing and placement of renewable integrated energy system with combined hydrogen and power technology in the active distribution network. Sci. Rep. 14 (1), 28354 (2024).
Akbari, E. et al. Multi-objective economic operation of smart distribution network with renewable-flexible virtual power plants considering voltage security index. Sci. Rep. 14 (1), 19136 (2024).
Mohammadzadeh, M. et al. Application of mixture of experts in machine learning-based controlling of DC-DC power electronics converter. IEEE Access 10, 117157–117169. (2022).
Pirouzi, S., Zadehbagheri, M. & Behzadpoor, S. Optimal placement of distributed generation and distributed automation in the distribution grid based on operation, reliability, and economic objective of distribution system operator. Electr. Eng., 1–14. (2024).
Zadehbagheri, M., Dehghan, M., Kiani, M. & Pirouzi, S. Resiliency-constrained placement and sizing of virtual power plants in the distribution network considering extreme weather events. Electr. Eng 1–17 (2024).
Norouzi, M. et al. Risk-averse and flexi-intelligent scheduling of microgrids based on hybrid Boltzmann machines and cascade neural network forecasting. Appl. Energy. 348, 121573 (2023).
Yao, M. et al. and. Stochastic economic operation of coupling unit of flexi-renewable virtual power plant and electric spring in the smart distribution network. IEEE Access. (2023).
Norouzi, M. et al. and. Enhancing distribution network indices using electric spring under renewable generation permission. In 2019 International Conference on Smart Energy Systems and Technologies (SEST) (pp. 1–6). IEEE. (2019), September.
Bagherzadeh, L. et al. Coordinated flexible energy and self-healing management according to the multi‐agent system‐based restoration scheme in active distribution network. IET Renew. Power Gener. 15 (8), 1765–1777 (2021).
Zhang, J., Wu, H., Akbari, E., Bagherzadeh, L. & Pirouzi, S. Eco-power management system with operation and voltage security objectives of distribution system operator considering networked virtual power plants with electric vehicles parking lot and price-based demand response. Comput. Electr. Eng. 121 109895 (2025).
Pirouzi, S., Aghaei, J., Shafie-Khah, M., Osório, G. J. & Catalão, J. P. S. Evaluating the security of electrical energy distribution networks in the presence of electric vehicles. In 2017 IEEE Manchester PowerTech (pp. 1–6). IEEE. (2017), June.
Emdadi, K. & Pirouzi, S. Benders Decomposition-Based Power Network Expansion Planning According to Eco-Sizing of High-Voltage Direct-Current System, Power Transmission Cables and Renewable/Non-Renewable Generation Units. IET Renewable Power Generation. 19(1), e70025 (2025).
Navesi, R. B., Naghibi, A. F., Zafarani, H., Tahami, H. & Pirouzi, S. Reliable operation of reconfigurable smart distribution network with real-time pricing-based demand response. Electr. Power Syst. Res 241, 111341 (2025).
Norouzi, M. et al. Flexible operation of grid-connected microgrid using ES. IET Generation Transmission Distribution. 14 (2), 254–264 (2020).
Navesi, R. B., Jadidoleslam, M., Moradi-Shahrbabak, Z. & Naghibi, A. F. Capability of battery-based integrated renewable energy systems in the energy management and flexibility regulation of smart distribution networks considering energy and flexibility markets. J. Energy Storage. 98, 113007 (2024).
Nowdeh, S. A., Naderipour, A., Davoudkhani, I. F. & Guerrero, J. M. Stochastic optimization–based economic design for a hybrid sustainable system of wind turbine, combined heat, and power generation, and electric and thermal storages considering uncertainty: A case study of Espoo, Finland. Renew. Sustain. Energy Rev. 183, 113440 (2023).
Matpower software Case of 57-bus system. Available: https://matpower.org/.
Mani, M., Bozorg-Haddad, O. & Chu, X. Ant Lion optimizer (ALO) algorithm. Adv. Optim. nature-inspired Algorithms. 105, 116 (2018).
Zolghadr-Asli, B., Bozorg-Haddad, O. & Chu, X. Crow search algorithm (CSA). Adv. Optim. nature-inspired Algorithms. 143, 149 (2018).
Mirjalili, S. SCA: a sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 96, 120–133 (2016).
Rezaei, H., Bozorg-Haddad, O. & Chu, X. Grey Wolf optimization (GWO) algorithm. Adv. Optim. nature-inspired Algorithms, 81–91. (2018).
Rao, R. V. & Rao, R. V. Teaching-learning-based Optimization Algorithmpp. 9–39 (Springer International Publishing, 2016).
Karaboga, D., Gorkemli, B., Ozturk, C. & Karaboga, N. A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 42, 21–57 (2014).
Mirjalili, S. & Mirjalili, S. Genetic algorithm. Evolutionary Algorithms Neural Networks: Theory Appl. 43, 55 (2019).
Wang, D., Tan, D. & Liu, L. Particle swarm optimization algorithm: an overview. Soft. Comput. 22 (2), 387–408 (2018).
Author information
Authors and Affiliations
Contributions
Ehsan Akbari: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data Curation, Writing - Original Draft.Ahad Faraji Naghibi: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data Curation, Writing - Original Draft.Mehdi Veisi: Investigation, Resources, Data Curation, Writing - Original Draft.Sasan Pirouzi: Supervisor, Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data Curation, Writing - Original Draft.Sheila Safaee: Supervisor, Investigation, Resources, Data Curation, Writing - Original Draft.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Akbari, E., Naghibi, A.F., Veisi, M. et al. High voltage direct current system-based generation and transmission expansion planning considering reactive power management of AC and DC stations. Sci Rep 15, 15537 (2025). https://doi.org/10.1038/s41598-025-99875-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-99875-z
Keywords
This article is cited by
-
Stochastic economic placement and sizing of electric vehicles charging station with renewable units and battery bank in smart distribution network
Scientific Reports (2025)
-
Two-layer energy scheduling of electrical and thermal smart grids with energy hubs including renewable and storage units considering energy markets
Scientific Reports (2025)
-
Robust operation of renewable virtual power plant in intelligent distribution system considering active and reactive ancillary services markets
Scientific Reports (2025)
-
Capabilities of battery and compressed air storage in the economic energy scheduling and flexibility regulation of multi-microgrids including non-renewable/renewable units
Scientific Reports (2025)