Introduction

A jointless bridge is defined by the International Association of Jointless Bridges (IAJBs) as a bridge structure with a continuous superstructure without installing any expansion equipment within the whole bridge structure. This definition emphasizes the absence of expansion joints throughout the entire superstructure of a bridge1,2. One novel design of the fully jointless bridges (FJBs) utilizes a road-bridge link slab further to eliminate the gaps between the continuous bridge ends and the approach road3. Currently, FJBs are suitable for the construction of medium and small bridges to improve ride comfort at road-bridge connections4,5.

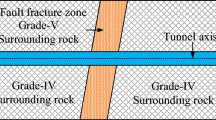
In preview research, an innovative road-bridge link slab made from engineered cementitious composites (ECCs), referred to as ECC road-bridge link slabs, as shown in Fig. 1, effectively utilizes the high-strain hardening characteristics of the ECC material, including its multiple cracking characteristics6,7,8 and strong crack width control capability9,10,11, thereby significantly enhancing the performance of FJBs12,13. Zhan et al.4,5 studied the tensile performance of the ECC road-bridge link slab, and the results demonstrated its substantial ability to absorb longitudinal deformations, which aligns with the requirements for FJBs to accommodate the deformations of bridge structures. However, ECC is quite expensive because of the use of silica sand. Zhang et al.14,15,16 and Zhan et al.12 developed a rubberized engineered cementitious composite (R-ECC) by using river fine sand and rubber crumb to completely substitute for silica sand and reduce its cost. The experimental results validated the suitability of the R-ECC material used in the road-bridge link slab to absorb longitudinal deformations caused by system temperature loads13.

Fig. 1
figure 1

ECC road-bridge link slab for FJBs13.

Full size image

Seasonal temperature loads is a key factor influence the performance of FJBs. Under seasonal temperature loads, micro-cracks developed on the surface of the R-ECC road-bridge link slabs of FJBs. But previous research proved that the microcracked R-ECC slabs exhibit strong crack control capabilities and meet the strength criteria for FJBs13. Compared to ECCs, R-ECCs have improved bending ability but lower compressive strength. At this point, whether the road-bridge link slab with micro-cracks can bear the vehicle load is worth studying. In order to demonstrate the successful application R-ECC in road-bridge link slabs for FJBs and establish a design theory for R-ECC road-bridge link slabs, further research is needed. This research should focus on the rebound deflection test of the microcracked R-ECC road-bridge link slab under vehicle loads. The objective was to evaluate whether the crack development and the bending deformation capacity of the R-ECC road-bridge link slabs with microcracks under vehicle load meet the durability and strength criteria of FJBs.

Rebound deflection test

Objective and overview

In practical projects, the road-bridge link slabs often develop microcracks due to seasonal temperature variations, particularly in winter. These slabs are subjected to pressure, impact, shear, and wear from vehicle loads, creating complex stress conditions that make it challenging to ensure the durability of microcracked slabs under these conditions.

The rebound deflection is directly related to the design strength of the pavement. It serves as one of the standards to check whether the construction of the pavement meets the design strength requirements. To explore the applicability of R-ECC road-bridge link slabs for FJBs, a vehicle load that directly acts on the most unfavourable cracking position of the R-ECC slab is used to test its rebound deflection.

The contact pressure, contact shape, and contact area between the vehicles and surface course are difficult to simulate in the laboratory. In accordance with the Specifications for the Design of Highway Asphalt Pavement in China, a dual wheel with one single-axle load of 100 kN is designed as the standard axle load, denoted as BZZ-100. The tire contact pressure is calculated to be 0.7 MPa, and the diameter of a single-wheel contact area equivalent circle is 21.3 cm17. Then, the diameter of the steel bearing plate used to simulate the wheel effect is determined to be 21.3 cm, with a thickness of 2 cm.

Model design

General description

The test model consists of an R-ECC slab measuring 5 m in length, 0.5 m in width, and 0.15 m in thickness, as shown in Fig. 2a,b13.There are three layers: a 15 cm R-ECC road-bridge link slab layer, a 25 cm 5% cement-stabilized gravel base layer, and a 20 cm grade gravel base layer, as shown in Fig. 2a. To prevent overflow of the base materials under vertical loading, the base materials are contained within a wooden box, as illustrated in Fig. 2c. As shown in Fig. 2d, a 2 mm thick emulsified asphalt sealing (EAS) layer is poured as a sliding layer between the 5% cement-stabilized gravel base layer and the R-ECC slab layer. Additionally, the detailed model design, casting process and reinforcement arrangement of the R-ECC slab are illustrated in Fig. 2c–h.

Fig. 2
figure 2

Model design and casting process of the R-ECC slab (units: cm). (a) Model elevation, (b) Model plan, (c) Wooden box, (d) EAS layer, (e) Steel bars, (f) Model casting, (g) Model Maintenance, (h) Test model.

Full size image

Model parameters

Based on previous research findings13, the R-ECC mix ratio for the design of the R-ECC road-bridge link slab is shown in Table 1.

Table 1 Material mix ratio of R-ECC.
Full size table

The detailed material parameters for the R-ECC slab test specimen are shown in Table 2.

Table 2 Detailed material parameters for the R-ECC slab.
Full size table

Loading location

Before conducting the rebound deflection test, a low-cycle tensile/compression test of the R-ECC slab must be performed to simulate the cracking that occurs in the slab due to seasonal temperature fluctuations18. In this case, a low two-and-a-half cycle tensile/compression test was simulated13. At the end of the two-and-a-half tensile test, lots of microcracks appeared on the surface of the R-ECC slab and the larger cracks are primarily concentrated near the tension end. The crack distribution within the slab are shown in Fig. 3a. To prevent a significant change in slab stiffness and to facilitate the placement of the bearing plate for vehicle load simulation, a position 50 cm away from the tension end is selected as the loading location, as shown in Fig. 3b.

Fig. 3
figure 3

Loading location (unit: cm) (a) crack distribution of the R-ECC slab, (b) loading point diagram.

Full size image

Layout of measuring instrument

Two bearing plates are used for vehicle load application, One is marked as 'B', located 0.5 m away from the tension end, as shown in Fig. 4a,b. Four dial gauges are arranged along the bearing plate ‘B’ and labeled as ‘B1’ to ‘B4’. The other bearing plate is labeled as ‘D’ and is positioned approximately 319.5 mm away from bearing plate ‘B’, at a distance of 1.5 times the radius (r) of the bearing plate. Additionally, four dial gauges are arranged along the bearing plate ‘D’ and labeled as ‘D1’ to ‘D4’, as shown in Fig. 4a,c. These gauges are used to measure the vertical displacement of the bearing plates under vertical load. In addition, a dial gauge labeled as 'A' is positioned at the centre of the two bearing plates to measure the rebound deflection.

Fig. 4
figure 4

Arrangement of the measuring points (unit: mm). (a) Schematic diagram, (b) picture of bearing plate ‘B’, (c) picture of bearing plate ‘D’.

Full size image

Loading process

The vertical load applied to the center of the bearing plate is divided into two levels, with each level carrying a load of 50 kN. After loading, the model rests for 5 min and the data is recorded. When unloading vertical loads, the process is completed all at once.

Results and discussion

Crack development

The largest crack width of the microcracks near the tension end is 65 μm, as shown in Fig. 5a. As the load increases, the crack width grows slightly, but remains constant beyond 100 µm, as shown in Fig. 5b. When the vertical loads reaches 100 kN, the maximum crack width (wmax) reaches 90 µm and after unloading, the crack width decreases to 85 µm. It indicates that the microcracked R-ECC slab possesses strong crack control capabilities and durability resistance under vehicle loads.

Fig. 5
figure 5

Maximum micro-cracking (unit:µm). (a) A picture of the maximum micro-cracking, (b) the relationship between the maximum crack width and the vertical load.

Full size image

Rebound deflection

The recorded vertical deflections are shown in Table 3. The vertical deflection results of bearing plate ‘B’ and ‘D’ are obtained by averaging the deflection measured from ‘B1’ to ‘B4’ and ‘D1’ to ‘D4’, respectively. The maximum vertical deflection at ‘B’ and ‘D’ is 0.279 mm and 0.282 mm, respectively, and the vertical residual deflection is 0.011 mm and 0.012 mm after unloading, respectively. Then the rebound deflection at ‘B’ and ‘D’ are 0.268 mm and 0.270 mm, respectively. While the rebound deflection at ‘A’ is 0.235 mm.

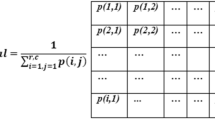
Table 3 The recorded vertical deflections(mm).
Full size table

The standard value for the rebound deflection of a 5% cement-stabilized gravel base is given in Table 4, and the acceptance rebound deflection can be calculated via the following equation19:

$$l_{s} = 2000\delta \left[ {\frac{{1.63l_{l} }}{2000\delta }\left( {\frac{{E_{0} }}{p}} \right)^{0.36} } \right]^{1/0.62}$$
(1)

where P is the tire contact pressure under the standard axle load, which is 0.7 MPa; \(\delta\) is the equivalent circular radius of the dual wheels, which is 16 cm; \(l_{l}\) is the theoretical deflection; and \(E_{0}\) is the rebound modulus of the base course.

Table 4 Standard values for the rebound deflection19.
Full size table

Therefore, the rebound deflection of the microcracked R-ECC road–bridge link slab is 0.235 mm, less than the acceptable rebound deflection of 0.345 mm. This indicates that the microcracked R-ECC road-bridge link slab meets the strength requirements under vehicle loads.

Sensitivity parameter analysis

An investigation of the sensitive influencing parameters (such as the slab thickness and the equivalent elasticity modulus of foundation) on the performance of the R-ECC road-bridge link slab was performed to obtain the design parameters for the R-ECC road-bridge link slab. In this paper, a finite element analysis model of R-ECC road-bridge link slab is established based on the experimental results13. The mechanical properties of the R-ECC road-bridge link slabs were simulated via the concrete damaged plasticity (CDP) plasticity damage failure criterion.

Model specifications

A finite element model of the R-ECC slab was established via the discrete simulation method. In this model, the R-ECC slab, tension end, anchor end, and base course were simulated with C3D8R solid elements, whereas the steel bars were simulated with T3D2 truss elements. To ensure computational accuracy, different parts of the model were divided into different grids. Therefore, the R-ECC slab and steel bars used a finer mesh, whereas the base course used a coarser mesh, as shown in Fig. 6a. The effect of slipping between the steel bars and the R-ECC slab was not considered. The anchor end and the base course of the R-ECC slab were fully constrained, as shown in Fig. 6b. The interaction between the R-ECC slab and the 5% cement-stabilized gravel base was simulated through surface-to-surface contact, allowing for separation after contact. The tangential interaction was modeled via Coulomb friction, with a friction coefficient of 1.1513. The base course at a depth of 20 m was treated as an isotropic elastic material with a Poisson’s ratio of 0.3, and variations in the Young’s modulus were used to simulate changes in the ERM of the base course. The PVA fibers were modeled by inputting their three-dimensional parameters with a fixed volume fraction of 2%. The steel bars were modeled via an ideal elastic–plastic material model.

Fig. 6
figure 6

A finite element simulation of the R-ECC road-bridge link slab. (a) Grid division and constraints, (b) loading simulation, (c) bilinear constitutive model.

Full size image

As shown in Fig. 6c, the R-ECC material follows a bilinear constitutive model20 based on results from material experiments13. It exhibits an initial cracking strength of 3.19 MPa, an initial cracking strain of 0.029%, an ultimate tensile strength of 3.70 MPa, and an ultimate strain of 2.40%.

Traffic loads simulation

As we mentioned before, the most unfavorable position (0.5 m away from the tensile end) was selected as the control point to apply the vertical vehicle load, as shown in Fig. 7 and the vehicle load for each bearing plate is 100 kN.

Fig. 7
figure 7

Location of loading point.

Full size image

Results and discussion

Influence of the slab thickness

The mechanical performance of R-ECC road–bridge link slabs with five different thicknesses (t = 100 mm, 120 mm, 150 mm, 180 mm, and 200 mm) was investigated. The influence of slab thickness on the maximum stress and tensile damage of R-ECC slabs was evaluated and the results are shown in Fig. 8.

Fig. 8
figure 8

Mechanical properties of R-ECC slab with different thicknesses: (a) maximum stress, (b) tensile damage.

Full size image

From Fig. 8a, it can be seen that the maximum stress decreased with the increase in the thickness of the R-ECC slab. But when the thickness of the R-ECC slab increased from 120 to 150 mm, the maximum internal force decreased rapidly, it decreased by 18.9%. From Fig. 8b, it can be seen that the tensile damage also decreased with the increase in the thickness of the R-ECC slab. But when the thickness of the R-ECC slab increased from 150 to 180 mm, the tensile damage decreased rapidly, it decreased by 91.2%.

Influence of the equivalent elasticity modulus of the foundation

The effects of six different equivalent elasticity modulus of the foundation (E = 200 MPa, 400 MPa, 600 MPa, 800 MPa, 1000 MPa, and 1200 MPa) on the maximum stress and tensile damage of the R-ECC slab were investigated and the results are shown in Fig. 9.

Fig. 9
figure 9

Mechanical properties of R-ECC slabs with different equivalent elasticity modulus of foundation: (a) maximum stress, (b) tensile damage.

Full size image

As seen in Fig. 9a, as the equivalent elasticity modulus of the foundation increases, the maximum decreases consistently. Meantime, the tensile damage in the R-ECC slab diminishes as the equivalent elasticity modulus of the foundation rises. Once the equivalent elasticity modulus of the foundation exceeds 800 MPa, there are minimal changes observed in the results.

Discussion

Based on the results of sensitive parameter calculations, a relationship between the slab thickness and the maximum stress and tensile damage of the R-ECC slab were established. It was found that the thicker the slab thickness, the better the performance. However, increasing the slab thickness also raises construction costs. We introduce the evaluation parameter “Ct” to quantify the relationship between the decrement of maximum stress/tensile damage and the increment of the construction cost. Here, the construction cost is calculated in units of 1000 USD. A larger value of “Ct” indicates a greater stress/tensile damage reduction for the same increment of the construction cost, suggesting that this structural type is a more cost-effective option. The calculation for this parameter is as follows:

$${C}_{t}=\frac{\text{Decrement of maximum stress}\,(\text{MPa}){/}\text{tensile damage }}{\text{Increment of construction cost }\,(\text{\$}1000)}$$
(2)

The value of “Ct” can be determined using Eq. (2), and the results are presented in Table 5.

Table 5 Ct with different slab thicknesses(t).
Full size table

It can be seen from Table 5 that the value of Cti decreases with the increase of slab thickness. Especially when the thickness of the slab increases from 150 to 180 mm, the value of Cti reduction decreases. This shows that when the slab thickness is greater than 150 mm, increasing the slab thickness can only slightly reduce the reduction of the maximum stress. And when the slab thickness reaches 180 mm, the value of Ctt is the largest. Therefore, this paper recommends a slab thickness of 180 mm to minimize the slab’s performance and construction cost.

Meantime, the relationship between the equivalent elasticity modulus of the foundation and the performance of the R-ECC slab also has been examined. It was found that a higher equivalent elasticity modulus of the foundation corresponds to improved mechanical properties of the slab. However, increasing the equivalent elasticity modulus of the foundation will also lead to higher construction costs. However, no research results have been found on the relationship between cost and the equivalent elastic modulus of the foundations. In this paper, we propose an evaluation parameter “Ce” to assess the relationship between the mechanical properties and the equivalent elasticity modulus of the foundation of R-ECC slabs. A larger value of “Ce” indicates a greater stress/tensile damage reduction for the same increment of the equivalent elasticity modulus of the foundation, suggesting that this structural type is a more cost-effective option. The calculation for this parameter is as follows:

$${C}_{e}=\frac{\text{Decrement of maximum stress}\,(\text{MPa}){/}\text{tensile damage }}{\text{Increment of equivalent elasicity modulus of the foundation}\, (\text{GPa})}$$
(3)

The value of “Ce” can be determined using Eq. (3), and the results are presented in Table 6.

Table 6 Ce with the different equivalent elasticity modulus of the foundation.
Full size table

It can be seen from Table 6 that the value of Cei decreases with the increase of equivalent elasticity modulus of the foundation. Especially when the equivalent elasticity modulus of the foundation is greater than 800 MPa, the value of Cei reduction decreases. This shows that when the equivalent elasticity modulus of the foundation is greater than 800 MPa, the increase of equivalent elasticity modulus of the foundation can only slightly reduce the reduction of the maximum stress. And when the equivalent elasticity modulus of the foundation reaches 1000 MPa, the value of Ctt is drops the most. Therefore, in order to minimize the performance and construction cost of the slab, this paper recommends an equivalent elasticity modulus of the foundation of 800 MPa.

In conclusion, in light of the mechanical properties and cost constraints of the R-ECC road-bridge link slab, this paper proposes that the design specifications for the R-ECC road-bridge link slab should be as follows: a thickness of 180 mm and an equivalent elasticity modulus of the foundation of 800 MPa.

Conclusions

Based on the results of this study, the following conclusions can be drawn:

  1. (1)

    Through the vertical bearing plate test, it is found that microcracked R-ECC road-bridge link slab has strong crack control capabilities and durability resistance. The vertical deformation of the microcracked R-ECC road-bridge link slab increased with increasing vertical load, and the rebound deflection was 0.235 mm, which is less than the calculated acceptable rebound deflection of 0.345 mm, meeting the design strength requirements for the road-bridge link slab.

  2. (2)

    Through the sensitivity parameter numerical analysis, the effects of the slab thickness and equivalent elasticity modulus of the foundation on the mechanical performance of the R-ECC road-bridge link slab were studied. The internal force and tensile damage of the R-ECC road-bridge link slab decrease with increasing slab thickness and equivalent elasticity modulus of the foundation. Based on the calculation results of the evaluation parameter “Ct” and “Ce”, this paper suggests that the design thickness and equivalent elasticity modulus of the foundation for an R-ECC road-bridge link slab should be 180 mm and 800 MPa, respectively.

  3. (3)

    Due to space limitations, this paper only studied the mechanical properties of micro-cracked R-ECC road-bridge link slabs under vehicle loads. To verify the applicability of R-ECC mixtures in the construction of road-bridge link slabs for FJBs, the following research areas need to be studied: the dynamic simulation analysis of the R-ECC road-bridge link slab and R-ECC road-bridge link slabs suffering uneven settlement of abutments/piers or with different anchoring quality situation of anchor beam as well.