Analysing the impact of digital technology diffusion on the efficiency and convergence process of the commercial banking industry of Pakistan

Abstract

In a dynamic financial ecosystem, digitalisation is supporting banks in revamping their business processes to be more efficient, reducing costs, coping with customers’ evolving demands, and keeping them abreast of market competition. This two-stage research aims to investigate three issues in Pakistan’s banking industry from 2006 to 2020: (i) banking efficiency; (ii) the impact of digitalisation on banking efficiency; and (iii) banking efficiency’s absolute and conditional convergence. In our first-stage analysis, bootstrap data envelopment analysis has been applied, which exhibits bias-corrected overall, pure, and scale efficiencies of 74, 77, and 96%, respectively. In the second-stage analysis, we executed Tobit and two-step dynamic panel data system generalised method of moments (DPDSYS-GMM) models, and the results uncover that digitalisation has a positive influence on banking efficiency. Findings confirm that return on assets, bank size, interest rate, and gross domestic product growth rate have a positive association with banking efficiency. Our research reveals that state-controlled banks outperform their private sector and special-purpose counterparts. Our DPDSYS-GMM findings validate β and σ-convergence, implying that initially, low-efficient banks caught up (converged) to the more efficient opponents, reducing cross-sectional efficiency dispersion and attaining common equilibrium. The findings of banking efficiency conditional β-convergence assert that the adoption of digital technology has played a critical role in the convergence process and that digitalisation has acted as a catalyst for less efficient banks to catch up significantly faster to their more efficient rivals. This study displays digitalisation’s disruptive influence on the overall transformation of Pakistan’s banking system in the modern era, resulting in significant efficiency gains.

Introduction

The banking industry in Pakistan plays a crucial role in driving the country’s economic growth. Banking performance analysis has captured the interest of scholars, the federal government, and financial regulators. While a range of different measures are used to examine the banking performance, the banking literature most extensively applies technical efficiency analysis. Moreover, technical efficiency analysis allows decomposition into pure technical and scale efficiencies, which provides a more meaningful and holistic view of identifying the sources of inefficiency. Suboptimal management abilities can lead to pure technical inefficiency, while unfavourable business environments cause scale inefficiency. International literature has extensively studied the issue of technical efficiency in the banking industry; however, in Pakistani banking literature, fewer studies have delved into banking technical efficiency analysis. For instance, (Usman et al., 2010; Chupradit et al., 2021) have employed non-parametric data envelopment analysis (DEA), while Afza and Yusuf (2012) have employed parametric stochastic frontier analysis (SFA). However, the main problem with the earlier strand of literature pertaining to DEA-based studies is that it lacks statistical properties. According to Simar and Wilson (2007), classical DEA generates biased and overstated efficiency estimates, which can be misleading for policy implications. Similarly, the latter strand of SFA-based literature has its own inherent limitations, mainly their lack of handling multiple inputs and outputs simultaneously and econometric functional form assumptions. Therefore, this study seeks to address this gap by estimating biased free efficiency estimates and proposes the following research question:

RQ1: What is the technical efficiency of Pakistan’s banking industry, and how has technical efficiency changed over the studied period?

On the other hand, the advent of the 21st century has resulted in a veritable eruption of modern innovations and technologies that have revolutionised business services and products. It has been particularly noticeable in the banking industry across the globe. The proliferation of digital technology has revolutionised the provision of financial services. Internet banking, smartphones with banking applications, and e-wallets have supplanted more conventional banking approaches. Digitalisation in the banking industry streamlines and reduces costs by using digital technologies. Conventional banks are digitising their operations to be more efficient and competitive in the market. Digitalisation refers to enhancing traditional banking services with forward-thinking technologies like internet banking, mobile banking, and electronic money digital payment systems. With ATMs and phone banking, digitalised banking emerged. The Internet and mobile banking applications, in particular, have made traditional banking products more ubiquitous.

According to several prior studies, the link between digitalisation and banking efficiency is still evolving and has not been conclusively established. Previous studies (Ekinci, 2021; Li et al., 2021; Wang et al., 2021; Zuo et al., 2021; Le et al., 2022) found a positive link between digital technology adoption and efficiency, while scholars (Martín-Oliver & Salas-Fumás, 2008; Chen & Xie, 2015) also identified a negative relationship between the two. Thus, the impact of digital technology adoption on banking efficiency remains unresolved. Moreover, there is no empirical evidence from Pakistan’s banking industry regarding this issue. There are several reasons why Pakistan’s banking industry has grown more competitive: (i) increasing competition from international banks; (ii) stricter statutory requirements; and (iii) higher investment costs resulting from decades of restructuring and deregulation. Likewise, Pakistan’s banking industry faces fierce market competition due to digital technologies ¹. Digital technology products greatly influence a bank’s capacity to offer its customer services. Additionally, digital technology can offer a competitive edge by automating transaction processing and accelerating the delivery of managerial data. It is vital to gain further empirical evidence, particularly from developing economies such as Pakistan, where the banking industry has been substantially growing through the adoption of digital technology. Therefore, we propose the following research question:

RQ2: What is the impact of Digitalisation on the efficiency of the banking industry of Pakistan?

Barro and Sala-i-Martin (1992) explained the term “convergence” in a stream of economic growth literature that addresses the notion that low-income nations are likely to expand more rapidly than richer ones, eventually catching up. Despite the lack of specific explanations for banking efficiency convergence, the macroeconomic paradigm suggests that initially less efficient banks will eventually catch up with more efficient ones, demonstrating a higher rate of efficiency increase to reach an equilibrium point. There are three key gaps related to banking efficiency convergence. First and foremost, the banking efficiency absolute convergence has rarely been investigated in the global banking literature, confirming it is worth additional investigation in this domain to enrich the prior empirical literature (Weill, 2009; Casu & Girardone, 2010; Matthews & Zhang, 2010; Kasman et al., 2013; Carvallo & Kasman, 2017; Olson & Zoubi, 2017; Chen et al., 2020; Mansour & El Moussawi, 2020; Thota & Subrahmanyam, 2020). Second, the issue of banking efficiency absolute convergence from the perspective of the banking industry in Pakistan has still not been brought into consideration. Thirdly, previous studies (Fung, 2006; Casu et al., 2016; Izzeldin et al., 2021) have neglected to adequately examine the issue of conditional banking efficiency convergence. Additionally, there is a dearth of research in international and Pakistani banking literature on the influence of digitalisation on the banking efficiency convergence process. This is particularly significant because different banks may achieve varying equilibriums due to external factors such as digitalisation, bank-specific factors, institutional idiosyncrasies, and banking firms’ operational situations. Therefore, we propose the following research questions to bridge the aforementioned gap:

RQ3: Does the efficiency of the banking industry of Pakistan have any absolute convergence?

RQ4: what is the impact of digitalisation on the efficiency convergence of the banking industry of Pakistan?

To conclude, this study seeks to achieve three main objectives: (i) banking efficiency; (ii) the impact of digitalisation on banking efficiency; and (iii) banking efficiency convergence. Our research examined 29 Pakistani banking firms from 2006 to 2020, which represents up to 90 percent of Pakistan’s overall financial industry asset size.

To meet the first objective, we have examined the evolution of the technical efficiency of Pakistan’s banking industry from 2006 to 2020. To provide bias-free efficiency estimates for Pakistan’s banking industry, we have employed a more robust and novel bootstrap data envelopment analysis (DEA) approach, coupled with traditional non-parametric DEA. We have also provided an efficiency decomposition for a deeper insight into Pakistan’s banking industry’s performance. Our results show that during 2006–2020, the average bootstrap bias-corrected overall technical efficiency was 74%, whereas the average bootstrap bias-corrected pure technical efficiency was 77%. Likewise, the average bootstrap bias-corrected scale efficiency was 96%. We conclude that bootstrap bias-corrected pure technical inefficiency (managerial inefficiency) of −23% accounts for the majority of bootstrap bias-corrected overall technical inefficiency.

Second, we have investigated how digitalisation and other contextual factors have influenced the efficiency of Pakistan’s banking industry throughout the course of the study’s period. We employed Tobit and two-step dynamic panel data system generalised method of moments (DPDSYS-GMM) estimators. The latter estimator exhibits greater robustness in panel data settings and effectively manages endogeneity, heteroskedasticity, and omitted variable bias; on the other hand, the former avoids the bias stemming from the first stage of bootstrap DEA’s bounded range (0, 1) of estimated efficiency scores. We examined the digitalisation using the number of internet-based transactions (IBTR), point-of-sale-based transactions (POSBTR), ATM-based transactions (ABTR), and digitalization index (DIG INDEX), the results reveal that digitalization significantly improves the efficiency of Pakistan’s banking industry. We observed that SIZE and return on assets (ROA) are two bank-specific factors that are positively associated with banking efficiency. Furthermore, macroeconomic factors which demonstrate a positive relationship with banking efficiency include the interest rate (INTRATE) and the gross domestic product growth rate (GDPGR).

Third, we have investigated efficiency convergence to comprehend the (catch-up) effect, that is, if there is any evidence that initially less efficient banks catch up (converge) with their more efficient counterparts over time. In this respect, we have inherited a concept from convergence models of growth economic i.e. β-convergence and σ-convergence (Barro & Sala-i-Martin, 1992; Quah, 1996). We have explored efficiency absolute β and σ-convergence. Our results reveal that less efficient banks have caught up with (converged with) their more efficient rivals, and that banks that initially had a higher dispersal from the cross-sectional mean efficiency have been able to narrow the gap between 2006 and 2020. Hence, we have concluded that efficiency absolute β and σ-convergence has occurred in Pakistan’s banking industry during 2006–2020.

Fourth, we have analysed the influence of digitalisation on the efficiency convergence process in Pakistan’s banking sector by looking at efficiency conditional β-convergence. We discover that digitalisation is positively associated with efficiency growth rates. Our empirical evidence reveals that the digitalisation has allowed less efficient banks to catch up with more efficient ones significantly faster during 2006–2020. Other control factors revealed that the loan growth ratio, prudent lending strategies, M2 money supply growth, and GDP growth rates positively influence the banking efficiency growth rate, validating that an upward shift in the M2 money supply could increase loan appetite. In conjunction with prudent lending practices, their snowball effect accelerates GDP growth and banking efficiency convergence process.

Literature review

Several studies investigating the influence of digitalisation on the banking sector have shown that the use of technology has significant implications for the banking system as a whole. Although significant investments in digital technology and the growing adoption of digital technologies have changed the banking industry, there is a lack of research on the influence of digitalisation on banking efficiency. Researchers (Ekinci, 2021; Li et al., 2021; Wang et al., 2021; Zuo et al., 2021; Le et al., 2022) investigated the impact of digital technology on banking efficiency. These studies conclude that digital technology positively influences banking efficiency. Innovations in technology can reduce intermediation costs, especially among underutilised workforces in the banking industry. However, contradictory results in fewer studies (Martín-Oliver & Salas-Fumás, 2008; Chen & Xie, 2015) concluded an inverse relationship between digital technology and banking efficiency.

However, banking efficiency convergence studies exhibit mixed findings. Studies (Weill, 2009; Kasman et al., 2013; Degl’Innocenti et al., 2017) reveal that EU banking efficiency and productivity converge. Degl’Innocenti et al. (2017) observed a persistent trend of banking productivity convergence in the European Union (EU) shortly after the worldwide financial crisis, as a result of Eastern economies’ catch-up movement and Western nations’ productivity decline. Similarly, Kasman et al. (2013) provided support for convergence in productivity across the EU nations. Moreover, evidence of convergence in EU banking efficiency is corroborated (Weill, 2009; Casu & Girardone, 2010), Latin America (Carvallo & Kasman, 2017), China (Matthews & Zhang, 2010; Chen et al., 2020; Matthews & Zhiguo, 2020), Arab countries (Olson & Zoubi, 2017; Mansour & El Moussawi, 2020), and India (Thota & Subrahmanyam, 2020).

Weill (2009) employed the banking cost efficiency convergence measure, which covers the years 1994–2005, to analyse the European Union banking market and determine the degree to which EU financial systems were integrated. The study’s findings of cost-efficiency β and σ-convergence imply that efficiency levels fluctuate between EU member states and have been gradually improving. Moreover, Kasman et al. (2013) also revealed evidence of β-convergence and σ-convergence in banking productivity, which coincides with the most recent study of Degl’Innocenti et al. (2017) within EU banking. Although Carvallo and Kasman (2017) showed insufficient evidence of convergence in banking cost and profit efficiencies between 1999 and 2013 in Latin American and Caribbean banking markets, two sub-clusters of economies managed to achieve convergence in that region. Some other studies, such as those from Arab countries (Olson & Zoubi, 2017; Mansour & El Moussawi, 2020), China (Matthews & Zhang, 2010; Chen et al., 2020), and India (Thota & Subrahmanyam, 2020), also confirmed the evidence of convergence.

However, there is a dearth of research (Fung, 2006; Casu et al., 2016; Izzeldin et al., 2021) on the issue of conditional banking efficiency convergence. For instance, Fung (2006) provides no validity to the hypothesis of “absolute convergence.” The findings validate the hypothesis of “conditional convergence,” which states that the equilibrium in banking productivity to which US banking holding companies (BHC) converge is dependent on the BHC’s own degree of X-efficiency. Furthermore, Izzeldin et al. (2021) have confirmed the convergence in efficiency between conventional and Islamic banks. Meanwhile, Casu and Girardone (2010) research on the European Union’s (EU) banking system revealed evidence of β-convergence and σ-convergence, suggesting that cost efficiency is converging towards an average level across the EU, yet they observed an obvious lack of convergence in profit efficiency. Likewise, Casu et al. (2016) expanded prior studies and identified significant productivity gaps over the long run, as well as a lack of productivity convergence in the EU banking industries.

To summarise, (i) the literature on digitalisation and banking efficiency nexus is still evolving, and there is a scarcity of empirical research on this issue in Pakistan’s banking industry; (ii) there is also a lack of research on banking efficiency convergence in Pakistan, in contrast to most studies conducted in developed banking markets such as the United States and Europe; (iii) there is a dearth of research on conditional banking efficiency convergence in international and domestic literature; and (iv) neither the global nor the domestic literature has yet evaluated the impact of digitalisation on the efficiency convergence process of the banking industry. Thus, the purpose of this research is to fill in these gaps.

Hypothesis development

Banking efficiency determinants

Relationship between banking efficiency and digitalisation

Electronic banking, or e-banking, is the use of the Internet to conduct financial transactions. In today’s world, electronic banking has made it possible for customers to monitor their finances and make investments from a distance quickly and effortlessly. Unlike traditional banking, which requires a customer to approach a branch physically, digital banking may be executed at any time and from any location. Because of the rapid technological advancements in digital technology, online banking has become more prominent in the e-payments industry. The banking industry has been the subject of previous studies (Ekinci, 2021; Li et al., 2021; Wang et al., 2021; Zuo et al., 2021; Le et al., 2022), which have explored the impact of technological advancements on banking industry efficiency. However, none of the above studies have ever explored the effect of digital services such as ATMs, the Internet, and point-of-sale (POS)-based transactions on banking efficiency. The growing Internet, ATM, and POS-based transactions imply that human resources are being substituted more often with modern digital technologies. These three mediums of digital banking have the potential to overcome the inefficiency challenges of traditional banking firms, such as restrictions on working hours, branches, insufficient expertise, and slower processing times. In today’s competitive banking ecosystem, Pakistani banks with larger human resources are under additional pressure to enhance efficiency. In light of this, ATM, internet, and POS transactions are generally regarded as one of the most practical solutions to substitute human labour and improve banking efficiency. According to Abbas et al. (2015), the three most important characteristics of ATM, internet, and POS-based digital transactions technologies are their dependability, speed, and security. Since a country’s economic standing increases with ICT infrastructure, Abbasi and Weigand (2017) assert that digital technologies improve banking efficiency. Therefore, in response to RQ2, we hypothesise:

H1a- Increased utilisation of digitalisation (ATM-based transactions) positively increases Pakistan’s banking industry efficiency.

H1b- Increased utilisation of digitalisation (Internet-based transactions) positively increases Pakistan’s banking industry efficiency.

H1c- Increased utilisation of digitalisation (point-of-sale-based transactions) positively increases Pakistan’s banking industry efficiency.

H1d- Increased overall utilisation of digitalisation (DIG INDEX) positively increases Pakistan’s banking industry efficiency.

The relationship between banking efficiency and profitability

Banking assets are vital to a bank’s revenues and profit margins. The conventional paradigm holds that banks are more efficient when their revenues are high, and vice versa. Bank efficiency may grow as profitability increases. (Das et al., 2005; Siriopoulos & Tziogkidis, 2010; Ekinci, 2021), utilised net interest margin (NIM), return on assets (ROA), and return on equity (ROE) ratios to assess banking profitability. A bank has a strong NIM when its interest income outweighs its interest costs. For the bank, primary lending and investment provide this profit margin. A higher NIM than the industry norm enhances bank efficiency. Bank efficiency improves with higher ROA due to superior cost control, interest, and other revenue gains. A higher ROE showcases a bank’s capital allocation and utilisation performance. Banks with a higher ROE are more efficient because they are in a stronger position to deliver long-term returns to their shareholders. Thus, we hypothesise:

H2a- The higher profitability (NIM) positively increases Pakistan’s banking industry efficiency.

H2b- The higher profitability (ROE) positively increases Pakistan’s banking industry efficiency.

H2c- The higher profitability (ROA) positively increases Pakistan’s banking industry efficiency.

Relationship between banking efficiency and management cost control ability

The cost-to-income ratio (CIR) often serves as an assessment tool for bank managers’ operational cost control. Several studies (Purohit & Mazumdar, 2003; Olson & Zoubi, 2017) have shown that CIR adversely influences banking efficiency. Consequently, we hypothesise;

H3- An effective cost control managerial ability (i.e., lower CIR) results in higher banking efficiency.

Relationship between banking efficiency and capitalization

The agency paradigm implies that highly leveraged banks ought to be efficient to avoid going insolvent by defaulting on interest payments. Several studies (Lee & Huang, 2016; Mansour & El Moussawi, 2020) suggest that bank capitalization elevates efficiency. A lower equity-to-asset ratio indicates more risk-taking and leverage, which could drive up borrowing costs and negatively impact efficiency. Therefore, we hypothesise;

H4- A higher equity-to-asset ratio (CAPT) results in higher banking efficiency.

Relationship between banking efficiency, AGE, SIZE, and other macroeconomic factors

The relationship between bank AGE and efficiency is complex. Mature banks have gained more knowledge and expertise over their long existence. Over time, they might have developed their business practices, risk assessment, and customer service policies (Chiu & Chen, 2009). Mature banks function more efficiently than newer ones. Thus, we hypothesise:

H5- Bank age has a positive link with banking efficiency.

The bank SIZE, measured as the natural logarithm of total assets, influences the ability of banks to achieve economies of scale across different business domains (Sufian, 2009; Phan et al., 2016). For instance, Sufian (2009) identified that larger Chinese banks are more profitable. While some studies reveal a negative relationship between bank SIZE and efficiency, being more efficient is more likely to be the situation for larger banks due to their larger fixed asset bases, human resources, and branch office networks. Thus, we hypothesise:

H6- Larger banks take advantage of economies of scale, which allows them to operate more efficiently.

We have additionally considered macroeconomic factors such as the inflation rate (INFRATE), interest rate (INTRATE), and gross domestic product growth rate (GDPGR) frequently used in prior studies (Avkiran, 1999; Perera et al., 2007; Anbar & Alper, 2011; Řepková, 2015; Carvallo & Kasman, 2017). The relationship between the inflation rate (INFRATE) and banking efficiency is convoluted. High inflation might make resource allocation challenging for banks. Effective resource allocation enables a bank to optimise revenues and remain profitable. However, inflation makes it challenging to assess investment alternatives, potential returns, and the cost of financing. Unforeseen circumstances might impede banks’ decision-making and efficiency. Thus, we hypothesise;

H7- There is an adverse relationship between the inflation rate and banking efficiency.

Moreover, higher interest rates (INTRATE) might increase loan revenues. Banks can increase revenue by charging higher interest rates on loans. With extra revenue, banks might invest in technology, infrastructure, and business operations, improving performance (Perera et al., 2007; Anbar & Alper, 2011). Thus, we hypothesise;

H8- Interest rate has a positive influence on banking efficiency.

The relationship between banking efficiency and the gross domestic product growth rate (GDPGR) may be complex and sensitive to context. Economic activity such as investment, consumption, and business expansion, which stimulates the appetite to open bank accounts, make deposits, and engage in other financial intermediation, contributes to GDPGR. Taking advantage of the growing economy and opportunities for profitable ventures can help banks enhance efficiency (Perera et al., 2007; Tan & Tan, 2016; Carvallo & Kasman, 2017). Therefore, we hypothesise;

H9- There is a positive association between gross domestic product growth rate GDPGR and banking efficiency.

Relationship between banking efficiency and ownership structure

The ownership structure of a bank might influence its business objectives. Because of their business focus, private banks might be more motivated to improve efficiency and revenue. Monetary inclusion or strategic funding may motivate public banks rather than efficiency. For instance, Ayadi (2014) argued that Tunisian private banks are more efficient than government banks. However, Karas et al. (2010) reported that public banks are more efficient than private ones. Therefore, we included ownership structure dummies to isolate Pakistan’s banking industry heterogeneity.

Banking efficiency convergence

Banking efficiency absolute convergence

As a performance benchmark, banking efficiency research sheds light on the best-practice frontier. However, empirical evidence on banking efficiency convergence/catch-up is crucial. Our analysis of banking efficiency convergence dynamics employs the convergence idea from the economic growth literature (Barro & Sala-i-Martin, 1992). Economic convergence takes place as emerging economies grow faster than developed ones, reducing the income gap. It analyses the economy’s performance globally or regionally, taking into account progress in technology, capital accumulation, monetary and fiscal policy, and productivity. Conversely, convergence in banking efficiency neutralises operational performance gaps between banks in a market over time (Casu & Girardone, 2010; Carvallo & Kasman, 2017). Thus, less efficient banks gradually catch up to their more efficient counterparts. It evaluates micro-level operational efficiency. Integration of operational performance measures, which might be influenced by managerial decisions, technology adoption (Casu et al., 2016), and legislative circumstances (Thota & Subrahmanyam, 2020).

Investigating bank efficiency convergence shows how efficient banking enhances the economy. Efficient banking allows banks to effectively allocate resources, lend funds, and manage risk, thereby stimulating investment and growth. To ensure financial stability, banking efficiency convergence ought to be thoroughly studied. Efficient banks reduce the likelihood of financial crises and downturns. Bank efficiency analysis might allow regulators to prevent financial instability and improve economic growth. Regulators and policymakers view convergence in banking efficiency as a key indicator of sector evolution. The convergence concept is relatively new to banking literature (Weill, 2009; Casu & Girardone, 2010; Matthews & Zhang, 2010; Kasman et al., 2013; Carvallo & Kasman, 2017; Olson & Zoubi, 2017; Chen et al., 2020; Mansour & El Moussawi, 2020; Thota & Subrahmanyam, 2020); however, there are several caveats to consider before applying it from macroeconomic growth to banking efficiency. There is a fundamental difference between the two economic disciplines.

First, macroeconomic convergence theorists (Barro et al., 1991; Barro & Sala-i-Martin, 1992; Quah, 1996) focus on regional or national growth indices. Banking performance convergence theorists (Casu & Girardone, 2010; Matthews & Zhang, 2010; Thota & Subrahmanyam, 2020) operate at the micro-level, and banks vary in scope, framework, and business style. Thus, heterogeneity between banks is vital for micro-level convergence. Second, macroeconomic convergence theories examine regional and national incomes, as well as GDP per capita convergence or divergence. This is dependent on government monetary and fiscal policies, as well as individual decisions. As emerging economies catch up, income disparities might narrow. Government spending and taxation, as well as central bank-supervised monetary policy, have an impact on economic growth. Global trade and technology spillover influence economic growth. Human education, labour participation, and migration decisions all contribute to human capital and economic growth. Managerial decisions beyond growth drive the microeconomic concept of banking efficiency convergence, which aims for long-term profitability, effective resource utilisation, higher productivity, and improved risk control. Managers’ micro-decisions have an impact on banking performance. Strategic decisions influence business activities, technology investments, and risk control. Optimising human resources, capital, and technology is vital for achieving financial objectives and providing high-quality services. To compete in evolving markets, banking management examines short-term trends in response to evolving regulations, technology, and circumstances. Banking efficiency convergence demands an in-depth approach, unlike macroeconomic convergence, which takes a broad context. Third, macroeconomic growth convergence is examined over an extended period of time. Banking efficiency convergence has short-term fluctuations in microeconomic settings due to legislation, technology, or rapidly evolving business circumstances.

Though economic growth and banking efficiency are intricate, convergence theory might be used for banking efficiency convergence in a microeconomic setting. This underscores the intricate similarities and underlying characteristics of macroeconomic trends involving economic growth convergence and microeconomic banking efficiency convergence.

Firstly, both economic growth and banking efficiency convergence share catch-up processes. For the former, developing countries aim for economic growth on par with developed countries, while for the latter, less efficient banks seek efficiency on par with more efficient banks (Casu & Girardone, 2010; Matthews & Zhang, 2010). Both convergence approaches involve catching up to narrow the gap towards convergence.

Secondly, structural reforms allow both convergence patterns to occur. To foster economic convergence, legislators undertake systemic reforms that foster organisational productivity, industry competitiveness, and aggregate output. Similar to banks, systemic changes (Matousek et al., 2015; Thota & Subrahmanyam, 2020) such as improved oversight, risk controls (Fiordelisi et al., 2011; Bryce et al., 2015; Sharma et al., 2015), and advanced technologies (Prakash et al., 2021) might increase efficiency.

Thirdly, technological leapfrogging affects economic growth and banking efficiency convergence. Innovative technology accelerates economic growth, allowing developing countries to catch up to advanced economies (Sala-i-Martin & Barro, 1995). In banking efficiency convergence, banks that employ digital innovation (Ekinci, 2021; Li et al., 2021; Wang et al., 2021; Le et al., 2022), automated processes, and data analytics are more likely to increase operational efficiency and catch up to more efficient competitors. Digitalisation leads to efficiency convergence in the banking sector and a paradigm shift in other sectors. Incorporating digital technology and practices that improve efficiency and growth allows less efficient banks to catch up with more efficient rivals. Economic convergence might result from digital transformation if less developed economies adopt digital technologies at the same rate as more developed ones.

Fourthly, market integration drives economic growth convergence and trade barrier reduction (Ben-David & Loewy, 1998). Market integration is essential to banking efficiency convergence. Banking sector integration facilitates competitiveness, knowledge spillover, and optimal process adoption, increasing efficiency convergence. In the banking industry, benchmark efficient banks transfer best organisational practices, risk control strategies, and client service tactics, which allow low-efficient opponents to catch up (Casu et al., 2016).

Finally, investing in training and education to improve economic growth convergence underlines the significance of human capital (Henderson & Russell, 2005), which also elevates banking efficiency convergence. Skilled decision-makers, advanced risk management, and high-quality service increase efficiency (Iliemena et al., 2019; Rahman & Akhter, 2021), enabling less efficient banks to catch up. Thus, human capital fosters both economic growth and banking efficiency convergence. In summary, this conceptual framework offers an in-depth understanding of macroeconomic convergence dynamics and illustrates the application of convergence theory to the convergence of banking efficiency in microeconomics by focusing on similarities and shared influencing factors. Therefore, we examine Pakistan’s banking industry’s efficiency convergence to discover how banks that were less efficient at utilising their input factors of production caught up to their more efficient counterparts over time. There are two approaches, β-convergence and σ-convergence, proposed by (Barro & Sala-i-Martin, 1992; Quah, 1996) and extensively applied in prior studies (Weill, 2009; Casu & Girardone, 2010; Matthews & Zhang, 2010; Kasman et al., 2013; Carvallo & Kasman, 2017; Olson & Zoubi, 2017; Chen et al., 2020; Mansour & El Moussawi, 2020; Thota & Subrahmanyam, 2020) to investigate banking efficiency convergence.

The concept of absolute β-convergence is one of the generalised aspects of the neoclassical theory of economic growth. In the broader context of banking efficiency convergence, absolute β-convergence represents the gradual narrowing of the efficiency gap between less efficient and more efficient banks. Absolute β-convergence asserts that banks with varying initial efficiency levels converge to a common equilibria if their long-run characteristics are homogenous. In a nutshell, absolute β-convergence applies if the rate of efficiency growth is inversely related to its initial level. Therefore, in response to RQ3, we hypothesise:

H5a- In the long run, initially, less efficient banks in Pakistan’s banking industry would eventually converge to more efficient counterparts, achieving the common equilibrium.

Banking efficiency σ-convergence describes the process of a gradual reduction in efficiency variance from the cross-sectional average over time. In the banking industry, any shock might momentarily widen the efficiency dispersion between banks, even when the banks are catching up to equilibrium. Quah (1996) underlines that β-convergence is a necessary but insufficient criterion for σ-convergence. Our research likewise investigates σ-convergence to confirm if the dispersion of banking efficiency levels from the cross-sectional mean diminishes over time. Therefore, in response to RQ3, we hypothesise:

H5b- In the long run, initially, the banks in Pakistan’s banking industry that experienced more dispersed efficiency levels from the cross-sectional mean would eventually diminish this dispersion and converge to the cross-sectional mean, achieving the common equilibrium.

Banking efficiency conditional β-convergence

Banking efficiency conditional convergence emphasises that banks converge to their own efficiency equilibrium, unlike absolute efficiency convergence. Since banks confront idiosyncratic and structural shocks, which influence them in a peculiar way, they may be at varying points towards efficiency equilibrium. The rate of convergence serves as an indicator of competitive advantage; a slower rate of convergence implies the ability to sustain advantages over an extended duration. In an ideal scenario, banks might maximize long-term efficiency. Economic conditions, varying business practices, industry regulations, and digital technology development influence the banking efficiency convergence process in the long run. We argue that banks exhibit varying efficiency levels due to bank-specific and technological factors. Several conditional factors can result in efficiency growth, such as the fact that in domains where resources are underutilised, digital technology tools help improve efficiency by lowering intermediary costs (Ekinci, 2021). Innovative digital banking technology gives banking managers more flexibility in pricing, reliability, and customer service. According to Abbasi and Weigand (2017) digital information and communication technology (ICT) might improve banking operations and mitigate risks. Meanwhile, (Delgado & Nieto, 2004; Vu, 2011; Hilal, 2014; Ekinci, 2021) found that digital ICT improves banking efficiency. Therefore, in response to our RQ4, we hypothesise:

H5c- In the long run, the utilisation of digital payment channels (ATM, internet, and point-of-sale-based transactions) support initially less efficient banks in Pakistan’s banking industry to converge faster to catch up with their more efficient counterparts.

H5d- In the long run, overall utilisation of digitalisation (DIG INDEX) support initially less efficient banks in Pakistan’s banking industry to converge faster to catch up with their more efficient counterparts.

H5e- In the long run, available digital information and communication technologies (ICT) support initially less efficient banks in Pakistan’s banking industry to converge faster to catch up with more efficient counterparts.

H5f- In the long run, utilisation of digital information and communication technologies (ICT) support initially less efficient banks in Pakistan’s banking industry to converge faster to catch up with more efficient counterparts.

Research methodology and data

First stage methodology

The 1^st stage DEA

A. Charnes and Rhodes (1978) introduced data envelopment analysis (DEA), which is an analytical approach based on linear programming and Farrell (1957) foundations. DEA aims to examine the optimal practice frontier by taking into account a set of decision-making units (DMUs) and the observed combinations of inputs and outputs associated with them². However, Coelli et al. (2005) argued that the DEA approach evaluates decision-making unit (DMU) efficiency by comparing ineffective DMUs outside the frontier to efficient ones within it. In this study, Pakistan’s banks are DMUs; hence, we apply the DEA to evaluate their efficiency. For instance, Färe et al. (1985) described the procedures using non-parametric DEA to construct a convex hull wrapping an array of observations. How far a bank is from an efficient production frontier is measured by technical efficiency (TE). We have applied the CCR model of A. Charnes and Rhodes (1978) and the BCC model proposed by R. D. Banker et al. (1984) to estimate technical efficiency (TE) based on the assertions of constant returns to scale (CRS) and variable returns to scale (VRS). We have estimated overall technical efficiency (OTE) using input-oriented CRS assumptions, which can be classified into two subcategories: pure technical efficiency (PTE) and scale efficiency (SE).

We applied VRS assumptions to determine pure technical efficiency (PTE) in production technology. However, scale efficiency (SE) describes the efficiency with which a bank might expand its operations. The SE is the ratio between CRS and VRS efficiency which reveals whether a bank should grow or downsize to maximise its business efficiency. Suppose a bank’s CRS and VRS efficiency scores deviate, proving that it is scale inefficient and not performing at its optimal level. The CCR-DEA model envisaged by A. Charnes and Rhodes (1978) and the BCC-DEA model extended by R. D. Banker et al. (1984) are two instances of DEA models that may be utilised to conduct efficiency analysis. There are two main orientations in the DEA framework: (i) input-oriented and (ii) output-oriented. The earlier approach lowers inputs while retaining outputs. While providing high outputs, banking management ought to reduce input resources. In the latter approach, constant inputs lead to optimised outputs. Most banking efficiency studies adopted an input-oriented approach because management is more cautious with inputs than outputs; thus, we use an input-oriented approach in this study.

In conclusion, the input-oriented CCR and BCC models evaluate the optimal use of the bank’s resources. With the constraint that all bank ratios must be less than or equal to 1, the DEA approach evaluates each bank’s inputs and outputs and rates their efficiency according to the highest ratio. Let’s suppose there are ${\mathscr{N}}$, 1………29 Banks, each of which has ${\mathcal{K}}\,{\rm{inputs}}$ and ${\mathcal{P}}$ outputs. It might be possible to obtain a solution to the problem presented previously to evaluate the relative efficiency of a specific decision-making unit (DMUs) reflected as ${{\rm{Bank}}}_{0}$.

$$\begin{array}{ccc}{\rm{Max}}{{{\phi }}}_{0} & & \\ & {\rm{S}}.{\rm{t}}. & \\ & & \begin{array}{c}\displaystyle{\mathop{\sum }\limits_{i=1}^{{\mathcal{m}}}}\,{{\mathcal{V}}}_{{\rm{r}}}{{\mathcal{K}}}_{{\rm{r}}}{\mathcal{N}},0\,\displaystyle{\mathop{\sum }\limits_{r=1}^{s}}\,{{\mathcal{U}}}_{{\rm{r}}}{{\mathcal{P}}}_{{\rm{r}}}{\mathcal{N}},0\le \!{{;}}\,\,{\mathcal{N}}={1,2,3},\ldots {\mathcal{n}}\\ {{\mathcal{U}}}_{{\rm{r}}}{{\mathcal{V}}}_{{\rm{i}}}\,\ge \,0;{\rm{r}}=1,2,3,\ldots .{\rm{s;i}}=1,2,3,\ldots {\mathcal{m}}\end{array}\end{array}$$

(1)

Where;

${{\mathcal{P}}}_{{\rm{r}}}{\mathcal{N}}$ = The amount of output r from unit ${\mathcal{N}}$

${{\mathcal{K}}}_{{\rm{r}}}{\mathcal{N}}$ = The amount of output i from unit ${\mathcal{N}}$

${{\mathcal{U}}}_{{\rm{r}}}$ = The maximum allowable weight to output r

${{\mathcal{V}}}_{{\rm{i}}}$ = The maximum allowable weight to input i

${\mathcal{N}}$ = The number of units

${\rm{s}}$ = The number of outputs

${\mathcal{m}}$ = The number of inputs

We will iterate the linear programming equation ${\mathcal{n}}$ times to derive the relative efficiency scores of the banks. Each bank’s optimal input and output weights maximize efficiency. For example, we consider a bank efficient if its efficiency index is 1, and consider it relatively inefficient if it is less than 1. Similarly, based on the A. Charnes and Rhodes (1978), framework CCR DEA input-oriented equation is as follows;

$${\rm{Max}}{{\rm{\phi }}}_{0}=\mathop{\sum }\limits_{j=1}^{{\mathcal{m}}}{{\mathcal{U}}}_{{\rm{j}}}{{\mathcal{Y}}}_{{\rm{j}}0}$$

(2)

S.t.

$${\rm{Max}}{{{\phi }}}_{0}=\mathop{\sum }\limits_{i=1}^{s}{{\mathcal{V}}}_{{\rm{i}}}{{\mathcal{X}}}_{{\rm{i}}0}=1$$

$$\mathop{\sum }\limits_{j=1}^{{\mathcal{m}}}{{\mathcal{U}}}_{j}{{\mathcal{Y}}}_{j{\mathcal{K}}}-\mathop{\sum }\limits_{i=1}^{s}{{\mathcal{V}}}_{{\rm{i}}}{{\mathcal{X}}}_{{\rm{i}}{\mathcal{K}}}\le 0$$

$${{\mathcal{V}}}_{{\rm{i}}}\ge 0,{{\mathcal{U}}}_{{\rm{j}}}\ge 0,{{\mathcal{U}}}_{0}$$

Based on Banker et al. (1984) framework BCC DEA input-oriented equation is as follows;

$${\rm{Max}}{{{\phi }}}_{0}=\mathop{\sum }\limits_{j=1}^{{\mathcal{m}}}{{\mathcal{U}}}_{{\rm{j}}}{{\mathcal{Y}}}_{{\rm{j}}0}+{{\mathcal{U}}}_{0}$$

(3)

S.t.

$${\rm{Max}}{{{\phi }}}_{0}=\mathop{\sum }\limits_{i=1}^{s}{{\mathcal{V}}}_{{\rm{i}}}{{\mathcal{X}}}_{{\rm{i}}0}=1$$

$$\mathop{\sum }\limits_{j=1}^{{\mathcal{m}}}{{\mathcal{U}}}_{{\rm{j}}}{{\mathcal{Y}}}_{{\rm{j}}{\mathcal{K}}}-\mathop{\sum }\limits_{i=1}^{s}{{\mathcal{V}}}_{{\rm{i}}}{{\mathcal{X}}}_{{\rm{i}}{\mathcal{K}}}+{{\mathcal{U}}}_{0}\le 0$$

$${{\mathcal{V}}}_{{\rm{i}}}\ge 0,{{\mathcal{U}}}_{{\rm{j}}}\ge 0,{{\mathcal{U}}}_{0}$$

Where;

${{{\upphi }}}_{0}$ = Comparative efficiency value for ${{DMU}}_{0}$

${{\mathcal{X}}}_{{\rm{i}}0}$ = Input vector of ${{DMU}}_{0}$

${{\mathcal{Y}}}_{{\rm{j}}0}$ = Output vector of ${{DMU}}_{0}$

${{\mathcal{X}}}_{{\rm{j}}{\mathcal{K}}}$ = Real value of utilized i input by ${{DMU}}_{{\mathcal{K}}}$

${{\mathcal{Y}}}_{{\rm{j}}0}$ = Produced real value of j output by ${{DMU}}_{{\mathcal{K}}}$

Finally, ${\mathcal{U}}$, ${\mathcal{V}}$ are characterized as input and output weights.

Likewise, scale efficiency can be derived as; ${\rm{SE}}=\frac{{{\rm{TE}}}_{{\rm{crs}}}}{{{\rm{TE}}}_{{\rm{vrs}}}}$

Where; ${{\rm{TE}}}_{{\rm{crs}}}$ and ${{\rm{TE}}}_{{\rm{vrs}}}$ describe the fraction of technical efficiency thereby utilizing CRS and VRS, respectively. Bootstrap DEA has been explained in following section.

Bootstrap DEA

Methods for efficiency analysis, such as DEA, use a deterministic approach. Similarly, DEA analyses the estimated efficiency scores based on the theoretical frontier, not the actual one. Moreover, sampling variations of the estimated frontier are likely to significantly affect the efficiency scores obtained from a limited sample. In light of this, researchers have proposed a statistical framework and reliable bootstrapping procedures to analyse technical efficiency using a nonparametric frontier method (Simar & Wilson, 1998; Simar & Wilson, 2000). According to DEA’s standard assumptions, the simulated production set is a smaller subset of the true production set, resulting in too-idealistic technical efficiency ratings. More robust bootstrap DEA delivers statistical inference to DEA analysis (Simar & Wilson, 2000; Simar & Wilson, 2007). Bootstrapping allows us to evaluate the confidence interval and bias of the original DEA estimations. Hence, we couple conventional DEA with the bootstrap DEA approach for our efficiency analysis to provide an accurate banking efficiency analysis of Pakistan’s banking industry. Simar and Wilson (2007) bootstrapping DEA algorithm (2) steps are explained (see supplementary file, Appendix C).

Second stage methodology

The 2nd stage DEA

In general, nonparametric methods, i.e., DEA, aim to identify how far a bundle of measured input-output combinations departs from a production-possibility frontier (PPF). However, they cannot provide a comprehensive understanding of the factors that influence the extent of this difference from PPF. In addition, investigating the factors that influence banking inefficiency in several empirical studies is more significant. Using a two-stage procedure, several prior DEA-based banking studies have investigated the influence of contextual variables on efficiency. The DEA approach estimates efficiency values in the first stage, and the regression approach regresses the estimated efficiency values on a set of contextual variables in the second stage. However, critics often question the selection of the regression model in the second stage of DEA.

Most studies have used OLS and Tobit regression. The DEA efficiency score varies from zero to one, suggesting it is challenging to apply prior models (Simar & Wilson, 2007). However, Simar and Wilson (2007) suggested an alternative regression approach to examine contextual factors’ influence on efficiency scores. One-sided inefficiency factors, driven by contextual variables, cause true efficiency to deviate from the PPF. The contextual variables could explain the variability of the left-truncated normal distribution in the inefficiencies of the banks observed during the study period. A more recent seminal study (Banker et al., 2019) showed that the two-stage DEA method combined with the OLS and Tobit regression methods provides more efficient estimates than the more complex double bootstrap truncated regression-based model suggested by Simar and Wilson (2007) in the presence of noise. Tobit models are censored class models. To be valid, our banking efficiency score, the dependent variable in the Tobit model, must satisfy bounded (range between 0 and 1) conditions (Tobin, 1958), which developed the maximum likelihood function-based Tobit regression model. There are two key characteristics of the Tobit framework. To begin, the dependent variable’s value must be truncated or censored rather than left continuous (such that it is recognized as a bounded trend). Secondly, to predict the model’s regression variables, the Tobit model uses the maximum likelihood approach. In light of this, the model is both highly robust and more consistent than the classical OLS (Banker et al., 2019). Hence, we used panel data tobit regression for our second-stage DEA research. The following is an illustration that highlights the probability distribution of the Tobit approach:

$${\rm{P}}\left({{\rm{EFF}}}_{{\rm{i}}}=0\right)={\rm{P}}\left({{\rm{EFF}}}_{{\rm{i}}}^{* }\le 0\right)={\rm{P}}\left(\frac{{{\rm{EFF}}}_{{\rm{i}}}^{* }-{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}}{\Psi }\le \frac{0-{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}}{\Psi }\right)={\rm{\phi }}\left(-\frac{{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}}{\Psi }\right)=1-{\rm{\phi }}\left(\frac{{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}}{\Psi }\right)$$

$${\rm{P}}\left({{\rm{EFF}}}_{{\rm{i}}}\right)={\rm{P}}\left({{\rm{EFF}}}_{{\rm{i}}}^{* }\right)=\frac{1}{\Psi \sqrt{2{\rm{\lambda }}}}{{\rm{e}}}^{-\left(\frac{{\left({{\rm{EFF}}}_{{\rm{i}}}-{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}\right)}^{2}}{{2\Psi }^{2}}\right)}$$

Below is the Maximum Likelihood-based panel-data Tobit Regression:

$${\rm{L}}={\coprod }_{{{\rm{EFF}}}_{{\rm{i}}} > 0}\frac{1}{\Psi \sqrt{2{\rm{\lambda }}}}{{\rm{e}}}^{-\left(\frac{{\left({{\rm{EFF}}}_{{\rm{i}}}-{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}\right)}^{2}}{{2\Psi }^{2}}\right)}{\coprod }_{{{\rm{EFF}}}_{{\rm{i}}}=0}1-{\rm{\phi }}\left(\frac{{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}}{\Psi }\right)$$

$$\mathrm{ln}{\rm{L}}={\coprod }_{{{\rm{EFF}}}_{{\rm{i}}} > 0}-0.5\left(\mathrm{ln}\left(2{\rm{\lambda }}\right)+\mathrm{ln}{\Psi }^{2}+\frac{{\left({{\rm{EFF}}}_{{\rm{i}}}-{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}\right)}^{2}}{{2\Psi }^{2}}\right)+{\coprod }_{{{\rm{EFF}}}_{{\rm{i}}}=0}\mathrm{ln}\left(1-{\rm{\phi }}\left(\frac{{{\rm{x}}}_{{\rm{i}}}{\rm{\beta }}}{\Psi }\right)\right)$$

Based on the Tobit framework’s probability distribution, ${\rm{P}}({{\rm{EFF}}}_{{\rm{i}}}=0)$ is the likelihood of uncovering a zero banking efficiency variable ${{\rm{EFF}}}_{{\rm{i}}}$. The probability is obtained by adjusting the cumulative distribution function (CDF) of the latent variable ${{\rm{EFF}}}_{{\rm{i}}}^{* }$. The formula reveals that the likelihood of ${{\rm{EFF}}}_{{\rm{I}}}$ approaching 0 is equal to 1 less the probability of the adjusted ${{\rm{EFF}}}_{{\rm{i}}}^{* }$ falling below or equal to 0. The P(EFF_i) formula illustrates the probability density function for banking efficiency measured by EFF_i. It uses parameters β, Ψ and λ from the normal distribution. The standard deviation (Ψ coefficient) for ${{\rm{EFF}}}_{{\rm{i}}}^{* }$ was simulated using Tobit regression. It assesses the association between the censored variable EFF_I and the latent variable ${{\rm{EFF}}}_{{\rm{i}}}^{* }$. In other words, the Ψ coefficient indicates the extent to which ${{\rm{EFF}}}_{{\rm{i}}}^{* }$ influences the censored EFF_i. If ${{\rm{EFF}}}_{{\rm{i}}}^{* }$ has a significant variance, such as a high value of Ψ, the chance of observing zero amounts or censoring the dependent variable EFF might fluctuate. Effective model estimation requires modifying the standard deviation Ψ using λ. In summary, we used the panel Tobit regression model with the right truncation/censor restricting the upper limit (UL) to 1 and developed the following generalised equation:

$${{\rm{EFF}}}_{{\rm{j}}}^{* }={{\beta }}{{\rm{x}}}_{{\rm{j}}}+{{\rm{\xi }}}_{{\rm{j}}}$$

(4)

$${{\rm{EFF}}}_{{\rm{j}}}=\left\{\begin{array}{c}{1,{\rm{otherwise}}}\\{{{\rm{EFF}}}_{{\rm{j}}}^{* },0\le {{\rm{EFF}}}_{{\rm{j}}}^{* }\le 1,{\rm{i}}=1,2,3,\ldots ..,29}\end{array}\right\}$$

where, ${{\rm{EFF}}}_{{\rm{j}}}$ is the banking efficiency of the jth bank, β are the vector coefficients of ${{\rm{x}}}_{{\rm{j}}}$ independent variables, ${{\rm{\xi }}}_{{\rm{j}}}$ is an unrelated randomized error term, and ${{\rm{EFF}}}_{{\rm{j}}}^{* }$ is the potential banking efficiency. Subsequently, in response to our RQ2 and proposed hypothesis H1a-H4, we have constructed the following base line regression equation:

$${{\rm{EFF}}}_{{\rm{i}},{\rm{t}}}={{\rm{\alpha }}}_{0}+{{\rm{\beta }}}_{1}{{\rm{DF}}}_{{\rm{i}},{\rm{t}}}+{{\rm{\beta }}}_{2}{{\rm{BSCF}}}_{{\rm{i}},{\rm{t}}}+{{\rm{\beta }}}_{3}{{\rm{OSD}}}_{{\rm{i}},{\rm{t}}}+{{\rm{\beta }}}_{4}{{\rm{MECF}}}_{{\rm{t}}}+{{\rm{\beta }}}_{5}{\rm{YD}}+{{\rm{\xi }}}_{{\rm{it}}}$$

(5)

The above Eq. 5’s dependent variable, EFF, represents the bootstrap bias-corrected banking efficiency, estimated in the first stage using bootstrap DEA. We have measured digitalisation factors (DF) using ATM-based transactions (ABTR), internet-based transactions (IBTR), point-of-sale-based transactions (POSBTR), and the digitalisation index (DIG INDEX). Following prior studies (see hypothesis development Section 3), we use bank-specific control factors (BSCF) such as net interest margin ratio (NIM), return on equity ratio (ROE), return on assets ratio (ROA), cost-to-income ratio (CIR), equity-to-assets ratio (CAPT), natural logarithm of total assets (SIZE), and age in years (AGE). To account for heterogeneity across different ownership types, we include the ownership structure dummies (OSD), such as state-controlled banks (SCBs) = 1 otherwise = 0, private sector banks (PSBs) = 1 otherwise = 0, and special purpose banks (SPBs) = 1 otherwise = 0. We include macroeconomic control factors (MECF) comprising the inflation rate (INFRATE), interest rate (INTRATE), and gross domestic product growth rate (GDPGR) to capture the influence of broader economic trends on banking efficiency. The year dummies (YD) demonstrates the effect of temporal variations, and ${{\rm{\xi }}}_{{\rm{it}}}$ is the error term. Additionally, we have estimated Eq. 5 by applying a two-step dynamic panel data system generalised method of moments (DPDSYS-GMM). At temporal horizons (T) smaller than a group of observed cross-sections (N), the DPDSYS-GMM estimator yields the most consistent results (Arellano & Bond, 1991; Mustafa et al., 2022, 2023). In endogeneity and omitted variable bias, DPDSYS-GMM estimates are more reliable than static panel data estimators. The dependent variable’s relationship with its lagged values might lead to endogeneity and spurious results. The DPDSYS-GMM also effectively tackles serial correlation and heteroscedasticity (Blundell & Bond, 1998; Bond et al., 2001; Roodman, 2009). The supplementary file, Appendix F, contains the extended variants of Eq. 5.

Banking efficiency convergence

Banking efficiency absolute β and σ-convergence

Our panel data analysis utilises the principles of β and σ-convergence as standard metrics to assess the progress of different banks in Pakistan’s banking industry in terms of efficiency growth and the degree to which they are catching up with their peers from 2006 to 2020. A β-convergence occurs when less efficient banks in an industry outperform their more efficient peers in terms of growth rate. In response to RQ3 and our proposed hypothesis H5a, we estimate Eq. 6 using a two-step DPDSYS-GMM to investigate the absolute efficiency β-convergence/catch-up effect in Pakistan’s banking industry from 2006–2020.

$$\Delta {\rm{Ln}}{{\rm{Eff}}}_{{\rm{i}},{\rm{t}}}={\rm{\alpha }}+{\rm{\phi }}\Delta {\rm{Ln}}{{\rm{Eff}}}_{{\rm{i}},{\rm{t}}-1}+{\rm{\beta }}{\rm{Ln}}{{\rm{Eff}}}_{{\rm{i}},{\rm{t}}-1}+{{\rm{YD}}+{\rm{\xi }}}_{{\rm{i}},{\rm{t}}}$$

(6)

Where, i represents the number of commercial banks in the sample, 1,….., 29, and t reflects time in years, 1,……,15. ${\rm{Ln}}{{\rm{Eff}}}_{{\rm{I}},{\rm{t}}}$ symbolizes the efficiency level of the commercial bank i at time t; ${\rm{Ln}}{{\rm{Eff}}}_{{\rm{I}},{\rm{t}}-1}$ is the initial efficiency level of the commercial bank i; $\Delta {\rm{Ln}}{{\rm{Eff}}}_{{\rm{I}},{\rm{t}}}$ = ${\rm{Ln}}{{\rm{Eff}}}_{{\rm{I}},{\rm{t}}}$−${\rm{Ln}}{{\rm{Eff}}}_{{\rm{I}},{\rm{t}}-1}$ denotes banking efficiency growth rate, while, ${\rm{\phi }}\Delta {\rm{Ln}}{{\rm{Eff}}}_{{\rm{I}},{\rm{t}}-1}$ indicates the first lag of efficiency growth rate, α is the constant, β denotes the convergence coefficient, year dummies (YD) are to account for dynamic time trends, and ${{\rm{\xi }}}_{{\rm{I}},{\rm{t}}}$ is the error term. A significant negative (inverse) β suggests absolute convergence, which likewise indicates speed of convergence. However, σ-convergence focuses more on the industry-wide trends of declining variations over time than it does on identifying possible catching-up occurrences. According to Quah (1996), although β-convergence is necessary for σ-convergence, it is not sufficient to stand alone. Therefore, in response to our RQ3, we proposed H5b and estimated the two-step DPDSYS-GMM Eq. 7 to analyse the narrowing of cross-sectional dispersal, also known as σ-convergence, which measures the rate at which individual banks’ efficiency levels converge or catch up to the panel mean during 2006–2020.

$${\Delta {\rm{DEff}}}_{{\rm{i}},{\rm{t}}}={\rm{\alpha }}+{\rm{\phi }}{\Delta {\rm{DEff}}}_{{\rm{i}},{\rm{t}}-1}+{\rm{\beta }}{{\rm{DEff}}}_{{\rm{i}},{\rm{t}}-1}+{{\rm{YD}}+{\rm{\xi }}}_{{\rm{i}},{\rm{t}}}$$

(7)

Where, ${{\rm{DEff}}}_{{\rm{I}},{\rm{t}}}={{\rm{LnEff}}}_{{\rm{I}},{\rm{t}}}{{\mbox{-}}}{\overline{{\rm{LnEff}}}}_{{\rm{I}},{\rm{t}}}$ and ${\Delta {\rm{DEff}}}_{{\rm{I}},{\rm{t}}}={{\rm{DEff}}}_{{\rm{I}},{\rm{t}}}-{{\rm{DEff}}}_{{\rm{I}},{\rm{t}}-1}$. Here ${{\rm{LnEff}}}_{{\rm{I}},{\rm{t}}}$ signifies natural logarithm of efficiency levels of banks i, in year t. on the other hand ${\overline{{\rm{LnEff}}}}_{{\rm{I}},{\rm{t}}}$ represents cross-sectional mean of ${{\rm{LnEff}}}_{{\rm{I}},{\rm{t}}}$ for each year. A significant negative (inverse) β coefficient value satisfies the criteria of σ-convergence.

Banking efficiency conditional β-convergence

Finally, analysing conditional efficiency convergence is vital because, in contrast to absolute (unconditional) convergence—which assumes that all banks would converge to a common steady state or efficiency equilibrium—conditional convergence takes into account the other contextual factors. Therefore, in response to RQ4 and our proposed hypotheses H5c-H5f, we have estimated base line regression Eq. 8 using two-step DPDSYS-GMM to investigate the conditional β-convergence during 2006–2020.

$$\Delta {\rm{Ln}}{{\rm{Eff}}}_{{\rm{i}},{\rm{t}}}={\rm{\alpha }}+{\rm{\phi }}\Delta {\rm{Ln}}{{\rm{Eff}}}_{{\rm{i}},{\rm{t}}-1}+{{\rm{\beta }}}_{1}{\rm{Ln}}{{\rm{Eff}}}_{{\rm{i}},{\rm{t}}-1}+{{\rm{\beta }}}_{2}{{\rm{BSDF}}}_{{\rm{i}},{\rm{t}}}+{{\rm{\beta }}}_{3}{{\rm{CSDF}}}_{{\rm{t}}}+{{{\rm{\beta }}}_{4}{\rm{BSCF}}}_{{\rm{i}},{\rm{t}}}{+{{{\rm{\beta }}}_{5}{\rm{MECF}}}_{{\rm{t}}}+{\rm{YD}}+{\rm{\xi }}}_{{\rm{i}},{\rm{t}}}$$

(8)

Where the natural logarithm of ATM-based transactions (lnABTR), the natural logarithm of internet-based transactions (lnIBTR), and the natural logarithm of point-of-sale-based transactions (lnPOSBTR) are bank-specific digitalisation factors (BSDF), and overall bank-specific DIG INDEX is created using PCA with lnABTR, lnIBTR, and lnPOSBTR. According to Ekinci (2021), the digital information and communication technology availability (DICTA) and digital information and communication technology utilisation (DICTU) indexes are used to measure country-specific digitalisation factors (CSDF). We computed the DICTA Index using fixed broadband subscribers per hundred (FBBSPH). To tackle the dimensionality and multicollinearity issues, we employed PCA to create a composite DICTU Index using two indicators: mobile cell phone subscribers per hundred (MCSPH) and fixed telephone subscribers per thousand (FTSPT). Moreover, bank-specific controls, natural logarithm of cost-to-income ratio (LnCIR) and natural logarithm of total assets (SIZE), are introduced, which are consistent with (Sufian, 2009; Phan et al., 2016; Olson & Zoubi, 2017). We have integrated other bank-specific control factors (BSCF), such as loan growth ratio (LGR) as specified by Dinger and te Kaat (2020), loan loss provisions to non-performing loans (LLPTNPL) ratio as reported by Bryce et al. (2015) and Sharma et al. (2015), and nonperforming loan-to-total loan ratio (NPLTTL) ratio as suggested by Fiordelisi et al. (2011) and Partovi and Matousek (2019), to measure the influence of banks’ loan-related performance, overall risk-taking behaviour, and prudential credit risk management on the banking efficiency convergence process. In addition, human capital—employee training, skills, and experience—is essential for efficient banking operations. Rahman and Akhter (2021) found a positive correlation between banking performance and staff training, expertise, and skills. Iliemena et al. (2019) found a positive relationship between human capital efficiency and Nigeria’s banking sector’s financial performance. Thus, we have considered the natural logarithm of the total number of employees (lnHR). We take into account macroeconomic control factors (MECF), which include monetary policy’s influence on banking efficiency convergence, using the M2 money supply growth rate (M2_GR) in line with (Williams, 2012; Carvallo & Kasman, 2017), the inflation rate (INFRATE) (Avkiran, 1999; Řepková, 2015), and the GDP growth rate (GDPGR) (Perera et al., 2007; Anbar & Alper, 2011). The supplementary file, Appendix F, contains the extended variants of Eq. 8.

Research data and DEA input and output variables selection

This study focuses on the commercial banking sector of Pakistan, which constitutes the majority of the market assets size of the financial industry. The dataset consists of state-controlled banks (SCBs), private-sector traditional banks (PSTBs), private-sector Islamic banks (PSIBs), special purpose banks (SPBs), and foreign banks (FBs). Nevertheless, this study excludes development finance institutions, microfinance banks, and investment banks. We retrieved bank-level balanced panel data for 29 commercial banks from 2006 to 2020 from the State Bank of Pakistan (SBP) database, which included 435 bank-year observations in the sample. The data on the availability and utilisation of information and communication technologies (ICT) indicators used to measure digitalisation is retrieved from the International Telecommunication Union (ITU) database. The database of the World Bank is mined for macroeconomic factors, i.e., inflation rate, interest rate, GDP growth rate, and M2 money supply growth rate. We rigorously examine the sampled data for inaccuracies, discrepancies, incomplete information, and anomalies.

Identifying which input and output variables are optimal for DEA is a divisive issue due to its wide-ranging implications. There are two approaches for determining the input and output variables in a DEA model: the former is known as the “intermediation approach (IA),” and the latter is called the “production approach (PA).” Since funds essentially serve as intermediary ‘raw material,’ one classic IA is utilised by Sealey Jr and Lindley (1977). Based on IA paradigm (Berger & Humphrey, 1991), integrated funds and their associated interest costs. However, the PA is required to bring attention to labour and capital. We favoured IA based on the concept that Pakistani banks facilitate the exchange of capital from savers to creditors; therefore, we have chosen the IA following Sealey Jr and Lindley (1977).

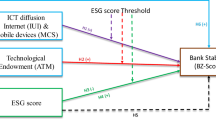
For inputs and outputs selection, we leverage four standard input parameters: (i) total deposits (TD), (ii) interest expenses (IE), (iii) fixed assets (FA), (iv) non-interest expenses (NIE), and on the output selection front, we have integrated four output parameters: (i) total loans (TL), (ii) interest income (II), (iii) non-interest income (NII), following a similar direction (Martín-Oliver & Salas-Fumás, 2008; Matthews & Zhang, 2010; Degl’Innocenti et al., 2017). Meanwhile, a conceptual model is exhibited in Fig. 1. On the right side, the 1st stage DEA illustrates inputs and outputs, whereas the original DEA assesses overall technical efficiency (OTE-O), pure technical efficiency (PTE-O), and scale efficiency (SE-O). We also used bootstrap DEA to estimate BSBC-OTE (bias-corrected overall technical efficiency), BSBC-PTE (pure technical efficiency), and BSBC-SE (scale efficiency). On the left, Fig. 1 shows the 2nd-stage DEA flow. In the second stage of DEA, we examined the contextual factors’ influence on the BSBC-PTE and banking efficiency’s absolute and conditional convergence. This research’s indicators, data, and sources are provided in the supplementary file Table S-4.

Fig. 1: Conceptual Model.

Our conceptual model Figure explains the two-stage DEA-based research design. In the first stage, we employ four inputs (total deposits (TD), interest expense (IE), fixed assets (FA), and non-interest expenses (NIE)) and use three outputs (total loans (TL), interest income (II), and non-interest income (NII)) to estimate banking efficiency by both original and bootstrap DEA methods (see top left side). First, we obtained the original overall technical efficiency (OTE: O) and then decomposed it into the original pure technical efficiency (PTE: O) and original scale efficiency (SE: O) using the original DEA estimator. Second, we estimate the bootstrap bias-corrected overall technical efficiency (BSBC: OTE) using the Bootstrap DEA, and further decompose it into the bootstrap bias-corrected pure technical efficiency (BSBC: PTE) and the bootstrap bias-corrected scale efficiency (BSBC: SE). On the right and bottom-left sides, Figure represents the second stage of the DEA research workflow. Here, the effects of digitalisation on banking efficiency (BSBC: PTE) and its convergence process are being analysed. A list of explanatory variables, examined in terms of their influence on BSBC: PTE, is located on the rightmost part of Figure. Factors related to digitalization: 1. ATM-based transactions (ABTR). 2. Internet-based transactions (IBTR). 3. Point-of-sale-based transactions (POSBTR). 4. Digitalisation Index (DIG Index). Bank-specific factors: 1. Net interest margin (NIM) ratio. 2. The return on equity (ROE) ratio. 3. The return on assets (ROA) ratio. 4. Cost-to-income (CIR) ratio. 5. Equity-to-asset (CAPT) ratio. 6. Bank ownership types (OWNERSHIP DUMMIES). Macroeconomic control factors: 1. Inflation rate (INFRATE). 2. Interest rate (INTRATE). 3. Gross domestic product growth rate (GDPGR). The second stage of DEA also investigates the efficiency convergence dynamics, which include efficiency absolute beta convergence and efficiency absolute sigma convergence. Absolute beta convergence is expanded to efficiency conditional beta convergence, examining the effect of digitalisation on the banking efficiency convergence process. The listed contextual variables at the bottom left are the ones used to estimate the efficiency conditional beta-convergence dynamics. In the following, there are the four bank-specific and two country-specific digitalisation factors that are included in this research: The natural logarithm of ATM-based transactions (lnABTR). 2. The natural logarithm of internet-based transactions (lnIBTR). 3. The natural logarithm of point of sale based ln of transactions (lnPOSBTR). 4. The Digitalization Index (DIG Index). 5. Digital information and communication technology availability index (DICTA Index). 6. Digital information and communication technology utilization index (DICTU Index). Bank-specific control factors: 1. The cost-to-income ratio’s natural logarithm (lnCIR). 2. The natural logarithm of the total assets (SIZE). 3. Loan growth ratio (LGR). 4. Loan loss provisions to non-performing loans (LLPTNPL) ratio. 5. Non-performing loans to total loans (NPLTTL) ratio. 6. The natural logarithm for the total number of employees (lnHR). Finally, macroeconomic control factors include M2 money supply growth (M2_GR), the inflation rate (INFRATE), and the gross domestic product growth rate (GDPGR).

Empirical results and discussion

Descriptive statistics

The summary statistics are depicted in Table 1, which illustrates observed mean, standard deviation (SD), minimum (Min), and maximum (Max) values throughout 2006–2020. We conducted an isotonicity analysis (Avkiran, 1999) to verify the appropriateness of our DEA efficiency research inputs and outputs. Cross-correlation analysis determines inputs and outputs to assess whether an increase in inputs influences outputs. Table 2 exhibits the Pearson correlation matrix (PCM) for Pakistani banks from 2006 to 2020 to assess whether the inputs supplied have a positive and significant relationship with the specified outputs. The inputs, which include total deposits, interest expenses, fixed assets, and non-interest expenses, and the outputs, which include total loans, interest income, and non-interest income, exhibit a positive and significant correlation at 1%. This correlation passes the isotonicity criterion and validates the feasibility of identifying inputs and outputs for our DEA analysis.

Table 1 Descriptive Statistics.

Table 2 Pairwise correlations.

The 1st stage DEA analysis

In response to our RQ1, Table 3 summarises the findings derived using Eqs. 2–3, input-oriented original DEA (A. Charnes and Rhodes (1978); R. Banker et al., 1984) and bootstrap DEA (Simar & Wilson, 1998; Simar & Wilson, 2000) with 1999 bootstrap replications (see supplementary file Appendix C algorithm 2) under both constant returns to scale (CRS) and variable returns to scale (VRS) assumptions from 2006–2020. Column 3 reveals that the Pakistani banking industry’s mean overall technical efficiency (OTE-O) was 87% during 2006–2020, using the original DEA under the CRS assumption. In contrast, Column 4 suggests that under the CRS assumption, our bootstrap DEA findings show a mean bootstrap bias-corrected overall technical efficiency (BSBC-OTE) of 74% for the examined duration, skewing efficiency estimates upward by 13%. As shown in Columns 5–10, the bootstrap DEA provides bias-corrected efficiency estimates and statistical confidence intervals. Thus, we favour bootstrap DEA efficiency estimates for discussion. Our results imply that Pakistani banks required 74% of the input resources to produce a comparable amount of output to operate on the bootstrap bias-corrected overall technical efficiency frontier and become fully efficient. Likewise, the mean BSBC-OTE was highest in 2018 (77%) and lowest in 2020 (68%), reflecting the COVID-19 ripple effect. The BSBC-OTE had a low coefficient of variation (CV) of 4.06 and a standard deviation (SD) of 0.03. We have categorised BSBC-OTE into bootstrap bias-corrected pure technical efficiency (BSBC-PTE) and bootstrap bias-corrected scale efficiency (BSBC-SE) to better reveal banking inefficiency drivers. In particular, the BSBC-SE is a ratio of the $\frac{{{\rm{BSBC}}-{\rm{OTE}}}_{{\rm{CRS}}}}{{{\rm{BSBC}}-{\rm{PTE}}}_{{\rm{VRS}}}}$.

Table 3 Efficiency Analysis.

As a scale-efficient bank approaches its optimal size, further expansion or contraction would reduce efficiency; hence, this metric provides more insight into economies of scale. Column 8 indicates managerial efficiency, or bootstrap bias-corrected pure technical efficiency (BSBC-PTE). From 2006 to 2020, Pakistani banks’ average BSBC-PTE was 76%. This indicates that Pakistan’s banking management could have reduced input resources by 22% and functioned on the bootstrap bias-corrected pure technical efficiency frontier. In 2009 (global financial crisis) and 2019, BSBC-PTE was at its lowest (74%) and highest (81%). Furthermore, the SD was relatively low at 0.02 and the CV was 2.76, suggesting that BSBC-PTE shows low variation.

Column 13 indicates Bootstrap bias-corrected scale efficiency (BSBC-SE). Between 2006 and 2020, we observed that Pakistani banks had a mean BSBC-SE of 96%. Although this percentage appears decent, there is still potential for growth of 3.56%. It also reveals that the Pakistani banks were 3.56% below their optimal scale size. We have also noticed that Pakistan’s banking industry has had the highest (99%) and lowest (89%) values of the observed BSBC-SE in 2011 (post-global financial crisis) and 2019, respectively. With a CV of 2.98 and an SD of 0.02 for BSBC-SE, our results reveal that the variance is fairly low. In sum, bootstrap bias-corrected pure technical inefficiency, unlike scale inefficiency, is the key driver of technical inefficiency in Pakistan’s banking industry. Our results contradict (Kumar & Gulati, 2008; Usman et al., 2010), who observed that scale inefficiency drove technical inefficiency. The former investigated Indian banks, while the latter analysed Pakistani banking institutions. However, our results coincide with the findings of Gulati (2011).

The 2nd stage DEA analysis

In response to our RQ2 and proposed hypotheses H1a–H9, Tables 4–7 provide interesting readings. For Eq. 5, we performed OLS, FE, RE, panel data Tobit regression, and two-step dynamic panel data system generalised method of moments (DPDSYS-GMM) estimations. However, for interpretation, we have opted for the reported findings under panel data Tobit regression and two-step DPDSYS-GMM. This is to prevent any bias resulting from the bounded nature (0, 1) of our efficiency scores, endogeneity, serial correlation, and heteroscedasticity in our estimated models. Before we start our discussions, the two-step DPDSYS-GMM estimator requires a few diagnostic tests to assure its accuracy. First, the AR1 test checks our model parameters’ first differences for autocorrelation. There is strong evidence against the first-order autocorrelation null hypothesis (P-values = 0.000). Tables 4–8 reveal an autocorrelation between our model parameters’ first differences. Second, we conduct the AR2 test to assess whether the first parameter differences reflect second-order autocorrelation. The test statistics (see Tables 4–8) do not support second-order autocorrelation. The P-values justify the view that second-order autocorrelation is not present. Thirdly, Sargan and Hansen’s tests validated our models’ over-identification constraints. All estimated models had greater P-values and lower test statistics (see Tables 4–8), suggesting the validity of over-identification constraints. Fourth, the estimated model does not include more instruments than groups.

Table 4 Influence of Digitalisation on the Efficiency of Pakistan’s Banking Industry.

Table 5 Influence of Digitalisation on the Efficiency of Pakistan’s Banking Industry.

Table 6 Influence of Digitalisation on the Efficiency of Pakistan’s Banking Industry.

Table 7 Influence of Digitalisation on the Efficiency of Pakistan’s Banking Industry.

Table 8 Influence of Digitalisation on the Efficiency of Pakistan’s Banking Industry.

In Table 4 (Models 4-5), we discover that our first digitalisation indicator, ATM-based transactions (ABTR), has a highly significant and positive effect on Pakistan’s banking industry’s bootstrap bias-corrected pure technical efficiency (EFF) at 1%, with an increase in EFF equal to the coefficient value for each thousand ABTR. ATMs associated with digital banking services allow clients to access and manage their accounts on various platforms. By integrating the internet and traditional banking, ATM interfaces make banking effortless. The ATM interface reduces duplicate activities and improves bank efficiency. Second, due to technological advancements, ATMs now offer more than just cash withdrawals and deposits. Customers might deposit, withdraw, and check balances at ATMs. By broadening their service offerings, banks can better satisfy client demands and reduce branch visits, enhancing banking efficiency. Therefore, we accept H1a.

Table 5 (Models 4-5) exhibits the results of our second digitalisation indicator, Internet-based transactions (IBTR), which has a positive relationship with banking EFF. Internet transactions are less costly and require fewer staff to handle financial data and operations than conventional banking. Internet banking allows clients to conduct transactions online, reducing the necessity for costly branch networks. Cost reductions increase banking efficiency because of more efficient resource utilisation and streamlined operations. This finding provides strong evidence in favour of our H1b; thus, we accept it. Our third digitalisation measure, point-of-sale-based transactions (POSBTR), has a positive association with EFF in Table 6 (Models 4-5). Since it reduces handling costs, speeds up payment processing, and improves precision, protection, and interaction with other business networks. These advantages simplify and speed up cash transactions for clients and businesses, resulting in improved banking efficiency. These results support H1c; hence, H1c is adopted.

Table 7 (Models 4–5) illustrates the overall influence of digitalisation (DIG INDEX) on EFF. We used principal component analysis (PCA) to capture the influence of each digitalisation indicator (e.g., ABTR, IBTR, and POSBTR) into a single factor (DIG INDEX)³ that captures digitalisation’s heterogeneity that follows Ekinci (2021). The working hypothesis asserts that each factor reveals unique information that cannot be gained from the others. Ekinci (2021) argued that the PCA-derived index has several econometric advantages, particularly that it can mitigate multicollinearity and over-parameterization. Table 7 (Models 4-5) reveals that the DIG INDEX positively affects our banks’ EFF. This finding support our H1d, thus, hypothesis is accepted.

The State Bank of Pakistan’s (SBP’s) yearly data indicates a significant increase in digital platform activities, validating our findings. In 2006, the volume of ATM-based transactions was 37.441 million. However, by 2020, this figure had increased significantly to 512.1 million. The volume of Internet transactions grew from 0.332 million in 2006 to 56 million in 2020, exhibiting a similar trend. The yearly data from SBP in 2006 revealed an aggregate of 18.896 million point-of-sale (POS) transactions. However, by 2020, this volume had significantly increased to 70.3 million⁴. Banks in Pakistan are investing more in digital technology infrastructure to comply with the SBP’s new digital payment system guidelines. A new Electronic Money Institution (EMI) received a business license in Q3 2022, accelerating digital payments. The existing two largest EMIs, Finja and Nayapay, have also expanded nationwide. As new EMI firms emerge, digital financial services will become more accessible. To promote digitalisation and financial inclusion, the SBP passed EMI legislation in 2019. New digital payment alternatives, such as quasi-FinTechs, are increasing digital penetration in Pakistan⁵. Pakistan’s banking industry appears to be becoming more efficient due to extensive banking digitalisation, according to our empirical findings, which coincide with previous studies (Ekinci, 2021; Li et al., 2021; Wang et al., 2021; Le et al., 2022).

Our H2a-H2c hypothesis results are shown in Tables 4–7. The Tobit model suggests that net interest margin (NIM) positively affects EFF, recommending that Pakistani banks’ lending is profitable. With a higher NIM, loan interest income outweighs deposit and borrowing interest costs. As its NIM grows, the bank benefits more from its asset-liability interest rate spread. Revenue growth allows the bank to cover operational costs and make revenue. The DPDSYS-GMM model shows a negative and insignificant association between NIM and EFF, implying nonlinearity (see Table 8). Tobit supports our H2a; however, DPDSYS-GMM rejects it. Tobit model results coincide with Das et al. (2005) but do not match DPDSYS–GMM. Tables 4–7 show that return on equity (ROE) exerts a positive but insignificant influence on EFF in both the Tobit and DPDSYS-GMM models. This clashes with prior findings (Siriopoulos & Tziogkidis, 2010). Our Tobit and DPDSYS-GMM results cannot support H2b; hence, we reject it. Both the Tobit and DPDSYS-GMM models (Tables 4–7) demonstrate a positive relationship between profitability, measured as return on assets (ROA), and banks’ EFF. This suggests that increased profitability leads to increased efficiency, a finding that aligns with Ekinci (2021) findings on Turkish banks. These findings confirm that efficient resource planning in the production process reduces bank costs, thereby boosting profitability and efficiency. Thus, we support H2c.

Moreover, while the Tobit model (Tables 4–7) indicates a significant positive association between the cost-to-income ratio (CIR) and EFF, the DPDSYS-GMM reveals an inverse and insignificant association, implying a nonlinear nexus (see Table 8). This contradicts earlier findings (Purohit & Mazumdar, 2003; Olson & Zoubi, 2017). Thus, H3 is rejected. Bank equity-to-asset ratio (CAPT) and EFF in the tobit model are positively associated in Tables 4–7. Although insignificant, DPDSYS-GMM shows a positive coefficient. Our tobit model results correspond to (Lee & Huang, 2016; Mansour & El Moussawi, 2020), who argued banks with a higher CAPT ratio experience lower financing costs. Since investors often seek a reduced rate of return on their investment in a bank that carries lower levels of risk, a lower cost of capital decreases the bank’s overall financing expenses, leading to increased revenue and efficiency. Therefore, the Tobit model adopts hypothesis H4, while DPDSYS-GMM rejects it. In Tables 4–7, we found a positive and insignificant relationship between AGE and EFF under both Tobit and DPDSYS-GMM, leading us to refute H5. Tables 4–7 reveal that the bank’s SIZE positively affects the EFF in both the Tobit and DPDSYS-GMM models, suggesting that bigger banks are more efficient due to economies of scale and scope that align with Phan et al. (2016) and Sufian (2009), who observed that returns to scale allow bigger banks to secure capital at lower costs. Thus, we accept H6.

In Tables 4–7, the Tobit model reveals a negative association between inflation rate (INFRATE) and EFF, whereas DPDSYS–GMM reflects a positive but insignificant relationship. Nonlinearity between INFRATE and EFF might explain these findings (see Table 8). Based on the evidence, we reject H7. The interest rate (INTRATE) favourably affects Pakistani banks’ EFF in the DPDSYS–GMM model but not in the Tobit model (Tables 4–7). Due to growing bankruptcy risk, credit-risky clients pay higher interest rates. Higher interest rates might assist banks in controlling credit risk and lowering credit losses by safeguarding credit portfolio quality. Thus, DPDSYS-GMM validates H8, which coincides with the earlier findings of (Perera et al., 2007; Anbar & Alper, 2011), while rejecting it based on the Tobit model. Tables 4–7 show that the gross domestic product growth rate (GDPGR) has a positive effect on EFF; however, in Tobit, the coefficient sign did not change and turned insignificant. An increase in GDPGR results in a boost in business activities, including the creation of new business entities and the expansion of existing ones, which allows banks to broaden their client base, increase profits, optimise business practices, and improve banking efficiency. Thus, based on DPDSYS-GMM, we accept H9, which is consistent with (Perera et al., 2007; Tan & Tan, 2016; Carvallo & Kasman, 2017). However, the Tobit model provides no statistical significance; hence, we reject H9 under the Tobit model.

Finally, our ownership structure control dummies provide interesting results in Tables 4–7. In most Tobit and DPDSYS-GMM models, state-controlled banks (SCBs) are more efficient than private sector banks (PSBs) and special purpose banks (SPBs); hence, ownership structure affects EFF. Pakistan’s SCBs focus on long-term objectives over short-term gains, unlike their PSBs. In Pakistan, SCBs facilitate socioeconomic growth, banking access, and several industries within the country. Strategic, growth-oriented investments allow Pakistani SCBs to increase their EFF over time. This finding matches Karas et al. (2010) on the Russian banking sector but contradicts Ayadi (2014) on the Tunisian banking sector.

Banking efficiency convergence analysis

In response to RQ3, we proposed H5a and H5b and estimated regression Eqs. 6–7 with OLS, panel data regression models for fixed effect (FE), random effect (RE), and two-step dynamic panel data system generalised method of moments (DPDSYS-GMM) by controlling for ${\rm{YEA}}{{\rm{R}}}_{{\rm{DUMMIES}}}$. In all static panel data models, the Hausman test recommends FE; however, we have preferred DPDSYS-GMM results for interpretation due to their superiority. It is essential to remember that a negative coefficient denotes a tendency toward convergence among the banks to validate the hypothesis. To start with absolute β-convergence, Table 9 (Model 4) provides strong evidence of efficiency absolute β-convergence since the coefficient of initial efficiency level is significantly and negatively linked with the efficiency growth rate, indicating that over time, initially, less efficient banks in Pakistan’s banking industry eventually converged with more efficient counterparts, hence achieving the common equilibrium at the rate of 41.43%. Therefore, we accept H5a.

Table 9 Efficiency Absolute β-convergence of Pakistan’s Banking Industry during 2006–2020.

Table 10 (Model 4) exhibits strong evidence of efficiency absolute σ-convergence, as the coefficient of the initial efficiency gap from the cross-sectional average is negatively and significantly associated with year-over-year fluctuations in each bank’s efficiency transition. This suggests that initially, the banks under study with more dispersed efficiency levels from the cross-sectional mean eventually caught up to the cross-sectional mean and attained the common equilibrium at 41.43%; thus, we accept H5b. These findings coincide with Kasman et al. (2013) in EU, Carvallo and Kasman (2017) in Latin America (Olson & Zoubi, 2017; Mansour & El Moussawi, 2020) in Arab countries, Matthews and Zhang (2010) in China, and Thota and Subrahmanyam (2020) in India.

Table 10 Efficiency Absolute σ-convergence of Pakistan’s Banking Industry during 2006–2020.

In response to RQ4, we proposed H5c and H5f to assess the banking efficiency conditional β-convergence. We estimated Eq. 8 by applying two-step DPDSYS-GMM to analyse how digitalisation influences Pakistan’s banking industry’s efficiency convergence process. Digitalisation’s pure influence on the efficiency growth rate has been evaluated in Table 11 by excluding all other controls to assess how it influences the convergence process. According to Table 11 (Models 1–4), we found that Models 1–3’s convergence speed improved from 41.43% (i.e., absolute β-convergence Tables 9) to 75.14%, whereas Model 4’s was 62.64%. To start, our bank-specific digitalisation indicators, the natural logarithm of ATM-based transactions (lnABTR), the natural logarithm of internet-based transactions (lnIBTR), the natural logarithm of point-of-sale-based transactions (lnPOSBTR), and digitalisation index (DIG INDEX), positively influence the efficiency growth rate. This is because digital technology has allowed Pakistani banks to broaden their reach beyond traditional branch locations. Banks adopt digital banking to serve clients in less densely populated regions or who are unable to visit traditional bank branches. A larger clientele allows for more business opportunities and client engagement, which can increase efficiency growth and accelerate banking industry convergence. Thus, we accept H5c and H5d.

Table 11 Efficiency Conditional β-convergence of Pakistan’s Banking Industry during 2006–2020.

Moreover, there are two country-wide digitalisation indicators: the digital information and communication technology availability index (DICTA Index), created using fixed broadband subscribers per hundred (FBBSPH), and the digital information and communication technology utilisation index (DICTU Index), constructed using principal component analysis based on mobile cell phone subscribers per hundred (MCSPH) and fixed telephone subscribers per thousand (FTPSPT), to assess the influence of country-wide digitalisation factors on the banking efficiency convergence process. Table 11 (Models 1–2) indicates the DICTA Index is inversely associated with efficiency increases. This finding challenges conventional wisdom and thus necessitates further investigation (see Table 13). Pakistani society’s digital disparity might explain this negative association. Since Pakistan’s low-efficient banks mainly target retirees or farmers in rural sections who have inadequate internet access, broadband coverage is more prevalent in larger towns in Pakistan; hence, this digital disparity in accessing digital technologies such as broadband appears to be impeding Pakistan’s banking industry’s efficiency catch-up process. Therefore, in light of the findings, we reject H5e. While the DICTU Index has a positive relationship with efficiency growth, the increase in mobile and landline telephone clients suggests a mature and more integrated communications network in Pakistan. As the country’s communication network grows, a wider population can access banking services and products, elevating the likelihood of adopting digital banking via mobile and internet banking, which enhances efficiency and allows low-efficient banks to catch up. These finding are in line with (Delgado & Nieto, 2004; Vu, 2011; Hilal, 2014; Ekinci, 2021). Thus, we accept H5f.

In Table 12, we re-estimated models 1–4 with additional bank-specific and macroeconomic controls to account for other control factors while retaining digitalisation factors. In all models, the coefficient signs and significance levels for bank-specific and country-wide digitalisation factors coincided with Table 11. Furthermore, convergence speed improved from 78.07 to 80.41% across Models 1–4 in Table 12. Tables 12–13 illustrate that efficiency growth is adversely impacted by the cost-to-income ratio (LnCIR) in all models, revealing that high LnCIR banks converge slower than rivals. Lower lnCIR might lead to cheaper banking services, allowing banks to invest in technology, improve customer service, and add value. Banks with greater LnCIR may lose business to less expensive competitors. This finding coincides with Olson and Zoubi (2017) yet conflicts with Jelassi and Delhoumi (2021). Table 12 (Model 4) and 13 (Models 1–4) exhibit that banking size positively influences efficiency growth rate and results in faster convergence. In other words, economies of scale and scope allow low-efficient banks to rapidly catch up (converge) with high-efficient ones. This supports Carvallo and Kasman (2017) but contradicts Jelassi and Delhoumi (2021).

Table 12 Efficiency Conditional β-convergence of Pakistan’s Banking Industry during 2006–2020.

Table 13 Efficiency Conditional β-convergence of Pakistan’s Banking Industry during 2006–2020.

Tables 12, 13 (Models 1–4) exhibit a positive association between loan growth rate (LGR) and banking efficiency growth rate. This is due to the fact that when banks expand their loan portfolio for profit, prudent lending leads to a decrease in impaired loans and a diversification of loan portfolios. More efficient banks assess borrowers’ creditworthiness, maintain loan portfolios, and harness prudent lending to reduce default risk, safeguard assets, ensure long-term income streams, and accelerate banking efficiency convergence. This finding is consistent with (Dinger & te Kaat, 2020). Tables 12 and 13 (Models 1–4) show that the loan loss provisions to nonperforming loans (LLPTNPL) ratio is positively associated with efficiency growth. More prudent banks with higher LLPTNPL ratios can cope with unexpected NPL losses and improve efficiency. Banks with sufficient loan loss reserves are more likely to comply with rules, avoiding penalties and litigation, implying that prudent risk management allows less efficient banks to catch up faster to their more efficient rivals. These micro-level decisions enable banks to manage risk during economic downturns by strengthening loan loss reserves and creating a feedback loop between macroeconomic conditions and banking risk control. Our results concur with (Bryce et al., 2015; Sharma et al., 2015). Table 12 (Models 1–4) and 13 (Model 4) suggest a significant association between the non-performing loans and total loans (NPLTTL) ratio and banking efficiency growth rate. A low NPLTTL ratio demonstrates prudent lending and risk control, indicating that the bank’s loan portfolio is stable and less risky, which accelerates efficiency growth. As the NPLTTL ratio decreases, the bank allocates fewer resources to recover losses, freeing up more resources for diversification and other business activities, potentially boosting efficiency growth and accelerating banking efficiency convergence. Banking management also tightens lending rules and micro-risk management during economic downturns. These micro-level shifts form a macroeconomic feedback loop, which influences banking system health and risk control. Human resources (lnHR) exhibits an insignificant adverse association with banking efficiency growth rate in Tables 12 and 13 (Models 1–4), opposing (Iliemena et al., 2019; Rahman & Akhter, 2021).

We also uncovered interesting insights into the influence of macroeconomic control variables’ on banking efficiency growth and convergence processes. Tables 12 and 13 (Models 1–4) indicate that M2 money supply growth (M2_GR) improves banking efficiency growth rates. A high M2_GR, which includes currency in circulation and bank deposits, indicates a healthy and growing economy. The central bank adopts an expansive monetary policy by expanding M2_GR, which lowers the interest rate and stimulates economic growth. Because M2_GR expansion elevates monetary liquidity; bank managers might lend more to consumers and businesses, stimulating corporate investment, consumer spending, and economic growth. Banking service demand expands during economic growth because, as the economy grows, the money flow and the volume of bank loans multiply. It enables banks to lend to businesses and customers, generating interest and fees, and allows less efficient banks to catch up faster to more efficient opponents by taking advantage of improved economic circumstances. These results corroborate (Williams, 2012; Carvallo & Kasman, 2017). Tables 12 and 13 (Models 1–4) demonstrate an inverse but statistically insignificant relationship between the inflation rate (INFRATE) and banking efficiency growth. Inflation indirectly influences banks by impacting the economy. Economic intuition validates INFRATE’s effect; however, statistical evidence is lacking to confirm its influence on banking efficiency convergence. Tables 12 and 13 (Models 1–4) reveal that the gross domestic product growth rate (GDPGR) positively affects banks’ efficiency growth. In a growing economy, banks increase lending as businesses and clients demand more of their products and services. Banks broaden branch networks, expand their digital presence, and offer more banking services, which increases interest revenue, fees, and commissions, allowing less efficient banks to catch up faster with more efficient ones. The results corroborate (Perera et al., 2007; Tan & Tan, 2016; Carvallo & Kasman, 2017).

Tables 11 and 12 reveal that the DICTA Index is inversely related to efficiency growth, suggesting that it has a negative effect on the efficiency convergence process. We investigated this relationship across different ownership structures to uncover the digital disparity in Pakistan’s banking industry. In Table 13, we interacted the DICTA Index with ownership dummies such as state-controlled banks (SCBs), private sector banks (PSBs), special purpose banks (SPBs), and foreign banks (FBs) with the DICTA Index while retaining the DIG Index, country-wide DICTA and DICTU, and bank-specific controls lnCIR and SIZE to isolate the index’s negative impact. Table 13 (Model 1) shows that the DICTA Index interaction with SCBs leads to lower efficiency growth. However, the influence of the interaction between the DICTA Index and PSBs in Table 13 (Model 2) is positive on efficiency growth, whereas the DICTA Index on its own turned negative but insignificant. In Table 13 (Model 3-4), the DICTA Index interactions with SPBs and FBs were insignificant.

Finally, we integrated the COVID-19 dummy in Table 14, interacted it with the DIG Index, and re-estimated the model to differentiate the influence of digitalisation on the efficiency growth rate during COVID-19. Although the coefficient has a positive sign, the results show that this has an insignificant influence.

Table 14 Efficiency Conditional β-convergence of Pakistan’s Banking Industry during 2006–2020.

Banking efficiency Phillips and Sul club convergence analysis

Conventional empirical models applying β-convergence and σ-convergence have investigated the economic convergence hypothesis (Quah, 1996; Sala-i-Martin, 1996; Sala-i-Martin, 2002). More recently, (Phillips & Sul, 2007b, 2007a, 2009) suggested a “log t” regression model to analyse the convergence hypothesis through a non-linear dynamic factor model. This novel framework offers several benefits: First, it allows different economic agents behaviours to evolve over time. Second, it is robust to the series’ normality since it does not presuppose trend normality or data random non-normality. Phillips and Sul (2009) argue that conventional convergence models have weaknesses. Because of unobserved heterogeneity and reverse causality, augmented Solow model estimates might be biased and inconsistent if temporal heterogeneity is evident. Since a unit root in the series difference does not always cause divergent inference, traditional co-integration models are less sensitive to stochastic co-movement. The convergence literature likewise detects convergent clubs. Conventional approaches partition the data sample based on characteristics and analyse convergence for each group independently. (Phillips & Sul, 2007b, 2007a, 2009) proposed a data-driven algorithm that identifies convergent clubs without the need for sample partitioning. Moreover, relative transition parameter classification approach coincides with convergence approaches (Phillips & Sul, 2009). Thus, for robustness, we apply a Phillips and Sul (PS) panel convergence approach with a log-t regression convergence test. The PS approach is based on a time-varying dynamic factor model, which allows us to account for generic and idiosyncratic fluctuations. With the PS approach, we can confirm if banks’ efficiency levels are converging and analyse their convergence speed throughout the study’s period. We use club convergence within the convergence process to identify convergence groups. We argue that applying such an approach in this study will augment the prior analysis. The supplementary file presents empirical results on banking efficiency club convergence dynamics (see Appendixes A-B).

Conclusions

This study aims to explore three key issues in Pakatan’s banking industry: (i) banking efficiency; (ii) the impact of digitalisation on banking efficiency; and (iii) efficiency absolute and conditional convergence during 2006–2020.

First, we examined Pakistan’s banking industry’s technical efficiency by applying Bootstrap data envelopment analysis from 2006 to 2020. The findings reveal a 74% average BSBC-OTE. The BSBC-OTE was further subdivided into BSBC-PTE and BSBC-SE. According to our analysis, the average bootstrap bias-corrected pure technical inefficiency (BSBC-PTIE) or managerial inefficiency (−23%) was the key source of overall inefficiency in industry. The findings demonstrate that Pakistani banks may have lowered interest and non-interest expenses by 23% to retain their current level of efficiency. The findings also suggest that banks underutilised their fixed assets and deposit portfolios by 23% to generate similar output.

Second, digital technologies have reshaped customer service, made banking operations more efficient, and driven innovation. Hence, in today’s dynamic banking ecosystem, digitalisation is crucial for banks to uphold their competitive advantage. Our research provides empirical evidence on the influence of digitalisation on the efficiency (EFF) of Pakistan’s banking industry. It is valuable for identifying trends, making informed decisions, and fostering long-term growth in the banking industry. The research reveals that all digitalisation indicators—ABTR, IBTR, POSTR, and DIG Index—significantly and positively influence Pakistani banks’ EFF. The internal banking dynamics indicate that ROA and SIZE positively and significantly affect the EFF. The research finds that SCBs are the most efficient, followed by PSBs and SPBs. Furthermore, in the macroeconomic context analysed, banks’ EFF has a positive association with INTRATE and GDPGR.

Third, we investigated banking efficiency absolute convergence. Our findings exhibit that efficiency absolute β-convergence has occurred, implying that initially, less efficient banks in Pakistan’s banking industry caught up (converged) at 41.43% to their more efficient counterparts. Absolute σ-convergence has also been confirmed suggesting that initially, banks with more dispersed efficiency levels were able to reduce this dispersion and catch up (converge) at the rate of 41.43% to the cross-sectional mean during 2006–2020 to obtain a common equilibrium.

Fourth, we investigate banking efficiency conditional β-convergence to examine how the adoption of digitalisation influences the convergence process. Our results reveal that bank-specific digitalisation indicators have shown a significant positive influence on the efficiency growth rate. The nation-wide scale digitalisation indicator DICTU Index illustrated a significant positive association with efficiency growth, whereas the DICTA Index shown a negative relation. Furthermore, ownership dummies differentiated the DICTA Index’s influence across ownership structures. The DICTA Index and ownership dummy SCBs interactions adversely influenced efficiency growth. However, the DICTA Index interaction with the ownership dummy PSBs positively influenced the growth rate, suggesting that the index’s influence is heterogeneous across ownership structures. The COVID-19 dummy and bank-specific DIG Index interaction enhances efficiency growth but is not statistically significant. Moreover, the absolute β-convergence speed is 41.43%; however, as we introduced digitalisation indicators and other bank-specific and macroeconomic controls to our conditional β-convergence model, catch-up improved significantly which fluctuates between 62.64 to 82.90%. Findings reveal that digitalisation promotes convergence in banking efficiency and allows banks to improve efficiency through ATM, internet-based, and point-of-sale transactions. Digitalisation allows banks to catch up to their more efficient counterparts significantly faster.

Fifth, expansionary monetary policy levers such as the M2 money supply and GDP growth might accelerate loan growth. These variables are interrelated and have a positive impact on efficiency growth, allowing initially less efficient banks to grow their loan portfolios through prudent lending practices as the M2 money supply and GDP growth rates increase. It enables them to catch up to more efficient rivals faster, accelerating banking efficiency convergence.

Sixth, prudent risk-control policies, assessed by LLPTNPL and NPLTTL ratios, accelerate convergence by allowing less efficient banks to catch up to more efficient ones. Thus, banks that effectively control and mitigate risks could capitalise on the money supply and economic growth. A systematic approach to prudent risk management safeguards lending operations from risky situations and balances risk and return.

Theoretical and practical contributions

First, this research broadens the banking literature by examining the evolution of Pakistan’s banking industry’s technical efficiency from 2006 to 2020. The research applied traditional and complex bootstrap DEA techniques to analyse banking technical efficiency, revealing that managerial inefficiency, or bootstrap bias-corrected pure technical inefficiency (BSBC-PTIE), drives industry inefficiency.

Second, this research investigates the influence of digitalisation on Pakistan’s banking industry’s efficiency. The results of this study provide novel empirical insights into the banking digitalisation and efficiency nexus, which is a relatively new area of research. This research adds depth to existing theoretical and empirical knowledge and demonstrates that adoption of digital technology has a tangible positive influence on banking efficiency, thus supporting the hypothesis that digitalisation enhances the efficiency of banks.

Third, this study augment the banking efficiency convergence literature. The study validates efficiency absolute β-convergence in Pakistan’s banking industry, implying that less efficient banks catch up to more efficient rivals. It also demonstrates efficiency absolute σ-convergence, implying that banking efficiency rates are becoming more uniform.

Fourth, by applying the conditional β-convergence paradigm, our research enriches the existing banking literature by assessing how digitalisation influences banking efficiency convergence process. This research is unique because there is a dearth of research on the influence of digitalisation on efficiency convergence process in the banking sector. The study provides empirical evidence on how the adoption of digitalisation allowed initially less efficient banks in Pakistan’s banking sector to rapidly catch up with more efficient counterparts and, thus, rapid convergence. The banking industry might become more equitable and efficient as convergence accelerates, driving sustainable economic growth. The study revealed how Pakistan’s banking industry’s digital transformation improves customer service, lowers costs, and leads to higher efficiency gains, thereby providing valuable insights to regulators and policymakers. As a result, the Pakistani government might encourage banks to invest in their digital networks and foster digital literacy.

Fifth, this study reveals how other financial variables involving loan growth and prudent lending practices, as well as macroeconomic drivers such as GDP growth and M2 money supply growth, influence banking efficiency convergence. The research reveals that adopting prudent lending practices has a positive impact on the banking efficiency convergence process and advances our understanding of the risk-return equilibrium in the banking industry. This indicates that banks that achieve efficiency convergence are effectively balancing the trade-off between risk and return, enhancing the broader understanding of risk control in the banking industry. This illustrates that the evolving dynamics of banking efficiency warrant a comprehensive approach.

Policy recommendations

According to this study’s theoretical and practical insights, we recommend:

First, the formation of a digital advancement authority in Pakistan involving regulators, experts, and academics might be a precursor to accelerating digital transformation. Other possible measures consist of media campaigns focused on improving digital literacy, tax breaks, and monetary incentives for banks to invest in technological platforms and novel technologies.

Second, Pakistan’s banking executives might collaborate with technology firms to develop new digital products and services. Technology adaptation for serving customers and synergies with local and foreign digital tech suppliers are essential for long-term economic gains. Digital technologies such as POS terminals, cash deposit machines (CDMs), and online banking APPs might reduce costs and improve efficiency.

Third, banking size enhances efficiency; therefore, smaller banks might benefit from mergers and acquisitions (M&A) to harness economies of scale. Banks in Pakistan might compete for deposit accounts by expanding their product lines, entering new markets, and improving customer service.

Fourth, at specific stages in the economic cycle, policymakers in Pakistan might institute expansive monetary policies, such as M2 money supply growth, to accelerate GDP growth while striking an appropriate balance between M2 money supply growth and inflationary control. In times of sluggish economic growth or recession, it has the potential to expand lending flow and accelerate economic growth. Banks may reap indirect benefits from a stronger flow of credit and lending activities when the central bank decides to raise M2 as a strategic move amid sluggish growth or recession. However, these measures need to be carefully balanced so as not to induce inflationary risks and assure long-term economic stability.

Fifth, policymakers and banking regulators in Pakistan might encourage banks to adopt prudent risk-control practices in their lending activities. To achieve the objective of a stable and efficient banking system, it might be crucial to formulate rules, perform periodic reviews, and incentivize banks that exhibit effective risk control practices.

Sixth, Pakistan’s financial regulators may focus on a flexible, responsive regulatory framework for the ever-changing economy. Flexible, swift regulatory framework is essential to foster efficient banking operations and prevent impulsive risk-taking.

In a nutshell, policymakers in Pakistan can learn from the exhibited findings by doubling down on attempts to overhaul the banking industry oversight and regulation apparatus and wrapping up the structural transformation to improve banking efficiency.

Research limitations and future research avenues

This research offers several novel insights; however, it is crucial to consider some limitations of this research.

Firstly, this research examines the efficiency of Pakistan’s banking industry using bootstrap data envelopment analysis; however, other parametric approaches, such as stochastic frontier analysis, could be utilised, and for comparative purposes, costs and profit efficiency analysis can also be valuable, which are understudied in Pakistani banking literature.

Secondly, this research applied bank-specific and country-wide digitalisation indicators to investigate the micro- and macro-level digitalisation influence on banking efficiency and its convergence process. Researchers in the future might broaden their focus by incorporating other indicators such as investments in digital technology, R&D, blockchain technology, artificial intelligence (AI), and fintech for analysing the influence of digitalisation on regional banking industry performance to draw more broader conclusions. Moreover, standard macroeconomic convergence approaches have been debated for decades in the literature on economic growth; they have recently become the focus of major attention in banking studies. This study used β and σ-convergence to analyse banking efficiency absolute convergence, augmenting the former with conditional β-convergence to analyse the influence of digitalisation on the banking efficiency convergence process. A novel club convergence approach using a non-linear dynamic factor model validated the main results and added robustness. Although convergence analysis can be a valuable tool for analysing the banking industry’s performance catch-up trends over time, it is crucial to carefully examine the inherent differences between economic growth and banking efficiency growth before applying it to analyse microeconomic-level banking efficiency convergence.

Thirdly, this research used a 15-year (2006–2020) panel data series since the data was a major constraint. Traditional economic convergence is a long-term process that requires a longer period to capture such trends; in contrast, banking efficiency convergence is sensitive to rapid changes and short-term fluctuations. To delve deeper into the banking efficiency catch-up processes and uncover broader and more persistent trends over the long run, future researchers might examine a longer panel series.

Finally, the study’s focus is on Pakistan’s banking industry, and its findings are context-dependent; they cannot be directly generalised to other economies or sectors. In other contexts, the dynamics of efficiency convergence are likely to be driven by different nuances of organisational and market frameworks, regulations, and socio-economic circumstances. Thus, it is vital to be cautious when extrapolating the study’s findings to other economic environments; further comparative research on regional banking industry might offer valuable insights for drawing broader implications.