Temporal and spatial effects of manufacturing agglomeration on CO₂ emissions: evidence from South Korea

Abstract

Studies have shown that industrial agglomeration has a facilitating effect on carbon emission reduction. However, discussions on the impact of manufacturing agglomeration on emission reduction have not simultaneously considered spatial correlation and temporal continuity. Addressing this gap, this study develops a dynamic spatial econometric model rooted in agglomeration economic theory to simultaneously assess the spatial and temporal impacts of manufacturing agglomeration on carbon emission reduction. Utilizing panel data from 17 major South Korean regions from 2013 to 2019, the research investigates the internal mechanisms and spatial effects of manufacturing agglomeration on reducing carbon emissions. The findings reveal that the relationship between manufacturing agglomeration (specialization and diversification) and carbon emissions in South Korea shows an inverted U-shape. Moreover, regarding the temporal continuity of carbon emissions, in the short term, specialized agglomeration is beneficial to reduce local and neighboring carbon emissions. In the long run, the effect of specialized agglomeration on the overall carbon emission reduction is still obvious. However, diversified agglomeration can only reduce local carbon emissions in the short term, but the spillover effect on neighboring areas is not obvious. In the long run, diversified agglomeration can effectively reduce local carbon emissions, but the spillover effect on neighboring areas is still not obvious. These nuanced insights are crucial for policymakers aiming to leverage industrial agglomeration for carbon emissions reduction effectively.

Introduction

Industrial growth has led to increased energy usage in countries, escalating levels of greenhouse gases, and global warming. This trend has prompted extensive research into the correlation between carbon emissions and economic development, with a heightened focus on CO₂ reduction driven by global concerns and international mandates (Tamazian et al., 2009; International Energy Agency report, 2018).

Manufacturing, pivotal in early economic stages and considered the primary driver of growth, exhibits higher energy intensity than other sectors as economies progress (Kuznets, 1971; Farla et al., 1998; Boyd et al., 1987). South Korea has strong government-driven industrial and energy policies. In Korea, energy consumption in the manufacturing sector has increased dramatically since the mid-1980s because of the vigorous development of energy-intensive industries such as steel, cement, and petrochemicals. South Korea released 709.1 million tons of greenhouse gases in 2017, ranking 11th in the world and fifth among the countries in the OECD. In South Korea, the manufacturing sector accounts for the second-largest share of the country’s CO₂ emissions, at 29.6%, following the public electricity and heat production industry, which contributes 32.7% of the CO₂ emissions (Ministry of Environment, 2022). Since the manufacturing sector accounts for a large share of CO₂ emissions in South Korea, the energy intensity of South Korea’s manufacturing sector has a strong impact on the formulation of the UNFCCC (Jung and Park, 2000).

With the successful implementation of the Paris Climate Agreement, South Korea must reduce 728 million tons of CO₂ by 2050 to achieve a carbon-free economy (Lee, 2021). This is a daunting task for the South Korean economy. Blindly limiting the proportion of industries is not conducive to effective industrial agglomeration, which has a negative impact on regional economic growth (Zhou and Fan, 2016). Achieving carbon emission reduction targets while ensuring stable economic growth has become one of the most important policy issues for the South Korean government. Therefore, it is necessary to explore ways to reduce CO₂ emissions from multiple perspectives and achieve carbon emission reduction targets more effectively.

Manufacturing sectors invest in research and development, leading to technological innovations that can significantly reduce the energy intensity and emissions per unit of production (Grossman and Krueger, 1991; Shao et al., 2021). The technological progress and innovation in the manufacturing sector may originate from the externalities of agglomeration economies (Han et al., 2018; Yuan et al., 2019, 2020). South Korea’s evident industrial agglomeration, driven by energy-intensive sectors, exhibits major manufacturing hubs like the Gyeongin zone around Seoul and the southeastern coastal area around Busan. These regions showcase specialized clusters such as steel in Pohang, automobiles in Ulsan, and non-ferrous metals in Jeolla Province, while the country’s second national land development plan (1982–1991) fostered rapid growth in smaller cities, extending diversified industrial clusters across the nation. In the existing literature, the impact of South Korea’s manufacturing agglomeration on carbon emissions has not been discussed in detail. The impact of different forms of manufacturing agglomeration on carbon emissions is also worth further study.

Carbon emissions demonstrate clear spatial dependence characteristics. Additionally, the impacts on carbon emissions vary significantly at different development stages of manufacturing agglomeration. At present, no study has simultaneously considered spatial correlation and temporal continuity when discussing the impact of manufacturing agglomeration on emission reduction. All studies have considered only one aspect when constructing the model.

Through the analysis provided, this study seeks to resolve several key questions: First, do specialized and diversified manufacturing agglomerations affect carbon emission reduction in South Korea, and what form does this impact take? Second, does this effect have spatial spillover implications, thereby broadly influencing neighboring regions? Third, is this effect subject to dynamic changes over time?

To address these questions, this study establishes an analytical paradigm. First, based on the data of 25 manufacturing sectors in 17 regions of South Korea from 2013 to 2019, this study calculates agglomeration indexes of manufacturing specialization and diversification in different regions of South Korea. Second, this study uses the Dynamic Spatial Durbin model to study whether manufacturing agglomeration has a positive impact on carbon emission reduction. This model can examine the impact of manufacturing agglomeration on emission reduction from both spatial and temporal perspectives. In terms of spatial, this study examines whether there is a spillover effect of manufacturing agglomeration on carbon emission reduction, that is, whether the carbon emission reduction of a region benefits from the development of manufacturing agglomeration in neighboring regions. In terms of temporal, this study can analyze the long-term and short-term impacts of manufacturing agglomeration on carbon emission reduction.

The unique contributions of this study can be summarized as follows: First, practically, the results provide a useful policy reference for governments to assess the current manufacturing agglomeration. Second, from a methodological perspective, this study uses the Dynamic Spatial Durbin model, so that the spatial and temporal effects of agglomeration economy on emission reduction can be analyzed simultaneously in one model. In addition, different spatial weight matrices were used in this study to verify the reliability of the model. In particular, asymmetrical spatial weight matrices are used in this study, which can reflect the imbalance of economic interactions between spatial elements.

The rest of this paper proceeds as follows: The next section introduces existing studies of relevant theoretical and empirical studies. The section next to this introduces the methodology and data used in this study. The penultimate section presents empirical results. The last section concludes the paper and provides policy implications.

Literature review

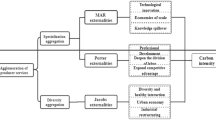
As for the agglomeration economy, Hoover (1937) first divided it into two parts: specialized agglomeration and diversified agglomeration. Marshall (2009) pioneered the idea that industrial geographic agglomeration benefits from externalities. He posited that the specialization resulting from the concentration of firms in the same industry within a certain region yields scale effects in the labor market and intermediate inputs. This concentration also facilitates knowledge spillovers and technological diffusion, thereby enhancing regional economic growth. Marshall’s externality theory was later modeled by Arrow (1962) and Romer (1990) to explain the effect of knowledge spillover on economic growth, which is known as the MAR (Marshall–Arrow–Romer) externality in academic circles. The agglomeration economy can also be explained from the perspective of competitive advantage. The intra-industry competition formed by the agglomeration of similar enterprises can accelerate the absorption and improvement of innovation achievements and help to improve productivity and reduce risks (Porter, 2011). On the other hand, diversified agglomeration emphasizes the externality of knowledge spillover between different industries and points out that important knowledge spillover often comes from outside the industry. The exchange of complementary knowledge between industries can promote innovation, and the regional agglomeration of a large number of diversified industries can drive economic growth more than the agglomeration of similar industries (Jacobs, 2016). Diversified agglomeration particularly highlights those externalities that arise from the differences and complementarities between industries. It underscores the unique role of diversified agglomeration in fostering the emergence of new ideas and stimulating regional economic growth, advocating for the diversified development of urban industries.

Based on Marshall and Jacobs’s externality theory, scholars have conducted many empirical tests on the impact of industrial agglomeration on regional economic growth. De Lucio et al. (2002) used dynamic panel data from 26 Spanish manufacturing sectors from 1978 to 1992 to analyze the impact of industrial agglomeration on economic growth, and the results showed that both specialization and diversification had a positive impact on employment. It is suggested that diversification and specialization play different roles in the different stages of the product life cycle. Comprehensive cities are more suitable for the early stage of the product life cycle, while specialized urban environments are more suitable for the mature stage of product development. A balanced urban system should be the coexistence of comprehensive cities and specialized cities, in which comprehensive cities can promote the integration of new ideas and new products, while specialization cities specialize in standardized products (Duranton and Puga, 2001). Henderson et al. (1995) found that there is both specialized and diversified agglomeration for emerging high-tech industries. This conclusion is consistent with the agglomeration economic theory from the perspective of the industrial life cycle; that is, emerging industries are generated and developed in large-scale comprehensive cities, and the production of mature products will be moved to specialized cities with the development of the industry. Batisse (2002) used Chinese provincial panel data to test the relationship between specialized/diversified agglomeration and industrial growth and concluded that diversified industrial agglomeration is beneficial to industrial economic growth, while specialized agglomeration is negatively correlated with industrial economic growth. Zhang et al. (2021) indicate that under the interaction of specialization agglomeration and diversification agglomeration, the impact of industrial agglomeration on urban economic resilience depends on the type of dual industrial agglomeration, showing significant heterogeneity. Gamidullaeva et al. (2022) utilized econometric methods based on the extended exogenous growth model to confirm the impact of territorial specialization factors on industrial economic growth. Fritsch and Slavtchev (2008) found that in high-tech industries, there exists an inverted U-shaped relationship between innovation and industrial agglomeration; that is, excessive specialization or diversification will lead to low efficiency of regional innovation.

Theoretically, although industrial agglomeration produces the total scale effect of carbon emissions and other pollutants, it will cause serious environmental pollution problems (Ver-hoef and Nijkamp, 2002; Duc et al., 2007). However, blind control of industrial development is not conducive to the generation of an agglomeration economy and the full effect of the agglomeration economy effect (Zhou and Fan, 2016). In addition, according to the traditional agglomeration theory and the new economic geography theory, the agglomeration economy will promote the application of clean technology in enterprises and improve the efficiency of resource use, thus contributing to the reduction of industrial carbon emissions (Krugman, 1998; Grossman and Krueger, 1991; Enrenfeld, 2003; Wang et al., 2020; Zhang et al., 2021). Wang et al. (2022) found information and communication technology (ICT) agglomeration can indirectly reduce carbon emissions through the mediating effect of technological innovation, while ICT agglomeration can positively affect carbon emissions by increasing economic scale. Shi and Shen (2013) showed that industrial agglomeration can promote technology spillover and improve energy efficiency. Han et al. (2014) investigated the impact of three external effects (knowledge spillover effect, economies of scale effect of intermediate input, and labor agglomeration effect) on industrial energy efficiency based on panel data from China. The results show that economies of scale and the knowledge spillover effect of intermediate input significantly improve industrial energy efficiency. In the process of diversified agglomeration, there exists a symbiotic relationship between enterprises (that is, the by-products or wastes of one enterprise may be the intermediate inputs or raw materials produced by another enterprise). Therefore, diversified agglomeration promotes the recycling of resources within the region, improves the efficiency of resource utilization, and thus reduces carbon emissions (Enrenfeld, 2003). The carbon emission reduction effect of industrial agglomeration is also reflected in the provision of a variety of environmental protection infrastructure and professional environmental protection industries. This is even more obvious in the case of diversification. Diversified agglomeration can provide various enterprises in the agglomeration with opportunities to share various low-carbon infrastructures (Han et al., 2018). Capello (2015) also shows that Cities with diversified agglomeration are more likely to share infrastructure than cities with just specialized agglomeration.

With the deepening of the research on the carbon emissions reduction effect of the agglomeration economy, many studies show that the impact of agglomeration economies on carbon emissions is nonlinear. BO and Jianfeng (2015) showed that urban agglomeration has an inverted U-shaped impact on carbon emissions. Xia et al. (2022) found fiscal decentralization’s effect on carbon dioxide emissions in China shows a U-shaped curve, initially decreasing with reduced coal consumption then increasing with the growth of the secondary industry. Li (2014) used threshold regression to study the inverted U-shaped relationship between industrial agglomeration and environmental pollution. When the degree of marketization is low, improving the level of industrial agglomeration will lead to environmental pollution. However, when the marketization level exceeds a specific threshold, industrial agglomeration improves the environment. The nonlinear relationship between industrial agglomeration and carbon emissions can also be explained from the perspective of the life cycle of an industrial cluster. Wang et al. (2022) discovered a significant U-shaped relationship between spatial agglomeration and carbon emissions. Scientific planning of urban clusters will achieve economies of scale and agglomeration effects, thereby reducing carbon emissions. In different life cycle stages, agglomeration shows different characteristics in R&D efficiency, resource allocation efficiency, inter-firm cooperation, and other aspects (Jircikova et al., 2013). Therefore, specialization and diversified agglomeration economies can be fully developed only when the agglomeration level exceeds a certain threshold, thus improving the energy efficiency of enterprises and reducing the marginal cost of carbon emissions.

The first law of geography, formulated by Tobler (2004), declares, “Everything is related to everything else, but near things are more related than distant things.” This principle highlights the importance of spatial proximity in understanding geographic phenomena and is a foundational concept in the field of spatial analysis and geography. Shan et al. (2023) develop a comprehensive method by integrating Bayesian maximum entropy, Weather Research and Forecast, and backward trajectory models to map PM2.5 transport trajectories and sources at a district level, demonstrating significant seasonal transport patterns and policy implications for urban air quality management in cities like Tianjin. Carbon emissions can be transmitted to surrounding areas through economic factors such as industrial transfer or natural factors such as atmospheric circulation, so carbon emissions are not simply a local problem (Han et al., 2018). Therefore, the total amount of carbon emitted in one region is inevitably affected by its neighbors. This may have resulted from the endogenous spatial interactions. For example, a region may emulate the environmental policies of its neighbors or even benefit directly from their efforts to reduce emissions (free-riders) (Han et al., 2018). In addition, the reduction in carbon emissions in a region may also arise from exogenous spatial interactions. For example, the reduction of carbon emissions in one area may benefit from the development of industrial agglomeration in nearby areas. On the other hand, carbon emissions are continuous over time. One region’s current carbon emission may be the result of previous economic activity or related decisions. Therefore, the dynamic economic model can better reflect the influence mechanism of the agglomeration economy on urban carbon emissions. In addition, industrial agglomeration has different characteristics in different evolutionary stages, which may produce different environmental externalities (Han et al., 2018). Therefore, it is necessary to study the impact of the agglomeration economy on carbon emissions in different periods (short-term and long-term), so as to understand the impact mechanism of agglomeration on carbon emissions more accurately and formulate corresponding environmental policies.

At present, there are some studies on the spatial correlation and temporal continuity of carbon emissions. Chuai et al. (2012) used a spatial error model (SEM) to analyze carbon emissions and their influencing factors. Spatial regression analysis shows that carbon emissions from energy consumption are closely related to GDP and population. Cheng et al. (2014) used the static spatial Durbin model (SDM) to analyze what factors influencing carbon intensity in China. The results show that energy structure, industrial structure, energy intensity, and urbanization rate are the leading factors influencing China’s carbon emission intensity. Du et al. (2018) developed a spatio-temporal analysis framework based on the maximum flux principle, to assess the low carbon development of China’s 30 provinces from 2003 to 2013, reflecting the dynamic evolution of low carbon progress. The results indicate that since 2008, China’s low carbon development level has been on an upward trend amidst fluctuations, yet provincial low carbon development is imbalanced. This imbalance is closely linked to socio-economic conditions, resource endowment, and geographic location. Yuan et al. (2020) combined a threshold regression model with a static spatial Durbin model to study the impact of financial agglomeration on green development. The results show that financial agglomeration is beneficial to urban green development. In addition, the study conducted a phase analysis of spillover effects. The results show that the spillover effect of high-level financial agglomeration is stronger than that of low-and medium-level financial agglomeration. Han et al. (2018) used the static spatial Durbin model to analyze the impact of specialized and diversified manufacturing agglomeration on carbon emission reduction in China. Their study found an inverted U-shaped relationship between manufacturing agglomeration (specialized and diversified) and carbon emissions. Both specialized and diversified agglomeration can significantly promote local carbon emission reduction through agglomeration externalities, while specialized and diversified agglomeration also has a positive spillover effect on carbon emission reduction in neighboring areas. Lan et al. (2021) found that specialization agglomeration in manufacturing has a significant impact on regional carbon emissions but does not have a noticeable spillover effect on the carbon emission levels of surrounding areas. Diversification agglomeration in manufacturing does not affect local carbon emissions but has a significant negative spillover effect on adjacent regions. Based on the panel error correction model, Lei et al. (2017) found that industrial agglomeration is conducive to reducing environmental pollution in the short term. But in the long run, there is no necessary causal relationship between industrial agglomeration and environmental pollution.

At present, no study has considered both spatial correlation and temporal continuity when discussing the impact of manufacturing agglomeration on emission reduction. All studies considered only one aspect when constructing the model. In addition, in the construction of a spatial econometric model, the existing research only adopts a symmetrical matrix and does not consider the differences in economic scale between regions. This study attempts to establish a dynamic spatial econometric model based on agglomeration economic theory. Based on the panel data of 17 major regions in South Korea from 2013 to 2019, this study explores the internal mechanism and spatial effect of manufacturing agglomeration on carbon emissions.

Variable selection and methodology

Variable selection

This study, referring to the relevant literature, proposes the following variables to establish the model: All data are defined at the metropolitan or provincial levels (Table 1).

It is well known that manufacturing is more energy-intensive than any other industry (Boyd et al., 1987). In South Korea, the energy intensity of the manufacturing industry has deteriorated since the mid-1980s because of the expansion of energy-intensive industries, such as steel, cement, and petrochemicals (Korea Energy Economics Institute, 1997). This phenomenon is unique compared to the energy intensity trends in other countries. As the manufacturing industry accounts for a large proportion of CO₂ emissions in South Korea, the CO₂ emissions of 25 manufacturing sectors in 17 major regions (metropolitan and provincial) published by the Korea Energy Agency were used as indicators to measure carbon emissions (I). Using this index can better match the specialized and diversified agglomeration index of manufacturing.

The specialized agglomeration index considered in this study is the proportion of manufacturing employment in region i divided by the proportion of manufacturing employment at the national level (Combes, 2000; Han et al., 2018).

$${{{\rm {SP}}}}_{i}=\frac{{{{\rm {emp}}}}_{i,m}/{{{\rm {emp}}}}_{i}}{{{{\rm {emp}}}}_{m}/{{\rm {emp}}}}$$

(1)

where emp_i,m and emp_m are the manufacturing employment in region i and South Korea, respectively. emp_i and emp are the total employment in region i and South Korea, respectively (Combes, 2000). For diversified agglomeration, we adopt the improved method referred to by Henderson et al. (1995):

$${{{\rm {DV}}}}_{i}=\sum _{S}\frac{{{{\rm {emp}}}}_{i,s}}{{{{\rm {emp}}}}_{i}}\left[\frac{1/\mathop{\sum }\nolimits_{{s}^{* }=1,\,{s}^{* }\ne s}^{n}{\left({{{\rm {emp}}}}_{i,{s}^{* }}/\left({{{\rm {emp}}}}_{i}-{{{\rm {emp}}}}_{i,s}\right)\right)}^{2}}{1/\mathop{\sum }\nolimits_{{s}^{* }=1,\,{s}^{* }\ne s}^{n}{\left({{{\rm {emp}}}}_{{s}^{* }}/\left({{\rm {emp}}}-{{{\rm {emp}}}}_{s}\right)\right)}^{2}}\right]$$

(2)

where emp_i,s represents the employment of manufacturing sector s in region i. emp_i represents the total quantity of employment in region i. ${{{\rm {emp}}}}_{i,{s}^{* }}$ represents the quantity of employment of sector s’ except sector s in region i. ${{{\rm {emp}}}}_{{s}^{* }}$ represents the quantity of employment of sector s’ except sector s in South Korea. emp_s is the employment of the manufacturing sector s in Korea. Here, emp is the total quantity of national employment.

Five control variables were included in this study. First, this study uses the total regional (metropolitan or provincial) population to measure the population size (P). Second, per capita affluence (A) is measured by regional GDP per capita. Third, many studies have shown that CO₂ emissions are related to local human capital. In this study, the proportion of bachelor’s, master’s, and PhD graduates was used to measure human capital (EDU) (Ang, 2009; Han et al., 2018). Fourth, the specialized and diversified manufacturing agglomeration is affected by industrial structure, which has different effects on environmental pollution at different stages of economic development. As environmental pollution mainly comes from the waste discharged in the industrial production process, this study chooses the proportion of employment in the secondary industry to the total local employment to measure the industrial structure (IND) (Poumanyvong and Kaneko, 2010; Han et al., 2018). Finally, scientific and technological innovation is closely related to environmental pollution. The input of scientific and technological innovation contributes to the optimization of the production mode and structure of enterprises and also provides the possibility for the improvement of environmental pollution, especially the innovation of green technology. This study selects the proportion of R&D expenditure of major institutions (universities and scientific research institutions) in the GDP of each region to measure the level of scientific and technological innovation in the region (TECH) (Zhou and Fan, 2016).

Data sources

The sample utilized in this study is derived from 17 main administrative regions (one special city, seven metropolitan cities, and nine provinces) in South Korea, observed from 2013 to 2019. The key variable data were sourced from the Korea Statistical Information Service (KOSIS) and the Korea Energy Agency.

Model specification

Dietz and Rosa (1994) found that factors affecting urban carbon emissions mainly include population scale, urban per capita affluence, and the technology level of energy utilization. Among them, the growth of urban population and per capita affluence will increase total carbon emissions, and the improvement of technology level of energy use is conducive to energy conservation and emission reduction. This study is based on the Stochastic Impacts by Regression on Population Affluence and Technology (STIRPAT) theoretical model established by Dietz and Rosa (1994) and expands the original theoretical model by introducing manufacturing agglomeration. The traditional STIRPAT theoretical model is as follows:

$${I=\alpha P}^{{\lambda }_{1}}{A}^{{\lambda }_{2}}{T}^{{\lambda }_{3}}e$$

(3)

where I represents carbon emission, α is a constant term, P is the population scale, A is per capita affluence, T is the technology level of energy utilization, λ₁, λ₂, and λ₃ represent their respective elastic coefficients; and e is other disturbance factors. With the development of the manufacturing industry, an agglomeration economy is formed. The scale effect and technology spillover effect produced by the agglomeration economy can improve energy recycling efficiency and reduce carbon emissions. Therefore, the technological level of energy use can be regarded as an increasing function of manufacturing agglomeration (AGG).

$$T={T}_{0}{{{{AGG}}}}^{\beta},{{\beta}}\, > \,0$$

(4)

where T₀ is a constant term, indicating other factors that can affect the technology level of energy use, except the technology spillover effect from agglomeration economic externalities. The AGG represents the level of manufacturing agglomeration. Due to the different stages of urban development, there may be two forms of manufacturing agglomeration, specialization, and diversification, and both can bring scale effect and technology spillover effect of agglomeration so as to improve energy utilization efficiency (Han et al., 2018). Therefore, the manufacturing agglomeration level (AGG) can be expressed as specialized agglomeration (SP) or diversified agglomeration (DI) (Zhang et al., 2021). β is the elasticity of the manufacturing agglomeration to the technology level of energy use. Substituting the above equation into the traditional STIRPAT theoretical model, the functional relationship between manufacturing agglomeration and carbon emissions can be obtained as follows (Han et al., 2018):

$${I=\alpha P}^{{\lambda }_{1}}{A}^{{\lambda }_{2}}{T}_{0}^{{\lambda }_{3}}{{{{AGG}}}}^{{\theta }_{1}}e$$

(5)

According to the theoretical model of STIRPAT, λ₁ > 0, λ₂ > 0, and βλ₃ = θ₁ < 0. After taking the logarithm of Eq. (5), the following form can be obtained:

$${\mathrm{ln}}I={\alpha }_{0}+{\lambda }_{1}{\mathrm{ln}}P+{\lambda }_{2}{\mathrm{ln}}A+{\theta }_{1}{\mathrm{ln}}{{{AGG}}}+{\theta }_{2}{({\mathrm{ln}}{{{AGG}}})}^{2}+{\theta }_{3}{\mathrm{ln}}X+\varepsilon$$

(6)

In Eq. 6, α₀ represents αλ₃lnT₀, X represents other variables that affect carbon emissions, θ₃ represents their elastic coefficients, and ε is the error term. Considering that the impact of manufacturing agglomeration on carbon emissions may be nonlinear, this study extends the quadratic term of ln AGG into Eq. (6) and with θ₂ as its elastic coefficient.

The carbon emissions were spatially correlated. Carbon emissions spread not only naturally across regions but also spatially spread with the development of transport infrastructure and communication technologies (Han et al., 2018). In addition, the externalities generated by a region’s agglomeration economy can also benefit neighboring regions by reducing carbon emissions. Therefore, in order to obtain consistent parameter estimation by considering the spatial interaction of carbon emissions, a spatial econometric model was adopted in this study. In addition, since carbon emissions are continuous in time, the time lag term of the dependent variables is added in this study to reflect the dynamic mechanism of carbon emissions. Based on the above analysis, this study constructs a Dynamic Spatial Durbin model that considers the spatial lag terms of both dependent and independent variables, and the time lag terms of the dependent variables (Elhorst, 2014). When the observed values of each unit of the cross-section at time t are written as vectors, the Dynamic Spatial Durbin model can be expressed as follows:

$${\mathrm{ln}}{I}_{t}=a+\varphi {\mathrm{ln}}{I}_{t-1}+\delta W{\mathrm{ln}}{I}_{t}+{\rho Z}_{t}+\eta {{WZ}}_{t}+\mu +v+{u}_{t}$$

(7)

where lnI_t is an N × 1 vector consisting of an observed value of the explained variable for each spatial unit i (i = 1, …, N) at time t (t = 1, …, T), Z_t is the N × K vector of independent variables including population scale, per capita affluence, manufacturing agglomeration level (SP or DV), the quadratic term of manufacturing agglomeration level (SP or DV), and other control variables; and μ and v are regional and time effects, which can be fixed or random effects. The choice between fixed effects and random effects can be determined through the Hausman test. φ is the corresponding parameter of the time lag value of the explained variable. δ represents the spatial autocorrelation coefficient, which directly influences the spatial interaction of carbon emissions across different regions; W is the spatial weight matrix with each element W_ij (i ≠ j), which represents the interaction effect among different regions. ρ and η explain the main and spillover effects of each independent variable on the dependent variable. In spatial econometric modeling, spatial interactions among error terms are also considered (u_t = ξWu_t + ε_t). where ξ represents the spatial autocorrelation coefficient of the error term. A model that includes only this spatial coefficient is referred to as a spatial error model (SEM). This term captures unobserved shocks that follow a spatial pattern. Instead of disregarding spatial dependencies in disturbances, the SDM offers an alternative specification for error dependence (LeSage and Pace, 2009). Moreover, the SDM model nests the SEM one since the latter can be derived after imposing an appropriate non-linear restriction on parameters. Additionally, if a spatial econometric model includes only the spatial lag of the dependent variable, it is referred to as a spatial autoregressive model (SAR).

When an equation includes a spatial lag of the dependent variable, parameter estimation cannot be interpreted as a marginal effect (LeSage and Pace, 2009). To address this issue, Lesage and Pace (2009) proposed decomposing the influence coefficient and further investigating the influence and its mechanisms using the partial differential method. They identified three distinct marginal effects: the direct effect, which gauges the impact of independent variables on local dependent variables and is similar to the regression coefficient; the indirect effect, which denotes the spillover effect of independent variables from one region on the dependent variables of other regions; and the total effect, which is the cumulative result of both direct and indirect effects. Since the dynamic Durbin model contains the time lag term of the dependent variable, direct and indirect effects can be calculated separately in the short and long term (Elhorst, 2014). To calculate the short-term and long-term effects, we can re-write the reduced form of Model 5:

$${\mathrm{ln}}{I}_{t}={(I-\delta W)}^{-1}\varphi {\mathrm{ln}}{I}_{t-1}+{(I-\delta W)}^{-1}({\rho Z}_{t}+{\eta {WZ}}_{t})+{(I-\delta W)}^{-1}R$$

(8)

where R includes a, μ, v, and u_t. At time t, the partial derivative matrix of the kth independent variable corresponding to the expected value of lnI_t can be expressed as

$${[\partial E({{\mathrm{ln}}I}_{t})/{\partial Z}_{1k}\ldots \partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{{Nk}}]}_{t}={(I-\delta W)}^{-1}{[{\rho }_{k}{I}_{N}+{\eta }_{k}W]}^{{{d}}}$$

(9)

$${[\partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{1k}\ldots \partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{{Nk}}]}_{t}={(I-\delta W)}^{-1}{[{\rho }_{k}{I}_{N}+{\eta }_{k}W]}^{{{{rsum}}}}$$

(10)

These partial derivatives represent the short-term effects of the explanatory variable k in spatial unit i on the explained variables in all spatial units. The superscript d denotes the operator that calculates the mean diagonal element of the coefficient matrix, which represents the short-term direct effects of each independent variable. The superscript rsum denotes the operator that calculates the mean row sum of the non-diagonal elements that represent the short-term indirect (spillover) effects of each independent variable. The long-term effect of the independent variable can be obtained by considering the time lag coefficient (φ) of the dependent variable (Debarsy et al., 2012).

$${[\partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{1k}\ldots \partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{{Nk}}]}_{t}=\left[\right.{(1-\varphi )I-\delta W\left)\right.}^{-1}[{{\rho }_{k}{I}_{N}+{\eta }_{k}W}]^{{{d}}}$$

(11)

$${[\partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{1k}\ldots \partial E({\mathrm{ln}}{I}_{t})/{\partial Z}_{{Nk}}]}_{t}={[(1-\varphi )I-\delta W)}^{-1}{[{\rho }_{k}{I}_{N}+{\eta }_{k}W]}^{{{{rsum}}}}$$

(12)

In the dynamic spatial Durbin model, the direct and spillover effects of explanatory variables depend on φ, δ, and η. Thus, the ratio between direct and indirect effects is different for different independent variables, allowing greater flexibility in coefficients (Elhorst, 2014).

When the spatial lagged dependent variable is added into the Spatial Durbin model as an explanatory variable, the use of OLS may lead to coefficient estimation bias (LeSage and Pace, 2009). This is because of the Spatial Durbin model violates the assumption of the standard regression model that $E\left[\left(\mathop{\sum}\nolimits_{j=1}^{N}({W}_{{ij}}{{\mathrm{ln}}I}_{{jt}}){u}_{{it}}\right.\right]=0.$ This research employs the quasi-maximum likelihood estimator introduced by Lee (2004), which explicitly accounts for the structural form of the endogeneity associated with the spatially lagged dependent variable.

Determining and testing for spatial autocorrelation

Spatial autocorrelation refers to the degree to which a spatial attribute is correlated with itself through space. It is a measure of the extent to which nearby or neighboring locations exhibit similar attribute values (LeSage and Pace, 2009). Theoretically, spatial autocorrelation is significant because many processes in nature, economics, and other fields are inherently spatial. For instance, in regional science and economic geography, the spatial arrangement of economic activity can significantly impact various outcomes. It contradicts the assumption of independence commonly used in standard statistical techniques, implying that observations nearby in space are more similar than those further apart. This can affect the validity of inferences about relationships between variables. Positive spatial autocorrelation occurs when similar values cluster together in space, while negative one occurs when dissimilar values do so. It can be global (affecting the whole study area) or local (affecting specific areas). Common tests for Spatial Autocorrelation include Moran’s I, Geary’s C, and the Getis-Ord General G. These tests help determine whether spatial autocorrelation is present and whether it is positive or negative. Moran’s I is a widely used measure that compares the spatial structure of the dataset to a random spatial arrangement to determine the presence and type of autocorrelation (Getis, 2009).

spatial weights matrix

In Eq. (6), W_ij denotes an N × N spatial weight matrix that illustrates the spatial arrangement of the observed units. The robustness of the findings was verified using various weighting matrices. Initially, the inverse distance matrix (W₁) was utilized, with the assumption that as the distance between two units increases indefinitely, their correlation approaches zero. In this context, d_ij represents the Euclidean distance (i.e., the simple straight-line distance) between region i and j, and d_ij⁻¹ is the reciprocal of d_ij, indicating the inverse distance between two regions.

Table 1 Definition of the variables.

Additionally, the distance matrix is weighted with regional GDP to represent a gravity function, illustrating the disparities in economic activity across regions (Bottasso et al., 2014). Matrix W₂ is defined as follows:

$${W}_{2}={{{{GDP}}}}_{i}\times {{{{GDP}}}}_{j}/{d}_{{ij}}^{2}(i\,\ne \,j)$$

(13)

W₂ is the inverse of squared distances, multiplied by the GDP levels of regions i and j. The ij entry is measured in the first year to mitigate potential endogeneity issues (Corrado and Fingleton, 2012). The final spatial weights matrix W₃ is the asymmetrical matrix with regional economic differences:

$${W}_{3}={W}_{1}\times {{{diag}}}({{{{GDP}}}}_{i}/{{{{GDP}}}}_{{{a}}})$$

(14)

where diag(GDP_i/GDP_a) represents a diagonal matrix and GDP_a represents the average GDP of all regions. In W₃, the mutual effects of the two regions are not identical (i.e., W_ij ≠ W_ji). The economic information in this matrix is directional, indicating that regions with higher economic development exert stronger spillover effects on those with lower development levels. This asymmetry highlights the varying degrees of mutual influence between regions (Zhang et al., 2018).

Analysis results

Data analysis and discussion

The details of all the variables are presented in Table 2. The relatively large standard deviations indicate significant differences in regional development and carbon emissions. Hence, accounting for regional heterogeneity by including regional fixed effects and control variables in the model specifications is necessary. Furthermore, the Jarque–Bera (JB) test results for the variables show that the null hypothesis, which states that the data comes from a normally distributed population, cannot be rejected at the 5% significance level for any of the variables.

Table 2 Descriptive statistics.

Prior to constructing the model, this study performed a correlation coefficient analysis and a variance inflation factor (VIF) test on the main variables to determine if significant collinearity exists among them (Table 3). The results showed that the correlation coefficient between SP and DV was high (−0.787), but the other main variables were not highly correlated. Moreover, the Variance Inflation Factor (VIF) values for SP and DV have reached 211.30 and 198.63, respectively, which are far >10, suggesting that there may be multicollinearity between the two variables. There was a significant inverse relationship between SP and DV, which is similar to the results of previous studies. This result shows that specialized and diversified agglomerations are obvious in each region of South Korea. To make reasonable use of the limited resources, each region is committed to developing one type of industrial agglomeration mode. Appendix A lists the index of specialized and diversified agglomeration in 17 main administrative regions of South Korea in 2019; it can be seen that Seoul and Jeju have a higher diversified agglomeration index, and the areas with higher specialized agglomeration index are concentrated in the industrial complex on the southeast coast of South Korea. In addition, because of the high correlation coefficient between SP and DV, the impacts of SP and DV on carbon emissions will be estimated separately in this study in order to prevent collinearity from biasing the estimation results. The software utilized in the empirical study included Stata16, Matlab 2022b, and its spatial econometrics toolbox.

Table 3 Correlation analysis.

Estimation procedure

First, this study employs the panel Moran’s I index to investigate the overall spatial dependence among the observed carbon emissions, aiming to understand the spatial transmission mechanism of carbon emissions in the selected regions. According to Table 4, Moran’s I values of carbon emission based on W₁, W₂, and W₃ are 0.216, 0.276, and 0.249, respectively, with p-values are at least <0.05. Therefore, carbon emissions exhibit significant positive spatial dependence throughout the entire panel period. This indicates that regions with high levels of carbon emissions tend to cluster together with other regions exhibiting similarly high emissions. This pattern aligns with the geographical distribution of the manufacturing industry in Korea, where most major manufacturing industries are concentrated in the southeastern coastal areas or around the capital. This result also suggests that there is a spatial correlation between the dependent variables, necessitating the introduction of a spatial econometric model for further analysis.

Table 4 Moran’s I values of carbon emission for the whole panel period.

In this study, the impact of SP and DV on carbon emissions was estimated separately. In Model 1, we measured the impact of SP on carbon emissions, according to Eq. (7). In Model 2, we measured the impact of the DV on carbon emissions.

In panel data analysis, the Hausman test is employed for model selection, with the null hypothesis suggesting that the preferred model is random effects rather than fixed effects (Greene, 2008). Lee and Yu (2012) extended the Hausman test to spatial panel models. Consequently, this study initially determined the model form using the Hausman test. For all model specifications, the Hausman test results (Table 5) exhibited p-values of <0.1. Therefore, a fixed-effects model was chosen over a random-effects model. Additionally, the likelihood ratio (LR) test (Table 5) indicated that the model should include both spatial and time-period fixed effects (Elhorst, 2014).

Table 5 Spatial econometric model test under W₁, W₂, and W₃.

When selecting the exact form of the spatial panel model, the LM test and robust LM test are commonly used to initially check the model form (Anselin et al., 2008). Table 5 indicates that the LM and robust LM statistics for the SAR model passed at least the 10% significance level in Models 1 and 2. The LM statistics for the SEM also passed at least the 5% significance level in Models 1 and 2; however, the robust LM statistics did not pass the significance test in Model 1 with W₂. This suggests that the SAR model may be preferable to the SEM, further confirming the spatial dependence of these influencing factors.

Although the LM and robust LM test statistics suggest that the SAR model is superior, a more generalized SDM should be further established (LeSage and Pace, 2009), and the optimal model type should be selected through the Wald and LR tests. The Wald and LR tests were employed to test the hypotheses H₀: η = 0 and H₀: η + δρ = 0. Table 5 shows that in all model specifications, the Wald and LR statistics for the SDM, simplified to the SAR model, passed the significance test at the 5% level. Similarly, the Wald and LR statistics for the SDM, simplified to the SEM, also passed the 5% significance test. This indicates that the SDM should be adopted instead of the SAR or SEM.

Empirical estimates of dynamic SDM

The estimation results of the dynamic SDM are presented in Table 6. It can be seen that the time lag term of CO₂ emissions (lnI_t−1) is positive under the three spatial weight matrices in Models 1 and 2 and passes the significance test at least 1% level, indicating that CO₂ emissions in South Korea have significant dynamic effects, that is, CO₂ emissions have significant path-dependent characteristics. Regions with high carbon emissions this year tend to stay that way for years to come. This also means that reducing emissions is a long-term task. The coefficient (δ) of the spatial lag term is positive under the three spatial weight matrices in Models 1 and 2 and passes the significance test at least at the 10% level, indicating that the CO₂ emissions show obvious spatial dependence under the effects of endogenous spatial interaction, and further verifies the existence of spatial correlation.

Table 6 Spatial regression results for the dynamic SDM with W₁, W₂, and W₃.

Because the spatial autoregression coefficient (δ) in Table 2 is significantly non-zero, it is not appropriate to directly use the model estimation values (point estimates) to judge the marginal effect of each independent variable on the dependent variable (LeSage and Pace, 2009). Therefore, this study uses the partial differential method to decompose the direct, indirect, and total effects of each explanatory variable on carbon emissions.

Table 7 shows the impact of specialized agglomeration on carbon emissions under each spatial weight matrix. First, in the short term, the direct effects of specialized agglomeration are not statistically significant, but their quadratic terms are significantly negative under each spatial weight matrix. The results show that with the increase in specialized agglomeration level, local carbon emissions show an inverted U-shaped trend of first increase and then decrease. The inflection point (k) of the inverted-U curve can be measured using the formula −m/2n, where m is the linear coefficient of the specialized agglomeration and n is the quadratic coefficient. Since the direct effect of specialized agglomeration is not statistically significant, this illustrates that the inflection point (k) of specialized agglomeration is zero. As can be seen from Table 2, the minimum value of the specialized agglomeration index is >0 (0.2214). This indicates that the specialized agglomeration of South Korea’s manufacturing has positive agglomeration externalities on carbon emission reduction. This result is consistent with previous studies (Han et al., 2018; Lan et al., 2021). The indirect effects of specialized agglomeration and its quadratic terms under each spatial weight matrix are significantly negative and represent an inverted U-shaped trend. The k values of specialized agglomeration are negative under each spatial weight matrix, but the actual indexes of specialized agglomeration are all >0. This indicates that the improvement of specialized agglomeration level in a region is also conducive to reducing the carbon emissions of its neighboring regions, which is due to the spatial spillover effect of specialized agglomeration. This may be because specialized agglomeration refers to the aggregation of enterprises in the same industry, and technology spillovers within the industry are more likely to occur. Once an enterprise has mastered relevant pollution control technology, other enterprises in the neighborhood can acquire relevant technology in a short time, thus significantly reducing the overall pollution emissions. Moreover, because specialized agglomeration involves the same types of enterprises, they also emit the same pollutants, making it easier to achieve economies of scale in the treatment of pollutants. This result differs from previous studies. For example, research set against the backdrop of China indicates that the spillover effects of manufacturing specialization agglomeration on carbon emissions in adjacent areas are not significant (Lan et al., 2021). This discrepancy may be attributed to South Korea’s relatively smaller territorial size, which could lead to more pronounced spillover effects. The total effect of specialized agglomeration and its quadratic term is significantly negative under each spatial weight matrix, also showing an inverted U-shaped trend. This suggests that specialized agglomeration can reduce overall carbon emissions in the short term.

Table 7 Direct, indirect effects, and total effects of Model 1.

In addition, in the short term, the direct effects of population size on carbon emissions are significantly positive in the estimation results for each spatial weight matrix, indicating that an increase in urban population size raises the carbon emission level. The direct impacts of GDP per capita on carbon emissions pass the significance test, indicating that there is a positive relationship between local carbon emissions and GDP per capita. The indirect impact of GDP per capita is also positive and statistically significant, which may indicate that an increase in GDP per capita in a certain region will also raise carbon emissions in neighboring regions. This proves that South Korea’s manufacturing industry generates a large amount of greenhouse gases along with its economic development. Carbon emission reduction and energy conservation remain an important task for the government. The direct effect of human capital is significantly negative in all spatial weight matrices, and the indirect effect is significantly negative only in W₂. Therefore, the promotion of human capital is conducive to the reduction of carbon emissions in the local manufacturing industry. This result illustrates that the high-level personnel represented by the ratio of bachelor’s, master’s, and PhD graduates can improve carbon emissions reduction through technological and productivity advances.

Second, in the long run, the total effect of specialized agglomeration is significantly negative under each spatial weight matrix, and their quadratic terms are also significantly negative. This suggests that, in the long run, an inverted U-shaped relationship between specialized agglomeration and carbon emissions is still evident. Specialized agglomeration can improve the utilization rate of resources and form agglomeration externalities more widely in the long run to achieve the goal of carbon emission reduction.

Table 8 shows the impact of diversified agglomeration on carbon emissions for each spatial weight matrix. First, in the short term, the direct effects of diversified agglomeration on carbon emissions are significantly negative under different spatial weight matrices, and their quadratic terms are also significantly negative. This shows that diversified agglomeration exerts obvious agglomeration externalities and promotes the reduction of local carbon emissions in the short term. The quadratic term of the direct effect is also significantly negative, suggesting that with the increase in diversified agglomeration, the regional carbon emission level presents an inverted U-shaped trend of first increasing and then decreasing. Because the inflection point k value is negative, the actual values of the diversified agglomeration index are all >0, indicating that the diversified agglomeration level of South Korea’s manufacturing industry is located on the falling side of the inverted U-shaped curve. This means that diversified agglomeration will continue to exert positive externalities on carbon emission reduction in the short run. On the other hand, the indirect effects and total effects of diversified agglomeration on carbon emissions are insignificant under different spatial weight matrices, and their quadratic terms are also insignificant. This result may indicate that the spillover effect of diversified agglomeration on carbon emissions in neighboring areas is not obvious. This result differs from that of specialized agglomeration. A possible reason is that the diversified agglomeration in South Korea is mainly concentrated in regions dominated by tertiary industry, and the tertiary industry is developed with low pollution, which does not have an obvious impact on the carbon emissions of other regions.

Table 8 Direct, indirect effects, and total effects of Model 2.

Second, in the long run, the direct effects and their quadratic terms of diversified agglomeration are also significantly negative under different spatial weight matrices. This shows that in the long run, diversified agglomeration promotes the development of tertiary industry and emerging industries, which will continuously improve the level of economic development of the city and enable the city to increase investment in environmental protection and gradually improve the environmental quality.

Endogeneity test

This study also addresses endogenous problems stemming from the bidirectional causality between carbon emissions and the agglomeration economy. To test the reliability of the model and investigate whether the model has endogeneity, this study also estimates the non-spatial fixed effects model and the non-spatial dynamic model (Appendix B). In the non-spatial fixed effect model, we still found an inverted U-shaped relationship between manufacturing agglomeration and carbon emissions. The positive effect of manufacturing agglomeration on carbon emission reduction was verified again.

A systematic GMM is a common method for the endogeneity test. It sets the difference and lag terms of endogenous explanatory variables as instrumental variables, which can solve the problem of inconsistent model estimates and overcome the problem of weak instrumental variables of differential GMM (Blundell and Bond, 1998). As a control for endogeneity, this study uses the systematic GMM method to estimate the panel data with the different terms of independent variables as the instrumental variable. The insignificant values of the Hansen test in the systematic GMM estimation show that the instruments used in the estimation are independent of the error term. Therefore, over-identification does not exist, and the instruments are valid. In addition, the Arellano and Bond tests showed that only first-order serial correlation existed in the error term, while the second-order serial correlation test was not significant, confirming that the model had no higher-order serial autocorrelation. The GMM estimates also found an inverted U-shaped relationship between manufacturing agglomeration (specialization and diversification) and carbon emissions. The results show that the estimation result of the dynamic spatial Durbin model is robust, and endogeneity may not be serious in this study.

Conclusion

South Korea intends to achieve zero carbon emissions by 2050, which makes its economic restructuring face the dual constraints of carbon emission control and economic growth. This paper uses the Dynamic Spatial Durbin model to investigate whether manufacturing agglomeration in South Korea is conducive to carbon emission reduction.

The relationship between manufacturing agglomeration (specialization and diversification) and carbon emissions in South Korea shows an inverted U-shape. That is to say, specialized and diversified agglomeration plays the role of first aggravating and then restraining carbon emissions. At present, the levels of manufacturing agglomeration (specialization and diversification) in South Korea are all above the critical value (k); that is, these regions have been on the descent position of the inverted U-shaped curve. Therefore, with the improvement in the manufacturing agglomeration level, carbon emissions can be continuously and effectively reduced.

Since this study adopts spatial econometric analysis, it is possible to measure the spillover effect of manufacturing agglomeration on carbon emission reduction in neighboring areas. The results show that specialized agglomeration not only benefits local carbon emission reduction but also has a positive spillover effect on carbon emission reduction in neighboring regions. One possible reason is that a region may benefit directly from its neighbors’ efforts to reduce carbon emissions (free-riders). In addition, specialized agglomeration is conducive to knowledge spillover and technology diffusion, thus promoting the adoption of environmentally friendly technologies in the adjacent industrial agglomeration areas to achieve the goal of carbon emission reduction. On the other hand, this study found that diversified agglomeration only has an obvious inhibitory effect on local carbon emissions, but the spillover effects on neighboring regions are not obvious.

In this study, a dynamic model was used to consider the temporal continuity of carbon emissions. Therefore, the short-term and long-term impacts of manufacturing agglomeration on carbon emission reduction can be analyzed. The results show that in the short term, specialized agglomeration is beneficial to reduce local and neighboring carbon emissions. In the long run, the effect of specialized agglomeration on the overall emission reduction is still obvious. However, diversified agglomeration can only reduce local carbon emissions in the short term, but the spillover effect on neighboring areas is not obvious. In the long run, diversified agglomeration can effectively reduce local carbon emissions, but the spillover effect on neighboring areas is still not obvious.

On this basis, this study has several policy implications. First, both specialized and diversified agglomerations can effectively reduce local carbon emissions. This means that the existing manufacturing agglomeration in South Korea has been able to fully generate agglomeration externalities, improve energy efficiency, and reduce carbon emissions. Therefore, the government should continue to support the long-term development of Korea’s major traditional manufacturing base by promoting the agglomeration of similar enterprises and improving the infrastructure manufacturing base. At the same time, the government should focus on promoting efficient, technology-driven agglomeration that maximizes productivity while minimizing environmental impact. This could include supporting innovation clusters and investing in green technologies within industrial areas. Second, specialized agglomeration of manufacturing is beneficial to carbon emission reduction in neighboring areas. This reflects that specialized agglomeration is more likely to induce knowledge spillover and technology diffusion. Therefore, the government should increase scientific research investment in specialized agglomeration areas, encourage the development of new technologies, and build an information-sharing platform to promote the exchange and popularization of new technologies. Furthermore, the government can investigate the optimal design and scale of policies to harness positive spillovers effectively, including regional collaboration and technology-sharing initiatives.

Based on the research result, several limitations might be inherent in the study that need to be acknowledged. First, while the dynamic spatial Durbin model is robust for spatial econometric analysis, it may not capture all nuances of the relationship between manufacturing agglomeration and carbon emissions, especially when considering the complex interplay of economic, technological, and policy factors. Second, the study’s reliance on specific types of agglomeration (specialized and diversified) may not consider other forms of industrial agglomeration that could also impact carbon emissions and economic growth. Third, the study’s conclusions are based on available data, which might have limitations regarding accuracy, completeness, and representativeness. Data constraints could affect the robustness of the findings and the derived policy implications. Last, while the results provide critical understandings applicable to countries with similar industrial structures and policy environments, the generalizability of the findings might be limited by regional specificities such as economic development stages, industrial policies, and environmental regulations.

This study not only contributes to the specific case of South Korea’s carbon neutrality goals but also enriches the broader discourse on sustainable development, economic geography, and environmental policy. It underscores the importance of considering both the economic structure and technological advancements in addressing environmental challenges, and it sets the stage for a multifaceted approach to future research and policy-making in the realm of sustainable industrial development and carbon management. The study’s findings on South Korea’s manufacturing agglomeration and its impact on carbon emissions intersect with existing environmental and economic theories and suggest several pathways for future research. First, the positive environmental impact of specialized agglomerations due to technology diffusion suggests a link between industrial clustering, innovation, and environmental sustainability. Future research might explore the specific mechanisms through which agglomeration affects carbon emissions, including the role of technology transfer, infrastructure development, and regulatory environments. Researchers might also investigate different types of agglomeration beyond specialization and diversification. Second, the study’s policy implications emphasize both specialization for knowledge spillovers and diversification for robust local emission reductions. Future research directions could involve designing and assessing policies that balance these aspects, understanding the optimal mix of specialization and diversification for different regions, and exploring how these strategies fit into broader national and international climate goals. Third, the use of a dynamic model to differentiate short-term and long-term effects offers a valuable perspective for understanding the temporal dynamics of environmental impact. The differing effects of specialized and diversified agglomerations over time highlight the complex nature of industrial evolution and its environmental implications. Future research might further explore these temporal aspects, considering how changes in industry, technology, and policy influence the speed and direction of environmental impacts over time. Besides, comparative studies across different countries or regions could also reveal how varying economic, cultural, and regulatory contexts influence this relationship.