Carbon emissions cap or energy technology subsidies? Exploring the carbon reduction policy based on a multi-technology sectoral DSGE model

Abstract

As global climate change becomes increasingly severe, energy technology innovation has become a key means of coping with the climate crisis and realizing green and low-carbon development. However, existing literature rarely examines the effects of carbon emission reduction policies based on the perspective of energy technology progress for both short-term economic fluctuations and long-term equilibrium. This paper introduces the fossil energy technology sector and the renewable energy technology sector into the dynamic stochastic general equilibrium (DSGE) model, and compares the effectiveness of the carbon emission cap policy, the fossil energy technology subsidy policy, and the renewable energy technology subsidy policy under the framework of China’s carbon trading market in promoting macroeconomic growth and controlling pollutant emissions. We found that in long-term, the emission reduction effect of the carbon emission cap policy falls short of the other two policies, and subsidizing fossil fuel technologies is more cost-efficient comparatively. The government expenditure shock can all stimulate macroeconomic growth with crowding out of private investment and household consumption, whereas the energy technology research productivity shock leads to a decline in total output and an increase in renewable energy technology demand. In addition, pollutant emissions are pro-cyclical under the impact of total carbon policies and counter-cyclical under the impact of energy technology subsidy policies. This article constructs a multi-technology sectoral dynamic stochastic general equilibrium model, expanding the research perspective and theoretical framework for evaluating carbon emission reduction policies. At the same time, it proves the importance of the government to implement the phased energy technology subsidy policy while implementing the carbon emission cap policy, which provides important enlightenment for the implementation and adjustment of carbon emission reduction policy.

Introduction

While fossil fuel energy is an essential driver of economic development, it is also the primary contributor to carbon emissions intensifying global climate change (Xu et al., 2023). The high reliance on fossil fuels will aggravate the energy shortage crisis and global warming (Zhou, 2022c). Against this backdrop, a growing global consensus has emerged advocating for collective action on climate change and strive towards carbon neutrality (Zhou, 2023). This was demonstrated in 2015 when the Paris Agreement established long-term climate goals, including the achievement of carbon neutrality. By the end of 2021, 136 regions worldwide have set targets for net-zero emissions. As a significant global energy consumer, China has also pledged to reduce emissions, with the goal of peaking carbon emissions by 2030 and reaching carbon neutrality by 2060 (Zhou, 2022b). Reaching carbon neutrality is poised to redefine global production paradigms and lifestyles, with technology innovation emerging as a pivotal cornerstone for nations worldwide to attain carbon neutrality objectives (Liu et al., 2022; Zhou et al., 2023). Therefore, formulating carbon reduction policies to foster energy technology innovation, optimize the energy structure, and achieve economic transformation of China represents a pressing issue that needs to be addressed.

Literatures have investigated the impacts of policies such as carbon tax, carbon trading, and carbon cap on carbon reduction and the macroeconomy (Lin and Jia, 2020; Qi et al., 2024; Rui et al., 2023). Studies have indicated that implementing carbon policies might lead to the migration of carbon-intensive industries to countries with more lenient carbon policies (He and Chen, 2023; Luan et al., 2023). With the diversification of global carbon policies, China may face increased pressure from the influx of carbon-intensive industries from abroad, compelling a shift from a high-carbon emission growth model to a new growth paradigm driven green technologies (Lin and Wang, 2023). Imposing a carbon tax effectively incentivizes reduction in emissions by manufacturing firms; however, merely increasing the tax rate would escalate the loss in social welfare (Chen, 2022). In contrast, the carbon emission trading system not only effectively reduces carbon emissions but also boosts production, stimulating technological innovation, particularly incentivizing technological advancements in the energy sector (Sun et al., 2023). Based on this, scholars further discovered a synergistic effect in reducing carbon emissions through China’s carbon trading market and administrative intervention in setting carbon cap (M. He et al., 2023a). By setting reduction targets through carbon cap, complemented by the carbon pricing mechanism of the carbon trading market, investors are encouraged to investment in low-carbon technologies through market signals, while enterprises are motivated to seek cleaner and more efficient energy technology solutions to minimize costs (Mandaroux et al., 2023; Shobande et al., 2024). Therefore, complementing carbon trading with carbon cap is among the most potent measures for China to achieve its carbon peak goals.

Considering the significant impact of energy technology innovation on carbon reduction, directly subsidizing low-carbon energy technology is a crucial policy measure. Compared to policies such as carbon trading and carbon cap control, the body of literature exploring the benefits associated with energy subsidy technology policies remains relatively underdeveloped. Furthermore, there exists some contention among the findings of existing studies regarding the effects of energy technology subsidies. For instance, empirical research based on panel data has indicated that subsidies for new energy technologies are conducive to the transition of energy structures and stimulate economic growth (Lin and Xie, 2023). However, some scholars have identified that R&D subsidies may exert negative effects on the macroeconomy. This controversy stems from the potential divergences between the long-term and short-term effects of energy technology subsidy policies, along with the notion that different intensities of subsidies may yield heterogeneous outcomes (Blanes and Busom, 2004). The literature is deficient in exploring the theoretical mechanisms by which energy technology subsidies directly or indirectly influence technological innovation, changes in energy structures, and macroeconomic output. Consequently, there is an inadequate understanding of the short-term fluctuations and long-term effects that energy technology subsidies impose on the macroeconomic environmental system. On the other hand, it is evident that policies such as carbon trading, carbon cap control, and subsidies for energy technologies all potentially contribute to emission reduction and foster technological advancement, enhancing energy efficiency and optimizing the energy structure. However, literatures predominantly focus on individual policies, with less comparative analysis on the heterogeneous effects of different policies and often overlooking the synergistic effects produced by policy interactions, despite the reality that policymaking involves weighing multiple approaches. Therefore, to achieve China’s dual carbon goals, further research is warranted to compare the heterogeneous effects of restrictive policies like carbon cap control and incentive policies such as subsidies for energy technologies on energy technology innovation, carbon reduction, and the macroeconomy under the carbon trading market.

As mentioned above, findings in numerous literatures have revealed that technology innovation constitutes a pivotal avenue for mitigating carbon emissions (Fernández et al., 2022; Hossain et al., 2022; Yu et al., 2024). Advances in energy technology can reduce the energy use intensity of industrial production activities while improving production efficiency (Wurlod and Noailly, 2018). Further, the heterogeneous effect induced by technological improvements in fossil and renewable energy on carbon emission reduction also received wide concern. Fossil fuel technologies encompass the techniques for the exploration, utilization, and management of fossil fuel resources, like Carbon Capture, Utilization, and Storage (CCUS) technology (McLaughlin et al., 2023). Their critical role in carbon emission mitigation primarily hinges upon augmenting energy efficiency and reducing the emission intensity per unit of energy (Su et al., 2023; Wurlod and Noailly, 2018). In contrast, the advancement of renewable energy technology directly catalyzes the utilization of renewable energy sources, displacing high-emission conventional fossil fuels such as coal (Zhou, 2022a; Zhou et al., 2024; Zhou and Lund, 2023). Many existing studies primarily focus on the effects of individual energy technologies on emission reduction as well as economic growth, overlooking the heterogeneous and integrated effects stemming from the interaction of fossil fuel and renewable energy technologies. This lack of understanding can be a limitation when formulating a policy package to encourage using both types of energy technologies.

Given the potential of technological innovation in achieving carbon neutrality without comprising economic growth, it becomes imperative to grasp the rhythm of economic fluctuations induced by carbon reduction policies (Iraola and Santos, 2017). A thorough examination of macroeconomic oscillations becomes indispensable to formulate judicious policies to promote technological innovation for carbon emission reduction within a context of economic stable advancements. A widely adopted method for assessing policy effects is the decomposition analysis, which can analyze the contributions of technological factors to carbon emissions. Additionally, numerous studies employ statistical models including IPAT, KAYA, STIRPAT models, among others, for assessments of technological factors influencing carbon emissions.(Bretschger, 2021; Lin et al., 2023; Solarin, 2020). However, it is imperative to acknowledge that those ex-post assessment methods relying on historical statistics confront the critique posed by the Lucas Critique. To predict the effects of carbon emission reduction policy for ex-ante risk controls, Integrated Assessment Models (IAMs) (Cai and Lontzek, 2019; Nordhaus, 1992) and Computable General Equilibrium (CGE) models (Chen, 2022; Jiang et al., 2023; Qi et al., 2024; Song et al., 2023) have become prevalent in recent years. Furthermore, technological progress wields an inescapable aura of uncertainty over both the economic and environmental realms. Apart from the technological advancements, the implementation of policies, enhancements in efficiency, and the expansion of public fiscal outlays also cast a shadow of uncertainty upon the dynamics of macroeconomic functioning (Xiao et al., 2021). However, Integrated Assessment Models (IAMs) and Computable General Equilibrium (CGE) models often presume a deterministic environment, delving solely into the static effects at equilibrium states, which typically disregard uncertainties, thereby rendering them ill-suited to providing a reasoned elucidation of economic phenomena. Therefore, environment policy research based on the dynamic stochastic general equilibrium (DSGE) has surfaced, which relies on representative agents optimizing their utility with intertemporal decisions based on future economic conditions, thus providing some resilience against the Lucas Critique while capturing the economic dynamics (Clift, 2019). The core of our study is to introduce various random shocks and carbon emission reduction policies related to energy technologies into the economy. By incorporating future uncertainty, we aim to simulate dynamic variations in both short-term economic fluctuations and long-term equilibrium.

Typically, DSGE models can be categorized into: the Real Business Cycle (RBC) framework and the New Keynesian (NK) framework, depending on the presence of nominal price rigidities. Angelopoulos et al. (2010) introduced environmental pollution into this framework, conceptualizing it as a byproduct of output and analyzing the welfare implications of environmental policies. For example, Fischer and Springborn (2011) found that emissions intensity reduction targets significantly impact on economic growth more than caps or carbon taxes. Further studies, such as those by Fischer and Heutel (2013) and Lintunen and Vilmi (2021), explored the impacts of policies like carbon taxes and carbon pricing in different economic cycles. The NK framework enhances the RBC model by including market frictions, imperfect competition, and nominal rigidities. It also expands uncertainty shocks beyond technology, such as those from fiscal and monetary policy changes, making it more suited to explain policy impacts in the real-world. Annicchiarico and Di Dio (2015) obtained the optimal environmental policy response to inflation under real and nominal uncertainty by introducing an environmental policy analysis model within the NK-DSGE framework. Furthermore, many studies have affirmed the positive role of fiscal and monetary policies in stabilizing carbon emissions (Chen et al., 2021), but some research has suggested that only fiscal policy can maintain emission levels while increasing household consumption and societal welfare (Chan, 2020). However, these studies assume production sectors to be homogeneous, which overlooks the differences in factor inputs between different production sectors and the heterogeneous impact of different production sectors on the economy and the environment. To explore heterogeneities within the production sector, pioneers represented by Dissou and Karnizova (2016) transformed the single production sector into a multifaceted landscape by subdividing the production sector into energy and non-energy sectors. Their work delved into the impact of heterogeneous production sectors on climate policies and found that the efficacy of climate policies is profoundly contingent upon the technological shocks experienced across various industries. According to the type of energy, Aminu (2018) constructed a DSGE model for oil and gas to explore the effects on energy price shocks. In addition, some studies have subdivided the energy sectors into the fossil fuel sector and the renewable energy sector, and examined the effects of a variety of carbon abatement policies, and analyzed the dynamic mechanism of action between different policy instruments (Argentiero et al., 2018; Xiao et al., 2021). Although previous studies have isolated the energy sector from the broader production landscape, aiming to analyze price dynamics and consumption patterns concerning fossil and renewable energy sources, they fall short of elucidating the profound effects on energy technology innovation on the economy.

In summary, formulating effective emission reduction policies to foster energy technology innovation is crucial to achieving China’s dual carbon goals, whereas the short-term fluctuations and long-term effects of carbon reduction policies that promote energy technology innovation on the macroeconomy remain to be further explored and compared. DSGE, a powerful tool for policy analysis, predominantly characterizes technological progress by simulating exogenous shocks on total factor productivity, while the incorporation of energy technology sector into modeling is still rare, despite the pivotal role of energy technology innovation in mitigating pollutant emissions. Furthermore, the failure of differentiating the heterogeneous effects induced by the energy technology sector and the commodity production sector may lead to an oversight or even misunderstanding of the contribution, substitution, and complementarity of energy technology in the total output. To address these gaps, we constructed a multi-technology sectoral NK-DSGE model to assess and compare the policy effects of the carbon emission cap, the fossil fuel technology subsidy, and the renewable energy technology subsidy. Specifically, the paper aims to make the following contributions.

Initially, extant DSGE models have yet to investigate the influence exerted by the energy technology sector on the broader economic system. Considering the crucial role of energy technology advancements in transitioning to a low-carbon economy, this study integrates sectors representing both fossil fuel and renewable energy technologies into an NK-DSGE framework. This integration aims to elucidate the theoretical mechanisms by which fossil fuel and renewable energy technologies contribute to efforts in carbon emission reduction and the facilitation of economic development.

Secondly, in comparison to policies such as carbon trading and carbon cap, the existing literature presents a relative dearth of research on the short-term and long-term effects brought about by energy technology subsidies. This paper constructs policy scenarios under the operation of the carbon emission permit for both fossil fuel subsidies and renewable energy subsidies. It analyzes the long-term effects of these subsidies on carbon emissions, energy allocation, employment, economic output etc. Additionally, this study introduces stochastic shocks to the intensity of both fossil fuel and renewable energy subsidies to unveil the short-term fluctuations within the macroeconomic environmental system caused by the uncertainty of subsidy intensity.

Finally, the extant literature typically focuses on the effects of an individual emission reduction policy, thereby lacking comparative studies on the heterogeneity of effects across different policies. We further compare the short-term and long-term effects of carbon cap, fossil fuel technology subsidy, and renewable technology subsidy. This comparison aids policymakers in weighing a variety of policy tools, facilitating the formulation of an efficient combination of carbon reduction policies.

The paper is organized as follows: “Methodology” presents the DSGE model; “Scenario setting” outlines the carbon emission reduction policy scenario setting; “Calibration and Bayesian estimation” offers parameters calibration and Bayesian estimation; “Results and discussion” provides the results and discussion of this research; “Policy Implication” provides the policy implications; “Conclusions” presents the conclusions; and “Limitations and future research” presents the limitations and future research.

Methodology

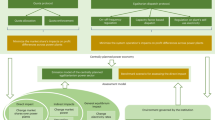
The DSGE model includes six economy sectors: the household sector, the intermediate goods sector, the final goods sector, the fossil fuel technology sector, the renewable energy technology sector, and the government sector. Figure 1 illustrates the basic structure of the DSGE model, where the dashed arrows indicate flows of materials while the solid arrows denote flows of funds. The household sector is the owner of the factors of production, and it supplies labor, capital, and energy to the various production sectors and receives income. Energy technologies produced by the fossil fuel technology sector and the renewable energy technology sector also enter the production process of the intermediate goods sector. The intermediate goods sector produces intermediate goods for supply to the final goods sector. The final goods sector produces final goods, which are supplied to the household sector for consumption, and pays profits to the household sector. The government sector collects revenue through taxes, partly to purchase final products, and partly to transfer payments to the household sector. We also incorporate pollutant emission, energy productivity, and carbon reduction policy components into the DSGE model framework. In this section, we will discuss this framework in detail.

Fig. 1

The framework of the DSGE model.

The most significant difference between this study and previous studies is the introduction of the energy technology sector in the DSGE framework, which is subdivided into the fossil energy technology sector and the renewable energy technology sector. This not only allows us to explore the heterogeneous effects of different energy technologies on economic development and carbon emission reduction, but also to simulate the impacts of carbon emission reduction policies on different energy technologies.

Households

The household sector is postulated to be homogeneous, with ownership of capital (${K}_{t}$), labor (${L}_{t}$), fossil fuel (${M}_{t}^{FF}$), and renewable energy (${M}_{t}^{RE}$). According to Xiao et al. (2018), the representative agent derives positive utility from consumption but negative utility from both labor and energy usage. The goal of the representative household is to maximize its lifetime utility as Eq. (1).

$$\max \ell =\mathop{\sum }\limits_{t=0}^{\infty }{\beta }^{t}\left\{{\mathrm{ln}}\,{C}_{t}-\frac{{L}_{t}^{1+\gamma }}{1+\gamma }-\frac{\chi {({M}_{t}^{RE})}^{1+\upsilon }}{1+\upsilon }-\frac{{[(1-e{r}_{t})\mu {M}_{t}^{FF}]}^{1+\nu}}{1+\nu}\right\}$$

(1)

where $e{r}_{t}$ is the proportion of emission reductions, $0\,< \,\beta \,< \,1$ is the discount factor, $\gamma \ge 0$, $\upsilon \ge 0$ and $\nu \ge 0$ are the inverse of the elasticity of labor supply, renewable energy supply, and fossil fuel supply, $\chi \,> \,0$ is the coefficient of the disutility of the renewable energy, and μ is the emission coefficient. Consequently, the intertemporal budget constraint is expressed in terms of goods as Eq. (2).

$$\begin{array}{c}{P}_{t}{C}_{t}+{P}_{t}{I}_{t}+{P}_{t}{B}_{t}\le (1-{\tau }_{t}^{K}){R}_{t}{K}_{t-1}+(1-{\tau }_{t}^{L}){W}_{t}{L}_{t}+(1-{\tau }_{t}^{FF}){P}_{t}^{FF}{M}_{t}^{FF}\\ +\,{P}_{t}^{RE}{M}_{t}^{RE}+(1+{R}_{t}^{B}){B}_{t-1}+T{r}_{t}\end{array}$$

(2)

The representative household owns the firms, and payments for capital (${R}_{t}$), labor (${W_{t}}$), fossil fuel (${P}_{t}^{FF}$), and renewable energy (${P}_{t}^{RE}$) are received by the representative household from the intermediate goods sector, fossil fuel technology sector, and renewable energy technology sector. And households need to pay a percentage of taxes to the government when it receives payment from capital (${\tau }_{t}^{K}$), labor (${\tau }_{t}^{L}$), and fossil fuel (${\tau }_{t}^{FF}$). In addition, the government pays a lump-sum transfer ($T{r}_{t}$) to the representative household and levies taxes at varying rates on factor incomes. After receiving income and transfer payments, the household allocates these resources towards consumption (${C}_{t}$), investment (${I}_{t}$) and financial activities such as purchasing government bonds (${B}_{t}$), and the household receives interest at bond interest rate (${R}_{t}^{B}$).

According to Dixit and Pindyck (1994), we incorporate Generalized Quadratic (GQ) investment adjustment costs into our model, which are a crucial component of contemporary DSGE models (Smets and Wouters, 2007). At the period t, the representative household holds capital and makes investments. The investment expression is as Eq. (3).

$${K}_{t+1}=(1-{\delta }_{K}){K}_{t}+\left[1-\frac{\vartheta }{2}{\left(\frac{{I}_{t}}{{I}_{t-1}}-1\right)}^{2}\right]{I}_{t}$$

(3)

where ${\delta }_{K}$ donates the capital depreciation rate, $[1-\tfrac{\vartheta }{2}{(\tfrac{{I}_{t}}{{I}_{t-1}}-1)}^{2}]{I}_{t}$ refers to the capital adjustment cost, and $\vartheta$ represents the corresponding capital adjustment cost coefficient.

Enterprises

Energy technology sector

In the DSGE framework, our model separates the production sector into the technology production sector and the good production sector, and further divides energy technology module into fossil fuel technology producers and renewable energy technology producers. Fossil fuel technology innovation will improve the efficiency of fossil fuel burning, thereby reducing carbon emissions, and improving production efficiency. Meanwhile, the innovation of renewable energy technology can reduce its costs, enhance its comparative advantage to a certain extent, and improve the usage of renewable energy by complementary effect to achieve the purpose of optimizing the energy consumption structure. Energy technology is the output of the two energy technology sectors and the production factors of the intermediate goods sector. In our research, we concentrate on one representative enterprise j.

We draw inspiration from Rivera-Batiz and Romer (1991), and establish the production function for the energy technology sector as a Cobb-Douglas production function, encompassing both capital and labor inputs. The representative fossil fuel technology producer donates the capital ${K}_{t}^{FF}$ and the labor ${L}_{t}^{FF}$ to produce fossil fuel technology, the production function of the representative fossil fuel technology producer is as Eq. (4). The objective of the representative fossil fuel technology producer is to maximize its profit as Eq. (5).

$$T{E}_{t}^{FF}(j)={A}_{t}^{T}{[{K}_{t}^{FF}(j)]}^{{\alpha }_{FF}}{[{\eta }_{t}^{L}{L}_{t}^{FF}(j)]}^{1-{\alpha }_{FF}}$$

(4)

$$\max {\varPi }_{t}^{FF}(j)={P}_{t}^{TEFF}(j)T{E}_{t}^{FF}(j)-{W}_{t}{L}_{t}^{FF}(j)-{R}_{t}{K}_{t}^{FF}(j)$$

(5)

where ${P}_{t}^{TEFF}$ is the price of the fossil fuel technology, ${A}_{t}^{T}$ is the energy technology research and development efficiency, and it follows an AR(1) process as Eq. (6).

$$\begin{array}{cc}{\mathrm{ln}}\,{A}_{t}^{T}-\,{\mathrm{ln}}\,{A}^{T}={\rho }_{AT}\,{\mathrm{ln}}\,{A}_{t-1}^{T}-{\rho }_{AT}\,{\mathrm{ln}}\,{A}^{T}+{\varepsilon }_{t,{A}^{T}} & {\varepsilon }_{t,{A}^{T}}\mathop{ \sim }\limits^{i.i.d.}N(0,{\sigma }_{AT}^{2})\end{array}$$

(6)

Similarly, the representative renewable energy technology producer donates the capital ${K}_{t}^{RE}$ and the labor ${L}_{t}^{RE}$ to produce renewable energy technology. The production function of the representative fossil fuel technology producer is as Eq. (7). The objective of the representative renewable energy technology producer is to maximize its profit as Eq. (8).

$$T{E}_{t}^{RE}(j)={A}_{t}^{T}{[{K}_{t}^{RE}(j)]}^{{\alpha }_{RE}}{[{\eta }_{t}^{L}{L}_{t}^{RE}(j)]}^{1-{\alpha }_{RE}}$$

(7)

$$\max {\varPi }_{t}^{RE}(j)={P}_{t}^{TERE}(j)T{E}_{t}^{RE}(j)-{W}_{t}{L}_{t}^{RE}(j)-{R}_{t}{K}_{t}^{RE}(j)$$

(8)

where ${P}_{t}^{TERE}$ represents the price of the renewable energy technology. The energy technologies produced by two energy technology sectors continue to participate in the production chain of intermediate goods as factors of production.

Intermediate goods sector

According to Dixit and Stiglitz (1977), there exists a multitude of final goods producers who operate within a perfectly competitive market and rely on intermediate goods to craft their final goods. These final goods producers employ a production function that consistently exhibits constant returns to scale. In contrast, the intermediate goods producers engage in competition under monopolistic conditions within their respective product markets, with no control over factor prices. This agent employs labor ${L}_{t}^{Y}(j)$, use capital ${K}_{t}^{Y}(j)$, and purchases fossil fuel ${M}_{t}^{FF}(j)$ and renewable energy ${M}_{t}^{RE}(j)$ to manufacture intermediate goods with the Cobb-Douglas technology. The production function of the representative intermediate goods producer is as Eq. (9).

$${Y}_{t}(j)={A}_{t}^{Y}{[{K}_{t}^{Y}(j)]}^{{\alpha }_{Y}}{[{\eta }_{t}^{L}{L}_{t}^{Y}(j)]}^{{\Delta }_{Y}}{[{\eta }_{t}^{FF}{M}_{t}^{FF}(j)]}^{{\sigma }_{Y}}{[{\eta }_{t}^{RE}{M}_{t}^{RE}(j)]}^{1-{\alpha }_{Y}-{\Delta }_{Y}-{\sigma }_{Y}}$$

(9)

where ${A}_{t}^{Y}$ means the total factor productivity (TFP), which represents the level of technology in intermediate goods production. And it also follows the AR(1) process as Eq. (10).

$$\begin{array}{cc}{\mathrm{ln}}\,{A}_{t}^{Y}-\,{\mathrm{ln}}\,{A}^{Y}={\rho }_{{A}^{Y}}\,{\mathrm{ln}}\,{A}_{t-1}^{Y}-{\rho }_{{A}^{Y}}\,{\mathrm{ln}}\,{A}^{Y}+{\varepsilon }_{t,{A}^{Y}} & {\varepsilon }_{t,{A}^{Y}}\mathop{ \sim }\limits^{i.i.d.}N(0,{\sigma }_{{A}^{Y}}^{2})\end{array}$$

(10)

According to Jorgenson (1984), energy efficiency is closely linked to the amount of energy technology input. Therefore, we introduce fossil fuel efficiency ${\eta }_{t}^{FF}$ and renewable energy efficiency ${\eta }_{t}^{RE}$ into the production function. Following “learning by doing” (LBD) proposed by Arrow (1962), we assume that the efficiency of energy inputs is closely related to the energy technology used in production.

$${\eta }_{t}^{FF}={\lambda }_{t}{(T{E}_{t}^{FF})}^{{\omega }_{FF}-1}$$

(11)

$${\eta }_{t}^{RE}={\lambda }_{t}{(T{E}_{t}^{RE})}^{{\omega }_{RE}-1}$$

(12)

where ${\lambda }_{t}$ represents the variable denoting the enhancement of energy technology efficiency throughout the LBD approach. And it adheres the AR(1) process as Eq. (13).

$$\begin{array}{cc}{\mathrm{ln}}\,{\lambda }_{t}-\,{\mathrm{ln}}\,\lambda ={\rho }_{\lambda }\,{\mathrm{ln}}\,{\lambda }_{t-1}-{\rho }_{\lambda }\,{\mathrm{ln}}\,\lambda +{\varepsilon }_{t,\lambda } & {\varepsilon }_{t,\lambda }\mathop{ \sim }\limits^{i.i.d.}N(0,{\sigma }_{\lambda }^{2})\end{array}$$

(13)

Consequently, the production function of the representative intermediate goods producer can be expressed as Eq. (14).

$${Y}_{t}(j)={A}_{t}^{Y}{[{K}_{t}^{Y}(j)]}^{{\alpha }_{Y}}{[{\eta }_{t}^{L}{L}_{t}^{Y}(j)]}^{{\Delta }_{Y}}{[{\lambda }_{t}{(T{E}_{t}^{FF})}^{{\omega }_{FF}-1}{M}_{t}^{FF}(j)]}^{{\sigma }_{Y}}{[{\lambda }_{t}{(T{E}_{t}^{RE})}^{{\omega }_{RE}-1}{M}_{t}^{RE}(j)]}^{1-{\alpha }_{Y}-{\Delta }_{Y}-{\sigma }_{Y}}$$

(14)

The representative intermediate goods enterprise emits pollutants, and μ is the emission coefficient. Under the pressure of environmental regulations and pollutant emission costs, the enterprise makes efforts to reduce emissions, where the emission reduction ratio is denoted as $e{r}_{t}(j)$, whose size depends on the input of fossil fuel technology $T{E}_{t}^{FF}$. Therefore, the emission reduction ratio $e{r}_{t}(j)$, pollutant emissions ${Z}_{t}(j)$ and emission reductions $R{E}_{t}(j)$ can be expressed as follows:

$$e{r}_{t}(j)=\phi \cdot T{E}_{t}^{FF}(j)$$

(15)

$${Z}_{t}(j)=\mu (1-e{r}_{t}(j)){M}_{t}^{FF}(j)$$

(16)

$$R{E}_{t}(j)=\mu \cdot e{r}_{t}(j){M}_{t}^{FF}(j)$$

(17)

According to the research of Nguyen (2023), the connection between emission reductions and the cost associated with those reductions can be approximately expressed as a quadratic function, which is illustrated as Eq. (18).

$$C{E}_{t}(j)={\phi }_{0}+{\phi }_{1}R{E}_{t}(j)+{\phi }_{2}{(R{E}_{t}(j))}^{2}={\phi }_{0}+{\phi }_{1}\mu \cdot e{r}_{t}(j){M}_{t}^{FF}(j)+{\phi }_{2}{\mu }^{2}\cdot {[e{r}_{t}(j)]}^{2}{({M}_{t}^{FF}(j))}^{2}$$

(18)

The labor efficiency coefficient (${\eta }_{t}^{L}$) is closely related to the pollutant stock ($S{T}_{t}$), and according to Xiao et al. (2018) and Heutel (2012), we set the labor efficiency shown as Eq. (19), where ${\eta }_{0}$, ${\eta }_{1}$ and ${\eta }_{2}$ are the damage function parameters. Due to the accumulation process of pollutant stock over time, it is assumed that the pollutant stock of any two periods follows the following relationship shown in Eq. (20), where ${\delta }_{Z}$ represents the depreciation rate of pollutant stock.

$${\eta }_{t}^{L}=1-({\eta }_{0}+{\eta }_{1}S{T}_{t}+{\eta }_{2}S{T}_{t}^{2})$$

(19)

$$S{T}_{t}=(1-{\delta }_{Z})S{T}_{t-1}+{Z}_{t}$$

(20)

The total production cost faced by enterprises, in addition to the cost of capital, labor, energy, and energy technology, also includes the cost of reducing carbon emissions. Therefore, the Lagrange function for maximizing the profits faced by enterprises in the production process can be determined as Eq. (21).

$$\begin{array}{l}\begin{array}{l}\max \mathop{\prod }\limits_{t}^{Y}(j)=\frac{{P}_{t}(j)}{{P}_{t}}{Y}_{t}(j)-\frac{{W}_{t}}{{P}_{t}}{L}_{t}^{Y}(j)-\frac{{R}_{t}}{{P}_{t}}{K}_{t}^{Y}(j)-\frac{{P}_{t}^{FF}}{{P}_{t}}{M}_{t}^{FF}(j)-\frac{{P}_{t}^{RE}}{{P}_{t}}{M}_{t}^{RE}(j)\\ \qquad\qquad\quad-\frac{{P}_{t}^{TEFF}}{{P}_{t}}T{E}_{t}^{FF}-\frac{{P}_{t}^{TERE}}{{P}_{t}}T{E}_{t}^{RE}-\frac{{P}_{t}^{Z}}{{P}_{t}}[\mu (1-e{r}_{t}(j)){M}_{t}^{FF}(j)]-C{E}_{t}(j)\end{array}\\ \begin{array}{ll}s.t. \,{Y}_{t}(j)={A}_{t}^{Y}{[{K}_{t}^{Y}(j)]}^{{\alpha }_{Y}}{[{\eta }_{t}^{L}{L}_{t}^{Y}(j)]}^{{\Delta }_{Y}}{[{\eta }_{t}^{M}{M}_{t}^{FF}(j)]}^{{\sigma }_{Y}}{[{\eta }_{t}^{M}{M}_{t}^{RE}{(j)}_{t}]}^{1-{\alpha }_{Y}-{\Delta }_{Y}-{\sigma }_{Y}}\end{array}\end{array}$$

(21)

To determine price adjustments, we adopt the method of Calvo (1983), positing that intermediate goods firms can only modify their nominal prices in reaction to a stochastic signal. The possibility of such price adjustments occurring in any given period is determined by the parameter $1-\omega$, where $\omega$ signifies the level of price rigidity prevalent in the economy.

$$\mathop{\max }\limits_{{P}_{t}(j)}\varPhi ={E}_{t}\mathop{\sum }\limits_{i=0}^{\infty }{(\beta \omega )}^{i}\frac{U^{\prime} ({C}_{t+i})}{U^{\prime} ({C}_{t})}{Y}_{t+i}\left[\frac{{P}_{t}(j)}{{P}_{t+i}}{\left(\frac{{P}_{t+i}}{{P}_{t}(j)}\right)}^{\phi }-M{C}_{t+i}{\left(\frac{{P}_{t+i}}{{P}_{t}(j)}\right)}^{\phi }\right]$$

(22)

Final goods sector

The representative final goods producer uses ${Y}_{t}(j)$ units of each intermediate good $j\in [0,1]$ to manufacture the final good ${Y}_{t}$, following Dixit and Stiglitz (1977) assumption of constant returns to scale, competitive firms produce ${Y}_{t}$ using a Constant Elasticity of Substitution (CES) technology, where $\varphi\, >\, 1$ denotes the elasticity of substitution between intermediate goods.

$${Y}_{t}={\left[{\int }_{0}^{1}{Y}_{t}{(j)}^{\frac{\varphi -1}{\varphi }}dj\right]}^{\frac{\varphi }{\varphi -1}}$$

(23)

The representative final goods producer seeks to maximize profitability by determining ${Y}_{t}(j)$ and ${Y}_{t}$, as expressed by Eq. (24).

$$\mathop{\max }\limits_{{Y}_{t}(j)}{P}_{t}{\left[{\int }_{0}^{1}{Y}_{t}{(j)}^{\frac{\varphi -1}{\varphi }}dj\right]}^{\frac{\varphi }{\varphi -1}}-{\int }_{0}^{1}{Y}_{t}(j){P}_{t}(j)dj$$

(24)

where ${P}_{t}$ represents the price of the final good, and ${P}_{t}(j)$ represents the price of the intermediate good $j$. The first-order condition generates the demand function for the intermediate goods are shown in Eq. (25) and Eq. (26), and we can clearly see that the price of final goods ${P}_{t}$ is also a reflection of the price level.

$${Y}_{t}(j)={\left(\frac{{P}_{t}(j)}{{P}_{t}}\right)}^{-\varphi }{Y}_{t}$$

(25)

$${P}_{t}={\left[{\int }_{0}^{1}{P}_{t}{(j)}^{1-\varphi }dj\right]}^{\frac{1}{1-\varphi }}$$

(26)

Government

The financing of public consumption ${G}_{t}$ comes from the taxes of labor, capital and fossil fuel, as well as the fees charged for pollutant emission permits. And the government adjusts lump-sum transfers $T{r}_{t}$ in a passive manner to ensure budget equilibrium in each period. So, the government budget constraint can be represented as Eq. (27).

$${P}_{t}{G}_{t}+(1+{R}_{t-1}^{B}){B}_{t-1}+T{r}_{t}\le {\tau }_{t}^{L}{W}_{t}{L}_{t}+{\tau }_{t}^{K}{R}_{t}{K}_{t}+{\tau }_{t}^{M}{P}_{t}^{FF}{M}_{t}^{FF}+{P}_{t}^{Z}{Z}_{t}+{B}_{t}$$

(27)

Aggregation and market clearing

Following Calvo (1983), we define the price dispersion as given in Eq. (28), and the production function can be written as Eq. (29).

$${V}_{t}=(1-\psi ){\left(\frac{{P}_{t}^{\ast }}{{P}_{t}}\right)}^{-\varphi }+\psi {\left(\frac{{P}_{t}}{{P}_{t-1}}\right)}^{\varphi }{V}_{t-1}$$

(28)

$${Y}_{t}={A}_{t}^{Y}{({K}_{t}^{Y})}^{{\alpha }_{Y}}{({\eta }_{t}^{L}{L}_{t}^{Y})}^{{\Delta }_{Y}}{({\eta }_{t}^{M}{M}_{t}^{FF})}^{{\sigma }_{Y}}{({\eta }_{t}^{M}{M}_{t}^{RE})}^{1-{\alpha }_{Y}-{\Delta }_{Y}-{\sigma }_{Y}}{({V}_{t})}^{-1}$$

(29)

To characterize the long-term equilibrium of the model, this study assumes that the commodity market in the model system is in long-term equilibrium, the market-clearing condition is defined as Eq. (30).

$${Y}_{t}={C}_{t}+{I}_{t}+{G}_{t}+C{E}_{t}$$

(30)

Scenario setting

We set up four policy scenarios summarized in Table 1. To accelerate the realization of carbon emission reduction, governments often prefer to implement policy tools from multiple dimensions (Rosenbloom et al., 2020). The restrictive policy represented by the carbon emission cap policy is often recommended by senior scholars and widely used worldwide (Hua et al., 2011). At the same time, the government also attempt a series of incentive programs to promote the low-carbon economy, subsidy policy is a representative policy because it can achieve carbon emission reduction and control by incentivizing enterprises to increase energy efficiency, optimize energy consumption mix, and carry out technological innovation (Y. He et al., 2023b). However, there is no research to compare the effect of subsidies for fossil energy technology and renewable energy technology. Therefore, we set up the fossil fuel technology subsidy policy scenario and the renewable energy technology subsidy policy scenario, and attempt to compare the economic and environmental effects of these policies.

Table 1 The scenarios.

Calibration and Bayesian estimation

The calibration method is used to determine some parameters based on a combination of existing research and related statistical data in this study. Meanwhile, Bayesian estimation is employed to determine the remaining parameters using quarterly data from China, which enables the DSGE model constructed in this paper to better simulate the practice in China.

Parameters calibration

We have calibrated most of the structural parameters based on the research of Heutel (2012), Annicchiarico and Di Dio (2015), Xiao et al. (2018), and summarized in Table 2. We have calibrated the values for parameters aligning with the actual socio-economic situation in China. For example, the discount factor β reflects the individual’s attitude towards future risks and uncertainties, as well as their preferences for current consumption and investment. Drawing upon existing research, this parameter typically ranges between 0.95 and 0.99. In this study, a value of 0.97 is chosen to mirror the relatively optimistic outlook and emphasis on the future among Chinese residents. The depreciation rate of capital δ_K is set at 0.025 in this paper, a value for which scholars have largely reached a consensus, reflecting alignment with the practical condition in China. The emissions per unit of energy μ is set at 0.6, and it aligns with the current technological proficiency and efficiency levels in the utilization of fossil fuels across various sectors with China’s economy. We assume the output elasticity of capital α_Y and labor Δ_Y is 0.33 and 0.5, which aligns with China’s labor-intensive characteristics. Besides, since capital input is crucial in determining energy structure in China, we set the capital elasticity for the fossil fuel technology sector α_FF and the renewable energy technology sector α_RE to 0.33 and 0.36, respectively.

Table 2 Calibrated parameters.

Bayesian estimation for shocks

To examine the endurance of exogenous shocks, we utilized the Bayesian estimation approach to evaluate the persistence of the AR(1) process. According to Smets and Wouters (2007), and Traum and Yang (2010), we assumed that the prior distributions of the parameters associated with the AR(1) processes (${\rho }_{{A}^{Y}}$, ${\rho }_{G}$, ${\rho }_{{A}^{T}}$, ${\rho }_{\lambda}$, ${\rho }_{\kappa }$, ${\rho }_{{s}^{FF}}$, ${\rho }_{{s}^{RE}}$) followed a beta distribution.

This study endeavors to illuminate the distinct characteristics of four distinct exogenous economic shocks: the total factor productivity (TFP) shock (${A}_{t}^{Y}$), the government expenditure shock (${G}_{t}$), the energy efficiency shock (${\lambda }_{t}$), and the energy technology research productivity shock (${A}_{t}^{T}$). First, the TFP shock represents the changes in efficiency in commodity production, which consequently influences carbon emissions and economic development. Second, government expenditure plays an essential role in reducing carbon emissions; for instance, the government can reduce carbon emissions by investing in green infrastructure. Third, energy efficiency reduces the intensity of energy inputs per unit of output, thereby reducing carbon emissions. Finally, the increase in energy technology research efficiency means that new fossil and renewable energy technologies can be developed more quickly with the same level of resource input, and the widespread adoption of these technologies will reduce reliance on traditional high-carbon energy sources. In conclusion, by simulating the four aforementioned exogenous economic shocks, we can better assess the significance of government support and incentives for technological innovation in achieving carbon reduction goals and promoting sustainable development.

In addition, this study also explores the effects of three carbon emission reduction policy shocks, namely carbon emission cap shock (${\kappa }_{t}$), fossil fuel technology subsidy shock (${s}_{t}^{FF}$), and renewable energy technology subsidy shock (${s}_{t}^{RE}$). By conducting Bayesian estimations of carbon emission reduction policy variables, it is possible to simulate how implementing these policies affects carbon emissions and macroeconomic fluctuations. This aids in evaluating the effectiveness of carbon emission reduction policies and, consequently, leading to better planning and adjusting these policies.

Data source

We employ quarterly data from 2000Q1 to 2020Q4 in China to estimate parameters, using observable variables such as total output (${Y}_{t}$), government expenditure (${G}_{t}$), fossil fuel technology ($T{E}_{t}^{FF}$) and renewable energy technology ($T{E}_{t}^{RE}$). Specifically, quarterly GDP data are obtained from the National Bureau of Statistics of the People’s Republic of China (NBS), while quarterly government expenditure data are collected from the Ministry of Finance of the People’s Republic of China. In addition, we conducted a patent search using the latest CPC patent classification system jointly administered by the European Patent Office (EPO) and the United States Patent and Trademark Office (USPTO). We utilized the Incopat patent search system to extract patent data related to Chinese energy technologies in the “Y02E” subclass.

We process the observed variables to align them with the variables in the model, following these steps: First of all, we deseasonalized the variables using the Census X12 technique. Secondly, we applied a logarithmic transformation to the observed variables. Lastly, we utilized the Hodrick-Prescott (HP) filter to remove the trend from the variables, extracting their volatile components.

Bayesian estimation

Table 3 shows the beta distributions for the persistence of AR(1) processes in relation to exogenous economic shocks and carbon emission reduction policy shocks. The exogenous economic shocks include the TFP shock of goods production, government expenditure shock, energy technology productivity shock, and energy efficiency shock. According to Annicchiarico and Di Dio (2015), and Xiao et al. (2018), the standard deviation for all processes associated with exogenous economic shock was 0.0045, while the means were 0.92, 0.92, 0.8, and 0.5, respectively.

Table 3 The Bayesian estimation results of the baseline scenario.

In addition, we exert a one-unit positive effect on variables ${\kappa }_{t}$, ${s}_{t}^{FF}$ and ${s}_{t}^{RE}$ to simulate the impact of carbon emissions cap shock, fossil fuel technology subsidy shock, and renewable energy technology subsidy shock, which means that the government will relax the total carbon emission target, and will increase the subsidies for fossil fuel technology and renewable energy technology. Similarly, we set the standard deviation for all processes associated with carbon emission reduction policy shocks at 0.0045, while the means were 0.08.

Then, a random walk Metropolis-Hastings (MH) algorithm is subsequently used to draw 300,000 samples from the posterior distribution, while the Markov chain Monte Carlo algorithm is utilized for estimating the distribution. The results of Bayesian estimation show that different types of shocks exhibit different persistence and long-term impacts across economic sectors. The TFP and government expenditure shocks are the most persistent, the energy technology shocks are the second most persistent, and the energy efficiency shock is the shortest of all shocks.

As shown in Fig. 2, it becomes apparent that the length of total sequence interval and mean length of the within sequence intervals of all parameters coincide and converge. Consequently, the Bayesian estimation results have high accuracy.

Fig. 2

The result of multivariate convergence diagnostic.

Results and discussion

Steady state

To facilitate a comprehensive comparison among the three distinct carbon emission reduction policies, following the methodology established by Xiao et al. (2018), we endeavored to align exogenous variables, thereby ensuring uniform levels of total output ${Y}_{t}$ across these three scenarios. This meticulous approach enables to scrutinize not only economic metrics but also the abatement effects when the three policies converge at an equivalent stage of economic advancement. Table 4 illustrates the equilibrium values of key variables within each scenario. Since FTS and RTS scenarios differ only in the energy technology sectors subsidized by the government, the steady-state values for most variables are essentially the same in both scenarios.

Table 4 Long term steady state values of the main variables.

Implementing carbon emission reduction policies negatively impacts consumption, which decreased by 15.04% in the CEC scenario and 19.8% in the FTS and RTS scenarios. Under the CEC scenario, several vital production factors, including labor, capital, and renewable energy inputs, exhibit a noteworthy ascent. Specifically, labor escalates by 8.55%, capital by 9.55%, and renewable energy inputs surge by a substantial 17.69%. In the context of the FTS and RTS scenarios, these factors undergo even more pronounced augmentations, with labor experiencing a rise of 11.73%, capital expanding by 10.78%, and renewable energy inputs soaring impressively by 23.02%. This amplified infusion of production factors consequently begets an uptick in total societal output, registering a substantial 4.99% increase within the carbon emission reduction policy scenarios.

It is evident that the implementation of policies has a salutary impact on the enhancement of environmental quality. Indeed, a marked reduction in pollutant emissions and pollutant stockpiles emerges as a conspicuous outcome across all three environmental policy scenarios when juxtaposed with the reference scenario of BAU. The pollutant emissions decreased by 27.84% under the CEC scenario and by 33.45% under the FTS and RTS scenarios, which shows that the emission reduction effect brought by the subsidy policy is better than that of the carbon emission cap policy. In addition, it can be calculated that the carbon intensity (Z_t/Y_t) is 0.648 in the BAU scenario, 0.445 in the CEC scenario, and 0.411 in the FTS and RTS scenarios, which represents a decrease of 31.26% and 36.61% compared to the BAU scenario.

In the CEC scenario, the government sets a target for total emissions, which will constrain firm’s production activities through coercive and commanding means. Obviously, both pollutant emissions and pollutant stocks will be reduced. The government’s imposition of charges for pollutant will serve as a compelling incentive, driving firms to substantially reduce the input of fossil fuel. Consequently, this dynamic is poised to engender a notable shift towards renewable energy utilization. And renewable energy related indicators such as renewable energy demand, renewable energy efficiency, and renewable energy technology demand have shown significant growth, with increases of 17.69%, 28.65%, and 24.83% compared with the BAU scenario, which suggests that the carbon emission cap policy promotes the development and application of renewable energy.

In the FTS and RTS scenarios, when the government implements an energy technology subsidy policy, it positively affects the production activities of companies due to the reduction of their production and operation costs. Subsidies, as a non-reimbursable transfer, follow the subsidy transfer and price transmission mechanism and will be transferred downstream through a cost-push process, and the wage level will rise by 0.12%, which also results in higher household disposable income, driving households’ investment and capital stock up by 10.78% while the level of capital interest rate remains unchanged. In the FTS scenario, subsidies have a crowding-out effect on capital factor inputs in the fossil energy technology sector, replacing firms’ own capital inputs and leading to a 4.45% decline in capital inputs in the fossil energy technology sector. In the RTS scenario, the introduction of renewable energy technology subsidy policies has driven significant growth in demand for renewable energy, renewable energy efficiency, and renewable energy technology, with increases of 23.02%, 40.26%, and 34.69% compared with the BAU scenario, suggesting that renewable energy technology subsidy policies stimulate the development of renewable energy. Additionally, the subsidy intensity is 0.0475 for fossil energy technologies and 0.05 for renewable energy technologies to achieve the same environmental and economic effects, which shows that the government subsidy intensity for fossil energy technologies is lower than that for renewable energy technologies to reach the same output level. As highlighted by Lin and Jiang (2011), China, as a developing country, still heavily relies on fossil energy, where subsidies prove to be more cost-effective. However, for the purpose of enhancing energy efficiency and optimizing the energy mix, it is imperative to shift the focus of subsidy policies towards renewable energy technologies.

Exogenous shocks

The above analysis revolves around the long-run deterministic steady state under each scenario, ignoring the potential impact of various short-term uncertainty on economic fluctuations. In this part, we examine how different exogenous stochastic shocks affect the macroeconomy and environment, comparing the responses of pivotal economic and environmental variables to these exogenous shocks within various carbon emission reduction policies.

Total factor productivity (TFP) shock

The impact of TFP shock in the commodity production sector is simulated by imposing a one-unit positive impact of ${A}_{t}^{Y}$. Figure 3 represents the results for four scenarios of total factor productivity uncertainty production: BAU, CEC, FTS, and RTS. The percentage deviations of each impulse response from the variables’ steady-state over 100 quarters are presented.

Fig. 3

Economic responses to the TFP shock.

When the economy is exposed to a positive TFP shock, many of the variables such as ${Y}_{t}$, ${C}_{t}$, ${I}_{t}$ and ${K}_{t}$ will positively deviate from the steady state values in all four scenarios, indicating that the expansion of production by firms and the increase in demand for various factors of production have a positive impact on the level of the economy and social consumption. In period 0, the output rises by about 1.33% in the BAU scenario, 1.25% in the CEC scenario, and 1.14% and 1.18% in the FTS and RTS scenarios, which shows that total factor productivity shocks cause the most pronounced fluctuations in output in the BAU scenario.

In response to the TFP shock, the investment rises in period 0, leading to increased capital stock. The capital stock follows a hump-shaped dynamic, where a substantial rise will gradually drive social capital accumulation until about the 17th period. Over time, investment growth will decelerate and arrive at an inflection point when capital depreciation outpaces capital expansion. This explains why the capital stock initially increases, then gradually declines approaching a steady state value. Furthermore, after the onset of the shock, the demand for the two energy technologies in business production shows opposite movements. In period 0, the need for renewable energy technologies is deviating from the steady state value in the negative direction, while fossil fuel technologies are deviating from the steady state value in the positive direction. This is due to the fact that the fossil fuel still dominates the energy consumption mix, and firms realize that using more fossil fuel technologies can rapidly increase the efficiency of fossil fuel use and maintain the continuity and stability of production using fossil energy (Semmler et al., 2022). Because of the substitution effect between energy technologies, companies will correspondingly reduce the demand for renewable energy technologies.

Additionally, there are variations in the responses of variables to the shocks across the four scenarios. First, the impact of the TFP shock is lower in the FTS and RTS scenarios than in the CEC scenarios, such as ${Y}_{t}$, ${I}_{t}$ and ${C}_{t}$. This is because the carbon emission cap policy, being a restrictive measure, is coupled with the carbon trading system arrangement. This system furnishes firms with clear economic incentives and market signals by acquiring carbon emission permits. Consequently, the changes in economic variables under the CEC scenario will be more pronounced than market-based policies such as subsidies. Second, there are significant differences in the effects of the four scenarios on pollutant emissions. Because of the government has set pollutant emission objectives, pollutant emissions in the CEC scenario will stay in a steady state and not react to TFP shocks. In addition, in period 0, the positive TFP shock will result in more pollutant emissions in BAU, FTS, and RTS scenarios, which is the negative effect of economic expansion in the short term.

Government expenditure shock

The macroeconomy can also be uncertainly impacted by fiscal policies, and we simulate the impact of government fiscal spending shocks on the economy by imposing a one-unit positive impact on the variable ${G}_{t}$. The results of government fiscal spending shocks are shown in Fig. 4. Similar to the TFP shock, variables in the CEC scenario exhibit more pronounced responses to the government expenditure shock compared to the BAU, FTS, and RTS scenarios.

Fig. 4

Economic responses to the government expenditure shock.

Increased government expenditure can stimulate economic activity. Under the expansionary fiscal policy, the total output in all four scenarios will rise in period 0. However, while bringing economic growth, it will have a “negative substitution effect” on investment, triggering a decrease in investment, and capital accumulation will be negatively affected, with both investment and capital stock declining. The government’s augmentation of public expenditure often aligns with considerations of environmental preservation and sustainable development. This translates to an increased fiscal baking for renewable energy technologies, concurrently fostering a transformation in energy consumption patterns. This transformation entails a reduction in the share of fossil fuels within the energy consumption spectrum, thereby mitigating greenhouse gas emissions and catalyzing a shift toward a low-carbon economy. In all four scenarios, the need for renewable energy technologies is anticipated to rise, while the demand for fossil energy technologies is expected to decline.

Except for the CEC scenario, where pollutant emissions remain constant, pollutant emissions in BAU, FTS, and RTS scenarios tend to increase with economic expansion, similar to the response observed with the TFP shock. Furthermore, the BAU scenario shows a more significant reaction of pollutant emissions to the shock compared to the FTS and RTS scenarios, indicating that the energy technology subsidy policies play a role in stabilizing pollutant emissions to some extent. Harting (2021) found that subsidy policies play a role in smoothing the economic cycle, and we found that the smoothing effect of subsidy policies plays out mainly in terms of pollutant emissions.

Energy technology research productivity shock

The impact of the energy technology research productivity shock is simulated by imposing a positive one-unit effect on the variable ${A}_{t}^{T}$. The results of government fiscal spending shocks are shown in Fig. 5.

Fig. 5

Economic responses to the energy technology research productivity shock.

The energy technology research productivity shock is obviously different from other shocks. The enhancement of energy technology research productivity results in increased marginal output in energy technology sectors. In contrast to the positive impact on total output observed by Xiao et al. (2021) due to the positive energy productivity shock, in our study, the positive energy technology research productivity has led to a decline in total output. This ensues because the shock can prompt resource reallocation, with production factors flowing from the intermediate goods sector to the energy technology sector. Such factor flows restrict output in the intermediate goods sector. The fall of output also has a negative impact on the demand for capital and labor.

In the four scenarios, the impact of the energy technology research productivity shock in period 0 leads to an upsurge in the demand for renewable energy technologies. This phenomenon arises from the progress in energy technology innovation efficiency, which triggers a reduction in the prices of renewable energy technologies, thus promoting enterprises to enhance their utilization of renewable technologies due to cost-effectiveness. However, in the initial stages of the shock occurrence, there is a transient increase in the demand for fossil fuel technology. This anomaly is attributed to the prevailing dominance of fossil energy in the energy consumption mix at the time of the shock. The complementary effects come into play, driving a corresponding initial increase in the demand for fossil energy technologies. Subsequently, the demand for fossil energy technologies consistently deviates from its steady-state value in a negative direction. This indicates that as the comparative advantage of renewable energy technologies strengthens, environmental consciousness gradually takes root within enterprises. Consequently, owing to substitution effects, the demand for fossil energy technologies diminishes over time.

Analyzing the impulse responses of pollutant emissions in the four scenarios reveals that, except for the CEC scenario where pollutant emissions stay constant, the pollutant emission levels in the other scenarios deviate from the steady state value in a negative direction, that is, after the energy technology research productivity shock, the pollutant emissions have decreased to a certain extent. Therefore, technology innovation plays an important role in curbing pollutant emissions, aligning with the findings suggested by Fernández et al. (2022). The rebound effect in carbon emissions, as mentioned in the study by Yang and Li (2017), does not appear to be significant. This is because as the concept of low-carbon development takes root, advances in energy technologies have not boosted large-scale growth in fossil fuels but promoted renewable energy to replace some high-carbon energy. Moreover, the process in energy technologies has also improved energy efficiency levels, reducing emissions caused by per unit consumption of fossil fuels.

Energy efficiency shock

We model the economic impact of the energy efficiency shock by imposing a one-unit positive effect on the variable ${\lambda }_{t}$. The results of the energy efficiency shock are shown in Fig. 6.

Fig. 6

Economic responses to the energy efficiency shock.

Augmented energy efficiency bolsters the economies of scale for the Cobb-Douglas production function in the intermediate goods sector. Evidently, positive energy efficiency shocks promote macroeconomic growth, with total output rising to 2.06% in the BAU scenario before gradually reverting toward the steady state value. As the economy balloons, vital economic variables exhibit positive expansion, including consumption, investment, capital stock, and labor. Based on the LBD approach, we posit that energy efficiency increases with the increased use of fossil fuel technologies. Consequently, ensuring a favorable shock to energy efficiency, rational firms’ demand for fossil energy technologies proliferates as a means to amplify production and enhance production efficiency. Similar to the TPF shock, the demand for fossil fuel technologies appears to ascend after the shock, attaining its apex around period 4. At this time, the competitiveness of renewable energy technologies is weak compared with fossil fuel technologies, and both energy technologies are used as factors of production for commodity-producing enterprises. The substitution effect makes enterprises expand the demand for fossil fuel technologies and suppress the demand for renewable energy technologies accordingly, so the demand for renewable energy technologies deviates from the steady state value in the negative direction in period 0.

For pollutant emissions, except for the CEC scenario where the government declares a fixed target for pollutant emissions and pollutant emissions keep unchanged, similar to the TFP shock, energy efficiency shocks contribute to higher levels of pollutant emissions in the CEC, FTS, and RTS scenarios while promoting economic expansion.

Carbon emission reduction policy shock

The effects of three carbon emission reduction policy shocks on ${Y}_{t}$, ${C}_{t}$, ${K}_{t}$, and ${Z}_{t}$ are shown in Fig. 7. Under the impact of the carbon emissions cap shock, the government will relax the emission cap target, so the total output, total consumption, and capital stock will respond positively. However, due to the reduction of environmental standards, pollutant emissions will also increase. Therefore, it can be concluded that pollutant emissions are pro-cyclical under the carbon emissions cap policy.

Fig. 7

Economic responses to the carbon emission cap shock, the fossil fuel technology subsidy shock and renewable energy technology subsidy shock.

Under the impact of the fossil fuel technology subsidy policy shock and the renewable energy technology subsidy policy shock, the government will increase subsidies to support energy technology innovation, and the total output, total consumption, and capital stock will also have a positive reflection. Heutel (2012) and Lintunen and Vilmi (2021) argued that carbon emissions are pro-cyclical under most environmental policies and that only optimal environmental policies can reduce the pro-cyclicality of carbon emissions to a certain extent. However, we can find that under the shocks of the fossil fuel technology subsidy policy and the renewable energy technology subsidy policy, pollutant emissions show a downward trend. This is because fossil fuel technology progress contributes to increased emission reduction rates, and developments in renewable energy technologies increase the use of renewable energy. Reduced pollution levels have been achieved in parallel with advances in the level of economic development.

In addition, the variables respond more sharply to shocks under the carbon emissions cap shock than the fossil fuel technology subsidy shock and the renewable energy technology subsidy shock. This is also consistent with our previous results that the economic variables respond more sharply to shocks under the CEC scenario. Unlike the view held by Annicchiarico and Di Dio (2015) that the carbon emission cap policy has a lease impact on economic fluctuations, energy technology subsidy policies exhibit a superior capacity to restrain economic volatility compared to the carbon emission cap policy. Thus, the magnitude of macroeconomic fluctuations is more moderate when governments subsidize fossil and renewable energy technologies than when they impose a cap on carbon emissions.

Policy implication

Policy makers need to contemplate a variety of policy instruments, including joint carbon trading, carbon cap, and subsidies for energy technology, to harness synergistic effects that efficiently promote carbon emission reduction and economic transformation. In pursuit of the goal to peak carbon emissions by 2030, China has preliminarily established a carbon trading market. Consequently, in our model, the imposition of emission permits on enterprises by the government is considered a manifestation of the carbon trading mechanism. Currently, China’s carbon trading market is in its nascent stage, with only the electricity sector incorporated into the national carbon trading market. The trading activity remains relatively low, failing to fully demonstrate the potential effects of the carbon trading market on the environment and economy. In contrast, carbon trading markets in places like the United States, the European Union, and Japan operate more maturely. In particular, the European Union Emission Trading System (EU ETS), is not only the largest in scale globally but also wields significant influence, effectively promoting the reduction of greenhouse gas emissions (Liu et al., 2022). On top of implementing carbon trading and carbon cap, the EU has also launched policies to support energy technology innovation. For instance, the “Horizon Europe” project has injected substantial subsidy funds into the energy technology sector, covering a wide range of key technologies from enhancing energy efficiency to decarbonizing fossil fuels (Baena-Moreno et al., 2020; Gowd et al., 2023). These energy technology subsidies essentially reduce the adoption costs of low-carbon technologies, and simultaneously enhance enterprises’ purchasing power in the carbon market, which is conducive to invigorating the carbon trading market. The synergy between energy technology subsidies and the EU ETS has effectively driven carbon emissions reduction. This is consistent with the core conclusion of this study that it is imperative to combine carbon cap and energy technology subsidy policies. On the one hand, setting clear emission reduction targets through carbon cap, and on the other, incentivizing enterprises to pursue low-carbon technological innovation via energy technology subsidies, bidirectionally stimulate the trading in the carbon market. Subsidies for energy technology supported by the project of “Horizon Europe” have not only achieved remarkable carbon emission reduction, but also favorably contributed to stimulating consumption, attracting investment, and creating jobs, thereby enhancing the EU’s innovation capacity and economic competitiveness. The promotional effect of energy technology subsidies on the macroeconomy, while achieving carbon emission reductions, is also corroborated in this study. Under the policy scenarios of subsidies for renewable and fossil energy technologies in this research, a reduction in carbon emissions was accompanied by an increase in capital stock and total output.

In addition to considering the synergistic effects among carbon reduction policies, decision-makers should also accurately recognize the short-term dynamics and long-term effects that emission reduction policies have on the environmental economic system, to effectively formulate phased policies by weighing the short-term and long-term effects. In the short term, our finding reveals that carbon cap may lead to a short-term increase in carbon emissions. When enterprises anticipate the stricter carbon emission restrictions implemented in the future, they might increase production or engage in carbon-intensive activities before the policy is enacted to avoid future high costs or constraints. Combining with the carbon trading mechanism considered in the model, if carbon price is lower than expected, enterprises might opt to purchase more carbon emission rights, which could also result in an increase in carbon emissions in the short term under the carbon cap scenario. In contrast to the carbon cap scenario, which may lead to an increase in carbon emissions in the short term, both types of energy technology subsidies have immediate effects on reducing carbon emissions. Compared to the respective impacts of two subsidy regimes, financial support for fossil energy technologies is more adept at facilitating immediate reductions in carbon emissions. This effectiveness is largely due to the prevailing dominance of fossil fuels within China’s energy structure, where subsidies directed towards fossil energy technologies can lead to swift and efficient emission mitigations. Conversely, subsidies allocated to renewable energy technologies not only contribute to emission reductions but also possess a superior capacity to stimulate short-term economic expansion. The advancement in renewable energy technologies catalyzes the development of sectors such as photovoltaic, wind power, and energy storage, alongside bolstering the construction of pertinent infrastructure. This dynamic engenders an increase in employment opportunities and invigorates investment inflows in the short term, culminating in a stimulative impact on economic growth (Bilgili et al., 2015). In the long term, reliance solely on carbon cap policy yields restricted emission mitigation outcomes. On the other hand, subsidization of both fossil fuel technologies and renewable energy technologies manifests superior emission reduction efficacies in the long term. Consequently, it becomes essential to concurrently implement energy technology subsidies alongside the carbon cap to facilitate the low-carbon transition in the long term.

As delineated in preceding discussions, the subsidization of both fossil fuel and renewable energy technologies is deemed essential, encompassing both short-term and long-term considerations. Acknowledging the unique benefits that subsidies for fossil fuel technologies and renewable energy technologies present in facilitating carbon emission reductions and stimulating economic growth, the formulation of a judiciously phased subsidy policy for energy technologies emerges as a paramount concern. Initially, the government must prioritize ensuring subsidies for fossil fuel technologies, recognizing that, against the backdrop of China’s existing energy structure, stimulating the advancement of these technologies serves as the most efficacious strategy for mitigating carbon emissions in the short term. Simultaneously, it is essential for the government to actively encourage technological innovation and augment the efficiency of research and development activities. The outcomes presented in this paper underscore the significance of enhancing energy technology research productivity as a catalyst for the proliferation of renewable energy technologies, thereby laying the foundational groundwork for a seamless transition towards sectors aligned with renewable energy. Secondly, the government needs to incrementally increase subsidies for renewable energy technologies, gradually shifting the focus of subsidies from fossil fuel technologies to renewable energy technologies. This approach is warranted by the findings of this paper, which suggest that subsidizing renewable energy technologies not only facilitates emission reductions but also more effectively promotes economic growth. Concurrently, the government should establish transition funds to support traditional energy enterprises venturing into the realm of renewable energy technologies. Furthermore, it is essential for the government to amplify its investment in renewable energy infrastructure, facilitating the market-based application and expansive growth of renewable energy technologies. This strategy is crucial for unleashing the full spectrum of economic and environmental benefits associated with the advancement of renewable energy technologies.

It is noteworthy that external factors, such as international trade, also exert an influence on the efficacy of China’s carbon emission reduction policies. The European Union has initiated the implementation of carbon tariff, a move that undeniably escalates the operational costs for Chinese export enterprises (Yang and Yan, 2023). Against this backdrop, it becomes imperative for the government to enhance subsidies for energy technologies, enabling these subsidies to serve as an endogenous motivation for enterprises to reduce emissions. This approach, in turn, could mitigate the impediments to international trade brought about by the carbon tariff, and assist enterprises in maintaining their competitiveness within the global trading arena. Moreover, enhancement of overall innovation capacity is pivotal to carbon emission reduction. According to the results of this study, enhancements in the efficiency of energy technology R&D can effectively propel the development of renewable energy technologies. This, in turn, is conducive to driving the growth of industries related to renewable energy, achieving a transformation in energy structure. Beyond international trade and technological progression, this paper reveals that an increase in government public expenditure can enhance public investment, elevate overall economic output, and also play a role in promoting the development of renewable energy technologies. Therefore, the combination of energy technology subsidies with an increase in government public expenditure can effectively promote the development of renewable energy technologies, enhance the innovation capabilities, and bolster competitiveness in global market.

Delving into the interaction between carbon emission reduction policies and other economic and environmental policies will constitute a crucial step towards refining the policy framework. China’s goal to double per capita GDP by the year of 2035, necessitates sustaining a high trajectory of economic growth. This imperative invariably escalates the challenges associated with enforcing carbon reduction measures. Hence, to balance the relationship between economic growth and carbon emission reduction, the implementation of energy technology subsidy policies becomes particularly significant, especially subsidies for renewable energy technologies. Additionally, China’s energy technology subsidy policies can be effectively integrated with the product subsidies for renewable energy related industries. For instance, the subsidy for new energy vehicles essentially serves as incentives for downstream low-carbon products, which in turn, catalyze technological innovation at the upstream of the supply chain, thereby engendering a synergistic policy effect. On the environmental policy front, there is a pronounced synergistic relationship between pollution reduction and carbon mitigation efforts. Prevailing studies affirm that targets of numerous pollution abatement policies are often significant sources of carbon emissions as well. Consequently, the deployment of policies aimed at pollution control can inadvertently foster reductions in carbon emissions. The total carbon control and energy technology subsidy policies under investigation in this discourse have the potential to facilitate pollution abatement concurrently with carbon emission reductions, thus achieving dual objectives of environmental preservation.

Conclusions

This research constructed a multi-technology sectoral dynamic stochastic general equilibrium model by integrating the fossil fuel technology sector and the renewable energy technology sector. We simulated the impact of energy technology innovations on macroeconomic fluctuations and assessed the policy effects of the carbon emission cap policy, the fossil fuel technology subsidy policy, and the renewable energy technology subsidy policy.

The findings of this article suggest that implementing carbon emission reduction policies can achieve long-term reductions in carbon emissions and improvements in total output. However, the carbon emission cap policy is not as effective as the other two policies in reducing carbon emissions. Additionally, to achieve the same emission reduction goal, the government needs to allocate more subsidies to renewable energy technologies than fossil fuel technologies.

In the short term, the implementation of total carbon control policies may lead to a simultaneous increase in carbon emissions and total output. However, the adoption of energy technology subsidy policies can result in an immediate reduction of carbon emissions, while macroeconomic variables such as total output and consumption experience growth. Contrastingly, subsidies directed towards fossil energy technologies are more efficacious in advancing carbon reduction efforts, while subsidies allocated to emerging energy technologies play a pivotal role in fostering economic progression. Additionally, the total factor productivity shock, energy efficiency shock, and government expenditure shock all stimulate macroeconomic growth, with the government expenditure shock and energy technology research productivity shock effectively promoting the development of renewable energy technologies.

Therefore, it is crucial to phase subsidies for energy technologies. When implementing the carbon emission cap policy, the government should prioritize subsidizing fossil fuels initially to achieve efficient carbon reduction. Then, gradually shift the focus towards renewable energy technologies to optimize energy structure and foster economic development. Furthermore, throughout the phases of implementing energy subsidy policies, it is imperative to consider the synergistic effects of other economic and environmental policies and factors of externalities, which entails making corresponding adjustments to subsidies to maximize potential economic and environmental benefits.

Limitations and future research

Further research could be expanded in the following areas. First, heterogeneous households can be introduced into the model to differentiate between the labor force engaged in energy technology research and production, in order to clarify the varied roles of different individuals in economic operation. Second, it would be meaningful to explore the interactions between carbon emission reduction policies and other economic or environmental policies. Finally, this paper mainly examines the impact of carbon emission reduction policies on China’s economy and environment, without considering cross-regional effects. As the process of economic globalization deepens, it is necessary to expand the closed economy model into an open economy model. In conclusion, future work should incorporate more factors affecting energy technology and carbon emissions to understand the complex mechanisms by which energy technology subsidies work.