Introduction

Problem-based learning (PBL) is a teaching strategy in which a facilitator assists students to solve real-world problems as they work in small groups; the facilitator’s aim is to help the students to gain new knowledge and improve their problem-solving skills (see Barrows, 1986; Goodman, 2010). PBL aims to improve students’ knowledge application (Hmelo, 1998; Hmelo and Lin, 2000; Schmidt et al., 1996), and attitudes towards learning the subject (Hung, 2006; Westwood, 2011).

In mathematics, PBL is an instructional strategy that contextualises mathematics knowledge (i.e., real-life problems) in a way that helps students to understand where, when and how to apply knowledge. In PBL, when students encounter a real-life problem, they should identify what they have already learned about the problem (i.e., activating their prior knowledge) and establish what they need to know in order to solve the problem (i.e., missing information). They have to search for missing information and then combine it with what they already know (i.e., relevant prior knowledge), applying this to a new context (Bokonjic et al., 2007). Therefore, using a PBL teaching strategy in mathematics should reflect on students’ improvement in applying mathematics. Applying mathematics is the concept of using mathematics in real life (Mumcu, 2016).

Contextualising knowledge can be prepared by embedding learning opportunities in real-life contexts, which could it also be of interest for students, and it shows students the value of the function of the subject matter in the real world (Hung, 2006; Westwood, 2011). In the mathematics context, the content of PBL settings (real-life problems) shows the function of mathematics in reality and gives meaning to learning mathematics (Westwood, 2011). This should place value on learning mathematics for students, leading to an increase in positive attitudes towards learning mathematics. Attitudes towards mathematics is a negative or positive emotional disposition toward mathematics (Zan and Di Martino, 2007). In a systematic review and meta-analysis, Suparman et al. (2021) determined that PBL is one of the best teaching strategies for primary school mathematics teachers to enhance students’ mathematical abilities. However, students’ learning processes need to be facilitated by teachers in their approach to solving problems (Collins et al., 1989; Hmelo-Silver and Barrows, 2006; Hung, 2011). Thus, it is essential for teachers to be able to do this effectively to produce a noticeable improvement in students’ outcomes. This might require teachers to complete training in facilitation processes. To date, little is known about how the training of teachers in PBL implementation affects students’ outcomes. The results of the present study will help educational decision-makers to understand how training teachers in implementing PBL affects students’ mathematical applications and attitudes towards mathematics.

This article begins with a review of previous studies on PBL, followed by a discussion of teacher training in PBL implementation. The experiment conducted as part of this research examined the effects of training teachers on students’ knowledge application in mathematics and students’ attitudes towards mathematics.

Previous studies in problem-based learning

The overall review of empirical studies shows that PBL tends to significantly improve knowledge application (Abdalqader and Khalid, 2014; Primadoni et al., 2020; Tong et al., 2021; Wirkala and Kuhn, 2011; Wong and Day, 2009) and generate positive attitudes among students compared with traditional teaching methods (TTM; i.e., teacher-centred instruction) in kindergarten to 12th grade (K–12) settings (Goodnough and Cashion, 2006; Lou et al., 2011; Merritt et al., 2017; Nowak, 2001; Tong et al. 2021). For example, a quasi-experimental study including control groups conducted by Tong et al. (2021) examined the effectiveness of PBL on 10th-grade students’ mathematical application knowledge and their attitudes towards mathematics. The results showed that the students taught by the PBL group improved significantly in the application of knowledge and attitudes towards mathematics compared to the students taught by conventional methods. The real-life problems used with PBL are expected to drive students’ curiosity and capture their interest (Schmidt et al. 2009); therefore, PBL pedagogy and content could enhance students’ interest and promote their knowledge application.

Most of the literature pertaining to PBL has been conducted in the field of medicine and its allied contexts at universities. A limited number of studies have been carried out in K–12 contexts, and very few studies have been conducted in primary schools see (Alshhrany and Mohammed (2010); Eviyanti et al., 2017). Additional empirical research is needed to investigate the effects of PBL on the outcomes of younger students.

Training in PBL implementation

Although training teachers to implement PBL is generally viewed as critical for improving students’ achievement (Arani et al., 2023; Barrows, 1996; Fernandes, 2021; Hmelo-Silver and Barrows, 2006; Leary et al., 2009; Wosinski et al., 2018) the effects of teacher training on students’ performance are still ambiguous. The agreement on the importance of training is supported by literature outside of PBL, where reports have shown that the most effective teachers are trained in how to use facilitation skills (Leary et al., 2009). A meta-analysis was conducted to investigate the relationship between teacher training and students’ learning outcomes, and 94 studies were selected for inclusion in the study. The results showed a significant relationship between teacher training and students’ achievement. The study suggested that untrained teachers have similar student outcomes to those of teachers who use TTM (Leary et al., 2013). The researchers concluded that the facilitator may be a key factor in students’ outcomes. In another study, Tawfik and Kolodner (2016) revisited PBL’s foundations from a case-based reasoning perspective suggested that novices must be trained to facilitate scaffolding students during PBL. Maxwell et al., (2005) suggested that PBL instruction can improve learning compared with conventional methods when teachers are trained well in PBL. El-Aziz El Naggar et al., (2013) found that training was necessary to improve facilitators’ skills in collaborative learning and self-directed environments. However, there is a lack of research studies that have experimentally examined the effects of teacher training on student learning. More primary research is required to measure the effects on students’ outcomes of training teachers in PBL.

The aim of training teachers in PBL is to develop teachers in their professional role (Friedman and Woodhead, 2008; Villegas-Reimers, 2003). Both teachers and students have a role in PBL. To delineate the role of teachers, first, we have to identify the role of students. In PBL, the role of students is to go through the PBL process. Students work in small groups to understand the problem, identify and learn what they need to know and generate hypotheses to solve the problem (Hmelo-Silver, 2004). The role of students also involves questioning, researching and using critical thinking in an active way to solve problems (Cerezo, 2004). Students are required to take responsibility for their learning and engage in meaning-making in terms of their knowledge (English and Kitsantas, 2013). For effective engagement in PBL, students must be responsible for their learning, and they must actively participate in constructing knowledge and making meaningful processes (English and Kitsantas, 2013). However, many students cannot easily shift into this role because they have developed ingrained habits from the typical traditional classroom experiences, and they rely on the passive receiving of knowledge (English and Kitsantas, 2013; Hung, 2011; Ronis, 2008). To shift effectively to the new role, students must develop self-regulated learning (SRL) skills (English and Kitsantas, 2013).

SRL refers to the extent to which the learner is motivationally, metacognitively and behaviourally active in their learning processes (Zimmerman, 1989). Self-regulated learners can set goals and plans, identify appropriate strategies, and self-monitor and self-evaluate their learning; they are intrinsically motivated to learn. Thus, for effective learning in PBL, SRL is an essential skill (English and Kitsantas, 2013). In PBL, teachers can consciously activate students’ behaviours, leading to SRL. When it comes to promoting students’ skills to be able to do this, the role of teachers is to structure activities to stimulate students’ motivation, encourage reflection and facilitate their learning processes through guidance, scaffolding feedback and prompting independent thinking (English and Kitsantas, 2013). The role of the teacher in PBL is to facilitate collaborative knowledge construction by students, monitor learning processes, model desired behaviours and concentrate students’ efforts on critical thinking (Hmelo-Silver and Barrows, 2006, 2008); this can be done by raising awareness of students’ higher cognitive thinking (Barrows, 1998).

Effective teachers should know how to facilitate groups’ learning processes (Dolmans et al., 2002; El-Aziz El Naggar et al., 2013). To enhance cooperation and production within groups, teachers should use intervention strategies, such as making decisions on what, when and how to intervene (Bosse et al., 2010). Teachers may need to be trained to implement such strategies in such a way as to facilitate tutorial processes, since it is teachers’ responsibility to guide students’ learning (Yew et al., 2011). In this study, we attempt to understand the effect of training in implementing PBL on students’ outcomes. We address the following questions:

  1. 1.

    How do trained and untrained teachers in PBL techniques implement PBL?

  2. 2.

    What are the effects of teacher training in implementing PBL on students’ mathematical applications?

  3. 3.

    What are the effects of teacher training in implementing PBL on students’ attitudes towards mathematics?

Methods

Study design

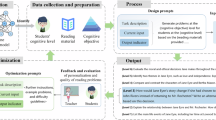
A quasi-experimental design was adopted in this study as the main quantitative approach to minimise bias in estimating the difference between traditional instruction and PBL classes. In addition, a qualitative approach was used during the intervention using field observation notes and after the intervention using interviews, as a secondary approach (see Fig. 1).

Fig. 1: Study design.
figure 1

The figure illustrates the study design; mathematical test and attitudes towards mathematics were applied before and after the intervention, while during the quasi-experimental implementation, field observation notes were taken, and at the end of the intervention semi-structured interviews were conducted with the teachers.

Full size image

Figure 1 illustrates the study design; during the quasi-experimental implementation, field observation notes documenting the authors’ observations were taken with the aim of observing how teachers implemented PBL, while semi-structured interviews were conducted with both types of the teachers who only implemented PBL (trained and untrained teachers) after the implementation of PBL as a supplement, with the aim of being used as part of the triangulation method for the author’s observations in how teachers implemented PBL.

School and participating students

The school was located in an urban district in a major city, Hail, which is situated in the north of Saudi Arabia. The school was randomly selected from ten private schools. Then, seven of the third-grade classes out of nine in the selected school were randomly chosen. The third grade is an important level, as it is the final grade of lower primary school. The classes were instructed by three teachers; one taught three classes, and the others taught two classes each. These classes comprised the three following groups: group A (three classes taught by a trained teacher using a PBL teaching strategy), group B (two classes taught by an untrained teacher using TTM) and group C (two classes taught by an untrained teacher using a PBL teaching strategy; see the study design in Table 1).

Table 1 Design of the main study.
Full size table

Ethical approval was obtained, and all participants signed consent forms to participate. They were informed that they could withdraw any time with no need to justify their decision, nor would there be any consequences of withdrawal.

In total, 127 pupils participated in the study, and their ages ranged from eight to nine years old. They were in the last semester of the third grade. Most of the students at the school were Saudis; in each group, two to four students had Arab backgrounds, such as from Syria, Egypt and Sudan. All students had a middle-class socioeconomic status. Academic school records and pre-test’ scores were used to ensure that the groups were similar in terms of mathematical achievement. Within each group, students showed a wide range of academic achievements; the students spanned from very low to very high achievers. There were no special education pupils within the groups.

Teachers

Three teachers were randomly selected from one large primary school to take part in this study. The first teacher was randomly selected to receive training courses in using the PBL teaching strategy. The second teacher did not receive any training, but he was provided with PBL materials—specifically, design problems and guidelines for implementing PBL; he was asked to conduct self-directed learning (SDL) to implement PBL in his classrooms. The aim of including a trained and an untrained teacher using PBL was to measure the effects of training teachers on students’ outcomes. The third teacher was not trained in PBL and was asked to teach students using TTM.

The teachers had similar characteristics in terms of qualifications, experience and expertise, as well as in their beliefs and perspectives on PBL and TTM. They are all male and they believed that the aim of teaching mathematics is to conduct real-life problem solving, and they considered active learning to be important for students. They had been teaching mathematics to third-grade school students for 10 years. They all had a first degree in mathematics. They were all Egyptians and aged in their late thirties. According to the teachers and the administration of the school, the teachers had all attended the same training courses in different aspects of education, such as active learning. However, none of them had ever been trained in using PBL teaching strategies.

Topics

The topic covered in the classes was ‘data display’. It covered representation through codes, interpretation of representation through codes, representation in columns and interpretation of representation in columns. The content was new to the students. The instruction took place during ten class sessions (45 min each) comprising four sessions per week over for two and a half weeks, with a total of 7.5 h for each group. To control for the time factor, all groups, whether PBL or traditional, were given the same amount of time.

Instruments

Six multiple-choice questions, short answer questions, fill-in table questions and drawing tests were applied at the beginning of the study (pre-test) and in the final experiment (post-test). Mathematics items were selected from Trends in International Mathematics and Science Study (TIMSS) 2003, 2007 and 2011 (see Mullis et al., 2012). The TIMSS items that were selected matched the objectives of lessons for knowledge application exactly; they had already been examined for the purpose of the test. We chose TIMSS mathematics items because they were verified as appropriate for the students’ ages. The students had nearly finished the third grade, and the curriculum for that grade contained many TIMSS topics (see TIMSS, n.d.). Each item on the test received a score of either one or zero. An example of the items is given in Appendix A. The measure ‘attitudes towards mathematics’ of TIMSS 2007 (Mullis et al., 2008) contains four items, as follows:

  1. 1.

    I would like to take more mathematics in school

  2. 2.

    I enjoy learning mathematics.

  3. 3.

    Mathematics is boring (reverse-coded).

  4. 4.

    I like mathematics.

This measure was adopted and assumed to meet the standard of a valid and reliable test (see, Mullis et al., 2008). Attitudes were assessed using four items applied twice as pre- and post-measures; four items with 4-point Likert scales (disagree a lot, disagree a little, agree a little, and agree a lot) were presented. Each item score ranged from 1 to 4. The total marks ranged from the number of items of the measure to multiply them by 4; the measure consisted of four items, so the total scores ranged from 4 to 16. Some items were reverse-coded; for example, for ‘mathematics is boring’, ‘disagree a lot’ would receive a score of 4, whereas ‘agree a lot’ would receive a score of 1.

The face validity method was used to assess the validity of the tests and attitude measures. Eight arbitrators checked and gave their opinions on the adequacy, clarity, and relevance of the items’ content. The opinions of the arbitrators were considered and included in the preparation of the final image of the tests and attitudes. However, no changes were reported, and face validity confirmed the tests’ validity. In addition, test-retest reliability was used to assess the reliability of the tests and attitude measures. The levels of reliability were acceptable, with a score of 0.86 for the mathematics test and 0.88 for the attitude measure. For further reliability, Cronbach’s alpha was used for each scale of the test and attitudes and for the whole test and attitudes. The results show that all items correlated with a good degree of total scales (no items scored less than 0.3), and the reliability for the test was 0.747, whereas that for attitude was 0.808. Therefore, the measures became high valid for the purposes of this study.

In qualitative methods, filed observation and semi-structured interview were used to assess teachers’ performance in PBL implementation. After filed observations completed, post- semi-structured interviews were conducted for the teachers to confirm the results of author observations of how teachers implemented PBL as a supplement for the methodological triangulation of the filed observations. Methodological triangulation involves a researcher using more than one method, such as interviews and observations, for collecting data to understand a phenomenon deeply (Flick et al., 2004; Neuman, 2000). The teachers’ responses to the questions in the semi-structured interviews were analysed and compared with the analysed observation data to enhance the validity of the study and to gain a deeper understanding of social events. As Neuman (2000) commented, “Looking at something from several different points gives a more accurate view of it” (p. 521).

The data obtained from qualitative methods were deductively analysed. Prior to conducting data collection from filed work. A structured categorisation matrix was developed by the authors based on a literature review (see Barrows, 1998; English and Kitsantas, 2013; Hmelo-Silver and Barrows, 2006, 2008). It aimed to assess PBL implementation conducted by teachers and consisted of two main categories: understanding the problem and using metacognitive strategies (see Appendix B). Field observation notes were used to describe how the teachers implemented PBL. In this study, field observation notes consisted of two parts: descriptive and reflective information (Patton, 1990). The descriptive part involved documenting the factual data obtained from inside the classroom. The main author moved between groups to make sure everything was proceeding well; the intention was to monitor the implementation of the study, and the authors had a diary that was used to document any observations, particularly the observations that took place during lessons and were made inside mathematics classrooms. The main focus was on teachers’ performance, particularly with respect to teacher intervention, individual and collective student practices, student responses, group interaction and PBL processes. In the reflective section, the authors reflected on the meaning of the observations outside of the classroom (see Appendix C). At the end of the experiment, ten lessons by each teacher were observed.

Semi-structured interview questions were developed according to analysed data of class observations which includes: The three main questions:

  1. 1.

    How was PBL implemented in your teaching strategies?

  2. 2.

    How did you assess your students in relation to understanding the problem?

  3. 3.

    How did you support your students to solve the problem?

In semi-structured interview, tape recordings were used for the interviews with each teacher, which ranged from 13 to 23 min in length. The interviews were conducted in Arabic, transcribed and subsequently translated into English by the authors.

The data were deductively coded (i.e., both the interview and observation) by the main author, and according to the identified categories mentioned above. When a deductive content analysis is used, a categorisation matrix is developed; following this, the data are coded according to the categories (Polit and Beck, 2004). In addition, if a structured matrix is chosen, only aspects that fit the matrix are selected from the data (Patton, 1990).

Professional development

The PBL programme used in this study aimed to train teachers by focusing on how to implement PBL in mathematics classrooms. The programme continued to provide feedback during the implementation after each session, taking advantage of the literature recommendations. Therefore, the trained teacher learned how to facilitate groups’ learning processes and guide students’ learning by adopting strategies such as posing meta-cognitive questions and focusing on the process of learning to model students’ learning strategies. The teacher was trained in intervention strategies, such as making decisions based on what, when and how intervention should occur to enhance cooperation. The programme included examples of PBL implementations. Teacher training lasted for one week (8–10 h), and daily meetings took place during the course of the training to provide an opportunity to present feedback and resolve unexpected problems. The programme for training the teacher to implement PBL in his class was developed by the author. It was expected that, following the teacher’s completion of the programme, the teacher would be able to do the following:

  • provide scaffolding and feedback as needed

  • prompt independent thinking

  • facilitate collaborative knowledge construction for students

  • monitor learning processes

  • model desired behaviours

  • concentrate students’ efforts on critical thinking.

  • use intervention strategies, such as making decisions on what, when and how to intervene

The programme included three real-life sessions, each lasting 45 min. The teacher was asked to implement the PBL strategy using an ill-structured problem, which was taken from a mathematics textbook and related to the topics that the students had been studying. A group of students from outside the study sample was selected to assess the teacher’s performance and establish whether he was able to implement PBL effectively. This was followed by providing the teacher with extensive feedback, which lasted more than an hour for each session.

The students were trained in two sessions in how to deal with the PBL teaching strategy.

Problem-based learning implementation

Problems were presented to the students. Students worked in small groups of four to six members. They discussed their understanding of the problems, and then the teacher discussed the understanding of the problem with the whole class. This was followed by students solving the problems. Finally, the teacher discussed the solution with all the students.

In this study, the six core characteristics of PBL mentioned by Barrows (1996) were adopted. These are as follows:

  1. 1.

    The student is the centre of the learning.

  2. 2.

    Learning occurs in small groups of students.

  3. 3.

    At the beginning of the learning, the students are presented with authentic problems.

  4. 4.

    The problems are used as a means of developing problem-solving skills.

  5. 5.

    New knowledge is gained through SDL. (Barrows, 1996)

  6. 6.

    The student is the centre of the learning.

From the literature review (see Barrows, 1986; Gallagher and Stepien, 1996; Hung et al., 2008), six characteristics were adopted in the problems after reviewing the literature related to the problem of PBL. These were as follows:

  • the role of students as stakeholders

  • ill-structured problems

  • real-life problems

  • age-appropriate problems

  • clear and short problems

  • not too difficult problems

Statistical analysis (quantitative analysis)

The study used mixed-factor analysis of variance (ANOVA) models (Field, 2013; Howell, 2012) within one factor (time: pre- and post-tests and between). Tukey’s post hoc test (Field, 2013; Howell, 2012) was applied when appropriate and where significant results were observed—that is, an effect size (partial eta squared [ηp2]). The effect size, classified as Cohen suggested, could be small 0.01; medium, 0.06; or large, 0.14. All analyses were performed on IBM SPSS v22 and at a 5% (0.05) level of significance.

Procedure

A quasi-experimental design was adopted in this study as the main quantitative approach, while a qualitative approach was used during the intervention using class observation notes and interviews, as a secondary approach. In total, 127 pupils participated in the study. They were in the last semester of the third grade. Ethical approval was obtained, and all participants signed consent forms to participate. Three teachers were randomly selected from one large primary school to take part in this study. The first teacher was randomly selected to receive training courses in using the PBL teaching strategy. The second teacher was not trained and asked to conduct SDL to implement PBL in his classrooms. The third teacher was not trained in PBL and was asked to teach students using TTM. The topic covered in the classes was ‘data display’. The content was new to the students. The instruction took place during 10 class sessions. Instruments of the study include mathematics test and attitudes towards mathematics were prepared and verified. Applying a pre-test (a measure of attitudes towards mathematics and an exam to measure mathematics application). Conducting the study took about 2 and a half weeks. Applying for a post-test (a measure of attitudes towards mathematics and an exam to measure mathematics application). During the intervention, class observations were carried out for each lesson.

Results

Problem-based learning implementation of trained and untrained teachers

Unlike the untrained teacher, the trained teacher properly implemented PBL. The differences between their performances lay in differences in ‘giving students sufficient time to understand the problem’ and ‘using more metacognitive strategies to coach students in relation to their thinking skills’.

Table 2 and Fig. 2 summarise the difference between trained and untrained teachers after analysing both the teachers’ interviews and the author’s observations. The two following themes were extracted from the data analyses: ‘understanding the problem’ and ‘using meta-cognitive teaching skills’. These themes are detailed below.

Table 2 Summary of the difference between the trained and untrained teachers’ qualitative results.
Full size table
Fig. 2: Difference between the trained and untrained teachers.
figure 2

This figure illustrates the difference between trained and untrained teachers' performances in PBL implementation.

Full size image

Understanding the problem

The trained teacher did not allow students to solve the problem until they demonstrated their understanding of it. The author frequently noted that the trained teacher prevented the students from solving the problem until they demonstrated their understanding of it. When the trained teacher was asked how he knew that the students understood the problem, he replied, ‘I frequently asked random students… : ‘could you please explain to us the problem in your own words?’ If they did not do very well, I asked them how they could understand the problem more deeply? I waited longer … for them to solve the problem and gave them more time to reflect on their understanding and discuss with their group to deeply understand the problem’. The author observed that the teacher frequently and asked ransom students the following question: ‘Could [you] explain the problem [to us in] your own words’. Some students could, while others could not. Then, he encouraged them to understand the problem by asking them the following questions: ‘How can you understand the problem deeply? and Could you identify the obstacles and discuss [them] with your [respective] groups?’ Later, he again asked them whether they could explain the problem. However, the untrained teacher’s students had been given a shorter amount of time to understand the problem than those who were with the trained teacher (author’s observation).

In all lessons, the untrained teacher asked students whether they understood the problem; he often proceeded after hearing anyone shout ‘yes’ (author’s observation). The untrained teacher confirmed this when he was asked how he knew that his students had understood the problem before carrying on: ‘I always ask my students, if they do not understand the problem, to stop me any time and feel free to ask’. He did not ask his students to explain the problem in their own words (author’s observation). It was noted that the trained teacher gave more time for understanding the problem and questioned his students’ understanding more than the untrained teacher did.

Using meta-cognitive teaching skills

The trained teacher used more metacognitive strategies than the untrained teacher. Throughout all the lessons, the author observed that the trained teacher facilitated his students’ learning processes via PBL by using meta-cognitive strategies. He confirmed this in stating:

They [the students] work within groups to solve the problem, and I monitor them and coach their thinking with meta-cognitive questions …. For example, I ask students: what they did so far, and what next, did they consider this or that … and so on…. Sometimes, I think aloud and model right behaviours to let them engage in learning processes.

It was observed that students gradually began to depend on their own selves to solve the problems when they found their teacher pushed them to be independent. The trained teacher confirmed the following:

I did not want my students to depend on me. I never give them the solution, but encouraged them to depend on their own effort … And I found coaching their thinking improved their independence.

In contrast, the untrained teacher showed less ability to use meta-cognitive strategies through implementing PBL (author’s observation). The untrained teacher said: ‘They [the students] worked with their groups to solve the problem, and I helped them to solve the problem by indirectly explaining any difficulties, for example, by giving them some examples’. He explained the difficulties and led his students to solve the problem. He did not explain the solution directly, but he gave similar examples, which led them to the correct answer (author’s observation). In some ways, this strategy may be considered a metacognitive activation strategy.

The author observed that students frequently asked their teachers to give them more examples to understand how to solve the problems. The untrained teacher confirmed this: ‘My students are allowed to ask me to give examples to solve the problems, and I always meet their needs’.

Knowledge application in mathematics

From Table 3, it can be seen that the improvement in the ‘applying achievement’ mean scores increased in all groups. From the mixed-measures ANOVA, as shown in Table 4, it was found that a statistically significant improvement occurred for the average of students’ scores in knowledge application, F(2, 121) = 76.795, p = 0.000, with a large effect size at 0.388 (see row 1). However, when time was interacted with the groups (PBL with trained teacher, PBL with untrained teacher and TTM) the result showed a statistically significant effect, F(3, 121) = 4.333, p = 0.015. The partial eta squared effect size for this statistically significant result was medium, at 0.067 (see row 2). This effect shows that there was an effect on at least one group, but further analysis was needed to identify which group(s) might be affected. Tukey’s post hoc test was applied to determine which of the groups was statistically significantly different from the others. This test found that the mean scores of the group of students taught using the PBL teaching strategy by the trained teacher were statistically significantly different only from the scores of the students taught using TTM, p = 0.009 (see row 3). This indicates that the average of the PBL group’s scores with the trained teacher significantly improved more than the average of the traditional group’s scores did in ‘applying mathematics’.

Table 3 Summary statistics for applying scores within time and by groups.
Full size table
Table 4 Mixed ANOVA outcomes for knowledge application.
Full size table

Attitudes towards mathematics

From Table 5, it can be seen that the mean score for ‘attitudes towards mathematics’ increased in groups A and C, while the scores of group B, the traditional group, decreased.

Table 5 Summary statistics for attitudes towards mathematics scores within time and by group.
Full size table

From the mixed-measures ANOVA analysis, as shown in Table 6, there was no statistically significant improvement occurring for the average of students’ scores in attitudes towards mathematics, F(2, 121) = 0.480, p = 0.490 (see row 1). However, when time was interacted with groups (PBL with trained teacher, PBL with untrained teacher, and TTM), the result showed a statistically significant effect, F(3, 121) = 12.486, p = 0.000. The partial eta squared effect size for this statistically significant result was large, at 0.171 (see row 2). Tukey’s post hoc test was applied to determine which of the groups was significantly different from the others in attitudes towards mathematics. This test showed that using PBL with the trained teacher group was significantly different from using TTM, p = 0.000; using PBL with the untrained teacher group was also significantly different from using TTM, p = 0.008. However, there was no statistically significant difference between using PBL with the trained and untrained teachers (see row 3). This means that there was a statistically significant difference between the groups attributed to the types of treatment (PBL and TTM) in ‘attitudes towards mathematics’ and in favour of the PBL group, regardless of the different abilities of teachers in PBL implementation.

Table 6 Mixed-measures ANOVA outcomes for attitudes towards mathematics.
Full size table

Discussion

The study aimed to assess the effect of teacher training on students’ knowledge application and attitudes towards mathematics. The trained teacher demonstrated his ability to facilitate his students’ learning processes by using more metacognitive strategies than the untrained teacher. This result was expected, as many scholars think that training teachers on PBL implementation is critical for success (Barrows, 1996; Hmelo-Silver and Barrows, 2006; Leary et al., 2009; Wosinski et al., 2018). The results of the analyses of the interview data and the class observations were convergent. No noticeable difference was identified between the data analyses of class observation and the teachers’ interviews. Below, we consider how the teacher training affected student outcomes. Below, we consider how the teacher training affected student outcomes.

Knowledge application in mathematics

The current study’s quantitative results suggest that when PBL is taught by a teacher who can facilitate the students’ learning processes by using more meta-cognitive strategies, this could improve the application of mathematical knowledge of third-grade students’ significantly more than when they are taught using TTM (see Table 4). PBL theorists claim that, when compared with TTM, PBL is more successful in improving knowledge application (Hmelo-Silver, 2004; Hmelo-Silver and Barrows, 2008). This is because, with PBL, students engage in SDL by using their meta-cognitive learning strategies to solve real-life and ill-structured problems as a way of learning (Chin and Chia, 2006). This should reflect some improvement in the students’ ‘application’ ability over TTM (Fogarty, 1994). However, for such a method to be effective, skilled teachers who are also able to effectively use meta-cognitive strategies must be present to activate students’ meta-cognitive learning strategies. The trained teacher in PBL is better able to do so.

The role of the teacher in PBL is to facilitate learning processes (Hmelo-Silver and Barrows, 2006, 2008). The shift to PBL requires new teaching roles and skills (Wilkerson and Hundert, 1997). Teachers can facilitate PBL processes if they are using meta-cognitive strategies, such as ‘thinking aloud with students’ and ‘modelling behaviours’ (Delisle, 1997). In the current study, these skills were shown effectively by the trained teacher; consequently, such strategies were reflected in the improvements to the students’ ‘application’ achievements. However, when students were taught by an untrained teacher, their learning processes were less facilitated. He only responded to difficulties they were experiencing by explaining similar situations (i.e., an example). Even though this approach is considered a metacognitive activation strategy, the students’ solutions were led by these examples. Thus, the teacher’s performance is an important factor that will affect the application of mathematical knowledge among third-grade students.

In terms of teacher training, the findings of the present study are supported by the results of the meta-analysis conducted by Leary et al. (2013), which showed a statistically significant positive relationship between teacher training and student achievement. The study also suggested that untrained teachers resulted in student outcomes similar to those attained by teachers who use TTM. This is also supported by the results of the current study. Moreover, this study’s findings are in line with those of Maxwell et al. (2005); these researchers’ conclusion suggests that PBL instruction can improve learning more than TTM can when teachers are well trained in using the PBL strategy. However, the results of the current study support the conclusions of several studies that found students taught via PBL outperformed students taught via TTM in terms of application knowledge (see Tong et al., 2021; Wirkala and Kuhn, 2011; Wong and Day, 2009).

Attitudes towards mathematics

The current study’s results suggested that PBL could significantly improve third-grade students’ attitudes towards mathematics compared with TTM (see Table 6). This is supported by the findings of (Lou et al., (2011) and Tong et al. (2021). For example, Tong et al. (2021) suggested that students taught via PBL improved their attitudes towards mathematics more significantly than those taught via TTM. The reason for this is that the students liked active learning and working in groups. This idea was supported by Goodnough and Cashion (2006), who suggested that young students like this strategy because it encourages active learning, supports working in groups and provides students with a variety of learning approaches and methods. In addition, real-life problems that interest students can be used to motivate students to engage deeply in learning processes when students fully understand them. These kinds of problems are expected to drive students’ curiosity and capture their interest, resulting in more effective student engagement in SDL in order to solve the problems (Schmidt et al., 2009).

In this study, the role of the problem was to motivate the students in all lessons taught by teachers trained in implementing PBL. Students became intrinsically motivated when they worked on tasks that stimulated their interests and sense of satisfaction or that challenged them (Hmelo-Silver, 2004). The possible reason for this is that the untrained teachers did not give students sufficient time to understand the problem, in contrast with the trained teacher (teachers’ interview and author’s observations).

In sum, PBL could be an effective teaching strategy for improving students’ attitudes towards learning mathematics; this effect is probably due to PBL content (i.e., real-life problems) and the nature of the PBL environment (i.e., eliciting active learning). In addition, PBL could be an effective teaching strategy for improving students’ mathematics application when students’ processes are effectively facilitated; without such facilitation, the effect of PBL instruction will not differ from that of TTM.

Limitations of the study

This study had several limitations. Because of the study design, results could be generated only for young students and for learning mathematics. The sample selection was not completely random, which could also decrease the opportunity to generalise the results of this study. Because of the gender segregation system that is currently operational in Saudi Arabia, the study participants were all male students. Therefore, the results of this study should be generalised with caution, taking these contextualising factors into account.

Conclusion

This study attempted to assess how training teachers in PBL implementation affects student outcomes, including knowledge application and students’ attitudes towards learning mathematics compared with TTM. Overall, the third-grade students who were taught using PBL showed more positive attitudes towards learning mathematics, regardless of whether they were taught by trained or untrained teachers. The study provides evidence that supports the necessity of training teachers to implement PBL effectively, as this will improve students’ mathematics application.