Assessing economic losses with COVID-19 integrated models: a retrospective analysis

Abstract

The COVID-19 pandemic led to a global crisis that forced governments to implement restrictive measures to control the spread of the disease. Although these restrictions, such as community quarantines, played a pivotal role in stabilizing healthcare systems, they also caused forced closures of various economic sectors that resulted in huge societal costs and severely impacted the marginalized. In order to understand and quantify the economic impact of the COVID-19 pandemic in the Philippines, an integrated modeling approach, which combined an epidemiological compartmental model and an economic model, was utilized. The evolving nature of COVID-19 required continuous updating of the integrated model which this paper illustrates by applying three versions of the model in three different phases of the pandemic. Scenario-based estimates of active COVID-19 cases and economic losses, expressed in terms of foregone income, are produced for each of the model versions. Analysis of the results provided a retrospective view of the losses the economy had incurred during the pandemic, along with implications for public policy. The insights presented in this paper emphasize the importance of using an integrated modeling approach to guide pandemic response.

Introduction

Background

The threat of the COVID-19 compelled nations across the globe to adopt various measures to mitigate the spread of the disease. The goal of such measures was to reduce the number of cases and deaths, and to stabilize the health system, ensuring availability of public health services throughout the pandemic. The Philippines, a lower-middle income class country, relied heavily on lockdowns for COVID-19 disease control, enduring one of the longest lockdowns worldwide (Chiu 2021; Maradang 2021; Olanday and Rigby 2020). However, such measures came with harmful repercussions; this was due to closures (full or partial) on various economic sectors that led to widespread unemployment and income loss, worsening the poverty and hunger crisis in the country (de Guzman 2021; Jackson 2020; Lalu 2020). Furthermore, the national real gross domestic product contracted by 9.6% in 2020, which was the steepest decline in Philippine recorded history as reported by the Philippines Statistics Authority (PSA) (Bangko Sentral ng Pilipinas 2021). This also represented largest GDP percentage loss for that year among the ASEAN-5 countries (Senate Economic Planning Office 2022). In addition, according to the National Economic and Development Authority (NEDA) estimates, the net present value of pandemic cost over the next 40 years in the Philippines is at PHP41.4 trillion, and it would take 10 years for the economy to converge to the pre-pandemic growth path (National Economic and Development Authority 2021).

To support the pandemic response efforts of Philippine national government and local government units (LGU’s), the COVID-19 FASSSTER¹ platform was developed to provide data analytics and visualization. The platform provided nowcasting metrics such as case doubling time, daily positivity rate, daily attack rate, effective reproduction number, and so on. It also generated scenario-based case projections to provide a potential outlook of the COVID-19 situation at the local, regional and national level. The model that produced these outputs had been continuously reviewed and updated to adapt to the evolving conditions surrounding the COVID-19 pandemic.

The case projections generated from the epidemiological model are informative from a public health perspective, but they by themselves do not capture other significant ramifications of the disease, particularly on the country’s economy. To address this, an economic framework that builds on an epidemiological model can provide a broader perspective. In this paper, we present such integrated model that evolves over time due to the emergence of new COVID-19 variants, the progress of vaccine administration, and shifts in policy interventions. We then conduct a retrospective analysis by applying the integrated models to specific counterfactual scenarios. By doing so, we quantify economic losses, in terms of foregone income, associated with different policy decisions and compare them with the baseline. This allows us to gain insights on how such policies can affect economic outcomes during the pandemic.

Review of related literature

The effects of COVID-19 in the Philippine economy are consistent with the literature’s classification of a pandemic’s economic impact either as first-round effects or second- and subsequent-round effects (Benson and Clay 2004; de Lara-Tuprio et al. 2022b; Keogh-Brown et al. 2020, 2010; Lubangco and Tuaño 2024). First-round effects typically include the direct impacts of widespread infection and mortality on the labor supply, while second- and subsequent-round effects include the impacts on wealth, income, firm productivity, welfare, and the macroeconomy (Benson and Clay 2004; Keogh-Brown et al. 2020, 2010; Noy et al. 2020). Second- and subsequent-round effects occur due to restriction policies, social distancing measures, or supply chain disruptions (ASEAN Secretariat 2020; Geard et al. 2020; Genoni et al. 2020). It is evident in these typologies that the main channels through which pandemics inflict economic losses is through the population and the labor market (Lubangco and Tuaño 2024).

The empirical strategies to capture these economic losses vary across studies. These can be categorized between static and dynamic strategies, although the dichotomy is not entirely rigid as some static methods can be extended to capture multiple periods. Static models include methodologies that fall under partial and general equilibrium analyses in economics (Amewu et al. 2020; Ducanes and Ramos 2023; Keogh-Brown et al. 2020; Lubangco and Tuaño 2024; Porsse et al. 2020). Partial equilibrium analyses trace the effects of a change or a shock to another economic variable such as employment (Ducanes and Ramos 2023), food security (Chiwona-Karltun et al. 2021; Min et al. 2020), and industrial production (Deb et al. 2022), while holding other factors constant. The advantage of partial equilibrium strategies, which hinge primarily on econometric methodologies, is that causal effects can be established among variables of interest.

However, as pandemics are economy-wide phenomena, other studies use input-output simulations, social accounting methods, and general equilibrium analyses that may also be static in nature (Amewu et al. 2020; Keogh-Brown et al. 2020; Lubangco and Tuaño 2024; Pham et al. 2021; Porsse et al. 2020). While the same economic variables as above may be the subject matter of such strategies, system-wide static analyses allow researchers to capture these economic losses from the perspective of the interlinkages between markets and sectors in the economy. For instance, poverty is simulated to increase following the reduction in labor supply and value added in a linked model between the computable general equilibrium and the microsimulation strategy (Laborde et al. 2021; Lubangco and Tuaño 2024). Through a social accounting matrix-based analysis, reduction in sectoral output is expected to occur following the implementation of social distancing measures (Amewu et al. 2020).

Capturing economic losses in dynamic simulations has an advantage over the use of static models as dynamic simulations allow researchers and policymakers to simulate the changes of economic losses over time. Therefore, these strategies may pinpoint which factors that exist at a specific point in time contribute the most or the least amount of economic losses overall. This is demonstrated in Dacuycuy (2021) where a parsimonious dynamic stochastic general equilibrium (DSGE) model was used to identify factors that countered demand and supply shocks in the early quarters of the pandemic. Although the economic model in Dacuycuy (2021) is not linked to an explicit model of COVID-19 spread, epidemiological models may complement economic models to provide a more comprehensive view of the how pandemics affect the economy. Previous studies attempt to use compartmental epidemiological models in simulating economic losses. The use of epidemiological models is advantageous as these simulate the evolution and transmission of illnesses through time while accounting for heterogeneities in geography, population, and the effects of policy interventions (Anand et al. 2020; Chen et al. 2020; de Lara-Tuprio et al. 2022b; Escosio et al. 2023; Mendoza et al. 2023; Reno et al. 2020). There have been a number of studies that take advantage of extending these epidemiological models to capture the economic losses associated with infections, deaths, and isolation in pandemics (Acemoglu et al. 2021; Bognanni et al. 2020; de Lara-Tuprio et al. 2022b; Eichenbaum et al. 2021; Goldsztejn et al. 2020; Makris and Toxvaerd 2020). In these recent studies, trade-off analyses between economic losses (or gains) and disease spread (or containment) can be conducted, and determine the optimal lockdown policy for a specific area.

While the literature on assessing the economic losses from the COVID-19 pandemic has grown over time, these studies are still insufficient in terms of addressing certain policy scenarios. For instance, analysis on economic losses due to the emergence of new variant strains have been limited. Moreover, while previous studies such as by Acemoglu et al. (2021), de Lara-Tuprio et al. (2022b), and Goldsztejn et al. (2020) investigate economic losses amidst pandemic restrictions using their respective variations of an integrated model, the Philippines’ policy shift from a stringent set of pandemic restrictions to a more relaxed and granular approach, which happened beginning the fourth quarter of 2021, has yet to be explored.

We also emphasize that this study differs from earlier published works which feature previous versions of the model. In particular, de Lara-Tuprio et al. (2022b) apply the integrated model during the first year of the pandemic before vaccines became available and do not offer any perspectives related to policy. On the other hand, de Lara-Tuprio et al. (2022a) focus solely on the first version of the epidemiological model and how it aided in policy making without quantifying economic impacts. For this study, we highlight how an integrated epidemiological-economic model has been adjusted over time as it adapted to the changes in the pandemic landscape. The assessment of economic losses is conducted as the integrated model evolves, taking into account a combination of changing pandemic restrictions, vaccination policies, and the emergence of new variants.

Evolution of FASSSTER integrated model

An integrated model was developed and updated accordingly to estimate the impact of the COVID-19 pandemic in the Philippine economy. This model is a combination of an epidemiological model that describes the transmission dynamics of the COVID-19 disease, and an economic model whose dynamics is based on the output of the epidemiological model. The epidemiological model is a compartmental model, expressed mathematically as a system of ordinary differential equations that describe the flow of individuals through the different compartments according to their infection status. The economic model is also a system of differential equations appended to the compartmental model, and it describes economic losses in the form of foregone income due to COVID-19 sickness and death, as well as foregone income due to pandemic restrictions which limit mobility and economic activities.

The first version of the integrated model was presented in the work of de Lara-Tuprio et al. (2022b). Its corresponding epidemiological model used an SEIR model to describe the movement of individuals in a population across 6 compartments: Susceptible (S), Exposed (E), Infectious and Asymptomatic (I_a), Infectious and Symptomatic (I_s), Confirmed (C) and Recovered (R).

As with any compartmental model, the transfer rates of individuals between the compartments correspond to the model parameters. Among these is the effective transmission rate β, which reflects the degree at which the disease spreads in a community. This measure has two main components: the baseline transmission rate β₀, and the transmission reduction parameter λ. The former is calculated by representing β₀ as a function of the basic reproduction number R₀ and other model parameters, and then setting a specific value for R₀. On the other hand, λ considers the effects of implementing COVID-19 policies such as community quarantines, as well as compliance of the general public to health protocols, such as social distancing, masking, and so on. The parameter β can then be expressed as β = β₀(1 − λ). Other parameters to consider are the death rates in the compartments I_s and C, given by ε_I and ε_T, respectively. These rates play an important role in the economic model. Additional details about the parameters used in the compartmental model can be seen in de Lara-Tuprio et al. (2022a, b).

The economic model appended to the compartmental model consists of two differential equations that describe the dynamics of two economic variables: Y^E which represents foregone income due to COVID-19 sickness and death, and Y^CQ which represents foregone income due to pandemic restrictions which limit mobility and economic activities.

The dynamics of Y^E is given by:

$$\begin{array}{ll}\frac{d{Y}^{E}}{dt}\,=\,\mathop{\sum }\limits_{k=15-{T}_{5}}^{{T}_{1}}\frac{{\iota }_{1}\left[{\varepsilon }_{I}\frac{d{I}_{SS}}{dt}\,+\,{\varepsilon }_{T}\frac{dC}{dt}\right]z}{{\left(1+{s}_{r}\right)}^{k}}+\mathop{\sum }\limits_{i=2}^{4}\mathop{\sum }\limits_{k=0}^{{T}_{i}}\frac{{\iota }_{i}\left[{\varepsilon }_{I}\frac{d\bar{I}}{dt}\,+\,{\varepsilon }_{T}\frac{dC}{dt}\right]z}{{\left(1+{s}_{r}\right)}^{k}}\\ \quad\quad\,\,\,\,\,\,\,+\,\kappa w\left(\left(1-{\varepsilon }_{T}\right)\frac{dC}{dt}+\left(1-{\varepsilon }_{I}\right)\frac{d{I}_{SS}}{dt}\right)\end{array}$$

(1)

where ${I}_{SS}\left(t\right)={I}_{s}\left(t\right)$. The money valuation of foregone income stems from the daily basic pay variable w and the average annual income variable z, which are calculated at a regional level. Further, note the dependence of Y^E on the infectious symptomatic and confirmed compartments, from which we consider the present value of all future income of those who died, as well as the total income lost due to sickness and isolation. On the other hand, the dynamics of Y^CQ is given by:

$$\frac{d{Y}^{CQ}}{dt}=\kappa w\phi \left[\frac{d\bar{S}}{dt}+\frac{d\bar{E}}{dt}+\frac{d\bar{I}}{dt}+\frac{dR}{dt}\right]$$

(2)

where ${\bar{S}}\,\left({t}\right)={S}\,\left({t}\right),{\bar{E}}\,\left({t}\right)={E}\,\left({t}\right)$ and $\bar{I}\left(t\right)={I}_{a}\left(t\right)$². In this case, Y^CQ is dependent on the other compartments to account for individuals who are unable to earn their income due to policy restrictions imposed by the government.

The economic model given by Eqs. (1) and (2) is also governed by several parameters. The quantities z and w represent the annual wage and daily wage of each worker, respectively. ι_i represents the percentage of the population with ages 0–14 $\left(i=1\right),$ and labor force with ages 15–34 $\left(i=2\right),$ 35–49 $\left(i=3\right)$ and 50–64 $\left(i=4\right).$ In addition, T_i is the average remaining productive years for people in age bracket i, s_r is the social discount rate, κ is the employed-to-population ratio, and ϕ is the displacement rate.

Solving the above equations, the foregone income due to COVID-19 sickness and death is expressed as:

$${Y}^{E}\left(t\right)={J}_{1}{I}_{SS}\left(t\right)+{J}_{2}C\left(t\right)$$

(3)

where ${J}_{1}={z}({K}_{1}+{K}_{2}){\varepsilon }_{I}+\kappa {w}(1-{\varepsilon }_{I})$ and ${J}_{2}={z}({K}_{1}+{K}_{2}){\varepsilon }_{T}+\kappa {w}(1-{\varepsilon }_{T})$, with ${K}_{1}={\iota }_{1}\frac{{\left({s}_{r}\,+\,1\right)}^{{T}_{1}+{T}_{5}-13}\,-\,\left({s}_{r}+1\right)}{{s}_{r}{\left({s}_{r}+1\right)}^{{T}_{1}+1}}$ and ${K}_{2}=\mathop{\sum }\nolimits_{i = 2}^{4} \iota_{i}\left(\frac{{({s}_{r}+1)}^{{T}_{i}+2}\,-\,({s}_{r}+1)}{{s}_{r}{({s}_{r}+1)}^{{T}_{i}+1}}\right)$. Meanwhile, the foregone income due to pandemic restrictions is given by:

$${Y}^{CQ}\left(t\right)=\kappa w\phi\,\left(\bar{S}\left(t\right)+\bar{E}\left(t\right)+\bar{I}\left(t\right)+R\left(t\right)\right).$$

(4)

The combination of the first version of the epidemiological model and the economic model shall be referred to in this paper as the FASSSTER Integrated Model I. A more detailed discussion of this model and its parameters can be seen in de Lara-Tuprio et al. (2022b).

The latter half of 2021 saw a huge surge of COVID-19 infections due to the highly virulent Delta variant. It was also during this period when the government implemented wide-scale vaccination in the country. Hence, the compartmental model had to be extended to account for the vaccinated population. The susceptible population was split into three compartments according to vaccination status: unvaccinated (S), partially vaccinated (V₁) and fully vaccinated $\left({V}_{2}\right)$. Unvaccinated individuals move to V₁ or V₂ depending on the kind of vaccine they receive. In particular, they move to V₁ if they receive the first of a two-dose COVID-19 vaccine such as Sinovac and Pfizer-Biontech, or they move to V₂ if they receive a single-dose COVID-19 vaccine such as Janssen. Moreover, partially vaccinated individuals in V₁ move to V₂ once they receive their second dose. From these compartments, individuals then transition to the corresponding exposed compartment (E, E₁ or E₂) when they have been infected with the SARS-CoV-2 virus. Once they become infectious, they either move to the corresponding asymptomatic compartments (${I}_{a},{I}_{1}^{a},{I}_{2}^{a}$) or symptomatic compartments (${I}_{s},{I}_{1}^{s},{I}_{2}^{s}$). Individuals from these infectious compartments who have been confirmed via RT-PCR test then transfer to compartment C. This compartment indicates the active cases in the population, where they are assumed to be isolated and receiving treatment. Finally, all individuals who recover from the disease transition to the R compartment. This second version of the epidemiological model is illustrated in Fig. 1.

Fig. 1: Second version of the epidemiological model.

This is the flow diagram representing COVID-19 disease transmission dynamics of the second epidemiological model (Estuar et al. 2022; Teng et al. 2024).

The additional compartments in this updated model resulted in additional parameters and transition flows. To be specific, given the new compartments V₁ and V₂, parameters that capture vaccine effectiveness have been introduced. These include parameters k₁ and k₂ which reduce disease transmissions for the partially vaccinated individuals and fully vaccinated individuals, respectively. The effects of vaccines are also present in the transition flows from the exposed to the infectious compartments, given by ${\alpha }_{1}^{a},{\alpha }_{2}^{a}$ for the asymptomatic, and ${\alpha }_{1}^{s},{\alpha }_{2}^{s}$ for the symptomatic. The rate of COVID-19 mortality is also assumed to be reduced through vaccination. Particularly, among partially vaccinated individuals, the COVID-19 death rate is given by ${\hat{\varepsilon }}_{I}=\hat{k}\cdot {\varepsilon }_{I}$, where $\hat{k}$ is a reduction factor associated to vaccination. In contrast, it is assumed that fully vaccinated individuals in ${I}_{2}^{s}$ will not die from the disease. A complete discussion of the model and its parameters can be found in Teng et al. (2024).

The changes in the epidemiological model resulted in minor adjustments to the economic model. The dynamics of the economic variable Y^CQ takes the same form as Eq. (2), where $\bar{S}\left(t\right)=S\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{2}{V}_{j}\left(t\right)$, $\bar{E}\left(t\right)=E\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{2}{E}_{j}\left(t\right)$ and $\bar{I}\left(t\right)={I}_{a}\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{2}{I}_{j}^{a}\left(t\right)$. Hence, ${Y}^{CQ}\left(t\right)$ follows the same expression as in Eq. (4), that is:

$${Y}^{CQ}\left(t\right)=\kappa w\phi \left(\bar{S}\left(t\right)+\bar{E}\left(t\right)+\bar{I}\left(t\right)+R\left(t\right)\right).$$

On the other hand, the dynamics of Y^E has to be expressed in an expanded form due to varying mortality rates of the different infectious compartments. That is:

$$\begin{array}{ll}\frac{d{Y}^{E}}{dt}\,=\,\mathop{\sum}\limits_{k=15-{T}_{5}}^{{T}_{1}}\frac{{\iota }_{1}\left[{\varepsilon }_{I}\frac{d{I}_{SS}}{dt}\,+\,{\varepsilon }_{T}\frac{dC}{dt}\right]z}{{\left(1+{s}_{r}\right)}^{k}}+\mathop{\sum }\limits_{i=2}^{4}\mathop{\sum }\limits_{k=0}^{{T}_{i}}\frac{{\iota }_{i}\left[{\varepsilon }_{I}\frac{d{I}_{SS}}{dt}\,+\,{\varepsilon }_{T}\frac{dC}{dt}\right]z}{{\left(1+{s}_{r}\right)}^{k}}\\ \qquad\quad\,+\,\kappa w\left(\left(1-{\varepsilon }_{T}\right)\frac{dC}{dt}+\frac{d{I}_{SUM}}{dt}-{\varepsilon }_{I}\frac{d{I}_{SS}}{dt}\right)\end{array}$$

(5)

where ${I}_{SS}\left(t\right)={I}_{s}\left(t\right)+\hat{k}{I}_{1}^{s}\left(t\right)$ and ${I}_{SUM}\left(t\right)={I}_{s}\left(t\right)+\mathop{\sum}\nolimits_{j = 1}^{2}{I}_{j}^{s}\left(t\right)$. This can then be solved as

$${Y}^{E}\left(t\right)={L}_{1}{I}_{SS}\left(t\right)+{L}_{2}\,C\left(t\right)+{L}_{3}{I}_{SUM}\left(t\right)$$

(6)

where ${L}_{1}=\left(z\left({K}_{1}+{K}_{2}\right)-\kappa w\right){\varepsilon }_{I},{L}_{2}=z\left({K}_{1}+{K}_{2}\right){\varepsilon }_{T}+\kappa w\left(1-{\varepsilon }_{T}\right)$ and L₃ = κw. The second version of the epidemiological model together with the adjusted economic model shall be referred to in this paper as the FASSSTER Integrated Model II.

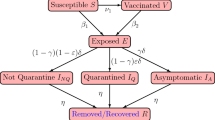
The third version of the epidemiological model was formulated in response to the spread of the Omicron variant in the country at the start of year 2022 (UNDP 2022). The new variant was characterized by its heightened transmissibility and immune evasiveness compared to the previous circulating strains in the country (Bálint et al. 2022; Ke et al. 2022; Manathunga et al. 2023). Moreover, booster doses became more widely administered during this period. To account for these, another susceptible compartment V₃ was added to the model, consisting of individuals who received an additional dose after completing their primary doses, that is, from V₂. Furthermore, unlike the previous two versions of the model, recovered individuals may be reinfected with COVID-19. Individuals from V₃ and R who become infected move to their corresponding exposed compartments E₃ and E₄, respectively, after which they become either infectious asymptomatic (${I}_{3}^{a},{I}_{4}^{a}$) or infectious symptomatic (${I}_{3}^{s},{I}_{4}^{s}$). These individuals may either get detected afterwards and move to C, or remain undetected. Upon recovery, these individuals move to compartment R. The diagram for this epidemiological model is presented in Fig. 2 (see also Fig. 2 of UNDP (2022).

Fig. 2: Third version of the epidemiological model.

This is the flow diagram representing COVID-19 disease transmission dynamics of the third epidemiological model (Estuar et al. 2022; UNDP 2022).

It is well-studied in literature that boosted individuals have a higher degree of protection against infection compared to those who only completed their primary doses (Zhu et al. 2022). Thus, the transmission rate from V₃ to the exposed compartment incorporates a reduction factor k₃, that is lower than k₁ and k₂. Likewise, recently recovered individuals acquire protective immunity against infection for a certain period of time (Kojima and Klausner 2022). Hence, a reduction factor k₄ is also introduced in the transmission rate from R. Booster doses and previous infection also affect the transition parameters ${\alpha }_{3}^{a},{\alpha }_{4}^{a}$ (asymptomatic) and ${\alpha }_{3}^{s},{\alpha }_{4}^{s}$ (symptomatic) towards the infectious compartments. An additional mortality rate $\tilde{\varepsilon}_I$ is applied to the compartments ${I}_{2}^{s}$ and ${I}_{4}^{s}$ which, similar to ${\hat{\varepsilon }}_{I}$, is expressed as a percentage $\tilde{k}$ of ε_I. It is also assumed that there are no COVID-19 deaths among infectious individuals in ${I}_{3}^{s}$ due to the increased protection offered by booster doses.

For the economic model, the dynamics of Y^CQ has the same form as Eq. (2), where $\bar{S}\left(t\right)=S\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{3}{V}_{j}\left(t\right)$, $\bar{E}\left(t\right)=E\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{4}{E}_{j}\left(t\right)$ and $\bar{I}\left(t\right)={I}_{a}\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{4}{I}_{j}^{a}\left(t\right).$ This implies that ${Y}^{CQ}\left(t\right)$ is given by Eq. (4) when solved. For the variable Y^E, the dynamics is also given by Eq. (5), where ${I}_{SS}\left(t\right)={I}_{s}\left(t\right)+\hat{k}{I}_{1}^{s}\left(t\right)+\tilde{k}\left({I}_{2}^{s}\left(t\right)+{I}_{4}^{s}\left(t\right)\right)$ and ${I}_{SUM}\left(t\right)={I}_{s}\left(t\right)+\mathop{\sum }\nolimits_{j = 1}^{4}{I}_{j}^{s}\left(t\right)$. Solving for Y^E then yields an expression given by Eq. (6). This economic model combined with the third version of the epidemiological model shall be referred to as the FASSSTER Integrated Model III.

Parameter estimation

Epidemiological parameters

The epidemiological model that was developed and updated through time has several parameters that describe the spread of COVID-19 in the population. These parameters are estimated using a variety of methods and sources. Details on parameter values and estimation procedures for the first two versions of the epidemiological model can been seen in Supplementary Section II (Tables 3 and 4) and in de Lara-Tuprio et al. (2022a, b), Teng et al. (2024).

For the third version of the epidemiological model, the transmission reduction parameter λ is estimated using the same method presented in Teng et al. (2024), that is, λ is fitted to the active COVID-19 case data using the L-BFGS-B Optimization through the optimparallel package (Gerber and Furrer 2019). The parameter λ is then decomposed into several components such as population mobility level (γ), degree of compliance to Minimum Public Health Standards or MPHS (η) and its corresponding level of protection (ζ). This is expressed mathematically using the equation $1-\lambda =\left(1-\Lambda \left(1-\gamma \right)\right)\left(1-\zeta \eta \right)$, where 0 < ζη < 1 and ζ is assumed to be equal to 85%. Moreover, the component γ is based on Google mobility data for retail and recreation. Finally, Λ is taken from a previous derivation in April 2020, where the mobility level γ is assumed to be zero (de Lara-Tuprio et al. 2022a).

Reduction parameters k₁, k₂, k₃ and k₄ to the transmission rate are dependent on the level of protection against COVID-19 infection provided by vaccines (for k₁, k₂, k₃) and previous infection (for k₄). These quantities vary every month, and the changes are based on the waning effectiveness of vaccines against infection and the cumulative number of doses administered for each vaccine type/brand. To estimate ${\alpha }_{j}^{s},{\alpha }_{j}^{a}$ for j = 1, 2, 3, 4, a quantity is computed based on vaccine effectiveness against infection and against symptomatic disease. The derivation is to be done for each j, after which it is applied as a reduction factor to the transfer rate α_s to arrive at ${\alpha }_{j}^{s}$. The relation ${\alpha }_{j}^{a}+{\alpha }_{j}^{s}=\frac{1}{\tau }$, where τ is the incubation period, is then applied to derive ${\alpha }_{j}^{a}$ for each j. Lastly, the mortality rate ε_I is calculated based on the linelist data, and is utilized in all versions of the epidemiological model, whereas ${\hat{\varepsilon }}_{I},{\tilde{\varepsilon }}_{I}$ are estimated by applying reduction factors $\hat{k}$ and $\tilde{k}$, respectively, to ε_I based on the effectiveness of vaccines against symptomatic disease. See Supplementary Section II for further details on the estimation procedure of these epidemiological parameters.

Economic parameters

The parameters in the economic model follow the derivation of the number of deaths according to age groups, their corresponding average remaining number of years, and the ratio between the employed over the total population of the subject region in de Lara-Tuprio et al. (2022b). Meanwhile, the valuation of economic losses are operationalized as wage losses or foregone income. The main parameter corresponding to do this is the average daily basic pay w, which can be derived as the weighted average of daily basic pay in a region from the Philippine Statistics Authority’s 2018 Labor Force Survey (LFS). Previously released in the first month of each quarter (Philippine Statistics Authority 2023), the LFS contains data pertaining to workers’ employment sectors as defined under the Philippine Standard Industrial Classification (PSIC). The 2018 LFS is used to capture the pre-pandemic baseline scenario that coincides with the year when the Family Income and Expenditure Survey (FIES) is conducted. During these rounds, the PSIC of workers is available at the four-digit level, or the more disaggregated classification, while non-FIES coinciding rounds give the PSIC of workers at the two-digit level only. These industrial classifications are useful in the derivation of the labor displacement rates.

On the other hand, the average annual income z of an individual is derived as a product of the daily basic pay w, the 22.5 working days in a month, and the 12 months in a year, that is, z = w ⋅ 22.5 ⋅ 12.

The changes in pandemic restrictions are operationalized in the integrated model as the labor displacement rate. The displacement rate pertains to the proportion of the working population that cannot come to work due to the restricted maximum operating capacity in an individual’s sector of work. The maximum operating capacity is adjusted following changes in the pandemic restriction policy of the government. The displacement rate is subsequently calculated using the LFS and the Department of Trade and Industry’s (DTI) guidelines in economic activity. The LFS allows us to map the sector of employment of workers at a more disaggregated level. Meanwhile, the guidelines released by the DTI gives us the maximum operating capacity per sector (Department of Trade and Industry 2020a, b; 2021a, b). The sectors under DTI’s releases are classified according to four categories, where lower categories are considered as essential sectors (see Supplementary Table 7). However, note that some sectors are reclassified from a higher category to a lower category depending on the government policy to gradually reopen the sectors. For instance, by 2021, sports facilities, libraries, and museums have transitioned from Category IV to Category III (Department of Trade and Industry 2021b).

The maximum operating capacities are lower for sectors belonging to higher categories. This can be observed for sectors in Category IV during the onset of the COVID-19 pandemic, where under more stringent pandemic restrictions, onsite operations were completely disallowed (Department of Trade and Industry 2020b). Over that period, these sectors can only also operate at their 50% capacity under the least restrictive pandemic policy (Department of Trade and Industry 2020b).

The pandemic restrictions imposed by the government mainly involve the following policy interventions: the Community Quarantine (CQ) and the Alert Level (AL) System. CQ policies were implemented from the onset of the pandemic until the third quarter of 2021, while the AL system was fully implemented from the fourth quarter of 2021. These are highlighted in the DTI guidelines. The CQ comprises of four levels that are relatively more stringent compared to the AL restrictions (de Lara-Tuprio et al. 2022b; Inter-Agency Task Force 2020, 2021a). These restrictions are enumerated as follows, arranged from the least to the most stringent: Modified General Community Quarantine (MGCQ), General Community Quarantine (GCQ), Modified Enhanced Community Quarantine (MECQ), Enhanced Community Quarantine (ECQ). Under ECQ, the strictest form of quarantine classification, stay-at-home measures are enforced while only essential sectors are allowed to remain operational. On the other hand, under GCQ, the restrictions are loosened to allow for increased mobility and economic activities. The quarantine classifications MECQ and MGCQ are slightly less strict versions of ECQ and GCQ, respectively. For additional details, the different CQ classifications are described in Table 1 of de Lara-Tuprio et al. (2022b).

The AL restrictions comprise of five levels (see Table 1), and aim to control the transmission of the virus on 3Cs: crowded places, closed contact settings, and closed spaces with poor ventilation (Inter-Agency Task Force 2021a). The highest level loosely reflects the restrictions imposed under the strictest community quarantine restriction (Department of Trade and Industry 2020a; 2021a, b). The four lower ALs are generally more relaxed and would allow sectors to operate at their 50% to 100% capacity. Moreover, under the lowest AL (Alert Level 1), all economic sectors are allowed to operate at their full capacity (Department of Trade and Industry 2021a). Hence, no labor displacement occurs under the said level of restriction.

Table 1 Operational definition of alert levels (Inter-Agency Task Force 2021a).

It is further understood that these restrictions are imposed at a provincial or regional level. However, during the AL system, looser province- or city-wide restrictions may be implemented together with more stringent granular-level restrictions (i.e., street level, village level). However, granular restrictions cannot be captured in the model anymore.

Using this information, the various lockdown restrictions in the country are translated into labor force displacement rates. The maximum operating capacity per sector is manually mapped with the sectors listed in the LFS. From here, the labor force displacement rates in a region can be calculated by designating the percentage maximum operating capacity of the sector where each representative individual j works in. Formally, the displacement rates are calculated as follows (de Lara-Tuprio et al. 2022b):

$$\varphi =\frac{\mathop{\sum }\nolimits_{j = 1}^{n}{p}_{j}{x}_{j}}{\mathop{\sum }\nolimits_{j = 1}^{n}{p}_{j}}$$

(7)

where x_j is the maximum operating capacity for j’s sector of work, and p_j is the probability weight assigned to individual j. The corresponding numerator and denominator are summed up to the size of the employed population in NCR, denoted by n. Given the sample frame of the LFS, the labor force displacement rates can be calculated according to the various regions and provinces of the Philippines. Further, the same procedure can be applied whether we use the CQ policies or the subsequent AL system.

Model applications and results

This section illustrates how integrated models can provide significant insights to inform policy, with particular focus on the National Capital Region (NCR). Different periods of the pandemic with varying epidemiological and social context are considered, to which we apply a version of the integrated model.

FASSSTER Integrated Model I application

From March 22 to April 4, 2021, the National Capital Region and some neighboring provinces, all under GCQ, were placed in a setup known as the “NCR Plus bubble” (Garcia 2021; Inter-Agency Task Force 2021b; Medialdea 2021). This measure was implemented to address the rising number of cases in the said localities, with the goal of containing the spread of COVID-19 within these areas. It was later reported that the surge was due to the Alpha and Beta variants of the COVID-19 virus. The bubble policy, however, did not seem effective in preventing further rise in the number of cases, so a more stringent lockdown policy after April 4 was considered.

Figure 3 shows projections of active cases in NCR generated on March 31, 2021 for the period April 1–30 using the first version of the compartmental model. Four CQ policies (ECQ, MECQ, GCQ, MGCQ) beginning April 5 and two values of the parameter δ_s (13%, 20%) for each CQ policy were considered, thereby producing 8 scenarios. Note that δ_s represents the rate at which infectious symptomatic cases were detected. It was assumed in the epidemiological model that an infected individual was immediately isolated upon detection. The value of 13% for δ_s was based on the actual data; while 20%, which denotes an average of 5 days between symptom onset and detection, represented an improvement over the actual rate. Expectedly, a higher detection rate resulted in lower case numbers. Since the NCR had never been previously placed under MGCQ at that time, it was assumed that MGCQ would reduce mobility in the region to 80% of pre-pandemic levels. On the other hand, for each CQ policy except MGCQ, it was assumed that the corresponding mobility was equivalent to the mobility when the same CQ policy was in place in 2020.

Fig. 3: Scenario projections of active cases in NCR.

These are the projected active cases using the first version of the epidemiological model for April 2021 across different scenarios based on CQ policy and detection rate δ_s.

The quantities Y^E and Y^CQ, which represent foregone income due to sickness/death and due to pandemic restrictions, respectively, were estimated by applying the FASSSTER Integrated Model I. Their graphs are presented in Fig. 4. The total foregone income, or the sum of the values of these two variables, is shown in Fig. 5.

Fig. 4: Projected foregone income in NCR.

These are the graphs of a Y^E and b Y^CQ over the period April 2021 across different scenarios based on CQ policy and detection rate δ_s.

Fig. 5: Projected total foregone income in NCR.

These are the graphs of the sum of Y^E and Y^CQ over the period April 2021 across different scenarios based on CQ policy and detection rate δ_s.

Note that the value of Y^E was generally lower while Y^CQ was higher when the CQ policy was more stringent. However, the value of Y^CQ dominated the sum of the two variables because it accounted for most of the population. Hence, for δ_s = 20% in particular, the sum was higher when the CQ policy was stricter.

The trade-off between total economic losses, given by foregone income, and healthcare utilization rate (HCUR), measured as the utilization percentage of designated ICU beds, was also analyzed. Based on data, there were 800 ICU beds in NCR at that time. Results are shown in Table 2. The third column indicates that in all scenarios there was a need to increase the number of ICU beds, and subsequently other health requirements, at some point during the period considered. The last scenario, MGCQ with 13% detection rate, was not feasible due to the extreme burden that this would pose on the health system. On the other hand, the GCQ scenario with 20% detection rate provided a better outcome than both ECQ scenarios. Despite similar levels of maximum HCUR, the former scenario yielded a significantly lower total foregone income.

Table 2 Total foregone income and maximum HCUR for April 2021 under different CQ and δ_s scenarios.

FASSSTER Integrated Model II application

The COVID-19 vaccination program in the Philippines commenced as early as the first quarter of 2021 (Congress of the Philippines 2021), but wide-scale vaccination efforts were initiated only in the second half of the year. The first to arrive were Sinovac vaccines from China (dela Cruz 2021; Department of Health 2021). Sinovac accounted for 63% of all first doses and 73% of all second doses administered in NCR as of July 31, 2021 based on the data provided by the National Vaccination Operations Center (NVOC). Inactivated vaccines, predominantly composed of Sinovac, remained the biggest chunk of cumulative doses every month, although mRNA vaccines steadily increased its share over time until the end of the year. Figure 6 shows the percentages of three vaccine groups over time in the second half of 2021.

Fig. 6: Percentage of cumulative number of doses administered per vaccine type.

The graphs represent the cumulative a first doses and b second doses per vaccine type as percentage of the total number of vaccines administered over time.

Several sectors questioned the effectiveness of the Sinovac vaccine; in fact, a petition was filed with the Supreme Court to stop the government from procuring and administering this brand of vaccine (Buan 2021; Gregorio 2020; Reuters 2021; Sabillo 2021). In addition, literature indicated that both first and second doses of Sinovac were less effective against both infection and symptomatic disease compared to the respective doses of mRNA vaccines (Muena et al. 2022; Pormohammad et al. 2021).

Thus, we consider in this subsection how the case trajectory over the period July to December 2021 might change under the counterfactual scenario in which both first dose and second dose of vaccines administered in NCR were all of the mRNA type. We then compare it with the baseline scenario given by the model output fitted to the actual data of active cases. Note that the actual data reflected the mixture of various types of vaccines administered during the period. The following events that took place over the same period are also worth mentioning: (1) In August–September, a surge due to the Delta variant occurred in NCR (and other parts of the country), prompting the government to impose ECQ for 2 weeks, followed by MECQ in NCR; (2) The government shifted policy from Community Quarantine to Alert Level System, with NCR as the pilot area in mid-September. Table 3 summarizes the community quarantine policies and alert levels implemented in NCR for the period July 1–December 31, 2021³.

Table 3 Timeline of restriction policies in NCR.

In Fig. 7a, the outputs under the two scenarios are presented together with the actual data on active cases. It is evident that the counterfactual scenario has resulted in significantly lower active case numbers compared to the baseline; this is due to the higher effectiveness of mRNA vaccines. The highest difference between the actual data and the output of the counterfactual scenario occurred in mid-September. Specifically, the active case numbers of the latter scenario was only around 50% of the actual number of active cases on that day. On the other hand, it is possible that with lower case numbers due to more effective vaccines, the government might not resort to the very restrictive ECQ in August. Imposing MECQ or GCQ instead would result in higher mobility and contact rate, potentially elevating the case numbers close to the actual data.

Fig. 7: Scenario projections of the FASSSTER Integrated Model II.

These are the model outputs on a active cases and b foregone income.

Assuming no change in CQ or AL timeline as indicated in Table 3, the total foregone income corresponding to the baseline scenario is around 164 trillion pesos, while the counterfactual scenario yields a loss close to this amount, around 161.5 trillion pesos.

Despite the significant drop in the case numbers under the counterfactual scenario, the decrease in the total foregone income is only 1.5% of the baseline. In fact, the maximum daily difference in economic losses is only 0.02% of the baseline. Figure 7b shows the graphs of the two economic variables for the two scenarios. The graphs of Y^CQ are almost identical for the two scenarios. The difference is seen only in the other variable Y^E. However, its contribution to the total foregone income is only minimal compared to Y^CQ. It should be recalled that Y^CQ is computed over the majority of the population in NCR at that time. This explains why the total foregone income under the two scenarios are very close to each other.

FASSSTER Integrated Model III application

When the COVID-19 case numbers became manageable after the Delta surge, the government had a paradigm shift beginning November 2021 to slowly reopen the economy. The Community Quarantine policies were replaced by an Alert Level System that imposed restrictions only on crowded places, closed contact settings, and closed spaces with poor ventilation.

However, the spread of the Omicron variant in January 2022 led to a surge of infections that surpassed previous reported numbers, resulting in reduced economic activities and slowing down progress towards recovery. It should be noted though that even if the Omicron variant was a lot more transmissible and immune escaping (He et al. 2021), it generally caused less severe disease, and it was associated with fewer ICU admissions and deaths compared to earlier SARS-CoV-2 strains (Wee and Elemia 2022). Consequently, the healthcare system remained stable despite high infection numbers as hospitalization rates remained low during the Omicron surge.

It was only in March 2022 when the government finally decided to put NCR and several parts of the country under AL1 (Inter-Agency Task Force 2022). Due to low healthcare utilization rates observed until the end of February 2022, there was a question whether it was more beneficial to fully open the economy much earlier. Conversely, it was also important to consider the economic impact if NCR and its neighboring areas remained under a more restrictive Alert Level for a longer period; this was a possible policy decision as several mass gatherings took place during the campaign period leading up to the May 2022 national elections (Rappler 2022).

In this subsection, we consider three scenarios on the Alert Level imposed in NCR for the period January to June 2022. The first is the baseline scenario (Scenario 1) which corresponds to what actually occurred—AL2 from January to February, followed by AL1 from March to June. In the second and third scenarios, it is assumed that NCR has been placed under one alert level for the whole period: AL1 for Scenario 2, and AL2 for Scenario 3. For each of these scenarios, we calculate the foregone income using the integrated model.

For the baseline scenario, the output of the compartmental model is fitted to the actual data of active cases. For the alternative scenarios, the output of the model is based on assumptions on the mobility. Figure 8 shows the graph of Google mobility data for retail and recreation in NCR over the period of January to June 2022, with the 100% horizontal line representing the pre-pandemic mobility level.

Fig. 8: Google mobility data for retail and recreation in NCR.

The mobility data is for the period of January to June 2022.

Observe that mobility for retail and recreation are nearly the same for February and March, with certain points in February even registering higher levels. This is despite NCR being under AL2 in February and AL1 in March. Moreover, there seems to be minimal increase in mobility for the same sector until June even when NCR was already under AL1; it remained below the pre-pandemic level. Based on these observations, the following assumptions are made. For Scenario 2 (AL1), the February mobility is as recorded in the Google mobility data, while the January mobility is obtained by extending a trend line fitted to the February data. For Scenario 3 (AL2), it is assumed that retaining AL2 for the period March to June will not alter the mobility level. Hence, in effect, the outputs of the compartmental model for Scenarios 1 and 3 are the same. Moreover, the output for Scenario 2 is very close to the other two scenarios. See graphs in Fig. 9a.

Fig. 9: Scenario projections of the FASSSTER Integrated Model III.

These are the model outputs on a active cases and b foregone income.

Although the epidemiological curves corresponding to the three scenarios are very close to each other, estimates of the total foregone income are quite different. This is mainly because the displacement rate during AL1 is 0, which greatly reduces the value of Y^CQ under that AL scenario. Table 4 summarizes the results, while Fig. 9b shows the graphs of the total foregone income over time.

Table 4 Total foregone income under different AL scenarios.

As shown above, the total foregone income is lowest under Scenario 2, where NCR is under AL1 the whole period. This essentially means imposing AL1 in NCR as early as January. This, however, was not an easy decision for the government. There were a lot of uncertainties about the virulence of Omicron when the variant first struck the country in January. Moreover, seeing the steep rise in the case numbers, there was a concern that the health system might be overwhelmed.

Policy implications

Restriction policies, while meant to slow down disease spread, had detrimental social and economic effects in the country. According to NEDA estimates, GDP growth was shaved off by 0.28 percentage points every week under ECQ/MECQ restrictions in the NCR and adjacent regions. This was equivalent to around 2.1 billion pesos in lost wages a day (National Economic and Development Authority 2021). Moreover, joblessness became more prevalent, especially during the early part of the COVID-19 pandemic when the restrictions enforced were at their strictest. Based on its regular Labor Force Survey (LFS), the PSA reported that the official unemployment rate went to a high of 17.6% in April 2020 compared to 5.13% in the same month in 2019 (Philippines Statistics Authority 2020). The impact of job loss was felt more by individuals and households from the marginalized sectors, including those who were reliant on informal jobs and other non-regular forms of employment (Ducanes et al. 2021). Hunger also became more widespread, tallying a new record high of 21.1% in 2020 that was more than twice the 2019 pre-pandemic year at 9.3% according to the Social Weather Stations (Social Weather Stations 2020).

We reflect on the policy implications of applying the three FASSSTER integrated models discussed in the previous section. Given near perfect hindsight, we analyze what has already transpired, as well as potential alternative outcomes.

Table 2 suggests that improving the health system capacity to detect-isolate-and-treat COVID-19 cases is better, both economically and epidemiologically, than imposing a blanket lockdown. This, however, was not always a ready option especially during the earlier part of the pandemic when everyone was still trying to understand the nature of the COVID-19 disease. Moreover, such improvement could not be achieved overnight, as it required budget and strategic planning that involved all stakeholders, including various government agencies. Hence, despite their detrimental effects to the economy, community quarantines were needed to be imposed on certain periods to ensure that our health systems remained stable and functional.

Based on the outputs of the integrated model shown in the “FASSSTER Integrated Model II application” section, a more effective vaccine, such as mRNA, could have provided a wider policy space for decision makers to maneuver. The significant decrease in the number of active cases could have allowed the government to choose a less restrictive policy, which would undeniably result in lower economic loss in terms of foregone income. While such a policy would push up the case numbers due to higher mobility and contact rate, it would have come with an upside of lesser economic burden.

Around the middle of January 2022, the epidemiological curve in NCR was steeply downwards (Fig. 9a) and this presented an opportunity of easing pandemic restriction with the objective of reducing foregone income. This is illustrated by Scenario 2 in Table 4. However, the government delayed the decision to shift to the less strict Alert Level I in NCR until the beginning of March 2022 despite the low number of recorded cases in the weeks prior. This cautious approach in decision making was driven by concerns where the COVID-19 situation might worsen once again. However, such an approach partially ignored the social and economic implications of policy decisions. Indeed, a few studies showed that on average, economic or social risks were not sufficiently considered (Shaw and Scully 2023; Siegrist et al. 2021). Balancing health and economic aspects of public policies was a difficult task, especially in the midst of a crisis where an immediate response was required. The policy trade-off also had far-reaching consequences to the daily lives of individuals, and hence required further study that could benefit future policy-making efforts.

The constantly changing population mobility, public behavior and the new emerging variants of the virus necessitated frequent updates on health policies and interventions within very short periods of time. The latter, however, adversely affected economic activities that usually operated and relied on longer term policy arrangements. Correspondingly, the FASSSTER integrated model captured the said evolving epidemiological and social context, thereby making it possible to provide and visualize economic assessment.

Conclusion

Health emergencies such as the COVID-19 pandemic has taught us that modeling plays a vital role in policy-making. More so, the use of integrated models, specifically combining health and economics, provides a wider perspective on the effect of the pandemic to the population. In this study, we have demonstrated how such models can provide insights to guide future COVID-19 responses and other disease control initiatives. Using our results, policymakers can better appreciate the interrelated health and economic implications of different policy decisions, and take them into account when dealing with similar future challenges. Thus, our work contributes to the ongoing discourse of identifying important lessons and experiences from the COVID-19 pandemic and utilizing these for crafting public policies towards pandemic preparedness.