The chain reaction of carbon emission trading policy in efficiency and rebound: evidence from spatial perspective in China

Abstract

Evaluating and improving environmental policies are significantly impacted by the question of whether increased energy efficiency results in an energy rebound effect. Utilizing carbon emission trading policies (CETP) as a quasi-natural experiment, this study created a spatial difference-in-differences (SDID) model with an endogenous spatio-temporal weight matrix. The analysis applied Chinese provincial panel data from 2008 to 2018 to assess the direct and spatial spillover effects of CETP on total factor carbon emissions efficiency (TCEE). On this premise, it is further explored to see if CETP causes the energy rebound (ER) effect via TCEE. It revealed that CETP exhibited positive spatial spillover effects on TCEE. Specifically, CETP was observed to enhance TCEE in pilot areas through green innovation (GI) but impede TCEE in neighboring regions due to siphoning and pollution haven effects. Further research, however, revealed that the CETP increased the ER in the pilot areas by improving the TCEE, causing the policy to fall into the trap of ineffective emission reduction, but it had a warning effect on the nearby areas. This study is of great significance for improving the emission reduction policy system and promoting the “dual carbon” goals.

Introduction

Increased extreme weather events (Shi et al., 2022), decreased biodiversity (Razzaq et al., 2021), and other negative effects of global warming brought on by excessive greenhouse gas emissions are gravely endangering ecosystems and the development of sustainable societies (Wei et al., 2021). Approximately 77% of total greenhouse gas emissions are attributed to carbon dioxide, making it the primary contributor to global warming (Ghosh et al., 2022). As the largest carbon emitter (Xu et al., 2023), China’s environmental issues are of great concern. By 2012, China emitted 28.8% of the world’s carbon dioxide emissions, whichby 2022 had reached 13.9 billion tons (Jiang et al., 2024; Li and Cheng, 2020). Under pressure to significantly reduce its carbon dioxide emissions, China pledged to achieve a “dual carbon” objective, aiming for a peak in carbon emissions by 2030 and carbon neutrality by 2060. Besides, the “14th Five-Year Plan” also focuses on controling energy consumption and intensity and enhancing ecosystem carbon sink capacity. Consequently, low-carbon development is not only a global imperative but also an inevitable trend for China.

To transition towards a low-carbon pathway and achieve a green economy, governments worldwide are exploring effective environmental regulatory measures (Lu et al., 2024). With the introduction of market mechanisms into environmental regulation, leveraging market-based approaches to achieve emission reductions has become increasingly important (Zhao et al., 2015). Specifically, the carbon emissions trading mechanism proposed in the 1997 Kyoto Protocol has been particularly favored (Weng and Xu, 2018). This market-based approach relies on price mechanisms, treating carbon emission rights as tradable commodities (Zeng et al., 2024). It aims to reduce greenhouse gas emissions through the cost pressures of purchasing carbon emission rights and the revenue incentives from selling them (Wang et al., 2024b). By 2018, 51 countries and regions worldwide had either implemented or were in the process of planning carbon emission trading systems (Qi et al., 2021), and by 2021, 33 mandatory carbon trading systems were in operation (Luo et al., 2022). 2023, several countries, including Indonesia, have progressively announced the establishment of carbon markets (Fu, 2024).The “Notice on Pilot Carbon Emissions Trading”, published in October 2011 by China’s National Development and Reform Commission, officially endorsing the initiation of carbon emissions trading in seven provinces and cities: Beijing, Tianjin, Shanghai, Hubei, Chongqing, Guangdong, and Shenzhen. The carbon emissions in these pilot areas accounted for around 20% of the total Chinese carbon emissions (Peng et al., 2021), geographically spanned the east coastal region and extended to the central region, and had high representativeness (Weng and Xu, 2018). In 2013, 445,500 tonnes of carbon were traded in the pilot areas, which by 2019 had reached 26.11 million tonnes (Wang et al., 2022), a cumulative trading volume of 1.562 billion yuan (Yu and Li, 2021). During the pilot period, 70% of the participating companies experienced reductions in both carbon emission intensity and total emissions (Wang et al., 2024a). Since the launch of the national carbon market in 2021, by the end of 2023, the cumulative carbon trading volume reached approximately 440 million tonnes, with a total transaction value of 24.9 billion yuan (Su and Chen, 2024).

The goal of China’s low-carbon development is to lower carbon emissions while fostering economic growth. Thus, it is not adequate to take into account merely how the CETP affects carbon emission reduction. One important metric for assessing whether CETP achieves a win-win situation for the economy and the environment is total factor carbon emission efficiency (TCEE), which can fully depict the relationship between economic growth and carbon emissions. Studies have suggested that CETP has had a direct effect on energy efficiency and green total factor productivity (Yu et al., 2022; Zhou and Qi, 2022) and that it also has had a spatial spillover effect (Li et al., 2022). However, inter-regional interactions frequently exhibit cross-period neighborhood effects (Fan and Darren, 2018), necessitating a thorough examination of the CETP impacts on TCEE from a temporal and spatial perspective.

Porter’s hypothesis claims that reasonable environmental regulations directly promote green innovation (GI) (Porter and Linde, 1995) and positively affect TCEE. However, according to the basic concept of the energy rebound effect, improving energy efficiency is the key factor leading to energy rebound. TCEE improvements could reduce the cost of energy use and generate greater revenue per carbon emissions unit; therefore, based on the profit maximization principle, enterprises may boost demand for energy services, which could partially or totally cancel out the reduction in carbon emissions brought about by TCEE improvement, cause an ER effect, and trap CETP into ineffective emission reduction. Therefore, in order to achieve the low-carbon sustainable development goals, it is crucial to assess the spatial spillover effect over time and GI mechanism of CETP on TCEE and further investigate the potential ER effect caused by TCEE improvement on this basis.

The study’s primary contributions and potential innovations are outlined below. First, given that the regional TCEE exhibited an intertemporal neighborhood relationship, this study took the time effect into account on the basis of the spatial effect, and constructed an endogenous spatio-temporal weight matrix-based spatial difference-in-differences (SDID) model to assess the CETP spatial effect on the TCEE evolution over time. Second, to thoroughly assess the CETP effects, the CI, TCEE and ER were combined into a unified analysis framework. This research can enrich the literature and evidence on the CETP driving and hindering effects, providing empirical support and theoretical reference for improving the CETP system and promoting China’s “dual carbon” goals.

The subsequent sections of this paper are structured as follows: Section 2 provides a summary of related studies, Section 3 establishes the theoretical model and presents the research hypotheses, Section 4 outlines the research methods and data sources, Section 5 offers the sresults analysis, and Section 6 summarizes the main conclusions and outlines the policy implications.

Literature review

CETP and carbon emissions reductions

In 1997, the Kyoto Protocol first introduced carbon trading as a crucial market-based mechanism for reducing carbon emissions (Adediran and Swaray, 2023). Since then, the CETP have gained significant attention globally. Since the early 20th century, developed countries such as Europe and the United States have implemented CETP. In 2003, the United States established the world’s first legally binding greenhouse gas trading platform, the Egal Climate Exchange (Hou et al., 2024). The European Union Emissions Trading System (EU-ETS) has been in operation since January 2005 (Hossain et al., 2024), involving more than 11,000 high-energy-consuming companies (Feng et al., 2024), which account for 45% of the total emissions in Europe. Compared to developed countries, China’s CETP started relatively late. In 2011, China launched the first batch of pilot projects for carbon emissions trading. By 2021, the carbon trading market expanded nationwide, becoming the largest carbon market in the world (Ren et al., 2024). As carbon markets become more refined, an increasing number of countries, including Indonesia, Vietnam, and Turkey, have started establishing their own carbon markets (Fu, 2024).

As a market-based approach to emission reduction, the essence of carbon trading is a cap-and-trade model. The government assesses the maximum carbon emissions based on the environmental capacity of each region, and assigns carbon emission allowances accordingly to companies. Carbon emission rights are given commodity attributes, allowing enterprises to emit within the initial quota (Xian et al., 2024). If a company’s total emissions exceed its carbon emission quota, it must purchase additional carbon emission rights (Zakeri et al., 2015). Conversely, if its emissions are below its allocated quota, it can sell surplus carbon emission rights to earn additional revenue. Therefore, CETP can leverage market mechanisms to convert environmental external costs into internal costs for businesses. This drives high-carbon enterprises to reduce their environmental costs and maximize profits, ultimately leading to a transition to lower-carbon development (Wu et al., 2024).

However, scholars have not reached a consensus on whether CETP effectively reduces carbon emissions. One viewpoint argues that CETP emission reduction effect is negligible and may even lead to negative externalities (Du et al., 2021a; Jaraite and Di Maria, 2016). Another viewpoint holds that CETP is effective (Ellerman and Buchner, 2008). Some scholars consider entities included in carbon trading as the experimental group, while those not included in carbon trading as the control group. They apply Difference-in-Differences (DID) methods to compare carbon emissions between these two categories of entities after the CETP implementation (Dechezleprêtre et al., 2023; Xuan et al., 2020). To further eliminate potential non-random selection bias in the experimental group and more accurately evaluate the emission reduction effects of CETP, Dechezleprêtre et al. (2023) and Feng et al. (2024) apply matched DID. This method identifies the most similar samples between implementing and non-implementing CETP entities, revealing that CETP has significant effectiveness in reducing carbon emissions. Some scholars have considered the significant differences in carbon emissions within CETP implementation regions. To evaluate CETP impact on high-emission county-level areas from a more detailed perspective, they employ a Difference-in-Difference-in-Differences (DDD) model. By comparing high-emission counties in CETP implementation regions with other counties, the CETP positive impact on high-emission counties is discovered (Gao, 2023). As the spatial spillover effect has been widely concerned, the method of combining DID and spatial metrology has been developed and applied (Bardaka et al., 2018; Chagas et al., 2016).Some scholars use the SDID model based on the spatial distance weight matrix to examine the CETP spatial effect on carbon emission reduction in regions where carbon trading has not been implemented, obtaining two distinct conclusions: positive and negative (Dai et al., 2022; Liu et al., 2023).

Technological progress and carbon reduction

Studies on the role of technological progress in reducing carbon emissions have yet to reach a unanimous conclusion. Numerous studies investigating the connection between technology and the reduction of carbon emissions underscore that technological progress serves as the fundamental driving force (Du et al., 2019; Khan et al., 2019). However, other studies have found that technological advances increase the negative impacts on the environment and have no significant impact on carbon emissions reductions (Amri et al., 2019; Cheng et al., 2018a), and others have also found that the carbon emissions reduction effects of technological progress have nonlinear characteristics, with the carbon emissions increasing when the technological level is low in the early stage, and the carbon emissions reduction effect increasing when the technological level improves in the later stages (Gu et al., 2019; Lin and Ma, 2022). Many studies that have explored the heterogeneous technological nature and technological source effects on carbon emissions reductions have shown that both production and environmentally related technological progress can drive carbon emissions reductions (Chen et al., 2020; You and Zhang, 2022) and that low-carbon technological progress can have a more significant effect on carbon emissions reduction than general technological progress (Liu and Zhang, 2021). There have been three main perspectives taken when examining technology source heterogeneity: independent research and development technology, provincial technology spillovers, and foreign technology spillovers (Yang et al., 2021a). Technological progress associated with independent research and development has been found to have a positive incentive effect on carbon emissions reductions (Paramati et al., 2021), and foreign technology spillovers from foreign investment have been shown to reduce carbon emissions to a certain extent (Hao et al., 2021). However, inter-provincial technology spillovers can have a positive effect on reducing carbon emissions through cooperation and technology transfers (Huang et al., 2020; Yang et al., 2014), but may also increase carbon emissions in surrounding areas due to the aggregation effect of low-carbon technologies (Li et al., 2021).

ER driving factors and calculation

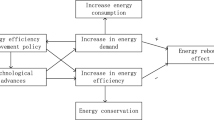
The concept of the ER effect originates from the “Jevons Paradox”: the contradiction between increased energy efficiency and reduced energy demand (Alcott, 2005). Although improving energy efficiency is considered an effective way to reduce energy consumption, the energy savings achieved through increased efficiency may be offset by new energy demands arising from substitution effects, income effects, and output effects. This can lead to energy policies falling into the trap of inefficient energy savings (Du et al., 2023). To better understand the mechanism behind the ER effect, many studies have explored the driving factors and mechanisms behind the ER effect and identified the influence of environmental regulations (Lee et al., 2020), technological progress (Wang et al., 2018b), energy efficiency (Liu et al., 2019), market reforms (Li et al., 2019a), energy price stickiness (Figus et al., 2020), and other factors on ER. Of these, environmental regulations have been found to affect the ER through technological progress and energy efficiency (Chen et al., 2021c), both of which have been seen to be keys for producing ER (Wang et al., 2022b). While technological progress can improve energy efficiency and reduce energy consumption, the economic benefits derived from technological progress can stimulate new energy demand and increase total energy consumption (Greening et al., 2000), and the lower energy service prices from improved energy efficiency can lead to higher economic output and higher energy consumption (Xing et al., 2020), resulting in the ER effect.

To avoid overestimating the CETP effectiveness, it is essential to examine whether CETP leads to the ER effect through an increase in TCEE. Therefore, accurate measurement of the ER becomes crucial. ER measurement methods have been mainly divided into four categories. First, the computable general equilibrium (CGE) model (Figus et al., 2020) has been used to estimate the ER effects at the macroeconomic level because of its ability to systematically incorporate policy and/or non-policy factors into the model (Turner, 2009; Zimmermann et al., 2021). Second, the technological progress contribution rate has been determined using the ER effect calculation method based on the Solow residual, assuming that energy efficiency is exogenous. This calculation is based on the idea that capital, labor, and energy have economic contributions that must be estimated and their respective impacts subtracted from the rates of economic growth (Jin and Kim, 2019; Wang et al., 2018a). Third, exponential technological progress decomposition, which is considered to be typically representative of the production frontier method, has been widely used to determine the ER effect because there is no need to set a specific form for the production function, and the technological progress and technological efficiency changes can be further decomposed (Chen et al., 2021a; Lin and Liu, 2012). Fourth, the endogenous economic growth theoretical model approach, which is based on “learning by doing” (Shao et al., 2013) Previous methods for measuring the ER have been based on the strict assumptions of neoclassical growth theory, which considers technological progress (i.e., energy efficiency) as exogenous and assumes constant returns to scale (Liu et al., 2018). These methods have the drawback of not being able to clearly determine the actual rate of growth in energy efficiency. However, endogenous growth theory emphasizes the endogeneity of technological progress and considers factors such as investment accumulation, production experience, and technological improvements (Zheng et al., 2022). Therefore, the ER calculated based on this theory overcomes previous methods limitations, providing a more realistic measurement framework and enhancing the flexibility and accuracy of the model (Zheng et al., 2022).

To sum up, a CETP has also been found to have a significant effect on carbon emissions reduction. Most studies have focused on the policy effects in pilot areas, and some scholarsr have considered the possible CETP spillover effects from a spatial perspective. However, spatial effects over time have been less studied. Further, while the incentive effects of low-carbon technologies on carbon emissions reduction and the ER effect from improved energy efficiencies have been widely proven, few studies have systematically considered these factors or studied the potential ER effects of CETP. This paper incorporated CETP, GI, TCEE, and ER into a unified analysis framework. Then, employing Chinese provincial panel data spanning from 2008 to 2018 and regarding the six Chinese carbon trading pilot areas as quasi-natural experiments, an SDID model based on endogenous spatio-temporal weight matrix was used to evaluate the CETP spatial spillover effect on TCEE evolution over time and the GI incentive path, and explore the ER effects caused by TCEE.

Conceptual framework and hypotheses

To accurately ssess the CETP-driven effect, the ER effect that may result from TCEE improvement must be considered, in addition to the consideration that CETP may drive or stimulate TCEE improvement via GI. Further, to fully consider the regional spatial demonstration and competition effects, it is necessary to expand the evaluation of the CETP effect from a direct effect to a spatial effect. The logical framework for this study is given in Fig. 1 and aims to address three main questions: Does CETP generate spatial spillover effects on TCEE? Can CETP enhance TCEE through GI? Does the TCEE improvement brought about by CETP lead to the ER effect? With these three key questions in mind, this article first based on the principle of maximizing profits and minimizing costs, theoretical models were constructed to analyze the transmission relationships of the carbon emissions trading policies (CETP), the TCEE, green innovation (GI), and the energy rebound (ER).

Fig. 1: Research framework.

The figure shows the research idea, and the possible relationships between these variables.

The driving effect and incentive mechanism of CETP on TCEE

The driving effect of CETP on TCEE

To regulate enterprise carbon emissions, the CETP takes the market price as the signal, aims at the basic principle of enterprise profit maximization, and promotes the free circulation and reasonable allocation of carbon emissions rights between enterprises (Chen and Lin, 2021).

In the theoretical analysis, minimizing purchase costs and maximizing carbon emissions permit sales profits were taken as the objective functions. It was assumed that the enterprise production was affected by capital $(k)$ and carbon energy $(e)$, where e is related to the carbon emissions quota $(G)$ granted by the government and the sold or purchased carbon emissions rights $(g)$. Here, considering that the initial carbon market quota is mainly allocated for free (Liu and Pan, 2024), $G$ is set as the free carbon quota. The initial carbon emissions rights quota is defined as 1 unit $G$. Based on this, the production function is written as $Q=f(k,e)$. Therefore, according to the Cobb-Douglas (CD) production function, the carbon trading enterprise production function is defined as shown in Eq. (1):

$$Q=A{k}^{\alpha }{e}^{\beta }$$

(1)

where $A$ is the established enterprise technical level, $Q$ is the maximum production output level, and $\alpha$ and $\beta$ respectively represent the relative capital and carbon energy importance in the production. It was assumed that the return to scale of the carbon trading enterprise production function remained unchanged, that is, $\alpha +\beta =1$.

If an enterprise is a carbon emissions rights buyer, then $e=G+g$. The objective function for minimizing the buyer’s carbon emission rights costs is as shown in Eq. (2):

$$\min \{rk+{p}_{1}g\}$$

(2)

where, $rk$ and ${p}_{1}g$ respectively represent the interest costs and transaction costs the enterprise needs to pay when using capital and carbon energy, ${p}_{1}$ is the cost per unit of the carbon emissions rights, and $g$ is the additional carbon emissions shares purchased by the enterprise. Therefore, the optimal cost minimization choice is shown in Eq. (3):

$$\min \varphi =[rk+{p}_{1}g]-\lambda \{A{k}^{\alpha }{[G+g]}^{\beta }\}$$

(3)

The first-order optimal selection condition under the cost function constraint is shown in Eq. (4):

$$\frac{\partial \varphi }{\partial g}={p}_{1}-\lambda \{\beta {[G+g]}^{\beta -1}A{k}^{\alpha }\}=0$$

(4)

If the enterprise is a seller of carbon emissions rights, then $e=G-g$. Therefore, based on the seller’s goal of maximizing profits under the condition that the cost is set, the objective function for maximizing profits is shown in Eq. (5):

$$\max \pi =\lambda \{A{k}^{\alpha }{[G-g]}^{\beta }\}-[rk-{p}_{2}g]$$

(5)

where ${p}_{2}$ is the carbon emissions rights sales price and $g$ is the carbon emissions rights sales share. The first-order conditions for corporate profit maximization under the profit function constraint are shown in Eq. (6):

$$\frac{\partial \pi }{\partial g}=-\lambda \{A{k}^{\alpha }\beta {[G-g]}^{\beta -1}\}+{p}_{2}=0$$

(6)

According to Eqs. (4) and (6), when the carbon emissions trading market reaches equilibrium, both sides of the transaction should meet the equilibrium price ${p}_{1}={p}_{2}$, which means the CETP can push both the buyer and seller sides to strive for carbon emissions reductions through cost pressure and profit incentives to finally achieve an optimal state at $g=0$. Thus, in light of this discussion, the following hypothesis is put forth:

H1: The CETP has an incentive effect on TCEE.

Due to the spatial demonstration effect between regions (Quah, 1996), neighboring regions may adopt corresponding incentives or environmental regulation measures to reduce their carbon emissions. As a result, the TCEE in the surrounding regions benefits from the CETP operations in the pilot areas. The following hypothesis is put out in light of this discussion:

H2: The TCEE in the surrounding regions is impacted by policy spillover from the CETP.

Mechanism for the GI incentive effect

To explore the TCEE improvement path, the CETP mechanism on TCEE was analyzed from a GI motivation perspective.

CETP is widely believed to improve GI, thereby improving efficiency (Xuan et al., 2020). As shown in Fig. 2, when there is no GI, the relationship between output $q$ and carbon emissions $e$ is represented by q = f₀(e); the greater the output, the greater the carbon emissions quota required; at which point, the company produces at $A({q}_{0},{e}_{0})$ to maximize profit ${\pi }_{0}$. Based on the Porter effect hypothesis on innovation compensation, it is believed that to maximize profits under CETP restrictions, enterprises conduct GI activities to improve production efficiency. Therefore, the original production technology $q={f}_{0}(e)$ is upgraded to include current production technology $q={f}_{1}(e)$. Because of the new technology level, the original point $A$ becomes an inefficient production mode; therefore, to obtain greater profits, the enterprise production activities move from point $A$ to point $B$, at which point the enterprises emit less carbon ${e}_{1}$, have increased production ${q}_{1}$, and greater profits ${\pi }_{1}$.

Fig. 2: GI incentive effect.

This figure depicts the changes in the relationship between output and carbon emissions before and after the implementation of GI activities.

Further derivations using equations. Based on the analysis in the previous section, the carbon energy used by enterprises is $e=G+g$. If $R$ is the profit from a unit of carbon energy consumption, then the enterprise carbon consumption profit is $R(G+g)$. The GI level is a, and the carbon quota purchase cost is closely related to GI, which is defined as $aC(g)$, where $C(g)$ is a continuous function of $g$. The stronger the GI of an enterprise, the smaller the carbon quota purchase quantity, and the lower the purchase cost, that is, $C\text{'}(g) < 0,C\text{'}\text{'}(g) < 0$. The expression for the GI cost function is $I(a)$, which satisfies $I\text{'}(a) > 0,I\text{'}\text{'}(a) < 0$. Equation (7) thus depicts the firm’s profit function as follows:

$$\pi =R(G+g)-aC(g)-I(a)$$

(7)

Under the CETP constraint, enterprises can achieve profit maximization through GI. Therefore, the derivative of a in Eq. (7) can obtain the first-order condition for enterprise profit maximization, as shown in Eq. (8):

$$-C(g)-I\text{'}(a)=0$$

(8)

Equation (8) is then treated as a new function, and the derivative of a is calculated to obtain Eq. (9):

$$\frac{dC(g)}{da}=-I\text{'}\text{'}(a)$$

(9)

Based on Eq. (9) and the cost function nature of enterprise GI, Eq. (10) can be obtained:

$$\frac{da}{dC(g)}=-\frac{1}{I\text{'}\text{'}(a)} > 0$$

(10)

To sum up, in the face of the CETP carbon quota purchase cost pressure and driven by the principle of profit maximization, enterprises can be forced to carry out GI activities, improve energy utilization efficiency, reduce carbon consumption, and further improve carbon emissions reduction efficiency. The following hypothesis is put out in light of the above discussion:

H3: CETP can stimulate TCEE through GI.

ER based on TCEE mechanism

However, increasing TCEE raises revenue per unit of carbon emission. Under the profit maximization principle, businesses may increase energy consumption in order to gain more profit space, thereby increasing carbon emissions and causing an ER effect. As a result, it is necessary to investigate whether TCEE ultimately results in ER as a result of CETP driving TCEE improvement.

It is generally believed that although GI can improve energy utilization efficiency, the energy efficiency improvement can reduce the energy input for the same output and more profit per unit of carbon emissions can be gained, which further increases the energy consumption (Fan et al., 2016). As shown in Fig. 3, assuming that only capital $(k)$ and carbon energy $(e)$ are the production factors, the equal-cost curve $({K}_{0}-{E}_{0})$ and equal-yield curve ${Y}_{1}$ are first presented. Under the production cost constraints, the enterprise realizes production optimization at $A({k}_{1},{e}_{1})$. Due to the CETP on GI incentive effect, the TCEE can be improved, the carbon consumption can be reduced at the same output level and the carbon price can be lowered (Chen et al., 2021c). Therefore, when there is a constant capital price, the substitution effect generated by energy efficiency improvements means that the carbon energy partially replaces capital, and the enterprises realize production optimization at a new equilibrium point $B({k}_{2},{e}_{2})$. When the total production cost remains unchanged, when the carbon price decreases, the equal-cost curve shifts outward from $({k}_{0}-{e}_{0})$ to $({k}_{0}-{e}_{0}{\text{'}\text{'}})$, which generates a new equal-yield curve ${Y}_{2}$, and the production optimization is realized at a new equilibrium point$C({k}_{3},{e}_{3})$, at which point the enterprise achieves greater output and higher profits at the same production costs. Therefore, under the ER influence, GI not only fails to reduce the carbon emissions but increases the carbon emissions, which means that the enterprises need to purchase additional carbon quotas in the carbon market to meet their production needs.

Fig. 3: ER effect.

The figure illustrates the substitution effects of capital and carbon energy following improvements in energy efficiency.

Further derivations using equations. Assuming that TCEE can be improved after the success of GI, the enterprise not only reduces its carbon emissions but also generates a carbon quota surplus, at which point the carbon consumption is expressed as $e=G-g$, and the income from the carbon consumption is $R(G-g)$. The remaining quota $g$ can be used for carbon market trading, with the additional income from the enterprise’s carbon quota sale being closely related to GI, which is expressed as $aP(g)$. Greater carbon quota surplus and increased additional revenue are directly correlated with higher enterprise GI levels, namely $P\text{'}(g) > 0,P\text{'}\text{'}(g) > 0$. Equation (11) therefore displays the firm’s profit function:

$$\pi =R(G-g)+aP(g)-I(a)$$

(11)

Drawing from the concept of enterprise profit maximization, the first-order enterprise profit maximization condition can be obtained by taking the derivative of a in Eq. (11), as shown in Eq. (12):

$$P(g)-I\text{'}(a)=0$$

(12)

Equation (12) is then treated as a new function, and the derivative of a is calculated to obtain:

$$\frac{dP(g)}{da}=I\text{'}\text{'}(a) < 0$$

(13)

The derivation results in Eq. (13) indicate that the higher the enterprise GI level, the lower the income of the remaining carbon quota. Consequently, it is necessary to consider that although GI enhances TCEE, TCEE results in the ER effect, which raises carbon emissions and subsequently lowers the amount of remaining carbon quota. The following hypothesis is put out in light of the above discussion:

H4: CETP produces an ER effect by improving the TCEE.

Study design

Modesl construction

The SDID model and the GI and TCEE mediation effects models were built separately to assess the CETP spatial effect on TCEE over time and its GI excitation path, as well as to investigate if the TCEE improvement results in an ER effect.

SDID model

For evaluating policies, the difference-in-differences (DID) model has been widely employed. By comparing the differences between the pilot areas and the non-pilot areas before and after the policies are implemented, the model can overcome interference from other factors on the policy evaluation effect and evaluate the net driving effect of the policies on the pilot areas (Chen et al., 2021c). However, according to Anselin (1990), nearly all spatial data possessed fundamental traits of spatial interdependence, and studies have found that China’s regional carbon emissions efficiency is spatially interdependent (Wang et al., 2019; Zhu et al., 2021); therefore, if the spatial spillover effect of TCEE is ignored, the estimation results will be biased. Further, as the spatial interactions between the adjacent areas often have intertemporal effects (Chen et al., 2021b), the dynamic transfer of the TCEE spillover effect over time should be considered to ensure a more accurate estimation of the spatial dependence. Therefore, as in Fan and Darren (2018), the spatial factors were incorporated into the classic DID model, and an SDID model was formulated using an endogenous space-time weight matrix to examine both the immediate impact of CETP on TCEE and the evolving effects in the surrounding areas over time. The CETP was promulgated in 2011 and officially launched in 2013; Based on signal theory, an examination of the policy promulgation effects can provide valuable information for forward enterprise production decisions about whether to implement GI activities in advance of an expected carbon trading market launch (Gao et al., 2020). Therefore, 2011 was taken as the policy commencement threshold, 2011 to 2018 taken as the policy implementation time, and 2008 to 2010 considered to have been non-implemented. The experimental group consisted of six CETP pilot areas, while the control group consisted of the remaining non-pilot areas. The SDID model construction is shown in Eq. (14):

$$\begin{array}{l}TCE{E}_{it}=\alpha +\rho TW\,TCE{E}_{i,t-1}+{\beta }_{1}TES{T}_{i,t}+{\beta }_{2}ED{P}_{i,t}\\\qquad\qquad\quad+\,{\beta }_{3}I{S}_{i,t}+{\beta }_{4}FD{I}_{i,t}+{\beta }_{5}H{C}_{i,t}+{\gamma }_{1}TW\,TES{T}_{i,t}\\\qquad\qquad\quad+\,{\gamma }_{2}TW\,ED{P}_{i,t}+{\gamma }_{3}TW\,I{S}_{i,t}+{\gamma }_{4}TW\,FD{I}_{i,t}\\\qquad\qquad\quad+\,{\gamma }_{5}TW\,H{C}_{i,t}+{u}_{i}+{v}_{t}+{\varepsilon }_{it}\end{array}$$

(14)

where $\rho$ is the spatial autocorrelation coefficient, $i$ is the province $(i=1,2,\mathrm{..}.,30)$, and $t$ is the year $(t=1,2,\mathrm{..}.,t)$. $TW=I\otimes W$ is the spatio-temporal weight matrix that integrates the time weight matrix $(I)$ calculated using Moran’s index with the spatial weight matrix $(W)$ produced by geographical distance and constructed using the Kronecker product $(\otimes )$ (Liu et al. 2022) to capture the spatial effects of the CETP-driven TCEE evolution over time. $TCEE$ is the TCEE and $TES{T}_{it}=(trea{t}_{it}-\overline{treat})\times (tim{e}_{it}-\overline{time})$ is a policy dummy variable; if the area is a pilot area, $trea{t}_{it}=1$, and if the area is a non-pilot area, $trea{t}_{it}=0$, and if the year following the CETP promulgation, then $tim{e}_{it}=1$, otherwise $tim{e}_{it}=0$. $\overline{treat}$ and $\overline{time}$ are the average values for the event dummy variables and the time dummy variables, and $EDP$ (economic development level), $IS$ (industrial structure), $FDI$ (foreign direct investment) and $HC$ (human capital) are the control scalars, ${u}_{i}$ is the fixed effect for a province, ${v}_{t}$ is a fixed effect for time, and ${\varepsilon }_{it}$ is an error term.

Mediating effects model of GI

Based on the Porter effect, it is assumed that environmental regulations can promote GI and have an effect on TCEE. Therefore, from a GI perspective, the effect mechanism of CETP on TECC was examined. As in Baron and Kenny (1987), a model with multiple mediating effects was constructed in three phases. Equations (15)–(17) respectively represent the three-stage model expressions for GI as an intermediary variable:

$$\begin{array}{c}TCE{E}_{it}=\alpha +\rho TW\,TCE{E}_{i,t-1}+{\beta }_{0}TES{T}_{i,t}+\theta {X}_{i,t}\\ \,+{\gamma }_{0}TW\,TES{T}_{i,t}+\delta TW\,{X}_{i,t}+{u}_{i}+{v}_{t}+{\varepsilon }_{it}\end{array}$$

(15)

$$\begin{array}{c}G{I}_{it}=\alpha +\rho TW\,G{I}_{i,t-1}+{\phi }_{0}TES{T}_{i,t}+\theta {X}_{i,t}\\ +{\phi }_{1}TW\,TES{T}_{i,t}+\delta TW\,{X}_{i,t}+{u}_{i}+{v}_{t}+{\varepsilon }_{it}\end{array}$$

(16)

$$\begin{array}{c}TCE{E}_{it}=\alpha +\rho TW\,TCE{E}_{i,t-1}+{\beta }_{1}TES{T}_{i,t}+{\varphi }_{0}G{I}_{i,t}+\theta {X}_{i,t}\\ \,+{\gamma }_{1}TW\,TES{T}_{i,t}+{\varphi }_{1}TW\,G{I}_{i,t}+\delta TW\,{X}_{i,t}+{u}_{i}+{v}_{t}+{\varepsilon }_{it}\end{array}$$

(17)

Mediating effects model of TCEE

The ER effect holds that GI improves TCEE efficiency and reduces carbon emission per unit of output; however, the substitution effect holds that enterprises replace the input from other factors by consuming more energy, which leads to an increase in carbon emission (Chen et al., 2021a; Zimmermann et al., 2021). Therefore, further explore whether TCEE causes ER.The TCEE is taken as the action path for the CETP and the ER to investigate whether the CETP increased carbon consumption when there was an improvement in TCEE, thus falling into the trap of inefficient emission reduction. Equations (18)–(19) respectively represent the model expressions for the TCEE as an intermediary variable:

$$\begin{array}{c}R{E}_{it}=\alpha +\rho TW\,R{E}_{i,t-1}+{\beta }_{0}TES{T}_{i,t}+\theta {X}_{i,t}\\ \,+{\gamma }_{0}TW\,TES{T}_{i,t}+\delta TW\,{X}_{i,t}+{u}_{i}+{v}_{t}+{\varepsilon }_{it}\end{array}$$

(18)

$$\begin{array}{c}R{E}_{it}=\alpha +\rho TW\,R{E}_{i,t-1}+{\beta }_{1}TES{T}_{i,t}+{\varphi }_{0}TCE{E}_{i,t}+\theta {X}_{i,t}\\ \,+{\gamma }_{1}TW\,TES{T}_{i,t}+{\varphi }_{1}TW\,TCE{E}_{i,t}+\delta TW\,{X}_{i,t}+{u}_{i}+{v}_{t}+{\varepsilon }_{it}\end{array}$$

(19)

where, $GI$ and $TCEE$ are the respective mediating variables for GI and TCEE, ${\beta }_{0}$ and ${\gamma }_{0}$ are the total local and neighborhood effects, ${\beta }_{1}$ and ${\gamma }_{1}$ are the direct local and neighborhood effects, and $\phi$ and $\varphi$ are the mediating effects.

Research variables and data sources

TCEE index measurement: super- slack-based measure (SBM) model

As a non-parametric technique, data envelopment analysis (DEA) has been widely used in TCEE calculations because of its multi-input and multi-output characteristics (Meng et al., 2016). However, radial and angle selections are neglected in traditional DEA models, which can lead to deviations in the TCEE calculation results (Dong et al., 2022). Tone proposed a SBM model based on undesirable output (Tone, 2002), which improved the super-SBM model by adding slack variables into the objective function, taking the undesirable output into account, and excluding the decision making unit efficiency value to make the efficiency greater than 1, which made up for the shortcomings in the traditional BCC-DEA model, effectively improved the estimation accuracy, and became the mainstream TCEE measurement method (Xie et al., 2021). Therefore, the model in this paper was set as a super-SBM model with non-expected and expected output orientations, as shown in Eq. (20):

$$\min \rho =\frac{1+\frac{1}{m}\mathop{\sum}\limits_{i=1}^{m}\frac{{s}_{i}^{x}}{{x}_{i0}}}{1-\frac{1}{{s}_{1}+{s}_{2}}\left(\mathop{\sum }\limits_{r=1}^{{s}_{1}}\frac{{s}_{r}^{y}}{{y}_{r0}}+\mathop{\sum }\limits_{t=1}^{{s}_{2}}\frac{{s}_{t}^{z}}{{z}_{t0}}\right)}$$

$$\begin{array}{c}s.t.\,{x}_{i0}\ge \mathop{\sum }\limits_{j=1,j\ne 0}^{n}{x}_{j}{\lambda }_{j}-{s}_{i}^{x}\\ {y}_{r0}\le \mathop{\sum }\limits_{j=1,j\ne 0}^{n}{y}_{j}{\lambda }_{j}+{s}_{r}^{y}\\ {z}_{t0}\ge \mathop{\sum }\limits_{j=1,j\ne 0}^{n}{z}_{j}{\lambda }_{j}-{s}_{t}^{z}\end{array}$$

$$1-\frac{1}{{s}_{1}+{s}_{2}}\left(\mathop{\sum }\limits_{r=1}^{{s}_{1}}\frac{{s}_{r}^{y}}{{y}_{r0}}+\mathop{\sum }\limits_{t=1}^{{s}_{2}}\frac{{s}_{t}^{z}}{{z}_{t0}}\right)\, > \,0$$

$${s}_{i}^{x}\ge 0,{s}_{r}^{y}\ge 0,{s}_{t}^{z}\ge 0,{\lambda }_{j}\ge 0$$

$$\mathop{\sum }\limits_{j=1,j\ne 0}^{n}{\lambda }_{j}=1$$

(20)

where $n$ is the number of DMUs in the input-output system and ${x}_{i0},{y}_{r0}$ and ${z}_{t0}$ respectively represent the DMU’s input, expected output, and unexpected output variables. To be specific, capital, labor, and energy are taken as input factors, and economic growth and carbon emissions are taken as expected and undesirable outputs to construct a multi-input output system (Dong et al., 2022). The perpetual inventory method is used to determine the capital input, which is represented by fixed capital stock; ${K}_{it}={I}_{it}+{K}_{it-1}(1-{\sigma }_{it})$; where $i,t$ are province and time, $K,I$ are fixed capital stock and fixed capital investment, and $\sigma$ is the depreciation rate (10.96%). Labor input is represented by the number of urban employed at the end of the year. Energy input is measured by the total energy consumption and converted to tonnes of standard coal (Zhou et al., 2019). GDP is chosen as the desired output because it broadly reflects the national economy (Xie et al., 2021). To eliminate the inflation effects, capital inputs and economic output were converted to 2000 constant prices (Zhou et al., 2019). The calculating method supplied by The Intergovernmental Panel on Climate Change (IPCC) is used to determine the undesirable result; $C{O}_{2}=\mathop{\sum }\nolimits_{i}^{8}{E}_{i}\times NC{V}_{i}\times C{C}_{i}\times COF\times \frac{44}{12}$; where $C{O}_{2}$ is the carbon dioxide emissions, $i$ is the energy type. According to Tao et al. (2023), it mostly uses various fossil fuels, including coal, crude oil, and natural gas; $E$ stands for energy consumption, $NCV$ represents the average low calorific value, $CC$ is the carbon content, $COF$ is the carbon oxidation rate, $44/12$ signifies the carbon conversion coefficient into $C{O}_{2}$ (Cheng et al., 2018b), $m,{s}_{1}$ and ${s}_{2}$ are the quantities of the three types of elements, and ${s}_{i}^{x},{s}_{r}^{y}$ and ${s}_{t}^{z}$ are the relaxation variables for the three elements.

ER effect index measurement: CD production function

The macro-level ER effect defined by Saunders (2000) has been widely recognized by scholars and is therefore very representative. The ER effect mathematical definition is as follows:

$$RE=1+\eta$$

(21)

where $\eta =d\,\mathrm{ln}\,E/d\,\mathrm{ln}\,\tau =(\tau \times dE)/(E\times d\tau )$ ($E$ is the energy consumption and $\tau$ is the energy efficiency) is the elasticity of energy consumption to energy efficiency. Based on this Equation, if the following five situations occur in $\eta$, there are also five corresponding ER effect situations:

• 1. $\eta \,>\, 0$, then $RE \,>\, 1$, which means there is a reverse effect, indicating that an improvement in energy efficiency would fail to produce energy savings and increase energy consumption.

• 2. $\eta =0$, then $RE=1$, which means there is a complete rebound, indicating that the environmental policies failed to produce any regulatory effects.

• 3. $-1\, < \,\eta\, <\, 0$, then $0 \,< \,RE\, <\, 1$, which means there is a partial rebound, indicating a common situation where energy efficiency improvements generate energy savings but the actual energy consumption remains greater than the expected energy consumption.

• 4. $\eta =-1$, then $RE=0$, which means there is zero rebound, indicating that the energy saving generated by the energy efficiency improvements is fully realized.

• 5. $\eta \,< -1$, then $RE \,<\, 0$, which means there is super energy saving, indicating that the energy use is lower than anticipated.

Based on the above methods and the basic ideas of the “endogeneity” theoretical model proposed in Shao et al. (2013), and considering the basic assumptions for the endogeneity of energy efficiency and labor supply, a CD production function is adopted to measure the long-term ER effect, which includes technological progress, as shown in Eq. (22):

$$Y=a{K}^{\alpha }{L}^{\beta }{(\tau E)}^{1-\alpha -\beta }$$

(22)

where $Y,K,L$ and $E$ are respectively the output, capital, labor, and energy, and the variable sources are consistent with the above. $\tau$ is the energy efficiency, $\tau E$ are the energy services, $a \,>\, 0$ are the production efficiency parameters, and $\alpha ,\beta$ and $1-\alpha -\beta (\alpha +\beta < 1)$ are the respective output elasticities for capital, labor, and energy.

As energy efficiency improvements are not exogenous, they can be realized through endogenous approaches, such as improving the energy technology, adjusting the energy price, and enterprise management improvements (Zheng et al., 2022). Therefore, based on the endogenous growth theory of “learning by doing” (Arrow, 1962), this paper believes that the methods and experience to improve energy efficiency can be obtained from the energy use in the production process. The relationship between energy efficiency and the energy consumption is as follows:

$$\tau =G{E}^{\gamma }$$

(23)

where $G \,>\, 0$ is the efficiency parameter for the “learning by doing” process, and $\gamma \,>\, 0$ is the energy efficiency’s elasticity with respect to energy consumption.

The CD production function form is reset again:

$$Y=a{K}^{\alpha }{L}^{\beta }{(G{E}^{\gamma +1})}^{1-\alpha -\beta }$$

(24)

When the energy efficiency is internalized, the sum of the outputs for the three input factors is $\alpha +\beta +(1-\alpha -\beta )(\gamma +1)\, >\, 1$, which indicates that the “learning by doing” effect appears to make the CD production function have increasing returns to scale. In combination with Eq. (21), and assuming that capital, labor, and energy are all freely variable, the long-term rebound effect is:

$$RE=1+\frac{{(1-\alpha -\beta )}^{2}(1+\gamma )}{[1-\alpha -\beta -(1-\alpha -\beta )(1+\gamma )]{S}_{E}}$$

(25)

where ${S}_{E}$ represents the real elasticity of output to energy consumption, which can be directly calculated using statistical data. From the above ER effect equation, the long-term ER effect can be calculated after the capital-output output elasticity, labor output elasticity, and energy efficiency on energy consumption are obtained. Therefore, the natural logarithm for both sides of Eq. (24) can be taken to derive Eq. (26):

$${\mathrm{ln}}\,Y=\alpha \,{\mathrm{ln}}\,K+\beta \,{\mathrm{ln}}\,L+\theta \,{\mathrm{ln}}\,E+C+v+\varepsilon$$

(26)

where $C$ is a constant, $v$ is the individual effect, $\varepsilon$ is the residual term, $\theta =(1-\alpha -\beta )(\gamma +1)$, and the other variables are consistent with the above.

Core variable

Green innovation (GI). The number of granted and filed green patents has been utilized by numerous research to estimate the GI level (Liu and Sun, 2021). However, the number of patent applications only represents the importance enterprises attach to GI, but not the actual green technology progress (Chen et al., 2021d), whereas the number of granted patents more effectively reflects the enterprise GI capability. Green technologies are scattered across many fields and technology categories in the international patent classification system, such as biofuels, fuel cells, wind energy, rail vehicles, energy supply lines, general building insulation, mechanical energy recovery, and other related technologies not produced using combustion (Quatraro and Scandura, 2019). The World Intellectual Property Organization (WIPO) introduced the “Green List of International Patent Classification” (IPC Green List), which integrates the green patent classification locations and facilitates the collection of GI data. Therefore, the number of GI authorizations for each province was collected based on the IPC classification number (Costantini et al., 2017). To eliminate the influence of province size and to ensure the provincial GI was comparable, the per capita GI level was used to measure the provincial GI capacity.

Control variables

Economic development level (EDP). As economic development occurs at the expense of the environment, which leads to higher carbon emissions, the contradiction between environmental preservation and economic growth has garnered a lot of scientific interest. However, the higher a region’s output creation level, the higher its GI capacity, and the more conducive it is to carbon emissions reductions. As economic development also reflects domestic demand (Liu and Sun, 2021), the consumer demand for green products can also encourage enterprises to improve the TCEE to provide more green products to meet market demand. Here, GDP per capita was used to represent the provincial EDP (Dong et al., 2022).

Human capital (HC): HC refers to the capital derived from the investment in education and training (Qi et al., 2021), which is the main source of GI as it is the quality and quantity of innovative talent that drives TCEE improvement. It is generally believed that the richer the regional HC, the stronger the GI and carbon emissions reduction capacities. Consequently, the percentage of R&D employees in each province’s year-end population was utilized to calculate HC (Xie et al., 2021).

Industrial structure (IS): IS upgrading is seen as an effective measure to reduce carbon emissions (Xuan et al., 2020). In particular, a rising tertiary industry ratio is conducive to improving energy structures, optimizing resource allocations, and promoting energy conservation, emissions reductions, and green, low-carbon production (Liu and Sun, 2021). As in Sun and Huang (2020), IS was quantified by calculating the percentage of the overall output value that came from the tertiary industry.

Foreign direct investment (FDI): The entry of foreign enterprises has a significant impact on regional carbon emissions (Yu et al., 2019). While FDI may promote TCEE through advanced technology investments, it can also lead to a transnational migration of polluting enterprises to fuel economic growth, which can lead to a pollution haven effect and an increase in carbon emissions, which in turn hinder the TCEE (Nepal et al., 2021). To observe the relationship between FDI and TCEE, the foreign investment proportion in total investment was used as a proxy FDI variable.

Data sources

Panel data from 30 Chinese provinces (excluding Tibet, Hong Kong, Macao, and Taiwan) between 2008 and 2018 were chosen based on data consistency and availability. The data was sourced from the China Statistical Yearbooks, the China Science and Technology Statistical Yearbooks, the China Energy Statistical Yearbooks, and the China Population and Employment Statistical Yearbooks. Additionally, GI data for each province were gathered from the China Intellectual Property Office’s Information Service platform, using the “IPC Green List” code to match authorized green patents (Chen et al., 2021d; Quatraro and Scandura, 2019). To resolve the heteroscedasticity problem and eliminate the dimensional influences, the ratio approach was employed to normalize all of the data (Wang et al., 2022).

Empirical results

Parallelism trend test

The policy effect assessment premise was that the pilot and non-pilot areas would meet the basic parallelism trend assumption (Qi et al., 2021), that is, in the absence of CETP intervention, the TCEE trends in pilot and non-pilot areas would be consistent. Figure 4 displays the results from the parallel trend tests. The calculated coefficient prior to CETP’s implementation was not significant, indicating that TCEE in the pilot area was not impacted by the policy before to CTP’s implementation and essentially satisfied the basic no systematic difference requirements. After CETP was implemented, the estimated coefficient was significantly positive within the 95% confidence interval, showing that CETP significantly improved TCEE and satisfied the parallel trend hypothesis, which is a requirement for assessing the CETP effect from a local perspective.

Fig. 4: Parallelism trend test.

Comparison of the changes in the average level of the total factor carbon emissions efficiency before and after the carbon trading pilot policy. Data source: The total factor carbon emissions efficiency is computed using the super-slack-based measure (SBM) model.

Spatial correlation test

Overall spatial autocorrelation test

The parallelism trend test can only establish the foundation for investigating the driving impact of CETP on TCEE in the pilot areas. However, regions are often spatially related due to factor flow and knowledge spillover interactions, which means that provincial TCEE improvements depend on local environmental regulations, knowledge accumulation, technology input, and the spillover effect from neighboring provinces. Hence, in order to investigate whether CETP had a favorable neighborhood effect on TCEE in non-pilot areas, it was essential to conduct a premise test at the spatial level. Moran’s I is commonly employed as a fundamental spatial metric test due to its ability to articulate spatial dependence properties and summarize the spatial correlation features among neighboring areas (Balta-Ozkan et al., 2015). Table 1 shows the Moran’s I of TCEE calculated by geographical distance, geographical adjacency relationship, and economic distance weight matrixs. The Moran’s I for the TCEE spatial autocorrelation coefficient was positive at a 1% level throughout the sample period, which indicated that there was a positive neighborhood effect due to the intercorrelations between the regions. To promote sustainable low-carbon development, it is essential to establish a cross-regional collaborative emissions reduction mechanism.

Table 1 Spatial autocorrelation test.

Local spatial association test

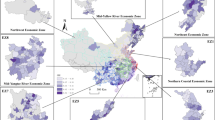
The overall spatial autocorrelation test can only macroscopically prove the dependence between regions; however, it cannot show the detailed correlations between the pilot and neighboring areas. Therefore, before assessing the CETP spillover effect, it was necessary to check whether the pilot areas formed an associated network with their neighboring areas. The gravity model was used to calculate the TCEE connection strength in each pilot area and the other areas because it considers geographical distance and also reveals the cross-sections in the dynamic spatial association network evolution (Jiang and Ma, 2021). The relationship between the regions with greater than average strength was assigned 1, which indicated a strong TCEE dependence between regions. Finally, the regional TCEE association diagrams for the six pilot areas were drawn (see Fig. 5a–f), in which it can be seen that all pilot areas were connected with the other areas, with most being strongly dependent on their neighboring areas, that is, the potential TCEE enhancement benefits in the pilot areas were likely to have affected the carbon emissions reduction behaviors in the neighboring areas and produce positive spillover effects (Yu and Li, 2021). This offers a more trustworthy foundation for assessing how CETP affects TCEE spatially.

Fig. 5: Local spatial correlation.

a Bejing local spatial association. The figure illustrates the relationship between the total factor carbon emissions efficiency in Beijing and other non-pilot regions. Data source: The regional correlation map was created using ArcGIS. b Tianjin local spatial association. The figure illustrates the relationship between the total factor carbon emissions efficiency in Tianjin and other non-pilot regions. Data source: The regional correlation map was created using ArcGIS. c Shanghai local spatial association. The figure depicts the correlation between the total factor carbon emissions efficiency in Shanghai and other non-pilot regions. Data source: The regional correlation map was created using ArcGIS. d Hubei local spatial association. The figure illustrates the correlation between the total factor carbon emissions efficiency in Hubei and other non-pilot regions. Data source: The regional correlation map was created using ArcGIS. e Guangdong local spatial association. The figure demonstrates the correlation between the total factor carbon emissions efficiency in Guangdong and other non-pilot regions. Data source: The regional correlation map was created using ArcGIS. f Chongqing local spatial association. The figure displays the correlation between the total factor carbon emissions efficiency in Chongqing and other non-pilot regions. Data source: The regional correlation map was created using ArcGIS.

CETP effect on TCEE

The CETP spatial spillover effect test

To more comprehensively test the CETP direct and spatial spillover effects on TCEE, the classical DID and SDID models were adopted to respectively evaluate CETP. This process extended the CETP test effect on TCEE from a direct effect to a spatial effect and from a static assessment to an inter-period dynamic assessment, which allowed for a comparison of the explanatory strength of the two models on the policy effects. Further, to increase the robustness of the regression results and more accurately evaluate the spatial spillover effect of CETP on TCEE, a double fixed effect model was adopted to control the time and regional effects (Liu et al., 2020). The evaluation results for the CETP effect on TCEE from the two models are shown in Table 2.

Table 2 CETP effect.

Both the DID and SDID estimation results showed that the CETP had a positive effect on the TCEE (Zhang et al., 2021). The comparison of the two models revealed that the goodness of fit of the SDID model was significantly higher than the goodness of fit of the DID model, that is, the SDID model had a higher explanatory power (Balta-Ozkan et al., 2015). The SDID model also solved the DID model deficiency by spatially testing the influence of the CETP on the TCEE in the adjacent areas, which further proved its reliability and robustness, with the spatial autoregressive TCEE coefficient being found to be significantly positive at a 1% level and proving the TCEE interdependence between the regions. If this spatial connection were not considered, the CETP effect would be underestimated (Yu and Li, 2021) and the results would be inaccurate. The CETP evaluation results were then further analyzed at the spatial level, from which it was found that the regression coefficient for the spatial term of the CETP on the TCEE was significantly positive at a 5% level, further proving that the policy implementation had a positive spillover effect.

The EDP, FDI, and HC had direct beneficial effects on the TCEE at 5% and 1%, according to the control variable regression. Economic development, innovative talent, and FDI provide the conditions for regional carbon emissions reductions, promote improvements in the regional TCEE, and promote green, high-quality regional economic development (Nepal et al., 2021; Xuan et al., 2020). FDI has also been found to have a positive effect on the TCEE in neighboring regions, possibly because of the flow of technical elements between the regions (Yang et al., 2021b). However, EDP can also seriously hinder the TCEE in the adjacent areas due to a siphon effect, as explained by the “pollution haven” hypothesis (Cole and Fredriksson, 2009). The direct and spatial effects of IS upgrading on the TCEE were not significant, possibly because industry remained the primary driver of economic development and the tertiary industry output value fraction was still underdeveloped, notwithstanding an increase (Sun and Huang, 2020). As the industrial sector is also the largest source of CO2 emissions at more than 80% of all carbon emissions (Li et al., 2019b), the impact of industrial structure upgrading on TCEE may be offset or even have a negative impact.

Robustness test

The policy effect test in the previous section proved that the CETP had direct driving and spatial spillover effects on the TCEE. To further verify the reliability of the test results, a counterfactual test, a change of spatial weight matrix test, and other environmental policy tests were conducted to test the robustness of the CETP effect.

Counterfactual tests

Counterfactual tests were conducted to further demonstrate that the TCEE was indeed caused by the CETP implementation. As in Yang et al. (2020), a false CETP implementation time was set and the model was re-estimated. If the estimation result was not significant, it indicated that the same conclusion could not be drawn when a CETP was not implemented, and the incentive effect of the CETP on the TCEE was stable. First, the samples after 2011 were deleted and 2010 and 2009 were set as the false starting years of the policy. The counterfactual test results are shown in Table S1 in the Appendix. As the SDID model regression results were not significant for the false pilot times in either 2010 or 2009, this proved that the TCEE was affected by the CETP rather than by some other accidental factors, which confirmed the evaluation results.

Change the spatial weight matrix test

The spatio-temporal weight matrix based on the geographical distance weight matrix applied to the SDID model proved that the CETP had a significant spatial spillover effect. However, spatial adjacency (Du et al., 2021a) and economic distance between provinces (Ge et al., 2021) both affect regional connections. Therefore, to prove the reliability of the CETP’s spillover effect on the TCEE, spatial adjacency weight and economic distance weight matrices were respectively used to construct an endogenous spatio-temporal weight matrix to evaluate the CETP spatial effect, that results for which are shown in Table S2 in the Appendix. The SDID model regression results based on the spatial adjacency and economic distance matrices showed that the CETP had a significant promotion effect on the TCEE in neighboring provinces, which further proved the robustness of research results and the need to consider policy spillover effects.

Control other environmental policy tests

Because of China’s energy conservation and emissions reduction emphasis, during the CETP implementation, the provincial TCEE was inevitably affected by other relevant environmental policies, which could have resulted in some CETP evaluation interference. Therefore, other major environmental policies during the same period were collected; the 12th Five-Year Plan for Air Pollution Prevention and Control in Key Areas (APPC), the Low Carbon City Pilot Policy (LCCP), and the Emissions Trading Policy (ETP). As in Dong et al. (2020) and Du et al. (2021a), to control these parallel environmental policies, the three environmental policies were successively incorporated into the regression model to test the robustness of the CETP on the TCEE’s direct and spatial spillover effects, the results for which are shown in Table S3 in the Appendix. The findings of the regression demonstrated that even when the three other pertinent environmental policies were progressively controlled, the CETP continued to have significant direct and geographical promotion impacts on the TCEE, which further confirmed the reliability of the evaluation results.

GI incentive mechanism

The policy evaluation results and the robustness tests proved that the CETP could significantly improve the TCEE in the pilot areas and also had a positive spatial spillover effect on the TCEE in adjacent areas. However, this spatial spillover effect required further exploration. In the theoretical model and research hypothesis section, the GI incentive mechanism was gradually deduced, which confirmed the research hypothesis that the CETP improved the TCEE through GI. Therefore, the effect of the GI’s specific incentive mechanism needed to be tested step by step using a mediation effect model. Table 3 lists the verification results for the GI incentive mechanism.

Table 3 GI mechanism.

The GI incentive mechanism regression results showed that the direct effect of the CETP was not significant; however, the direct effect of GI on the TCEE was significantly positive at a 1% level, indicating that GI had a mediating effect in the relationship between the CETP and the TCEE, that is, the CETP stimulated the TCEE in the pilot areas through the GI path, which verified hypothesis 3, proved the effectiveness of innovation compensation effect in the pilot areas. Although the CETP was found to have positive spillover effects on the TCEE in the adjacent areas, the GI regression results on the TCEE in the adjacent areas were significantly negative at a 1% level, which indicated that the GI had a masking effect on the CETP emissions reduction diffusion. Because of the inter-regional competition and pollution haven effects, GI weakened the spatial spillover effect of the CETP to some extent.

TCEE inhibition mechanism

The findings above demonstrate that CETP encourages TCEE through GI. Nonetheless, given that improving energy efficiency is the key to ER, neglecting the ER effect that could be brought on by TCEE will result in an overestimation of the CETP effect. On the basis of this, examine if CETP causes the ER effect via raising TCEE. Table 4 gives the verification results for the TCEE mechanism.

Table 4 TCEE mechanism.

Table 4 shows that the direct effect of CETP on ER was significantly positive at a 1% level, indicating that given the existence of ER, the actual CETP effect is less than anticipated. The mechanism test revealed that the CETP on TCEE and the TCEE on ER direct effects were significantly positive, that is, the TCEE played a partial intermediary role in the relationship between the CETP and ER, which verified hypothesis 4. The CETP carbon emissions reduction pressure forced the pilot areas to improve their TCEE; however, the efficiency improvements correspondingly increased the ER effect, which weakened the CETP effect to some extent.

The regression results for the spatial effect of CETP on regional ER were significantly positive at a 1% level, which was consistent with the direct ER result. As the above analysis showed, the CETP had a promotion effect on the TCEE in neighboring areas. However, it is worth noting that the TCEE mediating variable had a significant negative effect on the neighboring areas’ ER, which indicated that the TCEE had an inhibitory effect on the ER in the neighboring areas and a masking effect on the CETP on ER in the adjacent areas. This is because, driven by the environmental pollution warning effect, the CETP reduced its influence on the ER in the neighboring areas through the ER promotion in the pilot areas.

Conclusion and policy implications

Research conclusions

Taking the CETP in China as a quasi-natural experiment and based on Chinese provincial-level panel data from 2008 to 2018, this paper constructed an SDID model based on a spatio-temporal weight matrix from a “local—neighborhood” perspective to examine the direct and indirect effects of CETP on Chinese province TCEE, as well as the incentive channel via GI. Further research was conducted to determine whether CETP causes ER effects via TCEE, and the following conclusions were made.

• (1) The CETP not only benefitted the TCEE in the pilot areas but had a positive spillover effect on the TCEE in the neighboring areas. This conclusion was proven reliable from several robustness tests. This significant direct incentive effect that the CETP has on carbon emissions reduction and carbon neutralization has been found in many previous studies (Tan and Lin, 2022; Wang et al., 2022a). When a CETP is implemented, enterprises adjust their development strategies based on cost minimization and profit maximization principles (Xuan et al., 2020). As the cost increases associated with needing to purchase additional carbon emissions quota can weaken an enterprise’s market price advantages and market competitiveness (Wang et al., 2022), participating in carbon emissions trading can passively increase the TCEE. The extra income gained from selling excess carbon emissions quota and the product income increases brought by the unit carbon emissions after the TCEE improvements brings tangible and intangible benefits, which has an incentive effect on enterprise (Xuan et al., 2020). The CETP positive spatial spillover effect on neighboring regions has also been demonstrated by Liu et al. (2022). Because the spatial competition effect motivated neighboring regions to adopt similar carbon emissions reduction policies and improve the TCEE. This conclusion objectively proved the important contributions of market-oriented environmental regulations to carbon emissions reduction and the feasibility of establishing a national carbon trading market to achieve regional coordinated development, providing empirical evidence to support the advancement of the “dual carbon” goals.

• (2) The GI incentive mechanism results showed that the CETP enhanced the TCEE in the pilot areas and weakened the TCEE in the neighboring areas through GI. The direct incentive effect in pilot regions has been proven in previous studies (Chen and Mu, 2023; Xie et al., 2021). Because of the CETP’s significant pressure on carbon emissions reduction, traditional means such as reducing production can not only threaten enterprise profits and competitiveness but can also fail to achieve carbon emissions reduction targets. To ensure long-term development, enterprises need to make fundamental changes to their technology sources (Xuan et al., 2020). GI can improve the TCEE by reducing the carbon emissions per unit product through cleaner production and end processing innovations (Caparrós et al., 2013). Therefore, the carbon emissions cost pressure brought by the CETP can motivate enterprises to focus on GI activities to achieve green, high-quality development and reduce carbon emissions. The shielding effect in neighboring regions has been confirmed by Liu et al. (2023). Driven by cost pressures, due to their strong GI capacity, the pilot areas have a crowding-out effect on polluting enterprises, which then transfer to neighboring areas to reduce costs (Gao et al., 2020; Zhang et al., 2021), which is in line with the “polluted paradise” hypothesis. This conclusion reveals the adverse consequences of regional competition, further emphasizing the importance of regional cooperation policies and the necessity of establishing a national carbon market.

• (3) The ER effect results showed that the CETP increased the ER in the pilot areas and decreased the ER in the neighboring areas due to the TCEE improvements. The direct ER effect was reached a similar conclusion in Chen et al. (2021c), and Lee et al. (2020) also proved that climate policy effects could be affected by the ER. While the CETP improved the TCEE, it also led to greater gains per carbon emissions unit. Therefore, when the CETP promotes the TCEE in the pilot areas, cost theory and utility theory claim that to maximize their profits and balance the costs and benefits (Du et al., 2021b), the pilot area enterprises choose to increase their carbon consumption, putting the CETP in the trap of inefficient emission reduction, all of which poses a significant challenge to China’s “dual carbon” goals (Yuan et al., 2022). The negative ER effect in neighboring regions is because of the regional energy conservation and emissions reduction competition. The ER effect resulting from an increase in energy consumption in one region could have a warning effect on neighboring regions. The “competition for innovation” mechanism on neighboring regional governments (Wu et al., 2020) and the enterprise goal to obtain competitive advantages could incentivize neighboring areas to become involved in green production activities to obtain environmental benefits and green advantages. The ER effect reveals that the CETP emission reduction effectiveness is impeded, highlighting the importance of implementing both incentive and constraint mechanisms in parallel to ensure effective emission reductions.

Future research needs to explore the CETP-driven differences from a more micro-level industry and enterprise perspective, analyze the key entities in the ER effect, and develop a more targeted policy framework to achieve comprehensive carbon reduction. In addition to the spillover effects between regions, the CETP spillover effects among various micro-level entities are also worth exploring. Moreover, the heterogeneity of incentive effects across different GI types and their impact on the ER effect warrant further investigation.

Policy implications

The above research conclusions revealed the following policy implications.

• (1) Improve the national carbon emissions trading market and guarantee systems. The CETP in the six pilot regions has a significant positive effect on TCEE. Considering that the national carbon trading market is still in its early stages, relevant schemes need to be continuously reformed and improved based on pilot experiences. More industries and enterprises should be included in the carbon trading system to maximize the advantages of the carbon trading mechanism and significantly enhance national TCEE. Additionally, it is necessary to build a more systematic, equitable, and transparent policy framework. The government should ensure trading fairness and orderly national carbon trading market operations by optimizing the carbon emissions quota mechanism and the trading service system and ensuring an open, transparent trading mechanism.

• (2) Establish an effective regional coordinated development mechanism, narrow the development gap between regions, and prevent the “safe haven” effect. The research results indicate that, although CETP has had a certain stimulating effect on neighboring regions, the “safe haven” effect has still widened the low-carbon development gap between pilot and non-pilot regions. Therefore, full play should be given to the emission reduction synergistic driving role of the pilot regions, the efficiency of inter-regional green development communication and coordination should be improved. Leverage the comparative advantages of each region and implement carbon trading mechanisms according to local conditions. By addressing strengths and weaknesses, promote regional carbon trading coordination and interaction. Cross-regional carbon emissions trading mechanism building, factors sharing and exchange platforms, public information platforms, and green counterpart support strategy designs are needed to break down the “green technical barriers”, leverage the regional collaboration advantages.

• (3) Optimize incentive and restraint mechanisms to fully realize the CETP benefits. Although the TCEE improvement has increased the ER effect, in the long run, the GI incentive should be the main path for the promotion of the “dual carbon” goals. Therefore, the government needs to strengthen the policy bonus support for GI, increase R&D investment in green and low-carbon technologies. Create a favorable environment for GI, encourage clean energy development, and guide and support the development of clean industries.To minimize ER and maximize CETP emission reduction effects, effective constraint mechanisms must be established. Corporate carbon emissions penalties should be strengthened. An environmental oversight mechanism involving the central government, media, and public should be established and improved.