The effect of rare events on information-leading role: evidence from real estate investment trusts and overall stock markets

Abstract

The information relationship between real estate investment trusts and stock markets has garnered significant interest in finance; however, the time-varying information flow between the two can vary due to different market conditions. This study scrutinizes the information-leading roles between the real estate investment trust sector and overall stock markets under various market conditions. Shannonian transfer entropy, used for identifying information-leading roles, can reveal nonlinear interactions between two markets; however, the results can be hindered by rare events, such as sporadically occurring episodes. Therefore, this study introduces Rényian transfer entropy to examine the role of rare events in the information flow between the two markets. This conjecture is confirmed using the COVID-19 pandemic as a natural experiment setting of rare events. The results reveal notable findings. (i) Rényian transfer entropy can accurately capture the impact of rare events regardless of the sample period, including the changes in information-leading roles when volatility clustering strengthens. Furthermore, (ii) the significance of liquidity and market efficiency produces different information flows depending on market status. The findings suggest that investors can use Rényian transfer entropy to accurately identify information-leading roles between assets under various market conditions, facilitating optimal portfolio allocation. Moreover, policymakers can benchmark this approach to identify financial risk contagion paths, enabling regulators to implement timely policy actions to mitigate market risks.

Introduction

The REIT sector has experienced significant market capitalization growth over several decades (Topuz and Isik, 2009), underscoring its importance in the market and its advantages against physical assets, such as higher liquidity and ease of trading (Jain et al., 2017; Akinsomi, 2021; Ryu et al., 2021).¹ Financial liberalization and improved trading systems have facilitated the globalization of real estate and financial markets, which has been a primary driver of market growth in REIT (Lesame et al., 2021). The increasing expansion of the REIT market has fostered considerable interest in the price dynamics of the stock and REIT markets (Li et al., 2017). Specifically, investors and scholars are interested in the association between REIT and stock markets as a potential market diversification approach (Chandrashekaran, 1999) and a safe haven against systemic risk (Damianov and Elsayed, 2018). Therefore, previous research has intensively investigated the information flow in terms of spillover risks (Chiang et al., 2017), long-term relationships (Glascock et al., 2000), and market integration (Liu et al., 1990) between the two markets.

REITs and stock markets are significant components of the financial system, and the existing literature has extensively studied their interactions (Xu and Yin, 2017; Gokmenoglu and Hesami, 2019; Bustos and Pomares-Quimbaya, 2020; Mazur et al., 2021; Boungou and Yatié, 2022); however, the direction of information flow between these markets remain mixed. For example, previous studies have tested linear and nonlinear causal relationships² and documented the bidirectional information flow between REITs and overall stocks (Luchtenberg and Seiler, 2014; Lee and Chen, 2022). Furthermore, Hoesli and Oikarinen (2012) employed forecast error variance decomposition, revealing unilateral information flow in which office REIT shocks notably affect general stock market volatility. In contrast, Okunev et al. (2000) and Subrahmanyam (2007) used the GC test³ to determine that stock market returns can influence REIT market returns. This conflicting evidence may be attributed to specific market status depending on the sample period; therefore, this study considers various market conditions and generalizes the exploration of information flow between REITs and stock markets.

Previous studies used Shannonian TE as an instrument rather than the GC test, which can be constrained by several assumptions⁴ (Yi et al., 2021; Lee et al., 2022). Shannonian TE can capture linear and nonlinear interactions between two markets as a model-free measure, providing a more comprehensive assessment of market dynamics (He and Shang, 2017; Baboukani et al., 2020). Notably, Shannonian TE cannot capture specific aspects of a distribution, such as the impact of rare events (Assaf et al., 2022). This study introduces Rényian TE to address this challenge; this approach quantifies the diversity and uncertainty of rare events to capture information flow in various market conditions (Będowska-Sójka et al., 2021; Bossman, 2021; Aslanidis et al., 2022).

By answering the following two inquiries, this study explores the potential of Rényian TE to address the ongoing debate regarding the information flow between REITs and overall stock markets. (1) Can Rényian TE accurately capture the time-varying information flow between REITs and overall stock markets by considering the influence of rare events?⁵ (2) If so, what are the underlying factors for the shift in the information-leading role? This study’s findings have implications for investors and policymakers. First, investors can benchmark the approach to identify the information-leading role between REITs and overall stock markets; for example, such investors can consider market status to allocate optimal weights for each asset (Peralta and Zareei, 2016; Aromi and Clements, 2019). Second, policymakers can use Rényian TE to identify the contagion paths of systemic risk considering entropy-based networks (Kuang, 2021) to establish strategically targeted financial regulations.

Methodologically, this research advances the ongoing debate on the informational relationship between REITs and broader stock markets. This study clarifies TE’s applicability for identifying the information-leading role between REITs and overall stock markets by incorporating nonlinear characteristics of financial time series. This study also provides new insights into the applicability of Rényian TE for accurately assessing information flow in financial markets that consider tail regions in return distributions. Regarding rare events, Rényian TE can capture the variability in information flow across different market conditions—an aspect that traditional Shannonian TE cannot address. This outcome implies that Rényian TE can be benchmarked to identify information flows between financial markets when various market statuses are mixed. Furthermore, the research framework employs a natural experiment setting based on COVID-19 to ensure the consistency of the Rényian TE results and enhance the robustness of conclusions.

The remainder of this study is organized as follows. Section 2 investigates existing literature concerning information flow, and Section 3 describes the data and methodology. Sections 4 and 5 present and discuss the results. Section 6 concludes this study by providing relevant implications. Abbreviations denoted in this study are summarized in Table 1.

Table 1 Abbreviations.

Literature review

Measuring information flow

Investigating information flows between financial assets is a substantially debated topic in finance research. Tang et al. (2019) applied the commonly used GC test to construct a directed network, revealing the information flow between global stock markets beyond simple correlations. Similarly, Al-Yahyaee et al. (2019) conducted the GC test between the US stock market and those in GIPSI, revealing significant causal relationships. Nonetheless, the GC test is limited by its reliance on strict assumptions, including the linearity of time series and normality of residuals in the VAR process (Schreiber, 2000; Dimpfl and Peter, 2013; Jang et al., 2019; Joo et al., 2021; Yi et al., 2021; Lee et al., 2022; Jo et al., 2023). Furthermore, the nonlinear GC test often oversimplifies the complex nature of data series (Li et al., 2022).

In contrast, Shannonian TE captures linear and nonlinear market interactions, offering a broader assessment of market dynamics (He and Shang, 2017; Baboukani et al., 2020); however, Shannonian TE cannot capture rare events or specific aspects of distribution (Assaf et al., 2022). Therefore, several studies adopted Rényian TE, which can effectively capture the impacts of rare events on financial markets (Będowska-Sójka et al., 2021; Bossman, 2021; Aslanidis et al., 2022). Jizba et al. (2021) highlighted the importance of Rényian TE during turbulent periods, such as spikes or sharp rises, for a deeper understanding of directional information transfer. Furthermore, He and Shang (2017) contended that Rényian TE methods could advance analyzing informational relationships between assets’ return series.

This study adopts the Rényian TE to analyze information flow between REITs and overall stock markets across varying market conditions and confirms its robustness through a natural experiment. Therefore, the research framework of this study can provide additional insight into existing studies regarding information flow between REITs and overall stock markets.

Information flow between REITs and stock markets

REITs can make investment in real estate assets easier and mitigate liquidity issues by separating ownership rights, likened to stocks (Simon and Ng, 2009); thus, previous studies examined whether REITs exhibit an information-leading role against stocks. For example, Glascock et al. (2000) found that REITs shared no common information with the stock market from 1972 to 1991; however, a long-term relationship emerged from 1992 to 1996. Furthermore, Laopodis (2009) reported a reciprocal linkage between equity REITs and stocks and asymmetric information flows from mortgage REITs to stocks from 1971 to 2007. These findings highlight that the information flows between REITs and stocks have evolved, with the presence of information transmission between the two assets remaining inconclusive.

The varying market conditions during the sample period may be one reason for the mixed evidence on information flows; however, the existing literature primarily focused on the information flow between REITs and stocks under typical market conditions. The tail regions of return distributions arising from macroeconomic events have received little attention. Numerous studies utilized the COVID-19 pandemic as a proxy for volatile market conditions and explored the dynamics between various financial assets (Kartal et al., 2020; Depren et al., 2021; Kartal et al., 2021; Kartal et al., 2022; Kartal et al., 2024). Nonetheless, the relationship between REITs and the stock market during this period remains largely overlooked.

This study uncovers the relationship between REITs and stocks concerning the varying information flows between these assets across different market dynamics to address these apparent gaps. This study applies the Rényian TE and verifies the robustness of its results through a natural experiment using the COVID-19 pandemic. This approach allows to examine how information flow varies considering time-varying market conditions.

Research method

Data

The SPDR S&P 500 ETF (SPY) and iShares US Real Estate ETF (IYR) are widely used as proxies for overall stock markets and REITs, respectively (Bae and Kim, 2020; Kownatzki et al., 2023). Table 2 presents the specification of each variable. As the oldest and most respected ETF in the US, SPY accurately tracks the US stock market (Bae and Kim, 2020). IYR is the first traditional ETF in the US real estate sector. It serves as the representative for the US REIT market (Curcio et al., 2012; Kownatzki et al., 2023), benchmarking the Dow Jones US Real Estate Index, which tracks the performance of US REITs (Ryu et al., 2021; Ahn et al., 2024). This study obtains daily SPY and IYR closing prices from Barchart.com. The sample period covers from December 1, 2018, to June 30, 2021, including when the World Health Organization declared the COVID-19 pandemic (Ciotti et al., 2020). This period allows to investigate the relationship between REITs and the overall stock market, considering the exogenous shock caused by the pandemic (Onali and Mascia, 2022; Yang et al., 2023).

Table 2 Data description.

This study examines the descriptive statistics of two return series to understand the underlying patterns and distributions of SPY and IYR (Yi et al., 2021; Choi et al., 2023). Table 3 presents the descriptive statistics of the SPY and IYR return series, revealing that IYR has a more volatile return distribution than SPY regarding the minimum–maximum range and standard deviation. Both return distributions are negatively skewed, indicating investors’ risk-averse attitudes (Wen and Yang, 2009; Yi et al., 2022) in the marketplace. The highly leptokurtic return distributions⁶ for SPY and IYR indicate that the frequency of extreme returns is higher and more contingent in the distribution tails than in the normal distribution.

Table 3 Descriptive statistics of returns.

In summary, the two assets’ return distributions are far from the Gaussian distribution; hence, a traditional approach for analyzing two return series may suffer from an embedded normality assumption (Wu et al., 2011). Additionally, this study performs normality tests on both return series to examine whether each follows a Gaussian distribution. The null hypotheses of the normality tests for SPY and IYR are rejected at a 1% significance level. The Jarque–Bera, skewness, and kurtosis test results are 5.636, −1.029, and 17.312 for SPY and 16.039, −2.130, and 27.017 for IYR, respectively. This outcome shows that the return distributions of the two assets deviate significantly from a Gaussian distribution.

Figure 1 illustrates the return series of SPY and IYR, revealing the comovement of the two returns. According to Hoesli and Oikarinen (2012), REITs and overall stock markets move together in the short term with a less than three-year horizon because both markets share the noise from the equity market. The shaded area in Fig. 1 indicates that both assets were severely affected by the COVID-19 pandemic (NBER),⁷ with strong volatility clustering, demonstrating heteroskedasticity in both return series.

Fig. 1

Return series of SPY and IYR.

Methodology

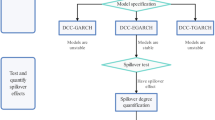
Figure 2 graphically summarizes the methodologies employed in this study. First, this study utilizes the VRT to test the weak-form efficient market hypothesis for REITs and the overall stock market. The TE approach captures nonlinear information flows between two assets. TE is further divided into two parts, i.e., the Shannonian TE for general market conditions and the Rényian TE for reflecting the impacts of rare events on information flows. Then, this study applies the AMIM method to identify the time-varying market (in)efficiency across the whole data period.

Fig. 2

Graphically summarized technical concepts.

Variance ratio test

The VRT has been widely used to investigate the weak-form EMH⁸ (Aumeboonsuke and Dryver, 2014; Ryu et al., 2021) and can examine whether the natural logarithm of a price series (${Y}_{t}$) follows a random walk⁹ (Choi et al., 2023; Jeong et al., 2023). In the VRT, the variance of the random walk increments increases linearly with the sampling interval. Accordingly, if the log price series follows a random walk, the variance of its $d^{\rm{th}}$ difference should grow proportionally with the number of differences ($d$). The log price series, ${Y}_{t}$, is as follows:

$${Y}_{t}=\mu +{Y}_{t-1}+{\varepsilon }_{t},$$

where $\mu$ is constant and ${\varepsilon }_{t}$ is an $i.i.d.$ random variable following a normal distribution with a zero mean and finite variance. The variance ratio ${VR}(d)$ is defined as follows:

$${VR}\left(d\right)=\frac{{\hat{\sigma }}^{2}\left(d\right)}{{\hat{\sigma }}^{2}\left(1\right)},$$

where ${\hat{\sigma }}^{2}$ corresponds to the maximum likelihood estimator of ${\sigma }^{2}$. ${\hat{\sigma }}^{2}\left(1\right)$ and ${\hat{\sigma }}^{2}\left(d\right)$ are variances of the first and $d^{\rm{th}}$ differences, respectively, referencing Lo and MacKinlay (1988):

$${\hat{\sigma }}^{2}\left(1\right)=\frac{1}{\left({nd}-1\right)}\mathop{\sum }\limits_{t=1}^{{nd}}{\left({Y}_{t}-{Y}_{t-1}-\hat{\mu }\right)}^{2},$$

and

$${\hat{\sigma }}^{2}\left(d\right)=\frac{1}{d\left({nd}-d+1\right)\left(1-\frac{d}{{nd}}\right)}\mathop{\sum }\limits_{t=d}^{{nd}}{\left({Y}_{t}-{Y}_{t-d}-d\hat{\mu }\right)}^{2},$$

with

$$\hat{\mu }=\frac{1}{{nd}}\left({Y}_{{nd}}-{Y}_{0}\right),$$

where ${Y}_{0}$ and ${Y}_{{nd}}$ are the first and last observations of the log price series, respectively.

The test acknowledges heteroskedasticity due to the observed time-varying conditional volatilities of the two markets. Under heteroskedasticity, the asymptotic variance is expressed as follows:

$$\varPhi \left(d\right)={\mathop{\sum }\limits_{k=1}^{d-1}\left[\frac{2\left(d-k\right)}{d}\right]}^{2}\hat{\delta }\left(k\right),$$

with

$$\hat{\delta }\left(k\right)=\frac{\mathop{\sum }\nolimits_{t=k+1}^{{nd}}{\left({Y}_{t}-{Y}_{t-1}-\hat{\mu }\right)}^{2}{\left({Y}_{t-k}-{Y}_{t-k-1}-\hat{\mu }\right)}^{2}}{{\left[\mathop{\sum }\nolimits_{t=1}^{{nd}}{\left({Y}_{t}-{Y}_{t-1}-\hat{\mu }\right)}^{2}\right]}^{2}}.$$

The $Z$-statistics under heteroskedasticity specification ($Z\left(d\right)$) can be expressed as follows:

$$Z\left(d\right)=\frac{{VR}\left(d\right)-1}{\sqrt{\varPhi \left(d\right)}} \sim N\left(0,1\right).$$

The null hypothesis of the VRT is that the log price series, ${Y}_{t}$, follows a random walk (i.e., ${VR}\left(d\right)=1$). If ${VR}\left(d\right)\,>\,1$, then the increment of the log price series is positively serially correlated, implying that the price series has long-term memory. Conversely, if ${VR}\left(d\,\right)\, <\, 1$, then the increment of the log price series is negatively serially correlated, and the price series is a mean-reverting process (Ryu et al., 2021).

Transfer entropy

This study employs TE¹⁰ using Shannonian and Rényian TE measures. First, Shannonian TE is a widely utilized methodology for analyzing information flow (Yi et al., 2021; Jo et al., 2023). Shannonian TE measures the cause–effect relationships between dynamic events hidden behind the correlation (Liang, 2013) and can also capture asymmetric interactions between two systems, serving as a nonlinear causality measure (Jo et al., 2023); thus, it provides a valuable alternative when the assumptions of the GC test do not hold (Yi et al., 2021). First, the average amount of information, $H$, leads to the general formula of Shannon entropy (Shannon, 1948), such that (Dimpfl and Peter, 2013):

$${H}_{J}=-\mathop{\sum}\limits_{j}\,p\left(j\right)\times {\log }_{2}p\left(j\right),$$

where $J$ denotes a discrete variable that takes the probability distribution $p\left(j\right)$; thus, $j$ indicates each value that $J$ can hold. Accordingly, the mathematical formula for Shannonian TE is as follows:

Suppose ${A}_{t}^{\left(k\right)}=\left({A}_{t},\cdots ,{A}_{t-k+1}\right)$ and ${B}_{t}^{\left(l\right)}=\left({B}_{t},\cdots ,{B}_{t-l+1}\right)$ are two distinct random processes of lengths $k$ and $l$, respectively. In this case, the conventional TE is as follows:

$$T{E}_{B\to A}\left(k,l\right)=H\left({A}_{t+1}|{A}_{t}^{\left(k\right)}\right)-H\left({A}_{t+1}|{A}_{t}^{\left(k\right)},{B}_{t}^{\left(l\right)}\right),$$

where $T{E}_{B\to A}\left(k,l\right)$ is the effect of ${B}_{t}^{\left(l\right)}$ on predicting ${A}_{t+1}$. $H\left({A}_{t+1}|{A}_{t}^{\left(k\right)}\right)$ is a conditional entropy that denotes the degree of uncertainty in predicting ${A}_{t+1}$ for a given ${A}_{t}^{\left(k\right)}$. $H\left({A}_{t+1}|{A}_{t}^{\left(k\right)},{B}_{t}^{\left(l\right)}\right)$ is a conditional entropy that represents the degree of uncertainty in predicting ${A}_{t+1}$, simultaneously considering ${A}_{t}^{\left(k\right)}$ and ${B}_{t}^{\left(l\right)}$ (Choi et al., 2023; Jeong et al., 2023).

Rényian TE can be benchmarked against Shannonian TE when a rare event arises in a financial time series in investigating information flow (Assaf et al., 2022). Rare events that occur at the edges or in the extreme portions of a distribution (often referred to as the “tail ends”), as well as various regions across the entire range of the distribution, can be accentuated by controlling the weighting parameter (Jizba et al., 2012). Therefore, this approach is preferable when the sample period depends on varying market conditions, such as the COVID-19 pandemic. Rényian TE is based on Rényi entropy, an extension of Shannon entropy that introduces an additional parameter ($q$).

Rényi entropy considers a distinct random variable ($J$) with probability distribution $p(j)$, where $j$ is the possible outcomes of $J$. The Rényi entropy (${H}_{J}^{q}$) is as follows:

$${H}_{J}^{q}=\frac{1}{1-q}\log\mathop{\sum}\limits_{j}{p}^{q}\left(j\right),$$

where $p$ denotes the event probability, and $q$ is a positive number. For $0 <\, q \,<\, 1$, rare events with low probabilities are weighted more heavily as $q$ approaches zero. If $q \,>\, 1$, central events with high probabilities receive more weight; however, as $q\to 1$, Rényi entropy converges to Shannon entropy (Będowska-Sójka et al., 2021; Bossman, 2021; Aslanidis et al., 2022).

Adjusted market inefficiency magnitude

Le Tran and Leirvik (2019) proposed AMIM, which captures the time-varying properties of market efficiency across different asset classes. AMIM can directly measure the significance of efficiency in a market over time using autocorrelation coefficients and associated confidence intervals.

This study first considers the AR process¹¹ (${AR}\left(m\right)$) of returns (${r}_{t}$) as follows:

$${r}_{t}=\alpha +{\beta }_{1}{r}_{t-1}+{\beta }_{2}{r}_{t-2}+\cdots +{\beta }_{m}{r}_{t-m}+{\varepsilon }_{t},$$

(1)

where $m$ is the number of lags in the AR model. ${\beta }_{m}$ is the AR coefficient with a lag of $m$, $\alpha$ is the constant, and ${\varepsilon }_{t}$ is the error term. $\hat{\beta }$ is an $(m\times 1)$ vector that includes the estimated AR coefficients ${\left({\hat{\beta }}_{1},{\hat{\beta }}_{2},\cdots ,{\hat{\beta }}_{m}\right)}^{{\prime} }$. $\hat{\beta }$ is asymptotically distributed as given by $\hat{\beta } \sim N(\beta, {\Sigma})$, where β is the $\left(m\times 1\right)$ vector of true AR coefficients, and ${\Sigma}$ is the $\left(m\times m\right)$ asymptotic covariance matrix of the estimated $\hat{\beta }$ vector. Through the Cholesky decomposition, ${\Sigma}$ can be decomposed into two triangular matrices, ${\Sigma} =L{L}^{{\prime} }$. After multiplying $\hat{\beta }$ into the inverse of triangular matrix $L$, the standardized $\hat{\beta }$ is obtained as follows:

$${\hat{\beta }}^{{\rm{standard}}}={L}^{-1}\hat{\beta },$$

where each component in ${\hat{\beta }}^{{\rm{standard}}}$ is independent.

The EMH requires that past and current returns do not predict future returns; therefore, if the market is efficient, all the coefficients $\left({\beta }_{1},{\beta }_{2},\cdots ,{\beta }_{m}\right)$ in Equation (1) should be close to zero. Meanwhile, ${\hat{\beta }}^{{\rm{standard}}}$ is normally distributed with a covariance matrix, an identity matrix under the null hypothesis that the EMH holds in the market. Therefore, MIM, which indicates the degree of inefficiency within the market, can be defined as follows:

$${MIM}=\frac{\mathop{\sum }\nolimits_{i=1}^{m}\left|{{\hat{\beta }}_{i}}^{{\rm{standard}}}\right|}{1+\mathop{\sum }\nolimits_{i=1}^{m}\left|{{\hat{\beta }}_{i}}^{{\rm{standard}}}\right|},$$

where ${{\hat{\beta }}_{i}}^{{\rm{standard}}}$ is the ${i}^{{th}}$ term of the standardized AR coefficient matrix ${\hat{\beta }}^{{\rm{standard}}}$, and MIM falls between 0 and 1.

This study uses an overlapping window of the daily return series to compute MIM measures for each time interval. Specifically, MIM is calculated at time $t$ using a moving window with ${r}_{t-m+1}$, where $1\le m\le w$ with $w$ window size. The optimal lag order of each moving window is determined using AIC.

The MIM value can lead to a false alarm regarding market efficiency as MIM and the number of lags in ${AR}\left(m\right)$ would be positively correlated. This study uses the AMIM value and a 95% confidence interval of MIM under the null hypothesis to avoid this undesirable outcome: ${{\hat{\beta }}_{i}}^{{\rm{standard}}}=0$. This study computes the confidence interval (${R}_{{CI}}$) for each of the lag numbers with simulated ${{\hat{\beta }}_{i}}^{{\rm{standard}}}$ values that follow the standard normal distribution. Finally, the AMIM is given as follows:

$${AMIM}=\frac{{MIM}-{R}_{{CI}}}{1-{R}_{{CI}}}.$$

(2)

The denominator in Equation (2) enables comparison across different periods and assets. Specifically, ${AMIM}\,\le\, 0$ indicates that a market is efficient. In contrast, ${AMIM}\, >\, 0$ implies inefficiency within the market (Le Tran and Leirvik, 2019; Okoroafor and Leirvik, 2022).

Results

Market efficiency

Efficient markets have been well documented as having an information-leading role against inefficient markets (Lu et al., 2018; Choi et al., 2023; Jeong et al., 2023); that is, more information flows from the market with a fair price to the market with a price anomaly. In this context, this study first investigates whether the VRT can support the random walk hypothesis of SPY and IYR.

This study considers the VRT under the heteroskedasticity specification due to observed time-varying conditional volatilities that can be supported by testing whether each return series’ residuals are homoscedastic (Box and Pierce, 1970; Ljung and Box, 1978; Breusch and Pagan, 1979). Considering the return series in the form of ${r}_{t}=\mu +{\varepsilon }_{t}$, the null hypothesis of each test is that residual, ${\varepsilon }_{t}$, is independently distributed (i.e., the series is homoscedastic). Table 4 shows that the null hypothesis is rejected for SPY and IYR at the 1% significance level, regardless of the testing methods, confirming heteroskedasticity in the two return series.

Table 4 Test statistics for homoscedasticity.

This study conducts the VRT under this specification based on heteroskedasticity in the return series. Table 5 reveals that the SPY does not follow a random walk at a 5% significance level; thus, the SPY market is inefficient in the weak form. In contrast, we cannot reject the random walk hypothesis for the IYR as the IYR market is efficient in the weak form; therefore, we hypothesize that the IYR market has an information-leading role over the SPY market.

Table 5 VRT results under the heteroskedasticity specification.

Information flow

This study determines the information flow between SPY and IYR markets by estimating the Shannonian TE, a conventional approach for investigating information flow between two interacting systems. Table 6 demonstrates unilateral information flow from IYR to SPY, confirming the conjecture based on the VRT results that the IYR market has an information-leading role over the SPY market. Consistent with previous studies (Lu et al., 2018; Choi et al., 2023; Jeong et al., 2023), the findings indicate that the IYR market (which has fair prices) transfers information unilaterally to the SPY market (which contains price anomalies).

Table 6 Shannonian TE.

Notably, financial markets lose market efficiency when a negative externality is eminent (Le Tran and Leirvik, 2019; Choi, 2021; Wang and Wang, 2021), implying that the information-leading role between the REITs and overall stock markets during a period of turmoil could change (Huang et al., 1996). Therefore, this study investigates the change in information-leading role using Rényian TE based on its capability of capturing the effect of rare events (i.e., extreme market conditions).¹²

Figure 3 presents the estimated Rényian TE values and standard errors. When $q=1$, the result is consistent with the Shannonian TE findings in Table 5;¹³ however, when $q < 1$, significant bidirectional information flows are evident, and information-leading role shifts from IYR to SPY. Moreover, the net information flow from the SPY to IYR rises as $q$ approaches zero. Therefore, this study contends that the information-leading role shifts from the REIT market to the overall stock market as negative externalities are imminent.

Fig. 3: Rényian TE.

Each error bar represents one standard error. Insignificant TE value is omitted (i.e., TE from SPY to IYR (the red dot) at $q=1$).

Natural experiment

This study uses a natural experiment (the COVID-19 pandemic) to confirm the results of the Rényian TE (Choi et al., 2023), revealing that the information flow between SPY and IYR changes across different market phases (Onali and Mascia, 2022; Yang et al., 2023). Considering the conditional volatility in the marketplace, this study divides the sample period into pre-turmoil, turmoil, and post-turmoil periods of the COVID-19 pandemic. This study employs the GARCH model, specifically the GARCH(1,1) model (Zolfaghari et al., 2020), as shown in Fig. 4.¹⁴ The findings indicate heteroskedasticity in the conditional variance of daily returns of the SPY and IYR. Furthermore, strong volatility clustering occurred in the early stage of the COVID-19 pandemic. In the shaded period of Fig. 4, most conditional volatilities in each asset deviate above the trend¹⁵ by more than one standard deviation; therefore, this study contends that the pandemic turmoil period (Period 2) ranges from February 2020 to April 2020. This result aligns with previous studies (Onali, 2020; John and Li, 2021; Joo et al., 2021; Jeong et al., 2023) and largely overlaps with the US recession period announced by the NBER.

Fig. 4: Conditional volatility of SPY and IYR.

Panels A and B indicate the conditional volatilities, trends, and thresholds for SPY and IYR, respectively. The shaded area is the turmoil period caused by the COVID-19 pandemic from February 2020 to April 2020. The data represent the conditional volatilities of SPY and IYR estimated using the GARCH(1,1) model. This study estimates the trend of conditional volatilities using the HP filter, with a smoothing parameter value of $\mathrm{13,322,500}$ for daily frequency data. Each threshold is one standard deviation above the trend.

This study uses Shannonian TE to investigate the information flow between SPY and IYR in the three subsample periods. Table 7 shows that information flow is only evident from IYR to SPY during the pre-turmoil period, which is congruent with information flow for the entire sample period reported in Table 6. Conversely, when volatility clustering strengthens during the turmoil period, the SPY exerts an information-leading role over the IYR, which is consistent with the Rényian TEs with a low value of parameter $q$ (i.e., assigning high weight to rare events). In the post-turmoil period, symmetric and bidirectional information flows are revealed between SPY and IYR. This outcome could be attributable to the relieved effect of the externality a few months after the pandemic since market return and volatility for both real estate and stock began to rebound after April 2020 (Hasan et al., 2021; Kuk et al., 2021).

Table 7 Shannonian TE for three different subsample periods.

This study next employs the t-test to determine whether a statistically significant difference is present between groups (Chernozhukov et al., 2018; Yao et al., 2022). This approach validates the findings of symmetric and asymmetric information flow between SPY and IYR in each subsample period. Table 8 shows that the $t$-test result can reject the null hypotheses for Periods 1 and 2, implying that the information flow from IYR to SPY (from SPY to IYR) dominated that from the opposite direction in the pre-turmoil (turmoil) period. Conversely, the null hypothesis cannot be rejected in Period 3, even at the 10% significance level, indicating bidirectional and symmetric information flow between SPY and IYR. In summary, the information-leading role immediately shifts from IYR to SPY after the external shock; however, both markets ultimately share equivalent information until the shock stabilizes. These results from the natural experiment align well with those of the Rényian TE per the different weights for rare events.

Table 8 t-test for each subsample period.

Discussion

This study first identifies the unilateral information flow from IYR to SPY over the entire sample period, which can be explained in terms of market efficiency. According to Ryu et al. (2021), the REIT market is efficient in the weak form due to high institutional ownership. Institutional investors have risen consistently, with the proportion of shares exceeding 60% on average from 1993 to 2020 (Aroul et al., 2023). Furthermore, for over two decades, the number of institutional investors in the REIT market has consistently surpassed that in the common stock market (Ryu et al., 2021; Bond et al., 2022). These institutional investors intensely monitor the REIT market; thus, information in the REIT market is effectively incorporated, lowering information asymmetry and enhancing market efficiency (Boone and White, 2015; Chen et al., 2020). Therefore, IYR has an information-leading role over SPY during the overall sample period because of the REIT market’s price fairness.

Nonetheless, both markets are inefficient during and after the turmoil period, and IYR loses its information-leading role against the SPY (Le Tran and Leirvik, 2019; Choi, 2021; Wang and Wang, 2021). Figure 5 illustrates the (in)efficiency of SPY and IYR in the time-varying form of AMIM values. A positive measure indicates market price inefficiency (Le Tran and Leirvik, 2019); thus, the SPY and IYR were inefficient during the turmoil period. This instability continued for several months in the post-turmoil period, maintaining the pandemic-related inefficiency in the REIT and overall stock market (${\rm{AMIM}}\, >\, 0$); therefore, the IYR’s efficiency no longer held an information-leading role.

Fig. 5: Market inefficiency estimated using the AMIM measure.

This study estimates daily AMIM with a 240-day overlapping window of the return series, smoothed with a 30-day moving average. This study determines the optimal lag length of the model using the AIC. The shaded area denotes the turmoil period from COVID-19 from February 2020 to April 2020.

Focusing on rare events shows that liquidity can be a primary factor (Chordia et al., 2008; Chung and Hrazdil, 2010) influencing the reversed information flow from SPY to IYR during the COVID-19 pandemic. Therefore, this study uses Amihud’s (2002) illiquidity measure, which is the ratio of the absolute value of daily returns to trading volume in dollars, to compare the liquidity of SPY and IYR for the entire sample period. Figure 6 reveals that SPY’s liquidity continuously exceeded IYR’s during the entire period. Chebbi et al. (2021) found that liquidity is crucial for investors, and its significance increases when the market suffers from high uncertainty, such as during financial crises. Ahn et al. (2019) and Lee et al. (2022) demonstrated that markets based on massive liquidity could include most information and subsequently act as information transmitters to less liquid markets. In this context, liquidity can be crucial in determining the role of information discovery between REITs and overall stock markets, in which both markets are inefficient. The SPY market is more liquid than the IYR market and unilaterally transfers information to the IYR during the turmoil period.

Fig. 6: Log-scaled Amihud illiquidity.

This study presents the logarithmic scaled values of illiquidity. The shaded area indicates the turmoil period caused by COVID-19 from February 2020 to April 2020. The dotted lines indicate each subsample period’s average illiquidity: Period 1 (pre-turmoil: December 2018–January 2020), Period 2 (turmoil: February 2020–April 2020), and Period 3 (post-turmoil: May 2020–June 2021).

Concluding remarks

Conclusion

This study explores Rényian TE’s potential as a promising instrument for investigating information flows between two financial assets under different market status periods. While Shannonian TE suffers from rare events, such as sporadically occurring episodes, this study demonstrates that Rényian TE can successfully detect changes in information-leading role across the sample period by effectively capturing the impact of rare events. Specifically, IYR holds an information-leading role over SPY during the overall sample period because IYR has weak-form market efficiency (as revealed by the VRT), unlike SPY; however, when volatility clustering is prominent, the information-leading role transfers to SPY over IYR. While both markets lose market efficiency as volatility clustering strengthens, liquidity can be a primary driver for explaining the information-leading role.

Implications

This study’s findings have managerial and policy implications for investors and regulators. First, the Rényian TE can help investors precisely identify the information-leading role between assets for various market conditions, allowing them to obtain valuable insights for allocating optimal weights to their portfolios. Furthermore, policymakers can employ the analytical approach to discern the contagion paths of financial risk captured by entropy-based networks, which may help regulators establish timely strategic policy actions to relieve market risks.

Limitations and future works

This study mainly focuses on daily returns, suggesting that future studies can use high-frequency data to benchmark the research framework in exploring market microstructure. In addition to return series, the information flow between markets based on volatility can deliver additional insights using intra-day prices. This study’s Rényian TE approach can be a desirable instrument in this procedure because a distribution’s tail regions are closely related to the extent of volatility. This study concentrated on ETFs; however, future studies can consider the research framework (including Rényian TE and the natural experiment setting) in unveiling dynamic information flows between futures and spot markets for the underlying assets.