A joint-training topic model for social media texts

Abstract

The burgeoning significance of topic mining for social media text has intensified with the proliferation of social media platforms. Nevertheless, the brevity and discreteness of social media text pose significant challenges to conventional topic models, which often struggle to perform well on them. To address this, the paper establishes a more precise Position-Sensitive Word-Embedding Topic Model (PS-WETM) to adeptly capture intricate semantic and lexical relations within social media text. The model enriches the corpus and semantic relations based on word vector similarity, thereby yielding dense word vector representations. Furthermore, it proposes a position-sensitive word vector training model. The model meticulously distinguishes relations between the pivot word and context words positioned differently by assigning different weight matrices to context words in asymmetrical positions. Additionally, the model incorporates self-attention mechanism to globally capture dependencies between each element in the input word vectors, and calculates the contribution of each word to the topic matching performance. The experiment result highlights that the customized topic model outperforms existing short-text topic models, such as PTM, SPTM, DMM, GPU-DMM, GLTM and WETM. Hence, PS-WETM adeptly identifies diverse topics in social media text, demonstrating its outstanding performance in handling short texts with sparse words and discrete semantic relations.

Introduction

The rapid growth of social media has revolutionized the way of communication, generating an immense volume of social media text that reflects diverse perspectives and insights. Platforms such as Twitter, Facebook, and Weibo, in particular, facilitate the widespread dissemination of brief yet information-rich messages, which pose significant analytical challenges due to their brevity and high variability (Qin et al., 2023). Consequently, the analysis of social media text has become an increasingly critical task.

Scholars have primarily approached this analysis from two aspects: sentiment analysis and topic analysis. For sentiment analysis, scholars have conducted extensive research. Faced with short and ambiguous Twitter messages, Bravo-Marquez et al. proposed Annotate-Sample-Average (ASA), a distant supervision approach that utilizes these two resources to generate synthetic training data for sentiment polarity classification. This method yields a classifier that significantly outperforms those trained on tweets annotated with emoticons and those trained without any sampling and averaging, based on the polarity of their words (2016). Wang et al. advanced sentiment analysis by integrating textual information of Twitter messages with sentiment diffusion patterns to achieve superior performance in analyzing on Twitter data (2019). Kumar et al. applied sentiment analysis to short texts using Enhanced Vector Space Model combined with a Hybrid Support Vector Machine classifier. And to further enhance the accuracy of this method when applied to short texts, Kumar extended the sentiment dictionaries through the expansion of Stanford’s GloVE tool during the sentiment analysis (2024).

For topic analysis, while scholars have focused on identifying topics within short texts (Xu et al., 2019), there is a paucity of topic models tailored specifically for social media text, which is characterized by brevity and discreteness. Compared to typical short texts, social media text exhibits greater discreteness, due to that contemporary social media text is carried on the social network platforms, which aggregate a wide array of internet slang and buzzwords (Zhang et al., 2021; Qin and Zhang, 2024). Consequently, the opinions shared on these platforms tend to be more informal and unexplainable, making it difficult for conventional models to perform accurate topic extraction and analysis. Thus, there is a pressing need for more sophisticated models capable of addressing the unique characteristics of social media text and providing deeper insights into the underlying topics.

To address these issues and accurately extract topics from social media text, the study introduces the short-text topic model PS-WETM. This model primarily incorporates a novel devised position-sensitive word vector training model and a self-attention mechanism. These innovations aim to capture the unique dynamics and semantic intricacies inherent more effectively in the brief yet complex expressions of social media text. In this short-text topic model, we utilize word vector similarity to enrich the corpus and semantic relations, thereby achieving dense word vector representations. And it employs the proposed position-sensitive word vector training model to differentiate relations between the pivot word and context words in various positions by assigning symmetrical weight matrices to words positioned symmetrically. Additionally, the model incorporates a self-attention mechanism to globally capture dependencies between each element in the input word vectors and calculate the contribution of each word to the topic matching performance accuracy. This method effectively captures the relationships within texts that are more discrete and contain scarce semantic relations. To evaluate the accuracy of short-text topic model PS-WETM, we conduct comparative analyses with six other topic models, utilizing perplexity and topic coherence as metrics. Finally, we select “COVID-19 explosion” as a case study, crawling relevant microblogs as data to verify the accuracy of PS-WETM, and employ Word Cloud visualizations and sentiment analysis of these microblogs to further evaluate the performance of the PS-WETM model and trace the evolving tendencies of their topics.

The contributions of this paper:

• To counterbalance the inherent scarcity of semantic relations in social media text, we implement a short text extension strategy utilizing word vector similarity, thereby enriching the semantic information conveyed by these texts.

• It defined a position-sensitive word vector training model equipped with a customized positional judgment mechanism, which considers the impact of word position on semantic relations, addressing the problem that current word vector training models ignore the position of context words. This innovation allows for a more nuanced understanding of word semantics, considering not just the words themselves but their specific positions within a text, thereby enhancing the model’s ability to accurately interpret and process language.

• To further enhance the performance of topic matching for social media text characterized by their conciseness and discreteness features, the model employs self-attention mechanism to post-process the extracted sentence features, which is capable of globally discerning internal semantic relations within a sentence and proactively determines the contribution of each word vector to the accuracy of topic matching. This approach leads to a more precise and representative depiction of word features, enhancing the model’s ability to accurately reflect the nuanced dynamics of social media text.

Literature review

Topic models for document

LDA is a basic topic model for identifying latent topics, playing a critical role in text classification, topic detection, evolution tracking, emotion analysis, and other tasks. However, LDA exhibits certain limitations, particularly when applied to document sets rich in metadata, where its performance often proves suboptimal. To overcome the limitations, researchers have proposed the Structural Topic Model (STM). STM extends the basic LDA framework by incorporating document-level covariates into the modeling process (Roberts et al., 2016). These covariates can include any attributes of the documents, such as publication date, author identity, or other contextual information. By integrating these covariates, STM captures not only the latent topic structures within documents but also the influence of covariates on topic prevalence and content. Nevertheless, both LDA and STM demand significant computational resources and and substantial time investment for training document weights when identifying topics from massive corpus (Jiang et al., 2019; Balikas et al., 2016; Huang et al., 2020). Moreover, their probabilistic foundations, adhering to the Bag of Words model and presuming word independence, diverge from the complexities of natural language (Bastani et al., 2019; Meng et al., 2020; Keya et al., 2023). Additionally, it ignores word order, resulting in poor semantic coherence and topic interpretability (Salehi et al., 2015; Ruas et al., 2019).

In response to these challenges, researchers have introduced several enhanced topic models incorporating word or document vectors (Li et al., 2020; Ma et al., 2019), and topic models combined with neural networks, which markedly improve semantic coherence in documents (Brown et al., 2020; Bender et al., 2021). For topic models incorporating word or document vectors (Steuber et al., 2021; Kumar et al., 2022), a notable advancement is the LDA2vec model. This model integrates Word2vec with LDA, where Word2vec utilizes a neural network framework to map input word vectors, and LDA employs probabilistic distributions for training topic weights (Moody Christopher, 2016; Mikolov et al., 2013; Le and Mikolov, 2014).

For topic models combined with neural network, scholars fused neural network with topic models to model topic distributions and learn topic representations (Hofmann, 1999; Blei et al., 2010; O’Callaghan et al., 2015; Belford et al., 2018; Bruni et al., 2014; Shahriare Satu et al., 2021; Chaturvedi et al., 2019). Specifically, Peng et al. introduced the Neural Sparse Topical Coding (NSTC), an advancement of the Sparse Topical Coding (STC) model (2018). NSTC addresses the issue of sparsity and demonstrates the versatility of neural networks with three extended applications without the need for re-deriving inference algorithms. In a further innovation, He et al. proposed a two-phase neural embedding network with redundancy-aware graph-based ranking, which optimizes the identified topics with fewer yet more representative terms. This approach the integrality and fidelity of topics while demonstrating how pre-trained neural embedding can be effectively applied to automatic topic labeling tasks (2021). Gupta et al. introduced a novel neural topic model named Discrete-Variation-Inference-based Topic Model. This model acquires dense topic embeddings that are homomorphic to word embeddings through discrete variational inference, conceptualizing words as mixtures of topics (2023). To further improve semantic relevance, scholars have combined the BERT pre-trained language model with topic models to extract latent topics from short texts, resulting in the BERTopic model (Grootendorst, 2022). The BERTopic model generates document embeddings using pre-trained transformer-based language models, clusters these embeddings, and finally generates topic representations with the class-based TF-IDF. Experimental results indicate that the BERTopic model performs exceptionally well in topic mining.

Topic models for short texts

Whereas social media text on platform like Weibo and Twitter typically manifests as short texts, the lexical characteristics of social media text exhibit greater dispersion compared to regular short texts, presenting significant challenges in the effective extraction of latent topics. These texts often amalgamate a broad range of internet slang and popular expressions, rendering the opinions shared on social network platforms more informal and less interpretable. On the surface, adjacent words may seem unconnected, yet within the context of the entire sentence, they frequently bear profound associations. Additionally, the limited number of words and the insufficiency of semantic information in these texts lead to sparse feature vectors. Consequently, standard document topic models are ill-suited for analyzing such short, semantically sparse texts as those found in social media.

Addressing this issue, several researchers have modeled texts as networks, wherein words are represented as nodes interconnected based on textual similarity. For instance, Machicao et al. characterized text networks to grasp informative spatio-temporal patterns and attributions of texts by considering both the topological and dynamic properties of networks (2018). Furthermore, one commonly method to enhance the performance of short-text topic mining is clustering short text via neural networks. Xu et al. have proposed a clustering technique via convolutional neural networks, which optimizes clustering by imposing constraints on learned features through a self-taught learning framework, eschewing the need for external labels (2015). Moreover, some scholars have attempted to extend or aggregate short text to solve its problem of sparse and unbalanced features. For example, the Bi-term Topic Model (BTM) was introduced to more effectively capture the co-occurrence relationships between words in short texts (Yan et al., 2013), which utilizes word pairs as the fundamental unit for modeling. However, BTM only considers the frequency of bi-term, neglecting the latent semantic relations between them, which may result in semantically similar words being categorized under different topics. Addressing this limitation, Li et al. improved the BTM for short texts and proposed the Latent Semantic Augmented Bi-term Topic Model (LS-BTM) based on BTM, which incorporates semantic information as prior knowledge to infer topics more accurately (2018). Beyond these advancements, researchers have explored incorporating external word-associated knowledge and prior understanding into short texts to improve the coherence of topic modeling. For example, Dieng et al. proposed Embedded Topic Model (ETM) to extract latent topics from short texts, employing a categorical distribution for each word. Within this distribution, the natural parameter is the inner product between word embeddings and specific topic embeddings. ETM has demonstrated the capability to uncover explainable topics within large vocabularies containing rare and stop words, thus outperforming traditional models like LDA in terms of topic quality and predictive performance (2020). Furthermore, another effective topic model for short texts is the fuzzy bag-of-topics model, developed from the fuzzy bag-of-words model (FBoWC). This model utilizes words communities that provide greater coherence than word clusters in FBoWC, replacing word clusters as basis terms in text vector (Jia and Li, 2018).

The above topic models for short texts present better performance compared to traditional topic models for documents. However, their effectiveness diminishes when applied to social media text, primarily due to their inability to specify unique positions of context words, the limited semantic content, and discrete semantic relations. To address these challenges, this paper introduces a joint-training short-text topic model —Position-Sensitive Word-Embedding Topic Model (PS-WETM). The model involves a proposed position-sensitive word vector training model and self-attention mechanism, which together facilitate a more comprehensive capture of global semantic relations within sentences. Additionally, it accurately evaluates the exact contribution of each context words in different positions, thereby significantly enhancing the model’s ability to precisely identify topics within social media text.

Methodology

Short text extension

To enhance the accuracy in identifying latent topics from brief contexts on platforms like Weibo and Twitter, we implement text extension techniques based on the semantic similarity of word vectors.

Initially, we generate word vectors using Word2vec. We select a word w from the corpus and verify whether its corresponding word vector is present within the set of generated word vectors. If the word vector for w is identified, we proceed to calculate the similarity between w ‘s word vector and the vectors of all other words in the corpus. Subsequently, we fill the new text with word w and the first k words with the highest similarity. The semantic similarity between words w₁ and w₂ is calculated as:

$${\rm{similarity}}\,({w}_{1},{w}_{2},)=\frac{{v}_{1}\times {v}_{2}}{{||}{v}_{1}{||}\times {||}{v}_{2}{||}}$$

(1)

where v₁ and v₂ are their word vectors. ${v}_{1}\times {v}_{2}$ denotes the dot product of two words’ vectors, and ||v₁|| represents the length of modulus.

In this paper, we utilize genism in Pycharm to calculate the similarity of words. And we use microblogs of event COVID-19 in Sina Weibo as corpus. The total number of words in the corpus is 188583, the number of unique vocabularies is 5929 and the dimension of feature vectors is 200. It uses negative sampling to get loss function, where negative samples = 5, size of window = 5. The top five words with the highest similarity of the example words are shown in Table 1.

Table 1 The similarities of exampled words.

The proposed short-text topic model PS-WETM

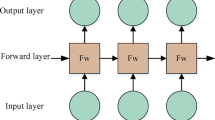
In this chapter, we propose a joint-training topic model PS-WETM, which integrates a proposed position-sensitive word vector training model, self-attention mechanism, document proportion and topic matrices obtained by LDA, aimed at enhancing the focus on contextual relationships between words and their associations with topics within documents. The proposed position- sensitive word vector training model in the PS-WETM short-text topic model assigns varying weight matrices to context words based on their relative positions to the pivot word, under the assumption that context words at symmetric positions share a comparable degree of semantic relation with the pivot word. With the proposed position- sensitive word vector training model, we extract sentence features encompassing the feature vectors of each word. In order to better characterize the feature vectors of each word, we employ a self-attention mechanism to obtain the degree to which each word’s features in a sentence contribute to the accuracy of topic matching and to adjust the feature representations accordingly, so that not only the semantic information of the word itself is taken into account, but also the internal relations of the sentence in which the word is embedded, so as to achieve the purpose of improving the performance of topic matching. It is worth noting that the self-attention mechanism only updates the training parameters by concentrating on its own information and does not require additional information, thus reducing the computational complexity of the model and making up the defects of the proposed position- sensitive word vector training model. Subsequently, by incorporating the word vector got from the self-attention mechanism with the document vector, we generate the context vector that is used in the topic model. Together, these components form the joint-training short-text topic model PS-WETM. Ultimately, we investigate the perplexity and topic coherence of the PS-WETM, comparing its performance with recent topic models under the data of online social media text. The framework of the proposed short-text topic model PS-WETM is as Fig. 1.

Fig. 1: The framework of the proposed short-text topic model PS-WETM.

A framework of the proposed short-text topic model, consisting of the positional-sensitive word training model, the document weight training model, and the self-attention mechanism.

The proposed position-sensitive word vector training model

In this paper, we described a proposed position-sensitive word vector training model to solve the constraint in prototypical word vector training models that it ignores the exact position of each context word and treats all context words equally. The proposed position-sensitive word vector training model operates on the premise that context words in symmetric positions relative to the pivot word share an equivalent degree of semantic relationship with it. It initially assigns different weight matrices to context words in asymmetric positions, and then judges the direction of context words, thereby differentiating the varying impacts of different context words in different positions on the pivot word and distinguishing the semantic relations between context words and the pivot word.

In comparison with the skip-gram word vector training model, the proposed position- sensitive word vector training model considers the exact positions of different context words, resulting in more concise performance. And compared with the structured skip-gram, it reduces the computation complexity. For instance, if a typical skip-gram has p parameters and the size of window is m, the structured skip-gram will contain 2 mp parameters while the proposed position-sensitive word vector training model contains only mp parameters. The proposed position-sensitive word vector training model is described in Fig. 2.

Fig. 2: The framework of the proposed position-sensitive word vector training model.

The training process of the position-sensitive word vector training model, depicting how to differentiate the distance between the pivot word and context words positioned differently.

V is the number of vocabulary and D is the number of features. The embedded matrix has a size of V × D, whereas the weight matrix has a size of D × V. In the proposed position-sensitive word vector training model, we proposed a new loss function based on the relative position of context words to the pivot word to update the embedded matrices and the weight matrices.

The proposed loss functions

In the proposed PS-WETM model, the dictionary is stored by hash algorithm. We generate an integer array called ${{\boldsymbol{voc}}}_{{\boldsymbol{hash}}}$, with each element initialized to −1. The size of this array is denoted as ${{\boldsymbol{voc}}}_{{\boldsymbol{hash\_size}}}$, which is calculated as:

$${{voc}}_{{hash}}[{h}_{v}({w}_{j})]=j$$

(2)

h_v (${w}_{j}$) signifies the hash value of word ${w}_{j}$. We calculate hash value h_v (w_j), and then we find the position of word w_j. If voc_hash [h_v (w_j)] = −1, it indicates that word w_j has not been included in dictionary V. Otherwise, compare w_j with ${w}_{{{voc}}_{{hash}}[{h}_{v}({w}_{j})]}$, where ${w}_{{{voc}}_{{hash}}[{h}_{v}({w}_{j})]}$ refers to the word with index ${{voc}}_{{hash}}[{h}_{v}({w}_{j})].\,$If ${w}_{j}$ and ${w}_{{{voc}}_{{hash}}[{h}_{v}({w}_{j})]}$ are the same, we set the index of ${w}_{j}$ to ${{voc}}_{{hash}}[{h}_{v}({w}_{j})]$.

During the construction of the dictionary, we selectively remove both low-frequency and high-frequency words. If the current scale |${V}_{{current}}$| of dictionary ${V}_{{current}}$ satisfies |V_current| > 0.7voc_{hash_size}, we proceed to eliminate words whose frequencies fall below the preset minimum threshold. Additionally, high-frequency words, such as is, are will also be deleted. To effectively manage high-frequency words, we adopt the subsampling approach proposed by Mikolov (Mikolov et al., 2013), which involves setting a probability prob(w) for each word, guiding the decision of whether to keep or discard these words. We set the probability prob(w) as:

$${prob}(w)=1-\left(\sqrt{\frac{t}{f(w)}}+\,\frac{t}{f(w)}\right)$$

(3)

$$f(w)=\frac{{[{counter}\left(w\right)]}^{\frac{3}{4}}}{\sum _{u\in v}{[{counter}\left(w\right)]}^{\frac{3}{4}}}$$

(4)

where f (w) refers to the frequency of word w. Accordingly, word w will be discarded with the probability prob(w). Given the hidden layer ${v}_{{w}_{c}}$, the proposed position-sensitive word vector training model will generate the predicted word vector $\hat{y}$. We first get the hidden layer through embedded matrix. ${v}_{{w}_{c}}$ is calculated as:

$${v}_{{w}_{c}}={x}_{{w}_{c}}{\rm{W}}$$

(5)

where ${x}_{{w}_{c}}$ refers to the one-hot vector of the pivot word, W refers to the embedded matrix, which is used as a look up table. Then we import m weight matrices for context words in asymmetric positions and there are sn words in the sentence. Note that if the skip window is 3, there will be 3 weight matrices. After assigning weight matrices, we get positional word vector ${z}_{n,{w}_{c+i}}$. It is calculated as:

$$\left\{\begin{array}{lll}{[{{v}_{{w}_{c}}v}_{{1,w}_{c-{\rm{i}}}}^{{\prime} },\ldots ,{v}_{{w}_{c}}{v}_{{1,w}_{c-2}}^{{\prime}},\,{{v}_{{w}_{c}}v}_{{1,w}_{c-1}}^{{\prime} },\,{{{v}_{{w}_{c}}v}_{{1,w}_{c+1}}^{{\prime} },{v}_{{w}_{c}}{v}_{{1,w}_{c+2}}^{{\prime} },\ldots ,v}_{{w}_{c}}{v}_{{1,w}_{c+{\rm{i}}}}^{{\prime} }]}\,{g}_{{\rm{i}}}\left({w}_{c-i}|{w}_{c}\right)+{b}_{c-i}={z}_{1,{w}_{c-i}}\\ {[{v}_{{w}_{c}}v_{{2,w}_{c-{\rm{i}}}}^{{\prime} },\,\ldots ,{v}_{{w}_{c}}{v}_{{2,w}_{c-2}}^{{\prime} },\,{{v}_{{w}_{c}}v}_{{2,w}_{c-1}}^{{\prime} },\,{{{v}_{{w}_{c}}v}_{{2,w}_{c+1}}^{{\prime} },{v}_{{w}_{c}}{v}_{{2,w}_{c+2}}^{{\prime} },\ldots ,v}_{{w}_{c}}{v}_{{2,w}_{c+{\rm{i}}}}^{{\prime} }]}\,{g}_{{\rm{i}}-1}\left({w}_{c-({\rm{i}}-1)}|{w}_{c}\right)+{b}_{c-(i-1)}={z}_{2,{w}_{c-(i-1)}}\\ \ldots \\ {[{{v}_{{w}_{c}}v}_{{{\rm{n}}-1,w}_{c-{\rm{i}}}}^{{\prime} },\ldots ,\,{v}_{{w}_{c}}{v}_{{{\rm{n}}-1,w}_{c-2}}^{{\prime} },\,{{v}_{{w}_{c}}v}_{{{\rm{n}}-1,w}_{c-1}}^{{\prime} },\,{v}_{{w}_{c}}{v}_{{{\rm{n}}-1,w}_{c+1}}^{{\prime} },{{{v}_{{w}_{c}}v}_{{{\rm{n}}-1,w}_{c+2}}^{{\prime} },\ldots ,v}_{{w}_{c}}{v}_{{{\rm{n}}-1,w}_{c+{\rm{i}}}}^{{\prime} }]}\,{g}_{{\rm{i}}-1}\left({w}_{c+(i-1)}|{w}_{c}\right)+{b}_{c+(i-1)}={z}_{{\rm{n}}-1,{w}_{c+({\rm{i}}+1)}}\\ {[{{v}_{{w}_{c}}v}_{{{\rm{n}},w}_{c-{\rm{i}}}}^{{\prime} },\,\ldots ,{v}_{{w}_{c}}{v}_{{{\rm{n}},w}_{c-2}}^{{\prime} },\,{{v}_{{w}_{c}}v}_{{{\rm{n}},w}_{c-1}}^{{\prime} },\,{{v}_{{w}_{c}}v}_{{{\rm{n}},w}_{c+1}}^{{\prime} },{v}_{{w}_{c}}{v}_{{{\rm{n}},w}_{c+2}}^{{\prime} },\ldots ,{v}_{{w}_{c}}{v}_{{\rm{n}}{,w}_{c+{\rm{i}}}}^{{\prime} }]}\,{g}_{{\rm{i}}}\left({w}_{c+i}|{w}_{c}\right)+{b}_{c+i}={z}_{{\rm{n}},{w}_{c+i}}\end{array}\right.$$

(6)

where i = {1, 2, 3, …m}, j = {1, 2, 3, …n}. ${w}_{c+i}$ refers to the feature vector of context word, and i refers to the relative position of context word.

Here, we regard the judgment of direction as a binary classification and use the sigmoid function to calculate the probability of selecting the direction. It is calculated as:

$${g}_{i}({w}_{c+i}|{w}_{c})=\left\{\begin{array}{l}\sigma \left({v}_{j,\,{w}_{c+i}}^{{\prime} \,T}{v}_{{w}_{c}}\right),\qquad{L}_{w+i}=1\\ 1-\sigma \left({{v}_{{j,w}_{c+i}}}^{T}{v}_{{w}_{c}}\right),\,{L}_{w+i}=0\end{array}\right.$$

(7)

Finally, we define a novel softmax function to normalize the probability of context words and get loss ${L}^{w}$. In this softmax function, the probability of each context word is normalized with all probability in ${z}_{n,{w}_{c+i}}$. It is shown as:

$$p\left({w}_{c+i}|{w}_{c}\right)=\frac{\exp \left(\mathop{\sum}\nolimits_{i=1}^{m}\mathop{\sum }\nolimits_{j=1}^{n}{z}_{n,{w}_{c+i}}\right)}{\mathop{\sum }\nolimits_{i=-m}^{m}\exp \left(\mathop{\sum }\nolimits_{i=1}^{m}\mathop{\sum }\nolimits_{j=1}^{n}{z}_{n,{w}_{c+i}}\right)}$$

(8)

Hence, the loss function L^w can be defined as:

$${L}^{w}=-\log \mathop{\prod }\limits_{i=-m}^{m}p\left({w}_{c+i}|{w}_{c}\right)$$

(9)

Optimization

The model optimization involves updating the embedded matrix and m weight matrices to optimize vector representation of words. We define u (w, i, m) as the following:

$$u(w,i,n)={\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}}{\left[\sigma ({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}})\right]}^{{L}_{w+i}}{\left[1-\sigma ({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}})\right]}^{1-{L}_{w+i}}$$

(10)

In the stochastic gradient descent, we update the embedded matrix and weight matrix as follows:

$${v}_{{w}_{c}}({\rm{new}})={v}_{{w}_{c}}({\rm{o}}{\rm{ld}})+\nabla {L}^{w}({v}_{{w}_{c}})$$

(11)

$${\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}({new})={\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}({\rm{old}})+\eta \nabla {L}^{w}\left({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}\right)$$

(12)

where $\nabla {L}^{w}$(${v}_{{w}_{c}})$ and $\nabla {L}^{w}$(${\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}$) represent the gradient for the embedded matrix and the weight matrix respectively. Then, the update rates of ${v}_{{w}_{c}}$ and ${\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}$ in gradient optimization are:

$$\begin{array}{l}\nabla {L}^{w}({v}_{{w}_{c}})=\frac{\partial {\rm{u}}({\rm{w}},{\rm{i}},{\rm{n}})}{\partial {v}_{{w}_{c}}}\\ \qquad\qquad\,\,\,=\frac{\partial {\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}}\,{[\sigma ({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}})]}^{{L}_{w+i}}{[1-\sigma ({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}})]}^{1-{L}_{w+i}}}{\partial {v}_{{w}_{c}}}\end{array}$$

(13)

$$\begin{array}{l}\nabla {L}^{w}({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}})=\frac{\partial {\rm{u}}({\rm{w}},{\rm{i}},{\rm{n}})}{\partial {\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}}\\\qquad\qquad\qquad=\frac{\partial {\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}}\,{[\sigma ({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}})]}^{{L}_{w+i}}{[1-\sigma ({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}{v}_{{w}_{c}})]}^{1-{L}_{w+i}}}{\partial {\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}}\end{array}$$

(14)

Hence, in the proposed position-sensitive word vector training model, ${v}_{{w}_{t}}$ and ${\mathop{v}\nolimits_{m,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}$ are updated as follows:

$${v}_{{w}_{c}}({new})={v}_{{w}_{c}}(old)+\eta \nabla {L}^{w}\left({v}_{{w}_{c}}\right)$$

(15)

$${\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}({new})={\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}({\rm{old}})+\eta \nabla {L}^{w}\left({\mathop{v}\nolimits_{n,\,{w}}^{\prime}}_{{c+i}}^{\quad{T}}\right)$$

(16)

where $\eta$ refers to the learning rate. The model will adjust the learning rate $\eta$ based on the following equations after every 10,000 words are processed.

$$\eta ={\eta }_{0}\left(1-\frac{{{word}}_{n}}{{{word}}_{c}+1}\right)$$

(17)

$${{word}}_{c}={\sum }_{{\rm{w}}\in {\rm{V}}}\,{counter}(w)$$

(18)

${{word}}_{c}$ represents the count of processed words. $\eta$ will gradually decrease during the processing. However, the learning rate cannot be too small. Hence, we set a threshold ${\eta }_{\min }$. Once $\eta \,< \,{\eta }_{\min }$, we initialize it to ${\eta }_{\min }$, where ${\eta }_{\min }$ = ${10}^{-4}$ $\times {\eta }_{0}$ and ${\eta }_{0}$ = 0.025.

Self-attention

We get the set of sentence feature = [w₁,w₂,…,w_j,…..w_n] through the above proposed position-sensitive word vector training model. Note that w₁ refer to the feature vector of the first word, and n means the number of words in the sentence. As shown in Fig. 3.

Fig. 3: The abstracted framework of self-attention.

The framework presents the process of generating new word vectors that containing richer semantic relations.

Feature vectors we got from the proposed position-sensitive word vector training model will be fed into the self-attention mechanism, yielding a revised set of feature vectors $\widetilde{W}=[{\widetilde{w}}_{1},\,{\widetilde{w}}_{2},\,{\ldots ,\widetilde{w}}_{j},\,\ldots ..{\widetilde{w}}_{n}]$, where ${\widetilde{w}}_{i}$ is the updated feature vector of the j^th word output by the self-attention layer. This self-attention mechanism is adept at learning the structure and contextual relationships within a sentence and updates the training parameters by concentrating on internal information, without the need for external data. Compared with the original feature vector $W=\left[{w}_{1},\,{w}_{2},\,{\ldots ,w}_{j},\,\ldots ..{w}_{n}\right]$, the new feature vector $\widetilde{W}=[{\widetilde{w}}_{1},\,{\widetilde{w}}_{2},\,{\ldots ,\widetilde{w}}_{j},\,\ldots ..{\widetilde{w}}_{n}]$ got from self-attention reflects the interconnections between different words in the sentence. What’s worth to say, the proposed position-sensitive word vector training model compensates for the failure that self-attention didn’t consider the influence of word position in the generation of feature vectors.

In this regard, we get three vector sequences by linear transformation based on the given sentence feature $W=[{w}_{1},\,{w}_{2},\,{w}_{3},\,\ldots ..{w}_{n}]$, which include the query vector sequence $Q$, the key vector sequence $K$ and the value vector sequence ${V}$, which is calculated as the followings:

$$Q=\,{H}_{q}\,* W=[{H}_{q}{w}_{1},\,{{H}_{q}w}_{2},\,{{H}_{q}w}_{3},\,\ldots ..{{H}_{q}w}_{n}]$$

(19)

$$K=\,{H}_{k}\,* W=[{{H}_{k}w}_{1},\,{{H}_{k}w}_{2},\,{{H}_{k}w}_{3},\,\ldots ..{{H}_{k}w}_{n}]$$

(20)

$$V=\,{H}_{v}\,* W=[{H}_{v}{w}_{1},\,{{H}_{v}w}_{2},\,{H}_{v}{w}_{3},\,\ldots ..{{H}_{v}w}_{n}]$$

(21)

where ${H}_{q},\,{H}_{k}$, and ${H}_{v}$ represents the initial parameters of the three linear transformations, and Q, K and V are the transformations of the sentence feature $W=[{w}_{1},\,{w}_{2},\,{w}_{3},\,\ldots ..{w}_{n}]$. Then, we calculate the attention weight distribution $A$ as followings:

$$A=\,Q\,{{\cdot }}\,{K}^{T}$$

(22)

$$A=\,[{H}_{q}{w}_{1},\,{{H}_{q}w}_{2},\,{{H}_{q}w}_{3},\,\ldots ..{{H}_{q}w}_{n}]\,{{\cdot }}\,{[{{H}_{k}w}_{1},{{H}_{k}w}_{2},{{H}_{k}w}_{3},\ldots ..{{H}_{k}w}_{n}]}^{T}$$

(23)

$$A=\,{H}_{q}* {H}_{k}* [{w}_{1},\,{w}_{2},\,{w}_{3},\,\ldots ..{w}_{n}]\,{{\cdot }}\,{[{w}_{1},{w}_{2},{w}_{3},\ldots ..{w}_{n}]}^{T}$$

(24)

$$A=\,{H}_{q}* {H}_{k}* [\,{w}_{1}* {W}^{T},\,{w}_{2}* {W}^{T},{w}_{3}* {W}^{T},\,\ldots \ldots {w}_{n}* {W}^{T}]$$

(25)

As depicted in the above, the length $n$ of the attention weight distribution $A$ represents the importance of each word’s feature vector. We normalize it using the softmax as followings:

$$\hat{A}={softmax}\left(\frac{A}{\sqrt{{d}_{k}}}\right)$$

(26)

where ${d}_{k}$ represents the length of the feature dimension. After that, we multiply the normalized attention weight distribution $\hat{A}$ by the feature vector, and get the new feature vector of the sentence $\widetilde{W}$ as follows:

$$\widetilde{W}=A{ttention}(Q,\,K,\,V)={softmax}\left(\frac{Q\,{{\cdot }}\,{K}^{T}}{\sqrt{{d}_{k}}}\right)\,{{\cdot }}\,V$$

(27)

$$\widetilde{W}=\hat{A}\,{{\cdot }}\,V$$

(28)

$$\widetilde{W}={softmax}\left(\frac{A}{\sqrt{{d}_{k}}}\right)\,{{\cdot }}\,V$$

(29)

$$\widetilde{W}={softmax}\left(\frac{A}{\sqrt{{d}_{k}}}\right)\,{{\cdot }}\,{H}_{v}* W$$

(30)

$$\widetilde{W}={softmax}\left(\,\frac{{H}_{q}* {H}_{k}* [\,{w}_{1}* {W}^{T},\,{w}_{2}* {W}^{T},{w}_{3}* {W}^{T},\,\ldots \ldots {w}_{n}* {W}^{T}]}{\sqrt{{d}_{k}}}\right)\,{{\cdot }}\,{H}_{v}* W$$

(31)

In this paper, the new feature vector considers both the position of context word and the semantic relations of the whole sentence, which significantly improves the accuracy of the output word vectors.

Document vector

The generation of the document vector is bifurcated into two parts: the document weight and the topic matrix. Document weight encapsulates the significance of each topic in a document. Initialize the document weight vector of each document in the corpus. Subsequently, a set of topic vectors is generated, subject to the constraints imposed by the document vectors ${{\boldsymbol{d}}}_{{\boldsymbol{j}}}$. Under these constraints, the latent topic vectors are represented as:

$${d}_{j}={p}_{j0}\times {t}_{0}+{p}_{j1}\times {t}_{1}+\ldots \ldots +{p}_{{jk}}\times {t}_{k}+\ldots \ldots {p}_{{jn}}\times {t}_{n}$$

(32)

${t}_{0}$, ${t}_{1}$, …, ${t}_{k}$, …, ${t}_{n}$ are latent topic vectors. ${p}_{{jk}}$ is the topic weight transformed by softmax, indicating the proportion of different topics in a document. The total sum of ${p}_{{jk}}$ for any given document is 100%. Topic vector ${t}_{n}$ is a shared part across all documents, with the document weight being instrumental in modulating its thematic prominence. To enhance the interpretability of topics, we set word vector’s dimension as the number of topics and initialize the latent topic vector to get ${p}_{{jk}}$. Then, optimize the Dirichlet(α) likelihood to sparse document weight ${p}_{{ij}}$ and the loss function is:

$${L}_{d}=-\lambda \mathop{\sum }\limits_{k=0}^{n}(\alpha -1){log} ({p}_{{jk}})$$

(33)

In this model, the parameter $\alpha$ plays a crucial role in determining the sparsity of the document weight vector. Specifically, if $\alpha$ > 1, the document weight vector tends to be more concentrated; conversely, if $\alpha \le$1, the document weight vector exhibits sparsity. Aligning with existing research (Zuo et al., 2023) set $\alpha =\frac{1}{n}$. After continuous iteration and optimization, the document weight vector becomes increasingly concentrated, culminating in the formation of an interpretable topic vector.

The total loss L of PS-WETM is the sum of ${L}_{w}$ generated by the proposed position-sensitive word vector training model and ${L}_{d}$ generated during optimizing the probability distribution of document weight.

$$L={L}_{w}+{L}_{d}$$

(34)

Topic vector and document weight vector are synthesized to produce the document vector. This document vector is then added to the word vector, resulting in the formation of the context vector. Finally, minimize the total loss L to train the context vector. Input the well-trained context vector into LDA topic model, the hot topic identification is completed.

Experiment and discussion

In this section, we perform comparative analyses between the newly proposed PS-WETM topic model and six recent proposed topic models, employing word cloud and sentiment analysis as assisted tools to gauge the accuracy of PS-WETM. This methodology aids in evaluating the model’s efficacy in capturing the nuanced essence of topics within online social media text.

Dataset

In this paper, we choose COVID-19 as the study case to verify the performance of short-text topic model PS-WETM. We chose to focus on microblogs on Sina Weibo from the initial outbreak period of January 2020 through June 2020, when the epidemic first showed signs of remission, for the research data. We crawled 6-month microblogs posted on Sina Weibo based on keywords epidemic, COVID-19, pneumonia, segregate, and mask, and obtained a total of 82,330 microblogs as the analysis data.

Performance analysis

We undertook a comparative analysis of seven topic models, evaluating their performance based on metrics of perplexity and topic coherence. The model assessed include DMM (Yin and Wang, 2014), PTM (Zuo et al., 2016), SPTM (Zuo et al., 2023), GPU-DMM (Li et al., 2017), GLTM (Liang et al., 2018), WETM (Rashid et al., 2023) and the proposed PS-WETM. When given a test set $W=\{{w}_{1},{w}_{2},{w}_{3},$…$,{w}_{N}\}$, the perplexity (PP) is calculated as follows:

$$PP(W)=P{\left({w}_{1}{w}_{2}{w}_{3}\ldots {w}_{N}\right)}^{-\frac{1}{N}}=\root{N}\of{\frac{1}{P({w}_{1}{w}_{2}{w}_{3}\ldots {w}_{N})}}=\root{N}\of{\mathop{\prod }\limits_{i=1}^{N}\frac{1}{P({w}_{1}{w}_{2}{w}_{3}\ldots {w}_{N})}}$$

(35)

The perplexity metric inversely relates to the conditional probability of word sequences; a higher conditional probability leads to a lower perplexity. We utilized the crawled microblogs as data to evaluate the performance of these models. The number of topics K is 5,10,15 and 20 respectively. The maximum iteration is 500. The results of this comparison are illustrated in Table 2.

Table 2 Perplexity score of seven topic models.

Topic coherence is another crucial metric for assessing the performance of a topic model. It is based on the co-occurrences of words within Wikipedia and has been demonstrated to correlate with human judgment. The calculation of topic coherence (C) is as follows:

$$C\left({z;}{S}^{z}\right)=\mathop{\sum }\limits_{n=2}^{N}\mathop{\sum }\limits_{l=1}^{n-1}\log \frac{{D}_{2}\left({w}_{n}^{z},\,{w}_{l}^{z}\right)\,+\,1}{{D}_{1}({w}_{l}^{z})}$$

(36)

For a specified topic z, the set of words in top n topics is ${S}^{z}$ = {${w}_{1}^{z}$, ${w}_{2}^{z}$, …, ${w}_{n}^{z}$}. ${D}_{1}$(w) signifies the frequency of word w in the document. ${D}_{2}$(${w}_{1},{w}_{2}$) is the co-occurrence of word ${w}_{1}$ and ${w}_{2}$. A higher value of topic coherence indicates better interpretability and clarity of the topics. The comparison of topic coherence among the models is depicted in Table 3.

Table 3 Topic coherence score of seven topic models.

As shown in Tables 2–3, PTM has the highest perplexity and the lowest topic coherence, presenting a relatively bad performance on topic extraction of short texts, followed by SPTM. And the topic model PS-WETM has the lowest perplexity and the highest topic coherence relatively, which demonstrates that compared with the other six topic models, PS-WETM has the best interpretability of topics.

Word cloud

The high-frequency Chinese words were translated into English and drawn in the Word Cloud. Word Cloud from January to June are shown in Fig. 4.

Fig. 4: Word Cloud of microblogs from January to June.

a, b, c, d, e, f represent the Word Cloud from January to June respectively.

The Word Cloud visualization reveals that during the initial period of the event, from January to February, there were three prominent topics reflected in the high-frequency words. Some words pertained to the topic of infection, such as case, health, cumulative, medical, while others are about the topic prevention, such as medical, observation, isolation, and still others are about the topic domestic places, such as Wuhan, Shenzhen, highlighting the areas most affected by the initial outbreak of COVID-19 in China.

In March and April, words rent, family, income, close arise in the Word Cloud, describing the situation that COVID-19 had a great impact on people’s daily lives. The shutdown of businesses led to reduced incomes, making it challenging for many to cover their rent and daily expenses. Additionally, words global, UK, overseas began to appear in the Word Cloud of April, albeit with less prominence compared to the aforementioned words.

As the timeline progressed into May and June, words work, death, test, close, market continued to feature in the Word Cloud, but with a declining frequency, indicating that efforts to control COVID-19 and treat patients were yielding positive results, as evidenced by the decreasing number of deaths and infections. In addition, businesses and workplaces in numerous cities started to resume production and work.

The Word Cloud in Fig. 5, encompassing data from 6 months of microblogs, demonstrates that topics epidemic and protection were persistent and dominant throughout this timeframe. Notably, the prominence of these topics did experience a slight decline during March and April.

Fig. 5: Word Cloud of 6 months microblogs.

It shows the Word Cloud and keywords of all the 6-month microblogs.

Sentiment analysis

In this chapter, we use the Emotion Dictionary of Dalian University of Technology, which contains seven emotions, to calculate the emotion value of microblogs and classify microblogs into seven emotions. The results are presented in Fig. 6.

Fig. 6: Count of seven emotions from January to June.

The statistical graph of seven emotions in each month from January to June, including emotion Love, Depress, Dislike, Fear, Anger, and Surprise.

The outbreak of COVID-19 led to a marked increase in the emotions of Love, Depress, Dislike and Fear in February, with Fear spiked the fastest. As the gravity of the COVID-19 situation dawned on people, there was a noticeable decrease in microblogs sharing moments of happy daily life and in expressions of Joy. However, there were also microblogs expressing encouragement for patients and frontline medical workers, which is why the emotion of Love remained predominant.

As the COVID-19 situation evolved, the prevalence of Anger diminished, reflecting a reduction in blame or resentment towards the virus’s origin. A significant moment of change occurred on May 21 and 22, with the convening of the NPC&CPPCC in Beijing, which instilled hope among the Chinese populace. Following this, widespread nucleic acid testing was implemented across China, and business operations began to resume, leading to improvements in the country’s situation. People’s lives started to show signs of recovery, and as a result, the emotions of Love and Joy experienced a resurgence.

The seven emotions identified in our study have been categorized into positive, negative, and neutral groups. Love and Joy are classified as positive emotions, Surprise is considered neutral emotion, while Depress, Dislike, Fear, and Anger are categorized as negative emotions. According to Figs. 7, 8, negative emotions slightly outnumber positive emotions. However, with the global spread of COVID-19, the prevalence of negative emotions significantly outweighs that of positive emotions due to events discussed above.

Fig. 7: Count of positive, negative, neutral emotions from January to June.

The statistic graph of three emotions, where emotion Love, Depress, Dislike, Fear, Anger, and Surprise are classified into positive, negative, and neutral emotion.

Fig. 8: Daily change of positive and negative emotions in 6 months.

The statistical graph of emotions each day, where emotion Love, Depress, Dislike, Fear, Anger, and Surprise are classified into positive and negative emotion.

Topic identification by the proposed topic model PS-WETM

In this part, we utilized the PS-WETM short-text topic model to identify topics from the extended texts. After we get the Chinese topics and corresponding keywords, we translate them into English and then visualize them. Topic visualization of January is shown as Fig. 9. (Topic visualization of other 5 months are shown in Supplementary Figs. S1–S5).

Fig. 9: Visualization of topics and key words of January.

The distribution and key words of topics, where circles represent topics, and words on the right are key words of the corresponding topics.

The number of topics is set to 6 according to the perplexity. And the number of keywords is set to 20. In Fig. 9, the absence of overlap between any of the circles indicates that the number of topics set here is reasonable. It is also observable that some topics and keywords recur across adjacent months. For better analyzing the identified topics, we combined microblogs of January and February as the first period, microblogs of March and April as the second period, microblogs of May and June as the third period. Then, new topics and keywords of three periods are presented in Figs. 10–12.

Fig. 10: Topics and key words of the first period in January and February.

The visualization of extracted topics and corresponding key words in the first period.

Fig. 11: Topics and key words of the second period in March and April.

The visualization of extracted topics and corresponding key words in the second period.

Fig. 12: Topics and key words of the third period in May and June.

The visualization of extracted topics and corresponding key words in the third period.

When identifying topics and keywords of the three periods, the number of topics is set to 8 according to the perplexity. Topics epidemic, support, protection and control, affection identified in the first period are consistent with key words infection, case, health, cumulative, medical, prevention, medical, observation, isolation drawn in Word Cloud of January. Topics international response, domestic places are dovetailed with key words Wuhan, hospital, Shenzhen, Guangdong, Beijing in Word Cloud of February. As described in Figs. 13, 14, in the first period, the number of confirmed cases and deaths in China suddenly climbed, and the places with confirmed cases gradually expanded, resulting in the emergence of domestic regions’ names.

Fig. 13: The total confirmed and deaths in China and the world.

In these two subfigures, the orange bar graph represents the count of China, and the blue bar graph represents the county of the World. a is the statistical graph of total confirmed cases in China and the World; b is the statistical graph of total death in China and the World.

Fig. 14: The map of places containing confirmed cases in China.

Subfigure a and b are respectively situations of China on January 21 and March 15.

During the second period, while China’s situation began to stabilize, the global scenario deteriorated significantly. There was a rapid increment in the number of confirmed cases and deaths worldwide. And as depicted in Fig. 14, the number of countries with confirmed cases also expands gradually. Hence, topics global and international events appear in the second periods. Furthermore, due to the global outbreak, the number of emotions Fear and Dislike both rise in the second period, which is also consistent with topics identified in these two periods.

In Fig. 15a, b, the map shows that China is in a severe situation where the number of confirmed cases accounts for the largest. On January 21, the first period, China has 386 confirmed cases, while the United States and Mexico each have only 1 confirmed case. On March 26, the second period, countries such as Italy, Brazil, Canada appear with a large number of confirmed cases, but the situation in China has flattened out, just like the description of topic global shown in Fig. 11. In Fig. 15c and Fig. 15d, it can be seen that in the third period, China’s COVID-19 has entered a period of remission, while other countries have entered an outbreak period. These all reflect the consistency between identified topics and emotion value, and the high accuracy of the proposed short-text topic model PS-WETM.

Fig. 15: The map of counties containing confirmed cases in the World.

a, b, c, d are respectively situations of the world on January 21, March 26, May 15, June 30.

Conclusions

In this study, we introduce PS-WETM, a joint-training short-text topic model grounded in deep learning, designed to precisely identify latent topics in online social media text of emergencies. Firstly, it extends short texts of online opinions according to the similarities of word vectors, solving the problem of sparse matrix, and improving the accuracy of PS-WETM in generating context vector. Secondly, it combines word vector and document vector to better deal with the semantic relations of words and topic coherence. Thirdly, we define a proposed position-sensitive word vector training model, which assigns different weight matrices to asymmetrically positioned context words and judges the direction of each context word, thereby thoroughly accounting for the precise positions of context words in weight prediction and making up for the deficiency that previous topic models treat context words in different positions equally. Fourthly, in order to enhance the performance of topic matching, we implement a self-attention mechanism that calculates the contribution of each word feature generated by the proposed position-sensitive word vector training model to topic matching accuracy. The mechanism not only adjusts the feature representations of individual words but also considers both their semantic relations and those within the entire sentence. In the short-text topic model PS-WETM, the proposed position-sensitive word vector training model differentiates the relation between context words in different positions, which compensates for the deficiencies that self-attention ignores the position of words. Concurrently, the self-attention mechanism learns the sentence structure solely from internal without the need for external information, which addresses the limitation that the proposed position-sensitive word vector training model relatively large parameters. And the comparison displays that PS-WETM outperforms than other six topic models, evidence by its lowest perplexity and highest topic coherence. Furthermore, the trend of identified topics is considerably consistent with that delineated through the Word Cloud and sentiment analysis.