Introduction

A dominant model of the origin of musical scales that is found in textbooks of psychoacoustics, music cognition, and musicology is a perceptual model in which musical intervals optimize the degree of harmonic purity between the pitches’ acoustic frequencies (Burns 1999; Hall 2002; Handel 1989; Howard and Angus 2009; Loy 2006; Patel 2008). In the theoretical system of just intonation, scale positions are defined as simple harmonic ratios of acoustic frequencies, such as 2:1 for the octave, 3:2 for the fifth degree of the scale, and 4:3 for the fourth degree of the scale. By the 19th century, a source for music’s harmonicity was proposed, namely the natural harmonic series (Helmholtz 1877; see also Rameau 1722). As Kreitler and Kreitler (1972) describe this theory, scales are derived from the “overheard overtones” assumed to be perceivable in the spectra of single pitched sounds. Along these lines, Gill and Purves (2009) synthesized a series of scales comprising combinations of justly-tuned frequency ratios, and calculated the mean similarity of every pairwise interval to the harmonic series. They observed that that several of the best known instrumental scales from a number of cultures ranked among the most harmonic of the scales they generated.

Mathematical theories of musical scales have been based exclusively on instruments (Daniélou 1943; A. J. Ellis 1885; Rahn 2019, 2022), mainly on fixed-pitch instruments such as chordophones. What has been strongly lacking is a comparative analysis of vocal scales, not least in indigenous cultures. This is evolutionarily important since the voice is almost certainly the original musical instrument (Darwin 1871; Rousseau 1781; Sachs 1943; Spencer 1857), and the voice’s tuning cannot be fixed. Therefore, an analysis of vocal scales provides a far more naturalistic understanding of the origins of music than does an analysis of musical instruments in cultures having mathematical tuning theories. In addition, scale theories have been presented as prescriptive regimens for how musicians should tune their instruments, which begs the very question of the origin of these tuning systems. A far more ecologically-valid approach is to examine how people produce music in actual practice, most especially vocal music, and most especially in cultures in which people are unbiased by academic tuning theories.

Previous ethnographic analyses of musical scales in traditional cultures, while rare, have provided important insights into the properties of scales cross-culturally. Savage et al. (2015) described a number of statistical universals in scale structure, most of which have been supported by subsequent findings. Scales tend to contain 5-7 pitch-classes per octave, arranged in small step-like intervals of at least 1 semitone (Li & Huron 2006; Shanahan and Huron 2011) and more commonly 2-4 semitones (Mehr et al. 2019; Sachs 1943). Scales are often non-equidistant, meaning that they are comprised of at least two distinct interval-sizes (Mehr et al. 2019; Patel 2008), although there is also evidence for equidistant scales in some cultures (Ambrazevičius & Budrys 2013; McBride et al. 2023; Ross & Knight 2019). Most scales contain one tone as a reference for the others, known as the tonic pitch (Ellis 1965; Mehr et al. 2019). They then typically contain pitch-classes that are approximately 2, 5, and 7 semitones above the tonic (Chiba et al. 2019; Ho et al. 2018; Kuroyanagi et al. 2019; McBride et al. 2023; McBride & Tlusty 2019; Sato et al. 2019). They also tend to contain a pitch-class that is either roughly 3 or 4 semitones above the tonic (i.e., a minor third or major third, respectively) (McLean 1969), but only rarely both, and sometimes a neutral third (Ambrazevičius & Budrys 2013). In addition, they tend to lack a pitch-class that is roughly 6 semitones above the tonic (i.e., the tritone) (McBride and Tlusty 2019). Most of these cross-cultural observations have been derived from musical corpora that contain both instrumental and vocal samples. Only Mehr et al. (2019) and Sato et al. (2019) examined cross-cultural samples that were purely vocal (and monophonic), although Ellis (1965) compared transcriptions of “pre-instrumental” indigenous vocal music to Western theoretical scales.

In the present study, we explore an influence on the structure of musical scales that is fundamentally different from harmonicity, namely the physiological imprecision inherent in vocal pitch production. Numerous studies have shown that the voice is highly imprecise as a pitch-generating instrument (Mauch et al. 2014), especially when compared to precisely tunable instruments like violins and flutes (Pfordresher et al. 2010; Pfordresher & Brown 2017; Phillips & Brown 2022b). For example, Pfordresher and Brown (2017) analyzed the sung intervals for the song “Happy Birthday” and found that the interval-classes had wide ranges, spanning a semitone or more on either side of the target interval. This was seen not just in amateur singers but in professionally-trained singers as well. This led the authors to formulate an Interval Spacing model of scales in which vocal imprecision creates a bottom-up motoric constraint on the intervallic properties of scales (Brown 2022; Brown & Phillips 2023; Pfordresher & Brown 2017; Phillips & Brown 2022b, 2022a). This constraint biases scales to optimize the spacing of pitch-classes in order for them to be distinguishable from one another (McDermott et al. 2010; Zarate et al. 2012) and to thus be meaningful during vocal communication. The alternative hypothesis is that people would be tolerant of imprecision and that scale intervals would not be completely distinguishable, in which case small intervals (e.g., consecutive semitones) should be common in music.

The principal objective of the present study is to analyze the structure of musical scales in field recordings of vocal songs cross-culturally with regard to the number of pitch-classes, the pitch-class distribution, the scale intervals, the number of different interval-types, and scale typology. This was done with an eye for how much such scales resemble instrumental Western diatonic scales, such as major and minor. In doing so, we wanted to analyze indigenous and traditional songs, since indigenous vocal music has been highly neglected as a source of information about musical scales. We carried out a global computational analysis of 418 field recordings of solo, unaccompanied vocal songs from across the 10 principal musical-style regions of the world, as based on a validation of these regions in Lomax’s (1968) Cantometrics project, a seminal musicological analysis of global song traditions. The aim was to capture global diversity in both scale systems and singing styles. We employed the results of a companion analysis (Phillips & Brown 2022b) to examine the connection between the scale properties of a region and a feature of vocal production, namely imprecision in the production of pitch-classes during singing. Finally, we analyzed all of the scales in two distinct manners, first through manual annotation of the scales based on a listening to the recordings, and second in a semi-automated manner by fitting Gaussian Mixture Models to the frequency distributions derived from the vocal recordings.

Based on the data of Pfordresher and Brown (2017) and the ethnographic studies mentioned above, we predicted that vocal scales would have fewer pitch-classes and larger intervals than the theory-based instrumental scales that form the foundation of Western music theory. In other words, we predicted that vocal scales would show greater spacing among pitches than in the diatonic instrumental scales of Western music. We also predicted that, across world regions, the size of the scales’ intervals would vary as a function of the imprecision with which people sing pitches, suggesting a possible mechanistic relationship between the way that people produce pitches vocally and the structure of musical scales culturally.

Methods

Vocal corpus

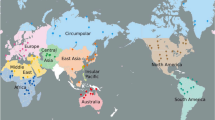
We constructed a global database of 418 solo, unaccompanied, monophonic field recordings of vocal songs from indigenous and traditional cultures. We obtained these recordings from various private ethnographic collections, independent record labels and, most commonly, the Smithsonian Folkways record label. We restricted our sampling to indigenous musical traditions as much as possible, supplementing them with folk traditions where appropriate, but avoiding art and pop traditions. Additional information about the corpus can be found in Phillips and Brown (2022b) and in the supplemental metadata file. Figure 1 presents a geographic map of the song sampling. The 10 regions are a modified version of the 10 musical-style zones characterized in Lomax’s (1968) Cantometric analysis of world singing style. Our goal was to be able to accommodate both the principal scale systems and singing styles found in traditional vocal musics from across the world.

Fig. 1: A geographic map of the song sampling according to the 10 principal musical-style regions of the world.
figure 1

This is color-coded by region. The 418 samples are distributed across the style-regions as follows: Africa, 41 songs; Australia, 17; Central Asia, 16; Circumpolar region, 52; East Asia, 50; Europe, 51; Insular Pacific, 52; Middle East-North Africa, 38; North America, 50; and South America, 51. The map was made in ArcGIS with further editing in Photopea.

Full size image

Instrumental scales

We used two corpora of instrumental melodies as a comparison to the vocal data, one of 35,275 traditional Irish melodies taken from thesession.com (https://github.com/adactio/TheSession-data), and the second of 2,367 traditional Dutch melodies taken from the Meertens Tune Collections (van Kranenburg & de Bruin 2019).

Manual scale analysis

For the vocal corpus, the scale analysis was carried out in parallel in two manners, one based on manually notating the scales by ear and the other using semi-automated inference methods (see next paragraph). First, we identified by ear major structural sections of the melodies, including repeated verses and points of considerable pitch shift or modulation. We then chose an excerpt (mean length 20.5 s, SD 8.52) that contained at least one complete melodic idea for further analysis and that had minimal pitch drift. For each melodic excerpt, we identified the scale series by ear. Scale series were notated using the closest possible Western alphabetical notes, from the lowest to the highest pitch. The perceived tonic – or the perceived focal tone of the melody – was assigned based on musical intuitions. When sung notes occurred in between keyboard notes, this was indicated with a slash (e.g., Eb/E). Non-discrete, unstable, or uncertain notes were indicated using parentheses. Three raters independently analyzed each song for its scale series, tonic pitch, and pitch-class boundaries. The amount and type of disagreement were recorded. Consensus was reached by listening to a given song together and discussing each point of disagreement. Occasionally, if two analysts failed to come to an agreement, the third analyst would act as the tie-breaker. These scales were also reported in Phillips and Brown (2022b). For the current interval analysis, we simplified the scales by “rounding down” ambiguous notes to the lowest perceived pitch (e.g., Eb/E → Eb) and either removing or “ratifying” uncertain or unstable notes. The results of the final agreed-upon analysis are presented here.

Semi-automated scale analysis

To obtain precise estimates of the relations between scale degrees, as well as to eliminate any concerns about Western subjectivity in the manual annotation of musical scales, we estimated scales by fitting Gaussian Mixture Models (GMM) to log2-pitch (cents) distributions (see Pitch estimation below), using the scikit-learn implementation in python. Scale degrees were inferred as the means of the GMM. The GMM-fitting algorithm is stochastic and so it was run several times to get the best fit (see Supplementary Methods). Fits were mainly evaluated by visual comparison of the GMM and the pitch-class histogram, inspection of the pitch trace, and comparison of GMM means with the manually-annotated scales. In some cases, additional filters were needed to obtain good fits. In 194 out of 418 cases, we found that additional filtering was necessary. We used three types of filters to deal with this (see Supplementary Methods): removing rare pitches (e.g., passing tones); sampling a portion of the excerpt (to avoid pitch drift); and high/low frequency filtering (e.g., to remove non-musical utterances). If a good fit could not be obtained, the quality of the pitch trace was improved, and the notation was manually re-analyzed by the original annotator. After reaching a consensus, the GMM procedure was followed again with the new pitch trace and/or notation. In 5 cases, we could not fit a GMM that matched the consensus notation, even after filtering; in 2 cases, audio files were not transferred correctly, and this was not discovered until the review stage. This left us with 411 scales for the semi-automated analysis, compared to 418 for the manual annotation. Data and figures for all pitch traces and best-fitting GMMs are available upon request.

For pitch estimation, we first used the pitch traces from Phillips & Brown (2022b), which were estimated using Tarsos (Six et al. 2013) and its built-in YIN pitch-tracking algorithm (de Cheveigné & Kawahara 2002). Some of the pitch traces had errors (e.g., octave errors, inclusion of non-vocal utterances, algorithm artifacts) that were identified during the semi-automated scale analysis. In such cases, we re-estimated pitch traces using in-house annotation software based on pYIN (Mauch & Dixon 2014), which included tools to fix octave errors and remove unnecessary pitches. (A Github link for this will be provided upon publication.) The parameter of “pitch-class imprecision” was defined as the standard deviation of the GMM component corresponding to a scale degree. The “joint imprecision” of two adjacent GMM components (scale degrees) is the square root of the sum of the variances of the two components.

Scale properties

We normalized each scale by transposing it to C in order to enable a global comparison of the pitch-class distribution of the 2301 scale degrees inferred from the scales. We quantified several basic features of each scale, including 1) the number of pitch-classes; 2) the mean intervallic spacing between pitch-classes; 3) the total range of the scale; and 4) the number of different interval-types in the scale (for example, a diatonic scale has two different interval-types: a semitone and a tone). Since intervals inferred from the semi-automated analysis are estimated to the nearest cent, a count of the number of interval-types per scale involves grouping them into categories. We carried out hierarchical clustering to group intervals using Ward’s method, and chose the smallest number of clusters for which the largest within-cluster interval-size standard deviation was less than 25 cents. This value was chosen to maximize the agreement with the number of interval-types identified through manual annotation.

Finally, we performed an exploratory typological analysis of the scales, as based on the manual annotation. Given the wide diversity of scale-types in our sample, we introduced a simplification that placed the focus on the “central pentachord” of a scale, spanning from the tonic (C) to the G above it. (This pentachord should not be confused with a pentatonic scale, which spans from C to C.) This is relevant since analyses of pitch-class histograms for music (including our own, see Results) demonstrate that the majority of pitches occur in this part of the scale, rather than in the upper tail of the scale (Chiba et al. 2019; Huron & Davis 2012; Kuroyanagi et al. 2019; Sato et al. 2019). From this analysis, we created the categories of “major-type” and “minor-type” scales, as well as scales that did not fit into either category. A major-type scale contains an E natural in its central pentachord, whereas a minor-type scale contains an Eb. Major-type scales include the following set of seven possible pentachord sequences: CE, CDE, CDEF, CDEG, CDEFG, CEFG, and CEG. Most scales contain pitches beyond those in the central pentachord. We therefore quantified the relative number of pitches above and below the central pentachord for the 418 scales.

It is important to note that we analyzed the scales in two different manners. In the standard “wrapped” representation, all of the pitches in a sample were compressed into a single octave, starting from the tonic. This is the typical means of representing scales in Western musicology. For example, a song having the melodic pitches of B-C-E (where C is the tonic) would get wrapped into a C-E-B scale sequence. We believe that this presents an artificial representation of the scale, since the ascending E-B interval does not exist in the melody. The second manner of scale representation is thus “unwrapped,” retaining the actual linear ordering of the pitches in a melody. In the case of B-C-E, the B is understood to be in the sub-tonic part of the scale. We performed all analyses using both wrapped and unwrapped formats. However, the present study is limited to an analysis of the properties of the unwrapped versions of the scales, since they offer a more accurate view of the relationship between scales and melodies.

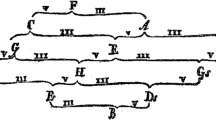
Figure 2 provides illustrative examples of GMM analyses for two melodies in the corpus, one from North America and one from Africa. This includes the pitch trace for the selected extract (panels A and D), the raw pitch-class histogram (panels B and E), and the pitch-class histogram after filtering and the fitted GMM (panels C and F). The unwrapped scale series is shown at the top. Two examples of filters are shown (see Supplementary Methods for more examples). The top example shows a low-count filter that removes rare pitches that are associated with glissandi and pitches in between notes. The bottom example shows a temporal filter where we select a short region that has all of the scale degrees in order to increase the relative density of rare notes in the histogram.

Fig. 2: Two examples of scales.
figure 2

The figure presents a two-note scale from a recording of the Kiowa-Apache people of the southern United States (A–C) and a triatonic scale from a recording from Ghana in west Africa (D–F). The unwrapped scale series is written to the right of the culture name, where the * indicates the tonic pitch. Pitch (fundamental frequency) traces (A, D) for selected excerpts are shown alongside the pitch-class histograms before (B, E) and after (C, F) additional filtering. Dashed grey lines and numbers on the y-axis indicate scale degrees obtained from Gaussian mixture models (GMMs) (A–F), while blue dashed lines indicate manual scale annotations (A, D). Fits to GMMs are shown as solid colored lines (C, F). In the top example, rare pitches are filtered out that correspond to non-discrete glissandi by applying a filter to the pitch-class histogram (B, red line). In the bottom example, filtering is done by time (D), selecting a short excerpt that includes all notes. This is done so that the tonic, which is heard much more often than the other notes (E), is less dominant in the filtered histogram (F), which makes it easier to fit a GMM.

Full size image

Results

Scale properties

Figure 1 presents a geographic map of the song sampling for the study, including a listing of the number of songs analyzed for each stylistic region. The 10 regions are a modified version of the 10 musical-style zones characterized in Lomax’s (1968) Cantometric analysis of world singing style.

Pitch-class distribution

Figure 3A presents the C-transposed pitch-class distribution for all of the vocal scales in unwrapped form (see Methods), where the histogram shows the manual analysis and the solid line the semi-automated analysis. In general, there was excellent agreement between the manual and semi-automated methods of inferring scales (Supplementary Figs. 1, 2). Specifically, we observed 95% agreement between the number of notes, as well as that 95% of scale degrees were within 1 semitone from each other (Supplementary Fig. 2). However, we did note a perceptual bias towards fourths and fifths (and against tritones) in the manual analysis, which is corrected by the semi-automated analysis (Supplementary Fig. 1). Another area where differences arose was in the determination of the number of distinct interval-sizes (Supplementary Fig. 1), since manually assigning scales to a 12-tone equal temperament system does not allow for microtonal interval-sizes. Importantly, these differences have now been quantified. This allays fears about Eurocentric bias, and highlights which scale features may be reliably estimated by ear (and which may not be).

Fig. 3: Pitch-class distribution of the 2301 scale tones for the unwrapped transposed representation of the full set of vocal scales.
figure 3

A The histogram shows the probability density for the manually annotated scales (in bins of 1 semitone), while the solid line is a kernel density estimation (KDE; bandwidth = 0.025) plot for the semi-automatically annotated scales. The pitches are shown as semitones relative to the tonic after transposition to C (which is indicated by 0). The corresponding letter names are shown below them. Note that all tonic degrees are excluded from the graph since they are present, by definition, in 100% of the scales. For aid in visualization, the pitches in the central octave (C-C) are shown with darker bars. B A quantification of the number of pitches per scale. C A quantification of the number of different interval-sizes per scale.

Full size image

In Fig. 3A, the pitch-class distribution spans nearly 3 octaves in pitch space, 32 consecutive pitch-classes, and 2301 scale pitches. The central tonic-pitch at C (at 0 semitones) is not shown in the figure since it is present, by definition, in 100% of the scales. As with previous analyses of vocal scales (see the Introduction), we can see that the demarcation between pitch-classes is not sharp, with individual pitch-classes spanning at least a semitone in width, and with there being overlap between adjacent pitch-classes. Peaks were seen in the region of D (2 semitones), F (5 semitones), and G (7 semitones), as well as at G below the tonic (-5 semitones), where all of these pitch-classes represent relative-pitch changes in the context of our C-tonicized scales.

The third degree of the scale was distributed nearly equally between Eb (3 semitones) and E (4 semitones), with a slightly larger presence of Eb. It is important to note that a pitch-class distribution is not able to reveal whether Eb and E are co-present in scales or whether they appear in distinct scale-types. This will be addressed below in describing the typology of the scales. The pitch-class distribution had a very low frequency of B-natural (11 semitones) and instead a higher frequency of Bb (10 semitones). Only European folk songs showed a predominance of B over Bb in the subtonic position; every other culture showed the reverse pattern (not shown). Finally, the pitch-class distribution revealed the general recurrence of pitch classes across octaves. For example, the equivalent prevalence of Eb and E is visible in the first two octaves in Fig. 3, as is the predominance of Bb over B (e.g., -2 vs. -1 semitones subtonically).

Scale tones and intervals

The remaining quantification of the scale features comes from the semi-automated analysis, except for the analysis of scale typology (see below). Table 1 provides a summary of some of the basic features of the unwrapped vocal scales across the 10 world regions. We compare them to the Western theoretical diatonic scales (major and minor) and to two corpora of European instrumental melodies. Overall, there was a trade-off between the number of scale tones and the mean interval-size between adjacent tones. The mean number of tones for the vocal scales was 5.5, compared to 7 for the Western theoretical scales and 7.1 for the European instrumental scales (in standard wrapped format). Vocal scales of 4, 5, and 6 tones were most prevalent (Fig. 3B; see Supplementary Fig. 3 for the wrapped scales).

Table 1 Basic properties of the vocal scales across regions.
Full size table

The mean interval-size of the vocal scales was 2.2 semitones, half a semitone larger than the 1.7 value for Western theoretical scalesFootnote 1 and the 1.8 value for European instrumental scales (Table 1). Figure 4 presents the distribution of interval-sizes between adjacent pitch-classes in the scales (see Supplementary Fig. 4 for the wrapped scales). Figure 4A presents this on a continuous scale, with a bin size of 0.2 semitones, whereas Fig. 4B shows this categorically up to the size of a perfect fourth (5 semitones), using interval categories from Western music theory. In the latter plot, the semitone corresponds to the intervals in the 0.5–1.5 semitone range, the tone to the intervals in the 1.5–2.5 semitone range, and so on. The results show that the whole tone is the predominant scale interval in world vocal music. Minor thirds were nearly as prevalent as semitones in vocal scales, in contrast to their absence in Western theoretical scales, although the Chinese pentatonic scale is an example of a theoretical instrumental scale that contains a large proportion of minor thirds. Overall, 90% of the sequential intervals in world vocal scales are comprised of just three interval sizes: the semitone, whole tone, and minor third, in other words “a whole tone +/– a semitone” (Pfordresher & Brown 2017).

Fig. 4: Scale interval-sizes across all scales (semi-automated) in the vocal corpus.
figure 4

A The probability density of interval-sizes is shown continuously, with a bin size of 0.2 semitones. The mean value is 2.2 semitones, with a positive skew. B The probability density of interval-sizes is shown categorically up to the size of a perfect fourth (5 semitones), where the category boundaries for each interval are shown in parentheses in semitones.

Full size image

A major finding of the interval analysis was that the vocal scales from the most indigenous cultures had larger scale-intervals than not just Western instrumental scales but also the European folk songs within the song corpus. Figure 5 plots the percentage of sequential scale-intervals that are larger than a whole tone – using a threshold value of 2.5 semitones – which is a parameter that we call %>T (where T=tone). This comprises mainly the minor third (m3), major third (M3), and perfect fourth (P4) intervals. The global distribution shows that the three regions having low values of 10–13% were the regions with the strongest historical traditions of instrumental heptatonic scales (Central Asia, the Middle East, and Europe). By contrast, the smaller-scale cultures, including many lacking melodic instruments, had %>T values that were 2–3 times higher than this, in the range of 28–38%. In general, vocal scales have larger intervallic spacings than Western instrumental scales, and vocal scales in small-scale cultures have larger intervallic spacings than vocal scales from regions where mathematical tuning theories have historical significance. The percentage of large intervals in the scales (%>T) was anti-correlated with the percentage of semitones (r = −0.47, p < 0.001 at the song level; r = −0.89, p < 0.001 at the region level), implying a trade-off between large and small intervals in vocal scales cross-culturally. This trade-off suggests that the whole tone is something of an optimal interval for the generation of musical scales.

Fig. 5: Percentage of sequential scale-intervals (semi-automated) larger than a whole tone across world regions.
figure 5

This is defined by a threshold value of 2.5 semitones. The results are presented in ascending order across the 10 musical-style regions.

Full size image

Interval-sizes per scale

The mean number of different interval-sizes in the scales was 2.4 types, compared to a prediction of 2.0 for a true diatonic scale (see Table 1). Figure 3C presents the global distribution of the number of different interval-sizes for the vocal scales (see Supplementary Fig. 5 for the wrapped scales). More than 90% of the scales were non-equidistant, according to the manual annotation. Interestingly, one third of the unwrapped vocal scales were not diatonic but were instead triatonic (manual 34%, semi-automated 34%), having three constituent interval-sizes, typically adding a larger interval such as a minor third or major third to the semitone and whole tone profile. The highest concentration of triatonic scales was found in Australia, with a value of 53% (manual; semi-automated 47%), with an additional 18% (manual; semi-automated 6%) of this region’s scales having four constituent interval-sizes. Triatonicity not only increases the spacing between adjacent scale-tones but also contributes to the diversification of scales.

Scale range

The mean range for the unwrapped scales was 10.0 semitones for the global sample. This is smaller than the 12 semitones of a Western heptatonic diatonic scale. Although this size difference may seem small, these ranges are quite different in nature from a musical standpoint. In the case of a Western diatonic scale, the pitches span from C-tonic to the C one octave above it. However, in the case of the unwrapped vocal scales analyzed here, the functional octave for melody production spanned roughly from the G below the tonic to the G above it in our C-tonicized relative-pitch system. In other words, the tonic pitch is located at the center of the pitch-class distribution in unwrapped form, not at its lowest point, as would be the case in a wrapped scale. The pitch-class distribution for the global sample falls off strongly on either side of these G’s (see Fig. 3). Despite this large range, there was also a preponderance of small vocal scales spanning a fifth or less, as will be discussed below.

Correlations among scale features

We examined correlations among the scale features just described. We observed a trade-off between the number of scale tones and the mean interval-size (Pearson’s r = −0.29, p < 0.001, n = 411, at the song level; r = −0.40, p > 0.05, n = 10, at the region level). Additionally, there was a correlation between the number of scale tones and the number of distinct interval-sizes (Pearson’s r = 0.43, p < 0.001, n = 411, at the song level; r = 0.37, p > 0.05, n = 10, at the region level). Larger scales not only had more scale tones but also a greater diversity of interval-sizes.

Correlations with vocal imprecision

We followed up on our previous study of vocal imprecision (Phillips & Brown 2022b) by examining correlations between the scale properties observed in the present analysis and vocal imprecision, as operationalized here as the standard deviation of the pitch-classes in the GMM analysis. Figure 6A shows that the mean interval-size between pitch-classes in the scales was significantly correlated with the level of imprecision in the singing of the pitch-classes (Pearson’s r = 0.49, p < 0.001, n = 411, at the song level; r = 0.83, p = 0.003, n = 10, at the region level). Scales containing larger intervals were found in geographic regions where imprecision in singing was greatest. As mentioned above, this was most prominent for the smaller-scale cultures in the corpus. Interestingly, European folk music was an outlier in this analysis, having a disproportionately high level of vocal imprecision for its relatively small scale-intervals (not shown). An analysis at the level of individual intervals presents a similar story (Fig. 6B), whereby interval-size is correlated with the “joint imprecision” of adjacent scale degrees (the square root of the sum of variances of two neighboring GMM components). The results in Fig. 6 are consistent with the Interval Spacing theory’s prediction that small interval-sizes should be performed with low imprecision in order to avoid miscommunication. Note that the theory does not specifically predict that large interval-sizes should be accompanied by high imprecision, but merely that this is a possibility. The fact that large interval-sizes are sung with higher imprecision may be due to stylistic considerations.

Fig. 6: Correlation (Pearson’s r) between scale interval-size and vocal imprecision for semi-automated scales.
figure 6

A Each point represents a song from the vocal corpus (n = 411). B Each point represents an interval-size between adjacent tones in a scale and the joint imprecision of the adjacent scale degrees (n = 1866).

Full size image

Scale typology

Figure 7 presents an exploratory typological analysis of the 418 vocal scales, as based on the manual annotation of the scales. Given the wide diversity of scale-types in our global sample, we placed our focus on the central pentachord of each scale, spanning from the tonic (C) to the G above it in the C-transposed scales (see Methods for details). The density plot in Fig. 3 reveals that 88% of the pitch-classes in the central octave occur in this pentachord, hence justifying our focus on this part of the scale. Based on this, we created the categories of “major-type” and “minor-type” scales for those scales that contained either an E or an Eb, respectively, at the third degree of the pentachord.

Fig. 7: A typology of world scales in the corpus of 418 songs (manual scale annotation).
figure 7

This is based on a classification of the scale sequence in the central pentachord (i.e., C to G) of the transposed unwrapped scales. A plurality of the scales (40.9%) were not part of the major/minor typology. Of these, 27.9% of the overall scales were “undefined,” since they were not of an established scale-type in the comparative musicology literature.

Full size image

The typological analysis revealed that 28.2% of the vocal scales were major-type, while 30.9% were minor-type. By contrast, a plurality of the scales in the corpus were of neither type (40.9%). This latter category included several well-known non-Western scales, such as Ritusen (CDFG in the central pentachord), Bayati (CDbEbFG), Lydian (CDEGbG), Hijaz (CDbEFG), and Okinawan (CEFG). However, even when these familiar scales were taken into account, more than a quarter of the overall scales (27.9%) were not of a known category in comparative musicological analyses. We designate them as “undefined.” Note that the prevalence of undefined scales would only increase if we used the full scales in the analysis, rather than the first pentachord alone. Minor-type scales were the largest category of known scale-types in the global sample. The minor pentatonic scale (CEbFG core) was the single most prevalent scale-type in the world. In addition, it was the most universal vocal scale, being found in all 10 of the stylistic regions. Europe and the Middle East had the lowest prevalence of this scale-type (not shown), suggesting that it could possibly be more of an indigenous scale.

Europe and Australia presented extreme examples of cultures containing a dominant type of scale, with 51% of the scales in Europe being major-type, and 47% of the scales in Australia being minor-type. Consequently, Europe and Australia both had low percentages of undefined scales. Other cultures that showed a high reliance on a single scale category – all of them for minor-type scales – were East Asia (42%), North America (40%), and the Circumpolar region (35%). The percentage of undefined scales varied from 12% to 53%. South America was an outlier in this analysis at 53%, followed by Central Asia at 38%.

Small scales

The corpus contained one 1-note scale, being found in East Asia. There were fourteen 2-note scales (3% of the total), with the highest prevalence in South America. Their mean interval-size was 3 semitones (range 1–7), thus defining the scale C-Eb. There were thirty-four 3-note scales (8%), with the highest prevalence in South America and North America. The mean interval-size between the first and second notes was 3 semitones (range 1–5), just as in the 2-note scales. The mean interval-size between the second and third notes was 2 semitones (range 1–4). The mean 3-note scale was thus C-Eb-F. It is interesting to observe that the mean 2-note scale (C-Eb) is embedded within the mean 3-note scale (C-Eb-F), which is itself embedded within the most prevalent and geographically universal scale-core in the dataset (C-Eb-F-G). This might reflect the antiquity of the minor pentatonic scale in world cultures (Reinhard 1958).

Scale positions

The pitch-class distribution in Fig. 3 demonstrated that Eb and E had roughly equal distributions in the global sample. However, the typological analysis revealed that Eb and E were nearly mutually exclusive in the vocal scales, rather than being co-occurrent. Of the 324 scales that contained the third degree of the scale, only 9% had Eb and E as co-occurrent. Therefore, the third degree of the scale seems to act as a pivot point in the generation of scale-types in world cultures. Similar to this, Gb (the tritone) and G were mainly mutually exclusive, although Gb occurred very rarely. Of the 33 Gb’s in the dataset, 88% (n = 29) were not adjacent to a G. Instead, they were either the terminal pitch of the scale or were adjacent to more-distant pitches, including Ab. Hence, the tritone appeared as an alternative to G in most of the instances in which it occurred. The same was not true of Db. Of the 46 Db’s in the dataset, only 61% (n = 28) were not adjacent to D. Instead, a certain amount of chromaticism occurred near the tonic. Finally, we already pointed out that Bb had a strong predominance over B natural in the dataset. In total, 75% of the B-pitches were Bb’s and 25% were B naturals. This suggests that major-type scales are far more likely to be Mixolydian than true major (Aeolian). Bb was especially prevalent in the sub-tonic position of the central octave.

Interval classes

The main source of the minor third scale-interval was the C-Eb in variants of the minor-type pentatonic scale. Two other principal sources were the D-F of the Ritusen scale and the G-Bb interval either above or below the central pentachord in many scales. The main source of the major third interval was C-E in major-type scales. The main source of the perfect fourth interval was G-C, since sub-tonic G’s were very common (see Fig. 3).

Notes below and above the central pentachord

Two thirds of all of the pitch-classes in the full pitch-class distribution were contained within the central pentachord of the central octave (67%). In all regions except Australia, there were more pitches below the central pentachord (21% of the total scale tones) than above it (12%). There was a significant negative correlation between the number of pitches above and below the central pentachord (Pearson’s r = −0.46, p < 0.001, n = 411, at the song level; r = −0.69, p = 0.03, n = 10, at the region level). These overall results support the notion that the functional octave for melody production in vocal music is G-G, more so than C-C.

Recurrence

We observed that 42% of the scales in the corpus spanned one octave or more. Of these, 97% showed a direct recurrence of pitch-classes across octaves, rather than the use of different pitches above and below the central octave.

Discussion

We carried out the first extensive analysis of the structure of vocally-produced musical scales from indigenous and traditional cultures, spanning the principal music families of the world. Vocal scales tended to have fewer tones and larger pitch spacings than both Western theoretical scales and European instrumental scales. The mean interval-size for the global sample was 2.2 semitones, half a semitone larger than the 1.7-semitone mean spacing for theory-based Western diatonic scales. The whole tone might be something of an optimal interval for the vocal spacing in scales. This is supported by the observation from our companion analysis of the same vocal corpus that the mean imprecision in producing individual pitch-classes is 1.5 semitones (Phillips & Brown 2022b). Next, we reported a significant correlation between the degree of imprecision in singing pitches and the mean interval-size of the scales across world regions. This establishes a relationship between a physiological feature of vocal production and a cultural feature of musical structure. This observation provides support for the Interval Spacing theory of scales (Brown & Phillips 2023; Pfordresher & Brown 2017; Phillips & Brown 2022a, 2022b), which argues that vocal imprecision is a fundamental motoric constraint on the generation of scale structure. The exploratory typological analysis of the 418 scales revealed that a plurality of them did not abide by a simple major/minor classification. Even when taking other familiar world scales into account, more than a quarter of scales did not have a recognized typology, thereby demonstrating a large degree of scale diversity in the world sample, including a number of scales containing only two or three tones. Finally, a comparison between the two methodologies that were used to extract the scale series for each song revealed that the manual method and the semi-automated method showed agreement in 95% of the songs, thus providing for an overall validation of the results.

Vocal scales, indigenous cultures, and the global map of musical style

The present study took a very different tack than the traditional approach to the analysis of musical scales for more than two millennia. Instead of looking at melodies produced by precisely tunable instruments such as chordophones, we examined ethnographic field recordings of vocal music from indigenous and traditional cultures, doing so across the principal musical-style regions of the world. The voice has been highly neglected as a source of information about musical scales. So has indigenous music. Many of the cultures analyzed in the present study have been unaffected by either prescriptive academic scale theories or melodic instruments as tuning references. They thus offer a more naturalistic view of the origin of musical scales. This is important since the voice’s tuning cannot be fixed, and so scales can only be learned through vocal imitation and oral transmission. Another important feature of the study is that we explicitly sampled from the 10 principal music families of the world in order to obtain the most complete picture of the global diversity of both scale systems and singing styles. Our selection of world regions for analysis was not driven by the availability of recordings from particular locations, but instead by a musicologically-validated conception of the regional diversity of musical styles throughout the world, as characterized in Lomax’s (1968) seminal Cantometrics project (Wood 2021).

Scale structure

The current study is the first analysis of musical scales to focus on unwrapped scale sequences, rather than on wrapped sequences that compress all pitches into a single octave. In doing so, we found that the functional octave for melody production was the span from G to G (with the tonic in the middle), rather than from C to C. Unwrapped scales provide a more accurate description of the relationship between scales and melodies. As mentioned in the Methods section, wrapped representations can distort this relationship. While the quantitative results were overall quite similar between the unwrapped and wrapped analyses (see Supplementary Figs. 3, 4), we believe that the typological analysis of the scale-types was more accurate by using the unwrapped sequences.

Structural analysis of the 418 vocal scales (and the 411-song subset for the semi-automated analysis) revealed some basic properties. These included a mean of 5.5 pitches per scale, a mean interval-size of 2.2 semitones between pitch-classes, and a mean of 2.4 different intervals-sizes in the scales, with nearly one third of the scales being triatonic. The observed value for the mean scale-interval of just larger than a whole tone is quite similar to measurements of melodic intervals in music, where values of a whole tone predominate cross-culturally (Huron 2006; von Hippel 2000; Vos & Troost 1989). This argues for an important relationship between scales and melodies (Meyer 1956). Next, there was a general trade-off between the number of scale tones and the mean interval-size. In addition, more than 90% of the scale-intervals were comprised of “a whole tone +/– a semitone,” arguing that a large diversity of scales can be generated combinatorially from a small number of building blocks (Brown & Phillips 2023).

The pitch-class distribution revealed that D, F, G, and the sub-tonic G were prominent scale tones, in accordance with previous studies of smaller corpora of vocal scales in traditional cultures (Chiba et al. 2019; Ho et al. 2018; Kuroyanagi et al. 2019; Sato et al. 2019). However, our results contrasted with the previous studies in that we observed that the third degree of the scale was split nearly equally between Eb and E, whereas the previous studies mainly observed a peak at E (4 semitones), but not Eb (3 semitones). Next, we observed that Bb was far more common than B. Gb was rare, but occurred as an alternative to G. Db was rare as well, but often co-occurred with D, creating chromaticism near the tonic. Consecutive semitones were extremely rare in the vocal scales. When semitones occurred in scales, they tended to be padded by a larger interval on the other side, as seen in the major, minor, and Hijaz scales in instrumental music (see also McBride et al. 2023). This overall picture is consistent with the tenets of the Interval Spacing model that scales seem to optimize pitch spacing in order to make adjacent pitch-classes distinguishable from one another in both production and perception.

One explanation for this prohibition against consecutive semitones arises from our companion analysis (Phillips & Brown 2022b), which revealed a universal propensity for singers to produce pitches in an imprecise manner, with a mean range of 1.5 semitones per pitch-class. Such imprecision provides a physiological – and vocal – rationale for why semitones are considered to be the smallest reliable scale-interval in world musics (Burns 1999). It also explains why consecutive semitones are not favored in musical scales: there is a strong tendency for their pitch-class distributions to overlap and to thus become blurred. The intervallic spacing between adjacent pitch-classes in the present study was 2.2 semitones, even larger than the 1.5-semitone imprecision of individual pitch-classes. This suggests that the true constraint on the structure of musical scales might stem not from the imprecision of pitch-classes per se, but instead from the imprecision of interval-classes (Pfordresher & Brown 2017), since intervals define the actual pitch movement of the voice during melody production. It also suggests that the whole tone might be an optimal interval for the production of both melodies and scales.

Interestingly, Lomax’s (1968) global analysis of correlations between the musical properties of a culture and features of its social structure revealed that melodic intervals tend to be smaller where populations are larger, a finding that was corroborated in the re-analysis of Anna Lomax Wood and colleagues (Wood 2021). While our study focused on scale intervals, rather than melodic intervals, it provided support for the idea that music in smaller cultures tends to have larger intervals than music in larger cultures, at the level of both scales and melodies. The emergence of mathematical models of heptatonic instrumental scales in various large-scale cultures (e.g., Europe, India, the Middle East, Persia, Central Asia) may have been the cultural-evolutionary driving force for institutionalizing scales having larger numbers of tones with smaller intervallic spacings than in traditional vocal music.

The mean range of the unwrapped scales was 10 semitones. In fact, a large number of the scales (60%) were less than an octave in span. This included small scales of one, two, or three pitches, which collectively comprised 12% of the corpus. Interestingly, Lomax did not consider musical scales to be a relevant feature for understanding the musical correlates of social structure. He thus excluded scales from his Cantometric classification system. However, a key finding of the present study was that the smallest scales were found exclusively in the most indigenous cultures in our sample, and not in Europe, the Middle East, or Central Asia. Hence, small scales might be a musical indicator of indigeneity, although there are certainly examples of monotone songs in large-scale cultures as well (e.g., Vedic chants in India, Buddhist chants in China). Further work is needed to examine this point. A generative model of the origin of scales proposed by Sachs (1943) argued that scales evolved over historical time through a process of “affixation” in which scales were initially small and became expanded in size by the successive addition of pitches. This evolutionary viewpoint argues that small scales are a feature of indigenous cultures. Such scales may have persisted in cultures where melodic instruments and written music theories have not replaced longstanding oral musical cultures. Whereas the instrumental scales of cultures having written music theories in Europe, the Middle East, India, and Persia are all heptatonic, the vocal scales in our traditional corpus were more commonly composed of 4–6 pitches. Heptatonic scales comprised only 11% of the wrapped scales in our sample (see Supplementary Fig. 3), and were mainly found in world regions known to contain heptatonic instrumental scales, most notably Europe and the Middle East.

Structure/performance correlations

We reported a correlation between a structural property of musical scales and a physiological feature of the way that people sing them. More specifically, we observed an increase in the mean interval-size of the scales as the degree of pitch-class imprecision in the singing style increased. In addition, larger scale-intervals were found to be more prevalent in the smaller-scale cultures than in the larger cultures (see Fig. 5), where the latter have more semitones in their scales. A previous study by Sato et al. (2019), looking at a much smaller corpus of 50 vocal songs, found a similar type of correlation. In their case, they observed a significant negative correlation between pitch-class imprecision and the number of scale tones (r = −0.23). We observed negative correlations of similar magnitude (Pearson’s r = −0.25,p < 0.001, n = 411, at the song level; r = 0.61 p < 0.06, n = 10, at the region level). Since the size of a scale tends to be inversely related to the mean interval-size (see Table 1), these correlations with vocal imprecision are not surprising. However, the positive correlation that we observed between mean imprecision and mean interval-size was larger in magnitude (Pearson’s r = 0.49, p < 0.001, n = 411).

This correlation is consistent with the Interval Spacing model’s central tenet that the structure of musical scales is a direct reflection of the properties of vocal pitch production, and that scales attempt to optimize spacing in order to make pitches distinguishable in production and perception. While we do not currently have the computational means of analyzing interval-class imprecision (although it is something we are working on), our prediction would be that large interval-classes would be produced with greater imprecision than smaller interval-classes during melody production. Because the relationship between scale properties and vocal imprecision is most likely bidirectional, an understanding of vocal scales cross-culturally will depend on a characterization of the factors that promote imprecision in a culture’s singing style beyond intrinsic motoric constraints related to vocalization. This includes stylistic features such as portamento, vibrato, and melisma. Lomax (1968) demonstrated that these and other features of singing style vary significantly across cultures. For example, he reported that the Circumpolar region, which had the highest level of pitch-class imprecision in our companion analysis, is a region that is high in both vocal glissando and tremolo.

Scale typology and scale diversity

The exploratory typological analysis, based on the central pentachord of the scales (C-to-G) from the manual analysis, demonstrated a large degree of scale diversity, both within and between musical-style regions. Had we analyzed additional scale degrees beyond the first pentachord, this would have only diversified the findings even more, indicating that the pentachord analysis is underestimating scale diversity in our sample. The results revealed that a plurality of the vocal scales (40.9%) were not part of a simple major/minor typology. Among those scales that were, the third degree of the scale revealed itself to be a clear pivot-point in the generation of scales. While the global distribution of pitch-classes demonstrated a nearly equal prevalence of Eb and E (Fig. 3), it was only the typological analysis that clarified that these pitch-classes did not co-occur in most scales, but instead contributed to distinct scale categories. In fact, 91% of scales containing the third degree of the scale did not contain a combination of Eb and E. This segregation is perhaps due to the contrasting emotion-based interpretations that are associated with these scale-types in musical communication (Huron 2006; Parncutt 2014), although the mechanisms by which third scale-degree achieves its significance as a contrastive emotional cue remain unclear.

Among the known scale categories in the corpus, minor-type scales had the largest frequency in the global sample. The minor pentatonic core (CEbFG) was the single most prevalent scale-type in the world. It was also the most universal vocal scale-type, being found in all 10 stylistic regions, with the highest prevalence in the smaller-scale cultures. However, the story was even more interesting than that. When we analyzed the small scales in the corpus, we observed that the mean 2-note scale (C-Eb) was embedded within the mean 3-note scale (C-Eb-F), which was itself was embedded within the most prevalent and universal scale-type in the dataset (C-Eb-F-G). Might this represent a musical scale having great antiquity in human evolution? The comparative musicologist Reinhard (1958) considered the 3-note sequence C-Eb-F to be a “pre-pentatonic” nucleus having a global prevalence. He wrote that “we must not think of the nucleus merely as part of a pentatonic series to which it owes its existence: it is probably the other way round, namely, that pentatonism actually first came into being as a consequence of the use of the nucleus in a particular way” (p. 17).

While we can do no more than speculate about the antiquity of this scale, our observation of a succession from C-Eb to C-Eb-F to C-Eb-F-G is consistent with Sachs’ (1943) generative model of the origin of scales, in which scales are built up through the successive affixation of tones (Brown & Phillips 2023; Phillips & Brown 2022a). Vocal imprecision would presumably serve as a guiding constraint on the affixation process, favoring intervals of a whole tone or larger, and disfavoring adjacent semitones or any interval smaller than a semitone. A generative model of scales has the potential to provide new insight into the combinatorial nature of musical systems (Bernstein 1976; Brown 2000; Patel 2008). In addition, it grounds the combinatoriality of music in vocal-production mechanisms, just as with the other major acoustic combinatorial system found in humans: speech (de Boer & Zuidema 2010; Jackendoff 2002; Verhoef et al. 2014). The analysis in Fig. 4 showed that more than 90% of the scale-intervals in the corpus were comprised of “a whole tone +/– a semitone,” arguing that the combinatorial employment of a small number of building blocks can lead to what Sachs (1943) refers to as “a kaleidoscopic infinity of variations and permutations” in musical scales (p. 39).

A final point about scale typology is that pitch recurrence was the norm for those scales that spanned more than an octave in unwrapped form. The present study is the first demonstration of recurrence in vocal music, not least in a global sample. Because the music in the corpus was not based on pre-tuned instruments – which would beg the very question of recurrence – it provides a much stronger and more natural basis for demonstrating the recurrence of pitch-classes across octaves. This observation was made possible by our analytical emphasis on unwrapped scales. While further work is needed to understand the basis of recurrence, we suggest that one source of it may in fact be harmonic, namely the widespread occurrence of unison singing in world cultures.

Limitations

Despite the fact that we sampled from all of the principal music families of the world (Lomax 1968), the world has far more scale diversity than could be analyzed here. Hence, our sampling was sparse in the context of global musical diversity. Many world regions were not covered in the analysis. A good case in point is Papua New Guinea, which is known to have a high level of scale diversity. However, this region had a dearth of solo songs for use in the present study, since much of the repertoire in our collection of over 300 ethnographic field recordings from Papua New Guinea was of choral music.

A similar limitation with regard to sampling was our exclusive focus on monophonic samples produced by solo singers. Our computational methods did not permit us to derive scale information from samples with more than one melodic line at a time. Hence, we had to limit the scope of our sampling to monophonic songs with no instrumental accompaniment. It is possible that scale properties differ between textured music and monophonic solos. In particular, solo songs might represent a “worst case scenario” for scales since the singer is not required to coordinate their musical line with other people. The same applies to the precision with which the singer produces pitch-classes and interval-classes. Choral samples might lead to a sharpening of scale properties in order for singers to coordinate their melodic lines with one another, for example during unison texture. This would be in line with the view that tonality functions as a coordinative device for group performance, similar to the way that rhythm is thought to provide a coordinative scaffold for group performance (Brown 2017, 2022). Advances in the computational analysis of choral samples will be required to be able to extract scale information from samples with simultaneous melodic lines.

The typological analysis was limited by a general dearth of knowledge about musical scales cross-culturally, most especially vocal scales in indigenous cultures. Hence, scales in the “undefined” category may be recognizable to other scholars with knowledge of scales from the regions that we sampled. For the present time, there is no general resource that catalogues musical scales in a cross-cultural manner. Lomax’s Cantometric analysis of world song in Folk Song Style and Culture (1968) describes 37 properties of song cross-culturally, but not scales. Within the ethnomusicology literature for a single region, it can be challenging to find information about scales. Hence, outside of institutionalized scale systems like the ragas of Indian classical music and the maqamat of Arabic classical music, it is difficult to find systematic analyses of scales, most especially in indigenous cultures that do not have theoretical systems for scales and instrument tunings. Hence, our typological analysis should be seen as provisional and in need of future validation.

Finally, while the current study provided a great deal of depth for vocal music, it was not able to provide comparable depth for instrumental music from the same cultures that were sampled for vocal music, with the exception of Europe. Methodology was a big factor here. The vocal scales of our corpus were derived from an acoustic analysis of field recordings, whereas the analyses of the Dutch and Irish instrumental scales were based on transcriptions of instrumental performances. At the present time, there is an insufficient corpus of instrumental scale measurements that is based on acoustic analyses so as to allow for a direct comparison between vocal and instrument scales. Future work will be needed to address this issue in a more regional manner by doing parallel analyses of vocal and instrumental songs from the same regions, and looking at the corresponding pitch-class distributions, scale intervals, and scale typologies.

We can imagine two general mechanisms by which vocal scales and instrumental scales could interact in human cultures. Vocal scales could mimic instrumental scales by perhaps becoming compressed in interval-size. Alternatively, instrumental scales could mimic vocal scales by perhaps becoming expanded. We have suggested that the smaller mean interval-size of vocal scales in Europe, the Middle East, and Central Asia, compared to other world regions, might have arisen as an accommodation to the known predominance of heptatonic instrumental scales in these regions. In regions where melodic instruments and heptatonic instrumental scales are less common, such as in the Americas and the Circumpolar region, vocal scales have larger spacings, and it will be a matter for future work to determine if instrumental scales in these regions are similar to the vocal scales or are instead more compressed.

In world regions where singing is principally an a cappella activity, as in many indigenous cultures, vocal scales and instrumental scales have the potential to diverge from one another. In regions where singing tends to be accompanied by melodic instruments, the scales have a greater opportunity to converge, as they might in regions like Europe and the Middle East. Comparative research is needed to analyze the relative features of vocal and instrumental scales within cultures, as well as to examine the impact of either a cappella or accompanied singing on the relative convergence of scale-types between voice and instrument. In addition, within vocal music itself, it will be important to know if the features of scales are similar between songs with words and songs comprised of meaningless vocables.

Conclusions

We have carried out the first global analysis of the structure of vocal musical scales in indigenous and traditional cultures, and have discovered a number of significant differences from the longstanding Western instrumental model of heptatonic diatonic scales comprised exclusively of semitones and whole tones. Vocal scales, on average, had fewer scale tones and larger intervallic spacings than instrumental scales, suggesting an accommodation to vocal imprecision in interval production. A significant correlation was shown between a physiological feature of vocal performance (imprecision in the sung pitch-classes) and a cultural feature of scale structure (the prevalence of large intervals). Typologically, the vocal scales showed a wide diversity of structures. More than a quarter of the scales defied known scale categorizations in comparative musicological analyses. This included 2-note and 3-note scales that were exclusively present in the small-scale cultures in the global sample.

Overall, the results of this study are consistent with the tenets of the Interval Spacing model that the structure of musical scales has been impacted by the physiological properties and constraints of what is likely the earliest human music, namely song. Vocal scales optimize pitch spacing in order to accommodate to imprecision in production. There is no question that musical instruments can be engineered to possess highly refined intervallic properties. However, our analysis of vocal scales in indigenous and traditional cultures from across the principal music families of the world suggests that theorizing about the origins of music should be based not on instruments but on the properties of the most ancient and universal of all musical instruments: the voice.