Introduction

Since the industrial revolution, global urban expansion has been significant, mostly faster than population growth (Seto et al., 2011; Angel, 2017; van Vliet, 2019; Sumari et al., 2020; Li et al., 2022c; Shi et al., 2022). For example, London expanded its built-up area by 63 times (from 36 km2 to 2300 km2) between 1800 and 2000, while its population only increased by ten times (from 1 million to 10 million) in the same period. Chicago, one of the six metropolises in the US, is another example. From 1970 to 1990, the area of its built-up increased by 45%, but its population only rose by 4%. In response to their rapid urban expansion and associated ecological and environmental problems, many countries have proposed varied solutions, such as the “Green Belt Act” in the UK, the “Smart Growth” in the US, and the “Compact City” in Japan and South Korea. These programs intended to curb urban expansion in the countries but failed to deliver the expected results (Jun and Hur, 2001; Amati and Yokohari, 2007; Ali, 2014; Li et al., 2018b). It is worth reflecting on the practical significance of excessive strict restrictions on urban expansion.

While China significantly increased its built-up area by almost nine times, from 7000 km2 in 1981 to 63,700 km2 in 2022, most of China’s provinces and cities reached their respective planning target 5-10 years ahead of schedule (Fei and Zhao, 2019; Liu et al., 2023). According to the trend that the urbanization level in China has increased from 17.9% in 1978 to 66.16% in 2023, more than 13 million people will relocate from rural to urban areas every year. It implies a rigid demand (rigid demand refers to a relief that people have to buy a house regardless of price (Wang, 2018)) from these new urban residents for houses in cities, which will pose unprecedented pressure and challenges to the management of urban space in China (Chen et al., 2020). It is, therefore, critical to research urban expansion, particularly regulation and spatial optimization of urban expansion.

Urban expansion studies have focused on the characterization and mechanisms of urban land use evolution and the simulation and optimization of urban expansion. Economists investigate the relationship between urban land use and land price and establish an economic model of land use (Du et al., 2016; Kane and York, 2017; Fitzgerald et al., 2019; Kvartiuk et al., 2022). Ecologists summarize the patterns of urban expansion from a large number of case studies (Salvati and Ricciardo Lamonica, 2020; Hai et al., 2020; Chakraborty et al., 2022). Meanwhile, there exist many theoretical studies on the expansion pattern, e.g., empirical judgment on factors that influence expansion patterns (transportation, culture, market, and the government) and theoretical explanations for the patterns using neoclassical urban economics and regulatory economics (Lei et al., 2021; Jia et al., 2022). Geographers mainly simulate urban expansion through various modeling methods, e.g., cellular automat (CA), Markov chain, and discrete dynamics (Wu et al., 2015; Zhang et al., 2020; Abijith and Saravanan, 2022; He et al., 2022; He et al., 2024). In addition, there has been an increasing number of studies on the identification of dominant influencing factors, the development of urban expansion simulation methods, and the regulation means of urban expansion through both qualitative and quantitative approaches (Mendonça et al., 2020; Xia et al., 2020; Wang et al., 2020; Basu et al., 2023; Kang et al., 2024). It is challenging to effectively manage and regulate urban expansion. The prevalent approaches to managing and regulating urban expansion are inflexible, limiting the scale of urban expansion and adjusting the urban spatial layout mainly through the formulation of planning and various policies, and lacking analyses of land demand (Yang et al., 2023b). Among these, urban growth boundary is one of the most commonly used means of guiding urban development and limiting urban expansion within a certain period by strictly controlling the incremental growth(Liu et al., 2024; Song et al., 2024). Such approaches remain in the “containment of expansion paradigm” and are limited in effectiveness.

Land prices directly affect the development and use of land resources, which in turn affects urban expansion(Yuan et al., 2019; Kichko, 2020). Urban expansion also affects land prices, and there is a complex interaction between the two (Livanis et al., 2006; Silva and Vergara-Perucich, 2021; Yang et al., 2023b; Zhang et al., 2023). Heterogeneity in land prices can also reflect differences in geographic space, and thus land prices can be an effective means of regulating urban expansion (Zang et al., 2015; Yang et al., 2020; Chai et al., 2021; Tan and Xu, 2023). Unfortunately, few studies have answered the theoretical propositions and regulation strategies for urban expansion regulation that conform to China’s reality. Therefore, it is worthwhile to conduct an in-depth study to propose measures for urban expansion regulation by integrating the economics perspective on land prices and the geography perspective on the urban space layout.

The main goal of this study is to propose urban expansion control strategies suitable for China’s urban development based on the analysis of urban expansion characteristics. Following a “characteristic diagnosis-theoretical analysis-empirical research” research framework, firstly, we characterized the urban expansion at different levels. Then, the theoretical propositions and regulation strategies for urban expansion were proposed based on the price equilibrium principle. Finally, we tested the theoretical propositions in Xuzhou, China, using a comprehensive method integrating various geospatial data and techniques, e.g., the fusion method of nighttime lighting and remote sensing index, the CA-Markov model, the price calculation model, and the spatial interpolation method. This study can provide new insights into urban expansion regulation and spatial optimization in China to support sustainable and high-quality urban development.

Characteristic diagnosis and theoretical analysis

Urban expansion characteristics

Global urban expansion

As shown in Fig. 1, global built-up land in 1990 was small and scattered on various continents and regions, mainly in the United States, Europe, East China, and Japan. The built-up land of central cities in the United States and Western Europe was the most densely distributed.

Fig. 1: The size of the built-up area in different countries around the world in 1990, 2000, 2010 and 2020, with a larger circle indicating a larger built-up area in that country.
figure 1

Distribution of global urban built-up land in a 1990, b 2000, c 2010 and d 2020.

Full size image

From 1990 to 2020, the area of global built-up land expanded significantly. Notably, the expansion in China, India, and Africa was the most prominent, concentrated in East and Southeast China (i.e., the Pearl River Delta, the Yangtze River Delta, and the Beijing-Tianjin-Hebei urban agglomeration), the middle and upper reaches of the Ganges River and the areas around New Delhi, and Kenya, Uganda, and Nigeria in Africa, respectively. The built-up areas in Western Europe and the United States showed a relatively large scale in 2020. Still, because their built-up areas had already begun to take shape in 1990, the growth rate was insignificant compared to the aforementioned developing countries. In the US, urban areas expanded primarily in its western and eastern states. In Europe, urban expansion mainly occurred in France, the UK, and large cities in neighboring countries. While urban expansion was concentrated along the eastern coast of South America (e.g., Rio de Janeiro and Sao Paulo in Brazil), Oceania saw a noticeable increase in urban areas on the southeast coast of Australia (e.g., Sydney, Melbourne, and Bristol).

Urban expansion in China

From 2006 to 2020, the area of China’s built-up land increased by 28,403.68 km2, with an average annual growth rate of 4.48% (data unavailable for Hong Kong, Macao, and Taiwan). At the provincial level (Fig. 2), the area of built-up land in 31 provinces (including municipalities and autonomous regions) showed an increasing trend. While Guangdong had the most extensive built-up land, immediately followed by the eastern provinces of Shandong and Jiangsu, the smallest area was found in Tibet, Qinghai, and Hainan. From 2006 to 2020, more than 70% of provinces expanded by more than 0.8 times. Among them, the built-up land area in Guizhou, Sichuan, Chongqing, Yunnan, and Hubei grew faster by over 1.3 times. The expansion rates of Tibet and Qinghai, which had a small area of built-up land, were also greater than once. However, with rapid economic development, Beijing and Shanghai only expanded by 0.17 and 0.44 times, respectively. The expansion of the built-up land in northeast China (i.e., Heilongjiang, Liaoning, and Jilin) was also relatively slow, expanding by 0.25, 0.47, and 0.55 times, respectively. The spatial evolution of China’s provincial construction areas from 2000 to 2020 is shown in Appendix Fig. A.

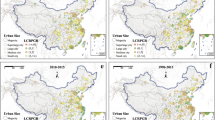
Fig. 2: Evolution of urban built-up land of 31 provinces (municipalities and autonomous regions) in China from 2006 to 2020.
figure 2

Figure llustrates the urban expansion rate and the changes in built-up land of 31 provinces (municipalities and autonomous regions) in China from 2006 to 2020. The left vertical axis is the changes in built-up land, which is represented by circles, and the right vertical axis is the urban expansion rate, which is represented by bars.

Full size image

At the municipal level (Fig. 3), the built-up land of municipalities (i.e., province-level cities in China) and provincial capital cities also showed an increasing trend. The areas of built-up land in Beijing, Shanghai, Guangzhou, and Chongqing were more significant, while Lhasa, Xining, and Yinchuan had more minor areas of built-up land. From 2006 to 2020, more than 50% of cities’ built-up land expanded more than double. Although the total areas of built-up land in Beijing and Shanghai were large, the expansion rate was less than 0.5. The expansion rate of built-up land in Nanjing, Guangzhou, Harbin, Lhasa, and Xining was relatively small.

Fig. 3: Evolution of built-up land of 31 provincial capital cities (municipalities) in China from 2006 to 2020.
figure 3

Figure illustrates the urban expansion rate and the changes in built-up land of 31 provincial capital cities (municipalities) in China from 2006 to 2020. The left vertical axis is the changes in built-up land, which is represented by circles, and the right vertical axis is the urban expansion rate, which is represented by bars.

Full size image

Theoretical propositions of urban expansion

According to our previous theoretical research (Jiang et al., 2015; Li et al., 2018b; Liu et al., 2021), urban expansion has three theoretical propositions, as shown in Fig. 4.

Fig. 4: Schematic diagram of the theoretical proposition of urban expansion.
figure 4

The image on the upper left side of figure illustrates the relationship between the current boundary, inertia boundary, and inertia space, corresponding to the first theoretical proposition. The image on the lower left side of figure illustrates the ideal, moderate and limit boundaries defined based on the principle of price equilibrium, corresponding to the second theoretical proposition. The picture on the right side of figure illustrates the regulation spaces for urban expansion, corresponding to the third theoretical proposition.

Full size image

(1) An essential proposition for urban expansion: Urban expansion, as a social phenomenon in the stage of economic development, shows an “S-shaped” (Logistic) growth in the process of economic development (Li et al., 2012; Shu et al., 2014; Xu and Gao, 2019; Wang et al., 2021), as shown in Fig. 5. Judging from the characteristics of global urban expansion, most central cities in Western Europe and North America are in the post-industrialization stage and have relatively mature urban development. Some cities in Oceania are in the transition period of industrialization and post-industrialization, and the rate of urban expansion is gradually slowing down. Most central cities in Asia, Africa, and South America are in the rapid rise period of industrialization, and the rate of urban expansion is continuing to accelerate. Judging from the characteristics of China’s urban expansion at the municipal level, cities such as Beijing, Shanghai, and Guangzhou are in the transition period of industrialization and post-industrialization, and their expansion rate of built-up land gradually slows down. The urban expansion will be further intensified around the new first-tier cities such as Changsha, Chengdu, Chongqing, Xi’an, Zhengzhou and Hefei, and other cities in the rapid rise period of industrialization. In summary, the trend of increasing built-up land will not be reversed (Fei and Zhao, 2019; Hai et al., 2020; Li et al., 2022c), so there is an “inertial boundary” and an “inertial space” for urban expansion. The inertial boundary defines the extent to which built-up land expand in the future, and inertial space is the space between the inertial boundary and the current urban boundary (Fig. 4).

Fig. 5: Logistic growth of urban expansion with economic development.
figure 5

Figure illustrates the relationship between urban sprawl and economic development, and the various stages in which different regions of the world and different cities in China find themselves.

Full size image

(2) China’s particular theoretical boundaries: In China, the rapid growth of economic demand has led to uncontrolled urban expansion, and the basic farmland and ecological land within the ample inertia space are swallowed up by construction land (Liu and Xin, 2022b). Therefore, increasing scientific regulation measures within the inertial space is necessary to provide reasonable regulation strategies for urban sustainable development. The price of agricultural land in China can be divided into three parts: economic price (APe), ecological price (APc), and social price (APs). Therefore, according to the relationship between agricultural land price (AP) and construction land price (CP), based on the land price equilibrium (Jiang et al., 2015; Li et al., 2018b; Liu et al., 2022a), the ideal, moderate, and limit boundaries of urban inertial space regulation in China can be defined (Li et al., 2011; Li et al., 2018b; Liu et al., 2021). As shown in Fig. 4, the ideal boundary refers to the spatial equilibrium curve when the sum of APe, APc, APs is equal to the CP under a sound land system and perfect market. The moderate boundary refers to the spatial equilibrium curve when the sum of APe and APc is equal to the CP under the condition that the current system is imperfect and the market cannot show the actual price of the agricultural land. The limit boundary refers to the spatial equilibrium curve when the APe is equal to the CP under the condition that the system and market are imperfect, and the government further depresses the land price.

(3) Alternative regulation zones for urban expansion: Overlaying the three boundaries within the inertial space, the three regulation zones for urban expansion in China, i.e. the ideal regulation zone (IRZ), cost regulation zone (CRZ), and alert regulation zone (ARZ) can be obtained (Fig. 4). The IRZ shows the economic, ecological, and social price of land loss from urban expansion. It has the optimal overall land resource allocation efficiency and the best regulation effect. The CRZ shows the economic and ecological price of land loss from urban expansion, has sub-optimal land resource allocation efficiency, and has a poor regulation effect. The ARZ only shows the economic price of land loss from urban expansion and has the lowest land resource allocation efficiency and the worst regulation effect.

Materials and methods

Study area

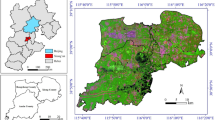
In the empirical research, we tested our theoretical propositions in the eastern Chinese city of Xuzhou. In the northwest of Jiangsu Province, Xuzhou is the central city of the Huaihai Economic Zone. Urban Xuzhou comprises the Gulou, Yunlong, Quanshan, Tongshan, and Jiawang districts. In 2023, the city’s GDP reached 845.78 billion Chinese yuan, with an urbanization rate of 67.60%. The built-up land increased from 61.80 km2 in 1990 to 292.98 km2 in 2022. However, such rapid urbanization was at the cost of losing ecological lands such as cultivated and forest land. From 2006 to 2022, cultivated land decreased by 237.10 km2. From 2006 to 2018, forest land decreased by 170.30 km2. Meanwhile, Xuzhou is a growing city at the stage of rapid expansion. Its balance between urban construction, food security, and ecological protection should be maintained. The regulation of urban spatial expansion is essential to promote sustainable development.

Data and processing

The data used in this study include Landsat satellite images, DEM data, nighttime light data, construction land price data, road network data, and other socioeconomic statistical data.

Both the Landsat satellite images and DEM data are obtained from the geospatial data cloud (http://www.gscloud.cn/), with a resolution of 30 m. The selected Landsat data consists of a Landsat 5 TM image acquired in October 2010 and two Landsat 8 OLI images acquired in October 2015 and September 2020, track numbers are 122/36 and 121/36. We performed radiometric calibration and atmospheric correction on the Landsat images using ENVI. The images were then extracted by mask and classified using a maximum likelihood classification method into six land use types, namely cultivated land, forest land, grass land, water, construction land, and unused land (Fig. 6). The three land use maps were accurately produced with overall accuracies being more significant than 90%, providing essential data and conversion rules for land use simulation and prediction.

Fig. 6: Land use of Xuzhou in 2010, 2015 and 2020, which was obtained by interpreting Landsat satellite images.
figure 6

Land use maps of Xuzhou in a 2010, b 2015, and c 2020.

Full size image

The nighttime light data used is the NPP-VIIRS data at a 500-m resolution, acquired in 2020 and downloaded from the National Oceanic and Atmospheric Administration (http://www.ngdc.noaa.gov). The nighttime light data was clipped to the extent of Xuzhou and reclassified to extract the active light area using ArcGIS. The resultant data supports the fusion extraction of the current urban boundary.

The construction land price data is extracted from the Xuzhou Benchmark Land Price Reports and Maps from 2008-2021, including three types of construction land: residential, commercial, and industrial. By vectorizing the Xuzhou Benchmark Land Price Maps, we built a construction land price database with 230 construction land price samples in this study area, including 85 for residential land, 114 for commercial land, and 31 for industrial land.

The road network data is obtained from the Open Street Map (https://www.openstreetmap.org/). The socioeconomic statistical data comes from Xuzhou Statistical Yearbooks from 2009 to 2022, including population, grain output, output price, per capita food demand, and per capita living consumption expenditure.

Methods

Empirical research flowchart

To verify the above theoretical propositions (Section “Theoretical propositions of urban expansion”), the following four tasks need to be completed in empirical research: (1) the extraction of the current urban boundary, (2) the simulation of the inertial boundary of urban expansion, i.e., the determination of the inertial space, (3) the extraction of the ideal, moderate, and limit boundaries, and (4) the delineation of urban expansion regulation zones, i.e., determining the scale and locations of IRZ, CRZ, and ARZ. The four tasks are shown in Fig. 7 and further described in the rest of Section “Materials and methods”.

Fig. 7: The flowchart of the empirical research verifying the theoretical propositions of urban expansion.
figure 7

Figure illustrates the four steps of the empirical research.

Full size image

Extraction of the current urban boundary

The overlay analysis of nighttime light data and remote sensing index data is used to extract the current urban boundary (Liu et al., 2019; Xie et al., 2019; Zheng et al., 2022). By eliminating the redundant information of construction land, bare land, and water outside the active area of nighttime light, the outer envelope surface of construction land in the active area is taken as the current urban boundary. Among them, the extent of construction land is extracted by the construction land index (CLI)(Liu et al., 2020a), and the area with CLI > 0 is taken as the construction land area. The calculation formula is:

$${CLI}={NDBI}\times {NDVI}-{MNDWI}$$
(1)

where NDBI is the normalized difference building index (Guo et al., 2015), NDVI is the normalized difference vegetation index (Li et al., 2018a), and MNDWI is the modified normalized difference water index (Du et al., 2016). Due to external factors such as seasonality and light, NDBI is often disturbed by vegetation in the calculation process, so it is necessary to eliminate the influence of vegetation and water. All three indices are calculated using the Band Math tool in the ENVI remote sensing image software package (Zheng et al., 2021).

Simulation of the inertial boundary

The CA-Markov model can be used for determining the pattern of land use change by a land use transfer matrix and suitability maps, and simulating future land use types(Kamusoko et al., 2009; Wang et al., 2019; Meng et al., 2021). Therefore, the model can help to predict the urban inertial boundary. The specific steps are as follows:

  1. (1)

    The Markov module in IDRISI was used to obtain the land use transfer matrices of the study area for the periods of 2010–2015 (Appendix Table A) and 2015-2020 (Appendix Table B).

  2. (2)

    By setting the limiting factors and constraint conditions (Appendix Table C), the MCE (Multiple Criteria Evaluation) was used to produce the suitability maps of land use conversion (Fu et al., 2018), providing conversion rules for the simulation of future land use.

  3. (3)

    Combined with the land use transfer matrices and suitability maps, the starting time and the number of cellular automata cycles were set to simulate land use types in the subsequent years (Abijith and Saravanan, 2022), and the outer envelope surface of construction land in the simulation results was taken as the urban inertial boundary.

Calculation of the land price

(1) Price of agricultural land

Considering the feasibility and representativeness of the research, we use cultivated land to represent agricultural land in this study. The economic price of agricultural land (APe) is expressed by the output price of grain or cash crops (Li et al., 2011; Jiang et al., 2015; Liu et al., 2021). The formulas are:

$$A{P}_{e}=\frac{{V}_{a}}{r}\times {\alpha }_{1}$$
(2)
$${\alpha }_{1}=\frac{{POP}\times {F}_{n}}{{F}_{q}\times A}$$
(3)

where Va is the agricultural added price per unit area of the study area (i.e., the ratio of the agricultural added cost to the actual cultivated land area at the end of the year), and r is the reduced interest rate, which is taken from the current year’s security interest rate. Since the banker’s deposit rate has been adjusted many times, the annual average is taken as the security interest rate of the year. α1 is the correction coefficient of agricultural land scarcity, POP is the number of permanent populations in the study area, Fn is the per capita demand for food crops in the study area, Fq is the unit area yield of grain crops in the study area, and A is the area of cultivated land at the end of the year in the study area.

The ecological price of agricultural land (APc) is expressed by modifying the ecosystem service value. Previous studies (Chuai et al., 2016; Xie et al., 2017) have shown that the agricultural land ecosystem’s ecological service value per unit area in 2010 was 6114.30 yuan/hm2. On this basis, the discount rate (taking the annual average of bank loan interest rates from six months to one year in that year) is used to modify the result. The formulas are:

$$A{P}_{c}=\frac{{V}_{C}}{r}\times {\alpha }_{1}\times {\alpha }_{2}$$
(4)
$${\alpha }_{2}=\frac{{F}_{q}}{{F}_{Q}}\times \frac{{GDP}{\prime} }{{GDP}}$$
(5)

where Vc is the ecological service value per unit area of the agricultural ecosystem after time point correction, α2 is the regional correction coefficient, FQ is the national yield per unit area of grain crops in China, GDP is the national per capita GDP, GDP’ is the per capita GDP of the study area, and the meanings of r, α1 and Fq are the same as in formula (2).

The social price of agricultural land (APs) mainly considers the price of agricultural land in three social functions, namely living security, medical security, and employment security (Li et al., 2011; Zhu et al., 2011; Jiang et al., 2015; Fang et al., 2019). The formula is:

$$A{P}_{S}=({V}_{L}+{V}_{M}+{V}_{W})\times {\alpha }_{1}$$
(6)

where VL is the living security price of agricultural land, VM is the medical security price of agricultural land, VW is the employment security price of agricultural land, and α1 is the correction coefficient of agricultural land scarcity.

VL is measured by the minimum living security fund for urban residents and given by:

$${V}_{L}=\frac{B}{r}\times \frac{{PO}{P}_{C}}{A}$$
(7)

where B is the annual minimum living allowance for urban residents in the study area, POPC is the total rural population in the study area, and the meanings of r and A are the same as in formula (2) and (3).

VM is measured by the per capita expenditure on medical and health care of rural households and given by:

$${V}_{M}=\frac{C}{r}\times \frac{{PO}{P}_{C}}{A}$$
(8)

where C is the annual per capita medical and health care consumption expenditure of rural households in the study area, R is the reduced interest rate, POPC is the total rural population in the study area, and A is the cultivated land area at the end of the year in the study area.

VW is measured by the study and training fees required by farmers for re-employment and given by:

$${V}_{W}=\frac{T}{r}\times \frac{{PO}{P}_{f}}{A}$$
(9)

where T is the per capita annual training cost, POPf is the rural labor force population in the study area, and the meanings of r and A are the same as in formula (2) and (3).

(2) Prediction of land price

Due to the limited access to land price data, a grey prediction model is used to construct a mathematical model and make predictions through a small amount of incomplete information for predicting the construction land price and agricultural land price (Dejamkhooy et al., 2017; Li et al., 2021). The grey prediction model is edited and run in the MATLAB R2016b platform.

The grey prediction model is constructed as follows:

1) With the known data sequence x(0) (formula 10), test whether the level ratio λ(k) (formula 11) of the sequence is in the admissible coverage interval (\({e}^{-\frac{2}{N+1}},{e}^{\frac{2}{N+2}}\)). If it is in, the sequence x(0) can be directly brought into the grey prediction model. If not, the sequence needs to be transformed (formula 12, c is a constant) to make its level ratio in the admissible coverage interval.

$${x}^{(0)}=\{{x}^{(0)}(1),{x}^{(0)}(2),{x}^{(0)}(3),{{...}},{x}^{(0)}(N)\}$$
(10)
$$\lambda (k)=\frac{{x}^{(0)}(k-1)}{{x}^{(0)}(1)},\,k=2,3,{{...}}\,N$$
(11)
$${x}^{(0)}={x}^{(0)}+c$$
(12)

2) The test-passing initial sequence x(0) is accumulated once to obtain the sequence x(1) (formula 13), and the nearest neighbor mean sequence x(2) of the sequence x(1) is constructed (formula 14).

$$\begin{array}{c}{x}^{(1)}=\{{x}^{(0)}(1),{x}^{(0)}(1)+{x}^{(0)}(2),{{...}},{x}^{(0)}(1)+{{...}}+{x}^{(0)}(N)\}\\ =\{{x}^{(1)}(1),{x}^{(1)}(2),{x}^{(1)}(3),{{...}},{x}^{(1)}(N)\}\end{array}$$
(13)
$$\begin{array}{c}{x}^{(2)}=\left\{\frac{{x}^{(1)}(1)+{x}^{(1)}(2)}{2},\frac{{x}^{(1)}(2)+{x}^{(1)}(3)}{2},{{...}},\frac{{x}^{(1)}(N-1)+{x}^{(1)}(N)}{2}\right\}\\ =\{{x}^{(2)}(2),{x}^{(2)}(3),{x}^{(2)}(4),{{...}},{x}^{(2)}(N)\}\end{array}$$
(14)

3) The grey differential equation (formula 15) is constructed using the initial sequence x(0) and the nearest neighbor mean sequence x(2).

$${x}^{(0)}(k)+a{x}^{(2)}(k)=b,\,k=2,3,{{...}},N$$
(15)

where a is the development grey number and b is the grey role quantity (endogenous control grey number).

4) The least squares method is used to estimate the parameter estimate \(\hat{\mu }=\left[\hat{a},\hat{b}\right]\) when j(µ) is a minimum.

$$j(\mu )={(Y-B\mu )}^{T}(Y-B\mu )$$
(16)
$$Y={[{x}^{(0)}(2),{x}^{(0)}(3),{{...}},{x}^{(0)}(N)]}^{T}$$
(17)
$$B=\left[\begin{array}{cc}-{x}^{(2)}(2) & 1\\ -{x}^{(2)}(3) & 1\\ {{\vdots}} & {\vdots}\\ -{x}^{(2)}(N) & 1\end{array}\right]$$
(18)

5) The estimated values of the parameters \(\hat{a},\hat{b}\) obtained from the above equation are used to establish the corresponding albinism differential equation (formula 19) and to solve the simulated and predicted values of the known sequence (formula 20).

$$\frac{d{x}^{(1)}}{dt}+\hat{a}{x}^{(1)}(t)=\hat{b}$$
(19)
$${\hat{x}}^{(0)}(k+1)={\hat{x}}^{(1)}(k+1)-{\hat{x}}^{(1)}(k)=(1-{e}^{\hat{a}})\left({x}^{(0)}(1)-\frac{\hat{b}}{\hat{a}}\right){e}^{-\hat{a}k}$$
(20)

6) The accuracy test of the simulation results is carried out to calculate the residual E (formula 21), the post-residual ratio C (formula 22), and the probability of small error P (formula 23).

$$E(k)={x}^{(0)}(k)-{\hat{x}}^{(0)}(k),\,k=2,3,{{...}},N$$
(21)
$$C=\frac{\sqrt{\frac{1}{N-1}\mathop{\sum }\nolimits_{k=2}^{N}{[E(k)-\bar{E}]}^{2}}}{\sqrt{\frac{1}{N}\mathop{\sum }\nolimits_{k=2}^{N}{[{x}^{(0)}(k)-\bar{X}]}^{2}}}$$
(22)
$$P=P\left\{|E(k)-\bar{E}| < 0.6745\sqrt{\frac{1}{N}\mathop{\sum }\nolimits_{k=2}^{N}{[{x}^{(0)}(k)-\bar{X}]}^{2}}\right\}$$
(23)

where \(\bar{E}\) is the mean value of E and \(\bar{X}\) is the mean value of x(0). The classification standards for accuracy test are shown in Table 1.

Table 1 Classification standard for accuracy test.
Full size table

Extraction of the ideal, moderate, and limit boundaries

Ideal, moderate, and limit boundaries are spatial indifference curves reflecting land price equilibrium under different conditions, which can be extracted by spatial interpolation of construction land price at monitoring points (Jiang et al., 2021). The formulas are as follows:

$$\,\begin{array}{cc}{\rm{Ideal\; boundary}} & {CP}=A{P}_{e}+A{P}_{c}+A{P}_{s}\end{array}$$
(24)
$$\begin{array}{cc}{\rm{Moderate\; boundary}} & {CP}=A{P}_{e}+A{P}_{c}\end{array}$$
(25)
$$\begin{array}{cc}{\rm{Limi}}{\rm{t}}{\rm{boundary}} & {CP}=A{P}_{e}\end{array}$$
(26)

where CP is the price of construction land, APe, APc, and APs are the economic, ecological and social prices of agricultural land, respectively.

Results

Extraction of the current urban boundary

The extracted construction land in Xuzhou in 2020 is shown in Fig. 8a. To some extent, the extracted construction land covers the built-up area of the city center, but construction land and bare land in the suburban areas are also included. There is a need to overlay the extracted construction land with the nighttime light active area (i.e., the area with an average night light intensity of greater than 50) (Fig. 8b). By the overlay analysis, we obtained the current urban boundary of Xuzhou in 2020 and the construction land within the boundary, which was 321.25 km2 (Fig. 8c).

Fig. 8: Extraction process and results of the current urban boundary in Xuzhou in 2020.
figure 8

a The construction land in Xuzhou in 2020. b The average intensity of nighttime light in Xuzhou in 2020. c The current urban boundary in Xuzhou in 2020 and the construction land within the boundary.

Full size image

Inertial simulation of urban expansion

Combined with the land use transfer matrix and suitability maps, the land use in 2020 is simulated. By comparing the simulated land use in 2020 with the actual land use in 2020, we performed an accuracy assessment. The Kappa coefficient was 0.85, indicating that the simulation effect is good. This model simulated the land use in 2025 to extract construction land (Fig. 9a). The patches with a high degree of aggregation were retained, with an area of 387.34 km2. The urban inertia boundary of 2025 was determined by the outer envelope of construction land, with an area of 679.07 km2 (Fig. 9b). The space between the current boundary of 2020 and the inertia boundary of 2025 was the inertia space of urban expansion with an area of 163.86 km2.

Fig. 9: The simulated land use and the inertial boundary of urban expansion in Xuzhou in 2025.
figure 9

a Land use types of Xuzhou in 2025 simulated using the CA-Markov model. b Spatial extent of the inertial boundary in Xuzhou in 2025 as well as the distribution of construction land within the inertial boundary.

Full size image

Delimitation of the ideal, moderate, and limit boundaries

Price calculation of agricultural land and construction land

As shown in Fig. 10, the economic, ecological, social, and comprehensive prices of agricultural land from 2008 to 2021 showed an overall increasing trend over the years. The comprehensive price increased from 454.79 yuan/ m2 in 2008 to 1312.00 yuan/ m2 in 2021. The proportion of economic price ranged from 33.38% to 45.13%, the proportion of ecological price ranged from 12.45% to 23.85%, and the proportion of social price ranged from 40.45% to 44.78%. Among them, economic and social prices showed abrupt changes in 2009 and 2011, respectively, due to the high setting of the bank deposit interest rate adjustment in that year. In addition, economic price and social price increase faster than ecological price, which was influenced by the higher growth range of economic price and social price measures than the discount rate used to estimate ecological price.

Fig. 10: Prices of agricultural land in Xuzhou from 2008 to 2021.
figure 10

The line graphs in figure represent the economic, ecological, social and comprehensive prices of agricultural land, while the bar graphs indicate the proportions of economic, ecological and social prices in the comprehensive price.

Full size image

According to the price data from 2008 to 2021, using the grey prediction model, the predicted economic price, ecological price, and social price of agricultural land in 2025 are 978.48 yuan /m2, 247.47 yuan /m2, and 899.82 yuan /m2, respectively, accounting for 46.03%, 11.64%, and 42.33% respectively. The prediction accuracy of agricultural land prices is shown in Table 2.

Table 2 Prediction accuracy of agricultural land prices.
Full size table

Similarly, the continuous series of the prices of 230 construction land samples from 2008 to 2021 was brought into the prediction model, of which 215 samples pass the accuracy test, and the predicted price distribution of construction land samples in 2025 can be obtained (Fig. 11a).

Fig. 11: Price of construction land, price contours, as well as the ideal, moderate, and limit boundaries extracted based on the principle of price equilibrium.
figure 11

a Construction land price contour in Xuzhou in 2025 and b ideal, moderate, and limit boundaries in Xuzhou in 2025.

Full size image

Spatial interpolation and boundary extraction

Within the inertia boundary in 2025, the interpolation analysis was performed on the construction land price monitoring points that have passed the accuracy test. According to Formulas (10)–(12), in 2025, the equilibrium price corresponding to the ideal boundary, moderate boundary, and limit boundary were computed, which were 2125.77 yuan/m2, 1225.95 yuan/m2, and 978.48 yuan/m2, respectively. Taking the price calculation results as breakpoints, the corresponding contours in the interpolation results were extracted, namely the ideal, moderate, and limit boundaries of urban expansion, as shown in Fig. 11b.

Delimitation of the urban expansion space regulation zone

Three types of urban expansion regulation zones were obtained by spatial overlay analysis of the current urban boundary identified in 4.1, the urban inertia boundary identified in 4.2, and the ideal, moderate, and limit boundaries identified in 4.3 (Fig. 12). The IRZ is the reserved regulation space for urban expansion within the inertial boundary, between the ideal boundary and the current urban boundary. It covers an area of 65.91 km2, including 28.83 km2 of construction land and 32.89 km2 of cultivated land. The CRZ is the reserved regulation space that can be provided for urban expansion further outside the IRZ, within the inertial boundary, between the moderate boundary and the current urban boundary. It covers an area of 66.57 km2, including 25.85 km2 of construction land and 38.54 km2 of cultivated land. The ARZ is the reserved regulation space that can be provided for urban expansion further outside the IRZ and CRZ, within the inertial boundary, between the limit boundary and the current urban boundary. It covers an area of 10.87 km2, including 5.10 km2 of construction land and 4.01 km2 of cultivated land.

Fig. 12: Urban expansion regulation zones in Xuzhou in 2025.
figure 12

Figure illustrates the spatial locations of three types of urban expansion regulation zones between the inertial boundary and the current boundary.

Full size image

In addition, in Fig. 12, the no-build area (20.51 km2) within the inertial boundary refers to the land where the price of land developed as construction land is lower than the minimum price of land used as agricultural land, i.e., the land resources in this area are more conducive to the efficient use of land resources and economic development as agricultural land.

Discussion

Global lessons of urban space governance

Given the imbalance of urban space and the destruction of the ecological environment caused by the rapid urban expansion, developed countries have put forward various governance models to control urban expansion strictly. This study mainly sorts out the specific measures, objectives, and problems in three countries in different periods, as shown in Table 3.

Table 3 Measures, objectives, and problems of urban expansion regulation in different countries.
Full size table

The above urban expansion control strategies based on the “containment of expansion” paradigm have more negative impacts in addressing the problem of urban expansion and urban space imbalance. Controlling urban expansion through the delimitation of urban boundaries and the protection of key resources is to a certain extent important for the regulation of urban expansion in China (Li et al., 2024; Song et al., 2024), but urban expansion caused by the population growth is inevitable, and space must be reserved to accommodate this new population (Jiang et al., 2022; Meng et al., 2024). Therefore, this study innovatively puts forward three theoretical propositions of urban expansion, especially forward three boundaries and three types of urban expansion regulation zones in China, which theoretically defines the spatial non-differentiated curve of land resources used as agricultural land and construction land, practically finds the equilibrium range of urban expansion, agricultural land protection and ecological environment maintenance, and managerially shows the spatial reference system for the regulation of urban expansion. Based on this, this study selects Xuzhou, which is in the rapid expansion stage, for empirical research. Our findings can provide a theoretical basis for urban expansion regulation and a practical reference for the space management of cities with similar development types.

Practical application analysis of theoretical propositions in China

Ideal boundary and IRZ

From the welfare economics perspective (Mackenbach, 2012; Inglesi-Lotz, 2016; Li et al., 2022b), it is most reasonable that the inertial boundary and spatial extent of future urban expansion fit on the ideal boundary of the regulation zone. At this time, the overall allocation efficiency of land resources is the highest, and the total social welfare is maximized. According to the schematic diagram of the theoretical propositions of urban expansion presented in Fig. 4, it can be seen that when the future urban expansion reaches the moderate boundary, it will over-consume the land resources between S1 and S2, in which process the overall allocation efficiency of the land resources will be reduced and the social welfare will be lost. When the urban expansion reaches the limit boundary, it will over-consume the land resources between S1 and S3, in which process the overall allocation efficiency of land resources will be further reduced, and social welfare will be further lost. Therefore, theoretically, the IRZ should be selected as the optimal strategy for future urban spatial expansion regulation. However, the arduousness of land system innovation and the long-term nature of market improvement determine that this most reasonable spatial regulation strategy is challenging in China (Li et al., 2018b; Liu et al., 2022a).

Moderate boundary and CRZ

From China’s practical experience, urban expansion is a spatial carrier to ensure China’s economic and social development and the improvement of urbanization in the new era (Li et al., 2018b; Liu et al., 2021; Zhang and Han, 2024). Reasonable urban expansion benefits regional development. This study suggests that regulating urban expansion space is more realistic within the CRZ. The reasons are as follows: (1) this “equilibrium state” not only meets the rigid requirements of urbanization and economic development on construction land but also shows the economic and ecological price of agricultural land, which is of great significance to the maintenance of the regional ecological environment and sustainable development. (2) It is undeniable that this “equilibrium state” is indeed at the expense of the social security price of agricultural land. Since the process of industrialization and urbanization is a critical stage that most countries must go through, if too much emphasis is placed on protecting agricultural land to restrict the rational growth of cities, it will undoubtedly hinder the advancement of China’s urbanization process in the new era. As long as the level of economic development reaches a particular stage, it is possible to compensate for the loss of social security functions sacrificed by rural farmers through other means, such as the social security systems for farmers’ medical care and pensions introduced by the central government (Yang and Chang, 2023a; Sun et al., 2023). The implementation of the concept of urban-rural integration (Lu and Yao, 2018; Wang et al., 2024) and rural revitalization strategy (Han, 2020; Liu et al., 2020b) are good examples.

Limit boundary and ARZ

The process of defining limit boundary and ARZ only shows the economic price of land loss from urban expansion, and does not incorporate the ecological services and social security functions to land resources into the comprehensive decision-making of resource allocation and spatial governance. If this expansion trend is followed, urban development will pay a huge cost in resources and produce a series of difficult-to-repair ecological and environmental problems (van Vliet, 2019; Guangdong Li et al., 2022a), so ARZ is a regulation zone that should be avoided in the management of urban expansion. But for some megacities, the space within the CRZ can no longer meet the needs of urban expansion, the ARZ is also an option for the regulation of urban expansion in such cities.

Selection of regulatory zones for urban expansion in Xuzhou

In the empirical research, we tested our theoretical propositions in the eastern Chinese city of Xuzhou, which is a growing city in the rapid expansion stage (Liu et al., 2021). Combined with the land use data (Appendix Table A and B), it can be seen that from 2010 to 2015, the construction land in Xuzhou has increased by 72.79 km2, and from 2015 to 2020, the construction land has increased by 52.95 km2. By 2025, Xuzhou will still need to add new construction land to support the urban expansion. In section “Delimitation of the urban expansion space regulation zone”, we get the scope of the three types of regulation zones and the construction land covered in them. There is only 28.83 km2 of construction land in IRZ, which is unable to meet the future development needs of Xuzhou, and CRZ has 25.85 km2 more construction land on the basis of IRZ, which is enough for Xuzhou to meet the demand of construction land in 2025, so Xuzhou should choose IRZ and CRZ as the reference system for the regulation of urban expansion.

Conclusions

According to the research framework of “characteristic diagnosis-theoretical analysis-empirical research,” we performed an in-depth analysis of urban expansion problems and drew the following conclusions. Firstly, by diagnosing urban expansion characteristics, we have found that global urban expansion has been rapid and characterized by concentrated patches. China, India, and Southeast Asian countries had the most prominent urban expansion. Meanwhile, most of the central cities in Western Europe and North America were in the post-industrialization stage. In China, the urban expansion will be further intensified around the cities in the rapid rise period of industrialization. Secondly, through theoretical analysis, we suggest that the use of ideal, moderate, and limit boundaries in the inertial space to define three types of urban expansion regulation zones, i.e., IRZ, CRZ, and ARZ, is the cornerstone of the choice of urban expansion regulation strategy. Regulating urban expansion space in the CRZ is more feasible, which conforms to the primary national conditions. Thirdly, through empirical research, we have found that the area within the current urban boundary of Xuzhou in 2020 was 515.21 km2, and the inertia space scale in 2025 would be 163.86 km2. The reserved space areas provided by the IRZ, CRZ, and ARZ for urban expansion are 65.91 km2, 66.57 km2, and 11.87 km2, respectively. Therefore, the urban expansion regulation strategy in Xuzhou should choose the IRZ and CRZ together with 133.48 km2 as the reference system of space optimization.

In summary, we proposed in this study that urban expansion regulation should choose the optimal scheme guided by theoretical propositions, considering the rigid demand and practical feasibility of rapid urbanization and high-quality development for urban space. The theoretical proposition and control strategy of urban expansion proposed in this study can provide a reference for the optimal regulation of urban space in Xuzhou and other cities with similar development.

There are still some limitations in this study. Firstly, we diagnosed the characteristics and trends of global urban expansion only at a macro scale. Still, it would be interesting to select the relevant static and dynamic indicators of urban expansion for quantitative comparative analysis. Secondly, many cities in China are currently characterized by multi-center development. The regulation model based on the principle of land price equilibrium is mainly suitable for single-center cities. The theoretical innovation and empirical analysis of the regulation model of multi-center cities need to be further explored. Thirdly, the characteristics of urban expansion in different development stages are heterogeneous. Due to the limitation of data acquisition, only Xuzhou was selected for the empirical research, and cities at different development stages will be selected for comparison our future work.