Abstract
Wood-carved window grilles in traditional Chinese historical architectures, as an important cultural heritage, bear profound historical value and exemplify the extraordinary craftsmanship of ancient artisans. However, due to natural weathering and human damage, protecting and preserving these artifacts has become a major challenge. This study proposes an optimization design method for wood-carved window grilles that combines the Stable Diffusion Model (SDM) with Intuitionistic Fuzzy VIKOR. First, 2476 window grille patterns were collected to create a diverse database to support algorithm training. Next, the SDM was employed to learn the design patterns of the window carvings, generating designs that blend traditional charm with innovative styles. After high-quality samples were selected by design experts, the Intuitionistic Fuzzy VIKOR was used to prioritize the esthetic appeal of the patterns, ensuring that the designs met contemporary esthetic standards. These innovative patterns were then integrated into creative lamp design, and optical simulation experiments were conducted using TracePro software to evaluate the best options based on translucency, surface illuminance, and uniformity. Through a hybrid approach combining artificial intelligence and multi-criteria decision-making, this paper provide traditional artisans with a steady stream of creative inspiration, shorten the R&D cycle for wood carving products, and offer new directions for the protection and modernisation of wood carving cultural heritage.
Similar content being viewed by others
Introduction
Wooden carvings in traditional Chinese ancient historical architectures are an important component of cultural heritage. Through a rich variety of motifs, such as flowers, birds, fish, insects, auspicious patterns, and religious figures, these carvings not only showcase the exceptional craftsmanship of Chinese artisans but also embody profound historical, cultural, and artistic values (Zhao et al. 2015; Fang et al. 2024). As a mark of ancestors’ lives and traditions, historical architectures record the passage of time and the accumulation of culture. However, with the rapid development of society, traditional timber structures are gradually being replaced by concrete and steel, leading to the disappearance of these unique architectural styles, which are now becoming precious fragments of historical memory (Wang et al. 2020). Wood-carved window grilles, as key decorative elements in historical architectures, are vital material evidence for studying ancient building structures, layouts, and esthetic styles. They provide crucial insights into ancient Chinese social life and cultural beliefs. Yet, the themes and artistic expressions of traditional wooden carvings are often fixed, with limited integration into modern life and fashion. This lack of innovation and contemporary relevance makes it difficult for these art forms to capture the public’s attention, resulting in a shrinking market for wooden carvings in the field of intangible cultural heritage (Cao and Bin, 2023; Li, 2016). The transmission of traditional woodcarving techniques primarily relies on collective memory and the master-apprentice system. However, due to the craft’s complexity, high labor intensity, long learning periods, and low economic returns, many young people are reluctant to learn the craft. This has led to a dramatic decline in the number of skilled practitioners and an increasing risk of these techniques being lost (Alfred 2016). Therefore, it is crucial to integrate advanced technology and innovative design into the woodcarving craft to revitalize it.
With the rapid development of Artificial Intelligence (AI), generative AI is good at high efficiency, scale and production of standardized content, but lacks the ethical judgment and emotional resonance of human creation, so human-computer collaborative creation is the main direction of future design. In addition, AI image processing technology is widely used in a variety of fields such as predicting diseases (Chakraborty 2024), accelerating the efficiency of complex data analysis (Huo et al. 2025) and precise production control (Mamat et al. 2022). Meanwhile, the application potential of AI in cultural heritage preservation and innovative design is also becoming more and more prominent (Saka et al. 2023), Chen et al. (2022) classified Chinese Cantonese opera singing based on the Cogcnet model; Zhang et al. (2023) applied the extended AISAS model to the field of ICH dissemination, Karadag, (2023) used the Conditional Generative Adversarial Networks to protect culturally significant buildings and sites by predicting the damaged parts of historical buildings within the boundaries of early Ottoman tombs, these studies demonstrate the diverse application scenarios of AI in ICH preservation and innovation.
Compared to the aforementioned models, the SDM offers greater flexibility and an advantage in generating highly realistic and detailed images. In addition, multi-scale processing improves the computational efficiency of the model, which has the advantages of good training stability, strong scalability, and accurate simulation. It shows broad prospects for application in various fields, including image enhancement, artistic design, and urban planning, Cheng et al. (2024) proposed a speckle removal model based on SDM, which can enhance the clarity and accuracy of images or data, and improve creative style and diversity. Wang et al. (2023) proposed using transfer learning to obtain novel paintings from latent SDM, promoting the development of image synthesis and painting creation. Cui et al. (2024) greatly reduced the creation time by learning to generate urban design images from conditional latent SDM. Yang et al. (2025) proposed a novel framework for high-fidelity Thousand Li of Rivers and Mountains image synthesis using SDM. Although It is an efficient tool for enhancing productivity and inspiring creativity, it still faces two major challenges that need to be addressed: (1) It is difficult to assess the quality of generated creative images. Due to the random nature of the generation process and the lack of a unified evaluation standard, it is challenging to provide objective assessments of the images produced. (2) Although models have powerful design assistance capabilities, their understanding of cultural connotations and depth of emotional expression remain limited, and therefore they cannot completely replace the role of human designers.
To address the above issues, we introduce the Multiple Criteria Decision Making (MCDM) method to solve problems involving multiple attributes that may conflict with each other and are difficult to compare directly. Commonly used MCDM method include the Analytic Hierarchy Process (AHP) (Xu and Nazir 2024), the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) (Yardimci and Kurucay, 2024), the Entropy weight method (Hu 2023), and Decision-Making Trial and Evaluation Laboratory (DEMATEL) (Fan et al. 2023). AHP was developed by Saaty (1986). Its core idea is to hierarchize complex problems and quantify qualitative problems (Li et al. 2019). However, although AHP has a clear structure and high flexibility, it relies too much on the knowledge and experience of experts, resulting in a certain degree of subjectivity in the evaluation results. The TOPSIS method was proposed by Hwang and Yoon (1981). It ranks the evaluation objects by calculating the distance between them and the ideal solution and the negative ideal solution. TOPSIS has the advantages of strong comprehensiveness, objectivity, and easy understanding, but it cannot solve problems such as indicator correlation. The advantage of the entropy weight method is that it can objectively reflect the amount of data information and avoid human bias in weighting; however, it relies entirely on the degree of data dispersion, which may overlook the actual importance of the indicators (Zeng et al. 2022). DEMATEL is a method for constructing a visual causal network by quantifying the mutual influence of elements within a system, focusing on the interdependence between evaluation criteria (Smidovnik and Groselj 2023). The DEMATEL method has the advantages of revealing the relationship between factors and determining key factors, but it also has disadvantages such as high processing difficulty and poor result interpretation. Compared with the above decision-making methods, Intuitionistic Fuzzy VIKOR can handle fuzzy information and uncertainty well, which is particularly important in the field of emotional design. Through its unique calculation approach, Intuitionistic Fuzzy VIKOR can avoid discrepancies between ranking results and actual conditions, ensuring consistency in the evaluation results. Therefore, this study combines SDM and Intuitionistic Fuzzy VIKOR to precisely assess the innovation and esthetic quality of generated images.
Technological progress has brought us many benefits, but it is also accompanied by new challenges and opportunities. AI is replacing repetitive and arduous manual labor in many fields by improving production efficiency. However, it also has problems such as lack of real-world applicability, low social acceptance, and low accuracy due to the scarcity of available data. Therefore, designers need to effectively supplement AI in terms of creativity, sociality, and complex cognition to achieve complementary advantages between man and machine (Villani et al. 2025).
In addition, the generative design of SDM is often constrained by training data, and is more about combining existing elements. Human designers can break through existing styles and forms through their creativity and create new artistic expressions. This kind of breakthrough creativity is difficult for AI to simulate. Moreover, in actual creation, designers will make adjustments based on their own esthetic experience and customer needs, and this flexibility is lacking in AI. Therefore, this paper explores the collaborative design model of AI and designers in ICH wood carving window patterns, using AI to improve production efficiency and replace repetitive and heavy human labor. Designers complement AI cognition in creativity, sociality, and complex cognition, promoting intelligent and digital innovation of wood carving patterns.
This paper combines SDM and Intuitionistic Fuzzy VIKOR to optimize the design of wood-carved window grilles in ancient dwellings. First, Model generates innovative patterns that combine tradition and modernity. Then, the Intuitive Fuzzy VIKOR method evaluates the esthetic ranking of the patterns. Designers combine their own practical experience to integrate the selected high-quality window grille patterns into modern lamp design. Finally, by optimizing lighting effects through TracePro software, we have developed a fashionable lighting product design that combines esthetics and functionality. This paper is the first to apply generative AI and fuzzy multi-criteria evaluation to the design of intangible cultural heritage (ICH) patterns, addressing the limitations of traditional generative AI in terms of esthetic quantification. In addition, it has also re-engaged the younger generation in the protection of traditional cultural heritage and established a digital decision-making framework for cultural heritage protection. The main contributions of this study are reflected in the following three aspects:
-
1.
Rapid generation and diversification of wood-carved window grille designs. By utilizing the SDM to learn the generation patterns and design logic of traditional wood-carved window grilles, innovative decorative patterns that retain traditional elements are generated. The AI algorithm quickly generates and optimizes complex patterns, improving design efficiency and exploring diverse innovative solutions (Bansal et al. 2024).
-
2.
Fuzzy MCDM optimization. The introduction of Intuitionistic Fuzzy VIKOR constructs a comprehensive evaluation system, addressing the lack of a unified evaluation standard for designs generated. This method not only enhances the precision and systematic nature of the selection process, but also effectively quantifies the quality of the evaluated images.
-
3.
AI-driven revival of traditional ICH. The wood-carved window grilles automatically designed not only retain the essence of traditional culture but also combine modern lamps for design, meeting the esthetic needs of the younger generation and realizing the inheritance and innovation of ICH in modern society (Zhou et al. 2025).
The remaining sections of this paper are organized as follows: Section “Literature review” introduces the theoretical foundations of generative design for wood-carved window grilles, the SDM, and Intuitionistic Fuzzy VIKOR. Section “The proposed research framework” describes the framework, process, and algorithm of the model used in this study. Section “Case study” presents the experimental procedures and result analysis. Finally, Section “Conclusion” provides a discussion and conclusion.
Literature review
Innovative design of wood-carved window grilles in historical architectures
The wood-carved window grilles in ancient residential buildings are unique components of Chinese historical buildings (Li et al. 2024; Wu and Kyungsun 2024), reflecting the unique form and cultural connotation of historical buildings (Hou et al. 2024). Although existing studies have explored the value of wood-carved window grilles from the perspectives of art (Yang 2013), history (Chen and Bai 2020), and esthetics (Pang 2014), these studies are mostly limited to a single discipline and lack interdisciplinary comprehensive research, making it difficult to meet the growing esthetic needs of contemporary society (Zheng et al. 2024). Therefore, it is necessary to use new technologies and interdisciplinary research to promote its innovation and development (Lungu et al. 2021).
As the second decade of the 21st century commences, technology-enabled innovation has emerged as a new research trend. Shi, (2023) developed a “literal-interpretive” dual-track design methodology, combining AI and IoT technologies to advance the adaptive conservation of ancient dwellings in Leizhou. Güzelci et al. (2024) made contributions to the field of digital archeology and heritage protection by using generative adversarial network to simulate and predict the architectural features and influences of the Dome of the Sinan Mosque. Kurucay and Ediz (2025) utilized digital tools to reinterpret the potential of traditional architectural elements, fostering their integration with contemporary design practices. In comparison, SDM demonstrates unique advantages in the design of wood carving window patterns due to its high-fidelity generation capabilities for complex structures and intricate details.
SDM
The concept of diffusion models was first proposed by Sohl-Dickstein et al. (2015), which achieves data generation through a forward process that simulates the diffusion of data distribution toward noise distribution, followed by a reverse process that restores noise to high-quality data (Yi et al. 2024; Croitoru et al. 2023). Diffusion models cover a wide range of tasks through two main branches: unconditional and conditional generation (Chen et al. 2024). Unconditional diffusion models only learn the data distribution, while conditional diffusion models introduce additional conditions during the generation process to control the generated content (Chen et al. 2025). With the improvement of engineering efficiency and reduction in computational costs of deep learning algorithms, SDM has demonstrated more intuitive and simpler characteristics due to its autoregressive training mechanism. Compared to the unstable adversarial training and mode collapse issues of GANs and the sequential generation of Transformers, It has significant advantages in parameter tuning and training stability. However, computational cost and sampling speed are its weaknesses, requiring hundreds of iterations for denoising, which is much slower than GAN’s one-step generation or Transformer’s parallel decoding, and it is also less efficient than Transformer in long sequence tasks. Nevertheless, SDM has been widely adopted and applied in fields such as image generation, natural language processing, and audio synthesis due to its exceptional generation quality and high stability during training, making it an important research direction in generative AI. Ke et al. (2024) proposed a text-guided image-to-sketch diffusion model, which can synthesize abstract and precise line-drawn human sketches at the object and scene levels. Wang et al. (2024) proposed a biomimetic product design based on knowledge graphs and semantic fusion diffusion models. Kang and Zhao (2025) proposed a ceramic morphology optimization design combining SDM and GRU-Attention.
Compared with other generative AI techniques, SDM can generate high-quality images and extraordinary creative flexibility, and the generated images provide clear formal features and high diversity, but challenges still exist (Wang et al. 2024). The complexity of wood carving window grille data, the lack of labels, and the randomness of the generation process pose challenges to the direct evaluation of generated patterns. To address this problem, this paper introduces the intuitionistic fuzzy VIKOR method, which aims to effectively balance the conflicts between multiple design goals and evaluation criteria.
Intuitionistic Fuzzy VIKOR
As early as 1965, L. A. Zadeh proposed fuzzy set theory, introducing membership functions to address problems involving fuzziness and uncertainty (Ainur et al. 2020). In 1989, Atanasov introduced the concept of Intuitionistic fuzzy sets (IFS) as an extension of fuzzy set theory. Unlike fuzzy sets, which consider fuzziness in a single dimension (Zadeh 1990), IFS must simultaneously account for support, opposition, and indecision (Mao et al. 2013). As the technical framework for addressing uncertainty in decision-making problems has gradually matured. Opricovic, (2011) jointly developed the VIKOR method in 1998, which is particularly suitable for complex scenarios involving conflicting and incommensurable evaluation criteria (Yang and Wu 2020). While the VIKOR method is efficient and flexible, it has limitations when addressing decision-making problems involving fuzziness and uncertainty. Given the advantages and widespread application of the VIKOR method and IFS, Zhao et al. (2017) extended the classical VIKOR method to develop a new approach called Intuitionistic Fuzzy Hybrid VIKOR (IFH-VIKOR) for supplier selection. The IFH-VIKOR model characterizes fuzziness through a two-dimensional framework of membership and non-membership, and employs a support/opposition/abstention multi-evidence mechanism to enhance the flexibility of subjective opinion expression (Yang et al. 2022), significantly improving the robustness and operability of the decision-making process. Experiments show that in scenarios involving conflicting indicators, dimensional heterogeneity, and high uncertainty, IFH-VIKOR can effectively generate compromise solutions, achieving a dynamic balance between maximizing group benefits and minimizing individual regret (Liu and Qin 2018), thereby providing more interpretable solutions for complex decision-making problems.
Intuition-based fuzzy VIKOR has been successfully applied in various fields such as engineering design, supply chain management, and sustainable development. Narayanamoorthy et al. (2019) first proposed a VIKOR-based industrial robot selection method using interval-based intuition-based fuzzy entropy. Later, Jing et al. (2021) evaluated the conceptual design process using fuzzy semantic variable fusion while considering conflicting beliefs, integrating Dempster-Shafer evidence theory and Intuitionistic Fuzzy VIKOR. Wang et al. (2024) combined Grey Relational Analysis with Intuitionistic Fuzzy VIKOR to explore the design of willow weaving cultural creative products. Considering the multiple criteria and potential uncertainties involved in pattern design, intuitionistic fuzzy VIKOR can flexibly handle the trade-offs between different design schemes. Therefore, this paper uses intuitionistic fuzzy VIKOR to screen ancient residential wood carvings that meet the emotional needs of customers, which solves the problem that SDM cannot quantitatively evaluate the innovation and esthetics of the generated patterns.
Although the above studies have explored the innovation of wooden carving window patterns from different perspectives, most existing studies focus on single generation mechanisms or independent evaluation models. Therefore, this study aims to construct an integrated “generation-evaluation-collaboration” closed-loop research framework to break through the bottlenecks of existing research and provide a new paradigm with greater explanatory power and practical value for the innovation of ICH.
The proposed research framework
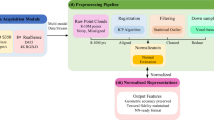
This study is divided into four steps (Fig. 1): First, Building a database of wooden window carvings by collecting 2,476 samples of traditional Chinese wooden window carvings from various styles, patterns, and details through multi-channel research. Second, Using a SDM to iteratively remove noise from random noise and generate innovative patterns that align with traditional wooden carving esthetic features. Third, Applying the Intuitive Fuzzy VIKOR method to evaluate the esthetic quality of the generated patterns, selecting high-satisfaction designs and combining them with modern lampshade shapes to develop creative products that meet the esthetic needs of the younger generation. Finally, validating the lighting performance of the lampshades (transmittance, illuminance uniformity, etc.) through Tracepro optical simulation, and finally optimizing and determining a lampshade design scheme that combines cultural value with practical functionality.
SDM generates innovative wood-carved window grille patterns
SDM excels in generating high-quality and high-resolution images. It achieves image generation through a process of adding and removing noise, where the image at the next moment is generated by adding noise to the image from the previous moment, \({{\rm{x}}}_{{\rm{t}}}\) represents the image at time t, \({\in }_{t}\) represents the randomly distributed noise image generated at time t, \({\beta }_{t}\) represents a constant specified at time t (Chen et al. 2025).
Noise Addition Formula:
The relationship between \({{\rm{x}}}_{{\rm{t}}}\) and \({{\rm{x}}}_{{\rm{t}}-1}\):
The relationship between \({{\rm{x}}}_{{\rm{t}}}\) and \({{\rm{x}}}_{0}\):
Normal distribution formula (Gaussian distribution formula) is used to generate these noisy images:
Back diffusion stage used a series of Markov chains to gradually remove prediction noise. For noise estimation and removal, the most commonly used U-Net, each step of the reverse diffusion process attempts to estimate the conditional probability distribution (Chen et al. 2022). According to the Bayesian formula:
Because \({\rm{P}}\left({{\rm{x}}}_{{\rm{t}}}\right)\) and \({\rm{P}}\left({{\rm{x}}}_{{\rm{t}}-1}\right)\) are difficult to estimate, we assume that \({{\rm{x}}}_{{\rm{t}}}\) and \({{\rm{x}}}_{{\rm{t}}-1}\) are obtained by adding Gaussian noise, \({\rm{p}}\left({{\rm{x}}}_{{\rm{t}}-1}|{{\rm{x}}}_{{\rm{t}}}\right)\) follows a Gaussian distribution, its mean and variance can be predicted by the U-Net network. The loss function is used to guide the model to learn how to effectively generate high-quality images from noise. Maximum likelihood estimation methods are often used to train model parameters, find a pair of mean and variance that maximizes the probability of these sample values sampled from the normal distribution. In order to realize the derivation of the maximum likelihood function, the problem of maximum likelihood derivation is converted to Evidence Lower Bound (ELBO). Evidence Lower Bound is a commonly used optimization objective in generative models. It provides an easily computable lower bound to approximate the log-likelihood function which is difficult to compute directly.
Continuously deduce and simplify the Evidence Lower Bound formula to obtain:
The formula contains the KL divergence between two Gaussian distributions, KL divergence is used to measure the difference between two probability distributions (distribution p and distribution q), The formula is:
First, let’s look at \({\rm{q}}\left({x}_{t-1}|{x}_{t},{x}_{0}\right)\), which represents the derivation of \({x}_{t-1}\) when \({x}_{t}\),\({x}_{0}\) is known. This formula can be solved, \({{\rm{p}}}_{{\rm{\theta }}}\left({x}_{t-1}|{x}_{t}\right)\) needs to use U-Net to predict the mean of the distribution. Finally, through continuous derivation, the formula is obtained:
Net is the formula for predicting the above, All the variables except ϵ in the above formula are known. So what the U-Net network actually predicts is ϵ, it makes more sense to perform this above method T times rather than trying to remove the entire noise. By repeating this process, the noise will gradually be removed, resulting in a “cleaner” image.
Intuitionistic Fuzzy VIKOR calculation priority ranking
Intuitionistic Fuzzy VIKOR introduces the IFS theory into VIKOR to deal with MCDM problems whose attribute values are intuitionistic fuzzy numbers. IFS not only consider the membership of an element to a set, but also the non-membership of an element that does not belong to the set and the hesitation of the element. IFS can be expressed as: Let X be a given set, then \({\rm{A}}=\left\{\left\langle x,{\mu }_{A}\left(x\right),{{\mathcal{V}}}_{A}\left(x\right)\right\rangle|x\in X\right\}\). Among them, \({{\mathcal{V}}}_{A}\left(x\right)\), \({\mu }_{A}\left(x\right)\) represent the membership and non-membership of element x to A respectively, and x is the hesitation degree. A and B are any two intuitionistic fuzzy numbers on X, and the euclidean distance between them is:
Let \({\rm{A}}=({{\rm{A}}}_{1},{{\rm{A}}}_{2},\cdots ,{{\rm{A}}}_{{\rm{m}}})\) represent a set of m selected samples (m ≥ 3),\(\,{\rm{B}}=({{\rm{B}}}_{1},{{\rm{B}}}_{2},\cdots ,{{\rm{B}}}_{{\rm{n}}})\) represents a set of n evaluation indicators; \({\rm{C}}=\left({C}_{1,}{C}_{2},\cdots ,{C}_{k}\right)\) represents a set of K evaluation experts \(({\rm{K}}\ge 5)\), \({\lambda }_{k}\) represents the weight of the bid evaluation expert \({C}_{K}\), \({\omega }_{j}^{k}\) represents the weight value assigned by expert \({C}_{K}\). The expert \({C}_{K}\) evaluation value is recorded as \({h}_{{ij}}^{k}.\) The initial evaluation matrix given by the expert \({C}_{K}\) is:
Qualitative indicators often use fuzzy language such as good, average, and poor to describe preference information. To facilitate evaluation, these fuzzy language information needs to be converted into specific numerical values to analyze specific problems. We describe the scores from 1 to 5 using fuzzy language of very poor, poor, fair, good, and very good. Then, invite relevant experts to truncate the expert scores based on the semantic strength of the language variables. Through linear transformation, \(\mu \in [0.15,0.85]\), \(v\in [0.10,0.80]\), \(\mu\) and \(v\) that meet the “very poor” and “very good” levels in the 5-level scale are symmetrically distributed, and the middle level is “fair” (0.50,0.40), \(\mu +v=0.90\). The special design retains fuzziness and reflects a clear tendency. The transition level follows the law of arithmetic decrease. Finally, these qualitative indicators are converted into corresponding intuitionistic fuzzy numbers (Table 1). The expert’s intuitionistic fuzzy evaluation matrix can be obtained using the information provided in Table 1.
Among them, \({\widetilde{h}}_{{ij}}^{k}=({\mu }_{{ij}}^{k},{\nu }_{{ij}}^{k})\) represents the intuitionistic fuzzy number, the size of intuitionistic fuzzy entropy is used to reflect the fuzzy uncertainty of expert evaluation information. The larger the intuitionistic fuzzy entropy is, the higher the degree of uncertainty in the evaluation given by the experts is, and the indicator should be assigned a smaller weight, otherwise it should be assigned a larger weight. the intuitionistic fuzzy entropy of expert \({C}_{K}\)‘s evaluation of indicator \({B}_{j}\) is:
Then the index weights determined by the expert \({C}_{K}\) intuitionistic fuzzy evaluation matrix can be expressed as:
The comprehensive weight of the indicators can be determined by establishing a minimum deviation optimization model. First, determine the reasonable range of weights \(\left[{\omega }_{j}^{k-},{\omega }_{j}^{k+}\right]\). They represent the minimum and maximum weights of the indicator allocation, and their deviations are used to reflect the consistency of expert opinions:
Secondly, build an optimization model to determine the comprehensive weight of indicators and obtain the comprehensive weight \({\omega }_{j}^{* }\):
In the formula, the indicator weight \({\omega }_{j}^{k}\) in the optimization model only includes the weights that meet the consistency test. Expert weights are determined based on entropy theory and weighted intuitionistic fuzzy entropy formula:
The intuitionistic fuzzy weighted average operator is used to aggregate the expert decision matrices into a group decision matrix:
Determine the positive ideal solution and negative ideal solution under each index:
VIKOR is used to calculate the group utility value S(\({A}_{i}\)), personal regret value R(\({A}_{i}\)), and compromise evaluation value Q(\({A}_{i}\)) of each sample, namely:
Where d is the euclidean distance between any two intuitionistic fuzzy numbers, \({{\rm{S}}}^{+}=\max \left[{\rm{S}}({A}_{i})\right]\), \({{\rm{S}}}^{-}={\rm{m}}{\rm{i}}{\rm{n}}\left[{\rm{S}}({A}_{i})\right]\), \({{\rm{R}}}^{+}=\max \left[{\rm{R}}({A}_{i})\right]\), \({{\rm{R}}}^{-}=\min \left[{\rm{R}}({{\rm{A}}}_{{\rm{i}}})\right]\), \(1\le i\le m\); \({\rm{\upsilon }}\) is the compromise coefficient, \({\rm{\upsilon }}\in \left[\mathrm{0,1}\right]\). This paper takes 0.5, which means the compromise decision of maximizing the group utility value and minimizing the individual regret value. sort the samples according to the values of \({\rm{S}}\left({A}_{i}\right)\), \({\rm{R}}\left({A}_{i}\right)\) and \({\rm{Q}}\left({A}_{i}\right).\) If the \({\rm{Q}}\left({A}_{i}\right)\) value of sample \({A}_{i}\) is the minimum and satisfies the following two conditions at the same time, it is the optimal sample for the bid evaluation decision.
Condition 1: \({Q}_{2}{-Q}_{1}\le \frac{1}{m-1}\), where \({Q}_{1}\) and \({Q}_{2}\) correspond to the minimum and second minimum values in the \({\rm{Q}}\left({A}_{i}\right)\) value ranking respectively, and m is the number of alternative samples.
Condition 2: The best window grille \({A}_{i}\) has the smallest value in both \({\rm{S}}\left({A}_{i}\right)\) and \({\rm{R}}\left({A}_{i}\right)\) value rankings.
If only condition 1 is met, it means that all samples are close to the ideal solution, if only condition 2 is met, it means that the samples corresponding to \({Q}_{1}\) and \({Q}_{2}\) are compromise solutions. After the optimal solution is selected, the optimal solution samples are eliminated and then the suboptimal solution is selected, and so on and so forth, and it is considered according to the actual situation.
Case study
In traditional Chinese architecture, doors and windows are considered part of the exterior decoration. Since the walls of wooden structures typically do not bear significant weight, doors and windows can be designed to be light and transparent. The various patterns carved on the window frames are placed at the visual focal point, serving both to allow ventilation and natural light, while also playing a key role in the building’s decorative design. Therefore, we have selected the decorative patterns of wood-carved window grilles from historical architectures as the case study for this research.
Collecting wood-carved window grille patterns of historical architectures
A wide range of traditional wooden carving window patterns were collected from various online and offline platforms, including websites, museums, and art galleries, with an initial total of 2476 images gathered. The data primarily originated from field research conducted at ancient residential dwellings, villages, ancestral halls, ancient towns, and temples. After excluding photographs with obvious defects such as blurriness, perspective distortion, or incomplete subjects, Ten professionals developed a three-dimensional evaluation standard covering artistic value, technical compatibility, and imaging quality. A systematic compilation of a sample database was conducted, encompassing eight regional categories (each with ≥150 specimens) such as the Huizhou and Jin categories, along with 15 foundational patterns (each with ≥50 specimens) including swastika and cloud motifs. Prioritization focused on complete patterns demonstrating rotational symmetry or expandable structures. Sample classification followed complexity-based grouping (simple: ≤3 types; medium: 4–6 types; complex: ≥7 types, allocated to 400/600/300 specimens respectively) to optimize data augmentation potential. Following expert quality validation, solid-color backgrounds were systematically removed and geometric features deconstructed using Photoshop, with precise extraction of 1,500 standardized line drawings achieved through Pen Tool processing (Fig. 2). This methodology retained critical decorative elements while enabling scalable pattern analysis. These wireframe diagrams are more unified than the original woodcarving patterns, ensuring that AI learning associates pattern shapes with cultural connotations. AI uses such image data for deep learning, automatically extracting and mastering design patterns and cultural logic, thereby generating innovative window patterns with cultural connotations.
SDM generates new creative wood-carved window grilles
Based on 1500 woodcarving window lattice line drawings, a dedicated training set was constructed. A pre-trained SDM model was combined with Low-Rank Adaptation lightweight fine-tuning technology to perform deep learning on traditional pattern features. The optimized model and inference engine were then embedded into the software to develop an interactive creation tool that supports intelligent generation of window lattice styles.
First, a multi-dimensional classification system was constructed based on the characteristics of wooden carving window patterns. After expert annotation to form structured metadata, a hierarchical sampling method was used to divide 1,500 line drawings into three categories-low, medium, and high-based on line density and topological complexity. A proportion formula was then used to extract 351 images to form the training set (covering 92% of core categories and including all eight rare patterns), and chi-square tests were used to verify the consistency of the distribution. The remaining 1,149 images were allocated to the validation set and backup repository in a 7:3 ratio. The validation set employed a sequential cross-validation strategy to distinguish between hyperparameter optimization (30%) and overfitting prevention (70%), while the backup repository implemented redundant storage to support model iteration optimization.
Subsequently, a “text-image” generative AI training dataset is constructed based on the AVE (encoder-decoder) structure. The encoder is responsible for extracting image features and generating a vector representing the image content. The decoder takes this vector as input and gradually generates a text description corresponding to the image content. A selection of 500 wireframe images depicting traditional Chinese window patterns has been compiled. For the generation of text description words for images, it is necessary to extract patterns and summarize semantics of wood carvings, and write accurate and inspiring description words to guide the model to correctly understand and perform tasks. We utilized the image captioning functionality of a vision-language multimodal large model, which is commonly implemented using an encoder-decoder architecture. The specific technical implementation involved invoking the open-source large model API interface provided by Zero One Infinity, an AI 2.0 company specializing in large model technology. Start inputting pictures one by one and outputting the corresponding description words. This completes the construction of the training data set.
We use Low-Rank Adaptation technology based on the opensource pre-trained SDM. During the training process of Low-Rank Adaptation, multiple parameters interact with each other, which can be roughly divided into two categories: training steps and training efficiency. The design of hyperparameters directly affects the training efficiency, generation quality and sampling speed of the model. The core parameters include Repeat, Epoch, batchsize, Learning Rate and Network Dimension. Before starting training, select the SDM v1.5 suitable for the training task, and then fine-tune the model on the constructed text data. The experimental environment used in this paper for model training and image generation is: torch 2.1.2 cuda 11.8 Graphics card is NVIDIA RTX 3070ti. The relevant parameters are: Optimizer AdamW, learning rate setting 1e-5 (Control parameter update step size, smaller learning rate helps stabilize training), The number of training set images is 351, the batch size is set to 16, the maximum number of training steps is 1600, the dimension of the Low-Rank Adaptation network is set to 128, the maximum resolution during training is 768×768, the training batch size is 3, and the step size of the Resolution Bucket is set to 64 pixels. Loss values are generated during the training process. The training status can be understood by observing the average Loss curve in the training log and the Loss value of each Epoch (Fig. 3).
Integrate the above carefully trained model and its reasoning function into an interactive UI interface (Fig. 4). The checkpoint in the figure is the checkpoint file of SDM, which determines the base model for generating images. The choice of VAE (Variational Autoencoder) model affects the latent space representation in image generation. The Clip skip parameter influences how well the model understands the text prompt during image generation. The sampling method refers to the sampling technique, which impacts image generation quality and speed. Sampling steps specify the number of sampling steps, determining the number of iterations during image generation. Batch count refers to the number of batches for generating images, and batch size sets the number of images generated per batch. These two parameters can help you generate multiple images at once. CFG Scale is the classifier free guidance scale, which affects how closely the model follows the text prompt. Seed is the random seed parameter used to initialize the generation process.
By inputting various text prompts to perform model inference and test the performance of the model in generating window grilles, the performance of the characteristic factors can be verified. To achieve controllability and image quality of window grille generation, other hyperparameters need to be set: The prompt word relevance is set to 7. Generate image resolution 512 * 512, the number of sampling steps for generating images is set to 20. Enable ControlNet to control the depth information of the image, making the comparison of fine-tuning effects more intuitive. The following is an example of model inference, the text prompt is “Traditional Chinese window decoration pattern, black and white, symmetrical design, high quality details, central floral graphics, draw interlocking shapes, high contrast, monochromatic”. Then the trained window grille model is called for prompt, and the influence coefficient of Low-Rank Adaptation is set to 0–1 to generate images.
Generate images when setting the weights of the Low-Rank Adaptation model to greater than 1, The generated results show: As the Low-Rank Adaptation weight increases, the generated image will deviate further from the original style, and the three-dimensional sense will increase and the complexity will become stronger, but at the same time the generation process will become unstable, and details will collapse or the overall effect will be out of control, which is not conducive to the extraction of patterns. The call weight of the Low-Rank Adaptation model is set between 0.2 and 3 to better express the characteristic factors, which is basically consistent with the requirements of the wood carving window patterns we need.
The evaluation of model performance involved selecting images of woodcarving window patterns created with the generative model and traditional designs for comparative analysis. We conducted a quantitative assessment across multiple dimensions, including features, details, and mathematical metrics (scored on a scale of 1 to 5). Calculations revealed that traditional woodcarving window patterns contain richer historical and cultural connotations. Traditional designs outperform generative designs in terms of deep feature extraction and design details, aligning more closely with traditional esthetic preferences. However, generative designs, due to their mechanized and random nature, exhibit superior symmetry and abstraction levels. Distribution similarity is more meaningful for generative designs, while the SSIM index shows limited distinction between the two design types. Nevertheless, generative designs may exhibit differences in certain aspects, as illustrated in Fig. 5.
Overall, generative modeling offers superior performance and many benefits in terms of creative generation. However, it does not outperform traditional methods in terms of creativity and image quality. Nevertheless, its dynamic and generative nature provides designers with a variety of solutions. It is important to balance the advantages of traditional methods with those of AIGC to maximize creativity.
Priority of wood-carved window grille patterns sorted by Intuitionistic Fuzzy VIKOR
In the previous phase, SDM generated 300 window patterns. The selection of window patterns this time adopted a combination of professional and public reviews: designers from fields such as fashion, interior design, and graphic design, as well as public representatives spanning various ages, genders, professions, and cultural backgrounds, were invited to form a review panel. They independently ranked and scored the 300 works based on a multi-dimensional evaluation guideline, then resolved discrepancies through collective discussion. Finally, by integrating professional opinions and public preferences, the top 40 works were selected based on their scores. When using the Fuzzy VIKOR method to assess design esthetics, if the evaluation criteria and indicators are not clearly defined, systematic methods can be employed to enhance the transparency of quantification and validation. Through three rounds of iterative screening using the Delphi method, the evaluation criteria and indicators were refined, ultimately identifying five core Kansei keywords: simple, modern, elegant, curved, and rounded. and validated the low redundancy of the indicators and the high consistency of expert scores using correlation coefficients (<0.5) and Cronbach’s α coefficients (0.87), ensuring the reliability and validity of the evaluation process. The research results indicate high internal consistency among the expert group, followed by the distribution of questionnaires using quantitative survey methods, a five-point Likert scale was used to semantically anchor 40 window patterns: 1–5 points (one point indicating strongly disagree with the selected adjective, three points indicating somewhat agree, and five points indicating strongly agree) were assigned to the five evaluation criteria for each of the 40 window patterns, with scores ranging from 1 to 5. To ensure the validity of the questionnaire, no restrictions were placed on the population or occupation, and a total of 82 questionnaires were distributed. After strictly screening and removing invalid questionnaires, the final data sample consisted of 53 questionnaires, yielding 53 expert evaluation samples.
According to the evaluation indicators of the previous stage, the questionnaire results can obtain the intuitionistic fuzzy evaluation matrix of 53 experts, The intuitionistic fuzzy entropy formula (10–13) is used to calculate the fuzzy uncertainty of the experts on the indicators, and then the minimum deviation optimization model is used to determine the comprehensive weight of the indicators. The calculated weights of the five indicators are 0.1991, 0.1991, 0.1914, 0.2077, 0.2027.
According to the obtained indicator weights assigned by all experts, based on the expert weight determination method proposed in the bid evaluation decision model, the weights of each bid evaluation expert are calculated in turn using formula (14–15). Weighted histogram obtained (Fig. 6).
The calculation results include 53 expert evaluation weight data points, with a minimum value of 0.0058 and a maximum value of 0.0440. The weight values are primarily concentrated between 0.0126 and 0.0262, with numerous values such as 0.0122, 0.0195, 0.0200, and 0.0239. Values below 0.01 are relatively rare, with only a few instances such as 0.0058 and 0.0068. The maximum difference in expert weights is 0.0382. Typically, the maximum difference does not exceed 0.15, indicating a high degree of consensus among experts.
The intuitionistic fuzzy weighted average operator in formula (16) is used to aggregate the expert decision matrices into a group decision matrix. According to the group decision matrix and formula (17), the positive ideal solution and negative ideal solution of each window grille under each indicator are determined.
According to the intuitionistic fuzzy Euclidean distance measurement formula and the VIKOR formula (28-20), the group utility value \({\rm{S}}\left({A}_{i}\right)\), personal regret value \({\rm{R}}\left({A}_{i}\right)\), and compromise evaluation value \({\rm{Q}}\left({A}_{i}\right)\) of each image are calculated respectively. We converted the comprehensive \({\rm{Q}}\left({A}_{i}\right)\) scores into a bar chart (Fig. 7).
The result of sorting by the size of the compromise value Q(Ai) shows that the value of sequence number 21 is the smallest 0, and the second largest value is 0.0374. According to condition one: Q2-Q1≥1/(m-1), Q2-Q1=0.0374 m is 40, 1/(m-1) = 0.0256, 0.0374>0.0256. Satisfying condition 1, the S(Ai) and R(Ai) values of sequence number 21 are both minimum values, which means that the 21st picture is the optimal solution. After eliminating picture No. 21, after calculating the minimum and second minimum values in the Q(Ai) value ranking, only condition one is satisfied, which means that all samples are close to the ideal solution. Because the sample satisfies the minimum value in Q(Ai) as a prerequisite and necessary condition, we select four optimal window grilles based on the minimum value of Q(Ai). Finally, it was concluded that among all the patterns, Nos. 21, 3, 12, 13, and 16 were the top five optimal solutions (Fig. 8). Pattern No. 3 is centered on a tiger’s face and combines floral patterns to form a concentric composition. Patterns 12 and 16 combine geometric circles with floral elements, primarily featuring symmetrical swirl patterns. Patterns 16 and 13 lack specific imagery, appearing more abstract, while patterns 21 and 13 primarily feature curling patterns. Finally, the ICH inheritors selected patterns 21, 3, and 13 as research subjects based on criteria including cultural semantics, esthetic balance, and image quality.
Creative product design of fashionable lamp
In recent years, the market for wood carving mood lighting has grown rapidly. This design combines modern home esthetics with traditional elements, with the theme of “classical elegance”. Wood carving window patterns are applied to mood lighting to create a warm and elegant space, bringing new inspiration to modern home design.
In the AI-assisted design process, the wooden carving window lattice design was deconstructed into three key elements: traditional pattern units, mortise-and-tenon structural modules, and lighting effects. Design compatibility validation utilized a traditional pattern database, with strict adherence to the classical proportion principle of “three parts empty, seven parts solid”. Guided by the core philosophy of “inheritance and innovation”, premium hardwoods such as rosewood and boxwood are integrated with geometric window lattice patterns into lampshade designs. Precision proportional adjustments yield an organic unity of traditional forms and modern functionality, targeting traditional culture enthusiasts and the home decoration market. Additionally, to address the challenge of adapting flat window lattice patterns to three-dimensional lamp structures, we adopted a three-dimensional planar structural design. This approach preserves the integrity of the window lattice patterns while optimizing the balance between decorative layout and lighting functionality, ensuring that light quality remains unaffected. Ultimately, three design scheme sketches were completed. We invited 200 design students to evaluate three design sketches using a Likert scale (1–5 points) based on five groups of Kansei words. Ultimately, sketch plan 2 emerged as the best option with an average score of 4.19 (compared to 3.37 and 3.28 for the other designs). A digital model of plan 2 was subsequently constructed using 3D modeling software and rendered with high-quality visuals in Keyshot (Fig. 9), establishing a robust foundation for the subsequent production phase.
TracePro optical system simulation experiment
TracePro is based on the ACIS solid modeling kernel and is the first simulation software to combine real solid models, powerful optical analysis capabilities, strong data conversion capabilities, and an easy-to-use interface. An optical model of a wooden carving window lamp was constructed using the TracePro optical simulation platform. Through simulating the light propagation path and distribution characteristics, we quantitatively evaluated the impact of different patterns on lighting uniformity (standard deviation, coefficient of variation) and softness. By combining experiments comparing translucent and opaque materials, we optimized the structural parameters of the lamp and the ratio of optical materials, ultimately selecting a window-carved ambient light design that balances artistic expression and optical performance. The specific experimental steps are as follows:
The lighting fixture model in STP format was imported into TracePro, where the light source was configured by defining its position, luminous intensity, and other parameters. In this setup, the light source was set to emit red light uniformly from the central cylindrical surface, with a radiative power of 1 W, generating 500,000 rays. The material properties were set to opaque, and the emitting area was defined as the surface area of a single window pattern (76 * 160 mm). After creating the receiving surface, ray tracing simulations were performed, resulting in light tracking maps and irradiance distribution analysis maps for the three window patterns. Finally, the light distribution uniformity was calculated for each design, \({\rm{U}}\left({\rm{u}}{\rm{niformity}}\right)=\frac{{E}_{\min }}{{E}_{\max }}\).
From the illuminance analysis maps, the following results were obtained: When opaque, the uniformity of light distribution for the three window patterns is 63.6 * 127.2 mm, 73.6 * 152 mm, and 71.6 * 151.2 mm, respectively.
With all other conditions unchanged, the materials of the three window patterns were set to transparent PMMA (polymethyl methacrylate), which has high transparency and a light transmittance of 90–92%. The ray tracing maps and illuminance analysis maps (Fig. 10) were then generated. Data analysis shows that when light passes through, the uniformity of light distribution for the three window patterns is 76 * 144 mm, 70 * 143.2 mm, and 79.6 * 151.2 mm, respectively.
In the irradiance analysis, the left side shows the candela diagram displaying the intensity distribution. The color gradient in the 3D diagram represents different illuminance values, with darker colors (e.g., blue) indicating lower intensity, and lighter colors (e.g., yellow) indicating higher intensity. The color gradient bar on the left is an important visual aid. It quantifies the relationship between color and intensity, correlating colors with specific illumination intensity values so that the illumination intensity represented by different colors in the figure can be understood intuitively. The regions are measured in millimeters. On the right side, the coordinate system shows the light distribution curve, where the x-axis represents the angle deviation from the axis, and the y-axis represents light intensity. The blue line represents the horizontal plane, and the green line represents the vertical plane. From Fig. 10, it can be observed that the illuminance in the horizontal angle for all three wooden-carved lamps increases in variability as the distance from the center point increases. In contrast, the illuminance in the vertical angle remains relatively stable and consistent, with greater variation occurring as the distance from the center increases. Additionally, it is evident that changes in material properties have a more significant impact on vertical illuminance, with the material variations in Window Pattern 2 having a more pronounced effect on the illuminance compared to the other patterns.
According to the experimental results, when the material is opaque, the illuminance uniformity follows the order: Window Pattern 2 > Window Pattern 3 > Window Pattern 1. Illuminance uniformity is a key indicator for assessing the evenness of light distribution, which is crucial for both visual health and work efficiency. When the illuminance varies significantly across the field of view, the pupils frequently adjust in size to accommodate the environment, which not only causes visual fatigue but may also lead to blurred vision, dry eyes, eye strain, headaches, and other discomforts. Therefore, when selecting lighting fixtures, products with good illuminance uniformity should be prioritized, making Window Pattern 2 the optimal choice. When the material is transmissive, the illuminance uniformity follows the order: Window Pattern 3 > Window Pattern 1 > Window Pattern 2, with Window Pattern 3 being the best. An optical model of the wooden carving window lamp was constructed using the TracePro platform, with opaque hardwood prioritized as the material and Window Flower 2 selected as the decorative pattern for lighting fixtures now in production. These simulation results can assist designers in carefully considering both the lighting effects and functionality when choosing window pattern decorations.
Results analysis and discussion
Innovative wood-carved window grille patterns generated by SDM
Through big data analysis, the SDM has mastered the principles of central symmetry, repetitive variation, and the distribution of patterns and lines in window carving designs, successfully creating 500 novel window patterns. These patterns integrate complex geometric shapes and curves, showcasing a harmonious and elegant esthetic while highlighting the unique charm of traditional Chinese art.
By comparing the differences in the generation trajectories of the same cultural symbol cue word in different scenarios, this paper found that the decision process of the diffusion model is essentially to establish a differentiable mapping between the noise space and the semantic space. The experiments revealed that when no specific keywords were input, the patterns predominantly consisted of cloud-like or curling designs, exhibiting conventional central symmetry. However, when specific elements (such as flowers, animals, people, etc.) were input, the patterns often became distorted, requiring multiple adjustments. The iteration results showed that the quality of the generated patterns ranked from highest to lowest as follows: plants, animals, people, and text, with the floral patterns performing the best and the textual patterns the worst. In terms of parameter settings, smaller weights resulted in more uniform window patterns with higher clarity and richer details. Increasing the weight led to greater variation and a stronger sense of layering in the patterns, giving them a more modern feel, but at the cost of decreased clarity. However, excessively large weights could cause the image quality to become unstable or even generate unrecognizable patterns. Overall, after parameter optimization, the window patterns generated by the SDM excelled in diversity, naturalness, and detail expression. When it is necessary to generate other cultural styles, we only need to build a special dataset and reuse the underlying feature extractor through the transfer learning framework for fine-tuning. We found that the advantages of modular data and reusable technical framework can make the model robust and universal, avoiding the generalization distortion of the model.
Experimental results analysis of Intuitionistic Fuzzy VIKOR
After the calculation of intuitionistic fuzzy VIKOR, we concluded that window grilles No. 21, 13, and 3 are the better ones. The composition of the window grilles No. 21 and No. 13 shows a perfect sense of balance, symmetrical up and down, left and right, and a harmonious beauty can be felt in their design and composition. The lines and visual elements guide the line of sight and enhance the expressiveness of the picture. The composition of the window grille No. 3 is different. The central body is prominent, and the surrounding leaf patterns not only echo the central circle but also increase the richness and dynamics of the entire design. Window grille No. 13 adds curling lines and dotted decorations, similar to twined twig patterns, symbolizing the continuous vines, which not only embodies the “endless” life view, but also implies the “continuous” family inheritance concept in Confucian ethics. Window grille No. 21 also has patterns similar to copper coin patterns, with a circle outside and a square inside, corresponding to the “round sky and square earth” cosmic view, symbolizing the pursuit of wealth. The Nian beast pattern in the middle of the No. 3 window grille is an important element in Chinese traditional culture, symbolizing courage and unity, implying the change of years and new hope, creating a specific atmosphere and emotion; it can trigger emotional resonance among users and also carries rich cultural heritage and diversity. There are also animal patterns in other window grilles, such as bats: homophonic to “Fu”, symbolizing “five blessings”, fish: implicitly referring to “year after year”, etc. These elements are still rejuvenated in contemporary design. Through the analysis of these three window grilles, we can find that balanced, symmetrical and harmonious window grille pictures with profound meaning and rich symbolic meaning are often more popular with people.
Comparative experiment between different decision-making models and intuitionistic fuzzy VIKOR
To validate the stability of the VIKOR algorithm for fuzzy intuition, this study conducted a comparative experiment using the same questionnaire data and three MCDM methods: AHP, TOPSIS, and DEMATEL. The AHP was used to evaluate the relationships among the five window flower indicators through expert assessments, resulting in a relationship matrix, followed by indicator weight calculations. TOPSIS combined the entropy weight method to determine weights and calculate the proximity of each scheme to positive and negative ideal solutions. DEMATEL assigned weights based on centrality and performed weighted ranking. Finally, the indicator weights and ranking results from the three methods were compared with those from the intuitionistic fuzzy VIKOR (Fig. 11).
In the calculation results of these methods, the weight of refined indicators in AHP is the highest, the weight of concise indicators in TOPSIS is the highest, and the weight of curve indicators in DEMATEL and intuitive intuitionistic VIKOR is the highest. From the ranking results, window grilles No. 21 ranks first in DEMATEL and intuitionistic fuzzy VIKOR, and has the highest ranking average among the four methods. Therefore, window grilles No. 21 is the optimal design scheme. The conclusions of the three evaluation methods effectively prove the theoretical adaptability and practical reliability of the intuitionistic fuzzy VIKOR ranking algorithm in the evaluation scheme.
By analyzing pairwise correlations based on the ranking results, can further demonstrate the similarity of rankings obtained through different methods, which we express using Pearson’s correlation coefficient. The data shows that the intuitionistic fuzzy VIKOR method exhibits positive correlations with both TOPSIS and DEMATEL, with correlation coefficients of 0.345 and 0.393, respectively, all of which are greater than 0. The correlation coefficient between the intuitionistic fuzzy VIKOR method and Analytic Hierarchy Process is -0.093, which is close to 0, indicating that there is no significant correlation between them.
Experiments show that TOPSIS, DEMATEL, and intuitionistic fuzzy VIKOR have a high ranking consistency when dealing with complex problems because they adopt a MCDM framework and a global optimization path, while AHP has significant ranking differences due to its reliance on subjective judgment, hierarchical information loss and sensitivity. The three robustness methods handle fuzziness through different mechanisms (VIKOR membership modeling, DEMATEL influence matrix, TOPSIS distance measurement), which are more suitable for high-dimensional coupled uncertainty decision-making scenarios; the deterministic scale of AHP limits its system analysis capabilities.
Performance comparison of Intuitionistic Fuzzy VIKOR and other MCDM methods
Intuitionistic Fuzzy VIKOR differs from other multi-criteria decision-making methods, such as AHP, TOPSIS, entropy weight method, and DEMATEL, in terms of performance and application scenarios. AHP uses a hierarchical structure to address complex problems, but the subjectivity of weights may affect objectivity; TOPSIS employs an objective ranking based on the distance from the ideal solution, which is efficient when there are few criteria, but weight sensitivity increases under multi-criteria conditions; the Entropy Weighting Method relies on data variability for automatic weighting, requiring strict data quality; DEMATEL excels at analyzing causal relationships between factors but has high computational complexity; the VIKOR method offers advantages such as strong comprehensiveness, high flexibility, and high resolution, but also has drawbacks such as susceptibility to uncertainty and sensitivity to weight selection. By incorporating intuitionistic fuzzy sets, it can more effectively handle fuzziness and uncertainty. In summary, intuitionistic fuzzy VIKOR performs exceptionally well in handling fuzziness, better describes the fuzzy characteristics of problems, and demonstrates outstanding accuracy and stability.
Discussion
This study proposes a cultural heritage revitalization plan based on AI and digital twin technology, achieving living inheritance by generating variants of endangered cultural patterns, and enabling deep integration with the home furnishings, apparel, and CNC carving industries. The research leverages smart manufacturing technology to drive personalized customization production, simultaneously enhancing efficiency and product value. It also specifies technical implementation conditions, providing practical guidance for industry applications. For example, processing a single style requires 500-1000 base samples, while multi-cultural styles or complex feature scenarios require over 2000-3000 samples to ensure model generalization capability. Hardware configuration recommendations include using NVIDIA Tesla/A100 high-end GPUs for deep learning training. For large-scale data processing or complex model training, a cluster of 4-8 GPUs can be configured to optimize efficiency through parallel computing. Team members should encompass multiple disciplines such as computer science, cultural studies, design arts, and manufacturing engineering.
Conclusion
This study pioneered the feasibility of human-machine collaborative design paradigms in the field of cultural heritage revitalization by establishing a complete technical closed loop for ICH digital innovation design. This framework successfully overcomes the technical limitations of traditional generative AI, which prioritizes form over cultural interpretation, by employing a fuzzy MCDM to achieve a multidimensional balance between cultural value, esthetic characteristics, and technical feasibility. This human-machine intelligent fusion design model not only provides a new pathway for the creative transformation of ICH, but also offers an innovative methodological framework for human-machine collaboration mechanisms in the era of intelligent design.
The main contributions of this study are:
-
1.
The design framework is versatile and replicable, and can be applied to the digital transformation of other traditional crafts, providing a replicable example of improving efficiency in the digital transformation of traditional crafts.
-
2.
The digital design process significantly shortens the research and development cycle of wood carving products, enabling craftsmen to quickly transform their ideas into products, improve production efficiency, and seize market opportunities.
-
3.
The simulation results of TracePro software compared the transmittance efficiency and visual comfort index of three different wood carved window pattern lamps, providing the best solution reference and parameter guidance for product development of related manufacturers.
Although the research process has yielded certain results, there are still issues and limitations: (1) Due to time and resource constraints, the data samples collected from field research on ancient wood-carved window grilles may not be comprehensive. Future studies could expand the data range to improve the generalizability of the conclusions. (2) When using the Intuitionistic Fuzzy VIKOR method, the setting of certain parameters may depend on subjective judgment. Future research could adopt more rigorous experimental designs to objectively assess the esthetic ranking of the window carvings. (3) While the TracePro ray-tracing engine is fast and accurate, the algorithm may face certain limitations when dealing with complex scenarios. In practical applications, many complex factors could cause slight deviations between the simulation results and actual conditions. During simulation analysis, numerous parameters such as light source characteristics, material properties, and surface attributes need to be configured. This study only considered window carving patterns and two materials, while many other complex factors were not accounted for. Future research may require additional measures or the use of other tools to support the simulation analysis.
Data availability
The datasets in this study of wood-carved window grilles are accessible through the following links https://pan.baidu.com/s/1WRQsqGnEPVU-QmuDMEbDhA?pwd=i7a9 Code: i7a9.
References
Ainur Z, Batyr O, Saya S, Kanagat D, Rita YML M, James C, Xiao-Guang Y (2020) Models for oil refinery waste management using determined and fuzzy conditions. Information 11(6):299
Alfred C (2016) Preservation of indigenous wood carving knowledge of African traditional people through the use traditional wood carvers database framework (Twcdf). Indian J traditional Knowl 15(3):370–377
Bansal G, Nawal A, Chamola V, Herencsar N (2024) Revolutionizing visuals: The role of generative AI in modern image generation. Acm Trans Multimed Comput Commun Appl 20(11):356
Cao ZH, Bin MM (2023) A study of ornamental craftsmanship in doors and windows of Hui-Style Architecture: The Huizhou Three Carvings (Brick, Stone, and Wood Carvings). Buildings 13(2):351–351
Chakraborty M (2024) Rule extraction from convolutional neural networks for heart disease prediction. Biomed Eng Lett 14(4):649–661
Chen H, Xiang Q, Hu JX, Ye ML, Yu C, Cheng H, Zhang L (2025) Comprehensive exploration of diffusion models in image generation: a survey. Artif Intell Rev 58(4):99
Chen J, He ZQ, Zhu DY, Hui B, Li RYM, Yue XG (2022) Mu-Net: Multi-path upsampling convolution network for medical image segmentation. CMES-Computer Modeling Eng Sci 131(1):73–95
Chen MS, Mei S, Fan JQ, Wang MD (2024) Opportunities and challenges of diffusion models for generative AI. Natl Sci Rev 11(12):254–276
Chen Q, Zhao W, Wang Q, Zhao YW (2022) The sustainable development of intangible cultural heritage with AI: Cantonese opera singing genre classification based on CoGCNet Model in China. Sustainability 14(5):2923
Chen RX, Fan JP, Wu MQ, Ma SN (2025) Conditional diffusion model for recommender systems. Neural Netw 185:107204
Chen WY, Bai GX (2020) Analysis of the historical and cultural roots of the rise and development of Jianchuan Bai ethnic woodcarving. Guangxi Ethn Stud 04:133–139
Cheng L, Xing YM, Li Y, Guo Z (2024) A diffusion equation for improving the robustness of deep learning speckle removal model. J Math Imaging Vis 66(5):801–821
Croitoru FA, Hondru V, Ionescu RT, Shah M (2023) Diffusion models in vision: A survey. IEEE Trans Pattern Anal Mach Intell 45(9):10850–10869
Cui XT, Feng X, Sun SW (2024) Learning to generate urban design images from the conditional latent diffusion model. IEEE Access 12:89135–89143
Fan ZM, Zhu BW, Xiong L, Huang SW, Tzeng GH (2023) Urban design strategies fostering creative workers’ sense of identity in creative and cultural districts in East Asia: An integrated knowledge-driven approach. Cities 137:104269
Fang XB, Li LL, Gao Y, Liu N, Cheng LS (2024) Expressing the spatial concepts of interior spaces in residential buildings of Huizhou, China: Narrative methods of wood-carving imagery. Buildings 14(5):1414
Güzelci O, Alaçam S, Bekiroğlu B, Karadağ İ (2024) A machine learning-based prediction model for architectural heritage: The case of domed Sinan mosques. Digital Appl Archaeol Cultural Herit 35:e00370
Hou JW, Zhou J, He YH, Hou B, Li J (2024) Automatic reconstruction of semantic façade model of architectural heritage. Herit Sci 12(1):400
Hu ZX (2023) Visual art evaluation methods in future digital works: From virtual reality to metaverse. J Intell Fuzzy Syst 45(2):2347–2365
Huo WW, Li RY, Zhu ZD (2025) Developing a program for quantification and characterization of microstructure: Application to BSE images of geopolymer recycled concrete. J Build Eng 104:112290
Hwang C, Yoon K (1981) Methods for multiple attribute decision making. Lect Notes Econ Math Syst 186:58–191
Jing LT, Shun H, Ma JF, Xie J, Zhou HC, Gao F, Jiang SF (2021) Conceptual design evaluation considering the ambiguity semantic variables fusion with conflict beliefs: An integrated Dempster-Shafer evidence theory and intuitionistic fuzzy -VIKOR. Adv Eng Inform 50:101426
Kang XH, Zhao ZT (2025) Optimal design of ceramic form combining stable diffusion model and GRU-Attention. Adv Eng Inform 64:103062
Karadag I (2023) Machine learning for conservation of architectural heritage. Open house Int-Sustain Smart Architect Urban Stud 48(1):23–37
Ke AH, Huang YJ, Yang J, Cai B (2024) Text-guided image-to-sketch diffusion models. Knowl-Based Syst 304:112441
Kurucay E, Ediz Ö (2025) Mimaride görsel karmaşıklığın hesaplamalı analizi: Şehzade Camii, Süleymaniye Camii ve Selimiye Camii. Gazi Üniversitesi Mühendislik Mimarlık Fakültesi Derg 40(3):1495–1508
Li Q (2016) Application of Traditional Woo dcarving Art in Modern Interior Design. Packaging Eng 37(12):41–44
Li R, Chau K, Zeng F (2019) Ranking of risks for existing and new building works. Sustainability 11(10):2863
Li WC, Xie Q, Shi WW, Lin HP, He JX, Ao JH (2024) Cultural rituality and heritage revitalization values of ancestral temple architecture painting art from the perspective of relational sociology theory. Herit Sci 12(1):340
Liu PD, Qin XY (2018) An extended VIKOR method for decision making problem with interval-valued linguistic intuitionistic fuzzy numbers based on entropy. Informatica 28(4):665–685
Lungu A, Androne A, Gurau L, Racasan S, Cosereanu C (2021) Textile heritage motifs to decorative furniture surfaces. Transpose process and analysis. J Cultural Herit 52:192–201
Mamat N, Othman MF, Abdoulghafor R, Belhaouari SB, Mamat N, Hussein SFN (2022) Advanced technology in agriculture industry by implementing image annotation technique and deep learning approach: A review. Agriculture-basel 12(7):1033
Mao JJ, Yao DB, Wang CC (2013) A novel cross-entropy and entropy measures of IFSs and their applications. Knowl-based Syst 48:37–45
Narayanamoorthy S, Geetha S, Rakkiyappan R, Joo YH (2019) Interval-valued intuitionistic hesitant fuzzy entropy based VIKOR method for industrial robots selection. Expert Syst Appl 121:28–37
Opricovic S (2011) Fuzzy VIKOR with an application to water resources planning. Expert Syst Appl 38(10):12983–12990
Pang Y (2014) Analysis of aesthetic characteristics of woodcarving decoration in Anhui Zhicheng Hall. Gd Stage 10:79–80
Saaty TL (1986) Axiomatic foundation of the analytic hierarchy process. Manag Sci 32(7):841–855
Saka AB, Oyedele LO, Akanbi LA, Ganiyu SA, Chan DMM, Bello SA (2023) Conversational artificial intelligence in the AEC industry: A review of present status. challenges and opportunities. Adv Eng Inform 55:101869
Shi Y (2023) Literal translation extraction and free translation change design of Leizhou ancient residential buildings based on artificial intelligence and Internet of Things. Sustain Energy Technol Assess 56:103092
Smidovnik T, Groselj P (2023) Solution for convergence problem in DEMATEL Method: DEMATEL of finite sum of influences. Symmetry-basel 15(7):1357
Sohl-Dickstein J, Weiss EA, Maheswaranathan N, Ganguli SD (2015) Unsupervised learning using nonequilibrium thermodynamics. Int Conf Mach Learn 37:2256–2265
Villani V, Picone M, Mamei M, Sabattini L (2025) A digital twin driven human-centric ecosystem for industry 5.0. IEEE Trans Autom Sci Eng 22:11291–11303
Wang DY, Chong M, Sun SW (2023) Novel paintings from the latent diffusion model through transfer learning. Appl Sci 13(18):10379
Wang TX, Yang L, Liu L (2024) Integrating GRA with intuitionistic fuzzy VIKOR model to explore attractive design solution of wickerwork cultural and creative products. J Eng Des 36(1):52–86
Wang YY, Agkathidis A, Crompton A (2020) Parametrising historical Chinese courtyard-dwellings: An algorithmic design framework for the digital representation of Siheyuan iterations based on traditional design principles. Front Architect Res 009(4):751–773
Wang Z, Fu C, Niu SF, Hu SJ (2024) Research on Bio-inspired product design based on knowledge graph and semantic fusion diffusion model. Adv Eng Inform 62:102797
Wang Z, Pan HR, Li JS, Niu SF (2024) Exploring product rendering generation design catering to multi-emotional needs through the Superiority Chart-Entropy Weight method and Stable Diffusion model. Adv Eng Inform 62:102809
Wu Y, Kyungsun K (2024) Automatic generation of traditional patterns and aesthetic quality evaluation technology. Inf Technol Manag 25(2):125–143
Xu YD, Nazir S (2024) Ranking the art design and applications of artificial intelligence and machine learning. J Softw-evolution process 36(2):e2486
Yang J (2013) Confucian interpretation of Huizhou style wood carving pattern design. One Hundred Artists 29:238–240
Yang R, Ota K, Dong MX, Wu XJ (2025) Semantic layout-guided diffusion model for high-fidelity image synthesis in ‘The Thousand Li of Rivers and Mountains’. Expert Syst Appl 263:125645
Yang S, Li K, Wu SL, Xu ZT, Liu TY (2022) Quality evaluation of wasteless mining in Dongguashan Based on Intuitionistic Fuzzy Set and VIKOR. Appl Sci 12(16):8249–8249
Yang WG, Wu YJ (2020) A new improvement method to avoid rank reversal in VIKOR. IEEE Access 8:21261–21271
Yardimci Y, Kurucay E (2024) LCA-TOPSIS integration for minimizing material waste in the construction sector: A BIM-based decision-making. Buildings 14(12):3919
Yi QH, Chen XF, Zhang CW, Zhou ZH, Zhu LA, Kong XJ (2024) Diffusion models in text generation: a survey. PeerJ Comput Sci 10:1905
Zadeh LA (1990) fuzzy-sets and systems. Int J Gen Syst 17(2-3):129–138
Zeng HL, Li RYM, Zeng LY (2022) Evaluating green supply chain performance based on ESG and financial indicators. Front Environ Sci 10:982828
Zhang B, Chen P, Deng LJ, Romainoor NH, Han JH, Luo GS, Gao TB (2023) Can AI-generated art stimulate the sustainability of intangible cultural heritage? A quantitative research on cultural and creative products of New Year Prints generated by AI. Heliyon 9(10):e20477
Zhao JS, You XY, Liu HC, Wu SM (2017) An extended VIKOR method using intuitionistic fuzzy sets and combination weights for supplier selection. Symmetry-Basel 9(9):169
Zhao SD, Guo HB, Wang YW (2015) Ecological environment and traditional craft: Taking Huizhou three carvings as an example. Anthropologist 21(1-2):80–88
Zheng Y, Jiao JN, Ye FG, Zhou YL, Li W (2024) Fast style transfer for ethnic patterns innovation. Expert Syst Appl 249:123627
Zhou YQ, Liu Y, Shao YX, Chen JM (2025) Fine-tuning diffusion model to generate new kite designs for the revitalization and innovation of intangible cultural heritage. Sci Rep. 15(1):7519
Acknowledgements
This study was funded by the National Natural Science Foundation of China (62206118), Jiangxi Province Humanities and Social Science Research Projects of Universities (JC24210), Jiangxi Province Degree and Graduate Education Teaching Reform Project (JXYJG-2024-008). Nanchang University Youth Talent Cultivation Innovation Fund Project (XX202506030027).
Author information
Authors and Affiliations
Contributions
XK: writing-review and editing, supervision, project administration and funding acquisition. JW: conceptualization, formal analysis and methodology, writing-original draft preparation, writing-review and editing. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This study was approved by the Ethics Committee of Nanchang University (approval number: NCUYG202401; date of approval: January 5, 2025) and was conducted in accordance with the Declaration of Helsinki and relevant ethical guidelines. Written informed consent was obtained from all participants after explaining the study’s purpose, procedures, and potential risks. All personal data collected was anonymized and kept strictly confidential, and was used solely for academic research without causing any adverse impact on the participants.
Informed consent
Informed consent was obtained from all participants and/or their legal guardians. Consent was secured between 12 January 2025 and 6 February 2025, before any data were collected. Each prospective participant (and, where applicable, their legal guardian) received a written information sheet outlining the study’s purpose, procedures, potential risks and benefits, confidentiality safeguards, and the voluntary nature of participation. After an opportunity to ask questions, respondents signed a paper consent form in the presence of a trained research assistant. The consent covered (i) participation in the study, (ii) the use of de-identified data for academic research, and (iii) the publication of anonymised results. Participants were assured that their responses would remain confidential and be reported only in aggregate form.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kang, X., Wang, J. Design optimization of wood-carved window grilles in historical architectures using stable diffusion model and intuitionistic Fuzzy VIKOR. Humanit Soc Sci Commun 12, 972 (2025). https://doi.org/10.1057/s41599-025-05388-5
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1057/s41599-025-05388-5