Introduction

According to the 2008/2009 State of the World’s Cities report, coastal cities account for approximately 65% of all cities worldwide (UN-HABITAT, 2008). With the rapid development of the marine economy, land use in coastal urban areas has exhibited significant boundary and spatial complexity (Eger and Courtenay, 2021; Verbavatz and Barthelemy, 2020; Wang et al., 2024). The spatial complexity of coastal land use evolves due to changes in coastal populations and economic sectors (Bettencour, 2013; Frolking et al., 2013). Coastal settlements are gathering places for human habitation and production as well as activities that have formed the coastal areas. Coastal settlements are the basic units of a coastal city where people interact with the marine environment (Chen et al., 2025). They are spatially interrelated and interdependent at the economic and social levels, and they constitute a complex system with a hierarchical structure and spatial connections. Therefore, understanding the land-use complexity of the spatial form of coastal settlements has important theoretical and practical significance for sustainable development.

Fractal theory offers a powerful tool to quantitatively describe the complexity of spatial forms in coastal cities. Mandelbrot (1983) proposed fractal theory to explore the length of the coastline of the United Kingdom. Batty and Longley (1994) used fractal dimensions to analyse the land use of the city of Swindon in the UK. Patuano and Lima (2021) examined the fractal dimension of Islamic and Persian fourfold gardens and emphasized their spatial layout and geometric complexity, which can inform the design of environmentally just and meaningful urban spaces. Shen (2002) calculated the fractal dimension to measure urban spatial growth in the United States. Chen (2013) calculated the fractal dimensions of urban forms and boundaries and determined the scaling laws in urban systems. Martínez et al. (2023) studied the fractal characteristics of the Chilean urban network and explored the application of fractal geometry to describe the morphology and organization of cities in developing countries. Lu et al. (2023) used fractal analysis to explore the patterns of heterogeneity at different spatial scales in cities and revealed patterns and trends of urban expansion. Song and Yu (2019) explored the application of multifractal analysis to understand the spatial variation in urban land use in Beijing, which provided valuable insights for urban planners. To bridge the gap between technical analysts and applied planners, Jahanmiri and Parkers (2022) reviewed the application of fractal geometry in urban planning. These studies suggest that fractal analysis of urban spatial forms may reveal the complexity of cities.

Coastal settlements, as the core sites for economic activities and population agglomeration in coastal urban areas, produce complex land use patterns. Recent studies have shown that the renewal of human habitats should prioritize balance among humans, the natural environment, and the social environment with a focus on resilience (Kurniawati et al., 2021) and adaptability (Fouad and Sati, 2021). Fractal theory has also been used to describe the dynamic spatial evolution of settlements. Yu and Zhao (2022) compared the fractal dimensions of three settlements and identified the distinct characteristics of their evolution. Jenerowicz et al. (2019) applied the multifractal method to predict the development of settlement spaces. A coastal city can produce a spatial pattern that includes numerous settlements. However, it remains unclear whether fractal analysis of the larger-scale and static characteristics of city space or urban patterns is suitable for analysing the small-scale and dynamic characteristics of coastal settlement land use. Additionally, the influence of socioeconomic variables such as the regional gross domestic product (GDP) and population on settlement land use has not been explored. Given the influence of highly dynamic socioeconomic factors, an examination of changes to the spatial complexity of settlements is urgently needed (Zhong, 2025).

The research questions of this study are whether fractal analysis is applicable to quantify the complex spatial patterns of coastal settlements and how socioeconomic factors influence the fractal characteristics of settlement land use. We apply the fractal analysis method to investigate the fractal characteristics of coastal settlement land use in Xiamen City, China. We calculate the fractal dimensions of typical geometries (such as circles and Koch snowflakes) and coastlines (such as the British coastline and the Norwegian coastline) to verify the numerical accuracy. Furthermore, we compare the fractal characteristics of the settlements of Inside Xiamen Island and Outside Xiamen Island and investigate the effects of socioeconomic variables on the fractal dimension. Nonlinear modeling is employed to describe the evolution of the fractal dimension for the settlement land use of Inside Xiamen Island and Outside Xiamen Island from 2003 to 2019, and the relationship between GDP and the permanent population is derived using the fractal dimension. The contribution of this study is to quantitatively reveal the fractal evolution of coastal settlements with regard to socioeconomic factors. This research presents an empirical study that applies fractal theory to analyse the morphology of coastal settlements and provides new perspectives and methods for sustainable development in settlement land management. This study presents several innovations that highlight its academic value and practical impact: (1) it explores the correlation between socioeconomic variables (such as GDP and permanent population) and the fractal dimension of coastal settlements and offers new theoretical insights and practical guidance for coastal settlement land use, and (2) it quantitatively reveals the small-scale and dynamic characteristics of fractal settlements to provide decision-making support for spatial planning and resource allocation in coastal settlements.

Materials and methods

Land use of the studied coastal settlement patterns

Xiamen City, located in China’s Fujian Province, is a typical coastal region with a highly concentrated population and a well-developed economy (See Fig. 1). After 2003, Xiamen City transitioned from an “island-type” to a “bay-type” urban spatial structure. Xiamen City is based on the island and has developed in the mainland around the western sea area, as shown in Fig. 2a. Xiamen City can be geographically divided into two regions: the island area, Inside Xiamen Island, and the off-island area, Outside Xiamen Island. Inside Xiamen Island and Outside Xiamen Island do not represent specific administrative regions. The boundary Inside Xiamen Island represents the boundary of the island area, whereas the boundary of Outside Xiamen Island represents the boundary of all areas of Xiamen City except Inside Xiamen Island, that is, the off-island areas. Inside Xiamen Island covers an area of 158 square kilometers and has been highly urbanized, while Outside Xiamen Island covers an area of 1542 square kilometers and has not yet been fully developed. Thirty-three coastal settlements were included in this study. The settlement information is presented in Table 1 of the Appendix.

Fig. 1
figure 1

The area delineated by the red border is the administrative area of Xiamen City, the brown area is Outside Xiamen Island, and the yellow area is Inside Xiamen Island.

Full size image
Fig. 2: Location and settlement patterns of Xiamen Island.
figure 2

a Location of Xiamen Island in Xiamen City; b-f Settlement patterns of Inside Xiamen Island and Outside Xiamen Island in 2003, 2009, 2012, 2015, and 2019.

Full size image

The data in this study include building outlines and AutoCAD maps of the settlements in Xiamen City in 2003, 2009, 2012, 2015 and 2019 provided by the Xiamen Geographic Information Centre. This study applied remote sensing image data (Lin et al., 2020) for Xiamen City from the Landsat 2/3 multispectral scanner (MSS), Landsat 5 thematic imager (TM), and Landsat 8 operational land imager (OLI) with spatial resolutions of 60 m (MSS), 30 m (TM nonthermal infrared band), 120 m (TM thermal infrared band), and 15–30 m (OLI), respectively. All images were geometrically and radiometrically corrected, and the WGS 1984 coordinate system was used to ensure the accuracy of the overlays and the consistency of the analysis of the spatial data (Lin et al., 2020). All data were downloaded from the National Geospatial Data Cloud Platform (http://www.gscloud.cn/). Additionally, we applied building outlines and CAD drawings with a spatial resolution of 30 m for settlement boundaries (Yu and Zhao, 2022). Field surveys were conducted on these settlements, and the AutoCAD maps were revised on the basis of the survey results. To extract the land-use patterns of the settlements from 2003 to 2019, building outlines were derived and the land area was filled in the maps. We removed the small-scale noise region and the large-scale saturation region to calculate the fractal dimension of a settlement. The spatial resolution of 30 m ensures that the scale invariant features of fractal dimension are prominent. In fact, between the noise region and the saturation region, the spatial resolution has a limited impact on the calculation of the fractal dimension in this study. Figure 2b–f show that the settlement boundaries exhibit irregular features.

Furthermore, we utilized industrial economic and demographic data provided by the Xiamen Municipal Bureau of Statistics to construct a model for the evolution of the fractal dimension of coastal settlements in Xiamen City. GDP is an important indicator of economic scale. In the process of urbanization, GDP reflects the economic development of coastal settlements and affects the spatial complexity of land use. To investigate the impacts of industrial structure, we use the primary industry, the secondary industry, and the tertiary industry. Furthermore, the permanent population is a key factor in the social structure. An increase in the population of coastal settlements leads to changes in housing, land use, and public services and results in high-density and saturated spatial forms. During the study period of this paper, data were collected on the GDP and permanent population. Therefore, GDP and population data were used for fractal dimension modeling, and other socioeconomic variables were not considered.

Fractal dimension

Fractal theory provides an important tool for quantifying the complex characteristics of spatial regions (Mandelbrot, 1983; Batty and Longley, 1994; Shen, 2002; Jevric and Romanovich, 2016; Batty, 1995). In fractal geometry, complex objects are fractal, whereas in Euclidean geometry, points, lines, surfaces, and cubes are zero-dimensional, one-dimensional, two-dimensional, and three-dimensional, respectively. To quantify the dimension D of a spatial object, r represents the scale and N represents the number of scales to satisfy the following formula:

Taking logarithms on both sides of Eq. (1), we have (Batty and Longley, 1994)

In Euclidean geometry, D is an integer value. For a line with

$$N={r}^{-D}$$
(1)

D = 1, if a line segment of unit length is divided into N = 3 equal segments, then the length of each line segment is r = 1/3.

$$D=\frac{\log N}{\log (1/r)}$$
(2)

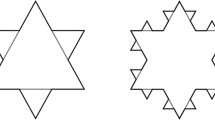
Similarly, for a square with D = 2, if a square of the unit area is divided into N = 9 equal squares, then the side length of each square is r = 1/3. However, for fractal geometry, D calculated by Eq. (2) is not an integer. As shown in Fig. 3a, the Koch curve fractal can be iteratively generated as follows: first, a line segment of unit length r = 1 is divided into three equal segments, the middle segment is removed, and the two line segments are connected with an equilateral triangle without the baseline, and then 41 line segments are generated, each with a length of r = 1/3. By applying the above operation to each line segment, 42 line segments are generated, each with a length of r = (1/3)2. This iteration process continues until the Koch curve is generated. In the N-th iteration, the length of each line segment is r = (1/3)N and the number of line segments is 4 N. By substituting these values into Eq. (2), we theoretically derive the fractal dimension of the Koch curve as D = (log4/log3 ≈ 1.258). Although the length (4/3)N of the Koch curve clearly increases with N, its dimension D is a noninteger value between 1 and 2.

Fig. 3: Koch fractal curve and corresponding dimensions.
figure 3

a The 1st, 2nd, and 5th iterations of the Koch fractal curve; b the corresponding dimensions.

Full size image

On the basis of fractal theory, for the geometry in a digital map, we apply the box-counting method to calculate the fractal dimension. This method has been widely used in urban fractal studies because of its simplicity and effectiveness (Encarnação et al., 2012; Purevtseren et al., 2018; Alam, 2018). First, the image is covered by a series of square boxes with side length r. The number N of square boxes that intersect with the geometry is recorded. Furthermore, the box length r is changed to obtain the box number N. Finally, a series of points (log(1/r), log N) are plotted, and least squares linear regression is used to fit (log(1/r), log N) to calculate the slope. When r is sufficiently large in the saturation region, N is 1 and the slope of the curve (log1/r, log N) is zero. Therefore, the box-counting method cannot obtain the fractal dimension D within this saturation region. However, a scale-free region exists in which the slope approaches D. Therefore, we calculate the fractal dimension of a geometry in the scale-free region. Figure 3b shows the corresponding curves (log(1/r), log(N)) of the geometries in Fig. 3a. For the regular lines, the dimensions are estimated as 1 (R2 = 0.999), indicating their nonfractal characteristics. However, for the Koch curve, the calculated dimension approaches 1.25 (R2 = 0.999), indicating its fractal characteristics.

To verify the accuracy of the box-counting method, we calculate the dimensions of typical geometries (such as circles and Koch snowflakes) and coastlines (such as the British coastline and the Norwegian coastline), as presented in Table 1. The geometry with a higher fractal dimension becomes more irregular and tortuous. For the regular circle, the estimated dimension is 1.002 (R2 = 0.999), whereas for the Koch snowflake, the estimated dimension is 1.258 (R2 = 0.999). Compared with the theoretical solution D = ln4/ln3 of the Koch snowflake, the calculated dimension of the box-counting method has only approximately 0.3% error. Thus, for both classical fractals and coastlines, the errors in dimension estimation are less than 2%, indicating the reliability of the fractal dimension algorithm in this study.

Table 1 Comparison of the literature dimension data with the calculated dimension result by the box-counting method.
Full size table

Modeling equation of the fractal dimension

For coastal settlement patterns, the variation in spatial complexity in relation to variables such as time, GDP, and population can be described by the modeling equation of the fractal dimension. Using the box-counting method, we can obtain a series of dimension data for variable k. The modeling equation of the fractal dimension is given

as follows:

$$D\text{'}(k)=F({\boldsymbol{\mu }},k)$$
(3)

where \({D}^{{\prime} }(k)\) is the fitted fractal dimension, k is the model variable (i.e., year), \(F(\bullet )\) represents the modeling equation, and \({\boldsymbol{\mu }}\) is the coefficient vector. We use \(F\left(\bullet \right)\) as a nonlinear quadratic function. On the basis of \({D}_{k}\), the nonlinear least squares algorithm can be used to determine \(F(\bullet )\) (Encarnação et al., 2012). The fitting error between the k-th fractal dimension and the fitting function is

$${e}_{k}={D}_{k}-F({\boldsymbol{\mu }},k)$$
(4)

According to the least squares principle (Zhang et al., 2011), the objective function is constructed as

$${\rm{Q}}=\mathop{\sum }\limits_{k=1}^{M}{e}_{k}^{2}=\mathop{\sum }\limits_{k=1}^{M}{[{D}_{k}-F({\boldsymbol{\mu }},k)]}^{2}$$
(5)

where Q is the total error for all fractal dimension values. The optimization estimation of \(\mu\) should make the objective function in Eq. (5) take a minimum value; that is, the modeling function \(F\left(\bullet \right)\) with coefficient \(\mu\) is fitted using the Gauss‒Newton iterative method (Yu and Zhang, 2013; Zhang et al., 2011) as follows:

$$\frac{\partial Q}{\partial {\boldsymbol{\mu }}}=0$$
(6)

The goodness of fit, R2, is used to evaluate the performance of the fit. The closer R2 is to 1, the better the fit of the nonlinear function is. We thus can obtain a proper function to model the fractal dimension of coastal land use patterns. The modeling equation is necessary to describe the correlation between the fractal dimension and other variables (such as time, GDP, and population).

Considering the variation in model fitting performance between different factors and fractal dimension, this study classifies the applicability of the models based on their R2 values:

When R2 ≥ 0.9, the model demonstrates good fit and can be used for predictive analysis;

When 0.7 ≤ R2 < 0.9, the fit is good, and the model is suitable for trend identification and estimation;

When 0.5 ≤ R2 < 0.7, the model shows relatively low fit and is more appropriate for analyzing structural relationships and exploratory research.

Meanwhile, because of limited data, a high R2 may not imply a causal relationship. An uncertain analysis is therefore included.

For example, by taking time as the variable, we derive a time-based fractal dimension modeling equation (Encarnação et al., 2012). Figure 4a shows the evolution of the Xiamen City boundary across the period from 2003 to 2019. Figure 4b shows the time evolution of the fractal dimensions of the Xiamen City boundary derived from satellite remote sensing images from 1990, 1995, 2000, 2005, 2010, and 2018. The time modeling equation can be derived as follows:

$$\begin{array}{c}D=-77.932+8.0879\times {10}^{-4}\times {\rm{Year}}\\ -2.0642\times {10}^{-5}\times {{\rm{year}}}^{2}({{\rm{R}}}^{2}=0.94)\end{array}$$
(7)
Fig. 4: Temporal evolution of Xiamen City boundary and its fractal dimension.
figure 4

a Time evolution of the Xiamen City boundary from 1990 to 2018; b time evolution of the fractal dimension of the Xiamen City boundary from 1990 to 2018.

Full size image

Like the British and Norwegian coastlines, the boundary of Xiamen City is also fractal. The fractal dimension of the Xiamen City boundary shows a decreasing trend, indicating that this boundary is gradually becoming smoother. This change is associated with the rapid urbanization of Xiamen City over the past thirty years. The complete utilization of land would lead to a nonfractal boundary with D = 1. Therefore, in this study, Dcr = 1 is defined as the critical boundary dimension. Dcr can be regarded as a quantifiable threshold to assess the complexity of land use. According to the annual reduction rate of 0.002 shown in Fig. 4, if the current linear trend persists, the fractal dimension of the Xiamen City boundary is projected to decrease to 1 by the early 22nd century. In terms of fractal theory, it is important to prevent the fractal dimension of the Xiamen City boundary from approaching Dcr. Maintaining the urban boundary above the critical boundary is of great theoretical and practical significance for its sustainable development.

Results

Fractal characteristics of the coastal settlement patterns

Figure 5 shows the curves (log(1/r), log N) of the settlement patterns of Inside Xiamen Island and Outside Xiamen Island in 2009. The result of log N shows the variability in the compactness of the settlement land uses at different scales of r. A significant change in log N leads to a sufficiently uneven land-use pattern. The settlement land uses of Inside Xiamen Island and Outside Xiamen Island show different distribution characteristics across the scaling regions. The log N curve of Inside Xiamen Island is less uniform, especially at smaller values of r. However, the log N of the land use of Outside Xiamen Island is more stable and shows good consistency in the entire scaling region. Because of high housing demand and spatial constraints, land use may become more homogeneous, resulting in lower fractal dimensions. During the early stage of development in Xiamen City, land use at a low scale of r, such as building construction and commercial district development, was mainly concentrated on Inside Xiamen Island. As coastal development extended to Outside Xiamen Island, land use in these larger regions was evenly distributed across various scales. The land-use patterns show power-law signatures, suggesting self-similarity. Linear correlations between log1/r and log N are found (R2 > 0.9) for the settlement land uses of both Inside Xiamen Island and Outside Xiamen Island. The fractal dimensions of the slopes of the scaling regions are calculated at 1.19 and 1.26, respectively, indicating the fractal properties of the settlement patterns of Inside Xiamen Island and Outside Xiamen Island. Therefore, the fractal dimension effectively describes the land-use complexity of the Xiamen settlements.

Fig. 5
figure 5

Comparison of fractal dimensions of the settlement patterns of Inside Xiamen Island and Outside Xiamen Island in 2009.

Full size image

The fractal dimensions of the settlements of Inside Xiamen Island and Outside Xiamen Island are sparse within the scale of (4.3 < log r < 4.9). This scale of r corresponds to the overall scale of settlements and reflects the degree of continuity of coastal settlement land use. In recent years, excessive demolition and land-use homogenization at this spatial scale have contributed to the scarcity of data. Therefore, urban planners should conduct comprehensive surveys, protect settlements at all scales, and avoid excessive demolition and construction. Xiamen City is undergoing intensive development. The fractal dimension may serve as a quantitative parameter to achieve the multiscale design and utilization of coastal settlement land use.

Fractal modeling equations of coastal settlement patterns

Figure 6 shows the time evolution for the fractal dimension of the settlements of Inside Xiamen Island and Outside Xiamen Island from 2003 to 2019. The growth trends of the fractal dimensions of Inside Xiamen Island differ significantly from those of Outside Xiamen Island. Over this 16-year period, the fractal dimension of coastal settlements of Inside Xiamen Island decreased by approximately 0.13, whereas the fractal dimension of Outside Xiamen Island decreased by approximately 0.06. This finding indicates that shoreline degradation had a substantial impact on the fractal characteristics of settlement land use in both regions. Compared with 2005, the fractal dimension of Inside Xiamen Island in 2018 decreased significantly. This is because the high degree of urbanization of Inside Xiamen Island makes the coastline smoother, which causes the fractal dimension to approach 1. The intensity of the development of Inside Xiamen Island was much greater than that of Outside Xiamen Island, leading to an accelerated decrease in the fractal dimension. Therefore, the imbalance in the distribution of coastal settlement spaces in Xiamen City affects the time evolution of the fractal dimension.

Fig. 6
figure 6

Time evolution of the fractal dimension of the settlements of Inside Xiamen Island and Outside Xiamen Island from 2003 to 2018.

Full size image

Furthermore, nonlinear modeling equations reveal that their fractal dimensions have the following nonlinear functional relationship with time:

Inside Xiamen Island:

$$\begin{array}{c}D=-2414.9+2.4119\times {\rm{Year}}\\ -6.0193\times {10}^{-4}\times {{\rm{Year}}}^{2}({{\rm{R}}}^{2}=0.75)\end{array}$$
(8)

Outside Xiamen Island:

$$\begin{array}{c}D=-2267.0+2.2602\times {\rm{Year}}\\ -5.6306\times {10}^{-4}\times {{\rm{Year}}}^{2}({{\rm{R}}}^{2}=0.77)\end{array}$$
(9)

Clearly, the fractal dimensions of Inside Xiamen Island and Outside Xiamen Island exhibit nonlinear evolutionary trends. These time-based modeling equations suggest that the development potential of Outside Xiamen Island may be greater than that of Inside Xiamen Island, which aligns with the observed urban expansion of Xiamen City. In recent years, the rapid development of Outside Xiamen Island has been actively promoted through cross-island development strategies and infrastructure enhancement. For Inside Xiamen Island, the model estimates a fractal dimension value of 0.9928 for 2021. The 75% confidence interval is [0.9109, 1.0748], indicating a 75% probability that the predicted value falls within this range. The residual standard deviation is 0.0237. For Outside Xiamen Island, the model estimates a fractal dimension value of 0.9981 for 2028 with a 75% confidence interval of [0.8767, 1.1195]. The residual standard deviation is 0.0138.

Figure 7 shows the relationship between GDP and the permanent population with the fractal dimension of Inside Xiamen Island and Outside Xiamen Island from 2003 to 2019. Their correlation functions can be derived as follows:

Fig. 7: Relationships between fractal dimension and socioeconomic factors in Xiamen.
figure 7

a The relationship between GDP and the fractal dimension of the settlements of Inside Xiamen Island and Outside Xia-men Island from 2003 to 2019; b The relationship between the permanent population and the fractal dimension of the settlements of Inside Xiamen Island and Outside Xiamen Island.

Full size image

Inside Xiamen Island:

$$\begin{array}{c}D=1.2037-2.8275\times {10}^{-5}\times {\rm{GDP}}\\ ({{\rm{R}}}^{2}=0.85)\end{array}$$
(10)
$$\begin{array}{c}D=1.32133-5.4043\times {10}^{-4}\\ \times {\rm{Permament}}\,{\rm{population}}({{\rm{R}}}^{2}=0.71)\end{array}$$
(11)

Outside Xiamen Island:

$$\begin{array}{c}D=1.2593-1.4619\times {10}^{-5}\times {\rm{GDP}}\\ ({{\rm{R}}}^{2}=0.71)\end{array}$$
(12)
$$\begin{array}{c}D=1.3158-2.6766\times {10}^{-4}\\ \times {\rm{Permanent}}\,{\rm{population}}({{\rm{R}}}^{2}=0.50)\end{array}$$
(13)

In Fig. 7a, the decrease in the fractal dimension of Inside Xiamen Island is more pronounced than that of Outside Xiamen Island. For Inside Xiamen Island, the prediction model yields a GDP value of 712.71 billion yuan at D = 1. The 75% confidence interval is [607.60, 896.89] billion yuan, indicating a 75% probability that the GDP value falls within this range. The residual standard deviation is 0.0180, whereas the critical value is 1. Furthermore, for Outside Xiamen Island, the prediction model yields a GDP value of 1751.75 billion yuan at D = 1 with a 75% confidence interval of [1301.30, 2902.90] billion yuan. The residual standard deviation is 0.0235 compared with the critical value of 1. These results suggest that Outside Xiamen Island has greater potential for future economic development. Although the R2 value is relatively low for this group, the model still reveals a meaningful exploratory trend.

In Fig. 7b, the fractal dimensions inside Xiamen Island and Outside Xiamen Island both decrease with an increase in the permanent population. For Inside Xiamen Island, the prediction model estimates a population of 588.39 × 10⁴ persons at D = 1. The 75% confidence interval is [514.11, 764.96] × 10⁴ persons. The residual standard deviation is 0.0329 compared with the critical value of 1. For Outside Xiamen Island, the prediction model estimates a population of 1166.97 × 10⁴ at D = 1. The 75% confidence interval is [854.25, 2542.64] × 10⁴ persons, and the residual standard deviation is 0.0238. This suggests that the population density of Inside Xiamen Island has approached saturation. To relocate the population of Outside Xiamen Island, city planning should improve the quality of life in these areas, such as by improving infrastructure and educational resources.

Similarly, we obtain the relationships between the three industries with fractal dimensions in Fig. 8. The fractal dimensions Inside Xiamen Island and Outside Xiamen Island exhibit a certain linear relationship with the three major industries. The primary industry has a weaker influence with poorer fitting performance, which is likely due to its relatively small share in the total GDP composition. however, the secondary and tertiary industries show more significant results, with a more significantly negative correlation with the fractal dimension Inside Xiamen Island and Outside Xiamen Island. In Fig. 8a, for Inside Xiamen Island, the prediction model estimates the primary industry of 2.69 billion yuan at D = 1. The 75% confidence interval is [2.04, 4.76] billion yuan. The residual standard deviation is 0.0329. For outside Xiamen Island, the prediction model estimates the primary industry of 47.09 billion yuan at D = 1. The 75% confidence interval is [35.40, 151.17] billion yuan, and the residual standard deviation is 0.0398. In Fig. 8b, for Inside Xiamen Island, the prediction model estimates a secondary industry of 1025.23 billion yuan at D = 1. The 75% confidence interval is [893.70, 1257.66] billion yuan. The residual standard deviation is 0.0239. For outside Xiamen Island, the prediction model estimates the primary industry of 5165.17 billion yuan at D = 1. The 75% confidence interval is [3819.82, 8738.74] billion yuan, and the residual standard deviation is 0.0188. In Fig. 8c, for Island Xiamen Island, the prediction model estimates a tertiary industry of 2826.83 billion yuan at D = 1. The 75% confidence interval is [2378.38, 3651.65] billion yuan, and the residual standard deviation is 0.0254. For outside Xiamen Island, the prediction model estimates the tertiary industry of 3243.24 billion yuan at D = 1. The 75% confidence interval is [2418.42, 5245.25] billion yuan, and the residual standard deviation is 0.0177. The estimated fractal dimensions show only slight deviations from the critical value of 1, indicating a stable pattern in spatial complexity. These results reflect coherent trends revealed by the model with limited variation. The findings suggest that the urban development strategy of Xiamen should not be limited to the tertiary industry. More efforts should be made to develop secondary industry Outside Xiamen Island. In particular, fostering high-tech industries could act as catalysts for economic development.

Fig. 8: The relationship between the fractal dimension and the in-dustrial structure of the settlements of Inside Xiamen Island and Outside Xiamen Island from 2003 to 2019.
figure 8

a Primary industry; b secondary industry; c tertiary industry.

Full size image

Discussion

In this study, the fractal dimensions of coastal settlements in Xiamen City were found to be between 1.1 and 1.3. This is similar to the fractal dimensions of coastlines in the UK, France, and Africa (Mandelbrot, 1983; Batty and Longley, 1994; Shen, 2002). Jiang and Liu (2012) reported that the fractal dimension of the Atlantic coast was much greater than that of the Pacific coast due to the complexity of the coastline. On the basis of remote sensing data, Ye et al. (2009) calculated the fractal dimension of the shorelines of Jiaozhou Bay and reported that the main factors that drove the change in the fractal dimension of the shorelines were the construction of aquaculture farms, reclamation, and port construction. The fractal dimensions of Xiamen’s coastal settlements are lower than those of some inland settlements, such as the Tea Horse Ancient Road (Gao, 2017) and traditional settlements of Houlinhe Village in Wu’an. A lower fractal dimension may be associated with overdevelopment. Compared with inland settlements, the morphology of coastal settlements is influenced significantly by marine activities, which provides a new perspective for understanding the fractal characteristics of urban morphology in different geographical environments. As shown in Fig. 2, due to the coastal location and economic development of Xiamen City, its coastal settlement patterns with complex coastlines are significantly influenced by human maritime activities. Less irregularity in urbanized land means that residents may have limited access to open spaces. In particular, the fractal dimension of Inside Xiamen Island is much lower than that of Outside Xiamen Island, as shown in Fig. 5. Clearly, more land uses were created for Inside Xiamen Island; however, Outside Xiamen Island may have greater potential for exploring land use. The sustainable development of Xiamen City should improve the fractal quality of Inside Xiamen Island, and the land use of Outside Xiamen Island can be further explored from the perspective of urban planning. Similarly, different fractal dimensions have been found in built-up urban and rural areas in Shanghai (Zhao et al., 2021). This finding indicates that the complexity and irregularity of land-use patterns vary significantly across different regions. Urban land management plays an important role in planning land use for sustainable development (Shen, 2002). Therefore, fractal theory provides an effective tool to describe the complex characteristics of land use in coastal settlements.

In addition, the time evolution of the fractal dimension of Inside Xiamen Island and Outside Xiamen Island are qualitatively consistent. The fractal dimension varies with the urban growth context. As shown in Fig. 6, the fractal dimension increases and then decreases, with the turning point occurring in 2009. The fractal dimensions of Inside Xiamen Island and Outside Xiamen Island are highest, with values of 1.19 and 1.26, respectively. In the first stage, due to the influx of migrants, the land-use area of coastal settlements increased, and the construction of urban transportation infrastructure resulted in the division of settlement land uses. Therefore, the complexity of the settlement land uses of Inside Xiamen Island and Outside Xiamen Island both increased, leading to an increase in the fractal dimension. The second stage involved optimization and upgrading of the urban industrial structure and functional layout of the coastal settlements. In particular, there was functional replacement at the periphery of coastal settlement land use areas. Commercial facilities replaced residential spaces, coastal settlement land use became more regular, and some small-scale settlements were demolished. These factors led to significant reductions in the number and complexity of buildings. Therefore, the fractal dimensions of the coastal settlement patterns of Inside Xiamen Island and Outside Xiamen Island decrease annually. This is associated with the profound impact of the optimization of the city’s transportation infrastructure and industrial structure on land use patterns.

In comparison with the Xiamen City boundary shown in Fig. 4, the settlements have much larger annual reduction rates in the fractal dimension. The coastal settlement patterns approach a highly ordered state in a shorter time than the Xiamen city boundary. This is associated with the highly developed coastline in Xiamen City, where the spatial characteristics gradually lose fractal features while the fractal characteristics of the boundaries of cities without coastlines remain relatively stable. The sustainable development of Inside Xiamen Island can significantly reduce the growth rate of the fractal dimension; thus, it is necessary to protect settlement land-use patterns. The fractal dimension of Outside Xiamen Island is much larger. This suggests that the land use of Outside Xiamen Island can further strengthen the utilization of space and improve its vitality to promote the development of the marine economy. In the 2013–2030 plan for Xiamen City, more land use is designated for Outside Xiamen Island. The fractal evidence in this study can reflect the evolution of land-use and urban development in Xiamen City.

Complex socioeconomic factors influence the fractal characteristics of coastal settlements. Previous studies have revealed that the social group size (Zhou et al., 2005), personal income distribution in metropolitan areas (Brelsford et al., 2017), and land price distribution demonstrate the power-law phenomenon (Hu et al., 2013). This phenomenon is shown in Fig. 5. The settlement land-use patterns exhibit fractal forms. Driven by the goal of maximizing economic benefits, settlement spaces are gradually compressed. As shown in Figs. 7 and 8, we correlate socioeconomic factors (GDP, permanent population, primary industry, secondary industry, and tertiary industry) with the fractal dimension of the settlements of Inside Xiamen Island and Outside Xiamen Island. Economic development and permanent population change the spatial morphology and boundary complexity of the coastal settlements, and the decrease in this dimension is subject to the impact of rapid urbanization. It is extremely unfavorable to settlement spaces with deep cultural heritage and distinctive regional characteristics. Good models of fractal dimensions may help planners identify “what-if” intervention scenarios (Batty, 2012; Batty and Milton, 2021). Therefore, understanding the correlation between the fractal dimension of settlement land use and socioeconomic variables will help in determining the main reasons for the reduction in complexity. To improve planning, land use should be balanced with socioeconomic growth to maintain fractal characteristics. This study links the fractal dimension to economic output and population growth and synthesizes the way these factors affect the spatial complexity of coastal settlements, which provides a novel analytical framework for urban spatial planning.

In Eqs. (10)–(13), the critical fractal dimension estimates that Inside Xiamen Island is approaching a GDP of 700 billion yuan and a permanent population of 6 million people. Thus, an intervention into the diversity and complexity of coastal settlement space is necessary. However, Outside Xiamen Island has a significantly larger GDP and population, suggesting its greater potential for land-use optimization and spatial expansion. This understanding may offer more flexibility for future urban planning and development. In response to the relatively low development intensity and abundant land resources in settlements of Outside Xiamen Island, exploration should be increased, and settlement land use should be expanded. This study highlights the guiding significance of fractal science for coastal settlement planning and land management.

As noted in the State of the World’s Cities 2008/2009 report (UN-HABITAT, 2008), approximately 65% of the world’s cities are situated along coastlines. Thus, understanding the land-use complexity of coastal settlements holds both theoretical and practical significance for sustainable development. The application of fractal theory in urban research provides a new perspective for urban planning and land management. Furthermore, strengthening environmental supervision and corporate social responsibility in relation to land-use complexity can improve the environmental, social, and governance performance of settlements, which has implications for urban sustainable development (Gao et al., 2024). The relationship between urban economic development and land use from the perspective of economic activity was previously examined (Zheng et al., 2024). The relationship between GDP and road freight value in different economic sectors provides empirical data to understand how urban economic activities shape the spatial structure. The significance of this study is that it not only presents a new empirical application of fractal theory to analyse urban morphology but also provides new perspectives and methods for settlement land management. By suggesting strategies such as improving the fractal characteristics of Inside Xiamen Island and enhancing the land use of Outside Xiamen Island, this study provides a basis in fractal theory to promote the sustainable development of coastal settlements. This study enriches the theoretical foundation of fractal settlements and provides practical guidance for policy makers in balancing conservation and development in coastal urban areas.

Conclusions

In this work, we investigated the fractal characteristics of coastal settlements in Xiamen City, China. The calculation errors for the fractal dimension of typical geometries (such as circles and Koch snowflakes) and coastlines (such as the British coastline and the Norwegian coastline) were less than 2%, indicating the reliability of the fractal dimension algorithm. The settlement patterns of Inside Xiamen Island and Outside Xiamen Island both exhibited fractal characteristics. The fractal dimension of Inside Xiamen Island was significantly lower than that of Outside Xiamen Island, indicating that the area outside the island has greater potential for land-use development. Furthermore, the fractal dimensions of settlements of Inside Xiamen Island and Outside Xiamen Island had different nonlinear equations over time. From 2009 to 2018, the fractal dimension of Inside Xiamen Island decreased by approximately 0.13, whereas the fractal dimension of Outside Xiamen Island decreased by approximately 0.06, suggesting shoreline degradation and land reclamation in these areas. The critical value D = 1 of the fractal dimension represents the quantifiable threshold for assessing land-use complexity. On the basis of the fitted evolution equation, the fractal dimension of Outside Xiamen Island is projected to decrease to the critical fractal dimension by 2028 if the current trend continues, highlighting the urgent need to protect settlement land use. In addition, the fractal dimensions of the settlements of Inside Xiamen Island and Outside Xiamen Island are negatively correlated with the regional GDP and permanent population. The critical fractal dimension of settlement land use predicts that in comparison with Inside Xiamen Island, Outside Xiamen Island should have a significantly larger GDP, population, primary industry, secondary industry, and tertiary industry, suggesting its greater development potential. In urban planning, the critical fractal dimension can be used as an important quantitative parameter to measure the spatial complexity of settlements. This study lays the groundwork for exploring the fractal mechanism of coastal settlements and optimizing land-use control strategies, which contributes to sustainable development.

This study has several limitations that should be acknowledged. First, although the correlation analysis between the fractal dimension, GDP, and the permanent population provides meaningful insights, the range of socioeconomic indicators used in this study was somewhat limited. Owing to data constraints, key variables such as land prices, industrial structure, and infrastructure investment were not included, which may affect the comprehensiveness of the analysis. Second, the time span of this study was relatively short and may not fully capture longer-term urban development patterns. Third, while this study reveals correlations, due to data limitations, it cannot establish definitive causal relationships. However, the findings provide a valuable reference for urban planning. Finally, although the fractal dimension model helps in understanding the evolution of the complexity of Xiamen City, there are potential risks when the results are extrapolated to other cities or different stages of urban development. Future research should incorporate additional indicators and more data to further explore the causal mechanisms.