Introduction

Widespread application of nitrogen (N) fertilizers, while significantly boosting crop yields, has led to a concurrent increase in N surplus (NS) (Chang et al., 2021; Gerten et al., 2020). When NS returns to the environment through various pathways, including surface runoff into nearby rivers and lakes (Dupas et al., 2018; Yu et al., 2019; Glibert, 2017), subsurface leaching into groundwater (Liu et al., 2010), ammonia volatilization into the atmosphere (Gu et al., 2021), and microbial denitrification releasing N₂O and NOₓ gases (Tian et al., 2020), it can cause a suite of negative consequences, such as eutrophication, groundwater contamination, greenhouse gas emissions and ultimately, water scarcity (Bai et al., 2022; Steffen et al., 2015; Galloway et al., 2008). These impacts highlight the urgent need for effective NS regulation and integrated NS management strategies. Results consistently indicated that NS is generally driven by a combination of natural factors, including climatic conditions (Sun et al., 2021; Ren et al., 2023), soil characteristics (Hansen et al., 2017), and human activities (Bai et al., 2022; Xu et al., 2024; Zhang et al., 2024) such as planting, fertilization, and irrigation. Effective regulation of these human activities seems a promising approach to promoting NS management and its induced water shortage.

On the one hand, improvement on crop structures and planting processes provides direct approaches for mitigating NS (Zhang et al., 2021; Quemada et al., 2020; van Grinsven et al., 2022). On the other hand, economic and financial policies offer indirect means to influence NS by promoting environmentally friendly agricultural practices (Zhang et al., 2015). Economically, the gross domestic product (GDP) has shown its linear or quadratic relations to NS across various countries; however, there is a challenge in the use of GDP as a straightforward tool for effective management (Zhang et al., 2015). Financially, agricultural insurance (AI) could be a viable tool for impacting NS by optimizing planting scales and/or stimulating the adoption of advanced agricultural technologies. AI has demonstrated its performance in improving crop production. For example, AI adoption could notably increase cotton planting acreage by 1.3–1.4 ha, representing a 60% increase, and subsequently elevate cotton output and income by approximately 40% (Elabed and Carter, 2015; Caifei, 2020); this implies that NS could have been simultaneously reduced by the tool of AI, though not yet evidenced.

As the relations between AI and NS and its associated water shortage have never been quantified, one can hardly gain insight into whether and how much AI has significant effects on environmental improvements in addition to agricultural gains. We here attempt to use the data from 333 cities across China to address the following issues: (1) find statistical evidence that AI did have an effect on NS, (2) identify spatially heterogeneous AI effects on NS while considering regional variability, (3) evaluate the AI contribution to impacting the NS-induced water shortage, and (4) establish respectively appropriate AI programs in terms of varied impacts for further promoting NS management.

We first developed an integrated N balance model (INBM) to compute NS values across the cities in China, which would be used as the response variable; the NS data were simultaneously used to compute the water shortage risk that is regarded to be indirectly influenced by AI. We then employed panel regression models under linear assumptions to represent the relation between AI and NS, by selecting AI as the explanatory variable. Because AI can hardly be the exclusive variable explaining NS, we introduced a set of control variables to co-explain the response variable NS. We also constructed different types of panel models by incorporating fixed effects, time trends, and their interactions, aiming to pinpoint the model that best captures the underlying AI effects and demonstrate the robustness of the model. To further illustrate the robustness of the models, we also conducted the following analyses on (1) the impacts of the uncertainty in statistical samples via Monte Carlo (MC) simulation, (2) the temporal heterogeneity effects using time-lagging and within-group stratification regression, (3) the potential endogeneity impacts through instrumental variable (IV) method, and (4) the difference between the AI effects on national-scale NS by panel regression models and those on the urban-scale NS as calculated by time-series-based regression models. Eventually, we utilized retrospective counterfactual analysis to quantify the AI contributions to NS and NS-induced water shortage with and without AI investments. To support this study, a total of 184,815 pieces of data were gathered, validated, and compiled through extensive literature review, expert survey, site investigations, and mathematical modeling for computing NS and NS-induced water shortage risk (NS-IWSR).

Materials and methods

Data collection and treatment

To calculate the NS across Chinese cities, we compiled a comprehensive dataset spanning the years 2006 to 2020. This dataset includes information on crop production (kt), N and compound fertilizers (kt), livestock numbers, crop sowing areas (ha), paddy field areas (km2), dry land areas (km2), precipitation (mm), permanent population, rural population, and per capita energy consumption (million tons of standard coal). To explore the AI (million RMB ¥) effects on NS (kt), we incorporated six control variables into our analysis: primary industry as percentage to gross regional product (PAV-GRP; %), the secondary industry as percentage to GRP (SAV-GRP; %), energy consumption metrics (ECM), cumulative precipitation (CP; mm), temperature (T; °C), and sunlight hours (SH; h). These variables were selected based on the following considerations: (1) they were proven to be substantially effective in statistics to support our regression modeling, (2) multicollinearity tests revealed no collinearity among these variables, (3) adding additional control variables did not enhance model performance and risked over-parameterization, and (4) certain variables were excluded because they served as “bad controls”—i.e., variables that are influenced by the treatment (AI) and, if included, would bias the estimation of causal effects by blocking part of the treatment-outcome pathway (Cinelli et al., 2022; Angrist and Pischke, 2009; Pearl, 2022). To ensure robustness, additional variables, including per capita GDP (RMB ¥), rural population (RP; ten thousand), and cropland area (CA; km2), were considered in within-group stratification regression. Furthermore, the density of internet users (DIU), measured as the DIU, was employed as an IV in separate analyses. DIU serves as a relevant and exogenous predictor of AI: greater internet access facilitates access to agricultural knowledge, digital financial services, and peer learning about insurance benefits, all of which can increase AI adoption. At the same time, DIU is unlikely to directly influence NS, which is largely shaped by agronomic decisions, thereby satisfying the exclusion restriction.

To support this study, we gathered, validated, and compiled a comprehensive dataset consisting of 184,815 entries through an extensive combination of literature reviews, expert surveys, site investigations, and mathematical modeling. Where publicly available data were incomplete, particularly for early years in less-developed cities and certain environmental and agricultural variables such as rural population, cropland area, and N fertilizer application, we employed supplementary methods to fill gaps. Site investigations were used to verify historical crop patterns and fertilizer use in selected provinces. Expert consultations helped estimate livestock densities, sowing areas, and fertilizer conversion ratios for some years when statistical records were missing. Web searches, including local government archives and agricultural bureau websites, provided auxiliary information on weather anomalies, policy events, or missing agricultural statistics. Linear interpolation was used primarily for climate variables (e.g., precipitation, temperature, sunlight hours) and socio-economic indicators (e.g., energy consumption, PAV-GRP) when missing values occurred intermittently between two known data points. To address potential redundancy, we calculated averages or excluded data exhibiting significant anomalies. Detailed descriptions of the datasets, variables, and their sources are presented in Tables S1 and S2. To capture spatial heterogeneity, we grouped all prefecture-level cities into three regions: west, central, and east, based on the standard regional division provided by the Resource and Environmental Science Data Platform (https://www.resdc.cn/data.aspx?DATAID=277). This classification is commonly used in national-scale socio-economic and environmental analyses. A detailed list of cities within each region is provided in Table S3.

Integrated N balance model (INBM)

NS (NS, kt N) is defined as the difference between total N inputs and N outputs. This balance can be expressed as:

$$N{S}_{{{ct}}}=I{{{N}}}_{put,{{ct}}}-{{{OutN}}}_{har,ct}$$
(1)

where INput,ct is the total N inputs (kt N) from various sources in city c (c = 1, 2, …, 333) in year t (t = 2006, 2007, …, 2020); OutNhar,ct is the total N outputs from the harvested crop (kt N) for city c in year t, which is calculated by

$$Out{N}_{har,ct}=\mathop{\sum }\limits_{i=1}^{7}Y_{i,ct}\times n_i$$
(2)

where Yi,ct is the production of crop i (i = 1, 2, … 7, representing rice, wheat, corn, soybean, peanut, rape, and vegetable, respectively) in city c in year t (kt); ni is the N content of each crop i (%), whose values are shown in Tables S4 and S5.

The total N input, INput, can be computed as:

$$I{N}_{put}=I{N}_{fer}+I{N}_{man}+I{N}_{fix}+I{N}_{dep}$$
(3)

where INfer is synthetic fertilizer application (kt N), INman represents animal N manure (kt N), INfix accounts for N fixation (kt N), and INdep corresponds to atmospheric N deposition (kt N). Detailed methodologies for calculating these components are provided in Method S2, with results illustrated in Fig. S1.

Benchmark regression model

Panel analysis

The two-way fixed-effects model was employed to address omitted variable issues, accounting for variables that change over time but vary across cities, as well as those constant across cities but change over time (Shaymal and Emir, 2020). In terms of the panel data gathered as mentioned above, we built regression models by introducing one explanation and six control variables and meanwhile considering fixed effect, time trend, and their combined effects (Tables S6 and S7). The basic model is specified as follows:

$$N{S}_{ct}={\beta }_{i}A{I}_{ct}+\mathop{\sum }\limits_{j=1}^{6}{X}_{ct,j}+{\theta }_{{1}_{i}}trend+{\theta }_{2i}tren{d}^{2}+{u}_{c}+{\varepsilon }_{ct}$$
(4)
$$\mathop{\sum }\limits_{j=1}^{6}{X}_{ct,j}={\alpha }_{i}PA{V}_{ct}+{\chi }_{i}SA{V}_{ct}+{\varphi }_{i}EC{M}_{ct}+{\gamma }_{i}C{P}_{ct}+{\eta }_{i}{T}_{ct}+{\kappa }_{i}S{H}_{ct}$$
(5)

where AIct is the explaining variable representing AI in city c in year t (million RMB ¥); PAVct (%), SAVct (%), ECMct (million tons of standard coal), CPct (mm), Tct (°C), and SHct (hour) are control variables for city c in year t, respectively (Tables S2 and S8), whose spatial distributions are presented in Fig. S2; the gradual changes in individual city’s NS that may be driven by slowly changing factors, such as demographic shifts, trade liberalization, and evolving political institutions, are addressed by the flexible city-specific time trends θ1itrend + θ2itrend2. Here, trend = t–2006 centers the time variable around the base year of the panel, improving numerical stability in estimating city-specific polynomial trends and mitigating multicollinearity between the linear and quadratic terms; uc represents the city-fixed effect at city c, accounting for the time-invariant city-specific characteristics to control for variables that could be evolving over localities (such as resource endowment or political institutions) that might explain differences in individual city’s baseline level of NS; εct represents modeling error for city c in year t; βi, αi, χi, φi, γi, ηi, κi, θ1i, and θ2i (i = 1, 2, 3) are regression coefficients representing the marginal effects owing to each unit change of a variable in east, central, and west regions, respectively.

Here, βi is called the “AI effect”, indicating that each unit variation in AI leads to how much change in NS every year. Models can be solved by the ordinary least squares (OLS) method on the platform of Stata 16.0. The comparisons of NS fitted values calculated by the base model with NS actual values are shown in Fig. S3.

Robustness analysis

To further demonstrate the robustness of our models and pinpoint the reliability of the observed AI effects on NS, we conducted a series of complementary analyses (Methods S3.2–S3.7). First, we constructed alternative panel models by incorporating fixed effects, time trends, and their interactions, identifying the most suitable model specification for capturing AI effects (Method S3.2). Second, we assessed the impact of uncertainty in statistical samples using MC simulations (Method S3.3). Third, temporal heterogeneity effects were examined through models incorporating lagged NS terms and within-group stratification regression (Methods S3.4 and S3.5). Fourth, potential endogeneity concerns were addressed via an IV approach using internet user density as the IV (Method S3.6). Finally, we compared the AI effects on NS derived from national-scale panel regression models with those calculated at the urban scale using time-series-based regression models (Method S3.7). These analyses consistently confirmed the robustness and reliability of our findings.

Impact quantification

NS-induced water shortage level model

NS-induced water shortage level (NS-IWSL) quantifies the degree of NS pollution within a watershed, reflecting the runoff’s capacity to assimilate N loads. It is calculated as:

$$NS-IWSL=\frac{{L}_{c}}{(a-b)\times {R}_{c}}$$
(6)

where a is the ambient water quality standard for N (maximum acceptable concentration, mg/L); b is the natural concentration in the receiving water body (0.1 mg/L) (Franke et al., 2013); Rc is the actual runoff of the hydrological basin (million m3/y) in city c; Lc is the N load to the water body from city c (kt).

To estimate Lc, we adopted the NS approach, subtracting the N removed by harvested crops to better represent the net N input (Muratoglu, 2020). The N load Lc is given by:

$${L}_{c}={\alpha }_{ct}\times N{S}_{ct}$$
(7)

where NSct is the NS in city c in reference year t (2020 in this study); αct is the leaching runoff fraction, calculated by

$${\alpha }_{ct}={\alpha }_{min}+\left[\frac{{\sum }_{k}{S}_{k}\times {W}_{k}}{{\sum }_{k}{W}_{k}}\right]\times ({\alpha }_{max}-{\alpha }_{min})$$
(8)

where αmin and αmax are the minimum and maximum leaching runoff fraction; they were determined to be 0.08 and 0.8, respectively (Franke et al., 2013); S is the score of each influencing factor; W is the weight of each influencing factor (Table S9).

To examine the difference between the NS-IWSL with and without AI effects, we further compute ΔNS-IWSL as follows (Ren et al., 2023; Erhardt et al., 2019):

$$\Delta NS={\beta }_{i}\times A{I}_{ct}$$
(9)
$$\Delta NS-IWSL=\frac{\Delta {L}_{c}}{(a-b)\times {R}_{c}}=\frac{{\alpha }_{ct}\times \Delta NS}{(a-b)\times {R}_{c}}$$
(10)

where AIct is the AI value in the reference year.

NS-induced water shortage risk model

Considering that parameters a and NS could be random variables, the computed NS-IWSL may be no more deterministic but also stochastic. We here propose a new concept to measure the NS-IWSR, i.e.,

$${\rm{NS}}-{\rm{IWSR}}={\rm{Probability}}\,\left({\rm{NS}}-{\rm{IWSL}} > 1\right)$$
(11)

This concept represents a novel approach, departing from the conventional deterministic definition of NS-IWSL. Previous studies typically assessed water shortage levels using binary values (Aldaya et al., 2020; Vorosmarty et al., 2000): 1 (when NS-IWSL > 1) and 0 (when NS-IWSL < 1), where 1 suggests water pollution and the presence of NS-induced water shortages, while 0 denotes an absence of pollution and no occurrence of water shortage. However, such measurements may be arbitrary, potentially leading to either exaggerated or overly conservative assessments, as they fail to capture a moderate status. Moreover, determining whether a water body faces shortages due to NS impacts is inherently uncertain and subject to various sources of uncertainty. Thus, adopting a probability-based definition of water shortage offers greater flexibility in accommodating the comprehensive impacts.

NS-IWSR can be calculated by using the MC simulation. We first assigned the uniform and normal probabilistic distributions to the allowable limit a (10 < a < 13) (Franke et al., 2013; Ministry of Ecology and Environment, 2002; Huang et al., 2017) and NSct. By simulating these distributions over 10,000 iterations, we generated a probabilistic distribution of NS-IWSL values. The NS-IWSR was then calculated as the proportion of simulations where NS-IWSL > 1. This probabilistic method accommodates the inherent uncertainties, offering greater flexibility and accuracy in evaluating water shortage risks.

Results

Figure 1A, B depicts the spatial distributions of NS in 2006 and 2020, respectively. The lowest NS levels were predominantly observed in the west region, encompassing the cities such as Wuhai, Nujiang, Karamay, and Jiayuguan exhibited the lowest NS levels, all below 10 kt. The higher NS levels were mainly in the central region, including cities such as Changsha, Luoyang, Harbin, and Wuhan. Conversely, the highest NS levels were identified in the east region, covering cities like Zhanjiang, Baoding, Shijiazhuang, and Xuzhou. Temporally, the vast majority of cities experienced a slight decline across the three regions from 2006 to 2020. Figure 1C shows the spatial annual average change of NS over the three regions from 2006 to 2020. There was an obvious NS increase in about 55% of the cities in the West. Notably, Chifeng and Tongliao in North China exhibited the highest annual increase in NS, exceeding 6 kt/year during 2006–2020. This trend likely reflects a combination of intensive maize-based agriculture, expansion of livestock farming, and historically high fertilizer application rates, which were further amplified by policy incentives for agricultural production in this region. In comparison, a remarkable NS reduction was observed in the remaining cities, with most of them concentrated in the southeast part close to the central and east. The central and east presented more positive NS improvement, with approximately 82% and 85% of the cities decreasing their NS considerably.

Fig. 1: Spatial dynamics of NS penetration in China.
figure 1

A, B The spatial distributions of NS results in 2006 and 2020; C The spatial variability of NS changes from 2006 to 2020.

Full size image

Specifically, based on the aggregated outputs from the INBM, the NS across all cities in the west increased by approximately 7 kt per year on average between 2006 and 2020. In contrast, the central and east regions experienced average annual decreases of about 153 kt per year and 190 kt per year, respectively. This implies that the NS-related environmental challenge facing the West was rather stringent than the others, because most of the cities were still at the stage of extensive agricultural development, where regional NS management had not yet been substantially controlled. The NS reduction in the cities could be attributed to various mechanisms, including improvements in N fertilizer use efficiency (You et al., 2023), increased agricultural investment (Duan et al., 2021), strict N pollution control (Cai et al., 2023; Gu et al., 2023), enhanced ecological protection policies (Gu et al., 2023), and adjustments in agricultural production structures towards eco-friendly practices with lower N emissions (Cai et al., 2023).

Figure 2A, B illustrates the spatiotemporal evolution of AI investment during the same period. Over the past 15 years, there has been a noticeable increase in total AI investment, driven by sustainable economic growth and increasing investment in agricultural practices aimed at enhancing food production. In China, AI increased by approximately 96 times from 838 million RMB ¥ in 2006 to 81,167 million RMB ¥ in 2020. Figure 2C illustrates that the AI across all cities in the west increased by approximately 1885 million RMB ¥ per year on average between 2006 and 2020. In contrast, the central and east regions experienced average annual decreases of about 1779 million RMB ¥ per year and 1688 million RMB ¥ per year, respectively. By 2020, the AI rapidly rose to 27,072, 19,938, and 34,158 million RMB ¥, respectively. In the West, government initiatives aimed at enhancing agricultural resilience in less-developed areas facilitated growth. In the central, balanced economic development and promotion of modern agricultural practices contributed to the rise. Conversely, in the east, proactive responses to evolving challenges in densely populated and economically dynamic areas led to exponential growth. These disparities reflect the diverse socio-economic and agricultural landscapes across China.

Fig. 2: Spatial dynamics of AI penetration in China.
figure 2

A, B The spatial distributions of AI results in 2006 and 2020; C The spatial variability of AI changes from 2006 to 2020.

Full size image

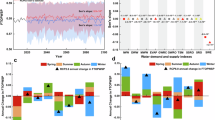
We here examined the AI effects on NS across the west, central, and east from 2006 to 2020 based on 24 linear panel regression models (Table S6), where coefficients β1, β2, and β3 represented the AI effects of the three regions, respectively. All the models achieved consistent coefficients (either positive or negative) in the three regions (R2 values > 0.93 and p values < 0.1‰). These implied AI can be an appropriate variable in explaining NS. While there were marginal discrepancies in the three coefficients as described in Fig. 3A–C, continuously increasing the number of control variables or fixed effects did not enhance the model’s quality, but rather augmented its complexity; this showed that the current models had been sufficiently capable of capturing the AI effects (Hsiang et al., 2013; Burke et al., 2018). Simultaneously, the consistently high performance of these models suggested that the potential impact of endogenous variables, such as AI, was effectively mitigated through the incorporation of suitable control variables (e.g., PAV-GRP) along with city-fixed, year-fixed, and/or year-trend effects (Burke et al., 2015; Ren et al., 2023). To illustrate without loss of generalization, we opted for model 3 as the base model for further analysis because it not only performed comparably well to the others without introducing an excessive number of explanatory variables and fixed effects, but also addressed potential issues related to omitted variables through the inclusion of pertinent fixed effects terms.

Fig. 3: Regional impact of AI on NS via panel regression analysis.
figure 3

A–C Demonstrate the influence of AI on NS across the west, central, and east, respectively, based on eight representative regression models. The slopes of the lines indicate the effect of AI on NS (βi, where i = 1, 2, 3) in each region. The shaded regions around the line correspond to the 95% confidence interval for the base model (model 3). Below each graph, bars illustrate the distribution of AI penetration levels across the regions. Annotations include “FE” for models incorporating fixed effects to control for unobserved, time-invariant differences among units, and “w/o control vars” to denote models executed without additional control variables. The dotted line represents the estimated effect after applying a 2% truncation to the variables, used to mitigate the influence of extreme observations. D–F Present the temporal dynamics of AI effects on NS over consecutive 5-year intervals throughout three regions, spanning the same 2006–2020 period. G Comparison of the fitting coefficients in China and the three regions achieved from 8 different models.

Full size image

We revealed significant spatially heterogeneous AI effects on NS among the three regions, with the west presenting positive (0.0452 ± 0.0236) and the central (−0.0311 ± 0.0307) and east (−0.0654 ± 0.0355) exhibiting negative. However, there was an obvious trend that β1 would turn to the opposite one after 2020, suggesting that the adverse AI effects had been lowering in this period and eventually AI would begin to contribute to decreasing NS (Fig. 3D). By comparison, the AI effects (as indicated by β2 and β3) in the central and east had been maintaining negative (Fig. 3E, F), showing that the AI had been playing a beneficial role in declining NS. Fig. 3G illustrates the overall fitting situation in China, which compares the fitting coefficients for the west, central, and east among eight representative models shown in Fig. 3A–C. All the models showed consistent AI effects in terms of both direction and statistical significance (p < 0.1), with positive effects in the west region and negative effects in the central, east, and national-level models. This consistency highlights the robustness of our findings and supports the spatial heterogeneity of AI effects on NS.

To demonstrate the robustness of the AI effects, we continued to employ the MC simulation by conducting a set of stochastic sampling experiments. We randomly drew either 2000 or 3000 samples from the comprehensive dataset (comprising 333 cities over 15 years) and iterated this process 10,000 times. Coefficient β1 exhibited remarkable stability, with values oscillating narrowly between 0.0444 and 0.0446 (Fig. S4). Coefficients β2 and β3 varied similarly tightly, ranging from −0.0306 to −0.0303 (Fig. S5) and from −0.0651 to −0.0647 (Fig. S6), respectively. Figs. S4B, S5B and S6B reveal a relatively higher variance in coefficients β1, β2, and β3, suggesting that increasing the number of statistical samples in regression model fitting decreases the uncertainty of the estimates. When we synthesized the outcomes from both experimental sets, the mean estimates were found to be 0.0445, −0.0304, and −0.0649 (Figs. S4C, S5C and S6C), respectively, aligning closely with those derived from the base model for each of the regions.

To evaluate the potential delayed effects of AI on NS, we introduced lagged NS terms into the base panel regression. The time-lagging models achieved the β1, β2, and β3 values close to those from the non-lagging model, indicating once again that the AI effects were robust enough, which were not influenced by time lagging (Fig. S7). In the west region (Fig. S7A), the AI effect is positive and gradually declines with time, suggesting delayed or dampened policy effectiveness, possibly due to structural limitations in policy uptake or implementation in that region. In the central region (Fig. S7B), the coefficients fluctuate slightly but remain relatively stable (−0.0362 to −0.0410), implying a more persistent influence of AI on NS. By contrast, in the east region (Fig. S7C), the AI effect remains negative and statistically significant across all lags, but its magnitude declines over time, from −0.0508 at t−1, to −0.0388 at t−2, and −0.0262 at t−3. This pattern suggests a temporal attenuation of AI effects on NS, where the strongest reductions occur shortly after implementation, and the effects diminish in subsequent years. Such a decline could reflect a short-term behavioral response among farmers (e.g., input adjustments or insurance-induced changes in nutrient application), which weakens over time unless reinforced by continuous policy engagement or complementary programs.

We also employed within-group stratified regressions to assess the heterogeneous effects of AI on NS across diverse climatic and socio-economic conditions. Specifically, we stratified the sample based on six key variables: temperature, precipitation, sunlight hours, GDP per capita, rural population, and cropland area. These stratification variables were selected due to their potential influence on NS outcomes, sensitivity in regression models, and the availability of consistent spatiotemporal data.

In the west region (Fig. 4A; Table S10), AI consistently exhibited positive and highly statistically significant effects on NS across all six stratification dimensions. Notably, the estimated coefficients (β1) ranged from 0.0148 to 0.0645, all significant at the 1% level, indicating a robust enhancing effect of AI on NS irrespective of local climatic or socio-economic conditions. This suggests that, in the West, AI may be intensifying agricultural intensification and input use, reinforcing its environmental impact. In contrast, in the central region (Fig. 4B; Table S11), AI effects were uniformly negative and statistically significant at the 1% level across all stratification variables, with coefficients (β2) ranging from –0.0182 to –0.0810. However, confidence intervals were notably wider across several strata, particularly those stratified by GDP per capita, suggesting greater heterogeneity or contextual variation in the AI–NS relationship, possibly due to transitional farming structures or diverse institutional environments in central China. The east region (Fig. 4C; Table S12), also showed predominantly negative and significant AI effects (β3 from –0.0285 to –0.0817). This pattern points to a consistently mitigating role of AI on NS in more developed or intensive agricultural systems.

Fig. 4: Heterogeneous effects of AI on NS by climatic and socio-economic factors.
figure 4

A–C Examine the differential impacts of AI on NS across various climatic and socio-economic variables in three regions.

Full size image

Across all models, AI coefficients were statistically significant at the 1% level, underscoring the robustness of these heterogeneous patterns. Moreover, the adjusted R² values were consistently high (R² > 0.9), supporting the strong explanatory power of the stratified models. These findings collectively highlight the robustness of these heterogeneous patterns and emphasize the importance of region-specific policy evaluation and design.

The endogeneity issues, potentially arising from omitted variables (e.g., crop rotation practices) or reverse causality between AI and NS, necessitate a cautious estimation strategy. To mitigate these concerns, we employed an IV approach using DIU, defined as the number of internet users per unit of cropland area, as a plausibly exogenous instrument for AI adoption (Method S3.6). While IV estimation helps address bias from endogeneity by breaking the correlation between the explanatory variable and the error term, it is important to acknowledge its limitations. These include sensitivity to weak instruments in finite samples and the fact that IV estimates may be biased if the instrument affects the dependent variable through channels other than the endogenous regressor.

Therefore, we performed a series of validity checks, including the under-identification test (Kleibergen-Paap LM), weak instrument tests (Cragg-Donald and F-statistics), and the Anderson-Rubin Wald test (Table 1). These diagnostics support the relevance and exogeneity of DIU across all regions. Moreover, the consistency in coefficient signs across OLS and IV regressions remained consistent, lending credibility to the causal interpretation, although we report IV estimates primarily for robustness and retain OLS estimates as the main reference for effect sizes.

Table 1 The instrumental estimate of AI on NS.
Full size table

We subsequently compared the AI effects with observations derived from regression analyses using time series data for individual cities (Table S13). Our investigation spanning the three regions revealed that the majority of cities followed the trends by our panel models. Notably, in the West, only 48.4% of cities have positive AI effects on NS. In contrast, the central and east regions demonstrated consistent patterns, with 78.7% and 87.9% of cities displaying the generalized negative AI effects on NS, bolstering the credibility of our regional analysis. This complex interregional disparity could be attributed to the following mechanisms.

First, agricultural diversity and economic disparity: the West displays varied agricultural practices (Zeng et al., 2020; Benami et al., 2021) and differing economic development stages, contrasting with the more uniform and economically advanced central and east. The positive correlation between AI and NS in the West may suggest the role of AI in promoting increased agricultural risk-taking and subsequent fertilizer use, potentially driven by suboptimal farming conditions such as poor soil quality and limited access to modern farming techniques. Second, policy enforcement and environmental regulation: variations in coefficient ratios across regions may result from differences in policy implementation. Stringent environmental regulations in the central and east could directly influence the sustainable use of AI, while relatively lax enforcement or the emerging adoption of AI in the West may explain the observed positive association with NS. Third, educational outreach and sustainable practices: proximity to academic institutions in the central and east likely fosters greater awareness and education on sustainable farming, empowering an informed agricultural community to utilize AI for effective NS management (Möhring et al., 2020; Hu et al., 2021). Fourth, climatic and geographical challenges: the unique climate and geography of the West require distinct farming methods and crop choices, which may be less N-efficient despite AI interventions (Zhan et al., 2021).

We compared the difference between the NS levels with and without AI effects using counterfactual analysis based on the reference year of 2020 (Fig. 5A). Owing to the development of AI investment in 2020, a total of 1282 kt of NS reduction was achieved in the entire China, with an increase by 1203 kt in the west and declines by 841 kt and 1644 kt in the central and east, respectively. We also examined how AI investments impacted the NS-induced water shortage using indicators of NS-IWSL and NS-IWSR. Results revealed that AI played a positive role in mitigating the water shortage challenge in the central and east (ΔNS-IWSL < 0), but negative in the west (ΔNS-IWSL > 0) (Fig. 5B). By comparison, its effects on NS-IWSR were inapparent. About 22%, 33%, and 31% of the cities, respectively, in the west, central, and east experienced high water shortage risks (NS-IWSR = 1) due to high NS and/or low water availability. Moderate water shortage risks (0 < NS-IWSR < 1) mainly occurred in about 10%, 4%, and 14% of the cities in the three regions, respectively (Fig. 5C). Unfortunately, these risks were not effectively improved even with the rapid development of AI investments. In 2020, we only observed 23 cities whose NS-IWSR was mitigated by AI, such as Jinan, Haikou, Changchun, and Shanghai. This implies that AI could take effect on the NS-induced water shortage problem, but its real contribution, considering various uncertainties, is still to be challenged. Thus, further improvement on current AI programs would be expected to address NS-induced water shortage challenges, and meanwhile, complex uncertainty impacts.

Fig. 5: Historical AI effects on NS and NS-IWS.
figure 5

A, B The change of NS and NS-IWSL in 2020 was only due to AI effects, respectively. C The nationwide distributions of the NS-IWSR in 2020.

Full size image

Discussion

AI has been widely implemented to stimulate agricultural investment, improve cropping structures, and introduce advanced technologies to mitigate potential risks arising from natural hazards. Despite numerous studies on the influence of AI on agricultural production, its potential impacts on environmental gains or deductions have been little known (Perry et al., 2020; Ahmed et al., 2022). This study revealed the strong positive or negative AI effects on NS and its resulting water shortage across 333 cities in China over the past 15 years. According to our knowledge, both the data (particularly on AI and NS) and findings were presented in this paper for the first time, which provided a scientific basis for establishing future policies on AI planning, agricultural development strategies, and environmental management practices.

AI has a consistent positive effect on NS in the West because of its rather undeveloped agricultural levels. In this region, AI investments primarily drove farmers to extensively expand their agricultural scales and production, rather than focusing on improving environmental quality (Benami et al., 2021). By comparison, in the other regions with generally higher economic development, AI investments have motivated farmers to introduce more and more green technologies (corresponding to higher cost) to mitigate the adverse impacts of strengthened agricultural activities on the environment (Möhring et al., 2020; Hu et al., 2021). These spatially heterogeneous AI effects hold valuable implications for policymakers. Specifically, the Ministry of Agriculture and Rural Affairs and China Agriculture Insurance Company (PICC) could initiate varied and environmentally friendly AI programs in terms of the AI effects to accommodate the discrepancies among the cities. Meanwhile, efforts such as the Action Plan for Fertilizer Use Reduction by 2025 and the Zero Growth Action Plan for Pesticide Use by 2020 offer a balance between agricultural production and environmental quality (Ministry of Agriculture and Rural Affairs of the People’s Republic of China, 2021; Shuqin and Fang, 2018). Finally, the Ministry of Ecology and Environment should develop appropriate pollution control measures, standards, or guidelines to match with or improve the associated AI programs and agricultural policies.

To validate the robustness of our findings obtained from panel regression, we conducted extensive analyses by comparing a total of 24 linear regression models to individually explore the AI effects, and observed statistically significant linear correlations existing in all of them within the three regions of China. We did not present more additional linear models due to their consistent performance within the same temporal range, with differences primarily in regression coefficients. Moreover, other validation approaches included (1) comparison of effects from multiple regression models with varied terms, (2) MC simulation, time-lagging, and stratified regressions for examining the stability of the effects subject to the samples’ uncertainty, and (3) introduction of an IV to mitigate potential endogeneity impacts. Results revealed that all identified AI effects were stable, indicating that the linear AI effects on NS in the three regions of China were substantially robust. Note that the IV approach was thought to be indispensable to mitigating endogeneity impacts and avoiding the appearance of spurious regression (Cao et al., 2023; Hao et al., 2023). Though there was much difficulty in finding a reasonable IV, we here successfully found a new IV (i.e., DIU) and demonstrated its validity in both mechanisms and statistics; this further bolstered the robustness of the identified exclusive AI effects.

We focused primarily on linear relationships in this study, as the hypothesized nonlinear effects, such as inverted U-shapes or other threshold behaviors, were not statistically identifiable within the observed range of AI levels. The study period (2006–2020) primarily captured the early phases of AI implementation, during which the variation in AI coverage across cities was relatively limited (Kramer et al., 2022; China Insurance Yearbook Editorial Board, 2007–2021). In particular, AI adoption was concentrated in the lower to moderate range of coverage, as many regions began scaling up AI programs only after 2007 (China Insurance Yearbook Editorial Board, 2007–2021). Consequently, the data did not encompass the broader range of AI levels that would be necessary to robustly identify nonlinear patterns, such as those associated with threshold effects or curvature (e.g., Kuznets-like curves). This limited variation in the AI policy variable restricted our empirical capacity to detect potential inflection points where the relationship between AI and the outcome variable might shift, which is a hallmark of nonlinear dynamics.

Such limitations are not uncommon in policy research using short panel datasets. When a policy variable like AI has not yet reached a saturation point or exhibited significant temporal variation, the dispersion in the variable is often too small to detect curvatures or thresholds (Burke et al., 2018; D’Orazio and Pham, 2025). In other words, without observing a sufficient range of AI levels, there is little opportunity to identify changes in the direction or magnitude of the effect that might be characteristic of nonlinear relationships. This issue has been observed in similar studies of policy impacts, where the detection of nonlinearity is constrained by the early or partial implementation stages of the policy. Missing latent inflection points, such as those resembling environmental Kuznets-type curves or other nonlinear structures, may therefore represent a risk in underestimating the complexity of the policy effects (Zhang et al., 2015; Burke et al., 2018). However, we note that this is an issue that could be addressed in future research, particularly with longer time series data or more mature AI systems, where the AI levels across cities are likely to exhibit more variability and where nonlinear relationships might become more apparent. In such future studies, the broader range of AI implementation may offer the empirical leverage necessary to capture curvatures and threshold effects that are currently beyond the scope of the present study.

“Premium” and “Indemnity” serve as critical indicators quantifying AI. In our analysis, we only focused on premium as the explanatory variable, while excluding indemnity based on two considerations. Conceptually, premium represents the proactive scale and policy commitment of AI, driven by insured area and policy uptake, while indemnity reflects reactive, event-driven payouts and may be more volatile and endogenous to shocks (e.g., floods or droughts). Empirically, the two indicators are highly collinear (VIF > 6; Table S14), suggesting that including both could distort coefficient estimates. Additionally, when we substituted the premium with the previous year’s indemnity in robustness checks, the explanatory power of the model weakened. In particular, the coefficient on indemnity was not statistically significant in the central region (p = 0.823; Table S15), indicating weaker explanatory consistency compared to premium. While our study concentrated on AI, it is crucial to acknowledge that other financial tools like agricultural subsidies (Springmann and Freund, 2022; Huffaker, 2008), loans (Rehman et al., 2024), and ecological compensation (Hou et al., 2021) also play significant roles in promoting agricultural development. These tools may also have positive or negative effects on NS and NS-IWSR, either directly or indirectly. It is thus desired that the potential individual or their combined effects be identified. Explorations of new evidence regarding the effects of these tools would provide valuable insights not only for developing well-considered financial programs but also for maintaining the balance between agricultural benefits and environmental quality.