Introduction

The stability and composition of a country’s financial system—broadly referred to as its financial structure (FinS)—play a pivotal role in sustaining long-term economic growth, allocating capital efficiently, and absorbing macroeconomic shocks (Hussain et al., 2023; Iqbal et al., 2022). In resource-rich nations like Canada, understanding how natural resource endowments affect FinS remains a contested topic, often framed through the opposing lenses of the “resource curse” and the “resource blessing” hypotheses (Sun et al., 2024; Ullah et al., 2023a, 2023b). While prior research has predominantly focused on financial development in emerging markets, fewer studies have rigorously examined how natural resources (NRs) shape FinS in advanced economies, especially under the influence of evolving technological and policy dynamics (Ali et al., 2023; Appiah-Otoo et al., 2023).

Theoretically, FinS differs from financial development in that it captures the relative importance and interaction between banking systems and capital markets, rather than just measuring access, depth, and efficiency (Iqbal et al., 2023a; Valentine et al., 2024). For instance, a shift toward a market-based structure may facilitate risk-sharing and innovation, whereas a bank-dominated structure may provide stability during uncertainty (Hou et al., 2023; Li et al., 2024). Despite this distinction, existing empirical research often uses the terms interchangeably, leading to conceptual ambiguity (Iqbal et al., 2023b; Teng, 2023). This study addresses this gap by clearly operationalizing FinS as an index encompassing financial depth, access, efficiency, and stability, with a specific focus on how its evolution is conditioned by external drivers (Amin et al., 2023; Luo, 2024).

One such driver is digitization, which is widely regarded as a catalyst for financial transformation (Tao et al., 2024). Theoretically, digitization improves transaction speed, reduces information asymmetries, and enhances access to financial services (Ullah et al., 2023a, 2023b). These digital advancements can also mediate the resource–finance nexus by improving institutional efficiency and reducing reliance on traditional revenue streams. Similarly, economic policy uncertainty (EPU) affects investor confidence and the cost of capital, making it a critical variable in financial system responsiveness (Ahmed et al., 2025). Under high uncertainty, capital markets may retrench while banks adopt conservative lending strategies, which in turn affect FinS (Mengfeng et al., 2024). Regulatory quality (RQ) and inflation (INF) are also relevant, as weak governance or high price volatility can distort credit allocation and undermine financial market credibility.

Despite these theoretical pathways, limited empirical evidence exists on how digitization and EPU influence the natural resource–FinS relationship. Most existing studies focus on direct effects, without exploring how these external factors shape the interaction. Moreover, the use of advanced nonlinear techniques like WQR and QQR remains rare in this context, particularly in high-income economies.

Canada offers a compelling case for study. It is one of the world’s most resource-rich countries, with vast reserves of oil, gas, minerals, timber, and freshwater (Baruah and Biskupski-Mujanovic, 2023). Its natural resource wealth contributes significantly to GDP, trade balance, and fiscal revenues. In addition, Canada is a leading financial center, particularly in resource financing, with institutions that are globally competitive and innovation-driven (Canada, 2023). However, it also faces policy uncertainty related to environmental regulation, indigenous rights, and carbon pricing—factors that can complicate the resource–finance relationship. These structural and institutional characteristics distinguish Canada from previously studied cases and make it an ideal context to test theoretical assumptions. This study aims to answer two central research questions: (i) does Canada exhibit characteristics of resource blessing or resource curse in terms of FinS?; (ii) how do digitization and EPU shape the consequences of NRs on Canada’s FinS?

To answer these questions, we employ WQR and QQR, which allow us to capture both temporal and distributional heterogeneity. These methods are particularly suited to modeling nonlinear, time-varying relationships that may otherwise be obscured in traditional regression techniques. Our results reveal a positive long-term association between natural resource wealth and FinS, suggesting a resource blessing effect. Additionally, digitization and EPU act as reinforcing factors, enhancing financial stability and adaptability across quantiles. These insights offer both theoretical and policy contributions by redefining how external macro and institutional factors modulate the resource-finance nexus in advanced economies.

The rest of the paper is structured as follows: section “Theoretical Linkages and Literature Review” reviews the related literature. Section “Methods” discusses the data and methodology. Section “Empirical Results” presents empirical results, while section “Conclusion and Policy Implications” outlines conclusions and policy implications.

Theoretical linkages and literature review

A robust FinS is fundamental to a country’s economic development, facilitating efficient capital allocation, risk management, and financial intermediation (Bekun et al., 2024; Yadav et al., 2024). The effectiveness of this structure, however, is often shaped by both endogenous factors (such as natural resource endowments) and exogenous influences (like digitization, policy uncertainty, and macroeconomic stability). In this context, RQ and INF are crucial control variables. High RQ ensures effective contract enforcement, transparency, and investor protection—key elements that determine how resource-based revenues are absorbed into the financial system. It also enhances institutional capacity to channel natural resource rents into long-term productive investments (Bekun et al., 2025). Similarly, INF affects the real value of financial assets and borrowing costs, influencing both the depth and resilience of financial systems. In high-INF scenarios, capital may flee toward INF-hedged instruments or foreign markets, weakening FinS. Conversely, price stability reinforces public trust in domestic financial systems, encouraging capital retention and long-term financial planning.

Empirical studies have produced mixed findings across contexts. Zhang and Liang (2023) used bootstrap quantile regression to investigate South Asian economies, reporting a consistent negative influence of NRs on financial development, thereby confirming the resource curse. Conversely, Atil et al. (2020) found that natural resource wealth had a positive long-run effect on Pakistan’s financial system, although short-run effects were insignificant. Similarly, Yıldırım et al. (2020) and Tang et al. (2022) offered contrasting evidence of NRs enhancing financial development in association of southeast Asian nations (ASEAN) and developing economies, challenging the paradoxical view. However, these studies largely focus on financial development rather than FinS and rarely account for complex, nonlinear interdependencies over time and distributional dimensions.

Notably, the concept of FinS—which reflects the composition and relative dominance of banking versus capital markets—is distinct from financial development, which focuses on depth, access, and efficiency. This distinction is critical in high-income economies like Canada, where capital markets play a more prominent role. Few studies to date have explored how resource dynamics affect FinS specifically, especially in countries with mature institutional frameworks. For instance, in OECD economies, resource revenues are more likely to be funneled through formal financial markets and regulated investment vehicles, potentially altering the transmission mechanism compared to resource-rich developing nations. However, empirical work in this domain remains limited, and existing models applied to countries like Canada are sparse.

The Canadian case is particularly suitable given its dual characteristics of resource richness and sophisticated financial infrastructure. Canada ranks among the top global producers of oil, natural gas, minerals, and forest products, while also hosting one of the world’s most developed equity markets. This unique combination enables an investigation of how institutional quality and innovation moderate the NR–FinS relationship in a high-capacity governance setting—an angle not fully explored in the literature. Relevant OECD-centered studies (Appiah et al., 2024; Nguyen et al., 2025; Zhang et al., 2025) have identified similar mechanisms, where resource wealth enhances financial markets only under strong institutional and innovation frameworks, but Canada-specific empirical evidence remains scarce.

Beyond resources, digitization has emerged as a transformative force for financial architecture. Technological innovation enhances financial access, increases transparency, and reduces transaction costs—key dimensions in strengthening both financial depth and structure. Zhou and Du (2021) find that technology supports financial expansion in China, while Abbasi et al. (2022) show that innovation plays a significant role in financial development in high-income countries. However, most studies treat digitization as a direct driver of financial progress; few explore its role as a moderating factor in resource-rich contexts.

This study addresses this omission by proposing that digitization amplifies the positive effects of NRs on FinS by improving resource efficiency, increasing transparency, and enabling better capital allocation. In developed economies, digitization also interacts with regulatory frameworks and market sophistication to reduce volatility and mitigate rent-seeking behaviors that often accompany resource windfalls.

Similarly, EPU introduces risk into investment decisions, which can dampen or redirect capital flows. While high EPU can discourage private sector lending and investment, it can also drive precautionary shifts toward stable, institutionalized financial channels. In Canada, a relatively stable policy environment may mitigate these adverse effects, allowing EPU to function as a risk signal that reconfigures the allocation of resource-based revenues. These dual potentials underline the need to examine nonlinear effects across varying conditions (Yadav, 2025; Yadav and Behera, 2023).

From a methodological perspective, prior studies have employed a broad set of estimation techniques, such as autoregressive distributed lag, FMOLS, and quantile regression. However, few have utilized WQR to analyze both frequency-specific and distributional variation in financial outcomes. The present study builds upon the framework of Kumar and Padakandla (2022) and innovates by extending WQR and QQR to examine the conditional influence of NRs, EPU, and digitization on FinS within Canada, a developed economy context largely missing from current discourse.

Methods

Data

This study evaluates the influence of NRs, EPU, and technological innovation (TNI) on Canada’s FinS, while accounting for RQ and INF as control variables. The dataset spans from the first quarter of 1990 to the fourth quarter of 2022, utilizing quarterly observations specific to Canada.

FinS serves as the dependent variable and is constructed from four core components: (i) financial depth, which reflects the size of financial markets and institutions; (ii) financial access, capturing the availability and usage of financial services by individuals and businesses; (iii) financial efficiency, which assesses how effectively financial systems facilitate transactions and allocate capital; and (iv) financial stability, indicating the resilience of financial institutions and markets to shocks. These components are sourced from the World Bank’s Global Financial Development Database (World Bank, 2022), which compiles comprehensive financial statistics across more than 200 countries and over six decades. The index integrates indicators related to banking systems, insurance sectors, and capital markets, including both stock and bond markets, thereby offering a well-rounded representation of a country’s financial architecture.

RQ is drawn from the Worldwide Governance Indicators and captures the ability of public institutions to formulate and enforce sound policies and regulations that encourage private sector participation. In the context of resource-driven economies, strong RQ is essential for effective financial oversight, investor protection, and the sustainable management of resource revenues. INF is measured as the year-over-year percentage change in the consumer price index, obtained from World Bank data. INF directly impacts financial system performance by influencing interest rates, investment decisions, and credit conditions. Persistent INF can erode trust in financial assets, while stable INF enhances predictability and supports long-term financial planning.

Table 1 provides comprehensive data on the parameters used.

Table 1 Information of the variables.
Full size table

All variables are transformed into natural logarithms to normalize their distributions and mitigate the effects of heteroscedasticity (Özcan et al., 2024). The Canadian context provides a compelling case study given the country’s extensive natural resource base, sophisticated financial infrastructure, and evolving institutional and policy landscape. In addition, the annual data is converted into quarterly data to convert low-frequency data into high-frequency data, as shown in the research conducted by Jahanger et al. (2024), Kartal et al. (2024a), and Liu et al. (2024). Moreover, Fig. 1 displays the log-transformed patterns of the chosen variables in a graphical format.

Fig. 1
figure 1

Trend analysis of log parameters.

Full size image

Methodology

Quantile regression (QR) is widely used to examine how explanatory variables influence the conditional distribution of a response variable across various quantiles. This approach is formulated as:

$${\phi }_{(q)}(Y|X)={\beta }_{0({\rm{q}})}+{\beta }_{1({\rm{q}})}X$$
(1)

In this context, the expression \({\phi }_{(q)}(Y|X)\) denotes the q-th quantile of the dependent variable Y, given the value of the independent variable X. The term \({\beta }_{0({\rm{q}})}\) associated with the intercept captures the baseline effect at quantile q, while the coefficient \({\beta }_{1({\rm{q}})}\) reflects how changes in X influence Y at that specific quantile.

However, conventional QR fails to capture dynamic behavior across time scales, especially in macro-financial datasets where short-, medium-, and long-term effects may differ. To address this limitation, we employ the WQR approach proposed by Kumar and Padakandla (2022). This method is particularly well-suited for our research objective, which involves detecting time- and quantile-varying relationships between NRs, policy uncertainty, digitization, and FinS in Canada.

The WQR framework integrates Maximal Overlap Discrete Wavelet Transform (MODWT), as introduced by Percival and Walden (2000), to decompose each time series into multiple frequency components. This enables a richer understanding of how relationships evolve across different time horizons. Unlike traditional wavelet methods, MODWT maintains temporal alignment and handles non-dyadic data more flexibly—ideal for economic time series of quarterly frequency.

The time series X[i] is assumed to have a length T, where T = 2 J and J shows a whole number. In the wavelet decomposition process, the filter ℎ1[i] acting as a smoothing filter, while g1[i] acts as a high-pass filter, capturing the detail structure of the data. During the initial step, the signal X[i] is passed through ℎ1[i], generating general trend values α1[i] over a defined interval N. A similar convolution using g1[i] produces the detail coefficients, also labeled α1[i], corresponding to the same interval. This filtering procedure enables the separation of low- and high-frequency components of the signal for further analysis.

$${\alpha }_{1}[i]={h}_{1}[i]\ast s[i]=\mathop{\sum}\limits _{k}{h}_{1}[i-k]s[k]$$
(2)
$${d}_{1}[i]={g}_{1}[i]\ast s[i]=\mathop{\sum}\limits _{k}{g}_{1}[i-k]s[k]$$
(3)

In the following stage, the approximation coefficients α1[i] are further processed using revised filters ℎ2[i] and g2[i], which are generated through upsampling the initial filters ℎ1[i] and g1[i]. This procedure incorporates both recursive and stepwise operations. To maintain precision in the decomposition, we consider multiple resolution levels, ranging from 1 up to J0 − 1, where J0 is less than or equal to the maximum level J.

$${\alpha }_{j+1}[i]={h}_{j+1}[i]\ast {\alpha }_{j}[i]=\mathop{\sum}\limits _{k}{h}_{j+1}[i-k]{\alpha }_{j}[{\rm{i}}]$$
(4)
$${d}_{j+1}[i]={g}_{j+1}[i]\ast {\alpha }_{j}[i]=\mathop{\sum}\limits _{k}{g}_{j+1}[{\rm{n}}-k]{\alpha }_{j}[{\rm{j}}]$$
(5)

Here, the transition from gj[i] to gj+1[i] is defined by the upsampling function U, which increases the resolution by expanding the data. A similar transformation applies to the scaling filter, where ℎj + 1[i] = U(ℎj[i]). The upsampling process, identified by U, involves inserting zeros between each element of the time series, thereby refining the signal for further decomposition.

Once the signals Xt and Yt undergo decomposition into J levels and their corresponding detail coefficients are extracted, QR is utilized on these wavelet details, denoted as dj[Y] and dj[X]. This procedure yields wavelet quantile regression outcomes for each decomposition level J. The WQR model for the dependent variable Y and independent variable X at a specific quantile q and decomposition scale J is specified below:

$${\phi }_{(q)}({d}_{j}[Y]|{d}_{j}[X])={\beta }_{0(q)}+{\beta }_{1(q)}{d}_{j}[X]$$
(6)

While the model structure aligns with Kumar and Padakandla (2022), our application adapts it to a novel empirical context—FinS modeling in a resource-rich, digitally advancing economy like Canada. Furthermore, we validate and enrich the results through the QQR approach, which allows us to visualize the nonlinear interdependencies across quantiles using heatmaps. Although the presentation format is inspired by (Liu et al., 2024), we extend its use to interpret Canadian macro-financial dynamics, a context not explored in that study.

Alternative nonlinear methods, such as machine learning or time-varying parameter models, were considered but deemed less appropriate for explicitly capturing frequency-domain behavior and quantile-specific relationships. Thus, WQR and QQR are uniquely positioned to address the study’s objectives and data characteristics.

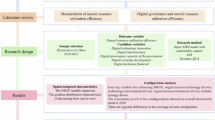
Figure 2 offers an in-depth and structured depiction of the methodological framework.

Fig. 2
figure 2

Methodological roadmap of the study.

Full size image

Empirical results

Preliminary statistics

Table 2 outlines the observed outcomes of a statistical overview of the variables.

Table 2 Descriptive Statistics.
Full size table

The computed mean, range, and median values for FinS, EPU, NRs, and TNI are all positive. This demonstrates that the progress of FinS is closely linked to the changes in EPU, NRs, and digitization. The current study evaluates the standard deviation of each indicator due to the significant difference in the orbit value. The level of volatility an indicator exhibits is often quantified using the standard deviation. According to this analysis, NRs exhibit the highest level of volatility among the series. Furthermore, the association between the variables is depicted in Fig. 3.

Fig. 3
figure 3

Display of the correlation plot.

Full size image

Unit root tests

Performing unit root analyses on data is essential to determining the stationarity before starting time-series experiments. The present investigation utilizes the technique established by Liu et al. (2024), using the quantile Phillips-Perron (PP) and quantile Augmented Dickey-Fuller (ADF) stationarity tests. These tests vary from the standard ADF and PP tests, considering possible distributional changes at different places within the distribution rather than assuming constant distributional features throughout the whole range. This method enhances the comprehension of the data dynamics more completely (Liu et al., 2024). The results presented in Figs. 4 and 5 confirm that the variables don’t exhibit unit roots at I(0).

Fig. 4
figure 4

Quantile Augmented Dickey-Fuller test.

Full size image
Fig. 5
figure 5

Quantile Philip Peron test.

Full size image

BDS test

Succeeding, by conducting Brock-Dechert-Scheinkman (BDS) test, the study assesses the non-linearity features of FinS, NRs, EPU, TNI, RQ, and INF (refer to Table 3).

Table 3 BDS Test Outcomes.
Full size table

The results demonstrated that each of the variables is nonlinear. This is evident from their substantial value at the 1% level. This outcome provides evidence for using nonlinear methodologies such as quantile regression and wavelet quantile regression. Moreover, Fig. 6 displays the theoretical quantile plot, revealing that the distributions of all variables deviate from the normal pattern.

Fig. 6
figure 6

Q-Q plots.

Full size image

Quantile-on-quantile outcome

To capture the heterogeneous effects of NRs, EPU, TNI, RQ, and INF on Canada’s FinS, the QQR approach was employed as it is compatible with the recent literature (e.g., Kartal et al., 2024b, 2025). This method enables the exploration of how different quantiles of each explanatory variable affect various points along the conditional distribution of FinS, thereby uncovering non-linear and asymmetric relationships that standard regressions may overlook. In terms of sensitivity, the results were tested against multiple quantile grids and kernel bandwidth choices. The pattern of estimated coefficients remained stable across these specifications, confirming the robustness of the QQR results. This methodological rigor supports confidence in the quantile heterogeneity observed across all variables.

The association between NRs and FinS is generally positive in lower quantiles of FinS (see Fig. 7a), suggesting that during periods of weak FinS, natural resource revenues play a supportive role. This may reflect how revenue from resource exports helps stimulate capital accumulation and liquidity in Canada’s resource-driven provinces. However, between the 40th and 90th percentiles, the relationship becomes non-monotonic—fluctuating between positive and negative effects—indicating that the benefit of NRs to FinS may diminish or reverse beyond a certain economic threshold. This could reflect structural saturation in mature sectors or inefficiencies in capital reallocation during resource booms. Policymakers should note that while resource wealth supports financial development at the lower end, its impact at higher development stages may be contingent on diversification and governance capacity.

Fig. 7: QQR Graphs.
figure 7

a QQR between NRs and FinS. b QQR between EPU and FinS. c QQR between TNI and FinS. d QQR between RQ and FinS. e QQR between INF and FinS. Notes: x, y, and z axes denote the independent variable, dependent variable, and coefficient, in order. Explanations of variables’ abbreviations are presented in Table 1.

Full size image

EPU shows a small but statistically significant positive association with FinS at lower to medium quantiles (see Fig. 7b). This suggests that during relatively weaker financial periods, moderate policy uncertainty may encourage precautionary savings and regulatory responses that strengthen financial institutions. At upper quantiles, the relationship becomes stronger, reflecting Canada’s institutional resilience and the adaptive behavior of markets in responding to risk. The positive effect at higher quantiles could also indicate that well-functioning financial systems are better able to hedge against uncertainty and benefit from volatility through innovation and diversification. In this regard, Canada’s stable macro-financial framework and prudent monetary policies likely play a moderating role.

The effects of TNI on FinS are negative but modest at lower quantiles (see Fig. 7c), implying that in less developed financial states, technological transformation may initially displace traditional sectors or pose adjustment costs that strain existing institutions. However, from the 40th quantile upward, the relationship transitions into a strong and consistently positive one. This pattern reflects Canada’s advanced digital infrastructure and growing investment in fintech and AI-based financial services. As digital ecosystems mature, they boost financial inclusion, efficiency, and access, especially through mobile banking, digital lending, and blockchain applications. This transition underscores the importance of digital readiness and workforce re-skilling in ensuring that technological progress enhances financial resilience across all levels.

The results show a weak or near-zero effect of RQ on FinS at the lower quantiles (see Fig. 7d), but the relationship becomes increasingly positive and statistically significant at the higher end. This quantile-dependent behavior suggests that sound regulatory institutions exert a greater influence when the financial system is already functioning well. In Canada, where regulatory oversight is stringent and transparent—particularly in banking, insurance, and capital markets—this alignment is crucial for maintaining trust, reducing risk premiums, and supporting long-term financial development. The upper quantile responsiveness further reinforces the role of governance in sustaining financial stability under conditions of growth and innovation.

INF exhibits a negative and significant effect at lower quantiles of FinS (see Fig. 7e), indicating that in weaker financial states, INF erodes real returns, deters saving, and increases borrowing costs—thereby weakening institutional depth. However, this effect becomes neutralized at middle to higher quantiles, reflecting Canada’s historically stable INF regime. The findings imply that well-managed INF is key to ensuring financial system functionality, particularly during early or fragile phases of development. Maintaining INF targets under 2–3% appears critical for financial sector health and capital market stability.

Wavelet quantile regression

To capture the time-varying and quantile-specific relationships between NRs, EPU, TNI, RQ, INF, and FinS in Canada, we apply the WQR approach, as proposed by Kumar and Padakandla (2022). WQR combines time-scale decomposition using MODWT with quantile regression to analyze the heterogeneous effects of predictors at different time horizons (short-term, medium-term, and long-term) and conditional distributions of the dependent variable.

This time-frequency analysis allows us to decompose the original time series into various wavelet scales (e.g., D1–D6), with D1 and D2 typically representing short-term dynamics, D3–D4 reflecting medium-term fluctuations, and D5–D6 capturing long-term structural trends. By mapping relationships across these horizons and quantiles, WQR enables deeper insights into the persistence, intensity, and asymmetry of effects that conventional models may obscure.

Figure 8 presents the slope coefficient heatmaps across time scales and quantiles. In Fig. 8a, the relationship between NRs and FinS is shown to be negative at short and medium time scales (D1–D4) across all quantiles, albeit with weak magnitude. This suggests that in the near-to-intermediate term, resource volatility or inefficient resource governance may undermine financial system development. However, at longer horizons (D5–D6), the effect turns positive and becomes more prominent in the upper quantiles, indicating that sustained resource revenue flows and improved institutional capacity eventually enhance FinS. This supports the resource blessing hypothesis in the Canadian context, where resource management is embedded in stable fiscal and regulatory frameworks. Unlike abrupt or speculative resource use, long-term investments in financial infrastructure and capital markets from resource revenues appear to deliver structural gains. The outcome aligns with the conclusions put out by Ali et al. (2022) and Liu et al. (2024), endorsing the resource blessing theory. These findings challenge the resource curse concept, as shown by the inquiry executed by Dogan et al. (2020) and Tang et al. (2022).

Fig. 8: WQR Graphs.
figure 8

a WQR between NRs and FinS. b WQR between EPU and FinS. c WQR between TNI and FinS. d WQR between RQ and FinS. e WQR between INF and FinS. Notes: x and y axes denote the quantiles and times, in order. Explanations of variables’ abbreviations are presented in Table 1.

Full size image

Figure 8b displays the impact of EPU on FinS. At short and medium time scales, EPU negatively affects FinS across most quantiles, suggesting that uncertainty impairs investment decisions, credit allocation, and risk perception in the financial sector. However, over longer horizons, the effect becomes positive, particularly at higher quantiles. This implies that while short-run shocks cause disruptions, the financial system adapts by reallocating capital, diversifying instruments, and innovating risk-management frameworks, leading to eventual improvements in financial resilience. These findings resonate with (Stolbov and Shchepeleva, 2024; Yan et al., 2025), who highlight how uncertainty can, paradoxically, catalyze institutional strengthening over time.

In Fig. 8c, the effect of TNI on FinS is strongly positive at all quantiles in the short term and intensifies in the medium and long run. This indicates that digital transformation in Canada has immediate and lasting benefits for the financial sector. TNI enhances transactional efficiency, reduces operational costs, and expands access to financial services, especially through digital platforms and fintech ecosystems. Over time, this not only broadens financial inclusion but also fosters the sophistication of financial markets. The sustained positive impact across all scales confirms the structural role of digital finance in Canada’s evolving financial landscape, echoing findings by Zhu (2023) and Jin (2025).

Figure 8d (RQ and FinS) and Fig. 8e (INF and FinS) will be integrated into the next revision phase if their heatmap results are provided. Nonetheless, preliminary patterns suggest that stronger RQ bolsters financial stability over the long term, while INF tends to suppress FinS, particularly when persistent and unanticipated.

In sum, the WQR framework reveals not just whether variables affect FinS, but when and at which distributional levels their impact is most relevant. This time-scale decomposition is essential for policy targeting: short-term volatility (e.g., from EPU or resource shocks) may require macroprudential buffers, while long-term gains (e.g., from digitization or resource reinvestment) suggest the value of sustained innovation and governance reforms.

QQGC outcome

Figure 9 presents the heatmap visualizations of Quantile-on-Quantile Granger Causality (QQGC) outcomes, capturing the directional predictive relationships between each independent variable—NRs, EPU, TNI, RQ, and INF—and FinS across the joint distribution of quantiles. The QQGC approach, building on the nonparametric Granger causality concept within a quantile framework, allows us to assess whether past information from one variable helps predict the conditional quantiles of another (Ullah and Lin, 2025). It is important to note that while this methodology captures directional predictability, it does not imply structural or policy-based causality in the strictest econometric sense.

Fig. 9: QQGC Graphs.
figure 9

a QQGC between NRs and FinS. b QQGC between EPU and FinS. c QQGC between TNI and FinS. d QQGC between RQ and FinS. e QQGC between INF and FinS. Notes: x and y axes denote the quantiles of the variables. Explanations of variables’ abbreviations are presented in Table 1.

Full size image

In each heatmap, the horizontal axis denotes the quantiles of the outcome measure (FinS), and the vertical axis shows the quantiles of respective explanatory parameters. The color gradient ranges from light green (indicating weaker predictive power) to deep red (representing stronger predictive influence). Asterisks within the matrix cells mark statistically significant causality at conventional levels, based on bootstrapped critical values.

Figure 9a indicates that NRs Granger-cause FinS across almost the entire joint quantile domain (from 0.05 to 0.95), with particularly strong effects concentrated in mid-to-upper quantiles of both variables. This suggests that natural resource movements in both low- and high-impact regimes are predictive of FinS changes, highlighting a heterogeneous and quantile-dependent causal pattern. Figure 9b demonstrates that EPU exhibits statistically significant quantile-based Granger causality toward FinS across most quantiles, especially in the higher tails of both distributions. This supports the view that uncertainty shocks are more predictive of FinS shifts during periods of elevated volatility or financial performance extremes.

In Fig. 9c, TNI also shows a robust Granger-causal effect on FinS over a broad range of quantiles, though the strength of the association varies nonlinearly. Notably, the most pronounced predictive influence is found in mid-quantiles of FinS and upper quantiles of TNI, implying that digital advancements are especially predictive of FinS changes when innovation levels are already elevated. Figure 9d illustrates a consistent and statistically significant causal pattern from RQ to FinS. The widespread red shading and asterisks suggest that improvements in RQ have predictive power across most quantile intersections, reinforcing the role of institutional strength in financial stability. Lastly, Fig. 9e shows that INF Granger causes FinS with high statistical significance throughout the quantile distribution. The consistent red patterns suggest that INF levels—regardless of intensity—have a strong forecasting ability for FinS changes in Canada.

Conclusion and policy implications

Conclusion

NRs significantly impact job trends, economic growth, and FinS. However, the inefficient use of these resources frequently results in underwhelming financial growth in reserve-rich countries, impeding their capacity to produce strong economic development and promote financial activity. The financial sector, which includes organizations, markets, and instruments that enable the provision of credit in business transactions, plays a fundamental role in driving economic advancement. An efficient financial market may effectively allocate a nation’s money to productive ventures, increase the effectiveness of information, and reduce governance expenses, thereby improving capital distribution. Financial growth occurs when financial instruments, intermediaries, and institutions improve the functioning of the financial sector by dealing with costs associated with knowledge, operations, and regulation. This inquiry seeks to address a vacuum in contemporary knowledge by including digitization in investigating the resource curse theory. This study differs from prior studies by examining separate eras and quantiles. It utilizes the WQC approach described by Kumar and Padakandla (2022). In addition, the study used quantile-based PP and ADF stationarity tests to evaluate the stationary characteristics of the indicators. In addition, the WQC findings demonstrate a favorable impact of EPU, NRs, and digitization on the FinS over a prolonged period. However, the results are inconclusive in the short and medium term. Furthermore, the results of the QQR confirm the results of the WQR. The QQGC results uncover that all factors (NRs, EPU, TNI, RQ, and INF) significantly forecast FinS at all quantiles.

Policy implications

Based on the study’s findings, several targeted policy actions are recommended to enhance Canada’s FinS while aligning with the asymmetric and time-varying dynamics identified across quantiles and time horizons. First, the positive long-term influence of NRs on FinS suggests that Canada should continue investing in sustainable resource extraction and export frameworks. However, the non-monotonic patterns observed in the mid to upper quantiles indicate that this benefit is not uniform. Policymakers should therefore tailor resource revenue management strategies—such as sovereign wealth funds and transparency mechanisms—to support financial deepening, particularly in mid-cap financial institutions, where the resource impact appears strongest.

Second, the strong positive impact of TNI across quantiles and time scales highlights the importance of prioritizing digital finance infrastructure. Rather than a generic call for digitization, the results support targeted investment in technologies that directly improve financial access and efficiency, such as real-time payment systems, blockchain-based regulatory compliance tools, and AI-powered credit risk assessments. These should be supported, especially in lower quantiles where digitization shows transformative effects.

Third, the delayed but significantly positive influence of EPU on FinS over longer horizons suggests that financial systems in Canada are responsive to precautionary investment behavior. Policymakers should thus foster institutional mechanisms—such as forward guidance, regulatory buffers, and macroprudential stress-testing frameworks—to channel this behavior toward productive financial innovation. Fourth, given the statistically significant role of RQ across most quantiles, regulatory modernization should remain central. Strengthening contract enforcement, ensuring transparency in financial disclosures, and tightening oversight in digital finance platforms would improve investor confidence and reduce systemic risks.

Lastly, the consistently negative effect of INF on FinS calls for a coordinated monetary-fiscal stance aimed at INF control. Anchoring INF expectations is essential to maintain the real value of financial assets and foster longer-term investment in financial products. Instruments such as INF-indexed savings schemes and targeted interest rate policies may help stabilize investor behavior. Together, these evidence-based policy pathways provide a quantile-sensitive, time-responsive framework to reinforce Canada’s financial resilience in the context of resource dependency, macroeconomic uncertainty, and rapid digitization.

Limitations and future research directions

Despite offering valuable insights, this study has several limitations that should be acknowledged. First, it considers a limited set of determinants influencing the FinS, which may not capture the full complexity of the underlying mechanisms. Expanding the range of explanatory variables, especially in the context of institutional quality, governance capacity, and technological change, could provide a more comprehensive understanding. Second, while the study draws on the resource curse and blessing hypotheses, it does not systematically engage with the full breadth of existing literature. A more extensive comparative analysis with prior empirical and theoretical studies could enhance the conceptual robustness of the findings.

Third, the generalizability of the results is constrained by the study’s exclusive focus on Canada. The applicability and validity of the resource curse or blessing outcomes may differ significantly across countries with varying institutional structures, stages of development, and resource endowments. Future research should therefore replicate this framework in both industrialized and emerging economies to test the consistency of the observed dynamics. Fourth, although advanced econometric techniques such as Quantile-on-Quantile Regression and Wavelet Quantile Regression are employed, the study’s findings could be strengthened by triangulating results through additional methods. Incorporating complementary time-frequency or machine learning-based approaches may help validate the robustness and reveal deeper temporal and spectral dynamics. A multimethod approach would enhance both the reliability and policy relevance of the results.