Quasi-Biennial Oscillation influence on Australian summer rainfall

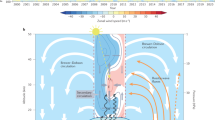
Abstract

The variability and distribution of Australia’s summer rainfall are influenced by modes of climate variability on multi-week to multi-year time scales. Here, we investigate the role of the stratospheric quasi-biennial oscillation (QBO) and demonstrate that the QBO influences rainfall variations and extremes’ responses across large regions of Australia. We find the QBO modulates convective heating to the east of the Maritime Continent and over the central South Atlantic Ocean in the austral summer. The baroclinic response and barotropic structure of the extra-tropical Rossby wave train induces anomalous circulation that affects the distribution and amount of rainfall over Australia. Our analysis and findings of QBO teleconnections with the dynamics that drive Australia’s rainfall variability and extremes represents a pathway to improve our understanding of rainfall potential predictability and scope to extend Australia’s rainfall prediction lead times.

Introduction

Knowledge of Australia’s rainfall variability and extremes is of the utmost importance to national water security considerations, including the potential for drought and flood events which can pose significant hazards and threats to the environment and society. Australia’s summer season rainfall is highly variable and linked to modes of climate variability including El Niño–Southern Oscillation (ENSO)^1,2, the Southern Annular Mode (SAM)³, Madden-Julian oscillation (MJO)⁴, and stratospheric polar vortex^5,6,7. Better understanding the relationships and mechanisms between relevant climate modes and rainfall is a vital step toward improved understanding of the potential predictability of Australia’s rainfall, rainfall extremes, and related extreme events^8,9,10,11,12.

One climate mode that has received little attention in the context of Australia’s rainfall is the tropical stratospheric quasi-biennial oscillation (QBO), although a few studies have implied QBO-rainfall relationships through related impacts, e.g., Ross River virus incidences on QBO time scales¹³ and tropical convection systems during different seasons¹⁴. Previous studies suggest that the QBO is a source of potential predictive skill for surface climate^15,16. This paper describes and quantifies the significant influence of the QBO on austral summer season (December-January-February) rainfall variability across large regions of Australia.

The QBO is a quasi-periodic fluctuation of the equatorial zonal winds within the stratosphere. The easterly (EQBO) and westerly (WQBO) phases are characterised by the downward propagation of easterly or westerly zonal-mean wind anomalies, respectively, from the upper stratosphere to the tropopause over an average period of approximately 28 months^15,17. The resulting strong wind shear alters the meridional temperature gradient and an anomalous meridional circulation emerges to maintain the thermal wind balance¹⁵. This secondary circulation is characterised by upwelling in the EQBO phase at the equator and downwelling in the vertical westward shear zone in the subtropics, with opposite signed circulation in the WQBO phase¹⁵.

The stratospheric QBO has been shown to impact the tropical troposphere and affect deep convection^18,19. The relationship between the QBO and tropical convection is significant during austral summer^20,21,22. One mechanism has been proposed that the MJO-related ascending moist-air in the lower stratosphere contributes to a local decrease in static stability. The EQBO-driven anomalous ascent/cooling in the lower stratosphere acts to reduce the static stability and contributes to more active convection²³. Conversely, increases in static stability due to WQBO-driven increases in the lower stratospheric temperature contributes to less active convection. Other proposed mechanisms suggest that increasing easterly winds with height during the EQBO phase induce a colder mid-stratosphere and associated reduced stability near the tropopause¹⁵. Previous research also suggests that the formation of tropical tropopause layer ice clouds is enhanced, caused by QBO-modulated deep convection and radiative reduction in the tropospheric stability²⁴.

The QBO’s influence on equatorial convection is associated with extra-tropical circulation and seasonal variability of the surface climate^25,26. Previous studies have proposed that variability in tropical convection induces the baroclinic response and structure of the extra-tropical Rossby wave that develops from baroclinic instability^27,28,29. The resulting changes in atmospheric circulation potentially influences surface climate in the Southern Hemisphere³⁰. For example, it has been shown that extra-tropical Rossby waves can induce changes in the distribution of Antarctic sea ice in austral spring—this was associated with low sea-ice anomalies in 2016, which were modulated by ENSO, the Indian Ocean Dipole (IOD) and SAM³¹. Additionally, it has been shown that the MJO is linked to a Gill type²⁸ baroclinic response^32,33,34,35 that impacts Australian rainfall and temperature^4,34. Recent studies have also proposed that the QBO affects precipitation in East Asia and South America through its modulation of MJO-related equatorial convection and the accompanying Rossby wave^36,37. Other research has shown that the QBO is associated with Antarctic sea ice variability in austral winter arising from the modulation of convection in the tropical Indian Ocean and the propagation of zonal waves in the high latitudes³⁸.

Although the relationship between the QBO and tropospheric circulation has been discussed in previous studies, very few studies have focused on the teleconnections between the QBO and regional weather and climate variations across the Southern Hemisphere subtropics to the midlatitudes. This paper investigates the role of stratospheric QBO phase variations on changes in the distribution of Australian summer rainfall, the statistical significance of these relationships, and the relevant tropospheric mechanisms. Importantly, we find that the QBO modulates the extra-tropical circulation via a Rossby wave train, inducing circulation anomalies over both eastern and western Australia, and which influences regional changes in Australian summer rainfall. Since the stratosphere has a longer memory than the troposphere³⁹, this study contributes to a broader understanding of Australia’s rainfall mechanisms and potential predictability.

Results

Distribution of rainfall anomalies and extremes

Our results show that much of western Australia (see Fig. 1 for Australian geographic information and features) is wetter in the EQBO phase (climatological mean rainfall shown in Fig. 2a and rainfall standard deviation in Fig. 2b), in the presence of a cyclonic wind anomaly that drives the onshore flow of moist air from the Indian Ocean (Fig. 2c, left panel). In the WQBO phase, however, anticyclonic wind anomalies drive offshore flow in conjunction with drier conditions over much of western Australia (Fig. 2c, middle panel). The EQBO cyclonic onshore wind anomalies are very apparent in the EQBO-WQBO difference and are statistically significant at the 5% level (Fig. 2c, right panel). The probability of occurrence of extreme rainfall over western Australia during the EQBO phase is up to two times higher than during the WQBO phase (Fig. 2d).

Fig. 1: The features and regions across Australia.

The features and regions across Australia referred to in this study are identified and highlighted. The Australian States and Territories are also identified, and boundaries indicated by the black lines.

Fig. 2: Composite of rainfall anomalies and extreme rainfall occurrence probabilities.

a Climatology of rainfall (mm day^-1) over 1982–2012. b Rainfall anomalies standard deviation (mm day^-1) calculated over 1981–2020. c Monthly rainfall anomalies (mm day^-1) in the EQBO phase (left), WQBO phase (centre), and the EQBO minus WQBO difference (right). d) top-decile weekly rainfall probability relative to climatology in the EQBO phase (left), WQBO phase (centre), and the ratio between EQBO and WQBO (right). The vectors in a) represent the climatology of monthly winds at 850 hPa over 1982–2012. The vectors in b) and c) represent the monthly winds at 850 hPa. The red dots/vectors indicate regions where the values are statistically significant at the 5% level, and the black dots/vectors indicate regions where the values are statistically significant at the 10% level. The wind vectors are defined as statistically significant when either the zonal or meridional wind anomalies are statistically significant.

For the Cape York Peninsula region (identified in Fig. 1) and much of northeast Australia, rainfall anomalies are negative during the EQBO phase and positive during the WQBO phase (Fig. 2c), with the difference statistically significant at the 5% level. The probability of occurrence of extreme rainfall in this region is also higher in the WQBO phase than in the EQBO phase (Fig. 2d). During EQBO, the anomalous air flow is predominantly south-westerly from the dry interior of Australia, whereas in the WQBO phase, the anomalous wind is predominantly easterly from the Coral Sea. The difference in wind anomaly vectors between EQBO and WQBO (statistically significant at the 5% level) suggests that strengthened south-westerly flow during the EQBO phase causes lower rainfall across northeast Australia.

Along Australia’s eastern seaboard, anomalous cyclonic winds occur during the EQBO off the central east coast, bringing anomalous onshore easterlies and increased rainfall to Australia’s south-eastern coastal regions that resembles an East Coast Flow (ECF) pattern⁴⁰. The ECF describes the prevailing austral summer climatological easterly wind flow across Australia’s east coast. This wind transfers moisture from the sea which, when combined with orographic uplift over the Great Dividing Range, results in higher rainfall along the eastern seaboard. For east and southeast Australia, including the southern Murray-Darling Basin to the west of the Great Dividing Range (identified in Fig. 1), rainfall anomalies are negative during the EQBO phase (significant at the 5% level) and positive during WQBO. The rainfall anomaly differences between EQBO and WQBO in this region are statistically significant (at the 5% level). Compared with the WQBO phase, the probability of occurrence of extreme rainfall is significantly lower in the EQBO phase in south-eastern Australia; extreme high rainfall is between 2.5 and 5 times less likely to occur in this region.

Mechanism for rainfall changes around the eastern seaboard

As noted above, we find the circulation difference between EQBO and WQBO phases resembles the East Coast Flow⁴⁰. As the QBO appears to modulate the circulation and associated rainfall along this eastern seaboard region, we now explore the mechanisms here.

In the EQBO phase, enhanced ECF was found across the eastern seaboard region, compared with the WQBO phase (Fig. 2). Figure 3 shows an average vertical cross-section of the vertical velocity anomalies across the eastern seaboard, from 30°S to 37.5°S, for the east coast box identified in Fig. 3a. At around 152.5°E, anomalous upward flow reaches a local maximum and is statistically significant (p < 0.1) from the surface to around 850 hPa in the lower troposphere. Conversely, in the WQBO phase, statistically significant (p < 0.05) anomalous downward motion is identified in the lower troposphere from 850 hPa to the surface. The difference in vertical velocity between the EQBO and the WQBO phases highlights that the difference in upward motion reaches a statistically significant local maximum near 155°E (blue shading in Fig. 3d) where the ECF is defined⁴⁰. Further west, from 140°E to 150°E, there is anomalous downward motion in the EQBO phase compared with the WQBO phase from the mid-troposphere to the lower troposphere.

Fig. 3: Composite of vertical velocity anomalies and wind vectors.

Composite of vertical velocity anomalies (shading) and wind cross-section (vectors) averaged between 30°S to 37.5°S in b) the EQBO phase, c the WQBO phase, and d) the EQBO minus WQBO difference (bottom panel). a The corresponding map from 30°S to 37.5°S and 135°E to 150°E, and the shading in (a) represents the topography (m). In (b)–(d), shading represents vertical velocity anomalies (×1000 Pa s^-1) and vectors represent wind flow anomalies (×1000 Pa s^-1 for vertical velocity and m s^-1 for zonal velocity). The red dots/vectors indicate regions where the values are statistically significant at the 5% level and black dots/vectors indicate regions where the values are significant at the 10% level. The wind vectors are defined as statistically significant when either the zonal or vertical velocity wind anomalies are statistically significant. The black topographic mask represents the highest point at each longitude. The grey topographic mask represents the average height at each longitude.

During EQBO, the stronger ECF results in enhanced upward motion and vertical moisture advection along the Great Dividing Range, contributing to higher precipitation east of the Divide and along Australia’s eastern seaboard. After moving westward across the Great Dividing Range (i.e., west of about 150°E), descending motion during EQBO (Fig. 3b) results in adiabatic warming and reduced rainfall in south-eastern Australia (Fig. 2).

Mechanisms for rainfall changes over western Australia

As shown in Fig. 2c, d, we found that rainfall tends to be enhanced over western Australia during the EQBO phase, whereas rainfall is reduced during the WQBO phase relative to climatology. Our analysis is supported by longitude-height anomaly composites of air temperature and wind flow, averaged between 15°S and 30°S (Fig. 4). Onshore flow of moist air from the Indian Ocean over western Australia during the EQBO phase can be seen with strong anomalous westerly flow in the middle- and lower-troposphere west of 120°E (Fig. 4). This appears to drive a region of relatively cool air near the surface and warm rising air aloft (Fig. 4d), which occurs in conjunction with the increase in rainfall (Fig. 2). This rising air occurs in a region of mid-level horizontal convergence over western Australia, promoting the enhanced convection (shown later) there. This corresponds to increased upward motion over western Australia in the middle-troposphere (shown in Fig. 4). The anomalous circulation during EQBO, which appears as a statistically significant difference (at the 5% level) to that during WQBO, thus drives enhanced rainfall over western Australia.

Fig. 4: Composite of temperature anomalies and winds.

Composite of air temperature anomalies and wind cross-section averaged between 15°S to 30°S in (b) the EQBO phase, (c) the WQBO phase, and (d) the EQBO minus WQBO difference (bottom panel). a The corresponding map from 15°S to 30°S and 15°S to 30°S. Shading represents temperature anomalies (K) and vectors represent wind flow anomalies (×100 Pa s^-1 for vertical velocity and m s^-1 for zonal velocity). The red dots/vectors indicate regions where the values are statistically significant at the 5% level and black dots/vectors indicate regions where the values are significant at the 10% level. The wind vectors are defined as statistically significant when either the zonal or vertical velocity wind anomalies are statistically significant.

Southern Hemisphere Rossby wave pattern

To relate the regional anomalous flow to the global circulation, we plot the geopotential height (GPH) anomalies at 200 hPa (Fig. 5a), 500 hPa (Fig. 5b) and 850 hPa (Fig. 5c). As part of the tropical-extratropical wave structure seen in Fig. 5, the decrease in GPH (most notable at 850 hPa) corresponds to the cyclonic wind anomaly near the Australian east coast in the EQBO phase, in contrast to the weak anticyclonic anomaly that occurs in WQBO (c.f. Fig. 2). Meanwhile, the increase in GPH over southeast Australia at 200 hPa and 500 hPa during the EQBO, relative to the WQBO, indicates an anticyclonic anomaly that supports the rainfall decrease within the southeast Australia box region (Fig. 2), in association with anomalous adiabatic warming at 300 hPa from descending air through the mid-troposphere (Fig. 6). The near-zero outgoing longwave radiation (OLR) anomalies – where significant OLR anomalies are a useful proxy for convection anomalies – in this region (Fig. 7) suggests that the rainfall decrease may be primarily driven by moisture divergence induced by the anomalous circulation.

Fig. 5: Composite of geopotential height anomalies and wind anomalies.

Composite of geopotential height anomalies (m; contours) and wind anomalies (m s^-1; vectors) at (a) 200 hPa, (b) 500 hPa and (c) 850 hPa in the EQBO phase (left panel), the WQBO phase (middle panel), and the EQBO minus WQBO difference (right panel). The red dots/vectors indicate regions where the values are statistically significant at the 5% level and black dots/vectors indicate regions where the values are significant at the 10% level. The wind vectors are defined as statistically significant when either the zonal or meridional wind anomalies are statistically significant.

Fig. 6: Composite of vertical velocity anomalies at 300 hPa.

Composite of vertical velocity anomalies at 300 hPa (unit: Pa s^-1) in the EQBO phase (top panel), the WQBO phase (middle panel), and the EQBO minus WQBO difference (bottom panel). The red dots indicate regions where the values are statistically significant at the 5% level and black dots indicate regions where the values are significant at the 10% level.

Fig. 7: Composite of outgoing longwave radiation anomalies.

The same as Fig. 6, but for outgoing longwave radiation anomalies (W m^-2).

In addition to the wave train emanating from the Maritime Continent / western Pacific Ocean sector, there exists a second concurrent wave train to the west of Australia that drives negative GPH anomalies at 500 hPa and 850 hPa off Australia’s west coast in the EQBO phase (whereas GPH anomalies are positive during WQBO; Fig. 5). This emanates from the central South Atlantic Ocean to the east of South America and combines with the mid-latitude zonal wave. The barotropic wave structure appears as a strong EQBO-minus-WQBO signal centred near 80°E at all levels (significant at 200 hPa and 500 hPa) that spans the southern Indian Ocean from 60°E to 100°E and 30°S to 35°S.

The negative GPH anomalies extend to western Australia where they are associated with anomalous ascending air at 300 hPa (Fig. 6) in concert with increased rainfall (c.f. Fig. 2). Notably, these GPH and circulation flow anomalies appear to be the combined product of (i) the baroclinic response at the equator to the QBO’s influence on tropical convective heating, and (ii) the barotropic response in the mid-latitudes associated with the extra-tropical Rossby wave trains that emanate from the central South Atlantic Ocean.

Outgoing longwave radiation

Here, we describe the QBO’s modulation of the OLR distribution, that is a proxy of convective heating. For northeast Australia, a significant decrease in convection (positive OLR anomalies) during EQBO compared to WQBO (Fig. 7, bottom) is consistent with the decrease in rainfall (Fig. 2, far right). Conversely, for western Australia, a significant increase in convection (negative OLR anomalies) during EQBO compared to WQBO is consistent with the increase in rainfall there.

As mentioned in the introduction, the Gill type²⁸ baroclinic response to tropical diabatic heating at the equator relates to the tropical-extratropical Rossby wave. In correspondence with the generation of the Rossby wave pattern over the central South Atlantic Ocean, there exists an anomalous increase in convection to the east of South America during the EQBO phase. One likely mechanism is that the QBO potentially influences the movement of the subtropical jets. There also exists an anomalous increase in convection east of the Maritime Continent centred near 155°E during EQBO, indicated by a statistically significant (at the 10% level) decrease in OLR in the western equatorial Pacific Ocean (Fig. 7, top panel), while an anomalous decrease in equatorial convection exists further east near 170°W during WQBO (Fig. 7, middle panel). The EQBO minus WQBO difference shows a strong increase in convection spans the western half of the tropical Pacific (Fig. 7, bottom panel) in the EQBO phase relative to the WQBO phase.

Next, we explore the mechanisms underpinning the QBO’s influence on equatorial convection. In the EQBO phase, positive temperature anomalies are evident at altitudes above 50 hPa (mid-stratosphere) and negative anomalies at altitudes below 50 hPa (Fig. 8b). In contrast, we observe a colder (negative temperature anomalies) mid- to upper-stratosphere and warmer (positive temperature anomalies) lower-stratosphere in the WQBO phase (Fig. 8c). This is consistent with the consequence of the thermal wind balance in each QBO phase.

Fig. 8: Composite of air temperature and static stability anomalies.

Composite of air temperature anomalies cross-section (averaged between 10°S and 10°N) in the (b) EQBO phase, (c) the WQBO phase, (d) and the EQBO minus WQBO difference. a The corresponding map between 10°S and 10°N along the equator. Shading represents temperature anomalies (K). The red dots indicate regions where the values are statistically significant at the 5% level and black dots indicate regions where the values are significant at the 10% level. e zonal distribution of static stability climatology (solid black line). The static stability difference (blue dashed-dotted line), temperature anomaly difference (green dotted line) and temperature anomaly difference (red dashed line) between the EQBO and the WQBO. All the variables are averaged between 10°S and 10°N and plotted along the equator.

To link the stratosphere to the upper troposphere, we define the upper-tropospheric static stability as the temperature difference between 100 hPa and 200 hPa, which has been applied in previous studies and is associated with the QBO via the thermal wind^21,23. Figure 8e shows the zonal distribution of static stability for the climatological mean (black solid line) and the difference between EQBO and WQBO phases (blue dash-dotted line). The climatological mean static stability (black solid line in Fig. 8e) minimum to the east of the Maritime Continent (at 152.5°E) provides the low-static stability background. Consistently, the negative difference in static stability between EQBO and WQBO phases is found to the east of the Maritime Continent. From the Maritime Continent and east across the western Pacific (from 120°E to 180°E), the temperature anomaly difference between EQBO and WQBO phases at 200 hPa is close to zero (red line in Fig. 8e) and is not statistically significant (Fig. 8d). Since the static stability depends on the temperature at 200 hPa and 100 hPa, therefore the static stability difference is attributed to the temperature difference at 100 hPa between 120°E to 180°E.

Rossby wave source

To understand the relationship between the convective heating and the origin of Rossby waves, the composition of the Rossby wave source (RWS) was analysed (Fig. 9). In the EQBO phase (top panel), an anticyclonic Rossby wave source to the east of the Maritime Continent from 148°E to 172.5°E is associated with southward divergent flow induced by the enhanced convection. In the WQBO phase (middle panel), a weak cyclonic Rossby wave source appears to the east of the Maritime Continent, slightly to the east of the positive anticyclonic Rossby wave source in the EQBO phase. The anomalous anticyclonic Rossby wave source during the EQBO phase appears to drive an anomalous cyclonic circulation across the north of Australia, a signature amplified in the difference between the EQBO and WQBO phases (significant at the 10% level).

Fig. 9: Composite of Rossby wave source and divergent wind anomalies.

Composite of Rossby wave source (contours) and divergent wind anomalies (m s^-1; vectors) at 200 hPa in the EQBO phase (top panel), the WQBO phase (middle panel), and the EQBO minus WQBO difference (bottom panel). The box region covers the area from 148°E to 172.5°E and 0° to 10°S. The red dots/vectors indicate regions where the values are statistically significant at the 5% level and black dots/vectors indicate regions where the values are significant at the 10% level. The wind vectors are defined as statistically significant when either the zonal or meridional wind anomalies are statistically significant.

Over the central South Atlantic Ocean, a positive Rossby wave source is apparent in the EQBO phase, accompanied with the southward divergent wind, which is opposite in sign to the signature during the WQBO phase. This corresponds to an anomalous cyclonic circulation in the EQBO phase and anomalous anticyclonic circulation in the WQBO phase at 200 hPa (upper troposphere). This Rossby wave source induces the cyclonic-anticyclonic wave pattern which propagates through to the Southern Hemisphere mid-latitudes.

Rossby wave trajectories

To diagnose the Rossby wave trajectories, the Rossby wave wavenumber (${K}_{S}$) and wave activity flux (WAF) at 200 hPa and 850 hPa were analysed (Fig. 10a and Fig. 10b, respectively). At these upper- and lower-troposphere pressure levels, the two-dimensional wave pattern is similar in form in the EQBO and WQBO phases.

Fig. 10: Composite of Rossby wavenumber and wave activity flux anomalies.

Composite of Rossby wavenumber ${K}_{S}$ and WAF anomalies (vectors, m²s^-2) at (a) 200 hPa and (b) 850 hPa in the EQBO phase (upper panel), the WQBO phase (lower panel). ${K}_{S}$ is masked where $\bar{U}$ < 0, (easterly wind, enclosed by green contours) and where the meridional gradient of absolute vorticity (${\beta }^{* }$) is negative (enclosed by magenta contours).

Over the central South Atlantic Ocean, the positive Rossby wave wavenumber in the upper troposphere (200 hPa, Fig. 10a) provides the pathway for the Rossby wave train to propagate poleward to the mid-latitudes. The Rossby wave is then guided by the mid-latitude westerly jets and propagates eastward. Over the South Indian Ocean, the wave train appears to propagate northward to Australia’s west coast. However, in the lower troposphere (850 hPa, Fig. 10b), the easterly winds (enclosed by the green contour) over the central South Atlantic Ocean prohibit the propagation of the Rossby wave from the Atlantic Ocean into the mid-latitudes. This indicates that the Rossby wave that emanates from the central South Atlantic Ocean can only propagate into the mid-latitudes in the upper troposphere.

To the east of the Maritime Continent, ${K}_{S} \,<\, 0$ and the Rossby wave propagation is limited by the easterly wind (enclosed by the green contour) in the upper troposphere (200 hPa, Fig. 10a). However, Gillett, et al.⁴¹ proposed that the Rossby wave can propagate at altitudes below (i.e., underneath) those where ${K}_{S} \,<\, 0$. As shown in Fig. 10b, ${K}_{S} \,>\, 0$ at 850 hPa (lower troposphere) in the southwest Pacific band around 10°S, and which extends from the South Indian Ocean west of the Maritime Continent, but ${K}_{S} \,<\, 0$ between 10°S and 30°S. However, there is a strong wave activity flux region to the north and northeast of Australia (vectors in Fig. 10b) which occurs in this 10°S region where ${K}_{S} \,>\, 0$. This exhibits strong convergence of the wave activity flux into the subtropical jet region where ${K}_{S} \,<\, 0$. The wave activity flux is generated on the poleward side of the jet, near New Zealand, showing a continuous Rossby wave train propagating from the Maritime Continent into the higher latitudes.

Discussion

This study comprehensively investigates the importance of the stratospheric quasi-biennial oscillation (QBO) on Australia’s summer rainfall variability and extremes. We have identified and quantified statistically significant relationships between QBO phase and the distribution of rainfall anomalies across the Australian continent and investigated the likely mechanisms underpinning these teleconnections. Importantly, we show clear evidence that the QBO modulates the teleconnection of the baroclinic response to convective heating in the western equatorial Pacific, to the east of the Maritime Continent, and over the central South Atlantic Ocean. The baroclinic response to adiabatic heating in the western equatorial Pacific and barotropic wave-structure over the mid-latitude Atlantic Ocean modulate the Southern Hemisphere extratropical circulation and induce anomalous flows across Australia’s east and west coasts. The anomalous cyclonic (anticyclonic) circulation in the EQBO (WQBO) phase induces statistically significant rainfall anomalies across the Australian continent. The QBO’s influence on rainfall is highlighted across northeast Australia, the eastern seaboard region, and across Australia’s southeast and southwest regions.

In austral summer, the EQBO-related wind shear leads to lower temperatures in the upper troposphere and lower static stability in the tropics. In the WQBO phase, the higher temperatures are in the upper troposphere and higher static stability is evident in the tropics. This is consistent with mechanisms proposed in previous studies^19,23. Over the western tropical Pacific, the climatological low static stability along the equator is evident to the east of the Maritime Continent and contributes to the formation of tropical tropopause layer (TTL) cirrus cloud⁴². The easterly (westerly) wind shear In the EQBO (WQBO) phase induces negative (positive) temperature anomalies in the lower stratosphere (100 hPa)¹⁵. During the EQBO (WQBO) phase, the increased (decreased) formation of cirrus cloud is likely to be responsible for the negative (positive) temperature anomalies at 100 hPa, corresponding to enhanced (suppressed) convection. The mechanism is consistent with the cirrus cloud radiative feedback that induces a stronger cold cap and a destabilised tropopause at 100 hPa driven by the MJO^{19,23,24,42,43,44}. The upper-tropospheric ice cloud fraction is associated with the deep convection⁴⁴. This is also a likely mechanism why the highlighted OLR difference between EQBO and WQBO phases appears in the western equatorial Pacific region. Yamazaki and Nakamura³⁸ previously investigated the QBO’s modulation of the Southern Hemisphere atmospheric Rossby wave train in the austral winter season. However, their study found no significant difference in the Rossby wave pattern between the EQBO and WQBO phases near Australia (Fig. 3 by Yamazaki and Nakamura³⁸). We contend that the teleconnection of the QBO on Australia’s rainfall depends on seasonal influences of the atmospheric convection along the equator.

In response to enhanced tropical convection over the Maritime Continent and western equatorial Pacific during the EQBO phase, an atmospheric Rossby wave train emanates and propagates poleward, and anomalous cyclonic circulation is produced across Australia’s eastern seaboard. In contrast, the suppressed convection over the Maritime Continent and western equatorial Pacific during the WQBO phase is found to induce an anomalous anticyclone over coastal eastern Australia. The easterly wind anomalies and negative wavenumber at 200 hPa limit the extent of the Rossby wave propagation to the east of Maritime Continent. However, in agreement with Gillett, et al.,⁴¹ the Rossby wave can propagate through the lower troposphere (seen at 850 hPa). We found that the strong wave activity flux converges in the subtropical region in the lower troposphere and then the Rossby wave propagates continuously as a train from the western South Pacific to the mid-latitudes. The mechanism here for the western South Pacific is consistent with that proposed by Mcintosh and Hendon⁴⁵ for the Rossby wave propagation in the South Indian Ocean.

The increased geopotential height in the lower troposphere and cyclonic circulation induced by the atmospheric Rossby wave train emanating from the tropical western Pacific warm pool region were found to be characteristic features associated with the lower rainfall in southeast Australia. We found that the probability of extreme high rainfall (identified by the top rainfall decile) across southeast Australia was significantly lower during the EQBO phase than during the WQBO phase. This indicates a potential predictor of rainfall variations that affect agriculture – including rice, cotton and grapes – of the southern Murray-Darling Basin (MDB) region⁴⁶, with relevant lead information providing potential benefits to water management in the MDB region⁴⁷.

This study has shown that the QBO phase-dependent anomalous circulations in the middle and lower troposphere can lead to altered zonal flows and enhanced temperature and moisture advection from the South Indian Ocean to western Australia. The upper troposphere geopotential height and circulation exhibit a Rossby wave train that emanates from the central South Atlantic Ocean. The barotropic wave structure induces an anomalous circulation in the middle and lower troposphere. During the EQBO phase, we found that there is an anomalous cyclonic circulation near the northwest Australian shelf in conjunction with enhanced convection and cooler near-surface conditions. The intrusion of the cold anomalies across the western Australian coast leads to increased rainfall over much of western Australia during the EQBO phase. This signal is particularly important for parts of subtropical western Australia, such as the Gascoyne and Pilbara regions, which sit under the subtropical ridge for much of the year and are typically influenced by dry conditions in austral winter and tropical cyclones in austral summer^48,49,50,51.

Taken together, it appears that the QBO modulates the baroclinic response to tropical diabatic heating and impacts the barotropic structure of the extra-tropical Rossby wave train (Fig. 5), where it acts to produce regional rainfall anomalies across Australia (Fig. 2). The QBO affects the tropical diabatic heating and related divergent winds but seems to have no impact on the Rossby wave tracks in the Southern Hemisphere. In the EQBO phase, the Rossby wave that emanates from the tropical western Pacific warm pool induces an anomalous cyclonic circulation along Australia’s east coast that causes high rainfall over the eastern seaboard and low rainfall across the broader southeast Australia. The Rossby wave emanating from the central South Atlantic Ocean contributes to an unstable atmosphere and increased rainfall over western Australia, and the anomalous circulation corresponds to reduced rainfall over northeast Australia.

Understanding the drivers of Australian summer rainfall can be beneficial to improving our understanding of Australia’s water security⁵² and potential flood and drought risk^53,54. Importantly, the relevant climate drivers that provide rainfall potential predictability at various lead times can be beneficial to enable appropriate management response strategies⁵⁵. This study contributes to better understanding of potential predictability of Australian summer rainfall through our understanding of the influence of the QBO on Southern Hemisphere circulation and local forcing of Australian summer rainfall. Our study focus has been on how the QBO influences Australia’s summer rainfall via tropical to mid-latitude Rossby wave teleconnections which act to modulate the extra-tropical circulation. Previous studies have proposed that ENSO impacts the amplitude and period of the QBO⁵⁶. Hence, it would be beneficial in future studies to also examine the potentially compounding effect of the QBO combined with other climate drivers (e.g., ENSO) on Australia’s regional rainfall, as well as other regions across the Southern Hemisphere.

Methods

Observational data

The gridded (mapped) observations analysed in this study are focused on austral summer daily rainfall totals across Australia (see Fig. 2) from December to February in the years from 1981 to 2020. These precipitation data are the gridded analyses from the Australian Bureau of Meteorology’s Australian Water Availability Project (AWAP)/Australian Gridded Climate Dataset (AGCD) v1⁵⁷, available on a 5-km grid. The data are based on an optimum interpolation of station observations available across Australia⁵⁷. The AGCD combines available rainfall data with state-of-the-art statistical modelling and the latest in scientific techniques to provide accurate information on rainfall and temperature across Australia⁵⁷. In this study, monthly rainfall data were used for the composite analysis of average rainfall in different QBO phases. Daily data were used to analyse extreme rainfall.

This study also used reanalysis data from the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/ NCAR) global reanalysis version 1 (NNR1)⁵⁸. The topography dataset was obtained from https://www.ncei.noaa.gov/products/etopo-global-relief-model. The outgoing longwave radiation (OLR) data were from the NOAA interpolated OLR dataset (https://www.psl.noaa.gov/data/gridded/data.olrcdr.interp.html). The sea surface temperature (SST) data were from the US National Oceanic and Atmospheric Administration (NOAA) Optimum Interpolation Sea Surface Temperature version 2 (OISST2) high-resolution dataset^59,60. Monthly mean fields were available on a 2.5° horizontal grid. A two-sided t-test was applied to test for statistical significance.

For the rainfall and reanalysis data, the long-term trends were firstly computed by linear regression and then removed from both the monthly and daily data. Next, the monthly and daily anomalies were computed relative to the climatology from 1982 to 2012.

QBO index

The QBO index is defined as the monthly zonal mean zonal wind at 50 hPa along the equator⁶¹, which we compute using the NNR1 dataset. The phase of the QBO was defined as easterly (EQBO) when the index was negative, and westerly (WQBO) when the index was positive. We define here the occurrence of an EQBO or WQBO summer when all three summer months (December-January-February) correspond to the same QBO phase. Hence, we detect 14 years of EQBO summers and 18 years of WQBO summers across the 39-year record, with 7 years being classified as QBO-neutral years.

Definition of extreme rainfall

Extreme rainfall was defined as seven-day running mean values exceeding the 90^th percentile in each season. This is a somewhat conservative but more statistically reliable estimate of the extreme rainfall, acting to smooth the results, and assuming some persistence of these climatic extremes. Extreme-event probability was calculated using the number of occurrences of extreme rainfall divided by the number of days in the chosen period, where the climatological probability was 0.1. Shown in Eq. (1), the probability anomalies were defined as the ratio of the probability of occurrences of each QBO phase composite and the climatological probability¹¹. The probability of occurrences of extreme rainfall is defined as the ratio between the number of occurrences (${{\rm{N}}}_{{\rm{EQBO\; or\; WQBO}}}$) and the number of days in the EQBO or WQBO phase (${{\rm{N}}}_{{\rm{days\; in\; EQBO\; or\; WQBO}}}$),

$${\rm{R}}=\frac{{{\rm{P}}}_{{\rm{EQBO\; or\; WQBO}}}}{{{\rm{P}}}_{{\rm{clima}}}}=\frac{{{\rm{N}}}_{{\rm{EQBO\; or\; WQBO}}}/{{\rm{N}}}_{{\rm{days\; in\; EQBO\; or\; WQBO}}}}{0.1}$$

(1)

Equation (2) represents the extreme rainfall probability ratio between the EQBO and WQBO phases, defined specifically as the ratio of the probability of occurrence of extreme rainfall in the EQBO phase (${{\rm{P}}}_{{\rm{EQBO}}}$) composite relative to the WQBO composite (${{\rm{P}}}_{{\rm{WQBO}}}$),

$${{\rm{R}}}_{{\rm{diff}}}=\frac{{{\rm{P}}}_{{\rm{EQBO}}}}{{{\rm{P}}}_{{\rm{WQBO}}}}=\frac{{{\rm{N}}}_{{\rm{EQBO}}}/{{\rm{N}}}_{{\rm{days\; in\; EQBO}}}}{{{\rm{N}}}_{{\rm{WQBO}}}/{{\rm{N}}}_{{\rm{days\; in\; WQBO}}}}$$

(2)

Significance test

A two-sided t-test⁶² was applied to assess statistical significance of the rainfall anomalies and reanalysis data composited in each QBO phase, as well as their difference between EQBO and WQBO phases. The vectors were defined as statistically significant when either the x- or y- component is statistically significant. The z-test for probability⁶³ of extreme rainfall occurrences was applied to establish statistical significance of the probability ratio, where it was assumed that the weekly-mean data in the EQBO and WQBO phases comprised of independent samples. The probability ratio for the occurrence of extreme rainfall was assumed to be statistically significant when $\left|{\rm{z}}\right|$ > 1.96 (5% significance level) or >1.645 (10% significance level).

For monthly and weekly mean rainfall, the autocorrelation was considered and the effective sample size was calculated as follows: ${{\rm{N}}}_{{\rm{eff}}}\cong {\rm{N}}\frac{1-{\rm{r}}}{1+{\rm{r}}}$, following Wheeler, et al.⁴ Here, r represents the lag-1 auto-correlation coefficient of the monthly rainfall anomaly or weekly mean rainfall anomaly in each grid box for each QBO phase. N represents the number of months for monthly rainfall and the number of days for weekly-mean rainfall.

Multivariate linear regression

ENSO has been shown to modulate the teleconnection between the stratospheric QBO and extratropical climate^38,56,64. Kuroda and Yamazaki⁶⁵ propose that the SAM is modulated by the QBO from October to December. In this study, multivariate linear regression was applied to the rainfall and reanalysis data to remove the ENSO and SAM signals, to better isolate the contribution from the QBO on Australia’s rainfall. A description of the indices and their sources are shown in Supplementary Table 1. To remove the eastern and central Pacific El Niño signals, the Niño3.4 index and ENSO Modoki index (EMI) were used. To remove the SAM signal, the Climate Prediction Center (CPC) Antarctic oscillation index was used. The equation for the multivariate regression that was applied is

$${{\rm{Var}}}_{{\rm{remove}}}={{\rm{Var}}}_{{\rm{Anomaly}}}-{{\rm{b}}}_{1}{\rm{Ni}} \tilde{{\rm{n}}}{\rm{o}}34-{{\rm{b}}}_{2}{\rm{EMI}}-{{\rm{b}}}_{3}{\rm{SA}}{{\rm{M}}}_{700{\rm{hpa}}}$$

(3)

Here, Var_Anomaly represents a particular variable anomaly, which could be any variable from the reanalysis data or the rainfall observations. The b_i represents the regression coefficients on the various climate mode indices. In this case, monthly indices were applied to the monthly rainfall and reanalysis data, and weekly-mean indices were applied to the weekly-mean rainfall data.

Rossby wave source, wave activity flux and wave numbers

Enhanced convective heating at the equator drives an anomalous divergent wind in the upper troposphere, which tends to excite and activate a Rossby wave train from the tropics into the higher latitudes^32,33,34,66. To diagnose the generation of the Rossby wave, the Rossby wave source (RWS) anomaly⁶⁷ is defined by the following equation:

$${\rm{RWS}}=-{{{\bf{v}}}^{{\prime} }}_{\chi }\cdot {\boldsymbol{\nabla }}\bar{\zeta }-\bar{\zeta }{D}^{{\prime} }\approx -{{{\bf{v}}}^{{\prime} }}_{\chi }\cdot {\boldsymbol{\nabla }}\bar{\zeta }$$

(4)

where $\zeta$ is the two-dimensional absolute vorticity, ${{\bf{v}}}_{\chi }$ is the divergent wind vector component, and D is the divergence of the horizontal wind vector. The prime and overbar represent the anomaly and mean climatology components (from 1982 to 2012), respectively. From Eq. (4), the RWS can be divided into two source components: S1 (${{{\bf{v}}}^{{\prime} }}_{\chi }\cdot {\boldsymbol{\nabla }}\bar{\zeta }$) represents the advection of the climatological mean absolute vorticity by the divergent wind anomaly, and S2 ($\bar{\zeta }{D}^{{\prime} }$) represents the vortex stretching term⁶⁸. Previous studies show that S1 (${{{\bf{v}}}^{{\prime} }}_{\chi }\cdot {\boldsymbol{\nabla }}\bar{\zeta }$) is more efficient for the RWS generated by convective heating^31,67. The RWS is calculated using the windspharm Python package⁶⁹.

Using wave tracing theory^70,71, the total wavenumber K for stationary Rossby waves (${K}_{S}$) is defined by Eq. (5). It is derived from the dispersion relation, assuming the zonal wavenumber is constant along the trajectory⁷¹. Here, $\bar{U}$ is the mean zonal flow, and ${\beta }^{* }$ is the meridional gradient of mean absolute vorticity which is defined in Eq. (6). In Eq. (6), f is the Coriolis parameter and y is the meridional spatial coordinate. From Eq. (5), ${K}_{S}$ will be real for regions where ${\beta }^{* }$ and $\bar{U}$ are positive. When the gradient of mean absolute vorticity (${\beta }^{* }$) is negative or zero, the ray paths of the Rossby wave will be reflected, and the propagation will be prohibited⁷⁰.

$$K={K}_{S}=\sqrt{\frac{{\beta }^{* }}{\bar{U}}}$$

(5)

$${\beta }^{* }=\frac{{df}}{{dy}}-\frac{{\partial }^{2}\bar{U}}{\partial {y}^{2}}$$

(6)

To diagnose the propagation of a stationary Rossby wave, the two-dimensional wave activity flux (WAF), here written as ${\bf{W}}$, is defined in Eq. (7)⁷² as:

$${\bf{W}}=\frac{{pcos}\varphi }{2\left|{\bf{U}}\right|}\left(\begin{array}{ll}{\frac{u}{{a}^{2}{cos }^{2}\varphi }\left[{\left(\frac{\partial \psi ^{\prime} }{\partial \lambda }\right)}^{2}-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial {\lambda }^{2}}\right]+\frac{v}{{a}^{2}cos \varphi }\left[\frac{\partial \psi ^{\prime} }{\partial \lambda }\frac{\partial \psi ^{\prime} }{\partial \varphi }-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial \lambda \partial \varphi }\right]}\\{\frac{u}{{a}^{2}cos \varphi }\left[\frac{\partial \psi ^{\prime} }{\partial \lambda }\frac{\partial \psi ^{\prime} }{\partial \varphi }-\psi^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial \lambda \partial \varphi }\right]+\frac{v}{{a}^{2}}\left[{\left(\frac{\partial \psi ^{\prime} }{\partial \varphi }\right)}^{2}-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial {\varphi }^{2}}\right]}\end{array}\right)$$

(7)

Here, $u$ and $v$ are the zonal and meridional components of the wind velocity, respectively. $\left|{\bf{U}}\right|$ represents the magnitude of the long-term background flow. $\psi ^{\prime}$ is the steamfunction anomaly, derived from the geopotential height anomaly based on the quasi-geostrophic approximation⁷³. $\lambda$ and $\varphi$ are the longitude and latitude coordinates, respectively. $p$ represents the pressure level, and $a$ is the radius of the Earth. The WAF (${\bf{W}}$) describes the perturbation on a two-dimensional horizontal basic background flow⁷². For stationary Rossby waves, the direction of the WAF is parallel to the Rossby wave trajectory.