Introduction

Air pollution is a persistent problem in developing countries, such as China and other emerging economies experiencing rapid industrialization1,2,3. Among the pollutants, the principal culprit is fine particulate matter (PM2.5), the airborne particles that can penetrate into human lungs, leading to premature deaths from cardiovascular and respiratory diseases and lung cancer4,5. To mitigate PM2.5 and its public health impacts, the Chinese government renewed its air-quality policies in 2021, aiming for a 10% reduction of urban PM2.5 concentration by 20256. Achieving this objective requires a clear understanding of the atmospheric chemistry producing PM2.5 in urban haze.

China’s haze differs from London fog or Los Angeles smog in several ways. First, gas pollutants coexist at high concentrations3,7,8,9, including SO2, NOx (NO and NO2), and NH3, emitted from industry, traffic, and agriculture10,11,12. These gases convert synergistically into PM2.5 through atmospheric multiphase reactions3,7,8,9. Second, the multiphase reactions occur rapidly, much faster than what aqueous chemistry predicts8,13,14,15. Such rapid kinetics may result from many factors, including enhanced chemical reactivities at the air-water interface14,16,17, the catalytic effects of transition metal ions (TMI)13,18, or the salt effects in the oversaturated aerosol water15,19 – or all these factors acting simultaneously. Recognizing these characteristics, scientists coined the term haze chemistry to describe how PM2.5 is formed during the severe urban air pollution in China3,7,8,9,20.

A decade-long debate in haze chemistry research concerns whether NO2 can effectively oxidize SO2 into sulfate, thereby contributing to PM2.5 formation. Why is NO2 considered an oxidizer of SO2? First, this redox reaction can occur in the atmospheric environments; NO2 can oxidize SO2 on the surfaces of primary particles (i.e., soot21 and dust9) and, more prevalently, in aerosol water7,22,23,24:

$$2{{\rm{NO}}}_{2\left({\rm{aq}}\right)}+{{\rm{HSO}}}_{3\left({\rm{aq}}\right)}^{-}+{{\rm{H}}}_{2}{\rm{O}}\to {{\rm{H}}}_{\left({\rm{aq}}\right)}^{+}+{2{\rm{HONO}}}_{\left({\rm{aq}}\right)}+{{\rm{SO}}}_{4\left({\rm{aq}}\right)}^{2-}$$
(Reaction 1)

Additionally, NO2 is abundant in the urban haze, especially when photochemical oxidizers such as O3, H2O2, and OH are inhibited in the polluted troposphere dimmed by haze8 or at night25. Field campaigns in China8,26,27 showed that sulfate and NO2 concentrations are positively correlated. A Beijing campaign25 found that the HONO produced by Reaction 1 can even further oxidize SO2. An air-quality model8 predicted that, at pH 5.8, the reaction between \({{\rm{HSO}}}_{3}^{-}\) and NO2 (hereafter, the \({{\rm{HSO}}}_{3}^{-}\)/NO2 reaction, and so forth) would produce sulfate by a rate of 10 µg m−3air hr−1. A laboratory study14 found that, at pH 6, a \({{\rm{SO}}}_{3}^{2-}\)/NO2 reaction would produce sulfate by 90 µg m−3air hr−1. These studies suggested that sulfate PM2.5 in China’s haze was produced mainly through the NO2 reaction pathway.

Yet equally compelling evidence indicates that NO2 contributed to SO2 oxidation negligibly. Although Reaction 1 can occur in the aqueous phase, it is unlikely to occur through a direct electron transfer, because the redox potentials between aqueous \({{\rm{HSO}}}_{3}^{-}\) and NO2 are close28,29. The reaction instead occurs through the formation of [NO2-SO3]2- adducts, which decompose to \({{\rm{SO}}}_{3}^{-}\) radicals slowly28. This kinetic constraint rules out a rapid sulfate formation through Reaction 1. Additionally, the average pH of urban aerosols in China30 is approximately 4, which is more acidic than what previous studies have assumed8. At acidic conditions, SO2 has limited solubility, leaving too few S(IV) ions (\({{\rm{HSO}}}_{3}^{-}\) and \({{\rm{SO}}}_{3}^{2-}\)) to facilitate a rapid sulfate formation13,31. At pH 4, the sulfate formation rate via \({{\rm{HSO}}}_{3}^{-}\)/NO28 and \({{\rm{SO}}}_{3}^{2-}\)/NO214 reactions are respectively 0.04 and 0.15 µg m−3air hr−1. Recent air-quality models13,32 showed that the \({{\rm{HSO}}}_{3}^{-}\)/NO2 reaction contributed approximately 0.1% of sulfate13; the \({{\rm{SO}}}_{3}^{2-}\)/NO2 reaction, approximately 0.4%32. A source apportion study31 showed that the NO2 reaction pathway contributed at most 1% of sulfate in China haze. A recent global-scale study33 found that the NO2 reaction pathway is unimportant unless aerosol pH is above 5, a condition rarely met worldwide.

These disagreements8,25,26,27,28,29,30,33 indicate a knowledge gap regarding how sulfate is produced in urban air pollution. Why does it matter whether NO2 contributes to sulfate formation? If so, then both SO2 and NO2 would be sulfate precursors, and effective abatement would require closer coordination between the industry and transportation sectors3,7,8,9,10,11. Bridging this knowledge gap requires us to answer the following question: Can the multiphase SO2 oxidation by NO2 occur rapidly at acidic conditions?

Here, we show that NO2 can oxidize SO2 into sulfate rapidly at acidic conditions when the reaction is catalyzed by copper (hereafter, Cu). Cu, albeit a transition metal, is a weak catalyst for S(IV) oxidation by O234. But Cu is a strong catalyst for NO2 reduction by S(IV) in flue gas de-nitrification35,36. Additionally, Cu is ubiquitous in urban air pollution37. A field campaign38 reported that Cu elements were on the orders of hundreds of ng m−3air during the air pollution in North China Plain (NCP). In Beijing, Cu mainly originates from traffic emissions, i.e., brake and tire wear39; in the broader NCP region, Cu mainly originates from coal combustions39. On the other hand, NO2 originates from both industrial and traffic emissions11,12, and its concentration can reach 40-to-80 ppb during heavy air pollution in NCP8. In other words, Cu and NO2 are companion emitters, and they may synergistically convert SO2 into sulfate during urban haze. Furthermore, we show that the kinetics of the ternary Cu/SO2/NO2 reaction depends more sensitively on NO2 concentration, rather than on SO2 concentration. This may explain why, over the past decade, a substantial decrease in SO2 emission has not led to a proportional decrease in sulfate concentration in China.

Results

Method summary

We studied the Cu-catalyzed reaction with Raman micro-spectrometry (hereafter, micro-Raman) and an aerosol optical tweezer (hereafter, AOT). The micro-Raman experiments provided information on the reaction mechanism, including the reaction products, the catalytic effect of Cu(II) ions, and kinetic dependence on droplet size (radius 5–30 µm) and acidity (pH 3–5). The AOT experiments provided kinetic data for the reactions in levitated droplets, under conditions closely mimicking urban air pollutions, such as droplet solute ((NH4)2SO4), acidity (pH 4), relative humidity (RH 60%), and reactant gases mixing ratio (SO2, 5–200 ppb; NO2, 50–500 ppb), and reaction time (hours). We designed these experiments based on literature values of aerosol pH13,30, gas concentrations8, and RH conditions14. Specifically, the ranges of these parameters encompass their average values during severe pollution events in Beijing (i.e., pH 4, SO2 40 ppb, NO2 66 ppb). Refer to the Methods section for details.

Copper-catalyzed SO2 oxidation by NO2

Figure 1A shows the Raman spectra of microdroplets, which served as reactors for the oxidation of SO2 (500 ppb) by NO2 (500 ppb). Droplet pH was buffered at approximately 4 with 400 ppb NH340. Ambient RH was approximately 80%. The left panel represents the reaction catalyzed by Cu(II) ions in the microdroplet seeded with a mixture of NH4Cl/HCl/CuCl2 (1:0.005:0.001). Here, the Raman spectrum exhibits a peak around 980 cm−1, indicating \({{\rm{SO}}}_{4}^{2-}\) formation (See Figure S1 for the full spectrum). This catalyzed reaction produced approximately 0.4 M sulfate in 240 min. Contrastingly, the right panel represents the uncatalyzed reaction in the microdroplet seeded with NH4Cl/HCl (1:0.005). This uncatalyzed reaction was too slow to be measured with the micro-Raman. In Figure S2, the AOT data shows that the reaction catalyzed by 0.1% Cu-in-solute was faster than the uncatalyzed reaction by two orders of magnitude. In both cases, the reaction did not produce \({{\rm{NO}}}_{3}^{-}\), which would exhibit a Raman peak at 1050 cm−3. In other words, NO2 served only as an oxidizer of SO2 and did not undergo disproportionation at our experimental conditions. Figure S3 shows another control experiment, where NO2 was not applied, and no sulfate was produced within 240 min.

Fig. 1: Cu-catalyzed oxidation of SO2 by NO2 at droplet surface.
figure 1

A In-situ Raman spectra of the microdroplets during the oxidation of SO2 (500 ppb) by NO2 (500 ppb). The left panel represents a droplet initially comprising a mixture of NH4Cl/HCl/CuCl2 (1:0.005:0.001); the reaction was catalyzed by 0.1%Cu-in-solute. The right panel, a droplet initially comprising NH4Cl/HCl (1:0.005). For both droplets, the pH was buffered at 4 with 400 ppb ambient NH3. The color indicates reaction time. The peak at 980 cm-1 was attributed to \({{\rm{SO}}}_{4}^{2-}\). B–D Reaction rate determined from Raman microspectrometry (micro-Raman). B During reactions, sulfate (\({{\rm{SO}}}_{4}^{2-}\)) molar concentration increased linearly with time. The size of the circle indicates droplet radius, \(a\). The color indicates droplet pH. Conditions were 500 ppb SO2 and 500 ppb NO2. Droplets comprised a NH4Cl/HCl/CuCl2 mixture (1:0.005:0.001) and were buffered at pH approximately 3, 4, or 5 with 40, 400, or 4000 ppb NH3, respectively. C Sulfate formation rate (\(d\left[{{\rm{SO}}}_{4}^{2-}\right]/{dt}\)) scales inversely with droplet radius \(a\) (red dotted line). The color indicates droplet pH. Error bar represents the 95% confident interval values of \({{\rm{SO}}}_{4}^{2-}\) formation rate, determined by linearly fitting the \(\left[{{\rm{SO}}}_{4}^{2-}\right]\) and \(t\) data. D Filled circles represent normalized reaction rate, \(R={Vd}\left[{{\rm{SO}}}_{4}^{2-}\right]/\left({Adt}\right)\) (mol sulfate per unit time per unit surface area), which is independent of droplet pH between approximately 3 and 5. The color indicates the droplet radius. Open diamonds and error bars represent the mean and standard deviation values, respectively, of the repeated measurements at each pH condition.

Full size image

Figure 1B–D show the kinetic dependence on droplet size and acidity. These experiments were conducted in NH4Cl/HCl/CuCl2 droplets (1:0.005:0.001), with a radius (hereafter, \(a\)) between 5 and 30 µm. Other conditions were 500 ppb SO2, 500 ppb NO2, 40-to-4000 ppb NH3, and 80%RH. Figure 1B shows that the reaction is faster in smaller droplets. Specifically, the \({{\rm{SO}}}_{4}^{2-}\) formation rate, \(d\left[{{\rm{SO}}}_{4}^{2-}\right]/{dt}\), (unit: M s−1) is inversely proportional to droplet radius, \(a\) (See the dotted line in Fig.1C). This relationship indicates that the reaction rate is proportional to the droplet surface-area-to-volume ratio, such as \(A/V.\,\)Hereafter, we will normalize kinetic data as below:

$$R=\frac{{Vd}\left[{{\rm{SO}}}_{4}^{2-}\right]}{{Adt}}$$
(1)

Here, \(R\) has a unit of mol s−1 µm−2 and it quantifies the reaction rate on a surface-area basis. Meanwhile, we also conducted experiments in the pH-resolved droplets, which were buffered at pH 3, 4, or 5 with 40, 400, or 4000 ppb NH3, respectively. Figure 1B–D show that the reaction rate is unaffected by pH between 3 and 5. Figure S4 shows that the reaction remains unaffected by acidity in the unbuffered droplets, where the pH decreased to a level between 0 and 1 owing to the production of sulfuric acid, H2SO4. In summary, Cu can accelerate SO2 oxidation by NO2 by two orders of magnitude. The reaction rate scales with droplet surface area and is independent of pH. These observations indicate that SO2 directly converts to sulfate at droplet surfaces.

Reaction mechanism

We propose the following mechanism for the Cu-catalyzed SO2 oxidation by NO2 on aerosol surfaces:

$${{\rm{SO}}}_{2}\cdot {{\rm{H}}}_{2}{\rm{O}}+{\rm{Cu}}\left({\rm{II}}\right)\mathop{\to }\limits^{{k}_{2}}{{\rm{SO}}}_{3}^{-}+{\rm{Cu}}\left({\rm{I}}\right)+2{{\rm{H}}}^{+}$$
(Reaction 2)
$${{\rm{NO}}}_{2}+{\rm{Cu}}\left({\rm{I}}\right)\mathop{\to }\limits^{{k}_{3}}{{\rm{NO}}}_{2}^{-}+{\rm{Cu}}\left({\rm{II}}\right)$$
(Reaction 3)
$${{\rm{SO}}}_{3}^{-}+{{\rm{NO}}}_{2}\to {{{\rm{NO}}}_{2}{\rm{SO}}}_{3}^{-}$$
(Reaction 4)
$${{{\rm{NO}}}_{2}{\rm{SO}}}_{3}^{-}+{{\rm{H}}}_{2}{\rm{O}}\to {{\rm{SO}}}_{4}^{2-}+{{\rm{NO}}}_{2}^{-}+2{{\rm{H}}}^{+}$$
(Reaction 5)
$${{\rm{NO}}}_{2}^{-}+{{\rm{H}}}^{+}\to {{\rm{HONO}}}_{\left({\rm{g}}\right)}$$
(Reaction 6)

Here, Reaction 2 is a direct electron transfer from SO2 hydrate to Cu(II) at aerosol surfaces. Cu(II) with a 3d9 outermost electron configuration can delocalize an electron from S(IV), producing \({{\rm{SO}}}_{3}^{-}\) radicals and Cu(I) ions41. This reaction between S(IV) and Cu(II) is widely applied in water treatment42,43. The viability of this reaction has also been confirmed with electron paramagnetic resonance in ref. 35. When this reaction occurs at aerosol surfaces, sulfate formation rate will not be constrained by SO2 solubility in the bulk aqueous phase. Reaction 3 is an electron transfer from Cu(I) to NO2, producing \({{\rm{NO}}}_{2}^{-}\) and Cu(II), and thus closing the redox cycle. This reaction is thermodynamically viable per the standard potential of the half-reaction (Table S1)44. This reaction has also been reported in refs. 35,45 on copper corrosion. Reactions 4 and 5 are radical reactions, in which \({{\rm{SO}}}_{3}^{-}\) and \({{\rm{NO}}}_{2}\) form \({{{\rm{NO}}}_{2}{\rm{SO}}}_{3}^{-}\) – an intermediate then dissociating into \({{\rm{SO}}}_{4}^{2-}\) and \({{\rm{NO}}}_{2}^{-}\)14,46. Reaction 6 is HONO degassing. The overall reaction is illustrated in Fig. 2A.

Fig. 2: Reaction mechanism and kinetics.
figure 2

A A schematic diagram for the reaction mechanism of Cu-catalyzed SO2 oxidation by NO2. Reactions 2 and 3 are the rate-limiting steps. R2 stands for Reaction 2 and so forth. B–D Reaction rate measured with an aerosol optical tweezer (AOT). B Normalized reaction rate \(R\) increases linearly with the total Cu ions molarity (\(\left[{\rm{Cu}}\right]\), which is also the initial Cu(II) ions molarity). Reaction conditions were 500 ppb SO2 and 500 ppb NO2. Droplets initially comprised (NH4)2SO4/NH4HSO4/CuSO4 at mixing molar ratio of 1:1:0.0002, 1:1:0.0004, 1:1:0.001, and 1:1:0.002. The droplet was buffered at approximately pH 4 with 800 ppb NH3. The dotted line represents a linear fit. During reactions, sulfate (\({{\rm{SO}}}_{4}^{2-}\)) molar concentration increased linearly with time. The size of the circle indicates droplet radius, \(a\). The color indicates droplet pH. Conditions were 500 ppb SO2 and 500 ppb NO2. Droplets comprised a NH4Cl/HCl/CuCl2 mixture (1:0.005:0.001) and were buffered at pH approximately 3, 4, or 5 with 40, 400, or 4000 ppb NH3, respectively. C Normalized reaction rate \(R/[{\rm{Cu}}]\) is plotted as a function of SO2 mixing ratio, \({P}_{{{\rm{SO}}}_{2}}\) (5–200 ppb). Data are colored per NO2 mixing ratio, \({P}_{{{\rm{NO}}}_{2}}\) (50–500 ppb). Droplets initially comprised a mixture of (NH4)2SO4/NH4HSO4/CuSO4 at a mixing molar ratio of 1:1:0.002. The droplet was buffered at approximately pH 4 with 800 ppb NH3. D The same data in C is further normalized as \(R/([{\rm{Cu}}]{P}_{{{\rm{NO}}}_{2}})\) versus \({P}_{{{\rm{SO}}}_{2}}/{P}_{{{\rm{NO}}}_{2}}\). Also overlaid is the kinetic data determined from the Raman microspectrometry (micro-Raman). The dashed-dotted line illustrates the piecewise trends of the dataset. In B–D, errors in AOT data arise from the 95% confidence interval values of droplet growth rate determined by analyzing the stimulated Raman spectra (see Methods for details). In D, the error in micro-Raman data represents the one standard deviation value of R amongst the 10 measurements shown in Fig.1.

Full size image

Considering the short lifetime of the radicals in Reactions 4 and 5, we assumed that Reactions 2 and 3 are rate-limiting steps. Thus, the apparent reaction rate is the rate at which Reaction 2 produces \({{\rm{SO}}}_{3}^{-}\), which scales with the mixing ratio of SO2, \({P}_{{{\rm{SO}}}_{2}}\), and the aqueous concentration of Cu(II), \(\left[{\rm{Cu}}({\rm{II}})\right]\):

$$R={k}_{2}{P}_{{{\rm{SO}}}_{2}}\left[{\rm{Cu}}({\rm{II}})\right]$$
(2)

Next, we assumed a steady state for \(\left[{\rm{Cu}}({\rm{II}})\right]\) and \(\left[{\rm{Cu}}({\rm{I}})\right]\) ions, such as:

$${k}_{2}{P}_{{{\rm{SO}}}_{2}}\left[{\rm{Cu}}({\rm{II}})\right]={k}_{3}{P}_{{{\rm{NO}}}_{2}}\left[{\rm{Cu}}({\rm{I}})\right]$$
(3)

The Eq. 3, when combined with a Cu mass conservation, yields:

$$\left[{\rm{Cu}}({\rm{II}})\right]=\left[{\rm{Cu}}\right]{\left(1+\frac{{k}_{2}{P}_{{{\rm{SO}}}_{2}}}{{k}_{3}{P}_{{{\rm{NO}}}_{2}}}\right)}^{-1}$$
(4)

Here, \(\left[{\rm{Cu}}\right]=\left[{\rm{Cu}}({\rm{I}})\right]+\left[{\rm{Cu}}({\rm{II}})\right]\), which is also the initial \({\left[{\rm{Cu}}({\rm{II}})\right]}_{t=0}\) in our experiments. Combining Eqs. 2 and 4, we get the expression of the apparent reaction rate:

$$R={k}_{2}{P}_{{{\rm{SO}}}_{2}}{\left(1+\frac{{k}_{2}{P}_{{{\rm{SO}}}_{2}}}{{k}_{3}{P}_{{{\rm{NO}}}_{2}}}\right)}^{-1}\left[{\rm{Cu}}\right]$$
(5)

Equation 5 indicates a piecewise trend in the reaction kinetics. Specifically, reaction rate \(R\) is determined by \({k}_{2}{P}_{{{\rm{SO}}}_{2}}\left[{\rm{Cu}}\right]\), when NO2 is excessive (i.e., \({k}_{3}{P}_{{{\rm{NO}}}_{2}}\gg {k}_{2}{P}_{{{\rm{SO}}}_{2}}\)); meanwhile, \(R\) is determined by \({k}_{3}{P}_{{{\rm{NO}}}_{2}}\left[{\rm{Cu}}\right]\), when SO2 is excessive (i.e., \({k}_{2}{P}_{{{\rm{SO}}}_{2}}\gg {k}_{3}{P}_{{{\rm{NO}}}_{2}}\)). In other words, the apparent kinetics is first-order in either SO2 or NO2, depending on which of the gases is excessive. This piece-wise kinetics differs from the second-order kinetics, \(R\propto {P}_{{{\rm{SO}}}_{2}}{P}_{{{\rm{NO}}}_{2}}\), which has been widely used in air-quality models for oxidation of S(IV) by NO28,14,22,23. The takeaway is that, when the reaction is catalyzed, the redox cycle is bridged by the Cu(I)/Cu(II) ions; the reaction does not occur through a direct interaction between SO2 and NO2. As Spindler et al. highlighted in ref. 28, a single-step reaction through a direct S(IV) and NO2 interaction is thermodynamically unfavorable.

Reaction kinetics

To verify the proposed mechanism, we next measure the rate of Cu/SO2/NO2 reaction in single droplets levitated by an AOT. Leveraging the cavity-enhanced Raman spectroscopy and the accurate droplet size information obtained from the whispering gallery modes47, one can measure the sulfate formation by a 10-14 mol precision48,49 in single droplets suspending in the air. These unique advantages allowed us to conduct kinetic experiments at conditions close to the real-world atmosphere, such as a ppb level of reactant gases and humidity conditions below the deliquescent point of ammonium sulfate.

Figure 2B shows that the reaction rate is first-order in Cu concentration, \(\left[{\rm{Cu}}\right]\), agreeing with our proposed mechanism. Cu(II) will not precipitate in water unless its concentration reaches 220 M at pH 3 or 22 mM at pH 534; these precipitation concentrations are much greater than the actual Cu(II) concentrations in our experiment. Hereafter, we will normalize the reaction rate per \(R/\left[{\rm{Cu}}\right]\). Figure 2C plots \(R/\left[{\rm{Cu}}\right]\) as a function of gases mixing ratio, \({P}_{{{\rm{SO}}}_{2}}\) and \({P}_{{{\rm{NO}}}_{2}}\). Specifically, at a fixed \({P}_{{{\rm{NO}}}_{2}}\), there exists a tipping point SO2 mixing ratio, \({P}_{{{\rm{SO}}}_{2}}^{* }\). When\(\,{P}_{{{\rm{SO}}}_{2}} < {P}_{{{\rm{SO}}}_{2}}^{* }\), the reaction rate is linearly proportional to \({P}_{{{\rm{SO}}}_{2}}\) but independent of \({P}_{{{\rm{NO}}}_{2}}\); when\(\,{P}_{{{\rm{SO}}}_{2}} > {P}_{{{\rm{SO}}}_{2}}^{* }\), the reaction rate is linearly proportional to \({P}_{{{\rm{NO}}}_{2}}\) but independent of \({P}_{{{\rm{SO}}}_{2}}\). In other words, the kinetics is piecewise; it is first-order in either SO2 or NO2, depending on which of the gases is excessive. The tipping point \({P}_{{{\rm{SO}}}_{2}}^{* }\) is also linearly proportional to \({P}_{{{\rm{NO}}}_{2}}\). Next, we normalize the data and plot in Fig. 2D the relationship between \(R/([{\rm{Cu}}]{P}_{{{\rm{NO}}}_{2}})\) and \({P}_{{{\rm{SO}}}_{2}}/{P}_{{{\rm{NO}}}_{2}}\). A universal trend emerges. Such a trend consists of a linearly increasing part, described with \(R/\left[{\rm{Cu}}\right]={k}_{2}{P}_{{{\rm{SO}}}_{2}}\) (red line), and a constant part, described with \(R/([{\rm{Cu}}]{P}_{{{\rm{NO}}}_{2}})={k}_{3}\) (black line). Extrapolating these trend lines to \({P}_{{{\rm{SO}}}_{2}}/{P}_{{{\rm{NO}}}_{2}}=1\) reveals the values of \({k}_{2}\) and \({k}_{3}\). The intersect of these lines reveals the tipping point, \({P}_{{{\rm{SO}}}_{2}}^{* }=\left({k}_{3}/{k}_{2}\right){P}_{{{\rm{NO}}}_{2}}\). Thus, we write:

$$R={k}_{2}{P}_{{{\rm{SO}}}_{2}}\left[{\rm{Cu}}\right],\,\left({P}_{{{\rm{SO}}}_{2}} \,<\, \frac{{k}_{3}}{{k}_{2}}{P}_{{{\rm{NO}}}_{2}}\right),$$
(6)
$$R={k}_{3}{P}_{{{\rm{NO}}}_{2}}\left[{\rm{Cu}}\right],\,\left({P}_{{{\rm{SO}}}_{2}} \,>\, \frac{{k}_{3}}{{k}_{2}}{P}_{{{\rm{NO}}}_{2}}\right).$$
(7)

where \({k}_{2}={2.95}_{-0.07}^{+0.14}\times {10}^{-19}\) and \({k}_{3}={4.57}_{-0.21}^{+0.11}\times {10}^{-20}\); both coefficients have a unit of \({{\rm{mol}}}_{{\rm{S}}({\rm{VI}})}\,{{\rm{M}}}_{{\rm{Cu}}}^{-1}\,{{\rm{ppb}}}^{-1}\,{{\rm{s}}}^{-1}\,{{\rm{\mu m}}}^{-2}\). Note that \({k}_{2}\) is approximately one order of magnitude greater than \({k}_{3}\). As a result, the tipping point \({P}_{{{\rm{SO}}}_{2}}^{* }\) is about one-tenth of the \({P}_{{{\rm{NO}}}_{2}}\) (Fig. 2D). That is, the SO2 is excessive in this reaction when its concentration is greater than approximately one-tenth of the NO2 concentration.

Excessive SO2 in air pollution

In China’s urban air pollution, SO2 and NO2 concentrations are on the same order of magnitude level. During the severe Beijing haze in January 2013, the average SO2 and NO2 mixing ratios were 40 and 66 ppb, respectively8. Despite the substantial decrease in SO2 emission over the past decade, its level is still greater than one-tenth of NO2 in recent pollution events (Figure S5). Therefore, when sulfate is produced through the Cu-catalyzed reaction pathway, SO2 remains to be excessive. In other words, the sulfate formation rate would depend on NO2 concentration, rather than on SO2 concentration. It may explain why, in field studies25,26,27,50, sulfate concentrations were observed to weakly correlate with SO2 concentration (Fig. 3A), but strongly correlate with NO2 concentration (Fig. 3B).

Fig. 3: Sulfate concentration correlates with NO2 rather than SO2.
figure 3

A, B Sulfate PM2.5 concentration as a function of SO2 and NO2 mixing ratios, respectively, as reported in past field campaigns conducted in Nanjing26, Beijing25, and Hebei at the Gucheng site50. Dots represent the data taken from the literature25,26,50. Circles with error bars represent the geometric mean and one standard deviation for the data inside each bin (data were binned per the gas mixing ratio, with a 10ppb increment). C National annual average concentrations of SO2 (blue), NO2 (yellow), and sulfate PM2.5 (gray) from 2013 to 2022. The SO2 and NO2 concentration data were acquired from the annual Report on the State of the Ecology and Environment in China53 published by the Ministry of Ecology and Environment of the People’s Republic of China. The sulfate PM2.5 concentration data were acquired from the Tracking Air Pollution in China database54,84 maintained by a team at Tsinghua University. D The concentration data in C are normalized to their respective values in 2013.

Full size image

When SO2 is excessive, reducing its concentration alone would not be effective in sulfate abatement. For example, China launched in 2013 its Air Pollution Prevention and Control Action Plan (hereafter, Action Plan 2013)51,52, implementing stringent industrial emission standards. As a result, the national annual SO2 concentration in the ensuing decade has decreased by 77% (Fig. 3C, D)53. This substantial decrease in SO2 emission, however, has not led to a proportional decrease in sulfate concentration. Instead, the moderate decrease in sulfate (about 50%) closely matches that in NO2 (Fig. 3D)53,54. This observation again indicates that SO2 may not be the limiting factor in sulfate formation during urban haze. In other words, sulfate can be produced rapidly at a very low SO2 concentration, as long as the NO2 concentration is high. Further abatement faces a greater challenge of reducing NO2 concentration because NO2 originates from both industry and traffic emissions, with the latter being a mobile and decentralized source52.

Copper in polluted air

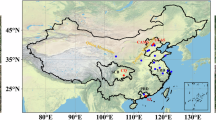
Traffic is the primary anthropogenic source of Cu in urban areas, such as Beijing39,55. Since Cu is an effective heat conductor, it is commonly used as a friction agent in automobile brake pads56. A higher Cu concentration was observed in the road dust collected from urban areas with denser traffic57. A Beijing campaign58 showed that the concentration of Cu in the PM2.5 sampled at the 4th Ring Road – a major traffic artery in the city – was consistently higher than those sampled at the Tsinghua University campus. A source apportion study39 reported that brake-and-tire wear contributed 69% of Cu in the PM2.5 during the air pollution in Beijing (See Fig. 4A and Table S2).

Fig. 4: Cu-catalyzed SO2 oxidation by NO2 as a sulfate source in urban air pollution.
figure 4

A The availability of Cu in PM2.5 in North China Plain haze events. On the map, circles (size) represent the concentration of total Cu elements in PM2.5 during the 2014 haze in Beijing, Tianjin, Langfang, Baoding, and Wangdu, as well as the 2016 haze in Shijiazhuang (See Table S2 for details). Data were acquired from refs. 38,59,60. Surrounding the map are the pie charts for the major Cu sources. Data were acquired from ref. 39. B Illustration for the Cu-catalyzed SO2 oxidation by NO2 in urban air pollution. C Sulfate PM2.5 formation rate through various heterogeneous SO2 oxidation pathways under urban haze conditions. The red solid line represents sulfate formation via the Cu-catalyzed oxidation of SO2 by NO2. The rate was estimated by using the kinetics expression in Equation 7. The red-shaded area represents the uncertainty arising from the one standard deviation of Cu concentration in urban air pollution (see Table S3). Also compared here are sulfate formation rates through other reaction pathways reported in literature, including the O3 pathway (purple curve)8, H2O2 pathway (blue curve)15, aqueous TMI-catalyzed oxidation (green curve)15, Mn-catalyzed oxidation on aerosol surface (yellow curve)13,32, and the uncatalyzed NO2 pathways (\({{\rm{HSO}}}_{3}^{-}\)/NO2 reaction8, red dashed-dotted curve; \({{\rm{SO}}}_{3}^{2-}\)/NO2 reaction14, red dotted curve). The conditions for urban haze follow that reported in ref. 8, which include 40 ppb SO2, 66 ppb NO2, 0.01 ppb H2O2, 1ppb O3, mean aerosol radius 0.15 µm, and aerosol water content (AWC) 300 µg m−3air. The water-soluble Fe and Mn were 18 and 45 ng m-3air, respectively32. The water-soluble and reactive Cu was 34 ± 19 ng m−3air. The gray shaded area represents the pH 4-to-5 range typical to China’s urban haze85,86.

Full size image

Yet traffic is not the only source of Cu and NOx in China’s air pollution. Industrial processes also contribute significantly to their co-emissions, especially in the broader NCP region39, i.e., in cities such as Tianjin and those located in the Hebei province (See Fig. 4A and Table S2). In these areas, a significant portion of Cu emissions (36–60%) originates from coal combustions, including power plants and industry boilers39. Additionally, in cities such as Tangshan and Handan, a considerable share of Cu (~29%) comes from ferrous metal smelting. Since these industrial processes also emit NOx, it is reasonable to consider Cu and NO2 as companion emitters across the NCP region. This pairing of the oxidant, NO2, and the catalyst, Cu, may contribute to the rapid SO2 conversion observed during haze events (See Fig. 4B)

The Cu concentration in urban air pollution38,59,60 is considerably higher than that in clean conditions37 or ambient conditions61. During severe haze events in 201438, the Cu concentrations in Beijing, Tianjin, and Baoding reached 200, 110, and 190 ng m−3air, respectively (see Fig. 4A and Table S3). The average Cu concentration among the six NCP locations was approximately 119 ± 66 ng m−3air (uncertainty refers to one standard deviation; see Table S3). Next, we assumed an approximately 35% solubility55 of Cu in aerosol water and a 300 µg m−3air liquid aerosol water content (AWC)8 in the urban haze. Under these conditions, the concentration of dissolved Cu in aerosol water is about 2.19 ± 1.22 mM. Details of the calculation can be found in Methods section Supplementary Table S3.

Not all the dissolved Cu species are reactive. Some Cu(II) ions may form complexes with dicarboxylic acids and lose their redox reactivity62,63,64,65. Following refs. 63,64, we examined the speciation of aqueous Cu(II) in Beijing PM2.5 by using the Visual MINTEQ model. The model input included the PM2.5 composition data acquired from Beijing campaigns38,66,67 (See Methods and Supplementary Table S4 and for details). The results show that metal-organic complexes constituted approximately 19% of dissolved Cu(II) in Beijing PM2.5. This percentage of metal-organic complexes is slightly lower than those reported from field campaigns at other locations worldwide (Table S5)62,63,64,65. This is because organic matter constituted a lower mass fraction of PM2.5 in NCP haze events, during which the secondary inorganic component and aerosol water content increased substantially67.

After excluding the metal-organic complexes (19%), we estimated the aqueous concentration of reactive Cu as 1.77 ± 0.99 mM (airborne equivalent concentration, 33.74 ± 18.82 ng m−3air, at AWC of 300 µg m−3air). We also assumed the SO2 and NO2 mixing ratios to be 40 and 66 ppb, respectively, per ref. 8. Using these parameters and our kinetic expression in Equation 7, we estimated that the sulfate formation rate via Cu-catalyzed oxidation of SO2 by NO2 can reach 11 ± 6 µg m−3air hr−1 (Red solid line and shaded area, Fig. 4C). The uncertainty was propagated from the one standard deviation of Cu concentrations reported in NCP field campaigns38,59,60. Also overlaid in Fig. 4C are the sulfate production rate via other heterogeneous reaction pathways reported in refs. 8,13,14,15,32. We highlight the comparison among the NO2 reaction pathways (Red curves), At acidic conditions, i.e., pH 4, the Cu-catalyzed reaction is faster than the uncatalyzed reactions8,14 by two to three orders of magnitude. Therefore, the reaction between SO2 and NO2 in the urban environment may occur predominately through the Cu-catalyzed route.

Discussion

In the present work, we studied an atmospherically relevant reaction with laboratory experiments. A major limitation of laboratory experiments is that the aerosol reactors cannot fully replicate the atmospheric conditions68,69, such as the complex aerosol composition in the real world. One potentially important aerosol constituent we did not consider is humic-like substances (HULIS). Under weakly acidic conditions, HULIS—both in protonated and deprotonated forms – can complex with Cu2+ ions70, thereby inhibiting their catalytic activity. Such a kinetic influence of HULIS may also exhibit seasonal variations, since the oxidation state of HULIS determines the distribution of organic functional groups, which in turn affects their complexation tendencies70. Without considering the influence of HULIS, our analysis of the sulfate formation rate is prone to overestimation. Additionally, the droplet size in our experiments is slightly larger than PM2.5. To account for this mismatch, we normalized reaction rates per the surface area of droplets. This normalized kinetics were then rescaled using the surface area concentration of urban aerosols. This extrapolation remains valid as long as the surface reaction rate is proportional to the area of the air-water interface where the reaction occurs. This extrapolation, however, may not be valid for droplets smaller than 100 nm, as the Kelvin effect becomes significant at that scale. The original data—without normalization and rescaling—may be applicable for polluted fog droplets19,25 within a similar size range.

Future studies may incorporate the Cu-catalyzed SO2 oxidation by NO2 in the atmospheric chemical transport models, so as to better constrain atmospheric reactions in general. For example, future studies may investigate the synergistic effects of the atmospheric reactions that involve Cu. For example, atmospheric hydroperoxyl (HO2) radicals can be converted into H2O2 through a Cu-catalytic cycle61,71,72,73. This reaction produces H2O2 that can in turn oxidize SO215. HO2 may also directly participate in the Cu cycle that converts SO2. Since HO2 radicals are much more reactive with Cu(I) than with Cu(II)61, they tend to keep the metal ions at a higher oxidation state, which favors the conversion of SO2. Another potential oxidant is Fe(III) ions, which can also convert Cu(I) to Cu(II)61, and such a metal ions synergism may further promote SO2 conversion. Additionally, for the uncatalyzed reaction between S(IV) and NO2, we suggest caution on using the second order kinetics, such as \(R\propto \left[{\rm{H}}{{\rm{SO}}}_{3}^{-}\right]\left[{{\rm{NO}}}_{2}\right]\)22,23, – a formulation widely adopted in the past. This second-order kinetics22,23 implies a single-step reaction through a direct interaction between \({\rm{H}}{{\rm{SO}}}_{3}^{-}\) and NO2, which is unlikely because the redox potentials between these reactants are close28,29. Furthermore, the uncatalyzed reaction is unlikely the case because metal ions always exist in urban aerosols, particularly at polluted conditions34. And when the redox cycle is bridged by Cu(I)/Cu(II), the reaction kinetics scale with either SO2 or NO2, but not with their product.

Electron transfer at the air-water interface is an important mechanism in atmospheric chemistry. Besides sulfate, this mechanism also contributes to the formation of secondary organic aerosols (SOAs). For example, studies by Guzman and coworkers74,75,76,77,78 have advanced our understanding of the oxidation of phenolic compounds, such as catechol and phenolic aldehydes, by NO375 and OH74,77 radicals as well as O374,78 at the air-water interface, leading to SOAs. These reactions can also be affected by the presence of TMIs79. Understanding these interfacial processes is crucial for evaluating the environmental impacts of biomass burning emissions76.

We conclude by reiterating the major findings of the present study. First, Cu can catalyze the multiphase SO2 oxidation by NO2, accelerating the reaction by up to two orders of magnitude at urban haze conditions. This reaction can be an important but hitherto unknown source of sulfate PM2.5 in China haze. This is because, not only is Cu concentration high during urban haze38, but it is also co-emitted with NO2 from anthropogenic sources—both industry and traffic39. Second, the Cu catalysts also alter the reaction order: When the reaction is Cu-catalyzed, SO2 tends to be excessive, and the sulfate formation rates scale instead with NO2 concentration. This observation challenges the widely perceived view that SO2 is always involved in the rate-limiting step of sulfate PM2.5 formation. From a policy perspective, further reducing SO2 emissions is difficult and may not be effective in sulfate abatement. Instead, cutting off NO2 emissions from industry and traffic may help further bring down sulfate PM2.5 levels. Another practice worth considering is reducing the amount of Cu in automobile brake pads56, thereby cutting down a catalyst for sulfate formation in the urban atmosphere, such as in Beijing, where traffic contributes to a larger share of both Cu and NOx.

Methods

Micro-Raman experiments

Spectrometer

The measurement was performed with a Renishaw inVia Raman micro-spectrometer. The spectrometer was equipped with a 514.5 nm laser, a Leica DMLM microscope, and an 1800 grooves/mm grating.

Droplets

Droplets were prepared by dispensing solutions onto polytetrafluoroethylene (PTFE) substrates. A medical syringe was used in the dispensing process. When investigating the Cu-catalyzed SO2 oxidation by NO2, we prepared the droplets per the following recipes: for the reactions occurring at pH between 3 and 5, the droplets initially comprised a mixture of NH4Cl/HCl/CuCl2, and these droplets were buffered with NH3 gas. The molar ratio of NH4Cl/HCl/CuCl2 was fixed at 1:0.005:0.001. With this recipe, the Cu(II) constituted approximately 0.1% of the solute. In this article, we occasionally denote this mixing arrangement as 0.1%Cu-in-solute. Not to confuse with the weight percent of Cu in aerosols. When investigating the uncatalyzed SO2 oxidation by NO2, we prepared the droplets per the following recipe: for the reaction occurring at pH 4, the droplets initially comprised a mixture of NH4Cl/HCl (1:0.005) and buffered with NH3. The chemicals, NH4Cl (purity 99.0%, Beijing Chemical Reagent Factory), CuCl2 (purity 99.99%, Sigma-Aldrich), and HCl (36-38% solution, Beijing Chemical Reagent Factory), were used without further purification.

Droplet ambient conditions

After the droplets were dispensed onto the PTFE substrate, the substrate was loaded into a sample cell. The relative humidity (RH, 77–80%) in the cell was controlled by mixing dry and humidified N2 gases. The RH was monitored with a hygrometer (CENTER-313, Qunte Technology Co., LTD). The temperature of the sample cell was maintained at room temperature (298 K). Reactants flowed through the sample cell with a prescribed mixing ratio. Specifically, both SO2 and NO2 were at 500 ppb. NH3 was at 40, 400, or 4000 ppb to buffer the NH4Cl/HCl droplets at pH 3, 4, or 5, respectively. We also conducted parallel experiments in the microdroplets that were unbuffered. In these unbuffered droplets, the formation of sulfurous acids can decrease the droplet pH to a range between ~0 and 1. The detailed experimental conditions for the micro-Raman study can be found in Table S6. Droplet pH was calculated with the extended aerosol inorganic model (E-AIM)40. Past studies80,81,82,83 have shown that E-AIM model predicted aerosol pH accurately as long as the compositions of the gas and aqueous phases of aerosols are well characterized. The model does not account for minor species, such as SO2(aq), SO2·H2O, HSO3-, and SO32-, because S(IV) contribute to pH negligibly compared to SO42-.

Raman spectral data collection and analyzes

It took about 20 min before the RH inside the sample cell became stable. After that, we started to collect the Raman spectra of droplet samples. For each droplet sample, the measurement lasted approximately 240 min. The Raman spectra were collected at intervals of about 20 to 30 min. The Raman mode at 980 cm-1, which corresponds to the O-S stretching vibration, was designated to \({{\rm{SO}}}_{4}^{2-}\). The Raman mode at 1650 cm−1, which corresponds to the H-O-H bending vibration, was designated to H2O molecules. We divided the intensity of \({{\rm{SO}}}_{4}^{2-}\) peak at 980 cm-1 with that of H2O peak at 1650 cm-1, giving a ratio \({A}_{{{\rm{SO}}}_{4}^{2-}}/{A}_{{{\rm{H}}}_{2}{\rm{O}}}\). Such a ratio is linearly proportional to the molar concentration of sulfate ions \([{{\rm{SO}}}_{4}^{2-}]\). Next, we retrieve the \([{{\rm{SO}}}_{4}^{2-}]\) by inverting the \({A}_{{{\rm{SO}}}_{4}^{2-}}/{A}_{{{\rm{H}}}_{2}{\rm{O}}}\) with a calibration curve: \({A}_{{{\rm{SO}}}_{4}^{2-}}/{A}_{{{\rm{H}}}_{2}{\rm{O}}}=0.95* [{{\rm{SO}}}_{4}^{2-}]\). We constructed this calibration curve by using the same spectrometer to measure the \({A}_{{{\rm{SO}}}_{4}^{2-}}/{A}_{{{\rm{H}}}_{2}{\rm{O}}}\) of bulk solutions comprising Na2SO4 solute with a molar concentration of 0.2, 0.4, 0.6, 0.8, and 1.0 M. In other words, the calibration curve can be used to invert [SO42−] below 1.0 M. See Fig. S6 for details of the calibration curve. See Fig.S7 for the Raman spectra of microdroplets during sulfate formation.

Determining reaction kinetics

we performed a linear least-square fitting on the dataset between \([{{\rm{SO}}}_{4}^{2-}]\) and time, \(t\). The slope was reaction rate, \(d[{{\rm{SO}}}_{4}^{2-}]/t\), on the basis of sulfate molar concentration. Next, the reaction rate \(R\) (unit mol s−1 µm−2) was calculated by dividing \(d[{{\rm{SO}}}_{4}^{2-}]/t\) with droplet surface area-to-volume ratio, \(A/V\). For each experiment, the values of \(R\), the uncertainties (95% confidence interval values of the linear fitting), and the number of data points used in the fitting can be found in Table S6.

Measuring droplet size

The droplet radius \(a\) was measured with the optical microscope equipped with the Raman spectrometer. We assumed droplets to be spheres, with volume \(V=\tfrac{4}{3}\pi {a}^{3}\) and surface area \(A=4\pi {a}^{2}\). See Fig. S8 for the optical microscope images of the droplets at the extreme size conditions.

AOT experiments

Aerosol optical tweezer

The reaction kinetics were measured in levitated microdroplets with a gradient-force, single-beam AOT. The optical trap was constructed with a 532 nm Gaussian beam, tightly focused with a 100x oil immersion objective scope (Olympus UIS2 PlanCN, numerical aperture of 1.25) inside a 6 mL sample cell. The 532 nm laser constituting the optical trap also served as the incident light for Raman scattering, and the backscattered Raman scattering signal was captured by using a spectrograph (Zolix Ominc λ-500, 1200 grooves/mm grating) with a temporal resolution of one frame per second.

Droplets

Droplets were prepared by aerosolizing solutions with a medical nebulizer (Yuyue 402AI model). When investigating the Cu-catalyzed reaction, we seeded the droplets with a mixture of (NH4)2SO4/NH4HSO4/CuSO4 at a molar ratio of 1:1:0.0002, 1:1:0.0004, 1:1:0.001, and 1:1:0.002. With these recipes, the Cu(II) respectively constituted 0.01%, 0.02%, 0.05%, and 0.1% of the solute. Again, we occasionally denote, for example, the mixture of (NH4)2SO4/NH4HSO4/CuSO4 at 1:1:0.002 as 0.1%Cu-in-solute. Not to confuse with the weight percent of Cu in aerosols. When investigating the uncatalyzed reaction, we seeded the droplets with a (NH4)2SO4/NH4HSO4 mixture (1:1). Chemicals, (NH4)2SO4 (purity 99.99%, Sigma-Aldrich), NH4HSO4 (purity 99.99%, Sigma-Aldrich), and CuSO4 (99.95%, Sigma-Aldrich), were used without further purification.

Droplet ambient conditions

The aerosolized droplets, led by an N2 flow, were then delivered to the optical trap inside the sample cell of the AOT system. This sampling process was considered successful when one of the droplets was captured by the optical trap. At this stage, the composition of the droplet is highly sensitive to the ambient gas phase, which should be maintained at stable conditions throughout the measurement. Specifically, the relative humidity (RH, 60 ± 1%) in the cell was controlled by mixing dry and humidified N2 gases. The RH was monitored with a hygrometer (CENTER-313, Qunte Technology Co., LTD). The temperature was maintained at room temperature (298 K) Reactant gases flowed through the sample cell with a prescribed mixing ratio. When investigating the Cu-catalyzed reaction, we applied the reaction gases per the following arrangements: SO2 was at 5, 10, 15, 25, 40, 50, 75, 100, 150, or 200 ppb; NO2 was at 50, 100, 250, or 500 ppb; NH3 was at 50, 100, 200, 400, or 800 ppb to buffer the (NH4)2SO4/NH4HSO4 droplets at pH 2.8, 3.1, 3.4, 3.7, or 4.0, respectively. When investigating the uncatalyzed reaction, we applied the gases per the following arrangements: SO2 was at 0.1, 0.25, 0.5, 0.8, 1.0, 1.5, 2.0, 3.0, 5.0, 7.5, 10.0, or 20.0 ppm; NO2 was at 10 ppm; NH3 was at 0.8 or 8.0 ppm to buffer the droplets at pH 4.0 or 5.0 conditions, respectively. The detailed experimental conditions for the AOT study can be found in Table S7. Droplet pH was calculated with E-AIM40.

Raman spectral data collection and analyzes

The backscattered Raman signal was collected with a time resolution of one second. During the reaction, the SO2 was continuously converted into \({{\rm{SO}}}_{4}^{2-}\), causing a continuous increase in droplet radius, \(a\). Such droplet growth, albeit slight in magnitude, can be precisely determined by observing the redshift of the whispering gallery mode (WGM) in the stimulated Raman spectra. At each time step, \(t\), we inverted the WGM wavelength \(\lambda\) to droplet size \(a\), by using the Mie-scattering calculation algorithm provided in ref. 47. Next, the increase in droplet volume \({dV}\), during a time interval \({dt}\), can be quantified as:

$${dV}=4\pi {a}_{t}^{2}\left({a}_{t+{dt}}-{a}_{t}\right)$$
(Equation S1)

This increase in volume was contributed by the (NH4)2SO4 produced by the reaction, and the corresponding increase in the mole of (NH4)2SO4 is therefore:

$${dn}=\left[{({{\rm{NH}}}_{4})}_{2}{{\rm{SO}}}_{4}\right]* {dV}$$
(Equation S2)

Here, \(\left[{({{\rm{NH}}}_{4})}_{2}{{\rm{SO}}}_{4}\right]\) is the molar concentration at an approximately 60% RH condition, calculated with E-AIM40. In summary, the reaction rate can be calculated from droplet growth rate per the following relationships:

$$\frac{{dn}}{{dt}}\left({\rm{mol}}{{\rm{s}}}^{-1}\right)=\left[{({{\rm{NH}}}_{4})}_{2}{{\rm{SO}}}_{4}\right]\times \frac{4\pi {a}_{0}^{2}{da}}{{dt}}\times \frac{{\rm{L}}}{{10}^{15}{\mu {\rm{m}}}^{3}}$$
(Equation S3)

and

$$R\left({\rm{mol}}{{\rm{s}}}^{-1}{\mu {\rm{m}}}^{-1}\right)=\frac{{dn}}{4\pi {a}_{0}^{2}* {dt}}=\left[{({{\rm{NH}}}_{4})}_{2}{{\rm{SO}}}_{4}\right]\times \frac{{da}}{{dt}}\times \frac{{\rm{L}}}{{10}^{15}{\mu {\rm{m}}}^{3}}$$
(Equation S4)

Here, \({a}_{0}\) is the initial radius of droplets (unit, µm). The droplet growth rate \({da}/{dt}\) (unit, µm s−1) was determined by linearly fitting the \(a(t)\) dataset. It is worth noting that Eqs. S1, S3, and S4 hold true only when the value of \({a}_{t}-{a}_{0}\) is much smaller than \({a}_{0}\) (so that the curvature of the droplet surface can be ignored). In the AOT experiments, the \({a}_{t}-{a}_{0}\) did not exceed 50 nm, which is approximately 1% of the \({a}_{0}\). For each experiment, the values of \({da}/{dt}\), the uncertainties (95% confidence interval values of the linear fitting), and the number of data points used in the fitting can be found in Table S7. Also, note that the treatment of Eqs. S3 and S4 requires that \({{\rm{SO}}}_{4}^{2-}\) is the sole product remaining in the condensed phase. Such a condition has been confirmed in our Micro-Raman study (See Fig.S7). We also assumed that the product was always (NH4)2SO4 when NH3 was in the ambient gases.

Aqueous copper speciation model

Visual MINTEQ

Following the method introduced in refs. 63,64, we estimated the chemical speciations of Cu(II) in the aqueous phase of Beijing PM2.5 by using Visual MINTEQ model version 3.1. The visual MINTEQ model, which was originally designed for chemical speciation analysis in natural aquatic systems, has also been successfully utilized for estimating metal speciation in aerosol water63,64. In other words, this model accounts for metal-organic complex formation and calculates the fraction of metals existing as organic complexes. The model input parameters included the aqueous concentrations of secondary inorganic matters (SO42−, NO3−, and NH4+), dicarboxylic acids (oxalate, malonate, succinate, and glutarate), and metal ions (Na+, K+, Mg2+, Ca2+, Al3+, Mn2+, As3+, Cr2+, Cu2+, Ni2+, Pb2+, Sb3+, Se4+, Zn2+, Fe2+, and Fe3+), as well as aqueous pH (fixed at 4) and temperature (fixed at 25 °C). These PM2.5 composition data were acquired from field campaigns conducted in Beijing38,66,67. Details of the composition data can be found in Table S4. Following that recommended in ref. 64, we adopted the specific interaction theory (SIT) for the ionic strength correction of the stability constants of the metal complexes. SIT correction was preferred because it is more appropriate for the high ionic strength condition (>1 M) of urban aerosols64.

Sulfate, nitrate, and ammonium

We estimated the aqueous concentrations of inorganic matters with the E-AIM model40 according to the hygroscopicity of a SO42−/NO3−/NH4+ mixture at a molar ratio of 1:1.5:3.5 and at an ambient RH of 80%. The molar ratio of the mixture was determined according to the mass fractions of SO42− (19.2%), NO3− (18.5%), and NH4+ (12.6%) in Beijing PM2.5 at heavily polluted conditions67.

Dicarboxylic acids

We took the concentration of dicarboxylic acids in Beijing PM2.5 from ref. 66 (Winter data, December 2013, Beijing Campaign, See Table S4). Then we calculated the aqueous concentrations (unit: mol kg−1) of the dicarboxylic acids by using their atmospheric concentrations (unit: ng m-3air), molar mass (unit: g mol-1), and atmospheric water contents, AWC, (300 µg m−3air)8.

Metals

We took the atmospheric concentration of metals in Beijing PM2.5 from ref. 38 (Winter data, January 2014, Beijing Campaign, See Table S4). Similarly, we calculated the aqueous concentrations (unit: mol kg−1) of the metals by using their atmospheric concentrations (unit: ng m-3air), molar mass (unit: g mol−1), and atmospheric water contents, AWC, (300 µg m−3air)8. The oxidation state of metal ions was assigned as follows: Al3+, Mn2+, As3+, Cr2+, Cu2+, Ni2+, Pb2+, Sb3+, Se4+, Zn2+, Fe2+, and Fe3+. The Fe2+ and Fe3+ were assumed to exist in equal amounts, per ref. 64. During calculation, the species that were predicted to be in an oversaturation state were allowed to precipitate63,64.

Calculating sulfate formation rates at urban haze conditions

Reactive Cu in aqueous phase

Table S3 provides the total Cu (ng m−3air) in the PM2.5 during past NCP haze events38,59,60. The total Cu refers to all forms of Cu elements existing in the PM2.5 sample, including both the water-soluble and insoluble fractions. The soluble fraction can be calculated by multiplying total Cu with the solubility of Cu (hereafter, \({f}_{{\rm{S}}}\)). A field campaign in China55 shows \({f}_{{\rm{S}}}\) ≈ 35% in acidic aerosol water. Among the soluble Cu, we assume that the fraction forming metal organic complexes (\({f}_{{\rm{OM}}}\) ≈ 19%, See Table S5) are non-reactive. That is, the reactive fraction can be calculated by multiplying soluble Cu with \(1-{f}_{{\rm{OM}}}\). To summarize, we write the following equation for reactive Cu concentration in the aqueous phase:

$$\begin{array}{l}\left[{\rm{Cu}}\right]\left({\rm{mM}}\right)={f}_{{\rm{S}}}\times \left(1-{f}_{{\rm{OM}}}\right)\times \frac{{\rm{Cu}}\left({\rm{ng}}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)}{{{\rm{M}}}_{{\rm{w}},{\rm{Cu}}}\left({\rm{g}}\,{{\rm{mol}}}^{-1}\right)\times {\rm{AWC}}\left({\rm{L}}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)}\\\qquad\qquad\qquad\,\times \frac{{10}^{-9}{\rm{g}}}{{\rm{ng}}}\times \frac{{10}^{3}{\rm{mmol}}}{{\rm{mol}}}\end{array}$$
(S5)
$${\rm{AWC}}\left({\rm{L}}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)=\frac{{{\rm{PM}}}_{2.5}\left(\mu {\rm{g}}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)}{{\rho }_{{\rm{water}}}\left({{\rm{kg}}\; {\rm{m}}}^{-3}\right)}\times \frac{{10}^{-9}{\rm{kg}}}{\mu {\rm{g}}}\times \frac{{10}^{3}{\rm{L}}}{{m}^{3}}$$
(S6)

Here, \({{\rm{M}}}_{{\rm{w}},{\rm{Cu}}}\) (63.55 g mol-1) is copper molecular weight; The AWC (L m-3air) refers to the volume of aerosol liquid water content per unit volume of air. For simplicity, we calculated the AWC (L m-3air) by dividing the AWC (300 µg m-3air) with water density \({\rho }_{{\rm{water}}}\) (103 kg m-3) (See Eq. S6). Refer to Table S5 for the concentrations of soluble and soluble-and-reactive Cu in Beijing PM2.5. Note that the aqueous [Cu] is on the order of millimolar level, which is three orders of magnitude lower than the Cu(OH)2 precipitation limit at pH 4 (approximately 2.2 M)34. Thus, the aqueous [Cu] concentration in urban aerosols can be regarded as pH-independent.

Extrapolation of reaction kinetics

The urban air pollution conditions follow that reported in ref. 8. Specifically, the average aerosol radius (a) was 0.15 µm, SO2 mixing ratio \({P}_{{{\rm{SO}}}_{2}}\), 40 ppb; NO2 mixing ratio \({P}_{{{\rm{NO}}}_{2}}\), 66 ppb; The mass concentration of AWC, 300 µg m−3air. Since SO2 mixing ratio is much greater than the tipping point mixing ratio, i.e., \({P}_{{{\rm{SO}}}_{2}} > \left({k}_{2}/{k}_{1}\right){P}_{{{\rm{NO}}}_{2}}\), the kinetic formulation in Equation 7 (in main text) was used to calculate sulfate formation rate at urban haze conditions. The reactive [Cu] concentration was calculated with Eq. S5. The resultant reaction rate \(R\) (unit: mol s−1 µm−2) was then extrapolated to an atmospheric sulfate formation rate (unit, µg m−3air hr−1), with the knowledge of sulfate molecular weight Mw,S(VI) (96.06 g mol−1), AWC (300 µg m−3air), average aerosol radius a (0.15 µm), and water density \({\rho }_{{\rm{water}}}\) (103 kg m−3), specifically:

$$\begin{array}{l}R\left(\mu{\rm{g}}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\,{{\rm{hr}}}^{-1}\right)=R\left({\rm{mol}}\,{{\rm{s}}}^{-1}\,{\mu {\rm{m}}}^{-2}\right)\times {{\rm{M}}}_{{\rm{w}},{\rm{S}}\left({\rm{VI}}\right)}\left({\rm{g}}\,{{\rm{mol}}}^{-1}\right)\times \widetilde{A}\left({\mu {\rm{m}}}^{2}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)\\\qquad\qquad\qquad\qquad\,\times \frac{{10}^{6}\mu {\rm{g}}}{{\rm{g}}}\times \frac{3600{\rm{s}}}{{\rm{hr}}}\end{array}$$
(S7)
$$\widetilde{A}\left({\mu {\rm{m}}}^{2}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)={4\pi a}^{2}\left({\mu {\rm{m}}}^{2}\right)\times {\rm{AWC}}\left(\mu {\rm{g}}\,{{\rm{m}}}_{{\rm{air}}}^{-3}\right)\times {m}^{-1}\left({\mu {\rm{g}}}^{-1}\right)$$
(S8)

and

$$m\left(\mu {\rm{g}}\right)=\frac{4}{3}\pi {a}^{3}\left({\mu {\rm{m}}}^{3}\right)\times {\rho }_{{\rm{water}}}\left({{\rm{kg}}\; {\rm{m}}}^{-3}\right)\times {\left(\frac{{10}^{-6}{\rm{m}}}{\mu {\rm{m}}}\right)}^{3}\times \frac{{10}^{9}\mu {\rm{g}}}{{\rm{kg}}}$$
(S9)

Here, \(\widetilde{A}\left({\mu {\rm{m}}}^{2}{{\rm{m}}}_{{\rm{air}}}^{-3}\right)\) is aerosol surface area per unit air volume; \(m\) \(\left(\mu {\rm{g}}\right)\) is the mass of a single aerosol particle.