Introduction

Greenhouse gas-driven warming is partially offset by aerosol-induced cooling mediated through clouds1. The effect of radiative forcing from aerosol-cloud interaction is estimated at −1.0 ± 0.7 W·m−2, and is the largest source of uncertainty in climate forcing2,3. The role of aerosols producing numerous smaller cloud droplets for a given cloud water content is well-established4, named as the Twomey effect. A key uncertainty concerns the aerosol effect on cloud water adjustment5. Most global climate models empirically parameterize aerosol-cloud interactions, assuming that increased aerosols enhance cloud water6,7,8. This assumption implies a stronger negative aerosol forcing than −1.5 W·m−2, which potentially offsets over half of the greenhouse gas radiative forcing9.

Aerosols exert two-sided effects on cloud liquid water path (LWP). The LWP adjustment is primarily controlled by the competition between evaporation and precipitation. Added fine aerosols (FA) produce more numerous and smaller cloud droplets, which can increase LWP by decreasing collision-coalescence and suppressing warm precipitation5. On the other hand, the aerosol-induced smaller cloud droplets enhance cloud-top evaporation and entrainment, decreasing LWP10. Substantial positive LWP adjustments were observed in invisible ship tracks11. However, direct observations from opportunistic experiments suggest a weak change in LWP due to anthropogenic and volcanic aerosols12,13. Overall, a predominantly negative aerosol-LWP correlation was demonstrated in most regions14, which is also validated by a dual field of view high spectral resolution lidar studies monitoring both aerosols and LWP simultaneously15.

The key question is what determines the direction of LWP adjustment? Glassmeier et al.16 suggest a cloud-regime dependence, which indicates precipitating stratocumulus typically exhibits positive LWP adjustments5, while non-precipitating stratocumulus exhibits negative adjustments17. The cloud-top humidity is also crucial in determining whether FA-induced precipitation suppression increases cloud water18. Drier environments amplify LWP depletion in response to increasing FA, where evaporation becomes more dominant19,20.

Both observations and models reveal an inverted “V” relationship between FA and LWP14,21. The FA-induced positive LWP adjustment is invigorated by precipitation suppression5,22. Recent model simulations, with improved entrainment and evaporation schemes, successfully capture the FA-induced negative LWP adjustment6,8. LWP adjustment exhibits contrasting trends between high and low FA21. Their linear correlation implies the entrainment-induced negative LWP adjustment at high FA is constant throughout the FA range21. Furthermore, model simulations reveal overall negative LWP adjustments in non-precipitating stratocumulus due to FA changes, controlled by evaporation and entrainment processes23. However, comprehensive observational evidence that accounts for both meteorological and aerosol influences remains limited.

Prior simulations and observations have primarily focused on anthropogenic or volcanic aerosols8,12, which are mostly FA. However, coarse sea salt aerosols (CSA, dry radius > 1 μm), which widely coexist with FA over oceans, remain relatively understudied. Doubling of coarse marine aerosol optical depth has been associated with a 1.4 ± 0.11 μm increase in cloud-top effective radius24, as the large initial size of CSA facilitates the rapid formation of large cloud droplets25. Large-eddy simulations indicate that CSA promotes precipitation, leading to cloud water depletion and cloud darkening26. Satellite observations further reveal opposing and comparable large effects of CSA and FA on regional warm rain flux27, suggesting a significant potential for CSA to influence cloud water adjustments. Therefore, disentangling the respective roles of FA and CSA in cloud adjustments is crucial.

Here, this study provides observational evidence of two-sided cloud water adjustments in marine stratocumulus clouds due to FA and CSA. Our results demonstrate that variations in cloud-top humidity can reverse the direction of LWP adjustments for both FA and CSA. Notably, FA and CSA exhibit opposing effects on LWP under similar cloud-top humidity and cloud thickness conditions. These findings have significant implications for resolving the ongoing debates on aerosol-cloud interactions and improving the parameterization of FA and CSA in global climate models.

Results

FA and CSA regulate cloud water dynamics

In this study, cloud parameters were retrieved from the Meteosat Second Generation (MSG) satellite, while aerosol and meteorological parameters were obtained from the global reanalysis. We utilized two key variables: cloud-top humidity, derived by interpolating NCEP relative humidity profiles to 50 hPa above the cloud top, and cloud temperature depth (CTD), defined as the temperature difference between cloud base and top, with larger values indicating thicker clouds.

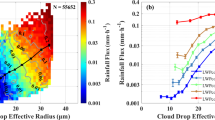
The opposite effects of FA and CSA on re are shown in Fig. 1a, suggesting distinct cloud microphysical processes. Both FA and CSA have non-monotonic impacts on LWP, with both first-increase-then-decrease trends (Fig. 1b), but with different sensitivities. Cloud fraction has a similar increasing trend for both FA and CSA, eventually saturating at high concentrations (Fig. 1c). These findings highlight the significant effects of FA and CSA on cloud properties. The inverted V-shaped relationship between LWP and FA (yellow line in Fig. 1b), as evidenced by multiple studies8,14, is attributed to arise from the synergistic influence of microphysical processes and large-scale meteorology28. Thus, it is essential to isolate the confounding influence of meteorological cloud-controlling factors29 and the mixed effects of FA and CSA27.

Fig. 1: The correlation between fine aerosol (FA) or coarse sea spray aerosols (CSA) and cloud properties.
figure 1

The yellow lines give the dependences of a cloud drop effective radius, b cloud liquid water path, and c cloud fraction as a function of fine aerosol mass concentration (bottom abscissa scale). The blue lines are the same as the yellow lines, but for CSA mass concentration (top abscissa scale). The solid lines connect the dots, which are the averaged cloud properties at 22 bins of fine (yellow) and CSA (blue) aerosol concentrations, respectively, including the 0–1%, 1–3%, 3–5%, 5–10%, 10–15%, …, and 95–100% quantiles. Vertical error bars indicate the standard error, which is too small to be visible.

Full size image

Gryspeerdt et al.14 observed significant geographical variations in aerosol-driven LWP adjustments, largely influenced by meteorological factors (especially relative humidity). Possner et al.30 found negative feedback of LWP to aerosols across stable, unstable, dry, and moist conditions, albeit with varying sensitivity. Therefore, constraining aerosol-meteorology covariation through cloud state and local meteorology is crucial. This study introduces cloud thickness and cloud-top humidity as key proxies of meteorological conditions. Cloud thickness, primarily driven by atmospheric thermodynamics, accounts for a substantial portion of meteorological influences22. Detailed calculations for CTD (Eqs. 1–3) and evaporation rate (Eqs. 4–6) are provided in the Methods section.

Variations in re are the primary drivers of both the precipitation and evaporation process (Fig. 2). Under a mid-range of fixed CTD (1–2 K) and CSA (20-40 μg·m−3), we examined the impact of cloud-top humidity on FA-induced precipitation and evaporation dynamics (Fig. 2a–c). Higher cloud-top humidity promotes stronger rain flux by creating a moist environment favorable for cloud droplet growth (Fig. 2a). It also promotes rain by weakening evaporative loss of cloud water (Fig. 2b, e). From low to high cloud-top humidity, FA consistently reduced re through the Twomey effect, with higher humidity leading to larger re due to enhanced condensational growth (Fig. 2a) and/or less drop evaporation10,31. FA-driven droplet reduction leads to a suppression of rain flux (Fig. 2b) and an enhancement of evaporation rate (Fig. 2c). Conversely, regardless of cloud-top humidity conditions, added CSA consistently increased re (Fig. 2d), as the large size of CSA can produce the early formation of large cloud drops25. CSA-driven droplet enlargement leads to an increase in rain flux (Fig. 2e) while reducing the evaporation rate (Fig. 2f).

Fig. 2: Aerosol-driven variations in cloud processes as functions of fine aerosol (FA) or coarse sea spray aerosol (CSA) concentrations under a fixed cloud temperature depth (CTD) of 1–2 K.
figure 2

The upper panels show (a) re, b rainfall flux, and c evaporation rate as functions of FA concentrations under fixed CTD (1–2 K) and CSA (20–40 μg·m−3). The rain flux (rain rate averaged for the whole 1° × 1° grid) is derived from the observed re and LWP, according to the relationship shown in Fig. 1a in our previous paper27. The evaporation rate is calculated using parameterization from Pruppacher et al.41. The lower panels show re, rainfall flux, and evaporation rate (d–f) as functions of CSA concentrations under fixed CTD (1–2 K) and FA (0.5–0.8 μg·m−3). Lines represent average re, rainfall flux, and evaporation rate at 10 concentration bins for FA and CSA, corresponding to the 0–10%, 10–20%, …, and 90–100% quantiles. Line colors transition from blue to red, indicating increasing cloud-top humidity. N indicates the number of cases. For each line, a slope was calculated using linear regression to fit cloud property variations to aerosol variations across the aerosol bins. Vertical error bars represent standard errors. The dashed 14 μm line indicates the typical precipitation initiation effective radius.

Full size image

The effect of FA on LWP is largely influenced by cloud-top humidity (Fig. 3a). Under dry cloud-top conditions (RH < 20%), evaporation processes dominated, leading to a 7.8 g·m−2 decrease in LWP as FA increased from 0.5 to 3.5 μg·m−3 due to enhanced evaporation (blue line in Fig. 3a). Conversely, under humid cloud-top conditions (RH > 80%), precipitation suppression dominated, leading to a 60.2 g·m−2 increase in LWP as FA increased from 0.4 to 4.5 μg·m−3 (red line in Fig. 3a). For intermediate cloud-top humidity, the overall FA-LWP relationship was the first-increase-then-decrease trend, consistent with previous findings8,14.

Fig. 3: Aerosol-driven variations in cloud water as functions of fine aerosol (FA) or coarse sea spray aerosol (CSA) concentrations under a fixed cloud temperature depth (CTD) of 1–2 K.
figure 3

The upper panels show (a) liquid water path (LWP) and b cloud fraction (Cf) as functions of FA concentrations under fixed CTD (1–2 K) and CSA (20–40 μg·m−3). The lower panels show LWP and Cf (c, d) as functions of CSA concentrations under fixed CTD (1–2 K) and FA (0.5–0.8 μg·m−3). Lines represent average LWP and Cf at 10 concentration bins for FA and CSA, corresponding to the 0–10%, 10–20%, …, and 90–100% quantiles. Line colors transition from blue to red, indicating increasing cloud-top humidity. N indicates the number of cases. For each line, a slope was calculated using linear regression to fit cloud property variations to aerosol variations across the aerosol bins. Vertical error bars represent standard errors.

Full size image

Across all cloud-top humidity, FA consistently increased Cf, saturating at FA concentrations above 1–2 μg·m−3. This indicates that precipitation suppression was the primary driver of the Cf enhancement (Fig. 3b). Moreover, Cf decreased with increasing cloud-top humidity, likely due to weaker radiative cooling with more humid cloud tops, which inhibits atmospheric convection32,33. The enhanced re and hence increased precipitation with more humid cloud tops can also explain the decreasing Cf.

Under fixed CTD (1–2 K) and FA (0.5–0.8 μg·m−3), we analyzed the impact of cloud-top humidity on CSA-cloud water regulation (Fig. 3c, d). The CSA-LWP relationship generally opposed the FA-LWP relationship under similar CTD and cloud-top humidity conditions (Fig. 3c). Under dry cloud-top conditions (i.e., RH < 20%), the buffering effects of precipitation and evaporation processes induce only a slight LWP increase of 4.2 g·m−2 as CSA increased from 8.8 to 44.8 μg·m−3. Under humid cloud-top conditions (i.e., RH > 80%), precipitation processes dominated, leading to a 35.3 g·m−2 decrease in LWP as CSA increased from 10 to 51.5 μg·m−3 due to enhanced precipitation (red line in Fig. 3c).

For intermediate cloud-top humidity (i.e., 20% < RH < 80%), the CSA-LWP relationship exhibited a non-monotonic trend, characterized by an initial positive correlation driven by suppressed evaporation followed by a negative correlation driven by enhanced precipitation. CSA also displayed a first-increase-then-decrease trend in Cf (Fig. 3d), with decreases dominating under humid conditions (red line in Fig. 3d). The above-mentioned trends were also observed for CTD values below 1 K and above 2 K (Figs. S1–S4).

FA effect on LWP remains consistent across different CSA conditions, whereas the CSA effect varies with FA concentration (Fig. 3; Fig. S5 and S6). When FA < 0.8 μg·m−3, CSA reduces LWP under high relative humidity but shows a slight increase at low cloud-top humidity (Fig. 3 and Fig. S5c). Conversely, when FA > 0.8 μg·m−3, CSA slightly increases LWP regardless of cloud-top humidity (Fig. S6). As precipitation is suppressed at high FA concentration, it prevents it from dominating even in humid cloud-top conditions.

FA and CSA susceptibilities under varying humidity

After isolating the effects of FA and CSA, we further explored their combined impacts. To quantify the cloud susceptibilities to FA and CSA, we introduce a bivariate linear fit method. More details are provided in the Methods section. Figure 4 shows the combined effects of FA and CSA on re, LWP, and Cf with a fixed CTD of 1–2 K. Across varying cloud-top humidity, similar FA and CSA concentrations exhibited comparable re values, suggesting that re is more sensitive to FA and CSA concentrations than to cloud-top humidity (Fig. 4a–e). The effects of FA and CSA on precipitation are correlated34,35. Figure 2e illustrates CSA’s stronger impact under low cloud-top humidity conditions, consistent with its more effective precipitation enhancement in non-precipitating environments36. Figure 4f–h further indicates that CSA enhances precipitation more at low FA under dry conditions, while its effect weakens at high FA due to the small collision efficiency of excessively small droplets.

Fig. 4: Combined effects of fine and coarse sea spray aerosols on cloud properties.
figure 4

a–e Cloud droplet effective radius (re), f–j rain flux, k–o liquid water path (LWP), and p–t Cloud fraction (Cf) under a fixed cloud temperature depth (CTD) of 1–2 K and cloud-top humidity. The columns, from left to right, represent low to high cloud-top humidity ranges: <20%, 20–40%, 40–60%, 60–80%, and >80%. The minimum sample size per bin is 50. The values in the upper and bottom two insets in the lower left corner of each panel are a–e dlnre/dlnFA and dlnre/dlnCSA, f–j dlnRain/dlnFA and dlnRain/dlnCSA, k–o dlnLWP/dlnFA and dlnLWP/dlnCSA, and p–t dlnCf/dlnFA and dlnCf/dlnCSA. These susceptibilities were derived from a bivariate linear regression within four quadrants based on FA (1 μg·m−3) and CSA (30 μg·m−3) thresholds.

Full size image

The combined effects of FA and CSA on LWP were complex, with cloud-top humidity significantly influencing both the sensitivity and trends (Fig. 4k–o). Cf responses were significantly stronger to changes in FA concentrations compared to changes in CSA concentrations (Fig. 4p–t). These findings are supported by statistical analyses for CTD values below 1 K and above 2 K (Figs. S7 and S8).

To address concerns about the absorbing nature of smoke particles37, we divided the data into two periods: the smoke season (June-October) and the non-smoke season (the remaining months). As shown in Fig. S9 (smoke) and Fig. S10 (non-smoke), high pollution levels (FA > 3 μg·m−3) are more frequent during the smoke season. However, the relationship between FA and cloud properties remains consistent across both periods, indicating that the potential absorption effects of smoke particles do not alter our conclusions. Cloud properties are influenced by factors beyond humidity, including surface wind speed, sea surface temperature (SST), and lower-tropospheric stability (LTS)38. To address concerns about meteorological covariation, we repeated the analysis of FA and CSA effects on LWP while further fixing surface wind speed, SST, and LTS, respectively. The consistent trends across conditions (Figs. S11–S13) support the robustness of our findings.

To quantify cloud susceptibility to aerosols, we calculated the dlnre/dlnFA, dlnRain/dlnFA, dlnLWP/dlnFA, dlnCf/dlnFA, dlnre/dlnCSA, dlnRain/dlnCSA, dlnLWP/dlnCSA, dlnCf/dlnCSA using the bivariate linear fit method (see Methods section). The dependence of these susceptibilities on cloud-top humidity and aerosol types was analyzed under four conditions: low-low (FA < 1 μg·m−3 and CSA < 30 μg·m−3), low-high (FA < 1 μg·m−3 and CSA ≥ 30 μg·m−3), high-low (FA ≥ 1 μg·m−3 and CSA < 30 μg·m−3), and high-high (FA ≥ 1 μg·m−3 and CSA ≥ 30 μg·m−3), represented by blue dotted, blue solid, yellow dotted, and yellow solid lines, respectively (Fig. 5). These thresholds (FA = 1 μg·m−3, CSA = 30 μg·m−3) correspond to the LWP maxima within the observed increase-then-decrease trends under intermediate cloud-top humidity (green lines in Fig. 3a, c).

Fig. 5: Sensitivity of cloud properties to fine aerosol (FA) and coarse sea spray aerosol (CSA) under varying cloud-top humidity.
figure 5

The cloud temperature depth is between 1–2 K. The top row shows the a dlnre/dlnFA, b dlnRain/dlnFA, c dlnLWP/dlnFA, and d dlnCf/dlnFA, respectively. The bottom row shows the e dlnre/dlnCSA, f dlnRain/dlnCSA, g dlnLWP/dlnCSA, and h dlnCf/dlnCSA, respectively. These susceptibilities are calculated under low-low (FA < 1 μg·m−3 and CSA < 30 μg·m−3), low-high (FA < 1 μg·m−3 and CSA ≥ 30 μg·m−3), high-low (FA ≥ 1 μg·m−3 and CSA < 30 μg·m−3), and high-high (FA ≥ 1 μg·m−3 and CSA ≥ 30 μg·m−3) conditions, represented by blue dotted, blue solid, yellow dotted, and yellow solid lines, respectively. The five data points per line at aerosol concentrations correspond to cloud-top humidity ranges of 0–20%, 20–40%, 40–60%, 60–80%, and 80–100%. These susceptibilities were derived from bivariate linear regression analysis presented in Fig. 4.

Full size image

The dlnre/dlnFA was consistently negative and unaffected by cloud-top humidity or CSA, indicating a robust negative relationship (Fig. 5a). Overall, the variation of rain flux with FA and CSA is consistent with that of re, further highlighting the dominant role of re in controlling precipitation (Figs. 4 and 5; Figs. S5 and S6). The dlnLWP/dlnFA increased with rising cloud-top humidity, reflecting the increased contribution of precipitation processes (Fig. 5c). Under high FA conditions, suppressed precipitation led to evaporation dominance, resulting in negative dlnLWP/dlnFA except under extremely humid conditions (yellow line in Fig. 5c). Conversely, under high CSA conditions, the enhanced precipitation led to more positive dlnLWP/dlnFA (solid lines in Fig. 5c). For Cf, the positive dlnCf/dlnFA was significantly larger at low FA (blue lines in Fig. 5d) compared to high FA (yellow lines in Fig. 5d), consistent with cloud cover saturation at high cloud droplet concentrations39.

Conversely, re exhibited a consistently positive response to CSA, with the dlnre/dlnCSA remaining stable across varying cloud-top humidity and FA concentrations (Fig. 5e). The dlnLWP/dlnCSA transforms from positive to negative as cloud-top humidity increases (blue lines in Fig. 5g). Under high FA conditions, suppressed precipitation led to the dominance of the evaporation process, which induced larger positive dlnLWP/dlnCSA (yellow lines in Fig. 5g). Conversely, under high CSA conditions, enhanced precipitation resulted in a more negative dlnLWP/dlnCSA (solid lines in Fig. 5g). Cf exhibited a generally weak response to CSA, with weak positive dlnCf/dlnCSA observed at the high FA condition and negative dlnCf/dlnCSA at the high CSA condition (Fig. 5h). These findings are also supported by statistical analyses for CTD values below 1 K and above 2 K (Figs. S14 and S15).

Discussion

Our prior work revealed that FA and CSA have opposing and comparable effects on re and warm rain27. This provided the physical basis for the current study’s investigation into LWP response, given its close link to re and precipitation changes. In this study, we interpret LWP adjustment as a competition between increased re leading to (a) gain of LWP due to less drop evaporation, and (b) loss of LWP due to enhanced precipitation. Current global climate model and cloud-resolving model simulations have demonstrated the process by which FA reduces LWP through enhanced evaporation6,8. However, existing cloud-resolving model simulations of CSA have primarily focused on their impact on precipitation, leading to the conclusion that CSA causes cloud water loss26. Our findings reveal that LWP adjustment is governed by the competitive dynamics between precipitation and evaporation, modulated by cloud-top humidity and cloud thickness. Critically, FA and CSA exert opposite effects on LWP under similar cloud-top humidity and cloud thickness, driven by their contrasting impacts on cloud droplet size and associated microphysical processes.

To illustrate the physical mechanisms, we added Fig. 6 to support our interpretation. FA consistently reduces re and rainfall flux, regardless of CSA conditions. Due to the competition between suppressed precipitation and enhanced evaporation, LWP increases until rain rate is mostly suppressed and then, with continued reduction of cloud droplets, the LWP decreases (Fig. 6a–c). Conversely, CSA consistently enhances re and rainfall flux, regardless of FA conditions. The competition between enhanced precipitation and suppressed evaporation dictates the direction of LWP adjustment (Fig. 6d–f). Overall, CSA generally first-increase-then-decrease LWP. We further analyzed CSA’s impact on LWP under varying cloud-top humidity, cloud thickness, and FA concentration. We found that CSA tends to decrease LWP under conditions where precipitation dominates: high cloud-top humidity, large cloud thickness, or low FA (Fig. 3a and Figs. S3–S6). In contrast, CSA tends to increase LWP where evaporation dominates: low cloud-top humidity, low cloud thickness, or high FA (Fig. 3a and Figs. S3–S6).

Fig. 6: Effects of fine aerosol (FA) and coarse sea salt (CSA) on cloud droplet effective radius (re), rainfall flux, and liquid water path (LWP).
figure 6

a–c Show FA’s effects across varying CSA concentrations, while d–f show CSA’s effects across varying FA concentrations. Lines represent average values of re (red), rainfall flux (green), and LWP (blue) for both FA and CSA, corresponding to the 0–10%, 10–20%, …, and 90–100% quantiles. Vertical error bars indicate standard errors.

Full size image

When 1 K < CTD < 2 K (Fig. 3a), cloud-top humidity regulates cloud evaporation efficiency, leading to the transition of LWP trends for FA and CSA across the humidity range of 40% to 60%. Specifically, for cloud-top humidity below 40%, evaporation dominates, with FA reducing LWP while CSA causes a slight increase. Conversely, for cloud-top humidity above 60%, precipitation dominates, with FA increasing LWP and CSA decreasing it. Thicker clouds (CTD > 2 K; Fig. S2 and Fig. S4) exhibit higher precipitation efficiency, making the precipitation the dominant process, leading to FA increasing LWP and CSA decreasing LWP.

This study also observed the inverted V-shaped FA-LWP relationship (yellow line in Fig. 1b), attributed to combined meteorological and physical processes28. Here, we isolate the confounding meteorological factors by limiting the analysis to specific CTD and the relative humidity above the cloud top in the marine stratocumulus regime. FA consistently increases Nd4. The FA-LWP relationship has an inverted V-shaped under moderate humidity. According to Fig. 4k, LWP decreases with FA in dry conditions above cloud tops due to the dominance of enhanced drop evaporation. Conversely, according to Fig. 4o, LWP increases strongly with FA in high relative humidity due to the dominance of suppressed precipitation over evaporation. In medium relative humidity (Figs. 4l–n), there is an increase in LWP with FA at low FA values due to the dominance of precipitation suppression in the high coalescence regime. At high FA values, there is decreased LWP with FA due to the dominance of evaporation in the low coalescence regime. This constitutes an inverted V shape, as shown by the green line in Fig. 3a.

Global climate modeling simulations often lack a comprehensive representation of FA and CSA effects. However, our observational evidence reveals that the mutual concentrations of FA and CSA significantly regulate cloud water adjustment. FA suppresses warm rain, while CSA enhances it (Fig. 2b, e). Under high CSA conditions, the enhanced precipitation results in a stronger positive LWP sensitivity to FA, primarily through precipitation suppression (Fig. 5c). Conversely, under high FA conditions, the weakened precipitation mitigates the LWP-depleting effect of CSA (Fig. 5g), leaving the effect of enhanced evaporation of smaller droplets dominant. Therefore, we suggest that modeling simulations should simultaneously parameterize the effects of FA and CSA, including their combined effect on cloud processes.

Aerosol-cloud radiative forcing remains highly uncertain in climate assessments, primarily due to a lack of knowledge over cloud adjustments. This study, based on observational data, clarifies how FA and CSA regulate LWP through physical mechanisms and environmental influences. The main findings are illustrated in Fig. 7 and summarized as follows:

  1. 1.

    In dry cloud-top environments, the evaporation process dominates (Fig. 6a, c). When CTD is between 1–2 K, increasing FA from 0.5 to 3.5 μg·m−3 reduces droplet size (Fig. 3a), enhancing evaporation and decreasing LWP by ~15% (7.8 g·m−2). Conversely, increasing CSA from 8.8 to 44.8 μg·m−3 enlarges droplets, with evaporation and precipitation processes buffering each other, inducing a slight ~8% increase in LWP (4.2 g·m−2, Fig. 3c).

  2. 2.

    In humid cloud-top environments or thick clouds with CTD above 2 K, the precipitation process dominates (Fig. 6b, d). When CTD is 1–2 K, increasing FA from 0.4 to 4.5 μg·m−3 reduces droplet size, suppressing precipitation, and more than doubles LWP, increasing it by 60.2 g·m−2 (Fig. 3a). Conversely, increasing CSA from 10 to 51.5 μg·m−3 enlarges droplets, enhancing precipitation, and nearly halves LWP, reducing it by 35.3 g·m−2 (Fig. 3c).

  3. 3.

    The respective responses of LWP to FA and CSA are influenced by the mutual concentrations of both aerosol types. Under high CSA conditions, enhanced precipitation induces a stronger positive LWP response to FA, primarily through precipitation suppression (Fig. 5c). Conversely, under high FA conditions, weakened precipitation induces a stronger positive LWP response to CSA, primarily through the reduction of the evaporation of the larger droplets that were induced by the added CSA (Fig. 5g).

Fig. 7: Conceptual illustration of the effects of fine aerosols (FA) and coarse sea spray aerosols (CSA) on marine stratocumulus clouds under dry and humid cloud-top conditions.
figure 7

The cloud temperature depth is between 1–2 K. a Depicts cloud properties under the lowest and highest 10% of FA concentrations, with cloud-top relative humidity less than 20% and CSA between 20–40 μg·m−3. b Shows the same conditions as (a), but with cloud-top relative humidity above 80%. c Depicts cloud properties under the lowest and highest 10% of CSA concentrations, with cloud-top relative humidity less than 20% and FA between 0.5–0.8 μg·m−3. d Shows the same conditions as (c) but with cloud-top relative humidity above 80%. Changes between these states are indicated by the adjacent numbers. Related statistics are presented in Figs. 2 and 3 and Figs. S1–S4.

Full size image

Our study demonstrates that both FA and CSA induce bidirectional LWP adjustments, determined by precipitation-evaporation dynamics. Cloud-top humidity and thickness are crucial in regulating the competition between these processes. Under similar cloud-top humidity and thickness conditions, FA and CSA exhibit opposing LWP adjustment. Current climate models often lack a representation of the combined FA and CSA effects. However, LWP adjustment is significantly influenced by the mutual concentrations of both FA and CSA. The causality of the observed relationships and the related insights from this study should be validated and further quantified by detailed simulations. Since this study focuses on marine stratocumulus regions with typically dry cloud tops, the scarcity of observations under high cloud-top humidity necessitates further investigation in more humid cloud regimes. Therefore, we recommend improved FA-CSA parameterizations in climate models, particularly to capture non-linear LWP responses across varying environmental and aerosol conditions.

Methods

To examine cloud adjustments to fine and coarse aerosols, this study combines geostationary satellite and reanalysis data, which are gridded to a 1° × 1° grid to capture marine water cloud characteristics under spatially varying meteorological conditions. The study area covers the marine stratocumulus-dominated region (10°W-10°E, 10°S-30°S) from April 2004 to January 2013.

Cloud properties, including cloud droplet effective radius (re), liquid water path (LWP), cloud-top temperature (CTT), and cloud fraction (Cf), are retrieved from the Meteosat Second Generation (MSG) satellite. The re and LWP are calculated as 1° grid-averaged values for water clouds. Cf represents the fraction of pixels classified as warm clouds (liquid phase, CTT > 265 K) by MSG within 1° × 1° grids. To avoid ice cloud contamination and minimize retrieval errors due to the solar zenith angle, data are restricted to warm clouds observed between 8:00 and 16:00 local time.

Cloud thickness is a key constraint on meteorological impacts as it reflects much of the thermodynamic influence22. However, retrieving both cloud-top height and cloud base height (CBT) relies on the adiabatic assumption (typically set to 1 in previous studies), which is sensitive to sea surface temperature40. The cloud temperature depth (CTD) is calculated as in Eq. 1:

$$CTD=CBT-CTT$$
(1)

where CTT is MSG-observed, and CBT is the cloud base temperature. In this study, CBT is approximated by the temperature at the lifting condensation level (\({{\rm{T}}}_{{LCL}}\)), assuming a dry adiabatic lapse rate from sea surface to cloud base, as shown in Eqs. 2 and 3:

$${Z}_{LCL}=1.23\times ({T}_{z}-{T}_{d})$$
(2)
$${T}_{LCL}={T}_{z}-0.98\times {Z}_{LCL}$$
(3)

Here, \({{\rm{T}}}_{z}\) and \({{\rm{T}}}_{d}\) are the sea surface temperature and dew point temperature from NCEP reanalysis. \({{\rm{Z}}}_{{LCL}}\) and \({{\rm{T}}}_{{LCL}}\) are the height and temperature of the lifting condensation level.

Cloud evaporation rate is estimated using the idealized approach. First, the evaporation rate of a single cloud droplet (kg·s−1) is calculated using parameterization from Pruppacher et al.41 as in Eq. 4:

$${E}_{droplet}=\frac{4\pi r{D}_{v}({\rho }_{v}^{\ast }-{\rho }_{v})}{\frac{{L}_{v}}{{R}_{v}T}+\frac{{R}_{d}T}{p{D}_{v}}}$$
(4)

Here, \(r\) is the cloud droplet radius. \({D}_{v}\), the water vapor diffusion coefficient, is 2.5 × 10−5 m2·s−1. Saturated and ambient water vapor densities, represented by \({\rho }_{v}^{* }\) and \({\rho }_{v}\) (kg·m−3), are determined using relative humidity. \({L}_{v}\), the latent heat of vaporization, is 2.5 × 106 J·kg−1. \({R}_{v}\) and \({R}_{d}\) are the gas constants for water vapor (461 J·kg−1·K−1) and dry air (287 J·kg−1·K−1), respectively. Temperature (\(T\)) and pressure (\(p\)) are obtained from NCEP reanalysis at 50 hPa above cloud top. Second, assuming the radius of all cloud droplets is re, thus total cloud droplet number per unit area with unit of m−2 is calculated in Eq. 5:

$${N}_{tot}=\frac{LWP}{\frac{4}{3}\pi {r}_{e}^{3}{\rho }_{w}}$$
(5)

Here, LWP and re are obtained from MSG satellite observations. \({\rho }_{w}\), density of water, is 1000 kg·m−3. Finally, multiplying cloud droplet number by the single droplet evaporation rate yields an approximate total cloud evaporation rate (\({E}_{{tot}}\)) with unit of kg·m−2·s−1 in Eq. 6:

$${E}_{tot}={N}_{tot}\times {E}_{droplet}$$
(6)

The aerosol data are obtained from the Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-2) reanalysis. FA is defined as the sum of surface mass concentrations of sulfate, organic carbon, black carbon, and sea salt with a radius <1 μm. CSA is defined as the sum of surface mass concentrations of sea spray with a radius >1 μm. Previous studies have validated the reliability of MERRA-2 aerosol data42. MERRA-2 simulations of sea salt mass concentration show good agreement with global aircraft observations, exhibiting correlation coefficients above 0.843. Cloud-top humidity is determined by linearly interpolating the relative humidity profile (from the National Centers for Environmental Prediction reanalysis) at 50 hPa above the cloud-top observed by MSG.

The GPM DPR dual-frequency radar remains a highly reliable instrument for detecting global warm rain. We combined MSG cloud data with GPM DPR precipitation data to create a lookup table. The results in Fig. S16 are consistent with Fig. 1a27, with the data period extended from 2014–2017 to 2014–2020. As shown in Fig. S16, rain flux is controlled by both re and LWP, enabling retrieval of rain flux values corresponding to specific re and LWP. The rain flux (rain rate averaged over each 1° × 1° grid) is thus derived from observed re and LWP using this relationship. The rain flux (rain rate averaged for the whole 1° × 1° grid) is derived from the observed re and LWP, according to Fig. S16.

To quantify the cloud adjustments to FA and CSA, we introduce a bivariate linear fit method. The following formula is fitted to quantify the impact of FA and CSA on cloud properties in Eq. 7:

$$y=\frac{d\,{\text{ln}}\,y}{d\,{\text{ln}}\,FA}\times \,{\text{ln}}\,FA+\frac{d\,{\text{ln}}\,y}{d\,{\text{ln}}\,CSA}\times \,{\text{ln}}\,CSA+c$$
(7)

The variable y represents re, LWP, or Cf, respectively. The dlny/dlnFA and dlny/dlnCSA represent the cloud susceptibility to FA and CSA, respectively. The term c is the constant term coefficient in the bivariate linear fit. Firstly, we binned the data into dense FA and CSA intervals, calculating binned averages for aerosol and cloud properties. Then, using these binned values, we derived dlny/dlnFA and dlny/dlnCSA via bivariate linear fit in log-log space to simultaneously quantify the cloud susceptibility to FA and CSA.