Introduction

Interlayer interactions in transition metal di-chalcogenides (TMDs) are complex, driven by both dispersive van der Waals (vdW) forces and orbital hybridization between adjacent chalcogen layers. Unlike the non-directional vdW interactions, interlayer hybridization is significantly dependent on the hybridization axis, which is highly sensitive to the stacking configuration. In this respect, interlayer hybridization in TMDs is expected to be more prominent when the hybridization axis aligns with the stacking axis to preferentially facilitate interactions between pz states of chalcogen atoms in adjacent layers. This hybridization may cause a large splitting between anti-bonding and bonding states near the Fermi level, leading to a significant change in the band structure when forming a layered structure - one of the characteristic features of TMD materials with strong interlayer coupling. This suggests that interlayer hybridization could be as influential as the vdW interaction in determining the phase stability and electronic properties of TMD materials.

In this work, we focus on PtSe2, a representative TMD material known for its strong interlayer coupling due to pronounced Se-pz interlayer hybridization1. Notably, its band gap was observed to be strongly dependent on layer thickness, leading to a metal-insulator transition (MIT) as additional layers are added2,3,4,5. The strong interlayer coupling in PtSe2 was also evident in various optical measurements such as Raman spectra6 and reflective index7, which vary with the number of layers. Interestingly, a series of these measurements have revealed various stacking modes beyond the ground-state AA stacking, each characterized by distinct optical signals. The observation of different stacking modes led to Kempt et al.’s suggestion of a possible stacking polymorphism in bulk PtSe28, which also aligns with the frequent formation of a polycrystalline phase upon its synthesis6,9,10. Furthermore, there was an experimental report that grain boundary formation between two different stacking domains in the bilayer structure can contribute to metallic transport through channels created by extra Pt or Se atoms in the boundary11, which is understood to be a potential source of differing experimental estimates for the critical layer count necessary for the onset of MIT2,3,4,5. Thus, accurately identifying the onset of MIT in well-controlled PtSe2 samples, free from grain boundaries and other defects, requires a thorough understanding of how the electronic band structure evolves across various stacking configurations. However, crucial elements such as the underlying mechanisms and their impact on band gap changes across these configurations remain largely unexplored in previous studies.

The theoretical description of the interlayer interactions in PtSe2 is challenging because of the intricate interplay of vdW forces, interlayer hybridization, and potential metallization. Currently available vdW-DFT functionals have produced widely scattered results for interlayer separations of layered PtSe2 systems. Accordingly, the DFT estimations for band gaps and the critical layer thickness for the MIT have also varied depending on the density functional employed4,12,13,14. Even on the experimental side, there has been considerable variations in the measurements of interlayer separation in bilayer PtSe2, ranging from 5.0 Å to 5.9 Å4,5,15. On the other hand, the diffusion quantum Monte Carlo (DMC) method has been successfully applied to accurately assess interlayer interactions of various 2D layered materials16,17,18,19,20,21,22,23,24,25. Its full incorporation of electron-electron correlations is not only highly beneficial in describing the vdW interactions, but also enables a simultaneous description of intralayer and interlayer interaction on an equal footing. Particularly, DMC successfully identified a semiconductor-metal transition in the A1B−1-stacked bilayer blue phosphorene22. This was achieved by the construction of the interlayer binding energy curve, which demonstrated a double-minima feature: the global minimum at a longer interlayer distance showed semiconducting behavior, while the local minimum, at a shorter distance comparable to the P-P bond length, exhibited metallic properties. From this, we expect the DMC calculations to provide a deeper and comprehensive understanding of the interlayer coupling in PtSe2 beyond the previous DFT studies.

Through DMC and DFT calculations, we have investigated the structural stability of various stacking modes in bilayer PtSe2 to explore the mechanisms of stacking polymorphism and its impact on band gap variations. For this, we first optimized the monolayer PtSe2 structures and then constructed the DMC interlayer binding energy curves in its bilayer forms. Interestingly, our findings reveal that while the AA stacking is most stable, an AB-r stacking is nearly degenerate with the AA stacking within statistical errors. This stacking degeneracy, which is hardly observed in other TMD materials, underscores a significant role of the interlayer hybridization in offsetting the energy cost associated with a larger interlayer separation in the AB-r mode. We have utilized our DMC results for bilayer PtSe2 to benchmark the performance of a variety of widely used DFT functionals that are known to represent well vdW binding, interlayer hybridization, or both. From these comparisons, we find that the r2SCAN+rVV10 exhibits good performance in describing the interlayer interactions in bilayer PtSe2. Finally, based on the benchmarked DFT-r2SCAN+rVV10 calculations, we have discovered the stacking polymorphism in few-layer PtSe2 systems, which turns out to be one of the main factors complicating the characterization of MIT in PtSe2. Our study not only unveils the stacking polymorphism in a few-layer PtSe2 system but also opens new possibilities for nanoelectronic devices based on a refined understanding of its layer-dependent MIT.

Results and discussion

Relaxed 1T and 2H monolayer structures

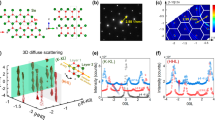
Firstly, we optimized the monolayer structures of 1T and 2H phases using DMC calculations. As depicted in Fig. 1a, d, the 1T and 2H phases are characterized by an octahedral and a trigonal structure, respectively, each consisting of a transition metal layer sandwiched by two chalcogen layers. Both monolayer phases of PtSe2 have been successfully synthesized in recent experiments26,27,28,29. These geometries are defined by lattice parameters and buckling heights labeled as a and h in Fig. 1a. We constructed contour maps of DMC potential energy surfaces (PESs) for varying structural parameters for both 1T and 2H phases, which are presented in Fig. 1b, c. For comprehensive mapping of the PESs, we evaluated 35 data points for the 1T phase, with lattice constants ranging from 3.63 Å to 3.75 Å at intervals of 0.02 Å, and buckling heights from 2.4 Å to 2.8 Å at intervals of 0.1 Å. Similarly, for the 2H phase, we analyzed 35 data points, with lattice constants from 3.47 Å to 3.59 Å and buckling heights from 2.8 Å to 3.2 Å, using the same intervals as those applied for the 1T phase. These calculations were conducted using a 4 × 4 × 1 supercell, balancing accuracy and computational cost. We anticipate substantial cancellation of finite-size effects on the PESs, especially near the equilibrium, given that they are derived from energy differences among DMC supercell energies. The DMC supercell energies were fitted to the 2D Gaussian functions to determine the equilibrium structural parameters, indicated by white stars with statistical errors in Fig. 1b, c. Our DMC results for the 1T phase structural parameters align closely with experimental values26, as illustrated in Fig. 1b, with deviations of approximately 1% for lattice parameter and about 3% for buckling height. We here note that the experimental values were obtained from monolayer PtSe2 grown on substrates, whereas our DMC calculations were performed on freestanding monolayers. The potential strain effects from the substrate could contribute to the discrepancies observed, as the substrate-induced strain might alter the structural parameters from their intrinsic freestanding values. While there have been several experimental reports for the synthesis of the 2H-phase monolayer PtSe228,29,30, none provide explicit values for their structural parameters. Meanwhile, our DFT calculations for monolayer PtSe2 yielded varying values for both lattice constant and buckling height, influenced by the choice of density functional used. Notably, for the 1T-phase monolayer, meta-GGA functionals and HSE06 hybrid functional demonstrated the great consistency with DMC results (see Supplementary Table 1). For the equilibrium monolayer structure of each phase, we made finite-size corrections to the DMC supercell energies by extrapolating to the thermodynamic limit (see Supplementary Fig. 1), which showed an energy difference of 1.922(3) eV/f.u. between 1T and 2H monolayer phases of PtSe2.

Fig. 1: DMC total energies of 1T- and 2H-phase monolayer PtSe2.
figure 1

a, d show their respective crystal structures and b, c present their potential energy surfaces (PESs) as functions of lattice constant a and buckling height h. The contour plots are in the same color scale denoted by the color table which is in units of eV/f.u. The white star symbols represent the optimal DMC values of a and h while the red symbol denotes the experimental ones.

Full size image

In Fig. 2, we compare this DMC energy difference with corresponding DFT results, where the DMC value is represented by a gray horizontal bar (see Supplementary Table 1 for detailed energy values). One can see that the DFT calculations significantly underestimate the energy difference, when compared to the DMC result, by ~0.6 eV/f.u at most. Furthermore, while incorporating vdW interactions has minimal impact on the monolayer energy difference, enhancing the description of electronic correlation with meta-GGA functionals or hybrid functional of HSE06 brings the DFT results closer to the DMC value. The substantial energy difference between two monolayer phases of PtSe2 as elucidated by our DMC calculations explains the rarity of the natural occurrence of 2H phase and its synthesis difficulties28,29,30.

Fig. 2
figure 2

Comparison of the DMC energy difference between 1T- and 2H-phase monolayer PtSe2 with the corresponding DFT values computed with several different density functionals.

Full size image

Interlayer binding properties of 1T and 2H bilayers

Next, we examined the interlayer binding properties of bilayer PtSe2 systems. For this, we constructed DMC interlayer binding energy curves as functions of interlayer distance, dPt−Pt, for both 1T- and 2H-phase bilayers. Here we considered the three stacking modes for each phase, as shown in Fig. 3a–c, e–g, which were identified experimentally via scanning transmission electron microscopy (STEM)11,31,32. The binding energy curves, plotted with the finite-size corrected DMC energies (see Supplementary Fig. 2), were fitted to the Morse potentials to determine the equilibrium interlayer binding energies and distances listed in Table 1. Figure 3d displays the interlayer binding curves for the 1T bilayer, where the AA stacking mode is shown to be the most energetically stable, mirroring bulk PtSe21,11. However, our DMC calculations also reveal that another stacking mode of 1T-AB-r, involving a 60∘ rotation of the AB stacking mode, is energetically equivalent to the 1T-AA stacking mode within statistical errors. Note that these two degenerate stacking modes, 1T-AA and and 1T-AB-r, correspond to 1TO and 2HO bulk phases, respectively, according to the nomenclature used in ref. 8.

Fig. 3: Interlayer binding in bilayer 1T- and 2H-PtSe2 across various stacking configurations.
figure 3

a–c show top and side views of the crystal structure for AA-, AB-, AB-r-stacked bilayer 1T-PtSe2, e–g display those for AB-, N-, AA-r-stacked bilayer 2H-PtSe2. The black parallelogram represents the unit cell of each structure and dPt−Pt in a corresponds to the interlayer separation. d, h present DMC interlayer binding energy curves of bilayer 1T- and 2H-PtSe2, respectively, as functions of the interlayer distance dPt−Pt.

Full size image
Table 1 DMC equilibrium interlayer binding energies (Eb), interlayer distances (dPt−Pt), and total energies relative to the AA stacking (ΔErel) for 1T- and 2H-phase bilayer PtSe2
Full size table

The 1T-AB-r stacking mode, identified to coexist and form grain boundaries with the AA stacking11, has a notably larger interlayer spacing at equilibrium, as presented in the Table 1. This finding suggests that not only vdW interactions, whose strength depends largely on the interlayer separation, but also significant interlayer hybridization, contributes to this structural degeneracy by offsetting the energy cost associated with larger interlayer distances. This is further supported by our Bader charge analysis, where the charge transfer in 1T-AB-r stacking (0.014 per Se atom) exceeds that in 1T-AA stacking (0.008 per Se atom). The Bader charge analysis was carried out using the PBE functional, specifically to isolate and examine hybridization effects on the stability of different stacking modes in the PtSe2 system, independent of vdW forces. The observed stacking degeneracy at different interlayer distances may relate to the widely scattered values (5.0 Å ~5.9 Å) reported for the interlayer distance in bilayer experiments4,5,15. The increased interlayer distance in the 1T-AB-r stacking mode reduces the spatial overlap between Se-pz orbitals across the upper and lower layers, leading to diminished splitting into antibonding and bonding states near the Fermi level1. This contributes to a larger band gap in the 1T-AB-r mode compared to the 1T-AA stacking mode (see Supplementary Fig. 3 and its related discussion).

The binding nature of bilayer PtSe2 is further analyzed through one-dimensional (1D) charge density profiles projected along the vertical z-axis, which allows observation of electron redistribution due to interlayer interactions. For this, we computed the 1D charge density difference between the bilayer and separate monolayers as Δρ(z) = ρbi(z) − ρupper(z) − ρlower(z) where each DMC charge density is computed using an extrapolated estimator (see Sec. Methods). Note that the positive (negative) sign indicates electron accumulation (depletion). Figure 4a presents the charge density difference profile for an interlayer spacing of 8.0 Å in the AA-stacked PtSe2 bilayer where the interlayer pz hybridization effects are expected to be minimal and vdW interactions are dominant. No charge accumulation is observed in the intermediate region between the upper and the lower monolayers, with slight charge accumulations near the interior Se planes due to intralayer charge redistribution, confirming that interlayer binding is mainly due to vdW interactions driven by fluctuating surface polarization. On the other hand, Fig. 4b, the charge density difference for the equilibrium distance of 5.37 Å, shows significant electron accumulation between the layers due to electron migration from the interior Se planes. This signifies substantial interlayer hybridization to form the covalent bond with electrons shared between the layers, which is sometimes referred as “quasi interlayer bonding” between the interior Se planes33,34. From this, we conclude that the binding nature in PtSe2 bilayers is characterized by interlayer hybridization as well as the vdW interactions.

Fig. 4: DMC 1D charge density differences per formula unit projected onto the vertical z-axis for the AA-stacked bilayer 1T-PtSe2.
figure 4

a, b present the charge density differences at interlayer separations of dPt−Pt = 8.0 Å and dPt−Pt = 5.37 Å, respectively, the latter of which corresponds to the equilibrium interlayer distance. The horizontal dashed lines denote the vertical positions of each Pt and Se planes while the vertical dotted line corresponds to zero density difference.

Full size image

For the 2H-phase bilayer, our DMC results show that the 2H-AB stacking is most energetically favorable, followed by the nearly degenerate 2H-N and 2H-AA-r stackings, with similar equilibrium interlayer separations (see Fig. 3e–h). This energetic ordering between 2H-AB and 2H-AA-r stackings is consistent with the stacking stability observed in other 2H-phase TMD materials such as MoS2 and MoSe235,36. Notably, interlayer binding energies for the 2H phase are larger than those for the 1T phase, reducing the energy difference between 1T- and 2H-phase bilayers by about ~0.1 eV/f.u. (see Table 1), compared to the monolayer energy difference of 1.922(3) eV/f.u.. Our PBE Bader charge analysis shows the increased charge transfer in the 2H-AB bilayer (0.020 per Se atom) compared to the 1T-AB-r bilayer, supporting the enhanced interlayer bindings in the 2H phase.

We now compare our DMC results for the 1T-phase bilayer PtSe2 with DFT calculations based on various vdW DFT functionals for different stacking modes (AA, AB-r, and AB). Figure 5a, b display the DFT equilibrium interlayer distances and binding energies, respectively, with the DMC results represented by colored regions to incorporate their statistical uncertainties. The DFT results display notable variations in interlayer distances and binding energies depending on the choice of density functionals, which was also noted in prior studies examining the effects of vdW corrections on layered materials37. Among the DFT functionals considered here, the r2sCAN+rVV10 functional is shown to produce the most consistent DFT results with the DMC ones for both energetics and separation distances, regardless of the specific stacking mode. The degeneracy between the AA and the AB-r stackings is also corroborated by the r2SCAN+rVV10 calculation, underscoring its effectiveness in capturing relative energetics across different bilayer stacking modes.

Fig. 5: Comparison between DMC and DFT calculations for AA-, AB-r, and AB-stacked bilayer 1T-PtSe2.
figure 5

a present the equilibrium separation distances and b show the interlayer binding energies, which were estimated by both DMC and DFT calculations. The DMC optimized values are represented by colored regions to reflect their statistical uncertainties.

Full size image

Furthermore, a comparison of charge density redistributions between DMC and DFT analyses, as illustrated in Supplementary Fig. 4, reveals that the r2SCAN+rVV10 functionals effectively represent the charge density redistributions of the AA stacking mode at its equilibrium distance, accurately capturing interlayer hybridization, albeit with minor quantitative differences from DMC results. Our r2SCAN+rVV10 calculations also show significant charge accumulation in the intermediate region between the upper and lower layers of the AB-r stacked bilayer, similar to the AA mode (see Supplementary Fig. 5). This similarity supports the observed stacking degeneracy between the AA and AB-r modes. Considering the extreme sensitivity of the band gap to even small changes in interlayer separation as well as the importance of interlayer hybridization, the geometry optimized at the DFT level with the r2SCAN+rVV10 functional is expected to provide a fine reference to assess an accurate band gap of a PtSe2 system.

Stacking polymorphism and band gap

Having verified its accuracy for bilayer systems, we further explored the interlayer binding properties of few-layer 1T-phase PtSe2 using DFT calculations with the r2SCAN+rVV10 functional. Specifically, we assessed the relative energetics of various stacking configurations up to five layers, featuring sequences of AA or AB-r stacking (see Fig. 6a for examples of five-layer stacking characterized by the number of AB-r interfaces, NAB−r). It is noted that these AA and AB-r stackings are nearly energetically indistinguishable for the bilayer. Figure 6b shows the relative energies of different stacking configurations with respect to the most stable stacking mode as a function of NAB−r for each layer count ((See Supplementary Table 2 for detailed energy values). In this figure, one can see several different stacking modes with energies closely matching the lowest energy configuration within a narrow range of 2.5 meV/f.u., indicating a significant stacking polymorphism in few-layer PtSe2 systems. This polymorphism is attributed to the near-degeneracy between the AA and AB-r stacking modes observed in bilayer PtSe2. Furthermore, as the layer count increases, more stacking configurations fall within this tight energy range, suggesting the potential for stacking fault (disorder) or coexistence of AA with other stacking modes as layer thickness increases. This stacking polymorphism would lead to grain boundaries between different stacking domains in few-layer PtSe2 samples, which could develop metallic electronic structures as discussed in ref. 11. We also identified similar stacking polymorphism in bulk PtSe2 (see Supplementary Fig. 7) as predicted in previous DFT studies8, influencing the synthesis of polycrystalline PtSe2 samples6,9,10. As shown in Fig. 6b, the energy difference between an N-layer system with only AA stackings (NAB−r = 0) and one with only AB-r stackings (NAB−r = N − 1) increases with N, reaching 40 meV/f.u. for bulk PtSe2. Considering that the AA and AB-r stackings are nearly degenerate in bilayers, this increase suggests that long-range vdW interactions progressively dominate over short-range interlayer hybridization effects with the increasing layer thickness. Notably, the use of cross-sectional STEM along the interlayer stacking axis has proven effective for directly identifying layer stacking disorder in MoTe238. Therefore, conducting similar STEM measurements on PtSe2 systems would be highly beneficial for providing direct evidence of their stacking polymorphism.

Fig. 6: Energetic stability and band gap of few-layer PtSe2.
figure 6

a shows side views of the crystal structures of AAAAA-, AAAAB-r-, AAAB-rB-r-, and AAB-rB-rA-stacked pentalayer 1T-PtSe2, where NAB−r indicates the number of AB-r interfaces. The yellow and blue dotted lines between adjacent layers represent AA and AB-r interfaces, respectively. b presents relative total energies of different N-layer stacking sequences of AA and AB-r modes with respect to the most stable configuration, i.e., the stacking sequence composed solely of AA interfaces (NAB−r = 0). While c shows band gaps of several different polymorphic stacking phases of N-layer PtSe2, d displays the band gap of AA-stacked N-layer PtSe2−x versus Se vacancy concentration x. All data presented here were obtained from benchmarked DFT-r2SCAN+rVV10 calculations.

Full size image

Finally, we discuss the impact of the stacking polymorphism on the band gap of few-layer PtSe2. Figure 6c presents the band gaps calculated with the r2SCAN+rVV10 functional for various stacking phases of N-layer systems (see Supplementary Table 2 for detailed band gap values). The band gap of the AA-stacked few-layer PtSe2 decreases from 1.57 eV in a monolayer to 0.09 eV in a five-layer system, aligning quantitatively with the HSE06 values reported for the 1TO phase in ref. 8. However, regardless of the stacking mode, an N-layer PtSe2 exhibits a finite band gap with an indirect nature for N ≤ 5, as shown in Supplementary Fig. 6, indicating no MIT up to five-layer systems. This is in contrast to earlier DFT calculations based on semi-local density functionals2,3,4,5, which suggested an MIT for N ≤ 3. Notably, HSE06 calculations by Kempt et al.8 also show finite band gaps up to a six-layer system while GW calculations9 confirm a semiconducting nature persists up to a four-layer system. These observations indicate that the r2SCAN+rVV10 functional is particularly effective at the DFT level for band gap estimations of PtSe2, offering a more cost-efficient alternative compared to hybrid functionals or GW methods. However, our DFT-r2SCAN+rVV10 results for pristine few-layer PtSe2 do not explain experimental observations of MIT at three to five layers2,3,4,5. Interestingly, we observed that Se vacancies, the most abundant defects in synthetic PtSe2 films39, significantly reduce the band gap (see Fig. 6d). Specifically, the band gap of a three-layer PtSe2 with a Se vacancy concentration of 1/9 disappears entirely, suggesting an MIT at thinner layers than in pristine conditions. In addition, as seen in Fig. 6c, a polymorphic stacking sequence with at least one AB-r interface tends to exhibit less band gap reduction with increasing layer thickness compared to a sequence composed solely of AA interfaces, due to the diminishing band splitting into antibonding and bonding states near the Fermi level with increasing interlayer separation at the AB-r interface. Therefore, the interplay between stacking polymorphism, potential metallic grain boundaries formed through this polymorphism, and defect formations complicates the MIT in few-layer PtSe2, necessitating careful interpretation of its band gap data.

This study provides a comprehensive understanding of the interlayer interactions and stacking polymorphism in few-layer 1T-phase PtSe2, employing a combination of DMC and DFT methods. Our DMC calculations reveal the near degeneracy between AA and AB-r stacking modes in bilayer PtSe2, along with their distinct interlayer separations. The increased interlayer separation in the AB-r mode leads to a notable increase in the band gap, which we attribute to diminished interlayer hybridization between adjacent layers. The DMC-benchmarked DFT study with the r2SCAN+rVV10 functional exposes a stacking polymorphism - a phenomenon established thermodynamically in ref. 8 - across different layer counts. It also builds on the insights from ref. 8 by elucidating the underlying mechanisms responsible for band gap variations across different stacking configurations, focusing on the number of AB-r interfaces and their impact on the critical layer count for the layer-dependent MIT. This polymorphism is likely instrumental in the formation of grain boundaries between different stacking domains and the emergence of metallic electronic structures in the few-layer systems.

Distinct from the thermodynamically-driven polymorphism at temperatures above 400 K addressed in ref. 8, our study explores stacking polymorphism in few-layer systems governed by degenerate AA and AB-r interfaces. This leads us to identify a broader range of polymorphic configurations than those covered in ref. 8. Additionally, the significant impact of Se vacancies on band gap reduction brings to light the interplay between vacancy defects and stacking polymorphism as crucial elements in analyzing the layer-dependent MIT of few-layer PtSe2. Our dual perspective aligns with experimental discrepancies regarding the critical layer count for MIT and contributes to a more complete understanding of the band gap variability observed in few-layer PtSe2.

In conclusion, the intricate interplay between stacking polymorphism, defect formations, and interlayer interactions in PtSe2 elucidates the broader challenge of understanding and manipulating the physical properties of TMDs. This study shows that the r2SCAN+rVV10 functional within the DFT framework offers a valuable tool for probing electronic properties of TMD materials as well as their strong interlayer interactions, providing a balance of computational efficiency and accuracy. Future studies should focus on refining the control of stacking faults and defect concentrations to tailor the material properties for specific applications, as well as expanding the investigation to other TMD materials to explore the generalizability of these findings.

Methods

Diffusion Monte Carlo calculation

Our fixed-node DMC calculations were carried out using the QMCPACK package40,41. We utilized the Slater-Jastrow type trial wave functions, comprising a product of the Slater determinants and correlating Jastrow factors that include up to three-body Jastrow factors to account for electron-electron-ion correlations. The Slater determinants were constructed using Kohn-Sham orbitals from the DFT-PBE calculations executed using the QUANTUM ESPRESSO42, with a plane-wave cutoff of 400 Ry and 18 × 18 × 1 Monkhorst-Pack k-point mesh43 for both monolayer and bilayer PtSe2. We used a norm-conserving scalar-relativistic energy-consistent pseudopotential by Burkatzki, Filippi and Dolg44,45 for Se atoms while Pt atoms were treated with a norm-conserving potential with pseudovalence state of 5s25p66s15d9, consistent with our earlier DMC studies20,24,46. To mitigate one-body size effects, twist-averaged boundary conditions47 were applied using 36, 16, and 9 twist angles for supercell sizes of 2 × 2 × 1, 3 × 3 × 1, and 4 × 4 × 1, respectively. The twist-averaged DMC supercell energies were then extrapolated to the thermodynamic limit (N = ∞) through linear fitting to address the two-body size effects.

The optimization of Jastrow parameters was conducted in variational Monte Carlo (VMC) calculations with the linear method proposed by Umrigar et al.48. Subsequent DMC calculations were performed with a time step of τ = 0.005 Ha−1 and size-consistent T-moves for variational estimation of non-local pseudopotential terms, as in our previous DMC studies for a cousin material of PtTe246. A vacuum distance was set to be 30 Å along the vertical direction to the PtSe2 plane to minimize spurious interactions between periodic images. For the estimation of densities, considering their non-commutative properties with the Hamiltonian, we used an extrapolated estimator defined as ρext = 2ρDMC − ρV MC, minimizing trial-function-dependent biases to second order49.

Density functional calculation

Complementary DFT calculations were performed using the VASP package50,51, where the Kohn-Sham equations were solved with the projector-augmented wave pseudopotentials52,53 for both Pt and Se atoms to include spin-obit coupling effects. A plane-wave cutoff of 400 eV and a 12 × 12 × 1 (12 × 12 × 4 for bulk) Monkhorst-Pack k mesh were employed. The convergence thresholds were set at 10−6 eV for electronic states and 5 × 10−3 eV/Å for forces during structural optimizations. We employed the meta-GGA functionals of SCAN54 and r2SCAN as well as semilocal density functionals of LDA55 and PBE56. These functionals combined with various vdW-corrected schemes, including PBE+MBD57, vdW-optB86b58, rev-vdW-DF259, SCAN+rVV1060, and r2SCAN+rVV1061, were used to deal with interlayer interactions.