Introduction

Layered transition metal dichalcogenide (TMD) based semiconductor heterojunctions have been extensively employed in optoelectronic devices and electrocatalysis1,2,3,4,5,6. In addition to the presence of a finite band gap, alignments of the valence band maxima and conduction band (CB) minima of the layers are also essential in determining their usage. For example, a type-II band arrangement, which is critical for solar cells, photodetectors, and photocatalysis3,7,8,9,10,11, results when the band edges of one layer are energetically higher than their counterparts in the other such that the valence band (VB) maxima falls in between the CB minimum and the VB maxima of the other material. This staggered arrangement can either drive the photogenerated charge carriers in opposite directions12,13,14,15 or perform redox processes based on the energies of the frontier orbitals of an adsorbate16,17. Recently such junctions are also being explored for the development of solar batteries18,19, where metal ion batteries can be directly charged using solar light.

Layered TMDs exist in multiple phases with very different physical and electronic properties. For example, the H-phase is semiconducting where the band gap is a function of the number of layers20 but the T-phase is metallic21. On the other hand, the quasi-metallic T’ phase22,23 shows an inverted band gap at the Γ-point in addition to a small fundamental gap24,25,26. The disposition of the d-orbitals in the D3h environment coupled to d2 configuration of the Mo centre ensures that the H-phase is semiconducting, whereas the octahedral chemical environment in the T-phase makes it metallic.

In TMD heterojunctions that are employed either as electrocatalysts or in photobatteries, ions from the solution phase can intercalate between the layers, thus altering their physical and electronic properties26,27,28. In one such well known example, the intercalation of Li-ions into MoS2 induces phase transition from the semiconductor H-phase to the quasi-metallic T’-phase.29,30,31 The atomistic mechanism of this solid state phase transition has been studied experimentally employing in situ STEM measurements32. Subsequently, the irreversible transformation of H-MoS2 upon lithiation at low potentials leading to the formation of Li2S has also been demonstrated experimentally33. A new intermediate state has also been observed in lithium intercalated twisted bilayer MoS234.

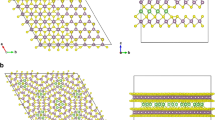
While Li-ion induced phase changes in H-MoS2 has been extensively studied, as discussed in the last section, corresponding changes in the presence of a heterostructure is not well documented. Here, we study the phase stability of lithiated MoS2 at various Li-ion concentrations, employing both density functional theory (DFT) and in situ Raman experiments, in the presence of another material that forms a type II heterojunction. For our study we chose MoS2/MoO3 combination because it has been shown to act as a photocathode before18. Our calculations indicate that the metallization requires ~ 1.5 times higher Li-ion consumption in MoS2 in the presence of MoO3. The emergence of the T-phase starting from the H-phase in the absence or presence of the heterostructure partner is tracked by Raman spectroscopy, as shown graphically in Fig. 1. The theoretical prediction of metallization at higher Li-ion concentration is validated by in situ experimental determination of electrical conductivity exclusively from the lithiated MoS2 at various concentrations of intercalated Li-ion with or without MoO3.

Fig. 1: Schematic diagram of phase transition from the semiconducting H-phase to the quasi-metallic T’-phase in lithiated MoS2 with or without the heterojunction.
figure 1

The Raman spectra is overlaid on top of the supercell units. Appearance of J1, J2 and E1g peaks indicate the emergence of the T'-phase. As indicated in the figure, these peaks appear at a much lower discharge voltage (higher concentration of intercalated Li-ions) in the presence of the heterostructure. From the computational perspective, the heterostructure is modeled explicitly only for the H-phase of MoS2. In order to compute the stability between the H- and the T'-phases in the presence of the heterojunction, an alternative computational set-up, as explained in the main text, is employed.

Full size image

Results and Discussion

Electronic Structure of LixMoS2/MoO3 Heterojunction

In LixMoS2 (where x is the fraction of intercalated lithium), there are additional electrons in the CB corresponding to the number of Li-ions that are present (see supporting information (SI), Table S1). On the other hand, in type-II heterojunction, this excess electron density can be delocalized onto the lower energy CB orbitals of the other material. In order to demonstrate this feature we built the LixMoS2 bilayer system in the absence and presence of MoO3 layers (lower panel in Fig. 1 and Supplementary Fig. 1) and computed their projected density of states (PDOS), as shown in Fig. 2a, b. It can be clearly seen that the CB electrons are shared between the orbitals of MoS2 and MoO3. We would like to point out here that the type-II character is maintained even if Li-atoms (ions and electrons) are intercalated either at the interface of MoS2/MoO3 (Supplementary Fig. 3a, c) or inside MoO3 (Supplementary Figures 3b, d). Since excess Li-ions are attached to the MoS2 layers, this electron delocalization will create a charge separation between the two materials (Fig. 2b). Hence, the electronic structure of LixMoS2/MoO3 is fundamentally different from LixMoS2 alone.

Fig. 2: Comparison of the PDOS of lithiated MoS2 in isolation and as part of the heterostructure.
figure 2

a PDOS of Li0.05MoS2 (LMS) for the supercell shown in Supplementary Fig. 1a. The Fermi level is denoted by a dotted line (b) PDOS of LMS/MoO3 for the supercell shown in Fig. 1 (bottom right) and Supplementary Fig. 1b. The band edges are marked with dashes. MoO3 bands are shown in red. The transfer of electron density from MoS2 to MoO3 would result in accumulation of net partial charges as depicted by δ+ and δ−, respectively.

Full size image

In many situations, only one of the partners is important for practical applications while the other plays a secondary role. In order to model those cases, it is sufficient to replicate the effect of the heterojunction partner rather than modeling the material explicitly. In the present scenario, the most important effect of the heterojunction partner (MoO3) is to extract the electron density from the lithiated MoS2. To replicate this effect, we have replaced MoO3 with a sheet of fluorine atoms ({Fn}). In this case, the electron density of the CB of lithiated MoS2 is extracted by the partially filled VB of {Fn}. While there are subtle differences in the PDOS of LixMoS2 in the presence of either MoO3 or {Fn} (Supplementary Fig. 2) due to explicit interaction between the MoS2 and MoO3 sheets at the interface, the band edges are very similar in both cases (Fig. 3a). In order to track the charge density transfer between LixMoS2 and either MoO3 or {Fn}, the cumulative differential electron density distribution is plotted in Fig. 3b. It is evident from the figure that {Fn} is able to extract more electron density from the lithiated MoS2 as compared to two layers of MoO3. This result is even more encouraging since multiple layers of MoO3 are usually present under experimental conditions, as mentioned later in the experimental section.

Fig. 3: Comparison of the band edges and total differential electron density between LMS/MoO3 and LMS/Fn.
figure 3

a The band edges of LMS/MoO3 and LMS/Fn. The PDOS of Fn is marked by the shaded black area. b Cumulative differential electron density distribution is plotted as a function of distance from the edge of the box. For the explicit heterostructure, MoO3 is on the left whereas for the LMS/Fn set-up, the fluorine sheet is on the right (see SI and Methods section for details).

Full size image

Phase Stability of LixMoS2/MoO3 Heterojunction

For MoS2 alone, the H-phase is more stable than the T’-phase at ambient conditions but the ordering can be reversed by adding excess electrons to the system. The reversal of the phase stability can be understood from the disposition of the partially filled d orbitals in the distorted tetrahedral or octahedral environment around the Mo center35. DFT calculations suggest that the critical electron doping concentration for the phase switch is 0.5 e per MoS2 unit36. Upon lithiation, not only does the MoS2 unit gains excess electron density but there is also associated structural change leading to a phase stability order that is critically dependent on the concentration of the intercalated Li-ion (Fig. 4a, blue plot)37.

Fig. 4: Switching the phase stability of MoS2 requires more lithium ions but the same number of electrons in the 'heterostructure'.
figure 4

a Energy difference between the two phases as a function of lithium ion concentration. The inset shows the relative energies of the H- and T'-phases. b Energy difference between the two phases as a function of the number of electrons per MoS2 unit in the conduction band of H-MoS2.

Full size image

Due to significant lattice mismatch between the T’-phase of MoS2 (3.305 Å × 5.806 Å) and MoO3 (3.9623 Å × 3.697 Å), constructing an explicit heterostructure with similar lattice strain as H-MoS2/MoO3 would require a significantly large supercell with thousands of atoms. The {Fn} construct, on the other hand, can be easily employed to compute the relative stabilities of the H- and T’-phases of LixMoS2 in the presence of the heterojunction (Supplementary Fig. 4). The difference in energy between the bilayer T’-and H-phases in the presence (red) or absence (blue) of {Fn} is plotted in Fig. 4a, with the inset showing the relative energies of each phase. It can be clearly seen that switching of the stability of the two phases occurs at a higher Li-ion concentration for the heterojunction, implying that the extraction of electron density stabilizes the H-phase more as compared to the T’-phase. The same change in the energy difference is plotted against the residual number of electrons (per MoS2 unit) in the conduction band of H-MoS2 in Fig. 5b. It is clear from the plots that irrespective of whether {Fn} is present or not, ~ 0.3 e per MoS2 unit is required in the conduction band of lithiated MoS2 to flip the stability of the phases. In other words, the number of electrons required to switch the phase stability is invariant to the presence of the heterojunction. However, due to the withdrawal of the electron density in the case of the heterojunction, more Li-atoms are required to supply the critical amount of electron density to the CB of MoS2.

Fig. 5: Band alignments from experiment and theory.
figure 5

a Band alignment of MoS2/MoO3 hetero-junction using UPS and UV-Vis spectroscopy. b Alignment of band edges between the bulk MoO3 and LixMoS2 as a function of the Li-ion concentration. The line plot, on top of the bar plots, is the graph of the difference in energies between the H- and T’-phases with the Fn sheet as shown in Fig. 3.

Full size image

Type-II Character of LixMoS2/MoO3

The switching of phase stability is preceded by a decrease in the underlying band gap of lithiated MoS2. This change in the band gap begs the question whether the type-II character is still maintained while the stability switches. In order to answer this question we looked at the change in the band edges of the lithiated MoS2 as a function of lithium ion concentration with reference to the band edges of the bulk MoO3 and compared it with the change in the phase stability in Fig. 5b. It is clear from the figure that both the processes, switch in the phase stability and the loss in the type-II character, occur at similar Li-ion concentrations. Additional calculations suggest that the Li-ion concentration required to induce phase in MoS2 might remain very similar even if MoO3 gets lithiated (Supplementary Fig. 6).

Experimental Evidence for Delayed Metallization in MoO3/MoS2 Heterojunction in the Presence of Li-ions

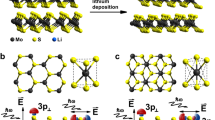
The MoS2/MoO3 vertical heterostructure was prepared by the partial sulfurization of sputtered MoO3 on FTO coated glass substrate (Supplementary Fig. 7b) films of around 50 nm thickness. In this partial sulfurization process, the MoO3 in the top layer is converted into a few layered MoS2 keeping the bottom MoO3 intact. The characteristics Raman mode at 999 cm−1 (Supplementary Fig. 8b) suggests the α-MoO3 remains unchanged38,39 whereas at the top it converted into a few layered MoS2 (Supplementary Fig. 8a). The separation of the E2g and A1g is found to be ~ 24 cm−1, indicates a few layered MoS240 film at the top layer. Additionally, a few-layered MoS2 prepared by chemical vapor deposition (CVD) method was used for the comparative study. To further check the chemical purity of the material, XPS was performed for the sputtered MoO3 and CVD grown MoS2 (Supplementary Fig. 9). The MoS2/MoO3 heterostructure has been also characterized using thin film XRD (blue plot in Supplementary Fig. 17). The type II band alignment of the formed MoS2/MoO3 heterostructure is suggested from UV-Visible and UV-photoelectron spectroscopy (UPS) measurements (Supplementary Fig. 10, S11 and Fig. 5a).

I n S i t u Raman Spectroscopy

A two electrode cell with lithium metal as one electrode and MoS2 or MoS2/MoO3 heterostructure film on FTO as the other electrode is constructed to track the changes in MoS2 with different extent of Li-ion intercalation. The electrodes are separated with a celgard separator soaked with electrolyte solution of LiPF6 in (1:1) EC/EMC (details of the cell construction are given in the SI (Supplementary Scheme 1 of SI).The open circuit potential of such an assembly is found to be ~ 2.9 V. The external circuit closing leads to the spontaneous intercalation of Li-ion in the other electrode and hence the discharge of the two electrode cell resulting in a decrease in the charge state (voltage) of the cell. In situ Raman spectra are acquired while the cell is getting discharged (Supplementary Fig. 12). Initially, the heterostructure shows the presence of H-MoS2 with the well identified Raman modes at 383 cm−1 (E2g) and 407 cm−1 (A1g) at ~ 2.9 V (x = 0) maintaining the gap of ~ 24 cm−1 between them. The presence Raman peaks at 127, 202, 228, and 289 cm−1 are due to the MoO3 (Supplementary Fig. 13b). We would like to point out here that powder XRD measurements from lithiated heterostructure (at 1.5 V) suggests minimal change in MoO3 due to lithiation whereas the MoS2 has already lost its H-phase (Supplementary Fig. 17). With insitu Raman spectroscopy, one can track the ballpark amount of Li-ion(x) at which phase transition initiates, and beyond which the quasi-metallic phase (T’) prevails. MoS2 shows the presence of H phase with the well identified Raman modes at ~ 2.9 V (x = 0). On gradual lithiation in pristine MoS2,when the potential reaches at about 1.6 V, new modes are found to be appearing in Raman spectrum (at about 224 cm−1, 284 cm−1, and 333 cm−1), corresponds to J2, E1g, and J3. Their presence became prominent after 1.53 V, (Supplementary Fig. 13a) suggesting the presence of T’ phase41. Unlike the pristine MoS2, the phase transition in MoS2/MoO3 heterostructure is not happening even at higher level of lithiation (lower voltages). It is found that only at ~ 1.1 V vs Li/Li +, the presence of the T’ phase of MoS2 starts appearing in MoS2/MoO3 heterostructure (Supplementary Fig. 13b). In this case, J2, E1g and J3 modes become prominent only at 0.566 V, indicating the higher level of lithium accommodation in heterostructure prior to the metallization.

Conductivity Measurements

It is well established in the literature that Li-ion intercalation in MoS2 begins close to 1.8 V vs Li/Li+42 so, It is expected that beyond 1.8 V, the conductivity of MoS2 will show an increase due to intercalation of Li-ions and will continue till the semiconducting phase transforms completely into the quasi-metallic phase. This has been tested by electron transport measurements of MoS2, as shown in Fig. 6. Conductivity measurements were performed from the top surface employing conducting Cu leads to analyze MoS2 electrodes at different states of discharge (Fig. 6a and explained in the SI). In all the samples, both the thickness and the separation between the Cu conducting leads are kept the same to compare directly the change in the MoS2 conductivity with variation in the Li-ion content. The current-voltage (I-V) curves indicate that lithiation in MoS2 leads the semiconducting to quasi-metallic phase transition at low amounts of lithiation (~ 1.36 V) as in Fig. 6b (details in Supplementary Fig. 15) whereas in the heterostructure, even at lower discharge voltages of 1.3 V, the non-linearity in the I-V plot still persists suggesting its semiconducting nature (Fig. 6d). In the heterostructure, the metallization happens at lower voltages, ~ 0.7 V vs Li/Li+ (Supplementary Fig. 16). Moreover, the variations in the nature of conductivity of MoS2 with lithiation is less drastic in the heterostructure as compared to the pristine case (Fig. 6c, e), indicating a distributed electronic charge density inside the heterostructure. This observation is in tune with the theoretical findings described above.

Fig. 6: The I-V measurements of MoS2 (pristine and MoS2 on the upper surface of heterostructure) with different extent of lithiation.
figure 6

The details of the experiment for incorporating different extent of Li-ion using Li- metal as the other electrode is given in the SI (Supplementary Figures 14-16) while the present schematic. (a) shows the I-V measurement setup on the heterostructure with the copper leads touching the top MoS2 layer. Copper (Cu) leads are shown in the figure where the heterostructure is placed on an FTO-glass substrate. Fixed separation between copper contacts and sample thickness are ensured in all the measurements. The light green blocks represent insulating polymer separators. (b and d) show the I-V plots of MoS2 in two different samples (pristine and heterostructure) before and after lithiation (upto nearly the same voltage vs Li/Li+ for both the samples) indicating the variation in the nature of MoS2 on lithiation with and with out heterostructure. Current values at bias voltage of 0.2 V for, (c) MoS2 and (e) for MoS2/MoO3 heterojunction with different degrees of lithiation. The changes in the I-V plots reflect the changes in the conductivity of MoS2 with Li-ion content, both in the pristine and heterostructure.

Full size image

In this work, we first put forth a theoretical prediction that the metallization of lithiated MoS2 can be delayed by forming a type-II heterojunction. An in-depth analysis of the electronic structure of the heterojunction shows that more Li-ions (+e−s) are required to reach a critical residual electron density in the conduction band of the lithiated MoS2 to switch the most stable phase from H to T’. This prediction is then validated by careful experiments to first characterize the two phases in the presence of Li-ions, employing InSitu Raman spectroscopy, and then track the metallization process by performing InSitu conductivity measurements. This study unlocks a hitherto unexplored dimension of type-II heterojunction, which can be exploited in future photo-devices.

Methods

Computational Details

Our calculations are based on Density functional theory (DFT) which uses PBE form for the Generalized Gradient approximation (GGA) and the hybrid functional HSE0643,44,45. These calculations were performed in the Vienna ab-initio simulation package (VASP) using a plane wave basis set with the projector augmented plane-wave method (PAW)46,47. For all MoS2 calculations a kinetic energy cut-off for plane-waves was set to be 360 eV, while a cutoff of 500 eV was used for MoO3 and the MoO3/MoS2 heterojunction calculations. The energy and force convergence criteria were set to be 10−4 eV and 0.02 eV/Å respectively. The Gamma Centred Monkhorst scheme of grid density 0.025 (2π/Å−1) in each direction was used to sample the Brillouin zone for all the calculations. As pointed out by Yan Hua Lei et al.48, accurate MoO3 calculations require Hubbard correction on top of DFT. Therefore we have used DFT+U calculations introduced by Dudarev et al.48,49 with a Hubbard parameter of 5.0 eV for both MoS2 and MoO3. For all multilayered systems, DFT+U was combined with the Grimes et al. dispersion correction (D3) to account for the long range interaction50.

Experimental Method

To prepare MoS2/MoO3 hetero structure we have first deposited 50 nm thick MoO3 on FTO coated glass by magnetron sputtering at 15 SCCM Ar gas flow, 5 × 10−3 mbar pressure and 12.6 MHz RF. The as deposited MoO3 is amorphous in nature to bring the crystallinity the deposited MoO3 was then annealed at 450 °C for 2 h.

Then sulfurization of the MoO3 is done in 2 zone CVD furnace in reducing (Ar/H2 mixture gas) environment for 5 min at 500 °C. Since only the MoO3 in top layer of thick deposition (~50 nm) is directly exposed to the Sulfur vapor, it converted into MoS2 keeping the MoO3 intact in the other parts. Thus sulfurization converting the MoO3 into MoS2/MoO3 heterostructure (Supplementary Fig. 7).

For insitu Raman study we have used our home build photo battery setup18. FTO coated with MoS2 or MoS2/MoO3 was used as one of the electrode to constract a cell with Li and 1.0 M solution of LiPF6 in 1:1 EC-EMC(50:50 vol%) was used as electrolyte. Before starting the discharge the laser of the Raman instrument was focused at a particular point and kept undisturbed throughout the experiment. In case of MoS2/MoO3 focusing was done in such a way to maximize the intensity of MoS2 Raman modes de-focusing the MoO3 part. Raman spectra was recorded while the battery is discharging at a constant current.

Multiple samples with different lithium content were prepared for I–V measurement by stopping at different discharge voltage. Those cells are then disassembled in Argon filled glove box (0.1ppm O2) and two copper contacts are then connected, precisely touching the top surface of the sample only. The whole setup was then kept inside the air sealed packet. I–V measurement was then performed for both the LixMoS2 and LixMoS2/MoO3.