Introduction

The anomalous Hall effect (AHE) in ferromagnetic materials arises from an extra Hall voltage proportional to the magnetization on top of the ordinary Hall voltage proportional to the inverse of the carrier density. Extensive studies over the past several decades have established three major physical origins of the AHE: one intrinsic and two extrinsic1,2,3,4. In particular, the intrinsic origin, suggested by Karplus and Luttinger in 1954, has received great attention since its direct link to momentum-space Berry curvature was recognized in the early 2000s5. Topologically nontrivial magnets such as a Chern insulator6,7 and a Weyl semimetal8,9 can indeed have uncompensated Berry curvatures in their electronic structures, resulting in large AHEs. Therefore, investigations of the AHE have become a viable tool to search for such topologically nontrivial magnets.

A two-dimensional (D) honeycomb lattice has been theoretically predicted to form symmetry-protected Dirac points in its electronic band structure that exhibit a large Berry curvature10,11. If time-reversal symmetry is further broken by, e.g., large exchange interactions of embedded magnetic ions, the 2D honeycomb lattice can naturally become a Churn insulator, resulting in a quantized AHE (QAHE) arising from a nonzero Chern number12. Recent theoretical studies13,14 have proposed that the ferromagnetic transition metal tri-chalcogenides (TMTCs) MBX3 (M = transition metals, B = P, Si, or Ge, X = chalcogens such as Se and Te) in a 2D form can be a promising system to search for such QAHEs. They form a layered honeycomb structure with different stacking sequences of 2D honeycomb lattices. Between layers, weak van der Waals interactions exist such that a 2D form can be fabricated. Moreover, the large magnetic exchange energy originating from transition metals allows spontaneous magnetic ordering, enabling time-reversal symmetry breaking.

CrSiTe3, a Cr-based TMTC semiconductor, is a promising candidate material for testing the above idea; it forms a layered honeycomb structure (space group R-3) with an ABC-stacking sequence (Fig. 1a, b). In a 2D layer, Cr ions, located in the center of a Te octahedron, form a honeycomb lattice via edge-sharing octahedra (Fig. 1a). The bulk form of CrSiTe3 exhibits ferromagnetic ordering with a Curie temperature of TC = 33 K and an easy c-axis at ambient pressure15,16. Owing to strong magnetic anisotropy, 2D ferromagnetism persisting to the monolayer limit has been observed in CrSiTe317. Thus, the monolayer form of CrSiTe3 is predicted to exhibit a QAHE with a high Chern number due to the combined physical properties of 2D ferromagnetism, spin‒orbit coupling, and multiple Dirac cones18.

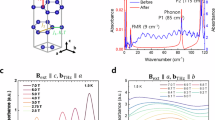
Fig. 1: Crystal structure and physical properties of CrSiTe3 at ambient pressure.
figure 1

a Monolayer form of CrSiTe3 with a Cr honeycomb lattice. b Crystal structure of CrSiTe3. c XRD pattern of a CrSiTe3 single crystal. The inset shows the ab-plane of the CrSiTe3 single crystal. d Temperature-dependent M/H and H/M of the CrSiTe3 single crystal measured at H = 1000 Oe. The green (blue) circles represent the corresponding curves for H//c (H//ab). From the slope of the H/M curve (for H//c) in the paramagnetic regime, an effective magnetic moment μeff = ~3.75 μB is extracted.

Full size image

Even if such a 2D sample is prepared, to observe the QAHE, the multiple Dirac cones located deep inside the conduction band also must be moved toward the Fermi energy EF. Electrical gating is an established method for tuning the EF in a layered material19. According to first principles calculations18, ~1 electron per 2D unit cell, i.e., ~2.5 × 1014 electrons/cm2, must be doped to place the EF of CrSiTe3 at the Dirac points. However, achieving this high doping concentration in electric gating experiments remains challenging. Moreover, conventional doping of such high concentrations via chemical methods is not only difficult but also could result in chemical disorder.

To reduce the large energy difference between the Dirac points and EF, we adopt pressure as a tuning knob. The application of hydrostatic pressure typically enables changes in energy levels on the order of a few eVs without causing chemical disorder. Because bulk CrSiTe3 is a semiconductor with a relatively small band gap of ~0.4 eV, the application of a moderately high pressure of ~10 GPa is likely to be effective for tuning the electronic structure, thus offering an opportunity to explore the electronic and topological properties of CrSiTe3 under high pressure.

In this work, we report our results on the crystal structure, magnetism and electrical transport of CrSiTe3 under high pressure, revealing the pressure-induced large AHEs in a pressure range where its honeycomb lattice and ferromagnetism are retained. Our results suggest that the intrinsic Berry curvature mechanism dominantly contributes to the AHE in CrSiTe3 because of the realization of a topologically nontrivial state at high pressures.

Results

Characterization of CrSiTe3 at ambient pressure

Plate-like single crystals as large as ~10 × 10 × 0.5 mm3 were grown via the flux method, as illustrated in the inset of Fig. 1c. In the X-ray diffraction (XRD) pattern of the CrSiTe3 single crystal, all the peaks can be indexed to the hexagonal (0 0 0 l) (l = integers) planes, indicating that the broad surface is oriented perpendicular to the c-axis. In order to check the stoichiometry of the grown crystal, wavelength dispersive spectroscopy (WDS) measurements were performed on at least ten different points of a sample surface using an electron probe microanalyzer (EPMA), resulting atomic ratios of Cr:Si:Te = 1.00( ± 0.01):0.98(±0.01):2.98(±0.01). This indicates that the grown single-crystal CrSiTe3 is close to the stoichiometry (see Supplementary Note 1 and Supplementary Fig. 1 for details). In all the subsequent measurements, we have used the single crystals from the same growth batch.

Figure 1d shows the temperature-dependent magnetic susceptibility M/H data measured in a magnetic field of H = 1000 Oe and its inverse curve. Both M/H curves measured along the c-axis and in the ab-plane steeply increase below TC ~ 33 K, indicating the development of ferromagnetism; at temperatures below the TC, the M/H values obtained on the H//c-axis are much greater than those measured in the H//ab-plane, indicating that the c-axis is a magnetic easy-axis near the ambient pressure regime. From a linear fitting in the paramagnetic region with the formula \(H/M=\left(T-{\theta }_{{\rm{CW}}}\right)/C\), an effective magnetic moment \({\mu }_{{eff}}=\sqrt{3{k}_{B}C/{N}_{A}{\mu }_{0}} \sim 3.75\,{\mu }_{B}\) is obtained, which is close to the predicted magnetic moment \({\mu }_{S}=2\sqrt{S(S+1)}\,{\mu }_{B}= \sim 3.87\,{\mu }_{B}\) with S = 3/2. Here, \({\theta }_{{\rm{CW}}}\) is the Curie–Weiss temperature, C is the Curie constant, \({k}_{B}\) is Boltzmann’s constant, \({N}_{A}\) is Avogadro’s number, \({\mu }_{0}\) is the vacuum permeability, and \({\mu }_{B}\) is the Bohr magneton. These structural and magnetic properties at ambient pressure are consistent with previous results20,21.

Structural stability under pressure

Although the high-pressure structures of CrSiTe3 have been reported previously, the published results to date are inconsistent with each other, and a unified conclusion has yet to be reached. Cai et al. reported the first high-pressure XRD study and found a structural phase transition at ~7.5 GPa22, while Pan et al., through a Raman scattering study, suggested a structural transition occurring from ~5 GPa23. Also, an infrared spectroscopy study performed by Musfeldt et al. reported a gradual structural phase transition occurring between 6 and 8 GPa, and a subsequent insulator-metal transition at ~9.5 GPa24. In contrast, Xu et al. found no structural transition up to ~15 GPa in their high-pressure XRD study25.

Because topological properties are determined by crystal symmetries and the published structural results are scattered, we have performed XRD at room temperature to reexamine the structural properties of CrSiTe3 under high-pressure conditions. We took extra care to reduce the exposure of the crystal surface to oxygen before loading into our diamond anvils. We found that oxidized surfaces indeed develop a considerable portion of TeO2 layers proportional to the exposure time, which can then affect the physical properties and interpretations significantly (see Supplementary Note 1 for details).

The contour plot in Fig. 2a presents the XRD patterns of the CrSiTe3 powder under pressures up to 12 GPa. The diffraction peaks from the (1 1 −2 0), (1 1 −2 3), and (3 0 −3 0) planes of CrSiTe3 can be traced up to 12 GPa, and all of them exhibit only a gradual shift to higher Q values; no peak splitting or sudden slope change is found. An apparently new peak emerging near the left wing of the (3 0 −3 0) peak from 8.0 GPa is identified as one coming from the Re gasket because a similar set of peaks also appear above 8.0 GPa in the XRD data obtained after X-rays are focused onto the gold foil (see Supplementary Note 2 and Supplementary Fig. 3 for details). Therefore, our XRD study indicates that the ABC-stacked honeycomb structure is stable until 12 GPa in CrSiTe3.

Fig. 2: Structural characterization of CrSiTe3 under pressure.
figure 2

a Contour plot of the XRD intensities of a CrSiTe3 powder at room temperature under pressures up to 12 GPa. For clarity, we removed the Q = 2.3–3.1 Å−1 region and the diamond (1 1 1) peak at ~3.1 Å−1. Evolution of the lattice constants b a, b, and c c with pressure variation. d Evolution of a unit cell volume V under pressure. The red solid curve is the fitted result of the third-order Birch–Murnaghan (B–M) equation of state (EoS).

Full size image

Unfortunately, Rietveld refinement could not be performed due to the limited number of diffraction peaks common in high-pressure XRD measurements. However, the lattice constants, a and c, and unit cell volume V for the hexagonal unit cell can be calculated from the three indexed peaks, as summarized in Fig. 2b–d. All these values decrease gradually with increasing pressure without showing any abrupt changes. The behavior of V under pressure fits well with the third-order Birch–Murnaghan (B–M) equation of state (EoS)26, yielding a bulk modulus B0 = 30.76 GPa and its first-order derivative B0′ = 5.972. The smooth variation in the lattice parameters and the successful fitting of V by the third-order B–M EoS again support the stability of the hexagonal symmetry R-3 in the high-pressure region below ~12 GPa. In addition, we find that our pressure-dependent Raman measurements also do not show any clear signature of the structural phase transition up to ~11.19 GPa (see Supplementary Note 1 and Supplementary Fig. 2 for details).

Magnetic properties under pressure

As topological properties and AHEs in CrSiTe3 are closely associated with the broken time-reversal symmetry, it is worthwhile to investigate the properties of ferromagnetism under high pressure. Up to now, several studies have discussed the magnetic properties of CrSiTe3 under high pressure. In 2020, Cai et al. first claimed that a ferromagnetic-to-paramagnetic transition occurs between 7.1 and 9.1 GPa based on the sign change in the magnetoresistance22. More recently, in 2023, Zhang et al. reported ferromagnetic properties under pressure through the magnetic circular dichroism (MCD) measurements on the CrSiTe3 flakes; they found a pressure-driven enhancement of TC and the coercive field Hc27. In their results, TC starts to increase from 4.6 GPa and reaches 138 K at 7.8 GPa. The authors concluded that the ferromagnetic-to-paramagnetic transition occurs beyond 7.8 GPa as they could not observe the MCD signals above 7.8 GPa. Finally, there was a more recent high-pressure DC magnetization study on CrSiTe3 in a limited pressure range below 1 GPa28.

Although those former studies, particularly the MCD study, have provided valuable information on the evolution of TC and Hc under pressure, the evolution of the absolute M values above 1 GPa has not been determined yet. Since the evolution of M with pressure and temperature can be crucial for interpreting the origin of the AHEs, it is highly demanding to measure M directly under pressure. Therefore, we have developed a turnbuckle-type diamond anvil cell that can fit into a magnetic property measurement system (MPMSTM, Quantum Design) and measured the temperature- and field-dependent magnetizations along the c-axis under static pressure.

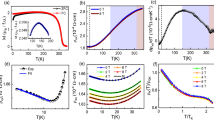
In Fig. 3a, b, we present the temperature-dependent M/H curve measured at H = 1000 Oe under constant pressure up to 11.3 GPa. The TC was determined from the minimum point in the \(d\left(M/H\right)/{dT}\) curve and is summarized in Fig. 3c. In the low-pressure region up to 4.5 GPa, the magnitude of M/H decreases gradually with pressure, whereas TC increases slowly from ~33 K at ambient pressure to ~40 K at 4.5 GPa. However, at a pressure of 5.9 GPa, the TC sharply increases to ~85 K, and the magnitude of M/H at 5 K returns to the M/H value at 3.0 GPa. As the pressure is increased further, the M/H value at 5 K decreases systematically, and the transition region seems to become broader. However, TC increases slowly from ~85 K at 5.9 GPa to ~97 K at 11.3 GPa. Thus, even at 11.3 GPa, a considerable M/H value of 2.28 emu/mol Oe is found at 5 K, indicating that ferromagnetism remains in the high-pressure region. Compared with the transport data in Fig. 4a, the pressure of 5.9 GPa, where a sudden increase in Tc occurs, is close to the pressure P1 ~ 6 GPa above which CrSiTe3 is in the metallic regime. Therefore, the closure of a charge gap and the simultaneous development of the itinerant electronic state are expected to be closely associated with the abrupt increase in TC at P1 ~ 6 GPa.

Fig. 3: Magnetic properties of a CrSiTe3 single crystal under pressure.
figure 3

Temperature-dependent M/H curves measured at H = 1000 Oe (H//c) under pressure (a) below P1 and (b) between P1 and 11.3 GPa after zero-field cooling (ZFC). c TC evolution with pressure. Note that a sudden jump in TC occurs at P1. d M vs. H curves (H//c) measured at 5 K and under several pressures indicated in the legend. e Magnified M vs. H curves in a low-field regime for pressures of 0, 8.6, and 9.8 GPa. f Pressure-induced variation in the saturation magnetization (Ms, red squares) and coercive field (Hc, blue squares), which are extracted from the M vs. H curves. All the magnetization data were obtained after subtraction of the background. (see Supplementary Fig. 2.).

Full size image
Fig. 4: Insulator–metal transition and Hall resistivity of a CrSiTe3 single crystal under pressure.
figure 4

a Temperature-dependent longitudinal resistivity \({\rho }_{{xx}}\) at selected pressures up to 15 GPa. The dashed line indicates the expected resistivity of the Mott–Ioffe–Regel (MIR) limit in two dimensions. The inset shows a photograph of a loaded CrSiTe3 single crystal and four Pt electrodes inside the diamond anvil cell. b Field-dependent Hall resistivity \({\rho }_{{yx}}\) at 300, 50, and 2 K at 10.4 GPa for H//c. Each dashed line is a linear fit of a high-field region, 4–9 T at each temperature. Note that the \({\rho }_{{yx}}\) curves start to deviate from the linear form at 50 K and show a large jump at ~4000 Oe at 2 K. c The \({\rho }_{{yx}}\) curve measured at 10.4 GPa and 2 K can be decomposed into two parts, i.e., the ordinary Hall (\({\rho }_{{yx}}^{N}\), dotted blue line) and anomalous Hall (\({\rho }_{{yx}}^{{AH}}\), dotted red line) terms.

Full size image

Interestingly, an analogous compound, CrGeTe3, also shows an abrupt increase in TC near ~5 GPa, where the insulator–metal transition occurs29. At ambient pressure, the ferromagnetism of CrGeTe3 and CrSiTe3 compounds is known to originate from the ferromagnetic superexchange interaction between the Cr-eg orbitals mediated by the Te-p orbitals30,31. Thus, CrGeTe3 and CrSiTe3 show similar types of localized ferromagnetic ordering at ~66 and 33 K, respectively, resulting in easy axes along the c-axis. In this regime, the superexchange interaction \({J}_{{\rm{SE}}}\) of both compounds can be expressed as \({J}_{{\rm{SE}}}\cong -\frac{{t}_{{pd}}^{2}{t}_{p^{\prime} d^{\prime} }^{2}{J}_{H}^{{\rm{Te}}}}{{\Delta }_{{\rm{CT}}}^{2}{\left(2{\Delta }_{{\rm{CT}}}+{U}_{p}\right)}^{2}}\), where \({t}_{{pd}}\) and \({t}_{p{\prime} d{\prime} }\) describe the hopping parameter between the Cr-eg and Te-p orbitals, \({J}_{H}^{{\rm{Te}}}\) is Hund’s coupling on the Te ion, \({U}_{p}\) is the Coulomb interaction on the Te site, and \({\Delta }_{{\rm{CT}}}\) is the charge transfer gap between the top of the Te-p valence band and the bottom of the Cr-eg conduction band. Based on its formula, \({J}_{{\rm{SE}}}\) is inferred to surge when \({\Delta }_{{\rm{CT}}}\) approaches zero29. Therefore, the sudden increase in TC found in CrSiTe3 and CrGeTe3 may be due to a rapid increase in \({J}_{{\rm{SE}}}\) resulting from the collapse of \({\Delta }_{{\rm{CT}}}\) near the insulator–metal transition.

We also investigated the M–H curves (H//c) at various pressures at 5 K, as summarized in Fig. 3d, e. Throughout the pressure window, the M‒H curves show a sharp saturation, indicating that CrSiTe3 remains in a ferromagnetic state up to 11.3 GPa. Figure 3f summarizes the evolution of the saturation magnetization Ms and Hc with pressure. Interestingly, Ms suddenly decreases from ~3 to ~1.5 μB/Cr at 5.9 GPa, which coincides with the sharp increase in TC. At the same pressure, the coercive field Hc also starts to increase and continues to increase until 9.8 GPa is reached. At a high pressure of 9.8 GPa, another sudden drop in Ms from ~1.5 to ~1 μB/Cr occurs. Above a pressure of 9.8 GPa, Hc remains nearly the same or even slightly decreases. The abrupt decreases in Ms to nearly Ms/3 and Ms/2 values at pressures of ~5.9 and ~9.8 GPa, respectively, suggest possible pressure-induced spin state transitions in CrSiTe3, presumably accompanied by changes in the electronic states at the Fermi level. In sharp contrast, the analogous compound CrGeTe329 exhibited only a small and continuous decrease in Ms from ~3 to ~2.8 μB/Cr at 5–6 GPa, around which the pressure-induced insulator–metal transition occurred. Moreover, no increase in Hc was found in the M–H curves of CrGeTe329, at least up to ~7.3 GPa. Therefore, the pressure-induced discontinuous drop in Ms and the sudden increase in Hc along the c-axis near its insulator–metal transition (~5.9 GPa) can be attributed to the unique properties of CrSiTe3. This behavior also indicates that the model based on itinerant ferromagnetism in a far metallic regime, which can, in principle, result in a small and noninteger magnetic moment, might not be sufficient to explain the abrupt changes in Ms.

Although the accurate spin ordering pattern in the high-pressure region still cannot be determined without further experimental and theoretical investigations, we discuss the possible constraints expected in the spin ordering of CrSiTe3. Several TMTC materials with a honeycomb lattice, MPX3 (M = Fe, Ni, and Mn; X = S and Se), are known to undergo a pressure-induced transition from a high spin state to a low spin state, thereby reducing the magnetization upon compression32,33,34. This transition is essentially due to the local spin state transition within a single MX6 octahedron. However, this explanation is unlikely to pertain to CrSiTe3; first, in contrast to those materials that have filled eg states in the ground state32,33,34, electrons in a CrTe6 octahedron fill the three Cr-t2g states only with ferromagnetic spin alignments among neighboring Cr ions via ferromagnetic superexchange interactions. Because its ground state has no Cr-eg electrons, CrTe6 is unlikely to undergo a pressure-induced low-spin transition from Cr-eg to -t2g states in a local CrTe6 octahedron. Furthermore, although the spin state transition in other TMTC materials, e.g., FePS3 or MnPS3, is often accompanied by volume collapse, no volume collapse occurs in CrSiTe3 up to 12 GPa. Therefore, the interaction among neighboring Cr ions rather than the single Cr site effect is expected to play a role in causing the abrupt decrease in Ms.

As CrSiTe3 has a smaller Tc = ~33 K than the Tc = ~66 K of CrGeTe3, CrSiTe3 should have weaker ferromagnetic superexchange interactions, such that the application of pressure might allow the material system to reach the competing antiferromagnetic phase more easily. If such competition between ferromagnetic and antiferromagnetic interactions under high pressure can stabilize an up-updown spin configuration involving at least three Cr ions in the in-plane or out-of-plane direction, it might explain why ~Ms/3 states are realized in the high-pressure regime above 9.8 GPa. Based on the observed increase in Hc along the c-axis, it is also speculated that high-pressure application can induce a spin easy-axis change in CrSiTe3. For example, Mn3Si2Te6, which has Mn honeycomb layers with self-intercalated Mn triangular layers, exhibits a spin reorientation transition from the ab-easy-plane to the c-easy-axis under high pressure because of competing spin interactions between the in-plane and out-of-plane directions35. If a similar kind of spin reorientation transition occurs in CrSiTe3, the spin easy-axis can lie toward the ab-plane in the high-pressure region. To confirm this scenario, the M‒H curves must be investigated in this plane, which is currently beyond our experimental ability.

Electrical transport under high pressure

To investigate the effects of the nontrivial band topology in CrSiTe3, we investigated the in-plane longitudinal resistivity \({\rho }_{{xx}}\) and Hall resistivity \({\rho }_{{yx}}\) under high pressure. The temperature dependence of \({\rho }_{{xx}}\) was measured at several pressures up to 15 GPa, as shown in Fig. 4a. At ambient pressure, CrSiTe3 exhibits insulating behavior with a high resistivity of ~4 × 103 Ω cm at room temperature. With increasing pressure, \({\rho }_{{xx}}\) decreases rapidly; \({\rho }_{{xx}}\) at room temperature decreases by seven orders of magnitude from ~103 to ~10−4 Ω cm. At 12.5 GPa, the \({\rho }_{{xx}}\) values at 300 K fall below the predicted 2D Mott–Ioffe–Regel (MIR) limit for metals, \({hd}/{\sqrt{2\pi }e}^{2}\approx 0.7\) \(\text{m}\Omega \text{cm}\), where d is the distance between each CrSiTe3 layer36. These transport behaviors provide clear evidence of a pressure-induced insulator–metal transition in CrSiTe3.

With decreasing \({\rho }_{{xx}}\) at 300 K, the temperature-dependent \({\rho }_{{xx}}\) curves start to indicate metallic behavior, i.e., \(\frac{{d\rho }_{{xx}}}{{dT}} > 0\) at 6.0 GPa, a pressure still much lower than 12.5 GPa, at which the \({\rho }_{{xx}}\) values at 300 K reach the 2D MIR limit. At 10.4 GPa, \(d{\rho }_{{xx}}/{dT}\) is positive at all temperatures below 300 K. These observations of metallic transport at much lower pressures before reaching the MIR limit imply that CrSiTe3 remains in a bad metallic state, possibly due to a strong correlation effect, as observed in the analogous compound, CrGeTe329. Moreover, we find that above 12.5 GPa, superconducting-like drops in resistivity appear at low temperatures, similar to the results reported in a previous study22. However, in contrast to the previous study, our CrSiTe3 sample did not show zero resistivity in the pressure range of ~12.5 to −15 GPa. Further studies are needed to determine how the superconducting volume fraction can vary with sample quality or stoichiometry.

When metallic transport appears above 6.0 GPa, the AHE starts to appear from the Hall resistivity data at low temperatures. Figure 4b shows the field-dependent \({\rho }_{{yx}}\) at 10.4 GPa as a representative example. At high temperatures above 50 K, \({\rho }_{{yx}}\) exhibits only a linear field dependence with a negative slope, indicating that electrons are the dominant charge carriers. However, at temperatures below ~50 K, the \({\rho }_{{yx}}\) curves deviate from the linear H behavior. Moreover, at 2 K, a large jump of \({\rho }_{{yx}}\) is observed at a field of ~4000 Oe. These features in the \({\rho }_{{yx}}\) data demonstrate the influence of an AHE.

In a typical ferromagnetic metal, the Hall resistivity can be expressed as an empirical relation:

$${\rho }_{{yx}}={\rho }_{{yx}}^{N}+{{\rho }_{{yx}}^{{AH}}=R}_{0}H+{R}_{s}{\mu }_{0}M$$
(1)

where \({\rho }_{{yx}}^{N}={R}_{0}H\) is the ordinary Hall resistivity proportional to an external H and where \({\rho }_{{yx}}^{{AH}}={R}_{s}{\mu }_{0}M\) is the anomalous Hall resistivity proportional to spontaneous M. By applying Eq. (1) to the low-temperature \({\rho }_{{yx}}\) data, we extracted \({\rho }_{{yx}}^{{AH}}\), as illustrated in Fig. 4c; after \({\rho }_{{yx}}^{N}\) is obtained from a linear fit of \({\rho }_{{yx}}\) in the high-field regime, \({\rho }_{{yx}}^{{AH}}\) is obtained by subtracting \({\rho }_{{yx}}^{N}\) from \({\rho }_{{yx}}\). The resulting \({\rho }_{{yx}}^{{AH}}\) curve shows a steep increase at low fields and saturation at H ~ 4000 Oe. Moreover, the M–H curve obtained at a pressure of 9.8 GPa exhibited saturation at a similar field of ~4000 Oe (see Supplementary Fig. 6). This finding strongly suggests that the jump as well as the nonlinearity appearing in the field-dependent \({\rho }_{{yx}}\) of CrSiTe3 is clearly due to the AHE appearing in the high-pressure region.

With a similar procedure, we can extract \({\rho }_{{yx}}^{{AH}}\) from \({\rho }_{{yx}}\) at various pressures and temperatures. For CrSiTe3, not only \({\rho }_{{yx}}^{{AH}}\) but also \({\rho }_{{xx}}\) change considerably with pressure and temperature, so \({\rho }_{{yx}}^{{AH}}\) might also strongly depend on \({\rho }_{{xx}}\). To compare the magnitude of the AHE after normalizing the effect of \({\rho }_{{xx}}\), we converted \({\rho }_{{yx}}^{{AH}}\) to the anomalous Hall conductivity \({\sigma }_{{xy}}^{{AH}}={\rho }_{{yx}}^{{AH}}/\left({\rho }_{{xx}}^{2}+{\rho }_{{yx}}^{2}\right)\approx {\rho }_{{yx}}^{{AH}}/{\rho }_{{xx}}^{2}\). Figure 5 shows the obtained \({\sigma }_{{xy}}^{{AH}}\) values at various pressures and temperatures. For all the pressures, the field-dependent \({\sigma }_{{xy}}^{{AH}}\) exhibits saturating behavior in high-field regions, similar to the traces of the M‒H curves. Notably, the \({\sigma }_{{xy}}^{{AH}}\) values are quite large; the maximum value of \({\sigma }_{{xy}}^{{AH}}\) at 10.4 GPa and 2 K reaches \(\sim 67\,{\Omega }^{-1}\,{\text{cm}}^{-1}\), which amounts to ~35% of \({e}^{2}/{hc} \sim 187\,{\Omega }^{-1}\,{\text{cm}}^{-1}\). Here, e is the electric charge of one electron, h is Plank’s constant, and c is the lattice constant of CrSiTe3. The observation of a large AHE indicates that the AHE from the intrinsic Berry curvature mechanism can be considerably included in the Hall effect signals.

Fig. 5: Anomalous Hall conductivity of a CrSiTe3 single crystal at high pressures.
figure 5

Field-dependent \({\sigma }_{{xy}}^{{AH}}\) at pressures of (a) 8.5, (b) 9.7, (c) 10.4, (d) 11.2, (e) 12.5, and (f) 13.5 GPa and at selected temperatures. Note that the \({\sigma }_{{xy}}^{{AH}}\) data at 2 K, measured at pressures of 12.5 and 13.5 GPa, are omitted in the low-field regime because the \({\sigma }_{{xx}}\) component is difficult to subtract in this regime due to the large variation in \({\sigma }_{{xx}}\) accompanying the superconducting-to-normal-state transition. For all the data, an external field is applied along the c-axis.

Full size image

To determine the origin of the AHE in high-pressure regions, we compared \({\sigma }_{{xy}}^{{AH}}\) and \({\sigma }_{{xx}}\) under various conditions. In typical ferromagnetic metals, the AHE exhibits a scaling relation with \({\sigma }_{{xx}}\), such as the Tian-Ye-Jin (TYJ) model37, and the contributions of each mechanism to the AHE can be distinguished using the scaling relations (see Supplementary Note 3 for details). Figure 6a shows the pressure evolution of the anomalous Hall conductivity at 9 T, \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\), and the longitudinal conductivity at 9 T, \({\sigma }_{{xx},9{\rm{T}}}\), both of which are measured at 2 K. \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) begins to appear at 6 GPa with a small value of \(\sim 0.4\,{\Omega }^{-1}\,{\text{cm}}^{-1}\), increases with pressure, and reaches the maximum value of \(\sim 67\,{\Omega }^{-1}\,{\text{cm}}^{-1}\) at 10.4 GPa. Above 10.4 GPa, \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) decreases with compression and finally disappears above 15 GPa. Consequently, the pressure-dependent \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) results in a dome-like shape. This dome-like behavior of \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) differs from the behavior of \({\sigma }_{{xx},9{\rm{T}}}\), which increases monotonically with pressure. Moreover, this behavior completely differs from the shape of the curve of pressure-dependent Ms in Fig. 3f. These features of \({\sigma }_{{xy}}^{{AH}}\), which cannot be explained by the behaviors of \({\sigma }_{{xx}}\) or Ms, distinguish the AHE of CrSiTe3 from that of typical ferromagnetic metals.

Fig. 6: Comparisons between the longitudinal conductivities and anomalous Hall conductivities of a CrSiTe3 single crystal.
figure 6

a Comparison of the pressure evolution of \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) (red squares) and \({{\rm{\sigma }}}_{{xx},9{\rm{T}}}\) (blue squares) at 2 K. b Comparison of the temperature evolution of \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) (red circles) and \({\sigma }_{{xx},9{\rm{T}}}\) (blue circles) at 10.4 GPa.

Full size image

Figure 6b displays the temperature dependence of \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) and \({\sigma }_{{xx},9{\rm{T}}}\) at 10.4 GPa. \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) starts to appear from 50 K, and as the temperature decreases from 50 to 2 K, the \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) values increase by ~40 times; \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) increases by ~30% even with a decrease of 1 K from 3 to 2 K. Thus, no sign of saturation of \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) is observed until 2 K is reached. Conversely, \({\sigma }_{{xx},9{\rm{T}}}\) is almost saturated below 20 K, exhibiting only a small percentage change. Moreover, M does not change much at temperatures below 50 K at ~10 GPa, as shown in Fig. 3b. This nonsaturating increase in \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\), in contrast with the nearly constant behavior of \({\sigma }_{{xx}}\) or M, reconfirms that the AHE in CrSiTe3 at high pressures differs from that of typical ferromagnetic metals.

Discussion

We recontemplate the possible origins of the AHE in CrSiTe3 observed under high-pressure regimes. First, the magnitude of the AHE is quite high, reaching a maximum value of \({\sigma }_{{xy}}^{{AH}}\) \(\sim 67\,{\Omega }^{-1}\,{\text{cm}}^{-1}\)(\(\sim 0.35{e}^{2}/{hc}\)), indicating that the side-jump mechanism is unlikely to be a dominant contribution to the AHE because it is usually on the order of \(\left({E}_{{SO}}/{E}_{F}\right)\times \left({e}^{2}/{hc}\right)\) 38. Here, ESO is the spin‒orbit coupling energy, and thus, \({E}_{{SO}}/{E}_{F}\) is less than 10−1 in typical ferromagnetic metals. In contrast, the intrinsic contribution of the anomalous Hall conductivity can reach the order of \({e}^{2}/{hc}\) when the Fermi level is located near the band crossing points39. Although the skew scattering mechanism can also generate this large anomalous Hall conductivity, it is often dominant at a clean limit (\({\sigma }_{{xx}} > {10}^{6}\,{\Omega }^{-1}\,{\text{cm}}^{-1}\)), thereby being rapidly suppressed with an increasing scattering rate39. Because the \({\sigma }_{{xx}}\) values lie within the order of \({10}^{1}-{10}^{4}\,{\Omega }^{-1}\,{\text{cm}}^{-1}\) in the high-pressure regime, the skew scattering contribution has difficulty becoming the main source of the AHE in CrSiTe3. Therefore, the remaining plausible explanation is the intrinsic Berry curvature contribution.

Since the magnitude of the intrinsic AHE is determined by the integral of the Berry curvature of the occupied electronic bands, it is highly sensitive to the Fermi level. When the Fermi level approaches the band crossing point, which is the source of the Berry curvature, the magnitude of the AHE increases, whereas when the Fermi level moves from the band crossing point, it decreases. In CrSiTe3, pressure induces an insulator–metal transition, accompanied by an increase in the number of electron carriers in the metallic phase. This outcome means that the conduction band of CrSiTe3 shifts toward and crosses the Fermi level via compression. If the band crossing point exists in the conduction band, it should also move toward the Fermi level with compression. Once the band crossing point reaches and finally passes through the Fermi level at a certain pressure, the magnitude of the AHE increases rapidly, approaching that pressure and being suppressed above it. In this way, the intrinsic AHE scenario can successfully explain the dome-shaped pressure evolution of \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\).

In Fig. 6b, \({\sigma }_{{xy},9{\rm{T}}}^{{AH}}\) increases with decreasing temperature without a change in \({\sigma }_{{xx}}\) or M. Theoretically, this kind of temperature dependence in the AHE can appear in a system with a massive Dirac cone with a small gap40. If the Fermi level is close to the gap of the massive Dirac cone, thermally excited electrons can fill the upper half partially and compensate for the total Berry curvature. As the temperature decreases, the number of thermally excited electrons decreases, and consequently, the anomalous Hall conductivity should be increased. Therefore, if the AHE in CrSiTe3 under high pressure originates from the intrinsic Berry curvature from the massive Dirac-like electronic band structure, all the features found in the AHE measurements can be successfully explained.

Next, we discuss where those topologically nontrivial bands can arise from and the possible topological phases of bulk CrSiTe3 under high pressure. As mentioned above, the DFT calculations of monolayer CrSiTe3 suggest that multiple massive Dirac cones exist in the Cr eg conduction bands because of the honeycomb lattice18. Thus, it is reasonable to start thinking of possible topological phases in a bulk system formed by stacking Chern insulators. According to a previous theoretical study by A. A. Burkov and L. Balents, three phases, the 3D QAH insulator, Weyl semimetal, and normal insulator, can appear in a Chern insulator multilayer, depending on the spin-splitting energy and relative magnitudes of the interlayer and intralayer hopping parameters41. The 3D QAH state is characterized by a bulk gap and quantized Hall conductivity from gapless chiral surface channels. In contrast, the Weyl semimetal state is characterized by gapless energy dispersion with point degeneracies and Fermi arcs on surface states. If the effect of disorder is considered, a diffusive metallic phase with an AHE can appear in addition to the aforementioned three phases42. In this phase, although distinguishable surface states remain, internode scattering due to disorder opens gaps at the Weyl nodes, and the bulk Fermi surface appears42,43. Because our experimental results suggest the existence of topologically nontrivial bands with gaps in bulk CrSiTe3 under high pressure, this diffusive metallic phase originating from the stacked Chern insulator is a promising candidate for the topological phase of bulk CrSiTe3 under high pressure. However, other possibilities, such as accidental band crossings occurring at high pressure, still cannot be eliminated. Further combined theoretical and experimental studies are needed to verify the true nature of the topological phase.

In conclusion, we studied the effects of pressure on the structure, magnetism, and electrical transport properties of the van der Waals ferromagnet CrSiTe3. The ferromagnetic phase in bulk CrSiTe3 not only remains under high pressure but also rapidly increases its transition temperature, nearly concomitant with the insulator–metal transition. In the metallic regime, a large AHE with an unusual pressure dependence has been found; our analysis reveals that the origin of the AHE should be related to the intrinsic Berry curvature mechanism. As the structure of CrSiTe3 at ambient pressure remains stable at high pressures up to 12 GPa, the topological Dirac cones from the honeycomb lattices are suggested to be the source of this large Berry curvature. Our findings indicate that atomically thin CrSiTe3 with electron doping or under high pressure can be a promising route to find a high-temperature QAHE, which originates from 2D ferromagnetism with a high Curie temperature and topologically nontrivial band structure.

Methods

Crystalline growth and sample characterization

Polycrystalline CrSiTe3 samples were grown via the solid-state reaction method. Cr (Alfa Aesar, 99.99%), Si (Alfa Aesar, 99.999%), and Te (Alfa Aesar, 99.99%) were mixed at a molar ratio of Cr:Si:Te = 1:1:3, put into an alumina crucible, and sealed in a quartz tube under an Ar atmosphere. The sealed quartz tube was held at 900 °C for 24 h and then cooled to room temperature at 100 °C/h. Single crystals of CrSiTe3 were grown via the Te flux method. Cr, Si, and Te were mixed at a molar ratio of Cr:Si:Te = 1:3:18, put into an alumina crucible, and sealed in a quartz tube under an Ar atmosphere. The sealed quartz tube was held at 750 °C for 8 h and then slowly cooled to 480 °C over 4 days. At this temperature, the quartz tube was centrifuged to separate the CrSiTe3 single crystals from the Te flux. The XRD experiment was performed via EmpyreanTM (PANalytical) with a Cu Kα1 source (λ = 1.5406 Å), and the magnetization measurements were conducted via a magnetic property measurement system (MPMSTM, Quantum Design).

WDS measurements

WDS measurements were performed using the field emission electron probe microanalyzer (FE-EPMA, JXA-8530F, JEOL Ltd) at the National Center for Inter-university Research Facilities (NCIRF). Insulating Cr2O3 (99.97%), SiO2 (99.995%), and TeO2 (99.99%) were used as standard specimens. The measurements were performed on at least ten different points of a sample surface.

High-pressure XRD measurements

High-pressure XRD measurements were performed at the 13-BM-C beamline of the Advanced Photon Source via a Mao-type symmetric diamond anvil cell (DAC). The wavelength λ of the input X-ray was fixed at 0.4335 Å. All the data were measured at room temperature. Ne gas was used as a pressure-transmitting medium. The pressure was determined via the well-known room temperature equation of state of gold44. The DIOPTAS program was used to integrate the powder XRD data. To fit the unit cell volume, the third-order Birch–Murnaghan equation of state,

$$P\left(V\right)=\frac{3{B}_{0}}{2}\left[{\left(\frac{{V}_{0}}{V}\right)}^{7/3}-{\left(\frac{{V}_{0}}{V}\right)}^{5/3}\right]\left\{1+\frac{3}{4}\left({B}_{0}^{{\prime} }-4\right)\left[{\left(\frac{{V}_{0}}{V}\right)}^{2/3}-1\right]\right\},$$

was used.

High-pressure DC magnetization measurements

High-pressure DC magnetization measurements were performed via MPMSTM (Quantum Design) and a custom-made turnbuckle DAC. A rectangular single crystal with dimensions of ~155 × 155 × 40 μm3 was loaded into the cell slightly after cleavage. The DAC for the magnetization measurements was made of a nonmagnetic Be‒Cu alloy, and silicone oil was used as a pressure-transmitting medium. The background signal from the DAC was removed by measuring the magnetization of the DAC without and with the sample and subtracting the former measured data from the latter (Supplementary Fig. 4). The pressure was determined via a ruby fluorescence line shift at room temperature45.

High-pressure electrical transport measurements

High-pressure electrical transport measurements were performed by using a physical property measurement system (PPMSTM, Quantum Design) and a screw-clamped DAC. A rectangular single crystal with dimensions of ~70 × 60 × 6 μm3 was loaded into the cell immediately after cleavage, and electrical contacts were made of Pt foils via a mechanical press. The van der Pauw method was used to measure the longitudinal and Hall resistivities of the samples (see Supplementary Note 4 for details). To remove the longitudinal resistivity contribution from the Hall resistivity signal, we obtained the Hall resistivity by anti-symmetrizing the raw data to the magnetic field, i.e., \({\rho }_{{xy}}(H)=[{\rho }_{{xy}}(H)-{\rho }_{{xy}}(-H)]/2\). The current flows in the ab-plane of CrSiTe3, and the field direction was H//c for all the magneto-transport measurements. NaCl was used as the pressure-transmitting medium. The pressure was determined via the ruby fluorescence line shift at room temperature.

High-pressure Raman spectroscopy measurements

High-pressure Raman spectrums at room temperature were measured by a commercial Raman spectrometer (Nanobase, XperRam200) equipped with a Nd:Yag laser with a 532 nm wavelength and a screw-clamped DAC. A single crystal was cleaved and loaded into the DAC inside an Ar-filled glove box (H2O < 0.01 ppm, O2 < 0.01 ppm). Silicon oil was used as a pressure-transmitting medium, and the pressure was determined via the ruby fluorescence line shift at room temperature.