Introduction

Topology and symmetry are fundamental principles in condensed matter physics, providing crucial insights into the classification and behavior of electronic states. The interplay between these concepts has revolutionized our understanding of topological electronic phases. One key advancement is the realization that electronic states with energy gaps can be categorized into distinct topological classes, often giving rise to gapless conducting state at interfaces between these phases, protected by specific symmetries1,2. For instance, topological insulators (TIs), the pioneering class of materials exhibiting topological properties, are protected by time-reversal symmetry (TRS)3,4,5,6,7. The exploration of TIs has sparked interest in the broader realm of symmetry-protected topology, leading to the discovery of topological crystalline insulators (TCIs), where surface states are preserved by crystal symmetry8,9,10. Recently, attention has turned to dual topological insulators (DTIs), which uniquely combine TI and TCI characteristics, enriching the landscape of topological phases11,12,13.

Acknowledging the profound influence of symmetry on topological properties, we delve into the exploration of DTI phases in van der Waals (vdW) layered materials. Unlike conventional bulk materials, where crystal symmetry is rigidly defined, vdW layered materials offer a unique ability to manipulate symmetry through stacking variations. Remarkably, even with identical monolayer structures, altering the stacking configuration alone can lead to striking differences in physical properties. Investigating these stacking-induced changes has proven instrumental in elucidating fundamental electronic and optical characteristics as well as topological properties14,15,16,17,18,19. By applying this concept to DTIs, we can achieve multiple levels of protection by adjusting the stacking configuration, allowing precise control over the robustness of the surface Dirac state and opening new possibilities for tailoring and manipulating the system’s topological properties. In our recent work, we successfully synthesized layered InTe and conducted a detailed analysis of its vdW stacking sequence20,21. Our findings highlight intriguing electronic phenomena, such as the unconventional hidden Rashba effect observed in vdW layered materials like InTe22,23. Notably, InTe’s polymorphic and stacking-dependent nature allows for the emergence of mirror symmetry, enhancing the stability and tunability of its topological surface states. Despite these fascinating discoveries, the topological aspects of this newly synthesized material remain largely unexplored, motivating the present study to bridge this gap and deepen our understanding of vdW-induced DTI phases.

In this study, we present the distinctive topological surface properties that arise in DTIs formed by stacking vdW layered materials, using InTe as a representative example. InTe’s notable polymorphism enables tunable symmetry and electronic structure through controlled stacking, allowing it to simultaneously host strong TI and TCI phases, protected by time-reversal and mirror symmetries, respectively. This duality makes InTe a versatile platform for exploring symmetry-protected topological states. Remarkably, the surface Dirac points remain gapless even under magnetic fields that break TRS, due to the protection from mirror symmetry. Moreover, the Dirac points shift away from time-reversal invariant momenta (TRIM) in a direction determined by the spin texture, offering a way to dynamically control their position via external fields. This controllable Dirac point motion, without gap opening, has direct implications for spintronic and magnetoelectric applications24,25. The robustness of surface conduction under magnetic perturbations can enable stable, low-dissipation transport, while the tunability of momentum-space features supports potential functionalities in topological transistors, memory devices, and magnetic sensors26,27. These properties position vdW-based DTIs such as InTe as promising candidates for quantum technologies. In particular, magnetic field–driven symmetry control could be used in quantum computing platforms where precise manipulation of topological states is essential. Our results thus not only advance the fundamental understanding of DTIs but also suggest practical strategies for developing functional topological materials.

Results and discussion

Stacking sequences and symmetries of vdW layered systems

All of vdW layered materials with hexagonal honeycomb lattices, such as transition metal dichalcogenides (TMDs) and III-VI monochalcogenides, are characterized by a mirror symmetry \({M}_{x}\) in their crystal structures, as seen in the top view shown in Fig. 1a, b. This symmetry, which maps \(x\) to -x, is inherent to the arrangement of metal atoms sandwiched between chalcogen atoms. In addition, these vdW materials in the hexagonal prismatic phase exhibits another mirror symmetry, \({M}_{z}\), perpendicular to the z-axis, arising from the individual layer structures, as shown in Fig. 1a. Unlike \({M}_{x}\), however, the presence of \({M}_{z}\) depends on the specific stacking configuration, which can vary due to the polymorphic nature of vdW materials.

Fig. 1: Stacking orders and crystal symmetry of vdW layered chalcogenides.
figure 1

Top and side view of the crystal structures of (a) the ε- and (b) γ-phases of vdW layered chalcogenides. Metal (M) and chalcogen (X) atoms are denoted by the red and green spheres. The blue and magenta lines represent the \({M}_{x}\) and \({M}_{z}\) mirror planes, respectively. c The orbital resolved electronic band structures of in-plane tensile strained ε-InTe with spin-orbit coupling (SOC). A band inversion occurs at the Γ point with SOC. d Bulk and surface Brillouin zone. The blue and magenta planes represent the Mx- and Mz-invariant planes, respectively. Note that special points on the surface BZs are denoted with –, ∼, and ⌃ for the 001, zigzag, and armchair surfaces, respectively.

Full size image

Typical examples illustrating these phenomena are the 2H and 3 R stacking in TMDs or the polymorphic phases of III-VI monochalcogenides, depicted in Fig. 1a, b as the ε- and γ-phases, respectively20,28. Both phases share an identical bilayer stacking pattern, yet differences arise in the crystallinity and bulk symmetry when three or more layers are stacked. The ε-phase exhibits an ABAB ∙∙∙ stacking sequence, forming a two-layer unit cell, whereas the γ-phase adopts an ABCABC ∙∙∙ stacking order with a three-layer unit cell. Consequently, as shown in the side view of Fig. 1a, b, the ε-phase possesses another mirror symmetry denoted as \({M}_{z}\) in addition to \({M}_{x}\), while the γ-phase lacks this symmetry. This disparity contributes significantly to the topological distinction between the two phases, as explained in more detail in our subsequent discussion taking InTe as a representative example.

To investigate the topological characteristics of InTe, we analyzed its behavior under in-plane biaxial strain. Remarkably, both the ε-phase and γ-phase exhibit band inversion with only a slight increase in tensile strain. For the ε-phase, which has an equilibrium in-plane lattice constant of a = 4.37 Å, band inversion occurs at a = 4.5 Å, as shown in Supplementary Fig. 1. In addition, Fig. 1c demonstrates that the spin-orbit coupling (SOC) opens local energy gaps at the crossing points due to band inversion. Similarly, the γ-phase, also with an equilibrium in-plane lattice constant of a = 4.37 Å, undergoes a comparable topological transition under tensile strain with a = 4.5 Å, as depicted in Supplementary Fig. 2. To further clarify the role of SOC in this process, we examined the evolution of the band structure of tensile-strained ε- and γ-InTe by progressively increasing the SOC strength from zero to its full value. As illustrated in Supplementary Fig. 1 and 2, SOC opens a gap at the crossing point of the inverted bands and increases the gap magnitude as its strength increases. These findings align with previous studies on tensile strain-induced topological phase transition in other III-VI monochalcogenides29. However, InTe, being the heaviest member of the III-VI family, benefits from a larger SOC strength and a smaller band gap, enabling band inversion and topological phase transition with minimal strain. This reduced strain requirement enhanced the feasibility of experimentally realizing the topological insulating phase via substrate engineering, making InTe a highly practical candidate for experimental implementation. Furthermore, recent studies have identified a trigonal anti-prismatic structure of InTe as an intrinsic topological insulator even without applied strain21. While our analysis focuses on the ε- and γ-phases under strain, we anticipate that the underlying mechanisms revealed in this study would also apply to the anti-prismatic structure, underscoring the robustness and versatility of InTe as a platform for exploring symmetry-protected topological phases.

Dual topological insulating phases

Upon evaluating the Wannier charge centers (WCC), we confirmed that both the γ- and ε-phases exhibit nontrivial \({{\mathbb{Z}}}_{2}\) band topologies, classifying them as strong TIs, as shown in Supplementary Fig. 3 and Supplementary Fig. 4. This classification implies that both phases host gapless surface state protected by TRS regardless of the exposed surface. To explore these surface states, we examined three representative surfaces: the 001 surface, the top surface perpendicular to the z-axis, and the zigzag and armchair surfaces, the side surfaces perpendicular to the y- and x-axes, respectively, as defined in Fig. 1a, b. The corresponding surface BZs and the mirror planes are shown in Fig. 1d.

Beyond their strong TI nature, the presence of mirror symmetries in InTe suggests the possibility of TCI behavior. As depicted in Fig. 2a, b, our calculations reveal that both the γ- and ε-phases possess a nontrivial mirror Chern number \({C}_{{M}_{x}}=+1\). Of particular interest, as mentioned above, is the presence of \({M}_{z}\) mirror symmetry in the ε-phase due to its stacking sequence. A similar calculation for \({M}_{z}\) confirms a mirror Chern number of \({C}_{{M}_{z}}=-1\), as shown in Fig. 2c, reinforcing the DTI nature of the ε-phase.

Fig. 2: InTe as a mirror Chern insulator.
figure 2

a The Wannier charge centers (WCC) flow for the Mx-invariant \({k}_{x}=0\) plane of the γ-phase. The WCC flows for (b) the Mx-invariant \({k}_{x}=0\) plane and (c) the Mz-invariant \({k}_{z}=0\) plane of the ε-phase. The red and blue dots represent the flow of WCCs for the +i and -i mirror eigensectors, respectively. The γ-phase possesses a nontrivial mirror Chern number \({C}_{{M}_{x}}=+1\), whereas the ε-phase, which has two mirror planes, possesses \({C}_{{M}_{x}}=+1\) and \({C}_{{M}_{z}}=-1\). Energy spectra for the armchair surface of the γ-phase (d) without (B = 0) and (e–g) with (B ≠ 0) the Zeeman perturbation. (h–k) Those of the ε-phase with the \({M}_{z}\) mirror plane (h) without (B = 0) and (i-k) with (B ≠ 0) the Zeeman perturbation. In (e–g), the gap is open for all applied field directions. In (h–k), the \({M}_{z}\) mirror symmetry protects the gapless Dirac surface states from gap opening when the field is applied along the \(z\) direction, whereas the gap is open for the other two field directions. l Surface Brillouin zone for the armchair surface. m Spin texture along the constant energy contour at the energy cut marked with a yellow line in (h). The size of the arrows and different colors, as given in the color scale bar, indicate the strengths of the in-plane and out-of-plane spin components, respectively.

Full size image

To further investigate the DTI properties of InTe, we examined the effects of an external magnetic field with 0.05 eV Zeeman energy, which breaks TRS as described in the Methods section. While TRS is entirely broken by the applied magnetic field, certain mirror symmetries persist depending on the field direction. In particular, a mirror plane perpendicular to the field direction remains intact, ensuring the protection of surface states. For instance, when a magnetic field is applied parallel to the x-axis, the \({M}_{x}\) mirror symmetry is preserved, allowing the topological surface Dirac states on the 001 surface to remain gapless, as summarized in Supplementary Figs. 5 and 6. Under field conditions that preserves mirror symmetry, the Dirac point remains protected but undergoes a shift along the line associated with the mirror-invariant plane.

From the perspective of a DTI, the armchair surface further distinguishes the γ-phase from the ε-phase due to their different responses to TRS-breaking perturbations. This distinction is evident in Fig. 2d–k where the armchair surface state of the ε-phase is protected by \({M}_{z}\) symmetry, whereas the γ-phase lacks this protection. As a result, the γ-phase exhibits a fully gapped armchair surface state under any applied magnetic field direction, as further verified in Supplementary Fig. 7. In contrast, the ε-phase retains a protected Dirac point when the magnetic field is aligned with the z-direction, preserving \({M}_{z}\) symmetry. This behavior highlights the crucial role of stacking-dependent mirror symmetries in determining the robustness of surface states in DTIs.

Determination of the direction of the Dirac cone shift

The results above suggest that in vdW layered systems, the manipulation of stacking configurations to introduce additional mirror symmetry provides a powerful means to control the Dirac cone when subjected to applied magnetic fields. This tunability allows for the controlled movement of the Dirac point away from the TRIM point while maintaining a gapless state. One crucial question to address is the specific direction in which the Dirac point moves. Since the Dirac point shift occurs along the line associated with the mirror-invariant plane, there are two possible directions for this displacement. We have established a way to determine the direction by analyzing the spin texture in the vicinity of the Dirac point, as elucidated in Supplementary Note 1. Our main result is that the shift of Dirac point is given by

$$\left({k}_{x},{k}_{z}\right)=\left(-\frac{B}{F},0\right).$$
(1)

Here, F is a real coefficient of the effective Hamiltonian \(H\left({k}_{x},{k}_{z}\right)=C{k}_{z}{\sigma }_{x}+D{k}_{z}{\sigma }_{y}+F{k}_{x}{\sigma }_{z}\), as derived in Equation (S3) in the Supplementary Note 1. This Hamiltonian represents the two-dimensional (2D) unperturbed surface state in the \({k}_{x}\)-\({k}_{z}\) plane, maintaining both TRS and mirror symmetry \({M}_{z}\). The constants \(C\) and \(D\) are real coefficients, while \(B\) represents the magnitude of the magnetic field applied perpendicular to the mirror-symmetric plane \({M}_{z}\). The shift direction of the Dirac point is determined by the sign of \(F\) in Eq. (1).

To illustrate this determination process, we consider the Dirac point shift shown in Fig. 2k. The corresponding spin texture along the constant energy contour, indicated by the yellow line in Fig. 2h, provides crucial information. As shown in Fig. 2m, along the positive kx-axis, the spin points towards the negative \({k}_{z}\) direction, meaning that \({\sigma }_{z} < 0\), resulting in \({k}_{x}{\sigma }_{z} < 0\). Since the yellow contour represents the lower energy band in Fig. 2h, the third term \({{Fk}}_{x}{\sigma }_{z}\) in \(H\left({k}_{x},{k}_{z}\right)\) should be negative. Consequently, this implies \(F > 0\), causing the Dirac point to shift toward the negative \({k}_{x}\) direction, consistent with the observed shift of the Dirac point in Fig. 2k.

Furthermore, to verify the linear relationship between the Dirac point displacement and magnetic field strength predicted by the effective model, we explicitly calculated the surface electronic structure of ε-InTe under various magnetic field conditions. As shown in Supplementary Fig. 8, the Dirac point on the armchair surface shifts progressively along the \({k}_{x}\) direction as the Zeeman energy increases. The extracted Dirac point positions exhibit a linear dependence on the magnetic field strength, as expected from Eq. (1).

The parameter \(F\) determines the dispersion of the surface Dirac cone along the \({k}_{x}\) direction and is directly related to the Fermi velocity, meaning its magnitude can be tuned by material-specific parameters such as doping, strain, or external pressure. Its sign is linked to the spin polarization of the surface states, which can differ between the top and bottom surfaces due to their opposite spin textures. Consequently, the sign of \(F\) can be effectively reversed by changing the surface termination or by reversing the direction of the applied magnetic field. This tunability in both the magnitude and the sign of \(F\) enables precise control over the location and dynamics of Dirac points in momentum space. Our analysis thus highlights how the interplay between spin texture and mirror symmetry governs the shift behavior of Dirac points in vdW layered dual topological insulators, which is an essential capability for spintronic and quantum devices that require controllable and robust surface states under external magnetic fields.

Two types of surface states in DTI with double mirror symmetry

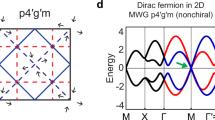
Among the various surfaces in the ε-phase, the zigzag surface exhibits particularly intriguing features resulting from the emergence of an additional mirror plane, \({M}_{z}\), through stacking. Remarkably, this surface exhibits double mirror symmetry along with \({M}_{x}\) mirror symmetry. The interplay between these two mirror symmetries leads to a unique classification of the four TRIM points in the 2D surface BZ into three distinct cases: (i) a TRIM point where two mirror-invariant k-planes intersect, (ii) a TRIM point lying on a single mirror-invariant k-plane, and (iii) a TRIM point that does not reside on any mirror-invariant k-plane. For example, in the zigzag surface of the ε-phase shown in the inset of Fig. 3a, \(\widetilde{\Gamma }\) belongs to case (i) as it is located at the intersection of the Mx- and Mz-invariant k-planes. In contrast, \(\widetilde{{\rm{X}}}\) and \(\widetilde{{\rm{Z}}}\) are case (ii) TRIM points that lie on the Mx- and Mz-invariant k-planes, respectively, while \(\widetilde{{\rm{U}}}\) represents case (iii), as it is not situated on either mirror-invariant k-plane.

Fig. 3: Two types of surface states with double mirror symmetry.
figure 3

Schematic band structures for Type I surface state with a single Dirac cone at \(\widetilde{\Gamma }\) (a) for unperturbed, under Zeeman perturbation with (b) \({\bf{B}}\parallel \hat{{\bf{x}}}\), (c) \({\bf{B}}\parallel \hat{{\bf{y}}}\), and (d) \({\bf{B}}\parallel \hat{{\bf{z}}}\). Insets show the surface Brillouin zones, with blue and magenta lines indicating k-planes invariant under \({M}_{x}\) and \({M}_{z}\), respectively. When mirror symmetry remains intact, the Dirac cone persists and shifts along the corresponding k-line associated with the mirror symmetry. Schematic band structures for Type II surface state with triple Dirac cones (e) for unperturbed, under Zeeman perturbation with (f) \({\bf{B}}\parallel \hat{{\bf{x}}}\), (g) \({\bf{B}}\parallel \hat{{\bf{y}}}\), and (h) \({\bf{B}}{||}\hat{{\bf{z}}}\). It consists of one TRS-protected Dirac cone at \(\widetilde{{\rm{U}}}\) and two (TRS + mirror)-protected ones at \(\widetilde{{\rm{X}}}\) and \(\widetilde{{\rm{Z}}}\). i–l Energy spectra for the zigzag surface of ε-phase terminated with In atoms, exhibiting a Type I surface state under magnetic field in the same directions as in (a-d). (m–p) Those terminated with a mixed atomic column of In and Te, exhibiting a Type II surface state under magnetic fields in the same directions as in (e–h).

Full size image

This categorization leads to two distinct types of surface states in DTIs with double mirror symmetry. Type I features a single Dirac cone located at the TRIM point where two mirror-invariant k-planes intersect, while Type II involves the formation of Dirac cones at the remaining three TRIM points, as illustrated in Fig. 3a, e, respectively. The main distinction between these two types lies in their response to an external magnetic field. In Type I, the Dirac point is protected simultaneously by TRS and both \({M}_{x}\) and \({M}_{z}\) symmetries, making it exceptionally robust to perturbations depending on the magnetic field direction. This behavior is illustrated in Fig. 3b–d, where the inset highlights the mirror-invariant k-plane that remains preserved under each specific magnetic field direction. Note that no mirror symmetries are preserved when the magnetic field is applied along the y-axis, as shown in Fig. 3c, eliminating all mirror-invariant k-planes. However, for other magnetic field directions, the Dirac point can shift within the k-plane while remaining gapless. In contrast, Type II consists of three Dirac points: two at \(\widetilde{{\rm{X}}}\) and \(\widetilde{{\rm{Z}}}\), which are protected by both TRS and a single mirror symmetry, and one at \(\widetilde{{\rm{U}}}\), which is solely protected by TRS in the absence of an external magnetic field, as shown in Fig. 3e. Upon applying a magnetic field, the TRS-protected Dirac point at \(\widetilde{{\rm{U}}}\) is always gapped out, while only one of the two mirror symmetry-protected Dirac points at \(\widetilde{{\rm{X}}}\) or \(\widetilde{{\rm{Z}}}\) remains, depending on the magnetic field direction, as shown in Fig. 3f–h.

To experimentally realize both Type I and Type II scenarios, we examined the surface states on the zigzag surfaces of the ε-phase with two distinct terminations. Our results reveal that a surface terminated with In atoms exhibits a Type I surface state (Fig. 3i), whereas a surface terminated with a mixed In-Te atomic column results in a Type II surface state (Fig. 3m). Furthermore, the behavior of these surface states under the applied magnetic field of different directions, shown in Fig. 3j–l, n–p, is consistent with the theoretical schematic surface energy spectra described in Fig. 3b–d, f–h. The displacement direction of the Dirac points is dictated by the spin texture in the vicinity of each Dirac point, as explained in Supplementary Fig. 9.

In this study, we have demonstrated that vdW layered systems, exemplified by the III-VI chalcogenide InTe, provide a versatile platform for realizing DTI phases with unique and tunable properties. The stacking-dependent mirror symmetries inherent to vdW materials enable the formation of multiply protected surface states that are highly robust against external perturbations. This underscores the potential of stacking engineering as a powerful tool for designing and stabilizing topological features. Furthermore, our analysis revealed that the spin texture of surface states dictates the directionality of Dirac cone motion under TRS-breaking perturbations, establishing a direct connection between spin-momentum locking and tunable surface state behavior. Additionally, we found that the response of surface states to magnetic fields varies significantly depending on the termination layer, presenting new opportunities for tailoring topological properties through surface engineering. These findings not only deepen our understanding of dual topological phases but also position vdW layered materials as an experimentally feasible platform for exploring and manipulating robust topological surface states.

The ability to control Dirac cone shifts and symmetry protection mechanisms opens promising avenues for applications in next-generation quantum computing and spintronic devices, where precise topological control is crucial. Moreover, since magnetic-field-induced symmetry breaking can lead to surface-state gaps under certain terminations, our platform may also offer a foundation for realizing higher-order topological phases featuring localized corner or hinge states, as suggested in recent theoretical studies30. In addition, since systems with magnetic substrates or magnetic doping can effectively generate internal magnetic fields, the concept developed in this work can be readily extended to a broader class of material platforms. Our results provide essential theoretical insights that can guide future experimental realizations, advancing the development of functional topological materials for technological applications.

Methods

Density functional calculation

Structural relaxations and electronic structure calculations were conducted using density functional theory within the Vienna ab initio simulation package (VASP)31. The electronic wavefunctions were expanded using a plane wave basis set with a kinetic energy cutoff of 500 eV. The exchange-correlation functional was treated using the generalized gradient approximation (GGA) of Perdew−Burke−Ernzerhof (PBE). The Brillouin zones (BZ) of the ε- and γ-phases were sampled with 19 × 19 × 5 and 19 × 19 × 3 k-point meshes, respectively, following the Monkhorst-Pack scheme32, taking into account the c-axis length of the unit cell. To perform Wannier charge centers (WCC) calculations, we utilized the WANNIER90 code to obtain maximally localized Wannier functions (MLWFs)33. The surface electronic spectra were computed using the iterative Green’s function method, implemented in the WannierTools code34,35.

Inclusion of Zeeman effect

To investigate the effects of an external magnetic field B on the dual topological nature of InTe, we included the Zeeman coupling \({H}_{Z}\) into the tight-binding Hamiltonian,

$${H}_{Z}={\mu }_{B}{g}_{J}{\bf{J}}\cdot {\bf{B}},$$

where \({\mu }_{B}\) is the Bohr magneton, \({g}_{J}\) is the Landé g-factor, and \({\bf{J}}\) is the total angular momentum. The tight-binding Hamiltonian was built using MLWFs derived from the s-orbitals of In atoms and p-orbitals of Te atoms. The contribution of the total angular momentum \({\bf{J}}\) in the Zeeman term was obtained from both orbital and spin states and added to the Hamiltonian. The Landé g-factor is given by

$${g}_{J}=1+\frac{J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}$$

where J, L, and S represent the quantum numbers of the total, orbital, and spin angular momenta, respectively.