Vacancy formation energy as a descriptor of the exfoliability of MAX phases to MXenes

Abstract

A thermodynamic descriptor for chemical exfoliation of MXenes remains elusive, primarily because the process is dynamic and MXenes are inherently metastable. Here we show that vacancy formation energies provide such a descriptor. Synthesized MXenes exhibit positive vacancy formation energies for M and X elements, while non-synthesized MXenes show negative energies for M or X elements, or both. Similarly, exfoliable precursor MAX phases are characterized by negative vacancy formation energies for A elements. Using this correlation, we identify seven hitherto unreported MXenes as potentially synthesizable in HF at pH = 2. At higher pH, additional unknown MXenes are identified as locally stable together with their exfoliable MAX phases but remain inaccessible in HF, highlighting the need for alternative alkaline etchants. The exfoliable precursor MAX phases are predominantly Al-based. The proposed descriptor is transferable to other 2D materials such as MBenes and may be adapted to other acidic or alkaline etchants.

Introduction

Mechanical or chemical (liquid) exfoliation is a predominant top-down synthesis route for two-dimensional (2D) crystals such as graphene^1,2, transition metal dichalcogenides (TMDs)³, hexagonal boron nitride (hBN)⁴, MXenes⁵, MBenes⁶ etc. While mechanical exfoliation suits the isolation of weakly bonded single-atom layers in three-dimensional (3D) van der Waals (vdW) materials, such as graphite^1,2, exfoliation of strongly bonded 3D materials requires harsher etching environments. One prime example is 3D MAX phases—ternary layered transition metal carbides, nitrides, and carbonitrides^7,8. These can be chemically exfoliated into 2D MXenes, typically by using aqueous hydrofluoric acid (HF)⁵. MXenes are promising in widespread applications such as energy storage^9,10,11, chemical sensing^12,13,14, catalysis^15,16, electromagnetic shielding^17,18, filtration^19,20, optoelectronics^21,22, etc. These applications are enabled by MXenes’ exceptional electrical conductivity, tunable hydrophilicity, and rich chemistry.

During chemical exfoliation, the A-layer of a MAX phase (M_n+1AX_n, M = Ti, Cr, Mn, etc., A = Al, Ga, etc., X = C and/or N, n = 1-3) is removed forming the MXene. Currently, 12 different MXenes (considering only pure, unalloyed compositions) are experimentally known to be exfoliable from a parent MAX phase in HF²³. Hypothetically, many more may exist. By simple multiplication, 84 carbon-based and another 84 nitrogen-based MXenes can be envisioned within the transition metal series from Sc to Hg (28 TMs x 3 n). However, since exfoliation requires the availability of a parent MAX phase, their actual number is more limited. In a recent study, we identified a total of 124 stable MAX phases²⁴. Out of these, all phases differing by only the A-element will yield the same MXene, assuming they can be exfoliated at all. Based on this, still a total of 42 MXenes may be exfoliable. The number will be higher if alloyed or doped MAX phases are considered. Understanding the discrepancy between the 42 potentially exfoliable MXenes and the 12 experimentally realized MXenes is essential for guiding future experiments toward the discovery of new MXenes.

At this point, atomic-scale modeling can greatly enhance our understanding of the exfoliation of MAX phases into MXenes. In this context, density functional theory (DFT) has been employed to calculate thermodynamic quantities and bonding properties, such as exfoliation energy (energy required to remove an A-element from a MAX phase)^25,26,27, formation enthalpy, reaction enthalpy^28,29, solvation energy (energy released when a MXene is dissolved in HF)³⁰, elastic bond constants^25,27, etc. However, predictions based on these quantities do not always align with experimental findings. Al-free MAX phases such as Cr₂GaC and Mo₂GaC are predicted to be highly exfoliable even though the calculations do not specify an etchant^25,27. In contrast, successful exfoliation has so far been reported mainly for Al-containing MAX phases^31,32. Some MXenes, like Zr₂C and Cr₂C, have been predicted as “formable”, but they so far have not been successfully synthesized in HF, the widely utilized etchant^25,27,30. The primary source of these discrepancies between theoretical predictions and experimental reality is the metastability of MXenes. Equilibrium thermodynamics only allows the prediction of stable compounds. A comprehensive understanding thus requires the determination of reaction rates and kinetic barriers in the appropriate environment.

In this context, Björk et al. identified a correlation between vacancy formation energies of M ($\Delta {E}_{f}^{{\rm{M}}}$) and A ($\Delta {E}_{f}^{{\rm{A}}}$) elements and the exfoliability of MAX phases^30,33. They found exfoliable MAX phases have formation energies positive for M (V_M) and negative for A vacancy (V_A). This criterion, however, only addresses the initial etching step, namely the removal of the A layer, but offers no insights into the subsequent metastability of the resulting MXene. Consequently, the successful removal of the A layer does not necessarily imply that the resulting MXene will exhibit local stability. To properly characterize exfoliation, an approach that also takes into consideration the resulting MXene is essential.

In this work, we extend the Björk et al. method and present an approach for exfoliation (in HF) that couples two thermodynamic requirements: (i) the intrinsic, local stability of the target MXene and (ii) a favorable driving force for removing the A layer from the parent MAX phase. On the MXene side, we consider M (V_M) and X (V_X) vacancies, whereas for the MAX phase, we employ the Björk et al. correlation solely to the A (V_A) vacancies. These vacancies are considered because we assume MXene formation as an intermediary step of a MAX phase reaction with an etchant (Fig. 1a, see the next section for further details). With this assumption, we find the following criteria (Fig. 1b) to exfoliate a given MAX phase into a metastable MXene. At a given pH (in HF).

Fig. 1: Exfoliation/etching process in HF.

a Schematic representation of an exfoliation reaction pathway on a representative potential energy surface (PES). The reaction begins with the removal of the A-layer leading to the formation of 2D MXene layers, which is thermodynamically favored (in HF). However, the reaction can further proceed exothermically, forming other products that reside at a global minimum on the PES. Having MXene formation as an intermediary step, vacancy formation energies are used as a suitable measure for the local stability of MXenes and the potential for further reactions. b For the initial step of exfoliation, i.e., MXene formation, the vacancy formation energy ($\Delta {E}_{f}^{{\rm{A}}}$) of the element must be negative to enable its removal from the precursor MAX phase. To assess if the resultant MXene is locally stable, the vacancy formation energies for the M ($\Delta {E}_{f}^{{\rm{M}}}$) and X ($\Delta {E}_{f}^{{\rm{X}}}$) elements must be positive.

• 1. V_A has a negative formation energy in the MAX phase.

• 2. Both V_M and V_X have a positive formation energy in the MXene.

Condition (1) ensures that a driving force exists for dissolving the A element in the MAX phase, while condition (2) assures that the dissolution of the resultant MXene is hindered. Using experimental data, we verify these conditions for synthesized MXenes and unsynthesized MXenes and find correlations between the sign of vacancy formation energies and synthesizability of MXenes. Using this correlation, we suggest seven so far unreported MXenes to be synthesizable, namely, Nb₃C₂, Ta₃C₂, V₃C₂, Ti₄C₃, Ti₃N₂, V₃N₂, and V₄N₃. MXenes, like Zr₂C and Cr₂C (mentioned above), on the contrary, are predicted to be locally unstable (non-synthesizable) in HF. Here, we demonstrate the approach for characterizing exfoliation in HF—the most commonly used etchant—while we note that it may also be applicable to other etchants, including acids and alkalis.

Results

Exfoliation pathway and metastability of MXenes

For a MAX phase in contact with HF, one possible reaction pathway is the formation of a MXene (surface terminations and stoichiometric coefficients are omitted here for clarity but are fully accounted for in our analysis),

$${\text{M}}_{{\rm{n}}+1}{\text{AX}}_{{\rm{n}}}+\,\text{HF}\longrightarrow {\text{M}}_{{\rm{n}}+1}{\text{X}}_{{\rm{n}}}+{\text{A}}_{x}{\text{F}}_{y}+{\text{H}}_{2}.$$

(1)

The potential energy surface (PES) of this exfoliation reaction is illustrated in Fig. 1. Firstly, the A element is removed from the MAX phase by reacting with the solution species (e.g., fluoride (F⁻) ions in HF) and dissolving into the solution as Al³⁺ ions. As a consequence, the M_n+1X_n (MXene) layers, previously bound by the A-layer, are separated and functionalized with surface groups such as F, OH, O, and others depending upon the environment.

The MXene formation reaction (Eq. (1)) with a negative reaction enthalpy (Δ_rG^MXene) across a relevant range of pH is thermodynamically possible (see Figs. S13–S14). However, MXenes only reside at a local minimum on the PES and are, therefore, metastable. Other competing reactions—such as those involving bulk transition metal carbides, nitrides, oxides, etc. as products—exhibit even more negative reaction enthalpies (see also Figs. S13–S14). This observation holds for all MAX phases, rendering MXenes as metastable. Reaction enthalpies associated with Eq. (1) can therefore not serve as an indicator for the synthesizability of MXenes (or the exfoliability of MAX phases).

Therefore, an alternative descriptor for exfoliability is necessary that describes the formation of a MXene through A-element removal and assesses the likelihood of further reactions, such as MXene dissolution or disintegration in HF (or any other etchant). Vacancy formation is critical in driving the removal of the A element from a MAX phase to form a MXene and subsequently influencing the MXene’s stability against dissolution. This process is evaluated using the vacancy formation energy (ΔE_f, see Eq. (2) in the Methods section), which is defined as the excess energy required to move an element into the etching environment. A negative excess energy thermodynamically favors the dissolution of the element. In contrast, a positive excess energy indicates a thermodynamic barrier for dissolving the element into the etching environment, preventing dissolution. For the first step of exfoliation—MXene formation—the vacancy formation energy of the A element in a MAX phase must be negative, as demonstrated by Björk et al.³⁰. To ensure that the formed MXene does not dissolve, the vacancy formation energies of both the M and X elements in the MXene must be positive. This absence of a thermodynamic driving force for MXene dissolution locally stabilizes the MXene, allowing it to reside in a local minimum on the PES, making it metastable. Conversely, if the vacancy formation energies of the M, X, or both elements are negative, the MXene is thermodynamically prone to dissolution in the etchant and is considered locally unstable.

The conditions for exfoliation are summarized in Fig. 1b. A MXene is considered to be metastable if the vacancy formation energies in the MXene are positive ($\Delta {E}_{f}^{{\rm{M}}} > 0$, $\Delta {E}_{f}^{{\rm{X}}} > 0$) and, simultaneously, the vacancy formation energy of the A element in a corresponding MAX phase is negative ($\Delta {E}_{f}^{{\rm{A}}} < 0$). In the following sections, we first verify these conditions for MXenes that are experimentally known to be (non-) exfoliable from parent MAX phases in HF. This analysis allows us to identify and confirm the correlation between the sign of vacancies and MXene synthesizability. Thereafter, to save computational resources, we first calculate vacancy formation energies of M and X elements for all possible new MXenes, 24 in total. From this set, we identify new metastable MXenes. Subsequently, we screen their precursor MAX phases for exfoliation potential based on the vacancy formation energies of the A elements. Eventually, the impact of variations in pH is discussed.

Exfoliation from vacancy formation energies

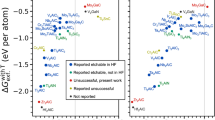
In Fig. 2a, we present vacancy formation energies of M ($\Delta {E}_{f}^{{\rm{M}}}$; y-axis) and X elements ($\Delta {E}_{f}^{{\rm{X}}}$; x-axis) in MXenes that have experimental reports on synthesis. In Fig. 2b, vacancy formation energies of A elements in corresponding precursor MAX phases are reported. All values are calculated at a pH of 2, a condition typically employed in experiments using HF (pH dependence is discussed further in the next section and Supplementary Section S2). For each MXene, various surface functionalizations are possible (see panel c) and have also been considered (see Fig. S16). In panel (a), however, only the most relevant surface functionalization is shown for better readability; see the discussion at the end of this section.

Fig. 2: Evidence of correlation.

a Vacancy formation energies of M elements($\Delta {E}_{f}^{{\rm{M}}}$;y coordinate) vs. X elements ($\Delta {E}_{f}^{{\rm{X}}}$; x coordinate) in MXenes, and (b) of the A elements ($\Delta {E}_{f}^{{\rm{A}}}$) in the corresponding parent MAX phases. c Schematic crystal structures of a MXene (M₂AX) with F, O, and OH surface terminations (T). A correlation for the metastability of MXenes and the exfoliability (etching of the A element) of MAX phases is identified. Synthesized MXenes in HF (green symbols) are located in the yellow-shaded region (x > 0, y > 0), while unsynthesized MXenes (red symbols) are situated in the turquoise-shaded region (x < 0, y < 0, or both). Simultaneously, A-etched MAX phases (green) are present in the yellow-shaded region ($\Delta {E}_{f}^{{\rm{A}}} < 0$), while non-etchable are positioned in the turquoise-shaded region ($\Delta {E}_{f}^{{\rm{A}}} > 0$). All values are calculated at a pH of 2, with an ionic concentration of 0.001 mol/l at room temperature.

For the MXenes (Fig. 2a) there is clear evidence for a correlation of the sign of vacancy formation energies with their synthesizability. MXenes that have been reported as synthesizable in HF (green symbols) are all located in the yellow-shaded area where both vacancy formation energies (for the M and the X element) are positive. There are two exceptions, V₂C and V₄C₃, which, however, lie only marginally (within 0.1 eV/vacancy) outside this region. At the same time, MXenes that have been reported to be not synthesizable in HF are exclusively situated in the turquoise-shaded area, where at least one vacancy formation energy (either for M or for X or for both) is negative. This correlation confirms the condition for the metastability of a MXene: $\Delta {E}_{f}^{{\rm{M}}} > 0$ and $\Delta {E}_{f}^{{\rm{X}}} > 0$.

For the MAX phases (Fig. 2b), we similarly find a correlation for A vacancy formation energies and their exfoliability in HF. Exfoliable MAX phases (green symbols) all show a negative vacancy formation energy (yellow-shaded region), with the exception of Mo₂Ga₂C—a double A-layered MAX phase. In contrast, non-exfoliable MAX phases (red symbols) such as Mo₂GaC, Ti₃SiC₂, Mn₂GaC, etc., are situated in the turquoise-shaded region. The exceptional behavior of Mo₂Ga₂C disappears when two A-element vacancies are considered, as shown by Björk et al.³⁰. However, in this study, we only evaluate single vacancies for all phases. We note that Cr₂AlC and Zr₂AlC both are located in the yellow-shaded region. Their non-exfoliability originates from the fact that the corresponding MXenes, Cr₂C and Zr₂C, are unstable, see panel (a). This highlights that understanding exfoliability requires considering vacancy formation energies in both the parent MAX phases and in the target MXenes.

In summary, the ability to exfoliate MAX phases into MXenes is correlated with vacancy formation energies in both materials. Only when the vacancy formation energy of M and X elements in MXenes is positive (indicating metastability in HF) and the vacancy formation energy of the A element in a parent MAX phase is negative (indicating the possibility to extract the A element in HF), successful exfoliation is possible.

We now return to the question of MXene surface functionalization. Since there are three relevant surface groups for every MXene (-F, -O, -OH; see Fig. 2c), there are three pairs of vacancy formation energies for V_M and V_X. In Fig. 3 we give examples of the three possibilities that may occur. The full calculated set of data is shown in Fig. S16. In case 1, we have one pair of positive formation energies and two pairs with at least one negative formation energy. The most relevant surface termination then is that with both vacancy formation energies being positive, since this yields a metastable MXene. Out of the three possible cases, only that one is shown in Fig. 2a. In case 2, we have two pairs of solely positive vacancy formation energies. In Fig. 2a we then only show the one with the largest distance from the origin. Finally, in case 3, there is at least one negative vacancy formation energy independent of the MXene surface group. In Fig. 2a we only show the data point that is closest to the origin.

Fig. 3: Schematic illustrating the relevant data point (right panel) chosen from three options (left panels; circles = F, triangles = H, stars = OH) for each MXene.

Depending on the scatter, in total three cases are possible.

New MXenes

We are now in a position to employ the correlation between vacancy formation energies and the possibility of synthesizing corresponding MXenes by exfoliation of MAX precursors in HF. The number of potential MXenes is naturally limited by the availability of a corresponding stable parent MAX phase (a maximum of 168 in total, see refs. ^24,34). This excludes, for example, Fe_n+1X_n MXenes, as Fe_n+1AX_n MAX phases are generally unstable²⁴. Also, since the family of M_n+1AX_n with fixed M and X all yield the same MXene upon exfoliation (if possible), the number of potential MXenes is further reduced to 39. A full list is given in Table S1. Excluding the 15 MXenes that have already been considered in the previous section and those with unstable precursor MAX phases, we are left with 24 potential MXenes.

Figure 4 catalogs the vacancy formation energies similar to Fig. 2, but of the new hypothetical (24 compositions not yet reported experimentally, whether synthesized or not) MXenes and precursor MAX phases of only metastable MXenes identified in panel (a). As before, we only show data points for the most relevant surface groups. Blue represents hypothetical new MXenes and MAX phases that are predicted or without any reported exfoliation behavior. The background color coding follows the same scheme as in Fig. 2. Panel (a) is constructed in the same way as panel (a) in Fig. 2. Refer to Fig. 3 for the construction of this panel. See Fig. S16(a–c) for vacancy formation energies of new MXenes with the three considered terminations.

Fig. 4: Applying the exfoliation descriptor to new MXenes.

a, b Same as in Fig. 2 but applied to (a) hypothetical MXenes and (b) precursor MAX phases of metastable MXenes identified in (a). We identify nine metastable MXenes. However, only seven are synthesizable in HF due to the presence of an exfoliable MAX phase in HF (b). Blue represents hypothetical MXenes and MAX phases that are either predicted or lack reported experimental exfoliation behavior. All values are calculated at a pH of 2, with an ionic concentration of 0.001 mol/l at room temperature.

From panel (a), we find that a total of nine MXenes are located in the yellow-shaded region, namely V₃C₂, Ti₄C₃, Ti₃N₂, Ta₃C₂, Sc₂C, Nb₃C₂, V₃N₂, V₄N₃, and Cr₂N (with ‘T’ not explicitly stated). These MXenes, owing to positive vacancy formation energies, are suggested to be locally stable in HF (at pH = 2). In contrast, the remaining 15 hypothetical MXenes are situated in the turquoise-shaded region, with negative vacancy formation energies of M, X, or both, indicating their disintegration or decomposition in HF.

Next, we examine the possible precursor MAX phases for the newly identified hypothetical MXenes. From panel (b), we find that seven among nine MXenes have exfoliable MAX phases in HF. These MXenes, i.e., Nb₃C₂, Ta₃C₂, Ti₃N₂, Ti₄C₃, V₃C₂, V₃N₂, and V₄N₃, have precursors MAX phases containing Al and Ga, which are located in the yellow-shaded zone ($\Delta {E}_{f}^{{\rm{A}}} < 0$, exfoliable). In these MAX phases, it is potentially possible to etch away the A element in HF (pH=2). The remaining non-Al-containing MAX phases are situated in the turquoise-shaded region ($\Delta {E}_{f}^{{\rm{A}}} > 0$, non-exfoliable). These phases contain Ga, Ge, In, Si, and Pb, which cannot be selectively removed in HF (at pH=2) from their corresponding MAX phases. Yet, there are phases such as Nb₃SnC₂, Ti₃SnN₂, V₃InC₂, and V₃GaN₂, which are located at the borderline $\Delta {E}_{f}^{{\rm{A}}}\approx 0$. These phases may also be potentially exfoliable, but the driving force for initial etching steps is minimal. The remaining two MXenes, Cr₂N, and Sc₂C, have the non-exfoliable MAX phases and cannot be synthesized in HF. Combining the results of panels (a) and (b), we suggest Nb₃C₂, Ta₃C₂, Ti₃N₂, Ti₄C₃, V₃C₂, V₃N₂, and V₄N₃, as locally stable and with an exfoliable precursor MAX phase in HF.

The correlation between vacancy formation energies and exfoliability can not only be used to predict novel MXenes; it also allows us to determine the dominant surface groups at individual MXenes. For instance, in Ti₂CT₂, the ΔE_f of V_Ti and V_C are both positive for T=OH and F surface groups, but not for the O surface group (Fig. S16(a–c)). Consequently, F and OH surface groups are prominent in Ti₂CT₂. We apply this approach to all the synthesized and newly predicted MXenes in HF. Table 1 provides the dominating surface groups for these MXenes. Focusing on the newly identified MXenes, we find the following trends: all F, O, and OH surface groups will be present in Nb₃C₂T₂ and Ta₃C₂T₂; both F and OH are dominant in Ti₄C₃T₂ and V₃C₂T₂; and finally, only the O surface group is dominant for Ti₃N₂T₂, V₃N₂T₂, and V₄N₃T₂.

Table 1 Dominant surface terminations in the synthesized MXenes and newly predicted MXenes

pH dependence

Our analysis suggesting seven novel MXenes to be exfoliable has so far been conducted at a fixed pH of 2 (typical synthesis conditions). However, the question arises as to whether varying the pH value could play an important role in (locally) stabilizing a MXene. To address this question, we investigate the change in vacancy formation energy over a pH ranging from −1 to 14. We note, however, that at pH >> 4, the formation of oxides and hydroxides in the etching reservoir becomes significant. These species are not included in our analysis, which would require further adaption of our analysis and additional calculations beyond the scope of the present manuscript.

Figure 5a illustrates how the vacancy formation energy of Ti increases monotonically with pH, even switching sign at a critical pH value (pH_cr = 1.2), above which the formation energy turns positive. This shift in ΔE_f arises from the variation in the chemical potential of Ti (μ_Ti) as a function of pH. The Ti chemical potential is referenced to the aqueous Ti^[2+] species up to a pH of about 6, beyond which it is referenced to the Ti^[3+] species. This change of reference is reflected by the change in slope in the vacancy formation energy. Details on the evaluation of the chemical potential using these species are provided in the Methods section.

Fig. 5: Role of pH in exfoliation.

a Ti vacancy formation energy (ΔE_f) in Ti₂CF₂ MXene as a function of pH in HF. ΔE_f reaches zero at the critical pH (pH_cr) and changes sign beyond this threshold. The pH range is divided into metastable (yellow-shaded) and unstable (turquoise-shaded) zones by pH_cr. The dissolved reservoir species are indicated in the legend. b Bar diagram illustrating critical pH values for M- and A-element vacancies in hypothetical and unsynthesized MXenes with F (top), O (middle), and OH (bottom) surface groups. The yellow-shaded bars highlight the exfoliable range, where $\Delta {E}_{f}^{{\rm{A}}} < 0$, $\Delta {E}_{f}^{{\rm{M}}} > 0$, and $\Delta {E}_{f}^{{\rm{X}}} > 0$. This range is bounded by ${{\rm{pH}}}_{cr}^{{\rm{A}}}$ (upper) and ${{\rm{pH}}}_{cr}^{{\rm{M}}}$ (lower) and disappears if ${{\rm{pH}}}_{cr}^{{\rm{A}}} < {{\rm{pH}}}_{cr}^{{\rm{M}}}$. MXenes with locally unstable ΔE_f values are excluded.

The variation of the chemical potential (monotonically increasing) with pH applies to most species as, does the occurrence of a slope change. Yet, depending on the species, the formation energy may change sign at a critical pH; it may strictly stay negative (Hf₂CF₂), strictly stay positive (Sc₂C(OH)₂), or not vary at all (Nb₂CF₂, Ta₂CF₂), see Fig. S11. In the latter three cases, no critical pH exists. A similar observation applies to vacancy formation energies in MAX phases (Fig. S12).

Figure 5b presents bar diagrams of stability regions for hypothetical and non-synthesized MXenes (in HF) with all three considered surface terminations. Each bar highlights the region where a MXene is both locally stable and exfoliable from any of its precursor phases, bounded by the upper critical pH value for A vacancies (V_A) and the lower critical pH value for M vacancies (V_M). If either the upper or lower critical pH value is absent, the bar extends to the limits of the accessible pH range. Bars are absent if ${{\rm{pH}}}_{cr}^{{\rm{A}}} < {{\rm{pH}}}_{cr}^{{\rm{M}}}$ (Hf₂NT₂ (T = O); first bottom label), indicating that the local stability of the MXene and exfoliability of its precursor MAX phase are mutually exclusive in pH. For each MXene, the precursor MAX phase that provides the largest exfoliable window is chosen. MXenes that are not locally stable and have corresponding non-exfoliable precursor MAX phases are excluded from the analysis. X vacancies do not exhibit a critical pH value for the considered MXenes.

In Fig. 5b, we identify additional MXenes, beyond those previously predicted, as locally stable with an exfoliable precursor MAX phase. Among these, Sc₂CT₂ (T=OH) features a yellow bar below a pH of zero, bounded by the critical pH of V_A. This means that its precursor MAX phase (Sc₂InC) could be exfoliated under harsh acidic conditions, which can not be achieved with HF. Conversely, Zr₂CT₂ (T=F and OH), and Zr₄N₃T₂ (T=O) exhibit yellow bars above a pH of seven, the pH of neutral water. Notably, Zr₂CT₂ has been reported as non-synthesizable in HF under acidic conditions (pH < 2). However, our analysis suggests that these MXenes could potentially be synthesized under basic pH conditions (7 < pH < 14), which are not accessible in HF. This finding underscores the potential for exploring the synthesis of these MXenes in alkaline solutions. For instance, alkali solutions such as potassium hydroxide have already been successfully used to prepare Ti₃C₂³⁵.

Figure 5b shows that Hf₂NT₂ (T=O) and Zr₃N₂T₂ have no yellow bars but exhibit a critical pH for V_M above a pH of seven. While these MXenes are locally stable under basic environments, they lack an exfoliable precursor MAX phase. These MXenes could be synthesized if new precursor MAX phases suitable for exfoliation are identified.

Discussion

In this work, we identified a strong correlation between vacancy formation energies, the local stability of MXenes, and the exfoliability of MAX phases in HF. Synthesized MXenes have positive vacancy formation energies for both M and X sites, while MXenes reported as non-synthesizable show negative vacancy formation energies for either M or X elements, or both. Similarly, exfoliable MAX phases exhibit negative vacancy formation energies for the A element. Using the correlation, we propose that seven out of 24 hypothetical MXenes— Nb₃C₂, Ta₃C₂, Ti₃N₂, Ti₄C₃, V₃C₂, V₃N₂, and V₄N₃—are locally stable and have an exfoliable precursor MAX phase at a pH of 2 in HF. These MXenes can likely form in HF. At higher pH values, we identified additional hypothetical MXenes, such as Zr₂C and Zr₄N₃ as locally stable and with an exfoliable precursor MAX phase in HF. However, at such pH values (pH > 7), our method is limited because of excluding oxides, which may become relevant in these conditions. The identified correlations may also guide the synthesis of other 2D materials (e.g., MBenes) via chemical exfoliation, potentially accelerating the discovery of novel 2D materials.

Methods

Computational details

DFT calculations are performed in the spin-paired state using the open-source code GPAW^36,37 within the projector-augmented wave (PAW) framework³⁸. Electronic exchange-correlation (XC) interactions are treated using the generalized gradient approximation (GGA) in the Perdew, Burke, and Ernzerhof (PBE) flavor³⁹. An energy cut-off of 700 eV is used for the plane-wave expansion of the wave functions. The reciprocal space for MAX phases and MXenes is sampled with a k-point density of 4 Å. Structural relaxations are performed by converging forces and stresses within 0.01 eV Å⁻¹ and 0.01 eV Å⁻³. For ideal structures (both MAX phases and MXenes), both the cell (planar directions only for MXenes) and atomic positions are fully relaxed during structural optimization. For defective structures containing a vacancy, only the atomic positions are relaxed; we also tested several cases with full cell and position relaxation and found that vacancy formation energies remained unchanged. For vacancy calculations in 2D MXene structures consisting of a single layer, (3 × 3 × 1) supercells are used, with a 10 Å vacuum layer along the c-axis; a dipole correction is added to avoid spurious electrostatic fields. For vacancies in MAX phases, a (3 × 3 × 1) bulk supercell is used.

Thermodynamic details

Vacancy formation energies of a particular vacancy V = V_M, V_A, or V_X in a MXene or MAX phase are calculated as,

$$\Delta {E}_{f}^{{\rm{V}}}={\Delta }_{f}{G}_{{\rm{V}}}+\Delta {\mu }_{{\rm{V}}}-{\Delta }_{f}{G}_{{\rm{ideal}}}.$$

(2)

Here, Δμ_V represents the chemical potential of the M, A, or X reservoir; Δ_fG_ideal is the Gibbs free energy of the formation of the ideal MXene or MAX phase; and Δ_fG_V is the Gibbs free energy of the formation of the defective phase. The latter two are approximated by the total DFT energy (E) without entropic contributions, i.e., Δ_fG ≈ Δ_fE. For gaseous species, entering in μ, the entropy and enthalpic contributions due to temperature at 25 °C are added to the DFT total energy. Detailed examples of the procedure used to compute vacancy formation energies for Ti₂CF₂ (Fig. S7) and Ti₃C₂F₂ (Fig. S9) along with their Al-containing MAX precursor phases, Ti₂AlC (Fig. S8), and Ti₃AlC₂ (Fig. S9) are outlined in Supplemental Section S2.

The chemical potentials of M, X, and A reservoirs are determined by the dissolved aqueous species present in the environment. For this evaluation, we followed the approach of Björk et al.³⁰. Dissolved species of an element in the presence of H and F are considered, with data sources from the NIST-JANAF thermochemical and ATLAS Pourbaix databases^40,41. Oxygen-containing species are excluded due to the limited availability of free oxygen or OH⁻¹ in HF. Solid bulk phases are also included in the evaluation, while inert gases such as methane (CH₄), and ammonia (NH₃), are excluded.

At a given pH, a species yielding the lowest chemical potential value is selected. Additional details on the determination of the M, X, and A reservoirs and the derivation of F and HF chemical potentials in terms of pH are provided in Supplemental Section S1. The procedure is applied to all the considered A, X, and M elements. Here we briefly show the procedure for titanium (Fig. S4). Titanium can exist in the dissolved state as

$$\,\text{Ti}+3{\text{H}}^{+}\rightleftharpoons {\text{Ti}}^{[3+]}+3/2{\text{H}}_{2}$$

(3)

or

$$\,\text{Ti}+2{\text{H}}^{+}\rightleftharpoons {\text{Ti}}^{[2+]}+{\text{H}}_{2}.$$

(4)

These equations can be used to evaluate the chemical potential of Ti (Δμ_Ti) relative to Ti³⁺ and Ti²⁺, respectively. These quantities depend on concentration by

$$\Delta \mu ={\Delta }_{f}{G}^{o}+RT\ln c,$$

(5)

where c is the concentration of dissolved ionic species, set to 0.001 mol/l throughout the analysis. Δ_fG^o represents the standard Gibbs free energy of formation, obtained from thermochemical databases under standard conditions.

Under standard Hydrogen electrode conditions, ${\Delta }_{f}{G}_{{{\rm{H}}}_{2}}$ is always zero. The chemical potential of H⁺ ($\Delta {\mu }_{{{\rm{H}}}^{+}}$) depends on its concentration and, consequently, on pH. In our first part of the analysis, we set pH to a value of 2, fixing this parameter for the evaluation.

The Gibbs free energy change of MXene formation (Δ_rG^MXene), using Ti₂CF₂ as an example,

$${{\rm{Ti}}}_{2}{\rm{AlC}}+2{\rm{HF}}\longrightarrow {{\rm{Ti}}}_{2}{{\rm{CF}}}_{2}+{{\rm{AlF}}}_{3}+{{\rm{H}}}_{2}$$

(6)

is calculated by

$$\begin{array}{rcl}{\Delta }_{r}{G}^{{\rm{MXene}}}&=&\left({\Delta }_{f}{G}_{{\rm{MXene}}}+{\Delta }_{f}{G}_{{{\rm{AlF}}}_{3}}+{\Delta }_{f}{G}_{{{\rm{H}}}_{2}}\right.\\ &&-\left.{\Delta }_{f}{G}_{{{\rm{Ti}}}_{2}{\rm{AlC}}}-2\Delta {\mu }_{{\rm{HF}}}\right)/{N}_{{\rm{MAX}}},\end{array}$$

(7)

Here, ${{\rm{N}}}_{{\rm{MAX}}}$ denotes the total number of atoms in the chemical formula of a MAX phase, and Δμ_HF is the chemical potential of HF, which depends on pH and falls within an accessible range. Further details on the evaluation of Gibbs free energy changes for Ti₂CF₂ (Fig. S13) along with Cr₂CF₂ (Fig. S14) are provided in Supplemental Section S3.