First-principles investigation of the resistive switching energetics in monolayer MoS₂: insights into metal diffusion and adsorption

Abstract

A deeper understanding of resistive switching (RS) in 2D materials is essential for advancing neuromorphic computing. The Dissociation-Diffusion-Adsorption (DDA) model offers a useful framework for probing RS mechanisms in non-volatile memory (NVM) and in-memory computing. We have employed first-principles density functional theory (DFT) to explore dissociation, diffusion, and adsorption phenomena within the DDA model, focusing on the interactions between exemplary metal atoms (Au, Ag, Cu) and monolayer MoS₂. Nudged elastic band (NEB) calculations evaluated diffusion barriers in pristine and sulfur-vacancy MoS₂. Charged systems were modeled to assess the impact of applied bias on migration pathways. We also examined metal dissociation from bulk electrodes and adsorption at S vacancies. Ag/MoS₂ shows the lowest dissociation barrier (~0.034 eV), while Au and Cu exhibit similar values (~0.32 eV). These insights highlight Ag as a promising candidate for low-energy RS applications and provide guidance for optimizing switching efficiency in 2D memory devices.

Introduction

The increasing demand for energy-efficient and scalable data storage has spurred interest in emerging non-volatile memory (NVM) technologies. Among these, resistive switching devices, including memristors, have shown promise due to their potential for low power consumption and high integration density¹. During the switching process, memristors transition between a high-resistance state (HRS, “OFF”) and a low-resistance state (LRS, “ON”)^2,3. In conventional memristors, the forming process typically requires a high voltage during the initial cycle to transition the device from HRS to LRS, with at least a 1 V difference between the switching voltages of the first two cycles⁴. By contrast, memristors based on 2D monolayers, such as MoS₂ and h-BN, exhibit unique features, including forming-free switching with operating voltages as low as 0.2 V^5,6,7. For instance, Yang et al. recently demonstrated switching at ~0.2V in a h-BN monolayer sandwiched between silver electrodes⁶. Although 2D material-based memristors are still in the early stages of development, understanding their switching mechanisms at the atomic scale is critical for advancing their future applications.

Several experimental and computational studies have demonstrated the potential of 2D monolayers for non-volatile memory (NVM) applications⁸. In conventional resistive random-access memory (RRAM) devices, resistive switching can occur through various mechanisms. These include the formation of conductive filaments via oxygen ion migration in oxides, switching between ferroelectric and paraelectric states in ferroelectric RAM (FRAM), or phase transitions between amorphous and crystalline states in phase change RAM (PCRAM)^9,10. Such mechanisms are well-established for memristors based on 3D materials⁴. In contrast, the switching processes in 2D materials remain an active area of research due to unique features such as forming-free switching, inconsistent evidence of conductive filament formation, and uncertainties regarding atomic-level structures. These challenges can hinder a comprehensive understanding of the switching mechanisms⁴. Nevertheless, various studies suggest that metal adsorption plays a critical role in initiating RS in 2D material-based devices.

For monolayer 2D materials, various mechanisms have been proposed to explain non-volatile resistive switching (NVRS). For instance, a recent study on multilayer h-BN memristors demonstrated RRAM-like behavior with a non-polar switching mechanism based on conductive filament formation¹¹. In contrast, for monolayer h-BN, Wu et al. reported both unipolar and bipolar switching without the need for a forming voltage (the high initial voltage required to transition the device to a low-resistance state)⁵. They attributed the switching behavior to the presence of vacancy sites, which facilitate the formation of conductive bridges, thereby enabling device switching.

Among 2D materials, transition metal dichalcogenides (TMDCs) have garnered significant interest for non-volatile memory applications. TMDCs have the general chemical formula MX₂, where M represents a transition metal (e.g., Mo, W, Re) and X is a chalcogen (e.g., S, Se). These materials exhibit semiconducting behavior and have been investigated for NVRS mechanisms like those observed in other 2D materials⁸. Among these TMDCs, molybdenum disulfide (MoS₂) has emerged as a promising candidate for non-volatile memory devices^12,13,14,15.

Monolayer MoS₂-based memory devices have been reported to exhibit enhanced memory characteristics, yet the RS mechanisms for monolayer TMDCs and other 2D materials remain a subject of ongoing research, with multiple mechanisms proposed^12,16,17,18. Wu et al. demonstrated non-volatile memory devices based on monolayer TMDCs - such as MoS₂, MoSe₂, WS₂, and WSe₂ - with gold electrodes, exhibiting forming-free switching behavior. They attributed the switching mechanism to the migration of gold atoms from the electrode to sulfur vacancy sites. When gold atoms adsorb at these vacancy sites, the device transitions to a low-resistance state (LRS)¹⁹. Notably, these sulfur vacancies are commonly present after the fabrication process, eliminating the need for a high forming voltage to initiate switching cycles. Mitra et al. explored the formation of a virtual filament in monolayer MoS₂ using classical molecular dynamics (MD) simulations. Their study revealed that sulfur atoms opposite to vacancy sites pop out and adjust within the molybdenum layer, creating localized metallic states that exhibit NVRS behavior²⁰. Building on this work, Mitra et al. extended their investigation to multilayer h-BN and MoS₂ using atomistic simulations. By incorporating metal electrodes such as gold, they analyzed metal atom migration through grain boundaries, which led to the formation of conductive bridges. Using metal-insulator-metal (MIM) structures and molecular dynamics (MD) calculations, they examined bond lengths, interface distances, and gold atom adsorption at various sites in MoS₂ under high applied voltages (0–20 V). Their simulations also demonstrated that gold atom migration occurs between the two metal layers through grain boundaries in MoS₂²¹. Li et al. employed the Keldysh non-equilibrium Green’s Function (NEGF) theory to simulate the current-voltage (I-V) characteristics of monolayer MoS₂, MoTe₂, and WSe₂. They investigated atomic migration and electronic transport properties in a MoS₂-based atomristor. Their findings revealed a two-step switching mechanism: first, gold atom dissociation from the electrode, followed by adsorption at a vacancy site within the monolayer MoS₂. These results highlight the crucial role of vacancy defects in governing the switching behavior of the device²².

Anvari et al. studied the interaction between Au(111) and MoS₂ heterostructures to simulate the gold substrate behavior with MoS₂ with density functional theory. Their analysis revealed how interfacial strain caused by lattice mismatch influences vacancy formation energies and the adsorption/desorption energies of Au-defect complexes. They observed that tensile strain in MoS₂/Au(111) heterostructures increases vacancy formation energy while lowering the adsorption/desorption energies of Au-adatom complexes, thereby favoring Au-adatom adsorption. Notably, moderate strain levels enhanced the switching ratio, but excessive strain suppressed the electronic states of the Au-adatom, reducing conductivity changes in the ON state²³. Ge et al. measured resistive switching (RS) behavior in a dozen 2D monolayers, including MoS₂, MoSe₂, MoTe₂, and WS₂, from the transition metal dichalcogenides (TMDC) group. They reported that RS occurs as metal atoms act as conductive points by adsorbing into chalcogen vacancy sites (e.g., S, Se, or Te vacancies)^7,24. To describe this phenomenon, they introduced the dissociation, diffusion, and adsorption (DDA) model, which explains how metal atoms dissociate from a bulk layer, diffuse along the 2D surface, and ultimately adsorb into vacancy sites, triggering device switching.

While many studies have explored RS in 2D materials, most have focused on devices with a single type of metal electrode, such as Ni/h-BN/Ni, Au/MoS₂/Au, or Ag/h-BN^25,26. This leaves a significant gap in understanding how the selection of the electrode material influences RS mechanisms. Key questions remain unanswered: How does the chemical identity of the electrode affect switching behavior? To what extent do interfacial interactions between the metal electrode and 2D material influence the resistive switching process? To address these questions, our research systematically investigates the impact of different group 11 metal electrodes—copper, silver, and gold—on the RS characteristics of MoS₂-based devices. We aim to explore how electrode material, defects, and charge transport mechanisms collectively shape the switching behavior. To further this understanding, we simulate the dissociation, diffusion, and adsorption processes of metal adatoms on MoS₂, aligning with the Dissociation-Diffusion-Adsorption (DDA) model. Our simulations include isolated metal adatom-MoS₂ structures and metal/MoS₂ heterostructures to analyze the diffusion of metal atoms from the bulk electrode and their adsorption into vacancy sites. By comparing the behavior of gold, silver, and copper adatoms, we elucidate how the choice of electrode material influences RS. These findings will provide critical insights into optimizing device performance, guide experimental efforts in selecting electrode materials for specific applications, and advance the design of next-generation NVM devices.

We outline the Dissociation-Diffusion-Adsorption (DDA) model to describe the resistive switching (RS) mechanism in 2D materials, using MoS₂/Au as an example. In this model, the transition of the device from the high-resistance state (HRS) to the low-resistance state (LRS) occurs in three steps: (1) a gold atom dissociates from the bulk electrode layer when a voltage is applied, (2) the atom diffuses along the surface of the MoS₂ monolayer, and (3) it adsorbs into a sulfur vacancy site⁷. While metal atom adsorption in vacancies has been studied for various 2D materials, research on the diffusion step has primarily been focused on gold atoms^7,27. Questions remain about how the energy barriers and diffusion process are influenced by different metal atoms. Moreover, the existence of multiple potential diffusion trajectories in 2D monolayers necessitates a detailed analysis to understand the factors that contribute to variations in switching voltages.

We hypothesize that the diffusion of metal atoms along the interface and surface is a crucial factor in the switching process. Barrier energies for diffusion are likely to vary based on factors such as the presence of sulfur vacancies and electrostatic charge effects. To refine the DDA model, we examine monolayer MoS₂ with three metals (Au, Ag, and Cu), chosen for their widespread use in electronic devices and compatibility with a standard fabrication technique^7,13. Two types of structures are analyzed: (1) monolayer MoS₂ with a single metal adatom and (2) heterostructures of monolayer MoS₂ with bulk metal layers. Figure 1a presents the side and top views of MoS₂ with a metal adatom, while Fig. 1b-d depict heterostructures for Au/MoS₂, Ag/MoS₂, and Cu/MoS₂, respectively.

Fig. 1: Structural models for MoS₂ and metal systems.

a Side and top views of a monolayer MoS₂ with metal atom adsorbed at the surface, Side and top views of heterostructure configurations for metal/MoS₂ systems: (b) Au/MoS₂, (c)Ag/MoS₂, and (d) Cu/MoS₂. Figure 1a shows the structure investigated for the diffusion of metal adatoms on monolayer MoS₂ along different trajectories. Figure 1b–d shows the heterostructures used for investigating the dissociation of the metal atom from the bulk layer and its consequent adsorption at the S vacancy. The relaxed interlayer distances between the metal layer and MoS₂ were determined to be 2.56 Å for Au/MoS₂, 2.76 Å for Ag/MoS₂, and 2.3 Å for Cu/MoS₂, consistent with reported literature^21,23,33,37.

This paper is organized as follows. First, we provide a detailed analysis of the trajectories for metal atom diffusion, starting with the adsorption sites available on MoS₂. Secondly, we analyze metal/MoS₂ heterostructures by simulating the migration of metal atoms from their respective position in the bulk structure to that at the S vacancy in MoS₂. Building upon these calculations, we interpret the DDA model in the context of switching energy, offering a more comprehensive explanation than previous studies.

Results

Adsorption site analysis for metal atoms on MoS₂ monolayer

For the analysis of the MoS₂ monolayer system, we first examine the different adsorption sites available for a metal adatom on the pristine, free-standing monolayer surface. The preferential adsorption sites determined here will be used to map the diffusion pathways of each of the adsorbate species. The potential adsorption sites for a metal atom on MoS₂ include: (i) topS (adsorption on top of the sulfur atom), (ii) topMo (adsorption on top of the molybdenum atom), (iii) hollow (adsorption site over the center of the hexagon), and (iv) bridge (adsorption site over the midpoint of the Mo-S bond), as shown in Fig. 2a–d and following previous labeling conventions²⁸. The identification of the optimal adsorption sites is crucial to determine favorable and unfavorable sites for metal atom adsorption.

Fig. 2: Structural configuration of metal atoms (Au, Ag, Cu) on various adsorption sites of Monolayer MoS₂.

a top S, b top Mo, c hollow, d bridge, e–g display adsorption energies at different sites for e Au, f Ag, and g Cu, comparing two relaxation methods: “Free-xyz” (all x-, y-, and z-coordinates relaxed) versus “Fixed-xy & Free-z” (only z-coordinate relaxed). Figure 2a–d depict the adsorption sites on the pristine monolayer MoS₂. Adsorption energies vary between the relaxation methods, highlighting the preference of specific metals for distinct sites. Gold shows the most stable adsorption on the topS site, while silver prefers the hollow site, and copper favors the topMo site. The difference in energy between the stable site and hollow site is observed to be ~0.021 eV <kT and ~0.057 eV ~2kT for Au and Cu, respectively. In this regard, Au and Cu adsorption on MoS₂ can be considered quite versatile as the difference in adsorption energies at three of the four sites are on the order of kT.

We focus on three metal atoms—gold (Au), silver (Ag), and copper (Cu)—which are chosen due to their noble metallic nature and widespread use as electrode/metallic layers in non-volatile memory (NVM) devices^8,26,29. To explore the optimal adsorption sites for each metal atom, we performed two types of relaxation: (i) free relaxation (labeled as free-xyz in Fig. 2e–g), where all atomic coordinates are allowed to relax, and (ii) fixed relaxation (labeled as fixed-xy & free z in Fig. 2e–g), where only the z-coordinate is allowed to relax, and the x and y coordinates remain fixed. These relaxation methods are referred to as “free” and “fixed”, respectively. Figure 2e–g display the adsorption energy (${E}_{{ad}}$) versus adsorption site plots for both free and fixed relaxation types.

For computing the adsorption energy, the following equation is used:

$${E}_{{ad}}={E}_{m}-{E}_{p}-{\mu }_{m}$$

(1)

where ${E}_{{ad}}$ is the energy required for the adsorption of metal adatom at the site, ${E}_{m}$ is the energy of the structure with adsorbed metal adatom, ${E}_{p}$ is the energy of pristine MoS₂ structure and ${\mu }_{m}$ is the energy of the metal adatom referenced to bulk energy of the individual metal atom. From the analysis of Fig. 2e–g, the adsorption energies are observed to be in the range of 2.53-2.66 eV, 2.03–2.23 eV, and 2.16–2.79 eV for Au, Ag, and Cu, respectively. The topS site is the most stable adsorption site for gold, whereas the topMo site is the least stable, with an energy difference of approximately 0.13 eV. For silver, the hollow site is the most favorable, while for copper, the topMo site is preferred. These adsorption site preferences are consistent with previous literature^30,31. Notably, when comparing the results between the free and fixed relaxation configurations, a significant shift in the atomic co-ordinates is observed for the adsorption of gold at the bridge and hollow sites. In both cases for bridge and hollow sites, gold (Au) relaxes closer to the topS site during free relaxation (Fig. S1). Similarly, for silver (Ag) and copper (Cu), the adatoms tend to relax towards the topMo site during free relaxation of the bridge site, rather than remaining at the bridge site, as depicted in Fig. S2 and S3.

Continuing with the analysis of adsorption energies, we next examine the bond lengths. The details of the adsorption energies, bond lengths, and bond angles for various adsorption sites in both free and fixed relaxations are presented in Tables S1–S4. The bond lengths for gold, silver, and copper adatoms range from 2.3 to 2.8 Å, 2.4 to 2.76 Å, and 2.24 to 2.29 Å, respectively, for both relaxations. Notably, for gold, the bond length at the topMo (for free and fixed relaxation) and fixed hollow sites is around 2.7–2.8 Å. Notably, for gold, the shortest bond length of ~2.34 Å is observed at the topS site, which also corresponds to the most stable adsorption site. This indicates a strong interaction and supports the identification of topS as the optimal site. For silver, the bond length is approximately 2.7 Å across most adsorption sites, except at the topS site (in both fixed and free relaxations) and the bridge site under free relaxation, where the bond length is closer to 2.4 Å. Nevertheless, the hollow site is energetically preferred, suggesting that symmetrical coordination plays a dominant role. For copper, the bond lengths at the topMo, hollow, and bridge sites range from 2.24 to 2.29 Å, while the shortest bond length of ~2.13 Å is observed at the topS site in both free and fixed relaxations. However, despite this shorter bond length, the topMo site shows stronger adsorption energy, indicating that bond length alone does not determine site stability. Instead, the optimal adsorption site results from a combination of factors, including local atomic coordination and charge distribution. These results emphasize that while shorter bond lengths generally imply stronger binding, the optimal adsorption site emerges from the interplay of geometric configuration, local electronic structure, and adsorption energy. To summarize the analysis of the optimal sites, we find that the topS is most favorable for gold, hollow for silver, and topMo for copper.

To understand the preference for different adsorption sites among the metals Au, Ag, and Cu, we visualize the charge density of the adsorbed structures by calculating the difference between the metal-adsorbed structure and the pristine MoS₂ surface. Despite the chemical similarities among these metals, their adsorption behaviors differ significantly. For Au, most of the charge is retained around the gold atom, with some redistribution observed around a few Mo atoms (Fig. S4a). In contrast, for Ag and Cu, the charge is more distributed towards the Mo sites, as shown in Fig. S4b and S4c, respectively. Notably, both Ag and Cu retain minimal charge compared to Au. This distinct charge distribution pattern is likely a key factor in determining the preferred adsorption sites, bond lengths, and subsequent diffusion pathways of these metal adatoms on the MoS₂ surface. This information will be crucial for analyzing the diffusion pathways of different metal adatoms on the MoS₂ surface in “Diffusion on MoS₂”.

Diffusion on MoS₂

Through a systematic enumeration of the possible diffusion paths, we find that the diffusion path is closely linked to the stability of adsorption sites. A detailed discussion of the criteria for pathway selection can be found in the Supplementary Information (Figures S5–S8). To understand the minimum energy pathway (MEP) for metal adatom diffusion on the MoS₂ surface, we identified five unique pathways, as illustrated in Fig. 3a. Each pathway in Fig. 3a is defined as follows:

• P_S: Diffusion occurs between two adjacent topS sites.

• P_H: Diffusion occurs between two adjacent hollow sites.

• P_M: Diffusion occurs between two adjacent topMo sites.

• P_SMH: A mixed-site pathway where the metal adatom moves from a topS site to a topMo site, as well as passing through a hollow site.

• P_MSH: A mixed-site pathway where the adatom moves from a topMo site to a topS site, also passing through a hollow site. The distinction between P_SMH and P_MSH arises due to the asymmetry in their diffusion trajectories.

Fig. 3: Diffusion pathways and energy barriers for metal atoms on pristine and defective Monolayer MoS₂.

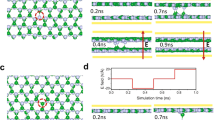
a Diffusion pathways analyzed for metal atoms (Au, Ag, Cu) on MoS₂ in pristine and sulfur vacancy configuration. b Example of metal atom diffusing along pristine MoS₂ surface showing a side view and top view. c Example of metal atom diffusing towards S vacancy on MoS₂ surface showing a side view and top view. Energy vs reaction co-ordinate graph for diffusion on pristine and S vacancy structures of MoS₂ for d gold along P_S, e gold along P_S-Vs, f silver along P_H, g silver along P_H, h copper along P_M and, i copper along P_M-Vs. Diffusion pathways in pristine MoS₂ are labeled as P_S, P_H, and P_M, while S vacancy pathways are denoted as P_S-Vs, P_H-Vs, and P_M-Vs. (Insets show the structure with metal atom diffusion on MoS₂, a black arrow indicating diffusion direction, Purple = Mo, Yellow = S, Teal = Metal atoms, Orange = Au, Gray = Ag, Blue = Cu, Red Circle = Vacancy). Figure 3 illustrates the structural evolution of metal atoms as they traverse different adsorption sites, providing insights into their preferred diffusion routes. The energy barrier analysis highlights how the presence of an S vacancy influences the diffusion process compared to pristine MoS₂.

To distinguish between pristine and vacancy-assisted diffusion paths, we adopted a systematic naming convention: pristine diffusion paths are labeled as P_S, P_H, P_M, P_SMH, and P_MSH, while vacancy-assisted diffusion paths include an additional “Vs” suffix (e.g., P_S-Vs, P_H-Vs). The energy barriers for these pathways are listed in Table 1. Figure 3b shows a representation of the side view and top view of diffusion along the pristine MoS_2, while Fig. 3c shows the side view and top view of diffusion towards a S vacancy site. A more comprehensive discussion of diffusion along each pathway is provided in the Supplementary Information, with Fig. S9 illustrating the NEB energy profiles for these pathways. The focus here remains on the minimum energy pathways for diffusion on both pristine and vacancy-defected MoS₂.

Table 1 List of Energy barriers for the diffusion of Au, Ag, and Cu along different paths on the pristine MoS₂ surface and the MoS₂ surface with S vacancy

The diffusion of each metal atom is closely linked to the stability of its adsorption sites. The topS site is the most favorable for gold, followed closely by the hollow site, while topMo is highly unfavorable. As a result, diffusion across P_M is unlikely. Among the considered pathways, P_S exhibits the lowest energy barrier of ~0.07 eV, which remains unchanged when diffusion occurs toward an S vacancy along P_S-Vs-Au (Fig. 3d, e).

For silver adatoms, diffusion primarily occurs along P_H, P_MSH, and P_SMH. Since the hollow site is the most stable adsorption site, the energy barrier for P_H is the lowest at 0.076 eV, while for P_H-Vs, the barrier is slightly reduced to ~0.07 eV (Fig. 3f, g). Diffusion along P_H follows a zigzag trajectory, moving from one hollow site to a topMo site and then to another hollow site, making it somewhat comparable to P_M. Conversely, diffusion along P_S is highly unfavorable for Ag, as topS is its least stable adsorption site.

For copper adatoms, diffusion along P_M follows a slightly zigzag trajectory, similar to Ag diffusion along P_H, and exhibits the lowest energy barrier of ~0.251 eV (Fig. 3g). Diffusion towards an S vacancy via P_M-Vs presents a slightly higher barrier of ~0.371 eV. Unlike Au and Ag, diffusion along P_S and P_S-Vs is the least favorable for Cu. As observed with the diffusion of Au and Ag, Cu diffusion follows its most stable site, topMo, making P_M its preferred pathway.

In Table 1, energy barriers for certain diffusion trajectories of Au, Ag, and Cu are not reported because the MEP relaxes into an alternative path. A similar issue arises with P_MSH-Vs for Ag and Cu diffusion, where calculations fail to converge. Notably, P_M and P_H exhibit similar behavior for Ag and Cu after relaxation. Therefore, P_H is chosen for Ag and P_M for Cu to avoid redundancy and emphasize the primary diffusion pathways. Figure 4a and b shows a bar graph illustration for the energy barrier along the different diffusion pathways on pristine and S vacancy MoS₂ for Au, Ag, and Cu. The calculated energy barriers for the MEP’s are consistent with values reported in the literature, generally falling within a reasonable range of ~0.1 eV^30,31,32,33.

Fig. 4: Energy barrier for metal atom diffusion on pristine and defective Monolayer MoS₂.

a Bar graph of energy barriers vs diffusion paths for metal adatoms (Au, Ag & Cu) on pristine MoS₂ surface, P_S, P_H, and P_M are the preferred pathways for the diffusion of Au, Ag, and Cu, respectively. b Bar graph of energy barriers vs diffusion paths for metal adatoms (Au, Ag & Cu) on MoS₂ surface with a sulfur vacancy nearby. c Bar graph illustrating the energy barriers for the diffusion of gold, silver, and copper along minimum energy pathways (MEPs) on pristine MoS₂ and S-vacancy structures under neutral, positively charged, and negatively charged conditions. NEB calculations show that for diffusion towards a vacancy, all three metals prefer the negatively charged system, while for pristine diffusion, gold and copper favor the negatively charged system, whereas silver prefers the positively charged system, which directly correlates with the preference for adsorption sites on MoS₂ for the different charged systems. P_S-Au, P_H-Ag, P_M-Cu labels path for pristine diffusion on MoS₂. P_S-Vs-Au, P_H-Vs-Ag, P_M-Vs-Cu labels the path for diffusion in the vicinity of a S vacancy in MoS₂.

The diffusion behavior of Au, Ag, and Cu is closely tied to their preferred adsorption sites. As a metal atom dissociates from a bulk structure and diffuses across the MoS₂ surface, it follows the MEP until reaching a vacancy site, where it ultimately adsorbs. For instance, gold primarily migrates between topS sites, silver follows a trajectory between hollow sites, and copper moves along a zigzag pathway between topMo sites, passing through hollow sites along the way. Notably, diffusion pathways that involve hollow sites tend to be either the most favorable or the second most favorable, suggesting that the hollow site plays a crucial role in facilitating metal adatom diffusion on MoS₂.

Energy barrier trends for diffusion in charged and neutral systems

The presence of charge impacts the diffusion barriers, with the presence of additional electrons tending towards the lower barrier and the presence of holes tending towards higher barriers. So far, we have identified the MEPs for neutral metal adatom diffusion. In this section, we investigate the diffusion of charged metal adatoms along these pathways. By simulating diffusion in both positively and negatively charged systems, we assess the impact of an applied electric field on the energy barriers, providing insights into how external stimuli modulate diffusion kinetics. While charged adatoms may not be stable defects under normal conditions, their transient presence during the switching process can significantly influence device behavior. Additionally, an external electric field can induce charge separation, leading to the formation of transient charged species. Studying the diffusion of these charged adatoms allows for a deeper understanding of the mechanisms governing RS in 2D materials. For this analysis, NEB calculations were performed on the lowest energy barrier pathways identified in “Diffusion on MoS₂”: P_S and P_S-Vs for gold, P_H and P_H-Vs for silver, and P_M and P_M-Vs for copper. The notation P_S, P_M, etc., refers to diffusion on pristine MoS₂, while P_S-Vs, P_M-Vs, etc., indicate diffusion in the presence of a sulfur vacancy. Figure S10 presents the energy vs. reaction coordinate graphs for these pathways in both pristine and sulfur-vacancy-defected MoS₂ involving adatoms in neutral, positive, and negative charge systems. A comparison of energy barriers across the different charge systems is shown in Fig. 4c, while the corresponding values are listed in Table S5 in the Supplementary Information. A discussion on preferred adsorption sites for metal adatoms on pristine MoS₂ is presented in the Supplementary information, where Fig. S11 shows the trends for adsorption energies across different adsorption sites for Au, Ag, and Cu.

Figure S10a illustrates the diffusion of gold along P_S. Although the diffusion trajectory remains visually similar across neutral, positive, and negative charged systems, the energy of Au at non-topS sites varies, indicating charge-dependent stabilization effects. Next, we compare the diffusion barriers between pristine MoS₂ and MoS₂ containing a sulfur vacancy. Figure S10b shows that while P_S follows a consistent trajectory, the energy barriers differ across the charged systems. Given that sulfur typically carries a partial negative charge, the energy barrier for metal diffusion on pristine MoS₂ is highest for the positively charged system (~0.11 eV) compared to the neutral (~0.07 eV) and negatively charged (~0 eV) systems. A similar trend is observed for P_S-Vs, where the positively charged system exhibits a higher barrier (~0.23 eV), while the negatively charged system has the lowest barrier (~0 eV). Figure S11a suggests that the relative stability of topS and hollow sites directly influences the diffusion barrier, with a larger energy difference leading to an increased energy barrier for diffusion. Overall, gold diffusion along P_S and P_S-Vs is significantly influenced by the presence of charge, with lower barriers observed in negatively charged conditions and higher barriers in positively charged environments (Fig. 4c).

For the trajectories of Ag along P_H and P_H-Vs, the negatively charged system exhibits the lowest energy barrier along P_H-Vs (~0.03 eV). The positively charged system shows a lower barrier (~0.06 eV) for P_H but a higher barrier (~0.13 eV) for P_H-Vs, compared to the neutral system (~0.076 eV and ~0.07 eV, respectively) (Fig. 4c). From Fig. S10c, we observe that for P_H, the negatively charged system has a higher energy barrier (~0.11 eV) compared to the neutral (~0.07 eV) and positively charged system (~0.06 eV). In contrast, for P_H-Vs, the negatively charged system corresponds to the lowest energy barrier (~0.03 eV) for silver diffusion toward the sulfur vacancy (Fig. S10d). An important observation is that while silver adsorbs into a vacancy in the positively charged system, it relaxes into a hollow site in the neutral system, which is the most favorable adsorption site for Ag. From Fig. S11b, we observe the higher difference in adsorption energy between the adsorption sites of hollow and topMo in negatively charged system as compared to neutral and positively charged systems. This trend correlates with the diffusion energy barrier observed for Ag along P_H in these charged states.

For copper, diffusion across pristine MoS₂ along P_M follows a trend similar to gold, where the energy barrier increases for the positively charged system by ~0.14 eV and decreases for the negatively charged system by ~0.1 eV (Fig. 4). A similar trend is observed for diffusion in the vacancy-containing structure along P_M-Vs, where the energy barrier increases by ~0.11 eV for the positively charged system and decreases by ~0.05 eV for the negatively charged system. Overall, the negatively charged system exhibits enhanced diffusion compared to both the neutral and positively charged systems. From Fig. S10e and S10f, we observe that while the pathways and trajectories for P_M and P_M-Vs remain similar, the energy landscape for diffusion varies significantly between the neutral, positively charged, and negatively charged systems.

In summary, the diffusion of metal adatoms in charged systems exhibits distinct trends compared to neutral systems, with energy barriers being significantly influenced by the presence of charge in the system. In MoS₂, sulfur atoms typically carry a negative charge, and their absence creates a vacancy that alters the local charge environment due to the localized dangling bonds³⁴. As a metal adatom diffuses across the MoS₂ surface, it adjusts its trajectory in response to the electrostatic interactions with Mo and S sites. The chalcogen vacancy preferentially adsorbs negatively charged adatoms, which aligns with the observed trend of lower diffusion barriers for negatively charged species^27,34,35. Conversely, positively charged adatoms experience stronger electrostatic repulsion near Mo sites, resulting in increased diffusion barriers. The presence of charged species, especially under the influence of external electric fields, further modulates diffusion kinetics, potentially impacting resistive switching behavior in 2D materials. Overall, positively charged systems generally exhibit higher energy barriers, whereas negatively charged systems tend to diffuse more easily, highlighting the role of charge interactions in governing atomic transport on MoS₂. To gain a deeper understanding of how the charge influences the diffusion process, we now turn to the Bader charge and charge density analysis of gold adatoms diffusing along P_S-Au and P_S-Vs-Au, focusing on the variations in charge distribution across different charge states.

Our calculations show different extents of charge localization around the adsorbate depending on the presence of charge in the system. To further investigate the impact of the charge on the energy barrier, we calculated the Bader charges of the metal adatom relative to the neutral atom for each point along the diffusion path. We use the gold atom diffusing along P_S and P_S-Vs for neutral, positive, and negative systems on MoS₂ as an example (Fig. S12). A positive change in the Bader charge indicates electron deficiency, while a negative change in the Bader charge signifies electron excess. Figure S13 provides a bar graph comparing the Bader charges of the adatom for the neutral, positive, and negative systems. For the neutral system, the gold atom initially carries a more negative charge along P_S, which fluctuates as it traverses the path, correlating with the energy profile (Fig. S12a). Along P_S-Vs, the gold atom maintains a negative charge throughout the diffusion process, with the highest charge observed for the adsorption of gold at the S vacancy site (Fig. S12d).

In the positively charged system, the gold atom exhibits a more positive charge along both P_S and P_S-Vs, i.e., diffusion along pristine and S vacancy MoS₂ (Fig. S12b, S12e). Along P_S-Vs, the charge decreases as the gold atom moves away from the sulfur atom and increases as it approaches the vacancy site. Ultimately, the gold atom still acquires a negative charge upon adsorption. For the negatively charged system, the gold atom initially carries a negative charge along both P_S and P_S-Vs (Fig. S12c, S12f). However, it struggles to maintain this charge during the diffusion process. At the final adsorption site, the gold atom adopts a more negative charge relative to the neutral atom in both the charge configurations for P_S-Vs.

We plot the charge density difference of the gold adsorbed at the sulfur vacancy in the neutral system with respect to the positively and negatively charged systems, shown in Fig. S14a and S14b, respectively. We observe that there is a greater charge density distribution in the final structure for the negatively charged system than for the positively charged system. In addition, the charge seems to be concentrated around the adsorption site for the negatively charged system (Figure S14a), while for the positively charged system (Fig. S14b), the charge is spread out. These findings underscore the pivotal role of charge in influencing the diffusion behavior and adsorption configurations of metal adatoms on MoS₂. By considering different charged systems, we gain a more nuanced understanding of electronic interactions and how atomic migration contributes to resistive switching mechanisms in 2D materials. With these insights, we now turn our focus to investigating the energy barriers for metal atom diffusion in metal/MoS₂ heterostructures, exploring how the presence of metal layers modifies the energy landscape and potentially enhances or hinders the diffusion process.

Energy barrier calculations for dissociation and adsorption in metal/MoS₂ heterostructures

The diffusion behavior of metal adatoms varies in both the diffusion paths and energetics depending on the properties of the individual metals. In the case of direct dissociation from the bulk electrode and the migration of the metal atom to the nearest sulfur vacancy does not necessarily involve a diffusion barrier. To explore this process further, we examine the metal/MoS₂ heterostructures, focusing on the dissociation and adsorption of the metal atom from the bulk layer into a vacancy within the monolayer MoS₂. Figure 5a presents the pristine heterostructure of metal/MoS₂, referred to as the pristine heterostructure. The structures for Au, Ag, and Cu with MoS₂ were constructed using the Interface Builder tool in QuantumATK, which facilitates efficient computation³⁶. The QuantumATK Interface Builder enables the creation of intricate interfaces by automatically aligning the 2D unit cells of two dissimilar surfaces and assessing the resulting strain. To minimize the strain, we selected the lowest-strain structure generated by the Interface Builder for subsequent relaxation. The atomic coordinates of these structures were then allowed to relax fully. The interfacial distance was determined to be 2.56 Å for Au/MoS₂, 2.76 Å for Ag/MoS₂, and 2.3 Å for Cu/MoS₂, aligning well with previously reported values^21,23,33,37. Figure 5b depicts the structure with a sulfur vacancy in the MoS₂ layer, referred to as Structure 1, while Fig. 5c illustrates the metal atom adsorbed at the vacancy site, referred to as Structure 2. NEB calculations are then conducted, where Structure 1 is the initial configuration and Structure 2 is the final configuration.

Fig. 5: Energetics and Charge for Heterostructure configurations of Monolayer MoS₂ and metal (Au, Ag, Cu) interface.

a Pristine metal/MoS₂ Heterostructure. b Structure 1: MoS₂ monolayer with a S Vacancy. c Structure 2: metal atom adsorbed at S Vacancy in the MoS₂ monolayer. d, e NEB results for the transition from structure 1 to structure 2 in the heterostructure for gold, copper, and silver. d Barrier Energy vs. reaction co-ordinate graph with an inset showing structural visualization of the diffusion path, where the inset shows the trajectory of the metal atom from bulk layer to S vacancy site, and e Bader charges of the metal atom at each co-ordinate along the diffusion path. Profile for the difference of charge density between structure 1 and structure 2 for f gold, g silver, and h copper (teal = metal atom, yellow = S, purple = Mo, red = Vacancy, gold = Au, Silver/gray =Ag, Blue = Cu). Structure 1 and Structure 2 are used as initial and final configurations in the NEB calculations. Ag/MoS₂ had the lowest energy barrier for the transition from structure 1 to structure 2, ~0.03 eV, while Au/MoS₂ and Cu/MoS₂ had energy barriers of 0.323 eV and 0.318 eV, respectively. Charge density difference plots show that while Ag/MoS₂ has a localized charge distribution and Au/MoS₂ and Cu/MoS₂ have a distributed charge density profile.

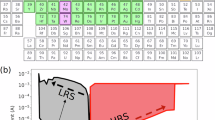
Figure 5d presents the NEB calculation results for the dissociation of gold, silver, and copper from their respective bulk structures, followed by adsorption into a sulfur vacancy site. The metal atom with the closest in-plane (xy) coordinates to the sulfur vacancy was selected to visualize the effect of an applied voltage triggering the dissociation and adsorption process. The overall trend reveals that, for gold, the energy initially increases after dissociation, reaching a maximum transition state energy. After this peak, the energy steadily decreases as the gold atom adsorbs into the vacancy site. For silver, the increase in energy is minimal compared to the transition state energies of both gold and copper. While copper exhibits a comparable energy barrier to that of gold (with a difference of only 5 meV), copper has a final adsorption energy that is slightly higher than the adsorption energy of gold by ~0.28 eV. Among the three metals, silver displays the lowest energy barrier of approximately 0.035 eV and the most negative adsorption energy.

The calculated energy landscape shown in Fig. 5d also provides some important insights into the adsorption stability of metal atoms at the vacancy site. For silver, the energy barrier from the metal surface to the vacancy site on MoS₂ is about 0.034 eV. However, in the reverse process where silver would return to the metal surface, the barrier for the Ag atom is significantly higher (~0.33 eV). This suggests that Ag is more energetically stable on the vacancy site and remains even after the removal of the external electrical bias, leading to nonvolatile switching. In contrast, for Au, the final adsorption energy is only slightly lower than the initial state, suggesting moderate stability on the vacancy site. However, for copper, the trend is reversed, and the adsorption energy is higher than its initial state, meaning that without an external electric field, the Cu atom will spontaneously return to the electrode, resulting in volatile switching. The energetics in Fig. 5d further confirm that silver is the most favorable metal for memristor devices, exhibiting the lowest energy barrier for switching and the highest stability. These results underscore the distinct dissociation and adsorption behaviors of each metal. To further explore the role of charge during this transition, we next examine the charge distribution in the heterostructure.

The charge distribution in the heterostructure system evolves during the transition from Structure 1 (S vacancy structure) to Structure 2 (metal atom adsorbed at vacancy) in the NEB calculation. We calculate the Bader charges of the metal atoms in the MoS₂ layer for each NEB image and present the results in Fig. 5e. For gold, as the Au atom begins to separate from the bulk gold layer, it initially acquires a negative charge. This negative charge diminishes as the gold atom approaches the transition state. Afterward, Au regains a negative charge as the atom moves toward its final position and becomes fully adsorbed into the vacancy. For silver, the Ag atom initially carries a negative charge as it begins to dissociate from the bulk. At the transition state, it briefly gains a positive charge before regaining a negative charge as it approaches the sulfur vacancy site on the MoS₂ surface. Upon adsorption, the negative charge decreases slightly, leaving the silver atom with a minimal negative charge. Copper exhibits a unique behavior compared to gold and silver. The copper atom maintains a negative charge throughout the entire dissociation and adsorption process, in contrast to gold and silver, which experience charge fluctuations. This behavior is likely due to copper’s higher reactivity compared to the other metals. Since the sulfur vacancy is an anion vacancy, the metal adatom tends to acquire a negative charge upon adsorption. Consequently, all three metal adatoms ultimately retain a negative charge after adsorption, which aligns with the negatively charged nature of sulfur atoms in MoS₂. This charge distribution suggests that the adsorption of metal atoms at the sulfur vacancy is energetically favorable due to electrostatic interactions.

Figure 5f–h depicts the plot of the charge density profile for the difference between structure 1 (S vacancy structure) and structure 2 (metal atom adsorbed at S vacancy), showing the redistribution of charge for gold, silver, and copper. For gold, the charge density increases notably within the MoS₂ monolayer, indicating a strong, delocalized interaction between the gold adatom and the MoS₂ surface (Fig. 5f). This spread of charge density reflects the robust coupling between the adatom and the underlying 2D material. In the case of silver, the charge density is highly localized around the adsorption site. Unlike gold, the interaction between silver and the MoS₂ surface is more confined to the vicinity of the vacancy, suggesting a more localized bonding nature (Fig. 5g). This localized distribution is evident in the sharp concentration of charge density around the vacancy site. Copper exhibits intermediate behavior compared to gold and silver. The increase in charge density around the copper adatom is considerable, but there is a more pronounced redistribution of charge among the copper atoms themselves (Fig. 5h). This observation suggests a more moderate interaction between copper and the MoS₂ surface relative to gold and silver. In summary, gold shows a delocalized charge distribution within the MoS₂ layer, silver exhibits a highly localized charge density at the adsorption site, and copper presents a mixed behavior, with charge redistribution at the adatom site but more noticeable changes among the copper atoms. These differences highlight the unique nature of the interactions for each metal and their corresponding charge transfer characteristics.

These observations also reveal a correlation between adsorption energy, Bader charge, and charge density for Structure 2. A higher adsorption energy is associated with a smaller Bader charge of the adatom. Similar findings have been reported by Frey et al., who noted a relationship between the binding energy of dopants/adatoms on 2D materials, including MoS₂, and implied that systems with lower binding energies require a lower set voltage for resistive switching²⁹. Lee et al. similarly showed that higher adsorption energies correspond to charge loss of the adatom to the 2D material surface²⁷. This relationship highlights the critical role of adsorption energy and charge transfer in influencing the electronic properties of metal/MoS₂ interfaces.

To examine the effect of vacancy proximity on the energy barrier for metal-induced switching, we performed NEB calculations for Au/MoS₂. Two separate structures were generated, each featuring a different gold atom, labeled Au-1 and Au-2, based on their proximity to the sulfur vacancy. In one structure, Au-1 was positioned approximately 0.5 Å closer to the vacancy, while in the other, Au-2 was farther away. The results showed that the structure with Au-1 had a lower switching energy barrier by ~0.07 eV compared to the structure with Au-2. (Fig. S15a). This shift in the MEP energies indicates that the proximity of the gold atom to the vacancy facilitates a more favorable transition path with reduced energy requirements. The difference, while minimal (~70 meV), suggests that the vacancy’s proximity can subtly influence the energy landscape and, consequently, the switching kinetics. The calculated energy barrier for Au/MoS₂ switching (~0.32 eV and 0.39 eV) aligns with the value of 0.378 eV reported by Li et al. for a similar Au/MoS₂ system²². A detailed comparison of local bonding environments, including bond lengths between the adatom and neighboring atoms, is provided in Table S6 of the Supplementary Information.

Furthermore, the Bader charge trends for Au-1 and Au-2, shown in Fig. S15b, reveal similar behavior, suggesting that the fundamental charge redistribution remains consistent regardless of the distance between the gold atom and the vacancy site. This indicates that while the proximity of the gold atom to the vacancy influences the energy barrier, the nature of charge transfer between the gold atom and the MoS₂ substrate remains largely unchanged. Additionally, the case of Ag/MoS₂, where silver has the largest Ag–S vacancy distance yet the lowest energy barrier, suggests that while distance plays a role in modulating the barrier within the same metal, it is not the dominant factor across different metals. Instead, the intrinsic nature of the metal element primarily governs the energy barrier. Vacancy proximity can still lead to variations in the barrier and, consequently, the switching voltage for the same metal electrode.

Discussion

We analyzed the dissociation, diffusion, and adsorption processes of metal atoms in monolayer MoS₂ using three different metals as adatoms and electrodes. The topS, hollow, and topMo sites were the most favorable for the adsorption of Au, Ag, and Cu, respectively. The MEPs contain the energetically favorable sites of adsorption. When considering the presence of excess charge (e.g., induced by an applied field), negatively charged systems generally exhibited lower energy barriers for diffusion compared to neutral and positively charged systems. For metal/MoS₂ heterostructures, the dissociation and adsorption of metal atoms from the electrode into the S vacancy leads to the formation of conductive points, which can eventually form conductive bridges across the interface. Gold, copper, and silver exhibited energy barriers of 0.32 eV, 0.31 eV, and 0.03 eV, respectively. Notably, this trend aligns with the bond dissociation energies of the respective metal dimers – Au₂ (2.33 eV), Ag₂ (1.66 eV), and Cu₂ (2.03 eV) – suggesting that a stronger metal-metal bond corresponds to a higher energy barrier for dissociation and migration toward the vacancy site³⁸. When the distance between the gold atom and the sulfur vacancy site increased by ~0.05 Å, the energy barrier increased by ~70 meV. While this increase is modest, it indicates that even small changes in the transition distance can substantially affect energy barriers.

From the Bader charge analysis, we observed that the metal atom or ion acquires a negative charge as it adsorbs into the vacancy site. Furthermore, we identified correlations between Bader charges, adsorption energy, and charge density profiles. Higher charge density systems, such as Cu/MoS₂ and Au/MoS₂, exhibited higher energy barriers, while Ag/MoS₂, which had lower charge density, showed lower energy barriers. Figure S16 highlights these relationships, showing that systems with higher adsorption energies correspond to lesser charge gain. These findings reveal the interplay between charge redistribution, structural configuration, and energetics in the switching process.

We propose that switching energy is governed by two main factors: dissociation energy and diffusion energy. A flow chart summarizing the switching process is provided in Fig. 6, depicting two scenarios for a device to switch to a low resistance state.

• Scenario A: The metal atom dissociates from the bulk structure, diffuses across the interface, and adsorbs at a nearby sulfur (S) vacancy site. Here, the diffusion path is the shortest. (Fig. 6a).

• Scenario B: The metal atom dissociates from the bulk structure, but the nearest vacancy site is farther away. Here, the dissociated metal adatom follows a minimum energy pathway (MEP) to diffuse across the MoS₂ surface (Fig. 6c). The MEPs for each metal are identified as (i) across topS for Au, (ii) across hollow for Ag, and (iii) across topMo for Cu (Fig. 6d). Upon reaching an S vacancy site, the metal adatom adsorbs, corresponding to the adsorption energy and the formation of a conductive bridge.

Fig. 6: Schematic representation of two proposed switching pathways in a 2D monolayer resistive memory device.

a Scenario A illustrates the dissociation of a metal atom from the bulk, followed by diffusion across the interface into a vacancy site. b Illustrates the barrier energy vs reaction-co-ordinate graph for NEB calculation corresponding to Scenario A, i.e., dissociation of metal atom from bulk, followed by diffusion across the interface and adsorption at S vacancy site. c Scenario B shows the dissociation, followed by diffusion along the pristine 2D monolayer surface toward a vacancy site, and subsequent adsorption. d Barrier energy vs. reaction-coordinate graph illustrating diffusion of metal atoms along their respective MEPs on pristine MoS₂ surface (Teal = metal atoms, yellow = S, purple = Mo, red/orange = vacancy). In Scenario A, where the vacancy is close to the dissociating metal atom, switching occurs without an additional diffusion energy barrier, as the metal directly migrates into the monolayer. In contrast, Scenario B requires an extra diffusion step, with an additional energy cost of ~0.07 eV for Au and Ag and ~0.25 eV for Cu. The overall switching energy, governed by both dissociation and diffusion, varies by metal, with silver exhibiting the lowest barriers for both interfacial (~0.03 eV) and surface diffusion (~0.07–0.2 eV). This makes silver the most energetically favorable option for switching, regardless of the scenario.

Our metal/MoS₂ heterostructure calculations indicate that silver has the lowest energy barrier to diffusion across the interface (0.03 eV), while gold and copper have the highest (0.32 eV and 0.31 eV) (Fig. 6b). Additionally, silver exhibits a significantly higher energy barrier (~0.33 eV) for returning from the S vacancy site to the metal surface compared to its adsorption barrier (~0.03 eV), reinforcing its stability at the vacancy site and its role in nonvolatile switching. Similarly, the calculated diffusion energy barriers for diffusion across the MoS₂ surface were 0.07–0.17 eV for Au, 0.07–0.2 eV for Ag, and 0.25–0.64 eV for Cu (Fig. 6d). In considering the individual energy contributions of the DDA model, silver is predicted to have overall the most favorable energetics compared to gold and copper. This trend aligns with experimental studies on electrode materials for graphene oxide, where silver exhibited the lowest formation voltage (~0.5 V), gold had the highest (~3 V), and copper showed an intermediate value (~2 V)³⁹.

Notably, the energy barriers observed for silver approach the fundamental thermodynamic minimum set by Landauer’s principle^40,41. This principle establishes a lower bound of ~2.8 zJ (zeptojoules) for irreversible bit operations at room temperature. In our study, silver’s dissociation and adsorption energy (~0.03 eV or ~4.81 zJ) is less than twice this limit, and its surface diffusion energy (~0.07 eV or ~11.2 zJ) remains within 4× the threshold. In contrast, gold’s switching energy (~0.323 eV or ~51.8 zJ) is nearly 19× the Landauer limit. These findings suggest that silver/MoS₂ systems are not only favorable for nonvolatile switching but are also uniquely positioned to enable ultra-low-energy memory operations that approach the thermodynamic limit, making them ideal for neuromorphic and edge computing applications.

Our study explored the switching process from multiple perspectives, integrating atomistic configurations with energetic analyses. Each electrode material, though chemically similar, exhibited distinct diffusion profiles and adsorption preferences. Negatively charged systems generally facilitated diffusion due to electrostatic attraction, while positively charged systems often experienced a hindered metal adatom migration. Additionally, interfacial interactions and the proximity of S vacancies significantly influenced the adsorption and diffusion processes. These factors—presence of charge in systems, diffusion profiles, defect location, and interfacial interactions—are critical for optimizing switching performance in memristors. To further refine the model, it would be valuable to analyze the impact of interfacial spacing between the bulk metal and monolayer MoS₂. Changes in spacing could affect dissociation, diffusion, and adsorption energy barriers. The combined effects of lower energy barriers for these processes could enhance the switching process, making it more efficient. Our findings highlight the importance of dissociation, diffusion, and adsorption energies in determining the switching efficiency of memristors. These factors influence the system’s total switching energy and, by extension, the required switching voltage. Our results also connect to the DDA model, where charge transfer, energy barriers, and structural factors were identified as critical to switching performance. The role of the metal adatom as a conductive point underscores the significance of selecting metals with favorable diffusion profiles and stable adsorption states. This study provides valuable guidance for the development of more efficient memristors. By prioritizing electrode materials with optimal dissociation and diffusion energies, engineers can improve memristor performance. Our atomic-level insights into switching mechanisms could facilitate the design of next-generation memristors for low-power, scalable neural networks and memory devices. By leveraging the unique properties of 2D materials, we can unlock the full potential of RS devices and accelerate the advancement of neuromorphic computing.

Methods

Density functional theory (DFT) based on the implementation in VASP is used, employing plane wave first principles calculations⁴². Plane augmented wave (PAW) pseudopotentials with the generalized gradient approximation and Van der Waals corrections are used^43,44,45. The pseudopotentials used incorporate the electronic configurations of Au ([Xe] 4f¹⁴5d¹⁰6 s¹), Ag ([Kr] 4d¹⁰5 s¹), Cu ([Ar] 3d¹⁰4 s¹), Mo ([Kr] 4 d⁵5 s¹), and S ([Ne] 3s²3p⁴), ensuring accurate representation of their valence states. This corresponds to 11 valence electrons for Au, Ag, and Cu, and 6 valence electrons for Mo and S. For the MoS₂ with metal adatom, a 3 x 3 x 1 k-mesh is chosen for the calculations, and a 20 Å vacuum is introduced. The structures are relaxed with an energy cutoff of 400 eV, and the forces were converged to less than 0.01 eV/Å. For the heterostructure, considering the large 6x6x1 supercell (>270 atoms), the calculations are carried out at the Gamma point. The heterostructures are initially generated using the Quantum ATK interface builder, which generates a structure with the least amount of strain for the given atomic arrangement³⁶. Following that, we optimized the structure at a cut-off energy of 450 eV, and residual forces were converged to below 0.01 eV/Å. The structure has ~21 Å vacuum. The relaxed structures are then studied for dissociation and adsorption of metal atom from the bulk into the 2D monolayer. For the Climbing Image Nudged Elastic Band (CI-NEB) calculations, the convergence criteria for cut-off energy are 350 eV, and forces are converged to below 0.05 eV/Å. The number of images for the metal adatom-MoS₂ structure was 8, and for heterostructure calculations, 6 images were used. CI-NEB calculations are carried out using the VASP Transition State Tools (VTST)^46,47. Bader charges and the charge density difference are calculated using the code provided by VTST⁴⁸.