Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A scalable universal Ising machine based on interaction-centric storage and compute-in-memory

Nature Electronics volume 7, pages 904–913 (2024)Cite this article

Subjects

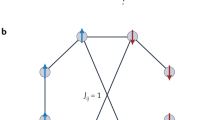
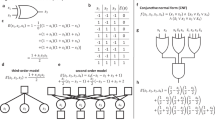
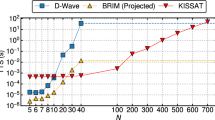
Abstract

Ising machines are annealing processors that can solve combinatorial optimization problems via the physical evolution of the corresponding Ising graphs. Such machines are, however, typically restricted to solving problems with certain kinds of graph topology because the spin location and connections are fixed. Here, we report a universal Ising machine that supports arbitrary Ising graph topology with reasonable hardware resources using a coarse-grained compressed sparse row method to compress and store sparse Ising graph adjacency matrices. The approach, which we term interaction-centric storage, is suitable for any kind of Ising graph and reduces the memory scaling cost. We experimentally implement the Ising machine using compute-in-memory hardware based on a 40 nm resistive random-access memory arrays. We use the machine to solve max-cut and graph colouring problems, with the latter showing a 442–1,450 factor improvement in speed and 4.1 × 105–6.0 × 105 factor reduction in energy consumption compared to a general-purpose graphics processing unit. We also use our Ising machine to solve a realistic electronic design automation problem—multiple patterning lithography layout decomposition—with 390–65,550 times speedup compared to the integer linear programming algorithm on a typical central processing unit.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Workflow and classification of Ising machine.
Fig. 2: Comparison between spin-centric design and interaction-centric design.
Fig. 3: Illustration of the CG-CSR method and its application to Ising computing.
Fig. 4: Illustration of implementing UIM on RRAM-based CIM module.
Fig. 5: Max-cut demonstration.
Fig. 6: Graph colouring demonstration.

Similar content being viewed by others

Data availability

Source data are available via Zenodo at https://doi.org/10.5281/zenodo.10686168 (ref. 41). Other data that support the findings of this study are available from the corresponding authors upon reasonable request.

Code availability

The core source code that implements the full-FPGA version of the UIM architecture is available via Zenodo at https://doi.org/10.5281/zenodo.10686168 (ref. 41). Other codes are available from the corresponding authors upon reasonable request.

References

  1. Karp, R. M. Reducibility Among Combinatorial Problems (Springer, 2010).

  2. Aadit, N. A. et al. Massively parallel probabilistic computing with sparse Ising machines. Nat. Electron. 5, 460–468 (2022).

    Article  Google Scholar 

  3. Schuetz, M. J., Brubaker, J. K. & Katzgraber, H. G. Combinatorial optimization with physics-inspired graph neural networks. Nat. Mach. Intell. 4, 367–377 (2022).

    Article  Google Scholar 

  4. Korte, B. H., Vygen, J., Korte, B. & Vygen, J. Combinatorial Optimization Vol. 1 (Springer, 2011).

  5. Lin, S. & Kernighan, B. W. An effective heuristic algorithm for the traveling-salesman problem. Oper. Res. 21, 498–516 (1973).

    Article  MathSciNet  Google Scholar 

  6. Kokash, N. An Introduction to Heuristic Algorithms (Univ. Trento, 2005).

  7. Tatsumura, K., Yamasaki, M. & Goto, H. Scaling out Ising machines using a multi-chip architecture for simulated bifurcation. Nat. Electron. 4, 208–217 (2021).

    Article  Google Scholar 

  8. Mohseni, N., McMahon, P. L. & Byrnes, T. Ising machines as hardware solvers of combinatorial optimization problems. Nat. Rev. Phys. 4, 363–379 (2022).

    Article  Google Scholar 

  9. Hu, F., Wang, B.-N., Wang, N. & Wang, C. Quantum machine learning with D-wave quantum computer. Quantum Eng. 1, e12 (2019).

    Article  Google Scholar 

  10. Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).

    Article  Google Scholar 

  11. Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354, 603–606 (2016).

    Article  Google Scholar 

  12. Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron. 4, 502–512 (2021).

    Article  Google Scholar 

  13. Moy, W. et al. A 1,968-node coupled ring oscillator circuit for combinatorial optimization problem solving. Nat. Electron. 5, 310–317 (2022).

    Article  Google Scholar 

  14. Takemoto, T., Hayashi, M., Yoshimura, C. & Yamaoka, M. 2.6 A 2 × 30k-spin multichip scalable annealing processor based on a processing-in-memory approach for solving large-scale combinatorial optimization problems. In IEEE International Solid-State Circuits Conference (ISSCC) 52–54 (IEEE, 2019).

  15. Takemoto, T. et al. 4.6 a 144 kb annealing system composed of 9 × 16 kb annealing processor chips with scalable chip-to-chip connections for large-scale combinatorial optimization problems. In IEEE International Solid-State Circuits Conference (ISSCC) Vol. 64, 64–66 (IEEE, 2021).

  16. Yamamoto, K. et al. 7.3 statica: a 512-spin 0.25 m-weight full-digital annealing processor with a near-memory all-spin-updates-at-once architecture for combinatorial optimization with complete spin-spin interactions. In IEEE International Solid-State Circuits Conference (ISSCC) 138–140 (IEEE, 2020).

  17. Chou, J., Bramhavar, S., Ghosh, S. & Herzog, W. Analog coupled oscillator based weighted Ising machine. Sci. Rep. 9, 14786 (2019).

    Article  Google Scholar 

  18. Su, Y., Kim, H. & Kim, B. CIM-spin: a scalable CMOS annealing processor with digital in-memory spin operators and register spins for combinatorial optimization problems. IEEE J. Solid-State Circuits 57, 2263–2273 (2022).

    Article  Google Scholar 

  19. Su, Y., Mu, J., Kim, H. & Kim, B. A scalable CMOS Ising computer featuring sparse and reconfigurable spin interconnects for solving combinatorial optimization problems. IEEE J. Solid-State Circuits 57, 858–868 (2022).

    Article  Google Scholar 

  20. Wang, T. & Roychowdhury, J. OIM: oscillator-based Ising machines for solving combinatorial optimisation problems. In Unconventional Computation and Natural Computation: 18th International Conference, UCNC 2019 Vol. 18, 232–256 (Springer International Publishing, 2019).

  21. Wang, T., Wu, L. & Roychowdhury, J. New computational results and hardware prototypes for oscillator-based Ising machines. In Proc. 56th Design Automation Conference (DAC) 1–2 (ACM, 2019).

  22. Tatsumura, K., Dixon, A. R. & Goto, H. FPGA-based simulated bifurcation machine. In Proc. International Conference on Field Programmable Logic and Applications (FPL) 59–66 (IEEE, 2019).

  23. Yamamoto, K. et al. A time-division multiplexing Ising machine on FPGAs. In Proc. International Symposium on Highly Efficient Accelerators and Reconfigurable Technologies 1–6 (ACM, 2017).

  24. Cook, C., Jin, W. & Tan, S. X.-D. GPU-based Ising computing for solving balanced min-cut graph partitioning problem. Preprint at https://arxiv.org/abs/1908.00210 (2019).

  25. Cook, C., Zhao, H., Sato, T., Hiromoto, M. & Tan, S. X.-D. GPU-based Ising computing for solving max-cut combinatorial optimization problems. Integration 69, 335–344 (2019).

    Article  Google Scholar 

  26. Verma, N. et al. In-memory computing: advances and prospects. IEEE Solid-State Circuits Mag. 11, 43–55 (2019).

    Article  Google Scholar 

  27. Roy, K., Chakraborty, I., Ali, M., Ankit, A. & Agrawal, A. In-memory computing in emerging memory technologies for machine learning: an overview. In Proc. 57th Design Automation Conference (DAC) 1–6 (IEEE, 2020).

  28. Yan, B. et al. Resistive memory-based in-memory computing: from device and large-scale integration system perspectives. Adv. Intell. Syst. 1, 1900068 (2019).

    Article  Google Scholar 

  29. Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. & Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 15, 529–544 (2020).

    Article  Google Scholar 

  30. Jiang, M., Shan, K., He, C. & Li, C. Efficient combinatorial optimization by quantum-inspired parallel annealing in analogue memristor crossbar. Nat. Commun. 14, 5927 (2023).

    Article  Google Scholar 

  31. Barahona, F., Grötschel, M., Jünger, M. & Reinelt, G. An application of combinatorial optimization to statistical physics and circuit layout design. Oper. Res. 36, 493–513 (1988).

    Article  Google Scholar 

  32. Goemans, M. Improved approximation algorithms for maximum cut and satisability problems using semidenite programming. J. Assoc. Comput. Mach. 42, 330–343 (1995).

    Article  Google Scholar 

  33. Coudert, O. Exact coloring of real-life graphs is easy. In Proc. 34th Design Automation Conference (DAC) 121–126 (ACM, 1997).

  34. Kahng, A. B., Park, C.-H., Xu, X. & Yao, H. Layout decomposition approaches for double patterning lithography. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 29, 939–952 (2010).

    Article  Google Scholar 

  35. Ciesielski, M. J., Yang, S. & Perkowski, M. A. Multiple-valued Boolean minimization based on graph coloring. In Proc. International Conference on Computer Design: VLSI in Computers and Processors 262–263 (IEEE, 1989).

  36. Smith, M. D., Ramsey, N. & Holloway, G. A generalized algorithm for graph-coloring register allocation. In Proc. ACM SIGPLAN Conference on Programming Language Design and Implementation 277–288 (ACM, 2004).

  37. Johnson, D. S. & Trick, M. A. Cliques, Coloring, and Satisfiability: Second DIMACS Implementation Challenge Vol. 26 (American Mathematical Society, 1996).

  38. Zhang, K., Qiu, M., Li, L. & Liu, X. Accelerating genetic algorithm for solving graph coloring problem based on CUDA architecture. In Bio-Inspired Computing—Theories and Applications 578–584 (Springer, 2014).

  39. Ma, Y., Zeng, X. & Yu, B. Methodologies for layout decomposition and mask optimization: a systematic review. In Proc. International Conference on Very Large Scale Integration (VLSI-SoC) 1–6 (IEEE, 2017).

  40. Li, W. et al. OpenMPL: an open-source layout decomposer. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 40, 2331–2344 (2020).

    Article  Google Scholar 

  41. Yue, W. Scalable universal Ising machine enabled by interaction-centric storage and compute-in-memory technology. Zenodo https://doi.org/10.5281/zenodo.10686168 (2024).

Download references

Acknowledgements

This work was supported by the National Key R&D Programme of China (grant no. 2023YFB4502200), National Natural Science Foundation of China (grant nos 61925401, 92064004, 61927901, 8206100486, 92164302 and 92364102), Beijing Natural Science Foundation (grant no. L234026) and the 111 Project (grant no. B18001). Fund grant nos 2023YFB4502200, 61925401, 92064004, 92164302 and L234026 were awarded to Yuchao Yang. Fund grant no. 61927901 was awarded to R.H. Fund grant no. 8206100486 was awarded to Y.T. Fund grant no. 92364102 was awarded to B.Y.

Author information

Author notes

  1. These authors contributed equally: Wenshuo Yue, Teng Zhang.

Authors and Affiliations

  1. Beijing Advanced Innovation Center for Integrated Circuits, School of Integrated Circuits, Peking University, Beijing, China

    Wenshuo Yue, Teng Zhang, Zhaokun Jing, Yuxiang Yang, Zhen Yang, Yibo Lin, Bonan Yan, Ru Huang & Yuchao Yang

  2. Institute for Artificial Intelligence, Peking University, Beijing, China

    Wenshuo Yue, Yaoyu Tao, Bonan Yan, Ru Huang & Yuchao Yang

  3. College of Electron and Information Engineering, Hebei University, Baoding, China

    Kai Wu

  4. Semiconductor Technology Innovation Center (Beijing) Corporation, Beijing, China

    Yongqin Wu, Weihai Bu, Kai Zheng & Jin Kang

  5. Guangdong Provincial Key Laboratory of In-Memory Computing Chips, School of Electronic and Computer Engineering, Peking University, Shenzhen, China

    Yuchao Yang

  6. Center for Brain Inspired Intelligence, Chinese Institute for Brain Research (CIBR), Beijing, China

    Yuchao Yang

Authors
  1. Wenshuo Yue
    View author publications

    Search author on:PubMed Google Scholar

  2. Teng Zhang
    View author publications

    Search author on:PubMed Google Scholar

  3. Zhaokun Jing
    View author publications

    Search author on:PubMed Google Scholar

  4. Kai Wu
    View author publications

    Search author on:PubMed Google Scholar

  5. Yuxiang Yang
    View author publications

    Search author on:PubMed Google Scholar

  6. Zhen Yang
    View author publications

    Search author on:PubMed Google Scholar

  7. Yongqin Wu
    View author publications

    Search author on:PubMed Google Scholar

  8. Weihai Bu
    View author publications

    Search author on:PubMed Google Scholar

  9. Kai Zheng
    View author publications

    Search author on:PubMed Google Scholar

  10. Jin Kang
    View author publications

    Search author on:PubMed Google Scholar

  11. Yibo Lin
    View author publications

    Search author on:PubMed Google Scholar

  12. Yaoyu Tao
    View author publications

    Search author on:PubMed Google Scholar

  13. Bonan Yan
    View author publications

    Search author on:PubMed Google Scholar

  14. Ru Huang
    View author publications

    Search author on:PubMed Google Scholar

  15. Yuchao Yang
    View author publications

    Search author on:PubMed Google Scholar

Contributions

B.Y. and Yuchao Yang directed the research. W.Y. and B.Y. conceived the idea and planned the study. W.Y., Z.J. and B.Y. designed the RRAM chip. W.Y. and B.Y. designed the UIM architecture. W.Y. implemented the closed-loop CIM-based UIM system. Y.L. extended the UIM to the EDA application. T.Z., Yuxiang Yang, Z.Y., Y.W., W.B., K.Z., J.K., R.H. and Yuchao Yang developed the RRAM integration processes. T.Z., W.Y., Yuxiang Yang, Z.Y., Y.W. and Y.T. optimized the RRAM device. W.Y. and K.W. developed the video demonstration. K.W. optimized the testing platform. All authors reviewed and edited the paper.

Corresponding authors

Correspondence to Bonan Yan or Yuchao Yang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Electronics thanks Bin Gao, Luke Theogarajan and Masanao Yamaoka for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–22, Notes 1–25 and Tables 1–12.

Supplementary Video 1

Computing process in the closed-loop system of the UIMe.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yue, W., Zhang, T., Jing, Z. et al. A scalable universal Ising machine based on interaction-centric storage and compute-in-memory. Nat Electron 7, 904–913 (2024). https://doi.org/10.1038/s41928-024-01228-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41928-024-01228-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics