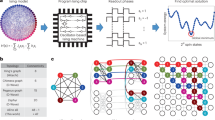
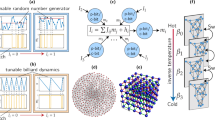
Abstract
Numerous practical problems—ranging from machine learning to bioinformatics—can be formulated as combinatorial optimization problems. However, the computational resources required to find an optimal solution to these problems using conventional von Neumann computers increases rapidly with problem size. Alternative solvers based on Ising machines, which directly leverage equilibrium characteristics of physical systems, offer a potential solution for such problems. Here we report a coupled-oscillator-based all-to-all-connected Ising chip that is manufactured in 65-nm complementary metal–oxide–semiconductor (CMOS) technology and operates at room temperature. The approach relies on logic-based coupling, which leads to low power consumption and a large number of all-to-all-connected spins. We show that the chip can solve representative combinatorial optimization problems in a more time- and energy-efficient manner than can optimized classical solvers in software and emerging quantum annealers. Due to its energy efficiency and all-to-all connectivity, our chip can also efficiently solve dense combinatorial optimization problems that cannot be effectively mapped or solved by quantum annealers.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data are available at https://figshare.com/s/99ae6e188bedee0d8ad5. Source data are provided with this paper.
References
Karp, R. M. in Complexity of Computer Computations (eds Miller, R. E. et al.) 85–103 (Springer, 1972).
Cook, W. J., Cunningham, W. H., Pulleyblank, W. R. & Schrijver, A. Combinatorial Optimization (Wiley, 1998).
Garey, M. R. & Johnson, D. S. Computers and Intractability: a Guide to the Theory of NP-Completeness (W. H. Freeman, 1990).
Fu, Y. & Anderson, P. W. Application of statistical mechanics to NP-complete problems in combinatorial optimisation. J. Phys. A 19, 1605 (1986).
Barahona, F., Grötschel, M., Jünger, M. & Reinelt, G. An application of combinatorial optimization to statistical physics and circuit layout design. Oper. Res. 36, 493–513 (1988).
Barahona, F. On the computational complexity of Ising spin glass models. J. Phys. A 15, 3241–3253 (1982).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001).
Lucas, A. Ising formulations of many NP problems. Front. Phys. https://doi.org/10.3389/fphy.2014.00005 (2014).
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).
Takemoto, T., Hayashi, M., Yoshimura, C. & Yamaoka, M. 2.6 A 2 × 30k-spin multichip scalable annealing processor based on a processing-in-memory approach for solving large-scale combinatorial optimization problems. In 2019 IEEE International Solid-State Circuits Conference (ISSCC) 52–54 (IEEE, 2019).
Yamamoto, K. et al. STATICA: a 512-spin 0.25M-weight annealing processor with an all-spin-updates-at-once architecture for combinatorial optimization with complete spin–spin interactions. IEEE J. Solid-State Circuits 56, 165–178 (2020).
Aramon, M. et al. Physics-inspired optimization for quadratic unconstrained problems using a digital annealer. Front. Phys. 7, 48 (2019).
Nakayama, H., Koyama, J., Yoneoka, N. & Miyazawa, T. Description: Third Generation Digital Annealer Technology (Fujitsu, 2021).
Goto, H. et al. High-performance combinatorial optimization based on classical mechanics. Sci. Adv. 7, 7953 (2021).
Tatsumura, K., Yamasaki, M. & Goto, H. Scaling out Ising machines using a multi-chip architecture for simulated bifurcation. Nat. Electron. 4, 208–217 (2021).
Johnson, M. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
Ebadi, S. et al. Quantum optimization of maximum independent set using Rydberg atom arrays. Science 376, 1209–1215 (2022).
Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron. 4, 502–512 (2021).
Moy, W. et al. A 1,968-node coupled ring oscillator circuit for combinatorial optimization problem solving. Nat. Electron. 5, 310–317 (2022).
Lo, H., Moy, W., Yu, H., Sapatnekar, S. & Kim, C. H. An Ising solver chip based on coupled ring oscillators with a 48-node all-to-all connected array architecture. Nat. Electron. 6, 771–778 (2023).
Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354, 603–606 (2016).
Clements, W. R. et al. Gaussian optical Ising machines. Phys. Rev. A 96, 043850 (2017).
Pierangeli, D., Marcucci, G. & Conti, C. Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
Wang, T. & Roychowdhury, J. in Unconventional Computation and Natural Computation. UCNC 2019 Lecture Notes in Computer Science Vol. 11493 (eds McQuillan, I. & Seki, S.) 232–256 (Springer, 2019).
Ising, E. Beitrag zur theorie des ferromagnetismus. Z. Phys. 31, 253–258 (1925).
Bian, Z., Chudak, F. A., Macready, W. G. & Rose, G. The Ising Model: Teaching an Old Problem New Tricks (D-Wave Systems, 2010).
Coffrin, C., Nagarajan, H. & Bent, R. Ising Processing Units: Potential and Challenges for Discrete Optimization Technical Report LA-UR-17-23494 (Los Alamos National Laboratory, 2017).
Cai, J., Macready, W. G. & Roy, A. A practical heuristic for finding graph minors. Preprint at https://arxiv.org/abs/1406.2741 (2014).
Hamerly, R. et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci. Adv. 5, 0823 (2019).
Könz, M. S., Lechner, W., Katzgraber, H. G. & Troyer, M. Embedding overhead scaling of optimization problems in quantum annealing. PRX Quantum 2, 040322 (2021).
Wang, T. & Roychowdhury, J. OIM: oscillator-based Ising machines for solving combinatorial optimisation problems. Preprint at https://arxiv.org/abs/1903.07163 (2019).
Shinomoto, S. & Kuramoto, Y. Phase transitions in active rotator systems. Progr. Theor. Phys. 75, 1105–1110 (1986).
Lyapunov, A. M. The general problem of the stability of motion. Int. J. Control 55, 531–534 (1992).
Graber, M. & Hofmann, K. A coupled oscillator network to solve combinatorial optimization problems with over 95% accuracy. In IEEE International Symposium on Circuits and Systems (ISCAS) 1–5 (IEEE, 2023).
Booth, M., Reinhardt, S. P. & Roy, A. Partitioning optimization problems for hybrid classical/quantum execution. GitHub https://github.com/dwavesystems/qbsolv (2017).
Chancellor, N., Zohren, S., Warburton, P. A., Benjamin, S. C. & Roberts, S. A direct mapping of Max k-SAT and high order parity checks to a chimera graph. Sci. Rep. 6, 37107 (2016).
McGeochand, C. & Farré, P. Advantage Processor Overview Technical Report 14-1058A-A (D-Wave, 2022).
Wurtz, J. et al. Aquila: QuEra’s 256-qubit neutral-atom quantum computer. Preprint at https://arxiv.org/abs/2306.11727 (2023).
Palubeckis, G. Multistart tabu search strategies for the unconstrained binary quadratic optimization problem. Ann. Oper. Res. 131, 259–282 (2004).
Johnson, D. S. & Trick, M. A. (eds) Cliques, Coloring, and Satisfiability: Second DIMACS Implementation Challenge, Workshop, October 11-13, 1993 (DIMACS Series in Discrete Mathematics and Theoretical Computer Science Vol. 26, American Mathematical Society, 1996).
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092 (1953).
Kawamura, K. et al. Amorphica: 4-replica 512 fully connected spin 336 MHz metamorphic annealer with programmable optimization strategy and compressed-spin-transfer multi-chip extension. In IEEE International Solid-State Circuits Conference (ISSCC) 42–44 (IEEE, 2023).
Sharma, A., Afoakwa, R., Ignjatovic, Z. & Huang, M. Increasing Ising machine capacity with multi-chip architectures. In Proc. 49th Annual International Symposium on Computer Architecture 508–521 (ACM Digital Library, 2022).
D-Wave Hybrid 2014; Ocean Documentation 6.7.1 Documentation—docs.ocean.dwavesys.com (D-Wave Systems, accessed 13 December 2023); https://docs.ocean.dwavesys.com/en/stable/docs_hybrid/
Tan, S. et al. HyQSAT: a hybrid approach for 3-SAT problems by integrating quantum annealer with CDCL. In 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA) 731–744 (IEEE, 2023).
Cılasun, H. et al. 3SAT on an all-to-all-connected CMOS Ising solver chip. Sci. Rep. 14, 10757 (2024).
Zielinski, S. et al. Pattern QUBOs: algorithmic construction of 3SAT-to-QUBO transformations. Electronics 12, 3492 (2023).
Nüßlein, J., Gabor, T., Linnhoff-Popien, C. & Feld, S. Algorithmic QUBO formulations for k-SAT and Hamiltonian cycles. In Proc. Genetic and Evolutionary Computation Conference Companion 2240–2246 (ACM Digital Library, 2022).
Bybee, C. et al. Efficient optimization with higher-order Ising machines. Nat. Commun. 14, 6033 (2023).
Kumar, S., Zhang, H. & Huang, Y.-P. Large-scale Ising emulation with four body interaction and all-to-all connections. Commun. Phys. 3, 108 (2020).
Puri, S., Andersen, C. K., Grimsmo, A. L. & Blais, A. Quantum annealing with all-to-all connected nonlinear oscillators. Nat. Commun. 8, 15785 (2017).
Böther, M. et al. What’s wrong with deep learning in tree search for combinatorial optimization. Preprint at https://arxiv.org/abs/2201.10494 (2022).
Liu, Y. et al. A 1024-spin scalable Ising machine with capacitive coupling and progressive annealing method for combination optimization problems. IEEE Trans. Circuits Syst. II 71, 5009–5013 (2024).
Graber, M. & Hofmann, K. An integrated coupled oscillator network to solve optimization problems. Commun. Eng. 3, 116 (2024).
Ahmed, I., Chiu, P.-W., Moy, W. & Kim, C. H. A probabilistic compute fabric based on coupled ring oscillators for solving combinatorial optimization problems. IEEE J. Solid-State Circuits 56, 2870–2880 (2021).
Mallick, A., Bashar, M., Truesdell, D., Calhoun, B. & Shukla, N. Overcoming the accuracy vs. performance trade-off in oscillator Ising machines. In IEEE International Electron Devices Meeting (IEDM) 40–42 (IEEE, 2021).
Bashar, M. K. et al. Experimental demonstration of a reconfigurable coupled oscillator platform to solve the max-cut problem. IEEE J. Explor. Solid-State Comput. Devices Circuits 6, 116–121 (2020).
Acknowledgements
This work was supported in part by the Defense Advanced Research Projects Agency (DARPA) Quantum-Inspired Classical Computing (QuICC) programme under Air Force Research Laboratory (AFRL) contract FA8750-22-C-1034 (W.M., T.I., H.L., C.H.K., Z.Z., R.S., A.K., S.S.S., H.C. and U.R.K.), National Science Foundation (NSF) under grants 2230963 (C.H.K., Z.Z., R.S., A.K., S.S.S., H.C. and U.R.K.) and 2142248 (C.H.K., H.C. and U.R.K.), Semiconductor Research Corporation under grant 2021-AH-3024 (W.M., A.V., M.A. and C.H.K.) and Intel’s Transformative HardWare for AI (THWAI) centre (W.M.).
Author information
Authors and Affiliations
Contributions
H.C. was responsible for the development of the software stack for application mapping and system-level benchmarking. W.M. was responsible for the schematic and layout design of the Ising core. Z.Z. worked on techniques for application mapping to the Ising hardware. T.I. led the integration and final sign-soff of the chip. H.L. assisted with the coupler design. A.V. and M.T. wrote the test program and performed the experiments. W.M., A.V. and C.H.K. jointly analysed the test data. M.A. assisted with the circuit simulation. R.S. and A.K. helped with software stack development. C.H.K. was the overall hardware lead and project coordinator. S.S.S. and U.R.K. led the application mapping and system-level benchmarking efforts.
Corresponding author
Ethics declarations
Competing interests
The authors declare the following competing interest: US patent no. 12,261,598 (Logic based ring oscillator coupling circuit) and US patent no 11,888,484 (Circuit having fully connected ring oscillators). C.H.K. is a co-founder and the CEO of COBI, which is developing quantum-inspired computing technologies. These interests have been reviewed and managed by the University of Minnesota in accordance with its conflict of interest policies. W.M. is a co-founder and the CTO of COBI. The other authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Klaus Hofmann and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–7, Discussion and Tables 1 and 2.
Supplementary Data Fig. 3
Raw data for Supplementary Fig. 3.
Supplementary Data Fig. 7
Raw data for Supplementary Fig. 7.
Source data
Source Data Fig. 3
Raw data for Fig. 3.
Source Data Fig. 4
Raw data for Fig. 4.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Cılasun, H., Moy, W., Zeng, Z. et al. A coupled-oscillator-based Ising chip for combinatorial optimization. Nat Electron 8, 537–546 (2025). https://doi.org/10.1038/s41928-025-01393-3
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41928-025-01393-3