Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A high-efficiency elementary network of interchangeable superconducting qubit devices

Nature Electronics volume 8, pages 610–619 (2025)Cite this article

Subjects

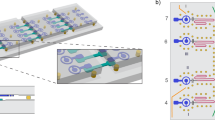
Abstract

Modular architectures could be used to scale quantum devices to the point of fault tolerance and utility. Such modularity is of particular value with superconducting qubits, where monolithically manufactured devices are limited in both system size and quality. However, although prototypical quantum device networks have been fabricated, the development of quantum systems with both interchangeability and high-fidelity operations remains challenging. Here we report a modular architecture for scaling quantum processors with reconfigurable and expandable networks. We develop a high-efficiency interconnect based on a low-loss detachable cable connection between two superconducting qubit devices. We overcome residual loss through a fast pump scheme, enabling intermodule SWAP efficiencies at the 99% level in less than 100 ns. We use the scheme to generate high-fidelity entanglement and operate a distributed logical dual-rail qubit. With an error rate of around 1%, our interdevice operations are at the threshold for fault tolerance.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experiment overview.
Fig. 2: Fast sidebands between qubit and high-Q detachable bus.
Fig. 3: Intermodule swaps.
Fig. 4: Dual-rail operations in the detuned Raman regime.

Similar content being viewed by others

Data availability

The experimental data that support the findings of this study are available at https://doi.org/10.13012/B2IDB-6176441_V1 (ref. 70).

Code availability

The code used for the data analysis and visualization is available at https://doi.org/10.13012/B2IDB-6176441_V1 (ref. 70).

References

  1. Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).

    Article  Google Scholar 

  2. Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).

    Article  Google Scholar 

  3. Awschalom, D. et al. Development of quantum interconnects (QuICs) for next-generation information technologies. PRX Quantum 2, 017002 (2021).

    Article  Google Scholar 

  4. Ang, J. et al. ARQUIN: architectures for multinode superconducting quantum computers. ACM Trans. Quantum Comput. 5, 19 (2024).

    Article  Google Scholar 

  5. Bravyi, S., Dial, O., Gambetta, J. M., Gil, D. & Nazario, Z. The future of quantum computing with superconducting qubits. J. Appl. Phys. 132, 160902 (2022).

    Article  Google Scholar 

  6. Smith, K. N., Ravi, G. S., Baker, J. M. & Chong, F. T. Scaling superconducting quantum computers with chiplet architectures. In 2022 55th IEEE/ACM International Symposium on Microarchitecture (MICRO) 1092–1109 (IEEE, 2000).

  7. Storz, S. et al. Loophole-free Bell inequality violation with superconducting circuits. Nature 617, 265–270 (2023).

    Article  Google Scholar 

  8. Ramette, J., Sinclair, J., Breuckmann, N. P. & Vuletić, V. Fault-tolerant connection of error-corrected qubits with noisy links. npj Quantum Inf. 10, 58 (2024).

    Article  Google Scholar 

  9. Roch, N. et al. Observation of measurement-induced entanglement and quantum trajectories of remote superconducting qubits. Phys. Rev. Lett. 112, 170501 (2014).

    Article  Google Scholar 

  10. Dickel, C. et al. Chip-to-chip entanglement of transmon qubits using engineered measurement fields. Phys. Rev. B 97, 064508 (2018).

    Article  Google Scholar 

  11. Narla, A. et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. X 6, 031036 (2016).

    Google Scholar 

  12. Gold, A. et al. Entanglement across separate silicon dies in a modular superconducting qubit device. npj Quantum Inf. 7, 142 (2021).

    Article  Google Scholar 

  13. Conner, C. R. et al. Superconducting qubits in a flip-chip architecture. Appl. Phys. Lett. 118, 232602 (2021).

    Article  Google Scholar 

  14. Zhong, Y. et al. Deterministic multi-qubit entanglement in a quantum network. Nature 590, 571–575 (2021).

    Article  Google Scholar 

  15. Niu, J. et al. Low-loss interconnects for modular superconducting quantum processors. Nat. Electron. 6, 235–241 (2023).

    Article  Google Scholar 

  16. Qiu, J. et al. Deterministic quantum state and gate teleportation between distant superconducting chips. Sci. Bull. 70, 351–358 (2024).

    Article  Google Scholar 

  17. Fowler, A. G., Stephens, A. M. & Groszkowski, P. High-threshold universal quantum computation on the surface code. Phys. Rev. A 80, 052312 (2009).

    Article  Google Scholar 

  18. Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014).

    Article  Google Scholar 

  19. Axline, C. J. et al. On-demand quantum state transfer and entanglement between remote microwave cavity memories. Nat. Phys. 14, 705–710 (2018).

    Article  Google Scholar 

  20. Campagne-Ibarcq, P. et al. Deterministic remote entanglement of superconducting circuits through microwave two-photon transitions. Phys. Rev. Lett. 120, 200501 (2018).

    Article  Google Scholar 

  21. Kurpiers, P. et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 558, 264–267 (2018).

    Article  Google Scholar 

  22. Burkhart, L. D. et al. Error-detected state transfer and entanglement in a superconducting quantum network. PRX Quantum 2, 030321 (2021).

    Article  Google Scholar 

  23. Zhou, C. et al. Realizing all-to-all couplings among detachable quantum modules using a microwave quantum state router. npj Quantum Inf. 9, 54 (2023).

    Article  Google Scholar 

  24. Leung, N. et al. Deterministic bidirectional communication and remote entanglement generation between superconducting qubits. npj Quantum Inf. 5, 18 (2019).

    Article  Google Scholar 

  25. Kurpiers, P., Walter, T., Magnard, P., Salathe, Y. & Wallraff, A. Characterizing the attenuation of coaxial and rectangular microwave-frequency waveguides at cryogenic temperatures. EPJ Quantum Technol. 4, 8 (2017).

    Article  Google Scholar 

  26. Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443–447 (2007).

    Article  Google Scholar 

  27. Axline, C. et al. An architecture for integrating planar and 3D cQED devices. Appl. Phys. Lett. 109, 042601 (2016).

    Article  Google Scholar 

  28. Gertler, J. M. et al. Protecting a bosonic qubit with autonomous quantum error correction. Nature 590, 243–248 (2021).

    Article  Google Scholar 

  29. Chakram, S. et al. Multimode photon blockade. Nat. Phys. 18, 879–884 (2022).

    Article  Google Scholar 

  30. Sivak, V. V. et al. Real-time quantum error correction beyond break-even. Nature 616, 50–55 (2023).

    Article  Google Scholar 

  31. Ni, Z. et al. Beating the break-even point with a discrete-variable-encoded logical qubit. Nature 616, 56–60 (2023).

    Article  Google Scholar 

  32. Milul, O. et al. Superconducting cavity qubit with tens of milliseconds single-photon coherence time. PRX Quantum 4, 030336 (2023).

    Article  Google Scholar 

  33. Koottandavida, A. et al. Erasure detection of a dual-rail qubit encoded in a double-post superconducting cavity. Phys. Rev. Lett. 132, 180601 (2024).

    Article  Google Scholar 

  34. Ganjam, S. et al. Surpassing millisecond coherence in on chip superconducting quantum memories by optimizing materials and circuit design. Nat. Commun. 15, 3687 (2024).

    Article  Google Scholar 

  35. Chou, K. S. et al. Deterministic teleportation of a quantum gate between two logical qubits. Nature 561, 368–373 (2018).

    Article  Google Scholar 

  36. Bergmann, K., Theuer, H. & Shore, B. W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 70, 1003 (1998).

    Article  Google Scholar 

  37. Wallraff, A. et al. Sideband transitions and two-tone spectroscopy of a superconducting qubit strongly coupled to an on-chip cavity. Phys. Rev. Lett. 99, 050501 (2007).

    Article  Google Scholar 

  38. Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).

    Article  Google Scholar 

  39. Shillito, R. et al. Dynamics of transmon ionization. Phys. Rev. Appl. 18, 034031 (2022).

    Article  Google Scholar 

  40. Abdurakhimov, L. V. et al. Identification of different types of high-frequency defects in superconducting qubits. PRX Quantum 3, 040332 (2022).

    Article  Google Scholar 

  41. Xia, M. et al. Fast superconducting qubit control with sub-harmonic drives. Preprint at https://arxiv.org/abs/2306.10162 (2023).

  42. Teoh, J. D. et al. Dual-rail encoding with superconducting cavities. Proc. Natl Acad. Sci. USA 120, e2221736120 (2023).

    Article  Google Scholar 

  43. Levine, H. et al. Demonstrating a long-coherence dual-rail erasure qubit using tunable transmons. Phys. Rev. X 14, 011051 (2024).

    Google Scholar 

  44. Chou, K. S. et al. A superconducting dual-rail cavity qubit with erasure-detected logical measurements. Nat. Phys. 20, 1454–1460 (2024).

    Article  Google Scholar 

  45. De Graaf, S. J. et al. A mid-circuit erasure check on a dual-rail cavity qubit using the joint-photon number-splitting regime of circuit QED. npj Quantum Inf. 11, 1 (2025).

    Article  Google Scholar 

  46. Kubica, A. et al. Erasure qubits: overcoming the T1 limit in superconducting circuits. Phys. Rev. X 13, 041022 (2023).

    Google Scholar 

  47. Place, A. P. M. et al. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 12, 1779 (2021).

    Article  Google Scholar 

  48. Somoroff, A. et al. Millisecond coherence in a superconducting qubit. Phys. Rev. Lett. 130, 267001 (2023).

    Article  Google Scholar 

  49. Wang, C. et al. Towards practical quantum computers: transmon qubit with a lifetime approaching 0.5 milliseconds. npj Quantum Inf. 8, 3 (2022).

    Article  Google Scholar 

  50. Kono, S. et al. Mechanically induced correlated errors on superconducting qubits with relaxation times exceeding 0.4 ms. Nat. Commun. 15, 3950 (2024).

    Article  Google Scholar 

  51. Safwat, A., Zaki, K., Johnson, W. & Lee, C. Novel transition between different configurations of planar transmission lines. IEEE Microw. Wireless Compon. Lett. 12, 128–130 (2002).

    Article  Google Scholar 

  52. Beeresha, R. S., Khan, A. M. & Reddy, H. V. M. CPW to microstrip transition using different CPW ground plane structures. In 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT) 667–671 (IEEE, 2016).

  53. Vool, U. et al. Driving forbidden transitions in the fluxonium artificial atom. Phys. Rev. Appl. 9, 054046 (2018).

    Article  Google Scholar 

  54. Nie, K., Bista, A., Chow, K., Pfaff, W. & Kou, A. Parametrically controlled microwave-photonic interface for the fluxonium. Phys. Rev. Appl. 22, 054021 (2024).

    Article  Google Scholar 

  55. Lachance-Quirion, D. et al. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 367, 425–428 (2020).

    Article  Google Scholar 

  56. Harvey-Collard, P. et al. Coherent spin-spin coupling mediated by virtual microwave photons. Phys. Rev. X 12, 021026 (2022).

    Google Scholar 

  57. Burkhart, L. Error-Detected Networking for 3D Circuit Quantum Electrodynamics. PhD thesis, Yale Univ. (2020).

  58. Pedregosa, F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).

    MathSciNet  Google Scholar 

  59. Geller, M. R. & Sun, M. Toward efficient correction of multiqubit measurement errors: pair correlation method. Quantum Sci. Technol. 6, 025009 (2021).

    Article  Google Scholar 

  60. Severin, J. B. Superconducting Qubit Readout In Theory, Experiment, And Simulation. Master’s thesis, Univ. of Copenhagen (2023).

  61. Lu, Y. et al. High-fidelity parametric beamsplitting with a parity-protected converter. Nat. Commun. 14, 5767 (2023).

    Article  Google Scholar 

  62. Dumas, M. F. et al. Measurement-induced transmon ionization. Phys. Rev. X 14, 041023 (2024).

    Google Scholar 

  63. Venkatraman, J., Xiao, X., Cortiñas, R. G., Eickbusch, A. & Devoret, M. H. Static effective Hamiltonian of a rapidly driven nonlinear system. Phys. Rev. Lett. 129, 100601 (2022).

    Article  MathSciNet  Google Scholar 

  64. Cohen, J., Petrescu, A., Shillito, R. & Blais, A. Reminiscence of classical chaos in driven transmons. PRX Quantum 4, 020312 (2023).

    Article  Google Scholar 

  65. Petrescu, A. et al. Accurate methods for the analysis of strong-drive effects in parametric gates. Phys. Rev. Appl. 19, 044003 (2023).

    Article  Google Scholar 

  66. Mavrogordatos, T. K. et al. Simultaneous bistability of qubit and resonator in circuit quantum electrodynamics. Phys. Rev. Lett. 118, 040402 (2017).

    Article  Google Scholar 

  67. Zhang, Y. et al. Engineering bilinear mode coupling in circuit QED: theory and experiment. Phys. Rev. A 99, 012314 (2019).

    Article  Google Scholar 

  68. Lescanne, R. et al. Escape of a driven quantum Josephson circuit into unconfined states. Phys. Rev. Appl. 11, 014030 (2019).

    Article  Google Scholar 

  69. Blais, A., Grimsmo, A. L., Girvin, S. M. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).

    Article  MathSciNet  Google Scholar 

  70. Mollenhauer, M. & Pfaff, W. Data for ‘high-efficiency elementary network of interchangeable superconducting qubit devices’. Illinois Data Bank https://doi.org/10.13012/B2IDB-6176441_V1 (2025).

  71. Krinner, S. et al. Engineering cryogenic setups for 100-qubit scale superconducting circuit systems. EPJ Quantum Technol. 6, 2 (2019).

    Article  Google Scholar 

Download references

Acknowledgements

The research was carried out in part in the Materials Research Lab Central Facilities and the Holonyak Micro and Nanotechnology Lab at the University of Illinois. We thank K. Chow and R. Goncalves for help with the fabrication, and B. DeMarco and A. Kou for critical reading of the manuscript. We acknowledge funding from the NSF Quantum Leap Challenge Institute for Hybrid Quantum Architectures and Networks (award no. 2016136), from the IBM-Illinois Discovery Accelerator Institute and the Army Research Office (grant no. W911NF-23-1-0096). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the US government.

Author information

Author notes

  1. These authors contributed equally: Michael Mollenhauer, Abdullah Irfan, Xi Cao.

Authors and Affiliations

  1. Department of Physics, University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Michael Mollenhauer, Abdullah Irfan, Xi Cao, Supriya Mandal & Wolfgang Pfaff

  2. Materials Research Laboratory, University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Wolfgang Pfaff

Authors
  1. Michael Mollenhauer
    View author publications

    Search author on:PubMed Google Scholar

  2. Abdullah Irfan
    View author publications

    Search author on:PubMed Google Scholar

  3. Xi Cao
    View author publications

    Search author on:PubMed Google Scholar

  4. Supriya Mandal
    View author publications

    Search author on:PubMed Google Scholar

  5. Wolfgang Pfaff
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.M. designed the device. M.M., A.I. and X.C. developed the theory models, conducted the experiment and analysed the data. S.M., M.M. and A.I. developed and tested the sideband pumping scheme. The paper was written by M.M., A.I., X.C. and W.P., with comments from all authors. W.P. supervised the work.

Corresponding author

Correspondence to Wolfgang Pfaff.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Electronics thanks Andrew Bestwick and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Experimental setup and wiring.

Most of the wiring follows standard best practices71. Noteworthy components: Low Pass (LP) filters: probe lines: 12 GHz (K&L 5L250-10200); pump lines: 1.8 GHz (Minicircuits VLF-1800+). Output line configuration: double-stage isolators (Low Noise Factory LNF-ISCIC4 12A), HEMT amplifier (Low Noise Factory LNF-LNC4 8C); room temperature low-noise amplifier (Low Noise Factory LNF-LNR4 14C). Room temperature electronics: signal modulation and demodulation: Quantum Machines OPX+ and Quantum Machines Octave; external RF generators: SignalCore SC5511A; pump signal amplifier: Mini-circuits ZHL-1-2W-S+.

Extended Data Fig. 2 Cable bus characterization.

a, Setup used to probe the modes of the coaxial cable in a reflection measurement. The inner conductor of the cable protrudes into a tunnel in the modules and capacitively couples to a pin connected to the SMA flange. b, CAD drawing of one of the cable modules. Top half has been made transparent to show the cable inner conductor (green) and coupling pin (gold) inside. c, Example reflection measurements of 3λ/2 modes of two cables (left: NbTi cable; right: Al cable) obtained with a vector network analyser; only phase response shown here. Fits (solid lines) to the data yield Qb = 3 × 104 (NbTi) and 5 × 105 (Al).

Extended Data Fig. 3 Sample holder design.

a, CAD drawings for a single transmon module, based on27. (Top) Full holder assembly, with cable clamp and cable bus included. Top half of the model made transparent to show the sample chip and exposed cable bus. (Middle) Side view of the holder. Copper clamps on each end hold the sample in place. Inside each clamp, a BeCu spring holds the chip in place with an estimated force of 250 grams. Aluminum cable clamp fastens around the cable and then mounts onto the side of the holder. (Bottom) Front view of the holder. Copper clamps made transparent to show the spacing between the cable inner conductor and sample. b, Exploded view of the actual device. c, Electric field simulation of the Al coaxial cable mode within one of the square modules shown in Extended Data Fig. 2a (left), and the sub-cut-off waveguide, with the sample and circuit elements modeled inside (right). Holders, cable clamp, and chip clamps have been outlined.

Extended Data Fig. 4 Bus-mediated qubit-qubit cross-Kerr.

Measurement of the direct dispersive interaction between the two qubits. We have measured Ramsey fringes on qubit 1, 4 μs after qubit 2 was prepared in either \(\left\vert {\rm{g}}\right\rangle\) or \(\left\vert {\rm{e}}\right\rangle\). Solid lines: sinusoidal fits.

Extended Data Fig. 5 Sideband spectroscopy and additional time-domain measurements.

a,d, Excited state population of qubits 1 (red) and 2 (blue) as a function of frequency and device input power of the microwave drives. Markers indicate where time-domain data was taken. Circles: Ω/2π ≈ 5 MHz (Fig. 2c,d). Triangles: Ω/2π ≈ 7 MHz (b,e). Squares: Ω/2π ≈ 10 MHz (c,f). Pentagon: Ω/2π ≈ 11 MHz (g). Qubit 1 displays additional transition(s) crossing the sideband resonance near the triangle marker, resulting in a broadened and asymmetric oscillation pattern (note the different scale on the detuning axis in b).

Extended Data Fig. 6 Time-dynamics of resonant Raman transitions.

a, Raman transitions between qubits 1 (red) and 2 (blue), immediately after tuning both sidebands individually to 5 MHz. The simulation (solid lines) matches the data (circles) with a 0.36 MHz detuning term on the bus (Eq. (6)). b,c, Simulation of the excited state population for qubits 1 (red) and 2 (blue) as a function of the drive detuning and time, assuming tuned up sidebands and no bus detuning. d,e, Data for the detuned swaps for the left and right qubit. In the simulation plots, ‘X’ marks a point of interest: in ref. 22 this point corresponds to an entangling gate. Here, we only predict a concurrence of 0.91 at this point, lower than what can be achieved using the stroboscopic approach shown in Fig. 3e of the main text.

Extended Data Fig. 7 Tuning up gates between qubits.

a, Example of a smooth pulse used to generate the swap gate. For this pulse shown, T = 160 ns, teff = 120 ns, and σ = 4 ns. Blacked dashed lines represent the effective gate time length. b, Excited state population for the right qubit as a function of consecutive gates for different effective gate times. Triangles, squares, and circles correspond to effective gate times of 139, 139.5, and 141.5 ns, respectively. Here, the 141.5 ns gate is best, as the exponential decay is indicative of least residual coherent error. c,d, excited state population for qubit 1 (red) and 2 (blue) as a function of the sideband gates applied where Ω/2π ≈ 5 MHz. Circles are data, squares are from simulation. Half-swap pulses are tuned between qubit 1 and bus, full-swap pulses between bus and qubit 2. The optimal effective sideband gate times for the left and right qubits are 52.6 ns and 101.8 ns, respectively.

Extended Data Fig. 8 Repeatability measurements.

Each iteration is a separate cycle of a bus re-mounted to a qubit package, cooled down and measured. Exception is iteration 8, where the device was not disassembled and reassembled from iteration 7, but only thermally cycled. Different markers represent different qubit samples and packages. Together, iterations 1 and 6 are the ones during which the main experiment data were collected. We have obtained ‘clean’ Sideband oscillations with Ω/2π ≈ 5 MHz in all iterations but iterations 7 and 8; there, we achieved only Ω/2π ≈ 4.5 MHz before observing high-power effects. a, Relaxation times (solid red), Ramsey (solid blue), and echo decay times (open blue). b, Qubit-bus dispersive shift χ (green) and bus lifetime (purple) across each iteration.

Extended Data Table 1 System parameters
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mollenhauer, M., Irfan, A., Cao, X. et al. A high-efficiency elementary network of interchangeable superconducting qubit devices. Nat Electron 8, 610–619 (2025). https://doi.org/10.1038/s41928-025-01404-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41928-025-01404-3

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing