Introduction

Over the past 30 years, task-based functional magnetic resonance imaging (fMRI) based on blood-oxygen-level-dependent (BOLD) signals has significantly advanced our knowledge of human brain function and organization. However, it has long been plagued with low reliability and reproducibility mainly due to the poor temporal signal-to-noise ratio of BOLD MRI data1,2. One of the main manifestations of this reproducibility issue is inconsistent activation locations across individuals for the same cognitive process. As a result, researchers have generally shielded away from studying individuals and resorted to group averaging to bolster the low statistical power of individual-level BOLD data to identify reliable group effects1. Unlike structural MRI, which reliably describes physical structures of individual brains and has clear clinical utility, the task fMRI study of individual differences and the translation to clinical applications has been limited to date due to the low reliability and reproducibility. Recent years have seen the research focus shifting from group averaging to individual subjects2,3,4,5, making the issue of reliability and reproducibility more pressing than ever before.

One issue concerning task fMRI studies is that reproducibility is mainly defined based on whether the same brain regions are activated6,7, ignoring connections between them. Recently, an increasing number of studies have indicated that brain functions better localize to connected networks than to isolated brain regions8,9,10. For example, Using lesion network mapping (LNM) technique developed by our group9, we found that neurologic and psychiatric symptoms such as prosopagnosia11, amnesia12, movement disorders13, and a variety of other symptoms9 correspond more closely to networks of connected regions than focal brain areas. In these studies, lesions that cause similar symptoms are located at different brain areas across patients but are part of the same network of connected regions. If heterogenous brain lesions across individual patients that cause the same symptoms are located at the same network9, why wouldn’t brain activations across individual subjects exhibit a similar pattern? Here, we propose that reproducibility of brain activations across individuals should be redefined in terms of brain connectivity and network. We hypothesize that the seemingly poor reproducibility of brain activations localizes, in reality, to a highly reproducible network of connected brain regions and that many of these heterogeneous brain activations are part of the same network.

As an initial test of this hypothesis, we focused on individuals’ brain activation during working memory (WM). We chose WM based on several factors. First, WM is one of the most studied cognitive tasks. Second, previous evidence suggests that WM localizes better to a brain network than to isolated brain regions14. Third, individual differences in WM behavioral performance within the healthy population are broader than those of other psychological processes that have been commonly evaluated with task fMRI protocols. This range of behavioral variation is crucial for brain-behavior prediction analyses. As a result, WM has been frequently employed to study individual differences and brain-behavior prediction analyses in healthy populations15,16,17,18,19,20,21.

To identify the brain network associated with WM in individuals, we used our recently proposed technique termed activation network mapping (ANM)22. ANM identifies the brain regions that are functionally connected to the location of brain activation using a large resting-state normative connectome database (n = 1000). The use of resting-state fMRI data is based on the critical observation that the degree to which brain regions are commonly activated together during a task state is reflected in resting-state network architecture23,24,25. ANM has been used to identify human brain networks associated with emotion processing22, substance use disorders26, suicide27, and a variety of other mental functions28,29,30. However, so far ANM has only been used as a network-based meta-analytic technique, in comparison to the discrete-brain-based activation likelihood estimation meta-analytic technique6,31, to integrate findings from multiple neuroimaging studies. No study has used this new technique to identify individual brain networks of cognitive processes.

In the present study, we combined publicly available, high-quality Human Connectome Project (HCP) datasets with the ANM technique to test whether individual activation locations associated with WM localize to a specific human brain network. First, we tested whether heterogeneous brain activations during WM across individuals localize to a common network. Second, we evaluated the specificity of the identified WM network by comparing it to those of other cognitive tasks included in the HCP dataset. Third, capitalizing on recent advances in machine learning techniques, we tested whether the identified individual-level WM brain network predicts individual differences in WM performance.

Results

Single-subject activations are heterogeneous

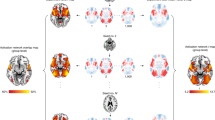
To identify the brain activations of each subject during a WM task, we contrasted brain activations during a 2-back condition with that during a 0-back condition at the individual subject level. Then, significantly activated regions were binarized and overlapped across all participants to identify regions consistently showing activation in the highest number of participants. As shown in Fig. 1a, b, there was significant heterogeneity in activation locations across individual subjects. Only 50% of subjects showed activations in the most convergent brain region (i.e., the cluster with the highest percentage of overlap). 25–50% of the subjects demonstrated activation in the bilateral dorsal and ventral prefrontal cortex, dorsal anterior cingulate cortex, and dorsal parietal cortex.

Fig. 1: Network localization explains the poor reproducibility of WM-related brain activations across individuals.
figure 1

a Activation maps of three representative subjects from the HCP dataset. b Percentage of single-subject activation maps overlapping in the same location. There is significant heterogeneity in the location of individual brain activations (N = 100), with only 50% of subjects showing activations in the most convergent brain region. c Percentage of single-subject activation network maps based on normative connectome overlap in the same location. These heterogeneous activations were functionally connected to a common set of brain regions. d Percentage of single-subject activation network maps based on the subject’s own connectome overlapping in the same location. Similar results were obtained when using each subject’s own resting-state connectome to derive activation networks, with roughly the same set of brain regions commonly connected. e Dice indices between each pair of activation network maps derived from either the normative connectome (t9898 = −248.55, p < 0.0001) or the subject’s own connectome (t9898 = −245.26, p < 0.0001) were significantly greater than those of the activation maps. Boxplots indicate the 25th to 75th percentiles (colored areas) and median (central lines). Whiskers represent the most extreme data points not considered outliers (minimum and maximum). Black circles show outliers (values more than q75 + 1.5 × (q75 − q25)) or less than q25 − 1.5 × (q75 − q25). ***P < 0.001.

Full size image

Heterogeneous activations across subjects localize to a common network

We hypothesized that heterogeneous WM brain activations across individuals would localize to a common brain network. To test this hypothesis, we utilized a recently developed technique termed ANM to identify the brain regions that were functionally connected to each subject’s location of activation. Although activation locations were heterogeneous among individuals, with no regions detected in >50% of participants (Fig. 1b), they were indeed functionally connected to a common set of brain regions (Fig. 1c). Specifically, more than 90% of subjects had activations commonly connected to the bilateral lateral prefrontal cortex, parietal cortex, cingulate gyrus, inferior temporal gyrus, and subcortical regions such as the thalamus and basal ganglia. Similar findings were obtained when using each subject’s own resting-state connectome to derive activation networks (Fig. 1d), with roughly the same set of brain regions commonly connected.

To provide a more quantitative measure of consistency, we computed the Dice index (DI) for each pair of binarized activation maps (see subsection “Activation map” of section “Methods”) and connectivity maps (see subsection “ANM” of section “Methods”) separately. A higher DI indicates greater similarity between the maps. As shown in Fig. 1e, the Dice indices for activation network maps derived from either the normative connectome (t9898 = −248.55, p < 0.0001) or the subject’s own connectome (t9898 = −245.26, p < 0.0001) were significantly greater than those of the activation maps.

Interestingly, although the consistency of brain activations between subjects was far lower than that between the activation networks, the patterns between these two maps were similar. The most commonly activated regions were also the most commonly connected regions. This indicates that these heterogeneously activated regions are located in different parts of the same network.

Robustness analysis

Matching the number of suprathreshold voxels between the activation map and activation network map

To confirm that the observed higher consistency across individual activation network maps was not driven by the presence of more suprathreshold voxels in the activation network maps than in the activation maps, we deliberately applied the same top 5% threshold to both the activation map and activation network map. This ensured that the number of suprathreshold voxels in these two types of maps remains equivalent. As illustrated in Fig. 2, our findings revealed that the interindividual consistency of activation networks remains notably greater than that of individual activations. Dice indices remained significantly greater for activation network maps derived from either the normative connectome (t9898 = −100.21, p < 0.0001) or the subject’s own connectome (t9898 = −91.59, p < 0.0001) compared to the activation maps (Fig. 2d).

Fig. 2: Interindividual consistency of the WM network map remains notably greater than that of the activation map when the percentage of suprathreshold voxels in these two types of maps was deliberately matched.
figure 2

a Percentage of single-subject activation maps (N = 100) overlapping in the same location. b Percentage of activation network maps based on the normative connectome overlapping in the same location. c Percentage of activation network maps based on the subject’s own connectome overlapping in the same location. d Dice indices between each pair of activation network maps derived from either the normative connectome (t9898 = −100.21, p < 0.0001) or the subject’s own connectome (t9898 = −91.59, p < 0.0001) were significantly greater than those of activation maps. Whiskers represent the most extreme data points not considered outliers (minimum and maximum). Black circles show outliers (values more than q75 + 1.5 × (q75 − q25)) or less than q25 − 1.5 × (q75 − q25). ***P < 0.001.

Full size image

Replacing the activation maps with the activation peaks as seeds in ANM analyses

To confirm that the pattern of the localized network was not driven by the distributed nature of the activation map used as seed, we repeated these ANM analyses solely using the peak of each activation map as the seed for each subject. As shown in Fig. 3, there was significant heterogeneity in the locations of the activation peak across individual participants, with only 8 out of the 100 activation peaks commonly located in the most convergent brain region. However, more than 80% of these peaks were functionally connected to common brain regions in the lateral and medial prefrontal cortex, parietal cortex, and inferior temporal gyrus. The pattern of the network is highly similar to that derived using distributed activation maps as a seed (spatial correlation r = 0.89 for unthresholded network overlap map). Of note, since the pattern of the activation peak overlap map (Fig. 3b) and activation network overlap map (Fig. 1c) are highly similar, it indicates that even though the location of the activation peaks are heterogeneous across participants, most of them are located in different parts of the same network derived from the ANM analyses.

Fig. 3: The pattern of the network derived using the activation peak as the seed is highly similar to that derived using the distributed activation map as the seed (spatial correlation r = 0.89 for the unthresholded network overlap map).
figure 3

a Activation peaks of the above three representative subjects from the HCP dataset. b The locations of the activation peaks across individual participants (N = 100) were highly heterogeneous, with only 8 out of the 100 activation peaks commonly located in the most convergent brain region. c However, these heterogeneous activation peaks were functionally connected to common set of brain regions. Notably, since the pattern of the activation peak overlap map (b) and activation network overlap map (Fig. 1c) are highly similar, it indicates that even though the location of the activation peaks are heterogeneous across participants, most of them are located in different parts of the same network derived from ANM analyses.

Full size image

Specificity of the WM network identified via ANM

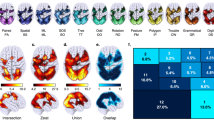
To determine whether the ANM-localized network was specific to WM, we used the remaining six tasks in the HCP dataset (emotion processing, social cognition, gambling, motor, relational processing, and language processing) as control tasks, and compared the localized WM network to those of the control tasks. We performed ANM analyses on activations of the control tasks as above, then pooled the resulting networks together, and compared it with those of WM. As shown in Fig. 4b, the significant overlap between the WM activation network overlap map (Fig. 1c) and specificity map (Fig. 4a) indicates that the above commonly connected brain regions were also specific to WM. In other words, activations during WM were significantly more connected to these regions compared with activations of the control tasks.

Fig. 4: The ANM-localized WM network is specific when compared to that of control tasks.
figure 4

a The specificity map associated with WM was obtained by comparing the ANM-localized WM network with the ANM-localized brain network of the control tasks using a nonparametric Liebermeister test. b The significant overlap between the WM activation network overlap map (Fig. 1c) and the specificity map indicates that the commonly connected brain regions (>80%) were also specific to WM.

Full size image

Networks identified using ANM predict individual differences in WM performance

Having identified each subject’s WM brain network using the ANM technique, we next investigated whether these networks could predict individual differences in WM performance. We used ridge regression, a machine learning technique, with nested leave-one-out cross-validation (LOOCV) paradigm for prediction. The accuracy of 2-back trials in the WM paradigm was used as a behavioral measure of WM performance. We used three types of binarized maps to predict WM behavioral scores separately: activation maps, activation network maps based on the normative connectome (n = 1000), and activation network maps based on the subject’s own connectome. We found that while activation maps accounted for only 6% of the variance in WM scores (Fig. 5a), the activation network maps derived from these activation maps based on the normative connectome explained 27% of the variance (Fig. 5b). Two-sample paired t-tests showed that activation networks performed better than activation maps in predicting WM scores (t98 = 2.11, p = 0.037). A similar predictive ability was obtained (R2 = 0.24, p < 0.0001) when using unthresholded activation network maps (based on the normative connectome) to predict WM behavioral scores.

Fig. 5: Subject-level brain network of WM identified using the ANM predicts individual differences in WM behavioral performance.
figure 5

Scatter plots show correlations between the observed WM behavioral scores and predicted scores from the activation-behavioral model (a) and activation network-behavioral models (b, c). Each dot represents one subject. Brain networks identified using ANM analyses with a normative connectome (b) predict WM performance significantly better than WM-related brain activations (t98 = 2.11, p = 0.037). Prediction models were iteratively trained based on image and behavioral data from n − 1 subjects and tested based on image and behavioral data from the left-out individual.

Full size image

The binarized activation network maps based on the subject’s own connectome explained 18% of the variance (Fig. 5c). Combining all three types of maps as predictors did not result in better predictive performance (R2 = 0.07, p < 0.0001).

To confirm that the observed differences in the predictions between the activation prediction model and the activation network prediction model were not solely driven by the presence of more suprathreshold voxels in the activation network maps than in the activation maps, we repeated the prediction analyses using the above “top 5%” thresholded activation map and activation network map as predictors. As shown in Supplementary Fig. 1, similar pattern of predictions was obtained, with activation maps accounting for 10% of the variance in WM scores, while the activation network maps derived from these activations explained 23% and 17% of the variance for normative connectome and the subject’s own connectome, respectively.

To assess the specificity of the prediction of the activation network, we repeated the prediction analyses by using activation network maps for each of the six control tasks to predict WM behavioral performance. The results (Fig. 6) indicate that the predictive ability of the WM activation network identified via the ANM analysis was specific. The activation network of all six control tasks failed to predict WM performance. Five of the six control tasks had a negative R2 values, indicating that the prediction performed poorly32.

Fig. 6: The predictive ability of the WM activation networks identified via ANM is specific compared to those of the six control tasks.
figure 6

To assess the specificity of the prediction of the activation network, we repeated the prediction analyses by using activation network maps of each of the six control tasks to predict WM behavioral performance. The activation networks of all six control tasks failed to predict WM performance. The red bar represents a significant prediction, whereas the blue bars represent nonsignificant or failed predictions. ***p < 0.0001.

Full size image

The weights from the activation and activation network prediction models were averaged across all leave-one-out models and projected back onto the brain, respectively (Fig. 7). For the activation prediction model, the most positive weights were mainly located in commonly activated regions, such as the lateral prefrontal cortex, somatosensory association cortex, and temporoparietal junction. Negative predictive weights mainly occurred in the primary motor and sensory cortices, thalamus, and occipital and temporal regions.

Fig. 7: Contribution weights from activation-behavioral and activation network-behavioral prediction models.
figure 7

Predictive weights for the activation-behavioral model (a) and activation network-behavioral models (b, c) are projected back onto the brain. For illustration purposes, the top 25% of voxels in terms of feature importance (i.e., the top 25% absolute contribution weight) are displayed. Red indicates positive weights (i.e., activation or positive connection predicts better WM performance), and blue indicates negative weights (i.e., activation or positive connection predicts worse WM performance).

Full size image

For the activation network prediction model based on the normative connectome, the most predictive positive weights occurred in the lateral prefrontal cortex, primary motor and sensory cortices, and occipital and inferior temporal regions, while negative weights occur in the medial and dorsal frontal regions and temporal cortices, among other regions. Similar contribution weight patterns were observed in the activation network prediction model based on the subject’s own connectome.

Discussion

We obtained the following noteworthy results in this study. First, although the results of subject-level discrete brain activations during WM indicate that reproducibility is relatively low, they are indeed highly reproducible in terms of connectivity and network. Second, prediction analyses using machine learning algorithms indicated that ANM-localized network can predict WM behavioral performance. This predictive ability is even better than that of the brain activations these networks were derived from. Finally, our study is the first to provide direct empirical evidence supporting the prevailing practice of approximating the subject’s own connectome using an indirect normative connectome in LNM studies. These results suggest that network localization may help reconcile heterogeneous brain activations across individuals, thereby improving our ability to link cognitive functions to neuroanatomy. It indicates that ANM can be used as a new technique for identifying individual brain networks of cognitive processes, thus promising broad potential applications.

Brain activations during WM showed common functional connectivity (FC) to the bilateral lateral prefrontal cortex, parietal cortex, cingulate gyrus, inferior temporal gyrus, thalamus, and basal ganglia, among other regions. Damage to most regions in this network has been associated with disruption of WM33,34,35,36,37,38,39,40. This network largely overlaps with the frontoparietal control network41,42, which has been shown to be crucial for WM43,44. The frontoparietal control network mediates a wide range of cognitive processes by flexibly adapting its functions in response to changing behavioral goals43. Studies using fMRI and electroencephalography in humans have shown that stronger frontoparietal FC45,46 and structural connectivity47,48,49 are associated with greater WM capacity. Furthermore, transcranial magnetic stimulation applied to the left dorsolateral prefrontal cortex can disrupt verbal WM performance in humans50. Training studies have also shown increased frontoparietal connectivity after WM training51,52,53,54. In addition, the basal ganglia contribute a selective gating mechanism that disinhibits thalamocortical loops and regulates the influence of incoming stimuli on the WM system55. Together with the lateral prefrontal cortex, these regions exert attentional control over access to WM storage in the parietal cortex in humans55. The inferior parietal lobules of the ANM identified WM network have been implicated in multiple problem-solving and visual-spatial tasks, both of which rely heavily on WM56,57,58.

The primary contributing factors to the low replicability of WM activation across individuals are the relatively short scan time (5–20 min) and low temporal signal-to-noise ratio of BOLD MRI data59. Because of these, fMRI research approaches have generally shied away from studying individuals, with the notable exception of projects focused on individuals such as MyConnectome60, Midnight Scan Club2, et al. Instead, much of Task based fMRI studies focused on examining the group-average brain. The low statistical power resulted from these contributors means that only strongly activated neural components (such as hub regions) of the network could survive the statistical threshold, leaving weakly activated regions undetected. A direct solution to the low statistical power problem is to increase the scanning time. For example, to understand functional brain organization at the individual humans, Gordon et al. 2 scanned 5 h of RSFC data and 6 h of task fMRI data for ten healthy subjects. They found that the set of brain regions activated during various motor tasks are highly replicable across these ten highly sampled subjects. Moreover, they found that these task-evoked BOLD responses align closely with individual-specific networks derived from resting-state data. However, due to the high cost associated with obtaining MRI data, acquiring such a large amount of data from a single subject is impractical for standard neuroimaging research. In this case, ANM can be viewed as an indirect solution to the low statistical power problem. The essence of ANM is to take advantage of the high statistical power guaranteed by the large resting-state normative human connectome (1000 subjects) and use seed-based RSFC approach to recover the undetected part of a distributed set of brain regions (i.e., network) responsible for a cognitive process22. Consistent with the above findings by Gordon et al, we found that the same set of distributed brain regions identified via ANM were commonly activated across individuals.

So far there are three main types of extensions of the LNM technique: ANM, atrophy network mapping and DBS network mapping. These extensions can also be called coordinate network mapping if the seed was derived from peaks or coordinates. Both LNM and its extensions use a third-party normative functional connectome to indirectly identify the FC network of each healthy subject or patient. The major difference is that ANM, atrophy network mapping, and DBS network mapping use brain activations, atrophy, and stimulation sites as seeds respectively, while LNM uses brain lesion instead. Since LNM was proposed, it has been successfully applied in numerous studies to investigate network dysfunction in a whole host of neurological and psychiatric conditions9,61. However, recent brain-behavior prediction studies62,63,64 have indicated that brain networks identified via LNM perform poorly in predicting behavioral deficits. In these prediction studies, the authors used both the brain lesions and brain networks derived from these lesions via LNM to predict behavioral deficits. They found that while brain lesions performed moderately in predicting behavioral deficits, the brain network identified via LNM exhibited surprisingly poor performance. In direct contrast to the findings of these studies, we showed that individual brain networks identified via ANM have a sound prediction of behavioral scores. In fact, it performed even better than brain activations it derived from in predicting WM behavioral scores.

A plausible explanation for the seemingly contradictory results of prediction between LNM and ANM may lie in the difference between using brain lesion and activation as seed. In LNM studies, large lesions, such as those from large vessel ischemic strokes, tend to be heavily represented in lesion cohorts. This is problematic in two ways62,65. First, these lesions can span both gray and white matter. LNM is quite limited in how it accounts for disrupted white matter contributing to deficits. Second, large lesions are likely to contain multiple regions that belong to different networks, thus the signal averaging of the BOLD signal within the lesion mask is problematic and the resulting FC map identified via LNM may be confounded by unrelated networks. In contrast, using brain activations as seeds in ANM studies can avoid these problems. Brain activations are normally limited to gray matter and are associated with the specific cognitive process of interest. Moreover, prior work has shown that individual task-evoked BOLD responses align closely with individual-specific networks derived from resting-state data2. Other possible explanations for the prediction difference between LNM and ANM are the recovery from brain injury and the time gap between the time of lesioning and behavioral testing.

A frequently cited limitation of LNM is the use of an indirect large normative connectome, rather than the individual’s own connectome, to identify regions functionally connected to each lesion location11,66,67. This approach is unable to account for individual differences in age, gender, or co-morbidities which can impact connectivity. Such an indirect approach for assessing functional connection is motivated by the objective difficulty of measuring functional MRI imaging in acute neuropsychiatric patients or rare patient groups. However, whether the normative connectome can replace the subject’s own connectome for connection estimation hasn’t been supported by empirical evidence so far. Our study is the first to address this gap by providing direct evidence in favor of this indirect approach. Our findings indicate that the brain network of WM identified using indirect normative connectome and the subject’s own connectome are highly consistent. Notably, the brain network of WM identified using indirect normative connectome, compared with the subject’s own connectome, were more consistent across individuals and performed better in predicting WM performance. This improvement is likely due to the highly improved signal to noise ratio guaranteed by the large sample size of the normative connectome. Alternatively, signal to noise ratio can be improved by increasing individual’s scan time. For example, Laumann et al. 4 repeatedly scanned one individual over more than a year, accumulating 14 h of resting state fMRI. They found that the individual’s systems-level network organization is broadly similar to that of a normative group. Together with Laumann’s findings, our findings provide direct support for the rationale of replacing the subject’s own connectome with a normative connectome in both LNM and ANM.

Notably, in the activation network prediction models, the brain regions exhibiting the highest weights, indicating the highest predictive power, are not necessarily the most commonly connected regions. This is expected, as we used the binarized activation network maps as predictors. The variances of voxel values in these most commonly connected regions are relatively low because more than 80% of subjects have a voxel value of 1 within these regions, meaning significantly connected, within these regions.

There are several limitations to this study. First, since our main focus here is the location of activation and connectivity, we binarized brain regions that are statistically significantly activated or connected and used it as input in the main consistency and prediction analyses, rather than the unthresholded activation map or activation network map. As such, some meaningful information in the unthresholded map might be lost. However, our findings indicated that both the unthresholded and binarized activation network map have similar predictive power. Second, functional neuroimaging research provides correlational but not necessarily causal information68. Even though previous lesion and neuromodulation studies of WM indicated that most components of the WM network identified via ANM were causally involved in WM (see “Discussion”), quantitative validation analyses are needed to test the causal role of our identified WM network in a data-driven manner. For example, since lesion studies allow for causal inferences between neuroanatomical structures and human behaviors, future studies can test whether the established ANM prediction model in this study can predict WM impairment in independent lesion dataset of patients with WM-related symptoms. Third, we found that heterogeneous brain activations across individuals share connectivity to common brain regions, but this does not preclude a role for individual WM networks that may differ between subjects. It rather suggests the coexistence of both common and distinct networks across individuals. Consistent with the findings from previous studies4,69, we found that the WM brain networks are similar overall between subjects, albeit with minor differences in detail. Finally, we focused on WM-related brain activations, which may have a higher probability of localizing to a common brain network than brain activations in other cognitive processes. To test whether the principle of “heterogenous activations across individuals during the same cognitive process localize to a common brain network” is a general rule, it will be necessary to use ANM to localize networks of other cognitive processes at individual level.

Methods

This work utilized the public HCP dataset and did not involve the collection of new data. The research protocol was approved by the Research Ethics Committee of Beijing Normal University. All analyses were conducted in voxel space and then projected onto surface space for illustration purposes. To be consistent, all voxel-level statistical analyses were thresholded at voxelwise familywise error (FWE)-corrected P < 0.05.

Participants

We used behavioral and functional imaging data from the Washington University-Minnesota Consortium HCP 1200 Subjects Data Release, which are publicly available at https://www.humanconnectome.org/study/hcp-young-adult. All ethical regulations relevant to human research participants were followed in the collection of this dataset. 100 subjects were randomly selected from a total of 850 healthy subjects that have completed the full HCP 3T MRI protocol, which includes 14 task scans (2 scans per each of the 7 tasks: WM, emotion processing, social cognition, gambling, motor, relational processing, and language processing) and four resting-state scans (two L/R phase encoding scans and two R/L phase encoding scans)70,71.

HCP WM task

In the WM task, a version of the N-back task was used to assess WM70. Specifically, within each scan, four different types of stimuli (pictures of places, faces, body parts, and tools) are presented in separate blocks. Half of the blocks used 0-back WM task, in which a target cue was displayed at the beginning of each block. Subjects are instructed to respond to any “target” stimuli that appeared during the block; the other half of the blocks used 2-back WM task, in which subjects are instructed to respond whenever the current stimuli match the stimuli two trials back within the same block. Each scan contains 8 task blocks (10 trials of 2.5 s each, for 25 s) and 4 fixation blocks (15 s). on each trial, the stimulus is displayed for 2 s, then followed by a 500 ms inter-trial-interval (ITI). The contrast of interest is 2-back > 0-back when modeling brain activations. The behavioral metric for WM performance is the mean accuracy across all four types of stimuli in the “2-back” group.

HCP control tasks

A detailed description of the remaining six control task paradigms included in the HCP dataset can be found in previous work70. Briefly, the gambling reward task consisted of a card-guessing game in which subjects were instructed to guess the number on the card to win or lose money. The contrast of interest was the reward versus baseline. The language task consisted of blocks of a story task that involved answering questions related to a story and a math task that involved basic arithmetic questions. Both tasks were auditorily presented. The contrast of interest was the “story” condition versus the “math” condition. In the motor task, participants were asked to either tap their left or right fingers, squeeze their left or right toes, or move their tongue. The contrast of interest was the movement versus baseline. In the emotion processing task, participants were instructed to make valence judgments on fearful, angry, and neutral faces. The contrast of interest was the emotional faces versus the shapes. In the social cognition task (theory of mind), participants viewed video clips of shapes (squares, circles, triangles) that either interacted socially or moved randomly on the screen. Subsequently, the subjects were asked whether the objects interacted in a social manner. The contrast of interest was social versus random interactions. In the relational processing task, participants were instructed to determine whether two sets of objects differed from each other along the same dimension (i.e., texture or shape). The contrast of interest was relational versus match.

fMRI data acquisition and preprocessing

Both resting-state and task-state fMRI data were acquired on a 3 T Siemens Skyra with a 32-channel coil using a slice-accelerated, multiband, gradient-echo, echo planar imaging (EPI) sequence with the following parameters: TR = 720 ms, TE = 33.1 ms, flip angle = 52°, resolution = 2 mm, multiband factor = 8, field of view = 280 ×  180 mm72,73. Scans were repeated twice using left-to-right (LR) and right-to-left (RL) phase encoding directions. Detailed description of the preprocessing procedure of resting-state fMRI data can be found in a previously published study from our lab22. Preprocessing of the task fMRI data was conducted using the HCP “fMRIVolume” pipeline74, which generate minimally preprocessed data. This preprocessing pipeline includes gradient unwarping, motion correction, fieldmap-based EPI distortion correction, registration of EPI to structural T1-weighted scan, non-linear (FNIRT) registration to standard space, and intensity normalization to a global mean of 10,000. Spatial smoothing was then applied using a 4 mm FWHM Gaussian kernel.

Activation map

To identify WM-related brain activations for each of the 100 subjects, we used the general linear model (GLM) implemented in FSL’s FILM to compute the model estimation of the preprocessed task fMRI data. Eight predictors were included in the model: four for 0-back condition (one for each of the four stimulus types) and the other four for 2-back condition. The duration of each predictor is 27.5 s, which covered the period from the onset of the cue to the offset of the final trial. To compensate for slice-timing differences and variability in the BOLD hemodynamic response (HRF) delay across regions, temporal derivative terms derived from each predictor were regressed as confounds of no interest. Subsequently, both the 4D timeseries and the GLM design were temporally filtered with a high-pass filtering at 200 s and prewhitened using FSL’s “film_gls” to correct for autocorrelations75. For each subject, fixed effect analyses were performed to estimate the average effect of the contrast between the 2-back and 0-back conditions across both runs. The resulting subject-level z-score maps were thresholded at voxelwise FWE-corrected P < 0.05 and binarized. The single-subject activation map for each of the six control tasks were identified using the same method as above.

Activation network mapping

Next, using a recently validated technique termed ANM Fig. 8 proposed by our group22, we identified the individual-level WM activation network map. This activation network was defined as brain regions that were functionally connected to the brain activations (i.e., the binarized activation map obtained in the previous step) of each subject during the N-back WM task. For a detailed description of ANM, please refer to our prior work22. Specifically, using a resting-state normative connectome of 1000 subjects (for a detailed description of this connectome, please see our prior work22, in which the same normative connectome was used), we regarded each single-subject binarized activation map as a seed (hereafter called the “activation seed”) and averaged the BOLD time course for all voxels within the activation seed. Then, we correlated this time course with the BOLD time course at every voxel in the whole brain. Each of the resulting 1000 r maps was converted to a Fisher z map using Fisher’s z transformation. To identify brain regions with significant connectivity, these 1000 Fisher z maps were compared against zero using a voxelwise one-sample t-test, yielding a network t map for each of the above 100 subjects. Each of the 100 individual network t maps was thresholded at voxelwise FWE-corrected P < 0.05 and binarized. The individual-level activation network maps for the six control tasks were obtained using the same method as above.

Fig. 8: Activation network mapping technique.
figure 8

a Task-based brain activations of three subjects. The activation map of each subject was generated by measuring changes in the BOLD signal associated with the WM task. b Brain regions functionally connected to each subject’s brain activations (activation map) were identified using a large resting-state functional connectivity database (n = 1000). c Overlap of the binarized functional connectivity maps identifying brain regions that were functionally connected to the greatest number of subject-level activations.

Full size image

Finally, as a way to evaluate consistency between subjects, all binarized activation network maps were overlapped and thresholded at 80% to create an activation network overlap map. The suprathreshold clusters in this overlap map were brain regions that were functionally connected to more than 80% of the activation seeds. To provide a more quantitative measure of consistency, we computed the DI of similarity for each pair of binarized activation network maps. The DI is calculated as follows:

$${{\rm{DI}}}=\frac{2\times {V}_{{{\rm{overlap}}}}}{\left({V}_{1}+{V}_{2}\right)}$$

where \({V}_{1}\) and \({V}_{2}\) represent the number of suprathreshold voxels in each pair of binarized maps and \({V}_{{\rm{overlap}}}\) is the number of overlapping voxels between these two binarized maps.

In addition to the above normative connectome, we used the subject’s own resting-state connectome to construct an activation network map. Specifically, the four resting-state scans from each subject were concatenated. Then, seed-based RSFC analysis was performed based on the subject’s own resting-state connectome to derive a correlation r map using each subject’s activation map as a seed. To identify significantly connected brain regions, the correlation r map was compared against zero and thresholded at voxelwise FWE-corrected P < 0.05 and then binarized.

Robustness analysis

Two control analyses were conducted to test the robustness of the results. First, when comparing the consistency between the activation map and the activation network map associated with WM, we performed a more balanced comparison, in which we deliberately matched the percentage of suprathreshold (top 5%) voxels between the activation map and activation network map from the same subject. Then, the thresholded activation maps and activation network maps were binarized and overlapped, as described above. Second, to confirm that the pattern of the ANM localized network was not driven by the distributed nature of the activation map used as a seed, we used the peak of brain activations as a seed instead. Specifically, we created an 8-mm radius sphere centered on each subject’s peak activation location (the maximum of the largest cluster in each subject’s activation map). Then, we repeated the ANM analyses using these spheres as seeds to test whether similar WM activation network maps were generated.

Specificity of ANM

The specificity of the WM network localized via ANM was assessed by comparing the activation network maps associated with WM to those associated with the six control tasks. Specifically, we compared the above binarized activation network t maps associated with WM (N = 100) with those associated with the control tasks (N = 600) using a nonparametric Liebermeister test implemented in NiiStat software (www.nitrc.org/projects/niistat). As recommended in prior work76, only voxels surviving more than 10% of the binarized activation network maps were included in the statistical analysis. Voxel-level FWE-corrected P < 0.05 were used for multiple comparison with a total of 5000 permutations.

Prediction of WM behavioral performance

The activation-behavior and activation network-behavior relationships were analyzed using multivariate nested leave-one-out ridge regression machine learning algorithms (Supplementary Fig. 1). Ridge regression differs from multiple linear regression by using L2 penalty to regularize model coefficients so that unimportant features are automatically eliminated or down-weighted. It prevents overfitting and improves the prediction accuracy and generalization77. Before training the machine learning algorithm, principal component analysis (PCA) was performed to reduce dimensionality while retaining meaningful differences in the input data. PCA was carried out on 238,955 2-mm2 brain voxels (whole brain), and each single brain voxel was treated as a predictor. All these predictors were standardized before applying PCA. The components that explained 95% of the variance were retained.

The ridge regression algorithm can be formulated as follows:

$${{\mbox{arg}}\,\min }_{w}\frac{1}{n}{\sum }_{i=1}^{n}{({\overrightarrow{w}}^{T}{\overrightarrow{x}}_{i}-{\overrightarrow{y}}_{i})}^{2}+{\lambda \Vert \overrightarrow{w}\Vert }_{2}^{2}$$

The x vector is the activation or activation network map (in PCA space). The y vector is the behavioral score. The ω vector indicates the relative importance (weight) of each feature in x to the prediction of y. λ is a regularization coefficient that is determined empirically. The closed-form solution for the weight vector is as follows:

Let \(X={\left[{\vec{x}}_{1},{\vec{x}}_{2},\ldots {\vec{x}}_{n}\right]}^{T}\) and \(Y={\left[{\vec{y}}_{1},{\vec{y}}_{2},\ldots {\vec{y}}_{n}\right]}^{T}\)

$$\omega ={\left(X{X}^{T}+\lambda I\right)}^{-1}X{Y}^{T}$$

We used the scikit-learn library to implement the ridge regression algorithm78.

We applied nested leave-one-(subject)-out cross validation (LOOCV), with the outer LOOCV loop estimating the generalizability of the model and the inner LOOCV loop determining the optimal parameter λ for the ridge regression model79. Nested cross-validation provides a more unbiased and reliable evaluation of a model’s performance by separating hyperparameter tuning from model selection, thereby reducing the risk of overfitting and selection bias compared to non-nested cross-validation79,80. The coefficient of determination was used to assess model accuracy:

$${R}^{2}=1-\frac{\sum {\left(Y-{Y}^{{\prime} }\right)}^{2}}{\sum {\left(Y-\bar{Y}\right)}^{2}}$$

where \(Y\) is the actual behavior score, \(\bar{Y}\) is the mean of the actual behavior scores and \({Y}^{{\prime} }\) is the predicted behavior score.

In each inner LOOCV loop, λ was optimized by identifying a value from 10−5 to 105 (logarithmic steps) that minimized the leave-one-out prediction error over the training set (i.e., maximizing the coefficient of determination \({R}^{2}\)). The optimal λ was then used in the outer LOOCV loop to train a model using n − 1 subjects in the training set. Then, the trained model was used to predict the outcome of the nth subject in the testing set.

A permutation test was performed to evaluate whether the prediction performance was significantly better than chance. Specifically, the above prediction procedure was repeated 10,000 times (permutations). In each permutation, the behavioral scores were randomly permuted across subjects, and the prediction accuracy (\({R}^{2}\)) was subsequently computed. The significance was calculated by ranking the actual prediction accuracy versus the permuted distribution; the p value of the model accuracy is the proportion of permutations that showed a higher prediction accuracy than that from the real data.

Statistical comparisons of prediction performance between models (i.e., the activation-behavior versus activation network-behavior models) were performed in terms of prediction errors, which were calculated as the squared difference between the actual and predicted behavior scores for each subject. Then, the prediction errors between these two models were compared using the two-sample paired t-test to determine which model performed better in terms of prediction.

To visualize the feature weights, the regression weight matrix was averaged across all outer LOOCV loops to obtain a single set of consensus weights. The statistical significance of each consensus weight was computed by comparing its value to the null distribution generated from the above permutation test and then FWE-corrected for multiple comparisons. The statistically significant consensus weights were projected back to the brain space using the transpose matrix of the principal component (PC) coefficients to construct a map containing the most predictive voxels. For illustration purposes, the top 25% of voxels in terms of feature importance (i.e., the top 25% absolute contribution weights) are displayed.

We also conducted an additional ridge regression analysis by combining an activation map and an activation network map as predictors to evaluate whether the combined information can increase the prediction accuracy.

Statistics and reproducibility

The activation-behavior and activation network-behavior relationships were analyzed using multivariate nested leave-one-out ridge regression machine learning algorithms. Before training the machine learning algorithm, PCA was performed to reduce dimensionality while retaining meaningful differences in the input data. A permutation test was performed to evaluate whether the prediction performance was significantly better than chance. two-sample paired t-test to determine which model performed better in terms of prediction. This analysis was two-sided, and statistical significance was assessed at the standard alpha threshold of 0.05. Two analyses were conducted to test the reproducibility of the results. First, when comparing the consistency between the activation map and the activation network map associated with WM, we performed a more balanced comparison, in which we deliberately matched the percentage of suprathreshold (top 5%) voxels between the activation map and activation network map from the same subject. Second, to confirm that the pattern of the ANM localized network was not driven by the distributed nature of the activation map used as a seed, we used the peak of brain activations as a seed instead.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.