Introduction

Cryogenic electron microscopy (cryo-EM)1 is a modern biophysical technique for protein structure determination. Protein complexes in solution are frozen and then imaged with electrons to produce various 2D projections (i.e., particles) within a digital electron micrograph. Individual particles in a micrograph are selected (i.e., picked), and then computationally aligned to produce 3D reconstructions of the imaged protein complex. Protein crystallization is not required before cryo-EM imaging, and complexes can theoretically be as small as 17 kDa2. However, micrographs have a low signal-to-noise ratio (SNR) due to limited electron beam exposure, which mitigates protein damage3. To overcome low SNR, cryo-EM studies require hundreds to thousands of micrographs4 from which as many as millions of particle images are selected. These datasets range in size from hundreds of gigabytes to several terabytes5, with modern microscopes generating 10–20 terabytes a day6.

Identifying particle images in a micrograph, called particle picking, is a major bottleneck for cryo-EM image processing because of low SNR, sample contamination (e.g., ice crystals), and image artifacts in micrographs. Manually picking all particles is impractical, given the large number of micrographs. Computational methods, called particle pickers, including reference/template-matching7,8,9,10,11,12,13,14,15,16,17 or machine learning algorithms (typically convolutional artificial neural network [CNN] based)18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35, have been developed to automate particle picking. Conventional pickers typically come pre-trained on a large dataset (including both real and simulated data). They can be used without further training, which we refer to as “out-of-the-box”, or they may be retrained on a new set of micrographs (ab initio). Due to a lack of ground truth for cryo-EM particle locations36, picker training is traditionally based on manually picked particles.

Particle pickers are useful but have practical limitations:

  1. 1.

    Consistency and predictability: State-of-the-art particle pickers are not consistent. Each picker selects a different particle set due to its individual particle-background decision boundary. Differences in decision boundaries arise from each picker’s algorithm and training data.

    One consequence of this limitation is that a priori, it is difficult to predict a good picker for a challenging protein. Since no single picker works best for all proteins and datasets, researchers ultimately rely on downstream classification and 3D reconstruction to evaluate the quality of picking.

  2. 2.

    Manual interactions: There are two stages in the particle picking pipeline where significant manual interaction is required. First, at an early stage in the pipeline, good-quality particles are manually picked to train a picker. Typically, 10s-100s particles are manually picked per micrograph. Novice cryo-EM users find this task difficult, and even experienced users can find it challenging for small molecular weight proteins. Second, a later stage of manual interaction is required when the picked particles are clustered into 2D or 3D classes. Classes are manually examined to remove “non-particles”. Typically 50% (and often 80%) of the picked particles have to be removed downstream by manual selection of 2D or 3D classes. Furthermore, these classes are not reproducible across cryo-EM pipelines (EMAN210, CryoSPARC16, RELION37, etc.).

These limitations pose a challenge to individual cryo-EM scientists. They are even more challenging for cryo-EM facilities. Cryo-EM facilities often limit microscope time and computational resources in order to serve multiple clients. In this situation, frequent manual interactions, iterative and fluctuating choice of pickers, requests for additional data collection, and the inability to quickly find a high-quality particle set can consume the center’s resources and become problematic. A stand-alone particle picking pipeline that can bootstrap the picking process without knowledge of the best picker for a particle, with minimal manual interaction, and which produces high-quality particles would be helpful for the optimal use of facility resources.

In this manuscript, we propose a consensus methodology that develops such a method. The key idea is to work at the “meta” level by deploying multiple pickers and finding a consensus set of particles. The consensus set is the set of particles that most of the deployed pickers agree are of good quality.

Choosing a consensus set from multiple pickers is far from trivial. We formulate the identification of the consensus set as an integer linear-programming (ILP) problem. The ILP problem is solved using a branch-and-bound technique. The solution is guaranteed to provide an optimal consensus set for the input particle sets.

A consensus approach has previously been reported by Sanchez-Garci et al. (2018)24. Called DeepConsensus (DC), it iteratively combines picker outputs to produce intersection and symmetric difference particle sets. A separate CNN is then trained to pick particles using both particle sets as training data. While promising, the various decisions made by DC make it a greedy algorithm and prevent global optimization. Finally, training a separate CNN has the potential to introduce false positives and false negatives when the CNN fits poorly into training data.

Our algorithm, called REliable PIcking by Concensus (REPIC), exhibits a number of emergent properties: First, the consensus set of particles found by the algorithm is of high quality. Second, because the ILP solution is guaranteed to be optimal, good consensus sets are found even if one of the deployed pickers performs poorly. Thus, the user need not know, or guess, which picker works well and which does not for any micrograph. This property addresses picker consistency and predictability issues. Finally, because the consensus set is of high quality, it can be used to iteratively train the underlying pickers. In this mode of use, a user can begin with very few picked particles to train the pickers. Although individual pickers may be undertrained and unreliable at this stage, the consensus particle set found by REPIC is of high quality. The consensus set can then be used to retrain pickers. The retrained pickers can be used with REPIC to find a new consensus set, which in turn is used to further train the pickers, and so on, iteratively improving picker performance. Our experiments show that even with very few initial manual particles (less than 10 in most datasets studied), this form of iterative training using REPIC quickly improves the performance of the underlying pickers and provides high-quality particles.

In this paper, we demonstrate the use of REPIC with three CNN-based particle pickers. However, REPIC is picker agnostic; other pickers, including ones yet to be developed, can be used with REPIC without modifying its algorithm.

Finally, there is a subtle but important point regarding REPIC. REPIC is a meta-level algorithm whose goal is not to compete with the best picker but to find a good quality set of particles without knowing the best picker, and to do this while using a set of pickers that might contain poorly performing pickers. All cryo-EM users face this practical scenario.

Results

REPIC algorithms

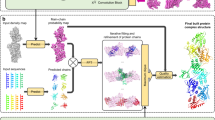
REPIC uses particles found by k pickers to form a consensus set in three steps (Fig. 1A):

  1. 1.

    Graph building—This step takes the set of picked particle bounding boxes from all pickers as input. Bounding boxes are represented as a graph where the vertices of the graph are the bounding boxes, and there is an edge between two vertices if the corresponding bounding boxes have a significant overlap as measured by the Jaccard Index. Edges only exist between bounding boxes of different pickers.

  2. 2.

    Clique finding—This step identifies k-tuples of bounding boxes that have significant overlap with each other by finding cliques of size k in the graph.

  3. 3.

    Clique optimization—This step selects the subset of cliques with the maximum bounding box overlap and quality score (see Methods) subject to the constraint that each vertex participates in only one clique. Selected cliques represent consensus particles. Optimally selecting cliques is a combinatorial optimization problem; bounding boxes often overlap in a dense way so that a globally optimal grouping is not obvious (see Fig. 1B middle). REPIC uses ILP to obtain a non-greedy solution for clique selection (see Methods and Supplementary Fig. S1 for more information).

Fig. 1: Identifying consensus particles with REPIC.
figure 1

A Schematic representation of consensus particle identification by REliable PIcking by Consensus (REPIC). Particle bounding boxes by individual pickers (SPHIRE-crYOLO29 [yellow], DeepPicker19 [green], and Topaz26 [blue]) are represented as vertices (yellow circles, green triangles, and blue squares) in a computational graph. Edge weights are the overlap between two bounding boxes calculated by the Jaccard Index (JI). Clique finding is then performed where all possible cliques in the graph are found, and an optimal subset of cliques is selected by integer linear programming (ILP–Supplementary Fig. S1). Consensus particles are then derived from optimal cliques (see Methods). B Normative (red–left), out-of-the-box picker (yellow, green, and blue–middle), and REPIC consensus (purple–right) particle bounding boxes, for example, β-gal (EMPIAR-10017–top) and TRPV1 (10005–bottom) micrographs. Picker boxes were randomly downsampled to a total of 256 particles. For comparison, an equivalent number of (the highest-scored) consensus boxes to the normative are shown. β-gal and TRPV1 micrographs represent high and low signal-to-noise ratio examples, respectively. Arrows indicate sample contamination present in β-gal micrograph, which both normative and consensus particle sets avoid. The TRPV1 micrograph has been low-pass filtered to make particles more visible.

Full size image

REPIC makes minimal assumptions: It assumes that there are k pickers, and that all pickers provide a bounding box and score for each picked particle. The score takes values in [0, 1] and reflects a picker’s confidence in the particle. REPIC results reported below use three (k = 3) CNN-based pickers: SPHIRE-crYOLO29, DeepPicker19, and Topaz26. SPHIRE-crYOLO and Topaz are modern (and widely accepted) pickers, while DeepPicker is an older picker. However, REPIC is not limited to CNN-based pickers and can be used with k-many pickers.

REPIC has two modes of use:

  1. 1.

    one shot—a single application of REPIC that takes the output of (possibly trained) pickers and finds high-quality consensus particles using the three steps above. This mode relies on individual pickers being well-trained on large datasets (Figs. 1B and 2). Please note that the term “one shot” used here does not pertain to “one-shot machine learning”.

  2. 2.

    iterative—Taking inspiration from the work of McSweeney et al. (2020)38: pickers are ab initio trained using either one-shot REPIC output or manually picked particles. Pickers are run, and one-shot REPIC is used to find consensus particles to retrain pickers. This pick-REPIC-retrain loop (Fig. 3A) is then executed for a user-defined number of iterations (see Pseudocode 1).

For cases where out-of-the-box pickers may fail, we show that REPIC’s iterative mode improves picker performance using one of the following three initializations:

  1. I.

    out-of-the-box picker output (Fig. 3)

  2. II.

    manually picked particles (Fig. 4)

  3. III.

    ab initio transfer learning (Supplementary Methods)

Datasets

REPIC is evaluated using five particle sets from the EMPIAR resource (https://www.ebi.ac.uk/empiar/): TRPV1 (EMPIAR-10005), β-galactosidase (β-gal—10017), T20S proteasome (10057), fatty acid synthase (FAS—10454), and no mechanoreceptor potential C ion channel (NOMPC—10093). All particle sets contain high-quality particles selected by downstream image processing (2D and 3D classification followed by manual selection) except β-gal, which contains particles manually picked by a cryo-EM expert. We refer to these sets as the “normative”, and are the ones that produced the final, published reconstructions. Picker output typically contains many false positives and requires extensive downstream filtering to produce high-resolution reconstructions. In the FAS dataset, for example, only 111, 000 particles of the original 857, 000 particles were used in the final published reconstruction. The rationales for choosing these particular datasets are as follows: all β-gal normative particles were manually picked by a cryo-EM expert, TRPV1 and NOMPC are examples of membrane proteins with low and very low SNR, T20S proteasome images were captured in-focus using the Volta phase-plate, and both FAS and NOMPC represent challenging-to-pick proteins for tested pickers. In addition, we make use of a negative control dataset (EMPIAR-12287) consisting of images containing only ice (no particles). Finally, to decrease processing time, we reduced the number of micrographs in the very large FAS and NOMPC datasets by randomly selecting 460 (10% of the total) and 375 (20%) micrographs, respectively.

Performance evaluation

Evaluating the quality of a cryo-EM particle dataset is a very difficult problem39. For lack of a direct-comparison metric, we perform a very stringent test: the 3D reconstructions resulting from REPIC output—with no downstream processing or curation—are compared to the corresponding 3D reconstructions obtained from the highly curated normative dataset. We make use of cross-Fourier shell correlations (cross-FSC—see Methods) to compare reconstructions. Since the cross-FSC is derived from non-disjoint particle image sets, the cross-FSC resolution is reported at FSC= 0.50. Cross-FSC curves indicate the resolution at which the similarity between the normative reconstruction and a consensus or picker reconstruction drops below 50%.

One-shot picking

To show REPIC can find useful consensus particle sets even when the pickers have variable performance, out-of-the-box pickers were used and one-shot REPIC was applied to find consensus particles.

SPHIRE-crYOLO picked high-quality particles for four of the five EMPIAR datasets (based on the resulting reconstructions and cross-FSC resolutions—Fig. 2 and Supplementary Fig. S2). Topaz picked good quality particles for three of the five datasets (FAS was the exception). DeepPicker picked moderate-quality particles for β-gal and TRPV1 and poor-quality particles for the T20S proteasome, FAS, and NOMPC datasets.

Fig. 2: One-shot REPIC using out-of-the-box pickers.
figure 2

Out-of-the-box SPHIRE-crYOLO (yellow), DeepPicker (green), and Topaz (blue) pickers applied to (top-to-bottom) β-gal (EMPIAR-10017); in-focus, Volta phase plate T20S proteasome (10057); TRPV1 (10005); FAS (10454), and NOMPC (10093) datasets. REPIC consensus (purple) particles are identified from picker output using one-shot REPIC and shown to produce high-resolution densities when most pickers perform well (i.e., β-gal, T20S proteasome, TRPV1). Cross Fourier shell correlation (cross-FSC) curves (see Methods) comparing picker and consensus maps to the normative (gray) are shown on the right. The normative curve is a half-map FSC, while all other curves are cross-FSCs (see Supplementary Fig. S2 for picker densities, and picker and consensus half-map FSC curves). SPHIRE-crYOLO produces the highest-resolution, most complete reconstructions for each dataset. REPIC consensus particle sets represent the performance of the three-picker ensemble and obtain reconstructions comparable to the normative for all proteins except for the FAS and NOMPC datasets.

Full size image

REPIC consensus particles achieved high-resolution reconstructions except for FAS and NOMPC where two or more of the three pickers failed. REPIC consensus particles were shown to have the highest precision when a majority of the deployed pickers succeed (Supplementary Table S1). A similar behavior was also observed with RELION 2D classes (Supplementary Fig. S3). These results show that when one-shot REPIC is used, the consensus particle set is consistent with the best picker, even when the best picker is not known a priori.

Finally, out-of-the-box pickers and one-shot REPIC were applied to the negative control dataset using the particle detection box sizes of the above EMPIAR datasets. Any particle detection in these micrographs is considered a false positive, as no particles were imaged. One-shot REPIC was shown to provide the lowest number of false positives across all box sizes, reducing the number of false positives by 35–99% when compared to individual out-of-the-box pickers (Table 1 and Supplementary Figs. S4–S6).

Table 1 Number of false positives picked by out-of-the-box pickers or REPIC when applied to the negative control dataset
Full size table

Iterative ensemble particle picking

To demonstrate how REPIC can be used on a novel particle, REPIC’s iterative mode (Fig. 3A) was initialized using out-of-the-box picker output, and pickers were then ab initio iteratively trained using the REPIC consensus set as training data in each iteration. This training was independently carried out for each of the five cryo-EM datasets for 16 iterations. For each dataset, 5% of micrographs were randomly selected as the training subset. The T20S proteasome dataset was processed for an additional eight iterations to observe a plateau in its precision curves. Figure 3B highlights the considerable improvement that can be achieved between the initial and final consensus particle sets, exemplified by the T20S proteasome dataset. DeepPicker showed the largest improvement, where the achieved reconstruction improved from an erroneous, disconnected map (4.57 Å) to a high-resolution map (3.37 Å). All four algorithms achieve reconstructions that are almost an Angstrom higher in resolution compared to normative particle coordinates (3.37-.42 vs. 4.22 Å).

Fig. 3: Iterative mode REPIC initialized using out-of-the-box picker output.
figure 3

A Training labels (i.e., particles) for iterative-mode REPIC can be either picker output (automatic) or manual particle picking (semi-automatic). Pickers are ab initio trained from training data (see Methods). REPIC identifies consensus particles from picker output, which replace training labels for the next iteration. This pick-REPIC-train loop is repeated for a user-defined number of iterations. B T20S proteasome reconstructions obtained from normative (gray–left), SPHIRE-crYOLO (yellow), DeepPicker (green), Topaz (blue), or REPIC consensus (purple) particles. REPIC identifies consensus particles from out-of-the-box picker output (top). All algorithm particle sets result in similar, final (24) high-resolution densities. C Evaluation metrics (precision, recall, and number of particles) of (top-to-bottom) T20S proteasome (EMPIAR-10057), β-gal (10017), TRPV1 (10005), and FAS (10454) datasets. Cross-FSC curves (see Methods) obtained from the initial and final iterations are shown on the right. Most algorithms improve over out-of-the-box pickers (Fig. 2B) and produce similar final densities (see Supplementary Figs. S8 and S9: S9 for NOMPC [10093] dataset), except for DeepPicker and the FAS dataset.

Full size image

Figure 3 C (and Supplementary Figs. S7 and S8) shows the successful results of REPIC’s iterative mode initialized with out-of-the-box picker output for four of the five tested cryo-EM datasets. REPIC processing of the T20S proteasome dataset demonstrates how the iterative mode can improve both precision and recall over multiple iterations. Convergence rates of the iterative algorithm vary from particle to particle, and the final particle set may be dissimilar from the normative. For example, REPIC processing of the β-gal dataset shows how the picker ensemble may converge during early iterations and have precision and recall remain stable across later iterations (Fig. 3C). The NOMPC dataset (Supplementary Fig. S9) demonstrates how the out-of-the-box pickers can perform poorly and prevent this initialization of REPIC’s iterative mode from achieving a high-resolution reconstruction.

Semi-automatic picking by iterative ensemble

Next, we asked if high-resolution reconstructions could be obtained using iterative-mode REPIC and a minimal, initial particle set. As before, 5% of micrographs were randomly selected as the training subset (Fig. 4A). For each micrograph in the training subset, 1% of normative particle coordinates were randomly selected to represent manually picked particles and ab initio train pickers. However, this percentage was increased to 2% for the NOMPC dataset because 1% resulted in pickers encountering exploding gradients or not converging during model training. In total, 6, 6, 8, 42, and 44 training particles were selected for the β-gal, T20S proteasome, FAS, NOMPC, and TRPV1 datasets, respectively. Initial training labels and micrographs were then provided to iterative-mode REPIC, and 16 iterations were performed.

Fig. 4: Iterative mode REPIC using minimal manual picking for ab initio picker training.
figure 4

A Three step, random selection analysis applied to each dataset: (1) 5% of micrographs are randomly selected as the training subset, (2) normative particles are randomly selected as training labels, and (3) training data is provided to REPIC's iterative mode (see Methods). B FAS reconstructions obtained from normative (gray–left), SPHIRE-crYOLO (yellow), DeepPicker (green), Topaz (blue), or REPIC consensus (purple) particles. Pickers are first trained from training data, and REPIC identifies consensus particles from their output (top). Each REPIC iteration, pickers are retrained on updated consensus particle sets (see Fig. 3A). FAS densities are obtained using either final REPIC consensus or picker particle sets (bottom). All algorithms (except DeepPicker) converge to similar final, high-resolution reconstructions. C Evaluation metrics (precision, recall, and number of particles) of (top-to-bottom) FAS (EMPIAR-10454), β-gal (10017), T20S proteasome (10057), and NOMPC (10093) datasets. Cross-FSC curves (see Methods) for densities obtained from the first and final iteration are shown on the right. Most algorithms produce similar final, high-resolution densities (see Supplementary Figs. S11 and S12: S12 for TRPV1 [10005] dataset).

Full size image

Figure 4B shows considerable improvement in FAS reconstructions between the first and last iteration using REPIC’s iterative mode. In the first iteration, the consensus particle set is unable to produce a reconstruction due to the poor performance of SPHIRE-crYOLO and DeepPicker (based on their respective reconstructions—Supplementary Fig. S10). After 16 iterations, the iterative framework produces both consensus and SPHIRE-crYOLO reconstructions at a resolution approaching the normative. These high-resolution reconstructions are achievable because the ensemble is composed of multiple pickers of different architectures and objective functions. Pickers that require minimal training data drive the initial iterations of iterative-mode REPIC (based on the resulting reconstructions). Later iterations are driven by pickers able to achieve higher-resolution reconstructions.

Initializing iterative-mode REPIC with a minimal particle set results in high-resolution reconstructions on par with (β-gal and TRPV1 datasets), approaching (FAS and NOMPC), and better than (T20S proteasome) the normative particle set (Supplementary Figs. S11 and S12). In fact, the NOMPC reconstruction obtained with minimal manual picking produces the highest-resolution density across all initialization strategies tested in this paper. β-gal, T20S proteasome, NOMPC, and TRPV1 precision and recall curves (Fig. 4C and Supplementary Fig. S12) show how the ensemble quickly improves and converges over a small number of iterations (six or less) from a small subset of initial training labels. SPHIRE-crYOLO and Topaz show instability for the FAS dataset across iterations even though the final reconstructions are comparable to the normative map (based on estimated resolution and cross-FSC analysis—Fig. 4C). Final DeepPicker particle sets are also improved (based on cross-FSC curves and obtained resolution) over automatic iterative picking. Similar to automatic runs of the iterative mode, the precision and recall of consensus particle sets remain stable across iterations and lead to high-resolution reconstructions that are comparable to the normative map.

Discussion

REPIC is a meta-level algorithm, designed to be used without the knowledge of the best picker, and to reduce manual interaction with pickers. The evaluation criteria for such a meta-level algorithm are: Whether the algorithm provides robustness against poor pickers, whether the algorithm can reliably reduce the amount of manual interaction, and whether the algorithm can produce high-quality consensus datasets that are comparable to the best picker (determined post hoc). The results of using REPIC show that REPIC performs well with respect to these criteria.

In one-shot mode, REPIC produces high-quality consensus particle sets when multiple out-of-the-box pickers are used, and the identity of the best picker is not known. REPIC works reliably as long as a majority of the pickers perform reasonably well. If most pickers fail, then the notion of consensus particles is not very meaningful. Such is the case with the FAS and NOMPC datasets in Fig. 2.

In the one-shot experiments, it is interesting to observe that SPHIRE-crYOLO obtained the highest precision and recall with the T20S proteasome dataset (Supplementary Table S1). We believe this result is due to SPHIRE-crYOLO being the only out-of-the-box picker trained on similar phase-plate data (EMPIAR-10050)40.

In all three initializations used with REPIC’s iterative mode (Figs. 3–4 and Supplementary Figs. S13–S15), consensus particle sets reliably produced high-resolution reconstructions, with resolutions comparable to the normative. We emphasize that the REPIC reconstructions did not involve any manual intervention, such as the inspection of 2D or 3D classes from which “good” particle subsets are chosen. This is notable for NOMPC, where the original authors performed multiple rounds of 2D and 3D classification to obtain their final particle set and reconstruction at 3.55 Å. A reconstruction from REPIC’s iterative mode initialized with only 42 manually picked particles resulted in a resolution of 4.57 Å compared to the reduced normative set’s 4.17 Å. While using REPIC iteratively for picking NOMPC particles, we did not carry out any 2D or 3D classification. All consensus particles found by REPIC were used in the 3D reconstruction, without any further selection (Supplementary Fig. S11). This result demonstrates how REPIC can reduce the need for one stage of manual interaction.

When using REPIC’s iterative mode, individual pickers improve their picking (as shown by initial/iteration 1 vs. final cross-FSC curves in Figs. 3C and 4C, and Supplementary Figs. S9A–B and S12A–B) and converge to similar reconstructions. This result is due to the ab initio training of individual pickers within each iteration using consensus particles. A minimal amount of training data (1% or 2% of particles per training micrograph) is required to initialize REPIC’s iterative mode, which substantially reduces the associated manual interaction by REPIC.

Figure 4B illustrates the benefits of using a picker ensemble: REPIC, along with pickers, can bootstrap from picking poor particles in the early iterations to picking high-quality particles in the later iterations (based on the resulting reconstructions). In Fig. 4B, early iterations of REPIC are driven by Topaz, which requires less training data due to its positive-unlabeled learning algorithm. Later iterations are driven by SPHIRE-crYOLO, which requires more training data but achieves higher-resolution reconstructions.

Furthermore, our results demonstrate that REPIC’s iterative mode can effectively handle multiple underperforming pickers in situations more strenuous than formal ablation experimentation. Pickers were shown to fail at early iterations producing many false positives and leading to incomplete or low-resolution reconstructions (Supplementary Figs. S7, S9A, S10, and S12A). Dealing with false positives is more challenging than ablation, where picker(s) produces no output. Through successive iterations, REPIC and (most) pickers progressively improved, achieving final reconstructions on par with or exceeding the normative (Supplementary Figs. S8, S9B, S11, and S12B).

One final point: NOMPC is a heterogeneous particle. This heterogeneity is caused by multiple ankyrin repeat domains that move with respect to NOMPC’s transmembrane domain. Despite this heterogeneity, REPIC’s iterative mode (initialized with manually picked particles) is able to find a consensus particle set that results in a 3D reconstruction approaching the normative (Supplementary Fig. S11). REPIC’s success with NOMPC illustrates the fact that reliable consensus particles can be found in spite of heterogeneity, as long as the underlying pickers are capable of picking such particles.

The above results support the main claims of this paper: (1) harnessing multiple pickers with REPIC can provide high-quality particles, even when the best picker is not known a priori, and when the set of pickers may contain poorly performing pickers, (2) REPIC substantially reduces the number of particles that have to be picked initially, and REPIC reduces the need for manual inspection of 2D classes, (3) reconstructions from consensus sets found by REPIC have resolutions close to that of the best picker (determined post hoc). Consequently, REPIC is likely to be useful for cryo-EM facilities and investigators: REPIC can be used with minimal interaction to obtain a high-quality set of initial particles and reconstruction. A limitation of REPIC’s consensus approach is the reliance on other pickers, which can reduce the amount of consensus particles when all pickers don’t agree. However, REPIC is designed to be robust to underperforming pickers (illustrated here by DeepPicker) and to reliably pick particles when the best picker is not known a priori.

The computational requirements of deploying pickers are likely comparable for 2D/3D classification and REPIC. The difference is in the following: (1) REPIC requires the pickers to be retrained, which 2D/3D classification does not; (2) a typical cryo-EM pipeline requires 2D/3D classification and 3D reconstruction with manual interaction, which REPIC does not. These two differences are difficult to compare but are likely to have similar complexity. REPIC has the advantage that no manual interaction is required, and it can be run without any oversight by a cryo-EM user. Within a REPIC iteration, the solution to the optimization problem requires minimal time and computational resources (Supplementary Fig. S16).

Future work will focus on improving the runtimes of both the one-shot and iterative modes of REPIC, and exploring extensions of REPIC to filament picking and cryo-ET (3D particle coordinates). Currently, an exhaustive search is performed when building the computational graph. A k-d tree approach could be used to significantly reduce the amount of bounding box comparison and improve REPIC runtime. During the iterative REPIC loop, pickers are run in sequence. Ab initio training of pickers contributes to a significant amount of REPIC’s runtime (Supplementary Fig. S16). Parallel application of pickers or a variant (i.e., only re-training the worst performing picker) can improve the speed of REPIC iterations.

Methods

Dataset description

Cryo-EM digital electron micrographs and normative particle coordinates were obtained from the Electron Microscopy Public Image Archive (EMPIAR) resource for entries EMPIAR-1000541, EMPIAR-1001737, EMPIAR-1005742, EMPIAR-1009343, and EMPIAR-1045444. Associated, published 3D volumes for each EMPIAR dataset were retrieved from the Electron Microscopy Data Bank from entries EMD-5778, EMD-2824, EMD-3347, EMD-8702, and EMD-4577, respectively. Due to the large number of micrographs in the EMPIAR-10454 (N = 4593) and EMPIAR-10093 (N = 1873) datasets, 10% or 20% of micrograph and paired particle coordinate files (N = 460 and 375, respectively) were randomly selected and used in this study (see Supplementary Data Files 1 and 2 for a list of the selected micrographs). Motion corrected, negative control (buffer images; no particles, only ice) cryo-EM micrographs were downloaded from EMPIAR (EMPIAR-1228745, N = 220—see Supplementary Data File 3 for a list of these micrographs). EMPIAR-10057 multi-frame micrographs were aligned and summed using MotionCor2 v1.5.046 in RELION v3.1.347. Contrast transfer function (CTF) estimation was performed for all datasets (except for the in-focus, phase-plate data of EMPIAR-10057) using CTFFIND4 v4.1.1448 in RELION. Please see Supplementary Data File 4 for a summary of RELION and CTFFIND4 parameters used to process each dataset. Standard micrograph preprocessing (i.e., low-pass filtering by SPHIRE-crYOLO29, image standardization by DeepPicker19, Gaussian mixture model [GMM] normalization by Topaz26) and false positive filtering is performed for each picker. Picker installation and application are described in Supplementary Methods.

REPIC algorithms

REliable PIcking by Consensus (REPIC—/rә’pik/) is a non-greedy approach to identifying consensus particles from k picked particle sets {S1, …, Sk}. The input to REPIC is the set of picked particle sets \({{{\mathcal{S}}}}=\{{S}_{1},\ldots ,{S}_{k}\}\), where each particle in a set is expected to have micrograph coordinates, a particle detection box size, and a quality score s expected to be in [0, 1]. REPIC output is a consensus particle set in BOX file format. REPIC represents all picked particles in a micrograph as an undirected, k-partite graph G = (V, E). Each vertex v in V corresponds to a particle detection box from a picked particle set. Each v is assigned a vertex score sv equal to quality score s provided by the picker. Each edge e in E represents a pair of overlapping particle detection boxes. The edge weight o between two vertices is the overlap (the Jaccard Index) of their corresponding particle detection boxes. Intuitively, the goal of REPIC is to find the set of non-overlapping k-size cliques in G that maximize particle overlap and score. For each clique c = (Vc, Ec), the clique weight wc is defined as the product of its median edge weight \(\tilde{o}={{{\rm{median}}}}\{{o}_{e}| e\in {E}_{c}\}\) and median vertex score \(\tilde{s}={{{\rm{median}}}}\{{s}_{v}| v\in {V}_{c}\}\). REPIC aims to find the disjoint set of cliques \({{{\mathcal{C}}}}\) that maximizes \({\sum }_{c\in {{{\mathcal{C}}}}}{w}_{c}\).

The details of the above steps are as follows:

  1. 1.

    Graph building—An undirected graph G is built from the output of k picked particle sets (as described above). In this study, picked particle sets are generated by three CNN-based pickers: SPHIRE-crYOLO29, DeepPicker19, and Topaz26. Edges with o < 0.3 are considered to be particle detection boxes that do not overlap and are excluded from G.

  2. 2.

    Clique finding—All cliques of size k are enumerated using a modified Bron-Kerbosch algorithm49, as implemented by the Python NetworkX package50.

  3. 3.

    Clique optimization—A clique in the graph G corresponds to a single consensus particle. However, each vertex in G (a picked particle) may participate in multiple cliques. To ensure each vertex associates with a single clique in the final set, cliques x are selected using Integer Linear Programming (ILP—Supplementary Fig. S1) as follows: Suppose that the result of clique finding is m cliques containing n vertices. Define an n × m matrix A, where the element Aij = 1 is the ith vertex participating in the jth clique, else Aij = 0. Then, the ILP is defined as below, where xj is a binary variable denoting whether the jth clique is selected (xj = 1) or not (xj = 0).

    $${{{\rm{maximize}}}}\quad {\sum}_{j}^{m}{w}_{j}\cdot {x}_{j}\qquad\qquad\qquad\qquad$$
    (1)
    $${{{\rm{subject}}}} \,{{{\rm{to}}}}\,\quad {\sum}_{j}^{m}{A}_{ij}\cdot {x}_{j}\le 1\,\,{{{\rm{for}}}} \,{{{\rm{all}}}}\,\,i\in [1..n],$$
    (2)
    $${x}_{j}\in \{0,1\}\qquad\quad$$
    (3)

    Equation (2) ensures vertices are only associated with a single clique by limiting row sums in A to 1. A globally optimal solution to the above problem is then found using ILP branch-and-bound optimization, as implemented by the Python Gurobi package51.

Graph building, clique finding, and clique optimization are performed on a per-micrograph basis. REPIC itself does not require a GPU (although the pickers do) and runs efficiently on a single workstation with a processing time on the order of seconds per micrograph. Graph building (specifically the exhaustive search for overlapping particle detection boxes) is the limiting step for REPIC (2-10 seconds per micrograph). The ILP solver is efficient (<0.2 seconds per micrograph).

One-shot mode

Given an initial set of picked particle sets \({{{{\mathcal{S}}}}}_{{{{\rm{init}}}}}\), one-shot REPIC executes the above steps once. In the discussion below, we denote the one-shot execution of REPIC with \({{{{\mathcal{S}}}}}_{{{{\rm{init}}}}}\) as REPIC\(({{{{\mathcal{S}}}}}_{{{{\rm{init}}}}})\),

Iterative mode

In the iterative mode, REPIC is used as described in Pseudocode 1. Here, I is the number of iterations chosen by the user. M is available cryo-EM micrographs split into cross-validation subsets. Ti is the set of training labels (particle coordinates) used for ab initio picker training in iteration i.

Pseudocode 1

REPIC—iterative mode

Cross-validation (training, validation, and testing) subsets M for Pseudocode 1 are created by sampling micrographs based on their mean defocus value. Mean defocus values are calculated from the output of a CTF estimation job in RELION v3.1.347 using CTFFIND4 v4.1.1448. Specifically, ‘defocus 1’ and ‘defocus 2’ values are averaged per micrograph. Micrographs are then grouped into three bins (low, medium, and high) using their mean defocus values. Subsets are generated by randomly sampling (without replacement) three micrographs at a time, one from each bin. If defocus values are not available (e.g., EMPIAR-10057), all micrographs are randomly grouped into three equally sized bins. Training and validation sets are built first to ensure algorithms are exposed to the entire range of defocus values during picker training. For each dataset, validation subsets consist of six micrographs, and the remaining micrographs were initially split 20-80 between the training and testing subsets.

Algorithm evaluation

For all EMPIAR datasets, picked and consensus particle sets are evaluated using published particle sets found on the EMPIAR resource. These published sets are used in place of a ground truth as the norm or expected picked particle set, which we refer to as the “normative”. Before evaluation, picker output was filtered for false positives using author-suggested thresholds (see Supplementary Methods).

Precision and recall were calculated using micrograph pixels P, where pi = 0 and pi = 1 are a pixel found in the background region of a micrograph or a particle bounding box, respectively. A true positive (TP) is pi = 1 for both the normative and compared particle set. A false positive (FP) is pi = 0 in the normative and pi = 1 in the compared set. A false negative (FN) is pi = 1 in the normative but pi = 0 in the compared set. TPs, FPs, and FNs are summed over P before calculating either evaluation. Reported precision and recall values are computed from all testing micrographs in a dataset.

$${{{\rm{precision}}}}=\frac{{{{\rm{TP}}}}}{{{{\rm{TP}}}}+{{{\rm{FP}}}}}$$
(4)
$${{{\rm{recall}}}}=\frac{{{{\rm{TP}}}}}{{{{\rm{TP}}}}+{{{\rm{FN}}}}}$$
(5)

When available, the final particle set that produced a published density (e.g., EMPIAR-10454) is used as the normative particle set. If this final particle set is not available (e.g., EMPIAR-10057), the normative particle set consists of all particles found in the EMPIAR entry.

Initial analyses showed that the published final particle set of EMPIAR-10005 produced lower-resolution reconstructions compared to the initial particle set. Missing summed frame micrographs in the EMPIAR entry reduced the final particle set from 35, 645 to 32, 387 particles. Therefore, the EMPIAR-10005 normative particle set was taken to be the published initial particle set reduced by the number of available micrographs (80, 443 particles - see Supplementary Data File 4).

3D reconstruction procedure

3D reconstruction was performed in RELION v3.1.347. Soft masks were generated from published maps (see Dataset description in Methods) using a RELION mask generation job. For each particle set, a RELION 3D auto-refinement job was provided with the corresponding soft mask, published density (low-pass filtered to 64 Å), and extracted particle images to produce a reconstruction. No particle filtering in RELION (either by 2D or 3D methodology) was performed on any particle set analyzed in this study. CTF correction was not performed for EMPIAR-10057 because it is an in-focus, phase-plate dataset. Final, unmasked reconstructions were generated using a RELION post-processing job. Unmasked normative reconstructions were then used to generate soft masks that were applied to their corresponding normative, consensus, and picker reconstructions (i.e., all reconstructions in the same row of a figure). RELION 3D auto-refinement jobs that had significantly longer runtimes (>24 hours) than the runtime for the normative particle set were aborted (e.g., DeepPicker EMPIAR-10005 reconstruction displayed in Fig. 2—see Supplementary Data File 5). For these particle sets (indicated by ‡ in figures), a single half map from the last-completed iteration of the RELION 3D auto-refinement job was used. Default RELION mask generation, 3D auto-refinement, and post-processing job parameters were used unless otherwise specified in Supplementary Data File 4.

3D reconstruction analysis

Masked reconstructions were registered to their corresponding normative reconstruction using UCSF Chimera52 (https://www.cgl.ucsf.edu/chimera/— ‘Fit in Map’ tool and ‘vop resample’ command) before Fourier shell correlation (FSC) calculation.

Reconstructions resulting from either picker or consensus particle sets were compared to their corresponding normative map by calculating an FSC between both the masked and registered maps (a “cross-FSC”). Since cross-FSCs violate the gold standard assumption of cryo-EM, we use a threshold of FSC = 0.5. To prevent spurious correlations at high frequencies, we applied a 3D Gaussian smoothing filter (μ = 0.0 and σ = 1.0 voxel) to normative volume masks. The reported cross-FSC resolution is the resolution where a map’s similarity to the normative map decreases below 50%. Half-map FSCs are included as a reference, and their reported resolutions use the gold standard FSC threshold (FSC=0.143).

UCSF Chimera was used to visualize all maps. Normative maps were used to set the density threshold for maps resulting from either consensus or picker picked particle sets. The density threshold for half maps from aborted RELION 3D auto-refinement jobs (indicated by ‡ in figures) was set in an ad hoc manner to better visualize the obtained map.

Statistics and reproducibility

No statistical analyses of the data or biological/technical replicates were conducted in this study.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.