Introduction

When we visit an unknown city, our ability to reach relevant places (the hotel, a tourist attraction, etc.) increases as we explore this new environment. This is enabled by the progressive implementation of navigation strategies of increasing efficiency1,2,3,4. This phenomenon, which here we named strategy progression, may reflect the active guidance of behavior from cumulative (remote or recent) experience, for which the prefrontal cortex (PFC) seems to play a critical role5,6,7. Of note, lesions to the rodent medial prefrontal cortex (mPFC) impair strategy progression during spatial learning8,9,10,11, and firing patterns in the mPFC represent several cognitive features relevant for strategy progression, such as strategy switching and implementation of efficient navigation strategies4,12,13,14. This suggests a critical role for the mPFC in executive aspects of spatial learning.

In order to accomplish this, the mPFC may integrate information represented across distributed brain areas15. Information concerning spatial-temporal sequences and active guidance of the body through the visual space is crucial for spatial learning16,17. This information is represented in the hippocampus (HPC) and posterior parietal cortex (PPC)18,19,20,21. Both structures are required for spatial learning1,9,10 and are structurally connected with the mPFC: whereas the HPC sends direct and indirect projection involving the nucleus reuniens of the thalamus22,23, the PPC sends indirect projections through the retrosplenial and anterior cingulate cortex24,25. Therefore, through these pathways, the mPFC may integrate relevant information from the HPC and PPC for strategy progression during learning. However, the mechanism underlying the prefrontal coordination with HPC and PPC during spatial learning is poorly understood.

The integration of information required for cognitive operations is supported by the transient synchronization of local and distributed neural activity patterns26,27,28,29,30,31. During awake state, low-frequency oscillations such as theta (6–12 Hz) and 4-Hz oscillations, are able to coordinate distributed networks. Whereas theta oscillation emerges in the HPC associated with spatial navigation32,33,34, 4-Hz oscillation appears coupled with respiration during awake immobility35,36. Both oscillations are detected in the mPFC, HPC, and PPC35,37,38, and synchronize gamma activity (30–100 Hz) and neuronal firing in the mPFC37,39,40. Parallelly, local gamma oscillations, which represent neural operations underlying information processing41, coordinate the firing of neural populations into particular computations, supporting the formation of task-relevant firing patterns in the mPFC37. Thus, two complementary low-frequency oscillations, though long-range coupling of gamma activity and firing patterns, may provide windows of efficient communication between distant neural networks, promoting large-scale information transfer and integration for the implementation of task-related neural operations in the mPFC42,43,44,45.

Here we performed simultaneous recordings of neuronal activity and local field potential (LFP) in the mPFC, the HPC, and the PPC of mice during a spatial memory acquisition task. Along navigation trials, we identified searching and exploratory task stages, in which strategy progression was observed during searching but not during exploration. Theta and 4-Hz oscillations were evident in the three recorded areas in relationship with locomotor activity. Importantly, gamma oscillations and neuronal firing in the mPFC were synchronized with hippocampal and parietal theta and 4-Hz oscillations according to task stages in a strategy progression-dependent manner. Lastly, firing patterns in the mPFC were dynamically modulated by strategy progression. Altogether, these results provide evidence for the neural mechanisms underlying the task-dependent coordination of distributed neural networks during spatial learning.

Results

Task stages and strategy progression during spatial learning

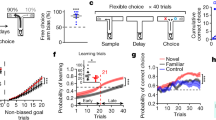
Adult mice (n = 12) were chronically implanted with microelectrodes simultaneously in the mPFC, the CA1 area of the dorsal HPC and the PPC and were subjected to training in the Barnes maze (Fig. 1a). In this behavioral paradigm, animals must escape from an aversive (elevated and illuminated) arena in which an escape hole is located in a fixed spatial location across all training trials (Fig. 1a); thus, a goal-directed spatial memory is formed across navigation trials. Representative occupancy color plots depicted in supplementary Fig. 1a show a progressive decrease in the path length to the goal and an increased occupancy near the goal across training days. Escape latency and the number of errors was significantly reduced across training days (latency: P = 0.026; Fig. 1b; errors: P = 0.025; one-way ANOVA; supplementary Fig. 1b). These results were not related to modification of locomotor activity, as no significant changes in mean and maximum running speed were observed across training days (mean speed: P = 0.719; max. speed: P = 0.951; one-way ANOVA; supplementary Fig. 1c, d).

Fig. 1: Behavioral performance during spatial learning in the Barnes maze.
figure 1

a Schematic diagram of the Barnes maze. b–d Escape latency (b), goal-nose poke latency (c), and path efficiency to nose poke in the escape hole (d) across acquisition days in the Barnes maze. Clear blue represents data of individual mice; solid blue indicates the mean ± SEM. *P < 0.05; **P < 0.01; Tukey’s multiple comparisons test after one-way ANOVA. e Schematic diagram of the criterion for the distinction between searching and exploration task stages. f Example occupancy colorplots in the Barnes maze during the searching and exploration task stages of the same trial for each acquisition day. g–i Comparison of average duration (g), error counts (h), and error incidence (i) across training days between searching and exploration task stages. Clear blue and clear grey represent data of individual mice; solid blue and solid grey indicate the mean ± SEM. *P < 0.05; **P < 0.01; Sidak’s multiple comparisons test after two-way ANOVA. j Example occupancy colorplots of the navigation strategies used to find the goal in the Barnes maze. Strategies were classified as non-spatial or spatial if animals were directed toward the goal quadrant. k Normalized distribution of navigation strategies implemented across training days during the searching and exploration task stages.

Full size image

We observed that mice do not necessarily enter the escape hole once they find it. Indeed, it has been considered that the first nose poke into the escape hole is a more reliable indicator of spatial learning2. We found that escape-nose poke latency and error counts before escape-nose poke significantly decreased across training days (latency: P = 0.023; errors: P = 0.020; one-way ANOVA; Fig. 1c and supplementary Fig. 1e, respectively), without changes on mean and maximum speed (mean speed: P = 0.635; maximum speed: P = 0.221; one-way ANOVA; supplementary Fig. 1f, g). Importantly, path efficiency to escape-nose poke increased significantly along training days (P = 0.033; one-way ANOVA; Fig. 1d), suggesting a progressive increase in the proficiency to find the escape. A detailed inspection of the trajectories suggests that after finding the escape, mice implemented a different behavior that was not necessarily related to finding the escape but related to the exploration of the unfamiliar environment (supplementary videos 1 and 2). To evaluate this possibility, we divided each navigation trial into two task stages with respect to the first encounter with the escape hole: before the first nose poke in the escape hole (which we called the searching stage) and after the first nose poke in the escape hole (exploration stage; Fig. 1e). Representative occupancy plots for both task stages of the same navigation trial across training days are shown in Fig. 1f. We found that duration, error counts, and distance traveled across training days were lower in the searching stage compared to exploration (P < 0.0001; two-way ANOVA; Fig. 1g, h, and supplementary Fig. 1h). We found no significant differences in mean or maximum speed between task stages (mean speed: P = 0.3860; max speed: P = 0.617; two-way ANOVA; supplementary Fig. 1i, j). Thus, mice spent most of the navigation time exploring the arena after they found the escape hole, even when they already knew its location. Occupancy plots in Fig. 1f also show that navigation was progressively concentrated near the goal in the searching stage, whereas mice navigated in a larger area of the arena during exploration. Indeed, path sparsity, which estimates the spatial distribution of the trajectory in the maze, was higher in the exploration stage compared to searching (P = 0.018; t test; supplementary Fig. 1k). Finally, we reasoned that the motivation to find the escape could be reflected as continuous attempts to find escape across training days, which could be highest during searching compared to exploration. To test this, we calculated the error incidence, i.e., the number of error counts per second for each stage across training days. Error incidence was highest in searching (P < 0.001; two-way ANOVA; Fig. 1i). Indeed, error incidence remained almost persistent across training days during the searching stage, consistent with the motivation to find the escape. Contrarily, error incidence in the exploration stage decreased across training days, suggesting a decreased motivation to find the escape (Fig. 1i).

We then evaluated the strategy progression across training. Given that escape-directed navigation was implemented during the searching stage, we first evaluated strategy progression in this stage. To this aim, navigation paths were qualitatively classified according to the Barnes maze Unbiased Strategy classification algorithm (BUNS46), which identifies six different navigation strategies: random, serial, long-correction, focused search, corrected, and direct. Representative occupancy plots for each navigation strategy are shown in Fig. 1j. We found significant differences across navigation strategies in path efficiency to goal-nose poke, path sparsity, latency to goal-nose poke, and number of errors (P < 0.0001; one-way ANOVA; supplementary Fig. 1l–o), with no significant differences in mean speed (P = 0.454; one-way ANOVA; supplementary Fig. 1p). This suggests that navigation strategies were related to changes in the trajectory but not in the velocity, which strongly impacts path proficiency and behavioral performance during the searching stage. Importantly, less efficient strategies were mostly implemented early during training, whereas those more efficient were mainly evident at the end of training, with an apparent continual progression from less-to-more efficient strategies across training days (Fig. 1k); the significant increase of the BUNS-cognitive score across training days agrees with this observation (P = 0.045; one-way ANOVA; supplementary Fig. 1q). Finally, if the exploration stage is not directed toward finding the goal, then strategy progression would be absent during the exploration stage. Occupancy plots in Fig. 1f show that, during exploration, random navigation prevailed (nearly 50% of trials), with no apparent strategy progression across training days. Indeed, the cognitive score did not change across training days in the exploration stage (P = 0.609; one-way ANOVA; supplementary Fig. 1r). Overall, these data show that two behavioral stages were clearly distinguishable during navigation: a first searching stage directed to find the escape, in which strategy progression was evidenced, and a consecutive exploratory stage with no evident strategy progression.

4-Hz and theta oscillations in the mPFC, HPC, and PPC during spatial learning

We asked if these behavioral findings were related to changes in neural activity patterns. LFP and neuronal firing were simultaneously recorded from the mPFC, HPC, and PPC during all training sessions. Examples of Nissl-stained sections showing the position of recording electrodes are shown in supplementary Fig. 2a. Good-quality recordings were obtained from 10 of 12 recorded mice (20 trials per animal, a total of 200 recording sessions).

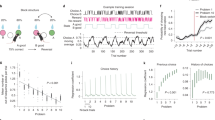
The raw LFP recording and spectrograms in Fig. 2a shows the presence of two low-frequency oscillations in the three recorded areas: 4-Hz and theta. Volume conduction between parietal and hippocampal LFPs appears to be a scarce possibility given the high variability and low similarity of instantaneous energy and phase between hippocampal and parietal 4-Hz and theta oscillations (supplementary Fig. 2b–h). The comparison of the representative instant energy between 4-Hz and theta oscillations suggests that these oscillations emerged contrarywise along time (Fig. 2b). Indeed, we found that when 4-Hz reaches its highest energy, theta reaches its minimum (Fig. 2c). This phenomenon was observed in the three recorded areas (Fig. 2c). As evidenced in Fig. 2b, this inverse relationship appears to be related to the dependence of these oscillations on locomotor activity33,36. To evaluate this possibility, we classified moments of navigation according to running speed at intervals of 2 cm/s, up to 8 cm/s, and we calculated the z-scored spectral power of 4-Hz and theta oscillations for each running speed interval. We found an apparent inverse relationship between 4-Hz power and running speed (supplementary Fig. 3a). However, this relationship only reaches statistical significance in the mPFC (mPFC: P = 0.014; HPC: P = 0.835; PPC: P = 0.497; one-way ANOVA). Contrarily, spectral power of theta oscillations seems to increase with running speed (supplementary Fig 3a); however, this relationship did not reach statistical significance in any recording area (mPFC: P = 0.878; HPC: P = 0.808; PPC: P = 0.496; One-way ANOVA). To facilitate the analysis, we identified episodes of mobility and immobility during navigation (running speed above and below 4 cm/s, respectively33); and compared the z-scored 4-Hz and theta spectral power for each episode. The proportion of time in immobility was higher than mobility in both searching and exploration stages (P < 0.001; Sidak’s multiple comparisons test after two-way ANOVA; supplementary Fig. 3b). We found that the spectral power of 4-Hz oscillation was higher during immobility compared to mobility in the three recorded areas (mPFC: P = 0.018; HPC: P = 0.009; PPC: P < 0.0001; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 2d). Contrarily, theta power was higher during mobility (mPFC: P = 0.042; HPC: P = 0.001; PPC: P = 0.0001; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 2d). Task stages did not affect the power of both 4-Hz and theta oscillations in the three recorded areas (supplementary Fig. 3c). These data indicate that 4-Hz oscillation was evident in the mPFC, HPC and PPC during immobility, whereas theta was present in these areas when mice moved in the maze.

Fig. 2: 4-Hz and theta oscillations in the mPFC, HPC, and PPC during spatial learning.
figure 2

a Upper panel: example of LFP recorded simultaneously from the mPFC, HPC, and PPC during training in the Barnes maze. Middle: magnification of segments of LFP recordings showing theta (left) and 4-Hz oscillations (right). Lower panel: spectrograms for LFP recordings shown in the middle panel. b Example of spectrogram of an LFP recorded from the mPFC comparing theta and 4-Hz spectral energy across time, and comparison of instantaneous energy of 4-Hz and theta frequency bands aligned with the instantaneous speed. Gray areas are periods of locomotion (instantaneous speed over 4 cm/s). c Upper panel: z-scored colorplot of energy of theta oscillation in turn to peaks of 4-Hz oscillation in the mPFC (left), HPC (middle), and PPC (right) for all training sessions. Lower panel: average theta z-scored energy in turn to 4-Hz peaks. Note that theta energy is minimal when 4-Hz reaches the maximum energy. Data are presented as mean (solid line) ± SEM (shaded area). d Box plot comparing the mean z-scored spectral power of the 4-Hz and theta oscillations in the mPFC (left), HPC (middle), and PPC (right) with respect to mobility (M) and immobility (I) episodes. For the box plots, the middle, bottom, and top lines of the box plot correspond to the median, lower, and upper quartiles, and the edges of the lower and upper whiskers correspond to the 5th and 95th percentiles. *P < 0.05; **P < 0.01 ***P < 0.001; Sidak’s multiple comparisons test after two-way ANOVA.

Full size image

4-Hz and theta oscillations from HPC and PPC modulated prefrontal gamma oscillations

Given that both theta and 4-Hz oscillations are able to entrain gamma oscillations in the mPFC37,39,40, we asked if these hippocampal and parietal low-frequency oscillations entrained gamma oscillations in the mPFC according to task requirements during spatial learning. The amplitude of prefrontal gamma activity seems to be coordinated by the phase of hippocampal and parietal 4-Hz and theta oscillations (Fig 3a, d). To quantify this entrainment, we computed the phase-amplitude cross-frequency coupling (CFC) of prefrontal gamma with respect to the phase of hippocampal and parietal oscillations47. Representative comodulograms are shown in supplementary Fig. 4a. Hippocampal and parietal entrainment strength (measured as modulation index, MI) of prefrontal gamma was higher for 4-Hz compared to theta (P < 0.0001; Sidak’s multiple comparisons test after two-way ANOVA), with no significant differences between areas (4-Hz: P = 0.634; theta; P = 0.373; Sidak’s multiple comparisons test; supplementary Fig. 4b). Despite the important variability in the frequency for phase for both hippocampal and parietal 4-Hz and theta oscillations (supplementary Fig. 4c), the mean frequency for phases of 4-Hz and theta was not different between HPC and PPC (4-Hz: P = 0.151; theta: P = 0.272, paired t-student test; supplementary Fig. 4d). We also observed an important variability in the frequency for amplitude of prefrontal gamma (supplementary Fig. 4c); however, the mean frequency for prefrontal gamma amplitude modulated by 4-Hz and theta oscillations was not different between HPC and PPC (near 80 Hz; 4-Hz: P = 0.371; theta: P = 0.378; paired t student test; supplementary Fig. 4d).

Fig. 3: Prefrontal gamma oscillations are modulated by hippocampal and parietal 4-Hz and theta oscillations according to task requirements.
figure 3

a, d Simultaneous LFP recording from the HPC (raw and 4-Hz filtered), the PPC (raw and 4-Hz filtered), and the mPFC (raw and gamma filtered) when 4-Hz oscillation was predominant. d Same as a, but when theta oscillation was predominant (HPC; raw and theta filtered; PPC: raw and theta filtered; mPFC: black; raw and gamma filtered). b, e Example of comodulograms of prefrontal gamma oscillations with respect to the phase of hippocampal 4-Hz (c) and theta (e) according to task stages and navigation strategies. c, f Box plot of modulation index of prefrontal gamma oscillations with respect to the phase of hippocampal 4-Hz (d) and theta (f) according to task stages and navigation strategies. ***P < 0.001; Sidak’s multiple comparisons test after two-way ANOVA. g Example of raw (upper, black traces) and gamma-filtered (lower, red traces) simultaneous LFP recordings from mPFC, HPC, and PPC. The panel on the right is a magnification of the dotted area from the left panel. Representative gamma events are pointed by black triangles. h Example of colorplot spectrograms of gamma oscillations of LFPs recorded from mPFC (left), HPC (middle), and PPC (right) according to task stages and navigation strategies. i Box plots of the incidence of gamma events in the mPFC (left), HPC (middle), and PPC (right) with respect to task stages and navigation strategies. *P < 0.001 Sidak’s multiple comparisons test after two-way ANOVA. For all box plots, the middle, bottom, and top lines correspond to the median, lower, and upper quartiles, and the edges of the lower and upper whiskers correspond to the 5th and 95th percentiles.

Full size image

We then asked if 4-Hz and theta oscillations from HPC and PPC modulated prefrontal gamma were task-related during spatial learning. To facilitate the analysis and data representation, we classified navigation strategies into two groups based on the criteria of movement toward the goal quadrant: random and serial strategies were considered “non-spatial”, whereas long-correction, focused search, corrected and direct were considered “spatial” (Fig. 1j)4. Examples of comodulograms are shown in Fig. 3b, e. We found that entrainment of prefrontal gamma by 4-Hz from HPC and PPC were highest in the searching stage respect to exploration during spatial strategies (HPC: P < 0.0001; PPC: P < 0.0001; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3b, c), with no differences between stages in non-spatial strategies (HPC: P = 0.986; PPC: P = 0.758; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3b, c). Theta long-range modulation of prefrontal gamma was also highest in searching compared to exploration during spatial (HPC: P < 0.0001; PPC: P < 0.0001; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3e, f), but not during non-spatial strategies (HPC: P = 0.884; PPC: P = 0.666; Sidak’s multiple comparisons test; Fig. 3e, f). This highest entrainment observed in searching during spatial strategies was not attributed to the duration of the stages (supplementary Fig. 4e). The coincident increased hippocampal and parietal modulation of prefrontal gamma during searching in spatial strategies may suggest simultaneous hippocampal and parietal CFC. To evaluate this possibility, we computed the “instantaneous” MI of hippocampal and parietal 4-Hz/gamma and theta/gamma CFC for all trials, and we calculated the regression between these two signals for each trial. Thus, low regression R2 values indicate low temporal coincidence, whereas high R2 values indicate high temporal coincidence (supplementary Fig. 5). We found trials with low coincident hippocampal and parietal CFC for both frequencies, as well as trials with high coincidence of hippocampal and parietal CFC (supplementary Fig. 5a–l). This was manifested as a high variability between trials in the parietal/hippocampal CFC-coincidence (supplementary Fig. 5m, n). The temporal coincidence of CFC was significantly higher for theta compared to 4-Hz (P = 0.037; t student test; supplementary Fig. 5m, n). We then evaluated if this temporal coincidence was modulated by task stages and strategy progression. We found that 4-Hz hippocampal/parietal CFC-temporal coincidence was highest during searching stage when animals implemented spatial strategies compared to non-spatial strategies (P = 0.011; Sidak’s multiple comparisons test; supplementary Fig. 5o). We found no significant temporal coincidence of CFC at theta frequency between spatial strategies and non-spatial strategies in the searching stage (P = 0.1002; Sidak’s multiple comparisons test; supplementary Fig. 5p).

The increased long-range entrainment of prefrontal gamma may impact gamma activity in the mPFC. Gamma oscillations appear as discrete oscillatory events (Fig. 3g); we identified these events and calculated the incidence of these events during the searching and exploration stages for every navigation trial. We found an increase in the incidence of gamma events in the mPFC when animals used spatial strategies during searching compared to subsequent exploration (P = 0.043; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3h, i), a difference not observed in non-spatial strategies (P = 0.274; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3h, i). No changes between stages and strategies were observed in the HPC (non-spatial: P = 0.749; spatial: P = 0.834; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3h, i) and PPC (PPC; non-spatial: P = 0.952; spatial: P = 0.552; Sidak’s multiple comparisons test after two-way ANOVA; Fig. 3h, i). In summary, these data suggest that 4-Hz and theta large-scale modulation of gamma in the mPFC, as well as gamma incidence in the mPFC, increase during the searching stage, specifically when mice implement spatial strategy.

Local and large-scale oscillations synchronized the spiking of prefrontal neurons according to task stages and navigation strategies during spatial learning

We then asked if local and large-scale oscillatory activity coordinate neuronal activity in the mPFC according to task demands. To this aim, we recorded and identified a total of 650 single units from the three areas during all training sessions: 343 from mPFC, 150 from the HPC and 157 from the PPC (supplementary Fig. 6a). According to the valley-to-peak waveform duration, 89% were classified as wide-spike (putative pyramidal neurons), and 11% as narrow-spike (putative interneurons) (supplementary Fig. 6b, c). We asked if local neural firing was phase-locked to this gamma and if this synchronization was modulated by behavioral demands. Examples of prefrontal neurons phase-locked to local gamma oscillation are shown in Fig. 4a. To quantify this phase-locking, we estimated the phase of gamma oscillation at which every spike occurred. From this, we obtained for every neuron the mean resultant angle of firing (expressed as degrees), and the magnitude (vector) of this mean angle (expressed as the mean resultant length, MRL). The angle phase histograms in Fig. 4b show that there was a wide distribution of phase preference of firing of prefrontal neurons with respect to local gamma, either in searching or exploring during non-spatial strategies. Instead, during spatial strategy, specifically in the searching stage, prefrontal neurons tend to concentrate their firing in the gamma trough (mean angle = 172°), the effect not observed in exploration (Fig. 4b). In agreement with this, the mean MRL to gamma was higher during searching compared to exploration in spatial strategies, with no differences between stages in non-spatial strategies (spatial: P < 0.0001; non-spatial: P = 0.306; Sidak’s multiple comparisons test; Fig. 4c).

Fig. 4: The firing of prefrontal neurons is modulated by local gamma and long-range hippocampal and parietal 4-Hz and theta oscillations.
figure 4

a Example of prefrontal raw (black, upper) and gamma-filtered (purple, middle) LFP recording, and raster plot of spikes of four simultaneously recorded neurons from mPFC (lower). b Angle phase histogram showing the proportion of prefrontal neuronal firing at a preferred local gamma phase (expressed in degrees) according to stages and navigation strategies. c Box plot of average phase-locking strength (measured as MRL) as a function of navigation strategy and task stage for all neurons recorded from mPFC with respect to local gamma oscillations. The middle, bottom, and top lines of the box plot correspond to the median, lower, and upper quartiles, and the edges of the lower and upper whiskers correspond to the 5th and 95th percentiles. ***P < 0.001; Sidak’s multiple comparisons test after two-way ANOVA. d Same as a but for prefrontal neurons modulated by hippocampal (upper) and parietal (lower) 4-Hz oscillations. e Same as b but firing at a preferred hippocampal (upper) of parietal (lower) 4-Hz phase. f Same as c but prefrontal firing phase-locking strength to hippocampal (left) of parietal (right) 4-Hz oscillation. The middle, bottom, and top lines of the box plot correspond to the median, lower, and upper quartiles, and the edges of the lower and upper whiskers correspond to the 5th and 95th percentiles. ***P < 0.001; **P < 0.01; Sidak’s multiple comparisons test after two-way ANOVA. g Same as a but for prefrontal neurons modulated by hippocampal (upper) and parietal (lower) theta oscillations. h Same as b but firing at a preferred hippocampal (upper) of parietal (lower) theta phase. i Same as c but prefrontal firing phase-locking strength to hippocampal (left) of parietal (right) theta oscillations. The middle, bottom, and top lines of the box plot correspond to the median, lower, and upper quartiles, and the edges of the lower and upper whiskers correspond to the 5th and 95th percentiles. ***P < 0.001; Sidak’s multiple comparisons test after two-way ANOVA.

Full size image

We then evaluated if long-range hippocampal and parietal oscillations modulated the spiking of prefrontal neurons according to task demands. Examples of prefrontal neurons modulated by hippocampal and parietal 4-Hz oscillations are shown in Fig. 4d. As observed in Fig. 4e, there was a wide distribution of preferred phase of firing to hippocampal 4-Hz during non-spatial strategies, both in searching as exploration. However, this distribution became narrower near the peak of 4-Hz oscillation (30 degrees) in spatial strategies, specifically during searching stage (Fig. 4e). Similar distribution was found for phase-locking to parietal 4-Hz oscillation (Fig. 4e). Statistical analysis revealed that mean MRL of prefrontal neurons to hippocampal 4-Hz was higher during searching compared to exploration stages during spatial, but not during non-spatial strategy (spatial: P < 0.0001; non-spatial: P = 0.824; Sidak’s multiple comparisons test; Fig. 4f). Similar results were found for parietal-4-Hz phase-locking of prefrontal firing (spatial: P < 0.0001; non-spatial: P = 0.995; Sidak’s multiple comparisons test; Fig. 4f). Then, we evaluated phase-locking to theta oscillations from HPC and PPC. Examples of prefrontal neurons phase-locked to theta from HPC and PPC are shown in Fig. 4g. As well as for 4-Hz oscillations, we observed a wide distribution of phase of firing to hippocampal and parietal theta during non-spatial strategies both in searching as exploration (Fig. 4h). However, this distribution became narrower near the theta oscillation trough (281 degrees) in spatial strategies, specifically during searching stage, both to hippocampal and parietal theta (Fig. 4h). Statistical analysis revealed that the phase-locking strength of prefrontal firing by hippocampal theta was higher during searching, irrespective of the strategy implemented (spatial: P < 0.0001; non-spatial: P < 0.0001; Sidak’s multiple comparisons test; Fig. 4i). Similar results were found for entrainment by parietal theta (spatial: P < 0.0001; non-spatial: P < 0.0001; Sidak’s multiple comparisons test; Fig. 4i). Taken together, these data suggest that phase-locking of prefrontal neuronal activity by local gamma, as well as by large-scale 4-Hz and theta oscillations, increase during the searching stage specifically when mice implement spatial strategy.

Reorganization of firing patterns during spatial learning

We then evaluated if firing patterns in the mPFC were modulated according to task stages and navigation strategies. Given that the variability of the duration of task stages does not allow a direct comparison of firing patterns between different training sessions, each stage was subdivided into an equal number of bins (warping), and the normalized (z-scored) firing rate was calculated for each bin. Thus, it is possible to compare the dynamics of spiking relative to relevant behavioral events independently of the duration of each task stage. These data are shown in the color-coded raster plot in Fig. 5a, in which normalized firing was segregated according to the magnitude firing in turn to the transition from searching to exploration. It can be observed that firing was increased during navigation with respect to start and goal stages (Fig. 5a). From this figure, it can be seen that, when mice used spatial strategies in the searching stage, several neurons changed their firing pattern between stages. Indeed, prefrontal units showed more complex firing during searching when they used spatial strategies. Contrarily, when mice used non-spatial strategies during searching, firing remained relatively constant during the entire navigation session (Fig. 5a). This is most evident in the normalized peri-event time histogram of the lower panel in Fig. 5a. To quantify the differences in firing patterns between stages, we calculated the stage-associated firing selectivity index (FSI) for each neuron (see methods). Thus, the firing of each neuron was expressed as a value between −1 and 1 that estimates its dynamics between stages; positive values indicate that firing was higher in searching compared to exploration; negative values indicate the opposite; values near 0 indicate no changes between stages; and the absolute value indicates the magnitude of the variation. To evaluate if firing dynamics changed with strategy progression, we compared the distribution of FSI values between navigation strategies. As shown in Fig. 5b, the values of FSI showed a distribution toward more extreme values during spatial strategies compared with non-spatial strategies. Statistical analysis revealed significant differences in the distribution of FSI values between non-spatial and spatial strategies (P = 9,7 e-21; Kolmogorov–Smirnov test; Fig. 5b). To quantify the strength of these dynamics, we compared the magnitude of change in firing patterns (absolute FSI value) between strategies (Fig. 5c). We found that absolute FSI values were higher during spatial strategies compared to non-spatial (P < 0.0001; Mann–Whitney U test; Fig. 5c). The same analysis was performed to hippocampal and parietal units (Fig. 5d–i). Similarly to prefrontal neurons, hippocampal and parietal neurons increased their firing during navigation (Fig. 5d, g). As well as for prefrontal neurons, we found, both for hippocampal and parietal neurons, significant differences between strategies in the distribution of FSI values (P = 0.018 and P = 0.036, respectively; Kolmogorov–Smirnov test; Fig. 5e, h) and in the absolute FSI value (P = 0.013 and P = 0.008, respectively; Mann–Whitney U test; Fig. 5f, i). In summary, these results suggest that neuronal populations in the mPFC, HPC, and PPC jointly increase their stage-selectivity of firing during the implementation of spatial strategies.

Fig. 5: Dynamics of firing patterns during spatial memory acquisition.
figure 5

a, d, g Upper panel: color-coded normalized time and z-scored firing rate for all neurons recorded in the mPFC (a) HPC (d), and PPC (g) aligned to behaviorally relevant events during non-spatial (upper) and spatial (lower) strategies. Lower panel: average z-scored peri-event time histogram during non-spatial (grey) and spatial strategies (purple). Shaded areas represent SEM. b, e, h Cumulative distribution of FSI for all neurons recorded in the mPFC (b) HPC (e) and PPC (h) during non-spatial and spatial strategies. c, f, i Box plot comparing the absolute value of the FSI between non-spatial and spatial strategies for all neurons recorded in the mPFC (c), HPC (f), and PPC (i). The middle, bottom, and top lines correspond to the median, lower, and upper quartiles, and the edges of the lower and upper whiskers correspond to the 5th and 95th percentiles. ***P < 0.001; Mann–Whitney test.

Full size image

Discussion

In this study, we found that mice sequentially executed searching and explorative behavior during goal-directed navigation, in which strategy progression was observed only in the searching stage. Interestingly, only when animals searched for the escape using spatial navigation strategies, 4-Hz and theta oscillations from the HPC and PPC synchronized gamma activity and firing patterns in the mPFC, which coincided with the highest incidence of gamma oscillations, the entrainment of firing patterns by these local gamma oscillations, and the task-related accommodation of firing patterns in the mPFC. These findings indicate that prefrontal ensemble synchronization with multiple brain structures varies with both task performance and stage of training.

Our behavioral analysis suggests that the searching stage was directed toward goal achievement (Fig. 1e–i). At the cognitive level, this requires the control and organization of behavior, a function supported by the mPFC7,48,49. Therefore, the increased prefrontal activity and local and large-scale synchronization (manifested as the increase of gamma incidence and CFC) observed during the searching stage may promote neural operations implicated in behavioral control for goal achievement. On the other hand, we found that, in agreement with current literature50, exploratory behavior was not goal-directed (Fig. 1e–i). In a consistent manner, the decreased local and large-scale coupling of the mPFC observed during exploration may imply reduced recruitment of the mPFC during this stage. Therefore, this evidence suggests that synchronization at both local (manifested as the increase of the incidence of gamma oscillations and the increased phase-locking of the neuronal spiking with this local gamma) and large-scale (manifested by the increased CFC and phase-locking of prefrontal spiking respect to hippocampal and parietal oscillations) is transiently increased when the subject requires guiding its behavior into a goal-directed manner. Notably, this prefrontal synchronization during searching was evidenced during the implementation of spatial navigation strategies, that were based on the modification of the navigation path (Fig. 1f; supplementary Fig. 1l, m) and strongly impacted behavioral performance (supplementary Fig. 1n, o). Spatial strategies occurred preferentially at the end of the training process (Fig. 1k), suggesting that the goal-directed accommodation of behavior, and the consequent recruitment of prefrontal activity, may require accumulated experience acquired throughout previous navigation trials3,4. It is proposed that a generalized internal map-like representation is gradually constructed during experience accumulation through the systematic organization, generalization, and extraction of commonalities from past similar episodes5,6,7. Thus, this generalized map can be subsequently utilized to flexibly guide goal-directed behavior according to current conditions51. Both the construction of the internal representation5,6,7, as well as the implementation of efficient strategies during spatial learning are supported by the mPFC8,9,10,11. Thus, our data suggests that the prefrontal neural processing required for goal-directed accommodation of behavior may emerge once sufficient experience has been accumulated.

For the execution of efficient strategies, the mPFC may integrate several sets of information into the current neural operations. Space-based information and action-based self-motion information are required for spatial learning52,53. These items of information are represented by neural spiking in the HPC and PPC, respectively21,54,55,56, structures that are anatomically connected with the mPFC22,23,24,25. Spatial information from the HPC is transmitted to the mPFC57, which synchronizes with the firing of prefrontal neurons58,59,60. Interestingly, whereas hippocampal representation of space remains specific, prefrontal spatial maps generalize across environments61. Considering that hippocampal spatial maps are formed in the first exposition to the environment62,63, it can be suggested that spatial information requires some “executive” processing before it can be used to guide behavior. Similarly, whereas neurons in the PPC represent accumulated evidence, prefrontal neurons encode categorical features in memory-guided tasks64,65. Therefore, the transference of information from the HPC and PPC into the mPFC may contribute to the formation of generalized categorical maps in the mPFC as required to guide behavior during learning.

Large-scale transference and integration of information across brain regions can be mechanistically promoted by the entrainment of local high-frequency oscillations by low-frequency oscillations42,44,66. Interestingly, we found that hippocampal and parietal 4-Hz and theta oscillations entrained gamma oscillations in the mPFC (Fig. 3). This entrainment was higher when animals executed spatial strategy in the searching stage (Fig. 3c, f). The CFC analysis also revealed that both 4-Hz and theta oscillations entrained gamma oscillations in a wide range of gamma frequencies averaged at 80 Hz (Supplementary Fig. 4c, d). Also, gamma oscillations increased their incidence at an analogous average frequency, specifically in the mPFC when animals executed spatial strategies during the searching stage (Fig. 3h, i). This suggests that 4-Hz and theta oscillations modulated gamma oscillations as a common neurophysiological process in the mPFC. Furthermore, spike timing of prefrontal neurons was modulated by local gamma oscillations (Fig. 4a–c), as well as by hippocampal and parietal 4-Hz and theta oscillations (Fig. 4d–i), which also increased when animals executed spatial strategy during the searching stage (Fig. 4c, f, i). Gamma oscillations emerge as a result of the excitatory and inhibitory interaction between local neural populations43. Entrainment of prefrontal neurons by long-range oscillatory synaptic input modulates the instantaneous spiking probability29, facilitating the interaction between local neurons and thus promoting the amplification of gamma oscillations. The increased proportion of prefrontal neurons modulated by the phase of 4-Hz or theta oscillations agrees with this idea (Fig. 4e, h). Hence, via the entrainment of neuronal spiking, large-scale CFC may promote the interaction between prefrontal neurons, increasing CFC and gamma incidence in the mPFC. Considering that gamma oscillations promote neural operations for cortical computations, as associative binding of distributed representations41,45,67, gamma oscillations may promote the integration of information for cognitive control during goal-directed spatial learning.

Our analysis of the CFC revealed that 4-Hz and theta oscillations are two distinct potential approaches to long-range entrain prefrontal gamma in the mPFC. These oscillations do not coexist during spatial learning (Fig. 2b, c) and they differ in their circuital origin in the mPFC, HPC, and PPC35,68,69. In awake rodents, theta emerges mostly during locomotion (Fig. 2d; supplementary Fig 3a); therefore, this rhythm is the main global integrator when animals move in the environment32,33,34. However, cognitive processing is also implemented in the absence of locomotion and, consequently, in the absence of theta oscillations. This occurs, for example, during deliberative processes70. Therefore, the exclusive role of theta as a long-range integrator seems insufficient. Considering that 4-Hz oscillation emerges widely in the brain in the absence of locomotion (Fig. 2d supplementary Fig. 3a36), 4-Hz oscillation may work as a global integrator of neural operations when locomotion is absent71,72. Interestingly, mPFC, HPC, and PPC are apparently simultaneously recruited by either 4-Hz or theta oscillations (Fig. 2a). Evidence supporting widespread brain synchronization by theta or 4-Hz oscillations has been previously reported38,68,73. Thus, the mPFC, HPC, and PPC may be coupled in two main large-scale configurations depending on locomotion: one dominated by the 4-Hz during moments of immobility, and the other dominated by theta oscillations during locomotion.

Finally, we found that prefrontal neurons modified their firing between stages according to the navigation strategy. Stage-associated FSI values were more extreme and had higher absolute value during spatial strategies (Fig. 5a–c), indicating that neurons in the mPFC increased the specificity of firing according to navigation efficiency. Indeed, the firing pattern of a large proportion of prefrontal neurons seems less dispersed during searching compared with the exploration stage in spatial strategies (Fig. 5a). This implies that firing patterns were adjusted during the searching stage depending on the strategy used. It has been previously found that prefrontal firing patterns signal the approach to the goal when mice use spatial strategy4. Therefore, firing patterns may be more specific to particular behavioral events during searching than during exploration. This issue will be approached in a subsequent and deeper analysis. Similarly to prefrontal neurons, hippocampal and parietal units also showed increased FSI during spatial strategies (Fig. 5d–i). This suggests that hippocampal and parietal networks locally accommodate their activity as the subject gains experience in a goal-directed manner. It has been that both hippocampal and parietal neurons accommodate in turn goals21,74. This accommodation may be promoted by executive-prefrontal-driven inputs. For example, the mPFC is necessary for the accommodation of hippocampal place cells in turn to the goal75. To our knowledge, the prefrontal-to-parietal relationship has not been assessed in rodent models during spatial learning. Future analysis will help to clarify this issue.

Overall, our results provide evidence for the large-scale coordination of the mPFC with the HPC and PPC as a putative neural mechanism supporting spatial learning. This mechanism was primarily implemented when mice organized their trajectory in an efficient goal-directed manner and were executed after sufficient experience had been acquired. It involved theta and 4-Hz oscillations that emerged differentially according to locomotor activity, which coordinated gamma oscillations and neuronal firing in the mPFC. This coincided with the increase of gamma oscillations and the task-related arrangement of firing patterns in the mPFC.

Methods

Animals

Adult male C57BL/6j mice (n = 12; age: 60–90 days) were used in this study. Mice were housed in a 12-hour light/dark cycle in a temperature- and humidity-controlled room (22 ± 2 °C) with ad libitum access to food and water. We have complied with all relevant ethical regulations for animal use. All experimental procedures related to animal experimentation were approved by the Institutional Animal Ethics Committee of the Universidad de Valparaíso (CICUAL-UV; protocol code: BEA178-22). Efforts were made to minimize the number of animals used and their suffering. For sample size estimation, we used the One Sample Design method (https://www2.ccrb.cuhk.edu.hk/stat/Means.htm) using data from previous pilot experiments (outcome measure: escape latency).

Custom-made microelectrode arrays (MEA)

MEA-carrying tungsten wire microelectrodes (SML coated; 50 µm diameter, California Fine Wire) were assembled for simultaneous LFP and single units recording from the mPFC, CA1 area of the HPC, and the PPC. Microelectrode wires were cut off with iris scissors (World Precision Instruments, Sarasota Instruments). The final impedance of each wire (100–500 kΩ) was measured in a saline solution at 1 kHz. Microelectrode arrays were composed of two bundles of seven stainless-steel cannula each (30 G; Components Supply Co., FL, USA), one directed to mPFC and the other to HPC/PPC. Six single wires were inserted in each bundle, and the length was adjusted to target the mPFC (length: 1.5 mm), the HPC (length: 1.5 mm), and the PPC (length: 0.5 mm). Each microelectrode wire was fixed to the bundle with cyanoacrylate and connected to a 16-channel interface board assembled with an Omnetic connector (Neurotek, Toronto, ON, Canada).

MEA implantation surgery

Animals were anesthetized with isoflurane (3% isoflurane with 0.8% O2) before being placed in a stereotaxic frame. Anesthesia was maintained until the surgery was finished (1–2% isoflurane with 0.8% O2). After the incision in the scalp, two craniotomies were drilled in the right hemisphere at stereotaxic coordinates targeting the mPFC (1.94 mm AP, −0.25 mm ML, from Bregma76) and region CA1 of the HPC (−1.94 mm AP, −1.5 mm ML, from Bregma). Stereotaxic coordinates targeting PPC were the same as for HPC. The dura was removed, and the electrodes were slowly lowered and inserted into the cortical surface. Two ground wires were attached to skull screws. Once in position, the MEA and the ground screws were affixed to the skull with dental acrylic. After surgery, animals were maintained in individual cages in a temperature- and humidity-controlled room (22 ± 2 °C) with food and water ad libitum and were supplied with a subcutaneous dose of analgesics (Ketoprofen, 5 mg/kg/day) and antibiotics (Enrofloxacine, 5 mg/kg/day) during the 5 days after surgery. Mice were allowed to recover for at least one week after surgery before beginning behavioral and recording experiments. During recovery, weight and general health were monitored daily.

Behavioral and electrophysiological recording procedures

After one week of recovery from surgery, mice were habituated and placed in the behavioral room for 15 minutes, and then they were trained for the spatial reference memory task in the Barnes maze77. The maze consisted of a white circular platform of 70 cm in diameter elevated at 70 cm from the floor with 16 equally spaced holes (9 cm diameter) along the perimeter and located at 2 cm from the edge of the platform. Visual cues were located on the walls of the room. Under one of the holes was located a black plexiglass escape box (17 × 13 × 7 cm) that allowed the mice to enter with the implanted MEA. The location of the escape box was consistent for a given mouse but randomized across the mice group. The spatial location of the target was unchanged with respect to the distal visual room cues. The maze was illuminated with two incandescent lights to yield a light level of approximately 400 lux impinging on the circular platform. To evaluate the acquisition of spatial memory, four navigation trials per day with an inter-trial interval of 15 minutes for 5 consecutive days were realized. In each acquisition trial, the interface board of the MEA was connected to the amplifier board (RHD2000 evaluation system; Intan Tech, CA, USA) via a 16-channel head-stage (model RHD2132 Intan Tech, CA, USA). Then, the recording system was turned on, and the mouse was placed in the start box in the center of the maze for 1 min with the room lights turned off (start stage). After time had elapsed, the start-box was removed, the room lights turned on, and the mouse was free to explore the maze (navigation stage). The session ended when the mouse entered the escape box or after 3 minutes elapsed. Once the mouse entered the escape, the lights were turned off, and the mouse was left to remain in the escape box for 1 min (goal stage). If the mouse did not enter the escape box within 3 minutes, the experimenter guided the mouse to the escape. When the trial was completed, the electrophysiological recording system was turned off, the mouse was disconnected from the electrophysiological recording system and returned to the home cage, and the maze was cleaned with ethanol 70% to prevent a bias based on olfactory or proximal cues within the maze. During the complete trial, the animal behavior was tracked and recorded with a webcam (acquisition at 30 fps and 640 × 480 pixels; camera model C920; Logitech Co.) located 1 mt above the maze and controlled with VirtualDub software.

Histology

After the complete experiment was finished, mice were anesthetized with 3% isoflurane, and the location of each microelectrode wire was marked by passing a small amount of current through each electrode (50 µA by 10 s). Two days after this protocol, mice were anesthetized with isoflurane (3%) and then transcardially perfused with ~40 ml of phosphate-buffered saline (PBS, pH = 7.4), followed by ~50 ml of paraformaldehyde (PFA) in PBS. The brain was removed and then stored in PFA with PBS overnight. PFA was washed with a solution of PBS containing 30% saccharose, and brains were stored in PBS with 30% saccharose until the cut session. Coronal brain slices (50 µm) from HPC/PPC and mPFC were obtained from a cryostat-microtome (Zhejiang Jinhua Kedi Instrumental Equipment Co., LTD) and stored in PBS containing 0.01% sodium azide. For visualization of the electrolytic lesions, slices were stained with Nissl-staining, and pictures were acquired with a microscope (Nikon). Electrophysiological data were excluded if recording electrodes were not positioned in the desired brain area. This was confirmed by two criteria: a) quality of the LFP recording (“typical” theta activity and presence of sharp-wave ripples in the HPC, for example) and b) proper histological location of electrolytic mark. Also, LFP recorded from electrodes with improper impedances (below 100 and above 1000 kOhms) were excluded from all analysis.

Behavioral analysis

Behavioral performance

Behavioral performance was analyzed by measuring the escape latency (the time to enter the escape hole), nose-poke latency (time elapsed for the first contact of the mouse nose with the escape hole), number of errors (nose-pokes in non-escapes holes), distance covered and path efficiency to the first nosepoke in the escape hole. To assess locomotor activity, the mean and maximum speed in all trials were measured. All these behavioral parameters were analyzed and measured with ANY-maze software (Stoelting Co.). Also, ANY-maze software provided for every trial a file containing instantaneous spatial coordinates of the animal’s trajectory and instantaneous speed. These were used to construct occupancy plots and for the detection of episodes of mobility (running speed >4 cm/sec for at least 2 sec) and immobility (running speed <4 cm/sec for at least 2 sec) during navigation. Both analyses were performed in MATLAB software with custom-made scripts.

Identification of task stages

For the identification of relevant task moments and comparison of electrophysiological parameters among them, each navigation trial was separated into two stages: searching, from the start of navigation to the first nose poke in the escape hole; and exploration, from the first nose poke in the escape hole to entering the escape hole.

Identification of navigation strategies

navigation strategies were defined and analyzed with the BUNS46 implemented in MATLAB software. Coordinates of animal trajectory obtained from ANY-maze software were entered in MATLAB by using the support vectorial machine and converted into cartesian coordinates to characterize animal trajectory features until the first contact with the escape hole. Data were adjusted at BUNS detector requirements, and then the strategies were classified according to the following definitions: random, when the animal navigates randomly in the maze until that it finds the escape-hole; serial, when the animal navigates of hole to hole (adjacent holes) until it finds the escape-hole; focused search, when the animal realizes a located scan of the escape-hole quadrant; long correction, when the animal navigates to erroneous hole and, then it adjusts the navigation trajectory to directly find the hole escape; corrected, when the animal slightly modifies its trajectory (go to the next hole, before the escape-hole); direct, when the animal uses the shortest path to find the escape-hole. All the results obtained from the strategy detector were compared with a visual analysis recording to determine possible errors. BUNS also provides a cognitive score according to the strategy (direct = 1 point; corrected = 0.75 points; long correction = 0.5 points; focused search = 0.5 points; serial = 0.25 points; and random = 0 points).

Path sparsity

Path sparsity, which represents the proportion of arena the animal occupied to reach the goal, was based on the method described by Jung et al.78. Briefly, to parametrize the sparsity for firing rate, trajectory sparsity was calculated as follow:

$${Sparsity}={\left(\sum {p}_{i}* {\varepsilon }_{i}\right)}^{2}/\sum {p}_{i}* {{\varepsilon }_{i}}^{2}$$

where pi is the probability of the animal being in the i th bin (occupancy time in the ith bin/total recording time) and εi is the total time, the animal visits the i th bin.

Electrophysiological analysis

LFP spectral power and instant energy

For analysis of the spectral power of oscillatory activity, electrophysiological recordings were down-sampled to 1000 Hz, and bandpass-filtered at 0.1–120 Hz. Power spectral density (PSD) was computed using multi-taper Hamming analysis using the Chronux toolbox (http://www.chronux.org79). For PSD analysis, field potentials were divided into 4000 ms segments with 400 ms overlap and a time-bandwidth product (TW) of 5-9 tapers. For the estimation of spectral power during mobility and immobility episodes, the down-sampled LFP recordings were filtered at 4-Hz or theta frequency bands using the Hilbert transform, and the resultant envelope (i.e., instant energy) was rectified, smoothed, and z-scored80.

Phase-locking value

For PLV analysis, we used the method described by Lachaux et al.81. Briefly, two simultaneously recorded LFPs signals were filtered at the same frequency (either 4-Hz or theta). Next, the Hilbert transform was applied to both signals, and the instantaneous phase was obtained. The phase difference between signals was computed using the following equation:

$${{{\rm{PLV}}}}=\frac{1}{N}{\sum}_{n=1}^{N}\exp (j\theta (t,n))$$

This gives values between 0 to 1, being 0 a random phase differences, to 1 indicating a fixed phase difference.

Granger causality

was calculated by the method described by Barnett and Seth82 using the Multivariate Granger Causality Matlab toolbox mvgc_v1.0. Briefly, the prediction (\(Fy\to x\)) of a time series (x) can be reflected in the measurement of a second time series (y) in a regression model (Verctor AutoRegressive (VAR) model), so if the second (Σ1) time series reflect the first (Σ2), it is said that there is a “Granger causality” of the first series on the second. If the prediction of the signal “x” is improved by incorporating the values of the signal “y”, it has a causal influence on “x”, as reflected in the following equation:

$${F}_{y\to x}={En}\frac{{\sum}_{2}\,}{{\sum}_{1}\,}$$

Gamma-event detection

For gamma event detection we used the method described by Logothetis et al. 83 with some variations from Csicsvari et al.84. Briefly, LFP was band-pass filtered (60–100 Hz) using a zero-phase shift noncausal finite impulse filter with a 0.5 Hz roll-off. Next, the signal was rectified and low-pass filtered at 20 Hz with a 4th-order Butterworth filter. This procedure yields a smooth envelope of the filtered signal, which is then z-score normalized using the mean and standard deviation (SD) of the whole signal. Epochs during which the normalized signal exceeded a 2.0 SD threshold were considered potential gamma events. The first point before the threshold that reached 1 SD was considered the onset, and the first one after the threshold reached 1 SD at the end of events. The difference between the onset and end of events was used to estimate the gamma event duration. We introduced a 50-ms-refractory window to prevent double detections. In order to precisely determine the mean frequency, amplitude, and duration of each event, we performed a spectral analysis using Morlet complex wavelets of 7 cycles.

Cross-frequency coupling analysis

For CFC analyses, the ModIndex toolbox47. CFC was computed using the MI. The MI is able to detect the strength of the phase-amplitude coupling between two frequency ranges of interest: the “phase-modulating” (theta and 4-Hz) and “amplitude-modulated” (gamma) frequency bands. First, LFP was filtered at the two frequency ranges under analysis. Next, the phase and the amplitude time series were calculated from the filtered signals by using the Hilbert transform. Specifically, the time series of the phases were obtained from the standard Hilbert transform, and to extract the amplitude envelope, we also applied the Hilbert transform. Then, the composite time series was constructed, which gave us the amplitude of the “amplitude-modulated” oscillation at each phase of the “phase-modulating” oscillation. The phases were binned, and the mean amplitude over each phase bin was calculated. The existence of phase-amplitude coupling is characterized by a deviation of the amplitude distribution P from the uniform distribution U in a phase-amplitude plot (if there is no phase-amplitude coupling, the amplitude distribution P over the phase bins is uniform). A measure that quantifies the deviation of P from the uniform distribution was determined by an adaptation of the Kullback-Leibler (KL) distance (DKL), which is widely used in statistics to infer the amount of difference between two distributions. The adaptation was to make the distribution distance measure assume values between 0 and 1. The MI is, therefore, a constant time, the KL distance of P from the uniform distribution (U). Thus, the higher the MI, the greater the phase-amplitude coupling between the frequencies and areas of interest. It is represented in the following equation:

$${{{\rm{MI}}}}=\frac{{DKL}(P,U)}{.\log (N)}$$

The instantaneous CFC was generated by repeatedly computing the MI in 10 seconds sliding windows with an overlap of 90%. LFPs were first band-pass filtered to avoid edge effects during phase extraction.

Spike sorting

Spike sorting was performed offline using Wave-clus, a MATLAB-based super paramagnetic clustering method for spike sorting85. To detect spikes, broadband recordings sampled at 20 kHz were filtered at 500–5000 Hz, and events with amplitudes reaching 4–50 SDs over the mean were considered candidate spikes. For each recording file, single channels from each single electrode were identified, and a single file was generated per channel. The spike features considered for clustering included peak amplitude (the maximum height of the waveform of each channel of each spike), timestamp (the time of occurrence of each spike), spike width (the duration in each channel of the spike), energy (the energy contained within the waveform of each channel of the spike), valley (the maximum depth of the waveform of each channel of the spike), and wave-PC (the contribution to the waveform due to the principal component). A file for every single unit, including timestamps of spikes, was generated and used in the subsequent analyses on MATLAB. To confirm the correct sorting of single units, the time stamps of every single unit were aligned with their 500–5000 Hz filtered LFP recording, and the concordance of timestamps with spikes was visually established.

Phase-locking analysis

Phase-locking analysis was computed using the Matlab toolbox CircStats (http://philippberens.wordpress.com/code/circstats/86); Briefly, LFP traces were bandpass filtered at 4-Hz, theta or gamma range (2–5 Hz, 6–12 Hz, and 60–100 Hz, respectively; zero phase shift non-causal finite impulse filter with 0.5 Hz roll-off). Phase locking was quantified as the circular concentration of the resulting phase distribution, which was defined as mean resultant length (MRL = (n/Z)0.5)87. The statistical significance of phase locking was assessed using the Rayleigh test for circular uniformity. To avoid bias, we only considered neurons with >50 recorded spikes.

FSI analysis

For the calculation of the stage-associated FSI, we used the following expression:

$${{{\rm{FSI}}}}=\frac{{FRs}-{FRe}}{{FRs}+{FRe}}$$

in which, for any given single unit, FRs is the mean firing rate during searching, and FRe is the mean firing rate during exploration. Values may range from −1 to 1. Positive values indicate that firing was higher in searching compared to exploration; negative values indicate the opposite; values near 0 indicate no changes between stages; and the absolute (abs(FSI)) value indicates the strength of the variation.

Statistics and reproducibility

Statistical comparisons were performed between task stages and/or navigation strategies. Comparison between the means of quantitatively normally distributed variables between two categories was analyzed using the t student test. Comparisons between the means of quantitatively non-normally distributed variables in two groups were analyzed using the Mann–Whitney test. Comparisons between the means of quantitatively normally distributed variables of more than two groups (as most behavioral variables) were analyzed using one-way ANOVA followed by Tukey’s multiple comparisons. Comparisons between the means of quantitative variables across two categorical independent variables (for example, MI or MRL between stages and navigation strategies) were performed using a two-way ANOVA followed by Sidak’s multiple comparisons test. Linear correlations between parameters were analyzed by the Pearson correlation test. Distributions (FSI values) were compared using the Kolmogorov–Smirnov test. Statistical analysis was performed with GraphPad Prism or MATLAB (2018a; The Mathworks Inc.) software. Significance differences were accepted at P < 0.05.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.