Introduction

Machine learning methods, particularly neural networks, have been a disruptive technology that has transformed numerous fields in the last decade. Machine learning and deep learning have completely reshaped the fields of biomedical image segmentation1, natural language processing2,3, protein folding4 and many more. The rise of deep learning can be attributed to three main factors. First, sufficiently large neural networks can approximate any function5,6. Neural networks are thus not constrained to linear combinations, but can find and leverage non-linear interactions between inputs. Secondly, neural networks scale well with data set size7. Neural networks thrive in large data sets with many examples as it allows the network to find complex patterns. Third, neural networks are flexible; their architecture can be easily modified for different tasks and different types of data. For the imaging domain, this led to convolutional neural networks (CNNs) while for natural language processing, transformers have deeply impacted the field8.

In population-based genetics where there is a large number of input SNPs, there is a domain-specific trend to embed neural networks with prior biological knowledge, such as gene and pathway information, to create sparse and interpretable neural networks that predict genetic risk9,10,11,12,13. These interpretable neural networks, coined visible neural networks14, provided a solution to the two main challenges for neural networks for genetic data. The large number of input features - up to millions of SNPs - and the need for neural networks that can provide more insight into its decision-making process. Prior knowledge such as gene and pathway information is embedded in the neural network architecture to define which node should connect and which not, resulting in a sparse and interpretable neural network. In these networks, each node represents a biological entity by the inputs it groups (e.g. SNPs are grouped by gene). The weights of the connections represent how predictive these entities (i.e., SNPs, genes and pathways) are for the final prediction.

However, although visible neural networks provide more insight into how important SNPs, genes and pathways are for prediction, they do not provide any information about interactions between SNPs or genes. Likewise, other post-hoc interpretability methods for standard types of neural networks, such as Layer-wise Relevance Propagation15, Integrated Gradients16 and DeepLIFT17, only provide the importance for each entity and do not provide insight in the nature of the relation between entities. Attributing entities with an importance score, a single value for each input, provides a simplified view of the decision process that ignores interactions. Neural networks thrive because they can learn (non-linear) combinations of features and these cannot be expressed by a single importance value. Thus, for a more complete overview of the decision process of neural networks and to understand the nature of the relation between SNPs, genes, and pathways, it is important to detect and understand which input features interact with each other in neural networks.

Non-linear effects are ubiquitous in biology. Detecting and understanding these interactions is necessary to fully model the complex biological mechanisms that exist between genotype and phenotype18,19. Detecting interactions between genes and, in particular, SNPs (epistasis) comes with an inherent computational challenge. Following Fisher’s20 definition of statistical epistasis, i.e., as a deviation from the additive expectation of allelic effects, the possible set of interactions exceeds \({{{\mathcal{O}}}}({p}^{2})\), with p the number of features. Thus, an exhaustive search is computationally unfeasible for a large number of inputs. In genetics, genome-wide association studies (GWASes) consider several millions of SNPs and detecting epistasis is thus infeasible to date without extra interventions to reduce the search space of possible interactions, due to the sheer number of possible combinations. Fortunately, there is a wide variety of non-exhaustive epistasis detection methods available. Epiblaster21, takes a two-step approach that first searches for a smaller number of likely candidates using correlation before performing full rank logistic regression to confirm significance. MB-MDR22, a non-parametric model often used to detect epistasis, conditions interaction testing on lower order effects. Other approaches, such as machine learning applications, build a prediction model first and then extract interaction information from this model. Tree-based classifiers can use the structure of the trees to find epistasis candidates23,24 or use the prediction model with permuted input data to find interacting features25. For neural networks, the field of explainable AI (XAI) provides many tools that aim to explain the trained neural network. Most of these tools focus on input feature attribution and place little emphasis on finding interacting features. However, Tsang et al.26 proposed a method for finding statistically significant feature interactions using the weights of a neural network. They demonstrated this method on synthetic datasets and real-world datasets such as California housing prices and bike rental counts. In genomics, only Greenside et al.27 introduced a feature attribution method for detecting interactions in sequences for neural networks predicting epigenetic markers.

Combining these methods with visible neural networks might enhance our understanding of these neural networks and thereby the underlying biology. In this paper, we evaluate the performance and consistency of several post-hoc interpretation methods on visible neural networks from the GenNet framework10. Primarily, we focus on epistasis detection, i.e., a pair of SNPs whose combination affects the phenotype. After training these networks, we apply: neural interaction detection (NID)26, PathExplain28 and Deep Feature Interaction Maps (DFIM)27 to investigate how well these methods explain interactions learned by visible neural networks. Moreover, on the learned network, we analyze which gene gives a relative local improvement in predictive power (RLIPP)13. We compare these methods to literature epistasis methods, such as light gradient-boosting machine, Epiblaster and MB-MDR, using simulated data from Epigen and Gametes. Finally, we apply these post-hoc interpretation methods to visible neural networks trained on data from the Inflammatory Bowel Disease Consortium.

Methods

To evaluate epistasis methods in a controlled environment with known ground truth, we used simulated data from two different methods: GAMETES29 for strict and pure epistasis models and EpiGEN30 for more complex simulations. Finally, we applied the methods to the data from the International Inflammatory Bowel Disease Genetics Consortium (IIBDGC) to test the approaches in human data.

GAMETES is an open-source simulation package to generate pure and strict epistatic models, thus epistasis models without linkage disequilibrium and marginal effects but with two loci contributing to a discrete phenotype in a strictly non-linear manner. Fourteen different sets of simulations were simulated with varying sample sizes {3000, 12000}, heritability {0.05, 0.1, 0.2, 0.3}, and number of SNPs {25, 100, 1000}. An overview of the simulation settings can be found in Supplementary Table 1.

EpiGEN, on the other hand, is a simulation pipeline built to simulate more complex phenotypes based on realistic genotype data. For example, EpiGEN allows the use of HAPGEN2 to simulate genotype data with similar characteristics (linkage disequilibrium, ethnicity, etc.). Additionally, EpiGEN was used to explore the effects of different epistasis models and SNPs with marginal effects. Using HAPGEN2 as a basis, we created simulations with varying sample sizes {3000, 12000}, number of SNPs {100, 1000}, interactions models {joint-dominant, joint-recessive, multiplicative and exponential}, and interaction strength {3, 10, 100}. Different interaction models mimic different structures of the epistasis. An interaction strength of, e.g., 10, means that an individual with the epistatic pair has 10-times the risk of someone without. Overall, we generated 384 different simulations: 288 with a marginal background effect and 96 pure epistasis models where only interaction effects lead to the response. All simulation parameters for EpiGEN can be found in Supplementary Table 1. For in-depth details on the simulations, we refer to the original paper30.

IBD dataset. We investigated the IBD dataset from the International Inflammatory Bowel Disease Genetics Consortium (IIBDGC). The data contains cases with non-infectious inflammations of the bowel, including Ulcerative colitis (UC) and Crohn’s disease (CD), the two main categories of IBD31. The dataset was genotyped on the Immunochip SNP array32. We performed quality control as in Ellinghaus et al.33, reducing the number of SNPs from 196,524 to 130,071. The final dataset contained 66,280 samples, including 32,622 cases (individuals with IBD) and 33,658 controls, thus with a feature:sample ratio of around 2:1.

Since the IIBDGC dataset aggregates multiple cohorts, confounders by shared genetic ancestry is a concern. As in Ellinghaus et al.33, we used the first 7 principal components to model population stratification. We adjusted the phenotypes for epistasis detection methods that cannot include covariates. The same quality control steps as in Duroux et al.34 were applied. We removed rare variants (MAF  < 5%) or in Hardy-Weinberg equilibrium (p-value  < 0.001). All risk SNPs described in Liu et al.35 were included.

Visible neural networks

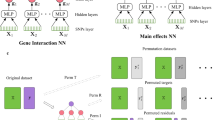
The GenNet framework10 was used to create sparse and interpretable neural networks. These visible neural networks use biological knowledge embedded in the neural network architecture to define connections between nodes. Figure 1 illustrates the employed neural network architecture. Each network had a depth of three or four layers, depending on the input encoding, and was structured according to Fig. 1. Several changes were made to the original framework to improve the neural networks for epistasis detection. First, we tested one-hot input encoding in addition to the standard (additive) input encoding. Secondly, we added multiple filters for each gene to allow the network to find and use multiple patterns per SNP and gene, followed by an extra layer to converge back to a single node per gene (Supplementary Fig. 1).

Fig. 1: An overview of the post-hoc interpretation methods applied in this study to detect interactions in visible neural networks.
figure 1

a Comparing the relative weights of the one-hot encoded input for each SNP reveals the model that the neural network is using for that particular SNP (e.g., linear spaced weights indicate an additive model). PathExplain applies Integrated Gradients on itself to find the Expected Hessians, which can be used to find interaction between inputs. RLIPP (c) is a method to detect if a node has non-linear behavior. The activations towards and from this neuron are regressed to the output with linear regression to provide an estimate of the non-linear gain of that node. d NID uses the assumption that edges with strong weights are more likely to interact with each other than edges with low absolute weights. DFIM (e) compares Deeplift’s attribution scores for all features before and after a feature of interest is perturbed, revealing all features that interact with the feature of interest.

Full size image

The simulated data from EpiGen and GAMETES lack gene annotations. For these simulations, we created the gene annotations dynamically by connecting neighboring inputs to a number of genes proportional to the input size of the simulation. More specifically, the number of neurons — the basic computational units in a neural network — was defined as the total number of inputs divided by 100, with a minimum of five neurons. The learning rate for the ADAM optimizer and the strength of L1 penalty on the kernel weights were optimized on the validation set. To reduce the computational cost, hyperparameters were only optimized for a single simulation for simulations similar in sample size and input size. Networks were trained using CPU since the sparse matrix operations used do not benefit from using a GPU.

For the IBD dataset we used similar neural networks but with gene annotations from FUMA36. To map SNP to genes, both positional and functional annotations were combined. In the positional annotations, SNP to genes were mapped via a positional mapping obtained from FUMA’s SNP2GENE function. A SNP was mapped to a gene when the genomic coordinates of a variant were within the boundaries of a gene  ± 10 kb. For the functional annotations, we used FUMA’s eQTL mapping that is based on eQTLs obtained from GTEx37. An eQTL SNP was mapped to its target gene when the association p-value was significant in any tissue (FDR < 0.05). Combined they map 38,225 SNPs to 25,139 genes with 126,899 connections.

One-hot encoding. The standard genotype encoding {0,1,2} may introduce a bias to the additive model between genetic variants and the outcome as it represents an additive model. Therefore, we train for each application two models. A standard model and a model with a one-hot encoded input for the genotype. For this model we modify the first layer of each network, leading to three inputs per SNP (as shown in figure 1a). Regular one-hot encoding is widely used in machine learning to treat categorical variables as numerical values. In one-hot encoding the three categories that the SNP can assume: both reference alleles, a reference and an alternate allele, or both alternate alleles are each represented with a single variable that assumes value 1 if the input individual has said configuration, and 0 otherwise. We designed a novel way of using this one-hot encoded input, the three inputs per SNP are connected to a node representing that SNP in the first layer of the network. The weights of these connections may be informative of the genetic model learned by the model for that SNP.

For an additive model, the expected strength of the weights should roughly adhere to: W0 − W1 ≃ W1 − W2. We, therefore, use the ratio Rw = \(\frac{{W}_{0}-{W}_{1}}{{W}_{1}-{W}_{2}}\) as a measure for the degree of linearity. Historically, the additive model is the standard model, and it has had great success as the underlying model explaining genetic effects. Accordingly, we initialized the weights for each SNP according to the additive model, which can be seen as a reference model under Fisher’s epistasis definition. During training the neural network may freely change the ratio between these weights, diverging from an additive model. Inspecting the weights and the ratio Rw may indicate for which inputs the model deviates from the additive model. However, it is important to note that the model may learn more complex models using subsequent layers of the network, thus additive weights in the first layer do not exclude the possibility of a deviation of an additive model.

Epistasis detection using trained neural networks

After training the visible neural networks we apply various methods to extract the non-linear patterns learned from the model.

Neural interaction detection (NID)

Ref.26 is a method to detect statistical interaction pairs in neural networks that works on the premise that relevant interacting features have large weights assigned. Pairs of features are ranked according to the strength of the weights connecting to the neuron and the importance of the neuron (defined by the weights of its successive connections). Adapting this algorithm to visible neural networks is straightforward, as the mathematical interpretation is unchanged. The most likely interaction candidates are the combinations of the absolute weights that result in the highest value. Multiplying this value with the importance of the node, expressed by a multiplication of all the weights between the node and the output node, results in the final interaction score.

$$NI{D}_{gene}={Z}_{j}* \min (| {W}_{cand}(1)| ,| {W}_{cand}(2)| )$$
(1)

with Wcand as a matrix sorted by the absolute weights per gene and Zj as the importance of the gene node (resulting from a multiplication of the absolute weights of all nodes between the selected node and the output).

Deep Feature Interaction Maps (DFIM)

Ref.27 assumes that perturbing a feature will result in a change in attribution score for a feature that is interacting with the perturbed feature. DFIM uses DeepLIFT17 to get attribution scores before and after mutating a variant and saves this difference in attribution score as the feature interaction score (FIS). Since a single DeepLIFT call provides the attribution scores for all variants, only two calls are necessary to gain all the feature interaction scores for all the unperturbed (target) features. In this work, we perturb the hundred most important features identified by DeepLIFT and save the feature that has the highest FIS score, however a larger number of features can be saved if one suspects more interactions per feature.

PathExplain

Ref.28 uses the Expected Hessians for identifying interacting features. We apply PathExplain on the hundred most important features identified with expected gradient38, the build-in feature importance method of PathExplain. For an input x, the feature interaction score (FIi,j(x)) is obtained using Integrated Gradients (ϕ)16 applied on itself in order to explain the degree to which feature i impacts the importance of another feature j:

$$F{I}_{i,j}(x)={\phi }_{j}({\phi }_{i}(x))$$
(2)

Thus, where DFIM mutates a feature and finds the change in importance for other features using the gradients in Deeplift, PathExplain directly finds the change in gradients by computing the expected Hessians.

Relative local improvement in predictive power (RLIPP)

Ref.13 is a method to detect in which nodes of the neural network statistical interactions occur. It compares the difference in predictive performance of a specific neuron’s inputs and outputs. The activations towards and from this neuron are regressed to the output with linear regression. In the original paper, the Spearman correlation was used to measure the performance gain for a regression task. We modified the algorithm in two ways to adjust it for the classification problem at hand. We compare the adjusted R2 of the two models and calculate RLIPP as:

$$RLIP{P}_{n,l}=\frac{{R}_{pa}^{2}-{R}_{ch}^{2}}{{R}_{pa}^{2}}.$$
(3)

For GenNet’s networks for each node (n) and for each layer (l), the phenotype based on its’ activations (Parent, pa) and all the incoming edges, i.e., the weighted SNPs defining the node (Child, ch).

Baseline methods

To compare the neural network to more traditional solutions, we use different epistasis detection models with different underlying mechanisms: LGBM, MB-MBDR and Epiblaster (see Table 1 for a comparison between the epistasis detection algorithms used in this study).

Table 1 Properties of the different epistasis detection algorithms used and associated input
Full size table

Light gradient-boosting machine (LGBM)

Ref. 39 is a classification model using gradient boosting decision trees. Light gradient-boosting machine (LGBM) is an open-source gradient boosting framework that is designed to be efficient and scalable, making it well-suited for large datasets and high-dimensional problems. LGBM is particularly effective for handling large datasets with a large number of features, as it is able to handle missing data and categorical features efficiently. Two techniques distinguish LGBM from other gradient-boosting decision tree classifiers. Gradient-based one-side sampling allows LGBM to grow decision trees faster than traditional approaches, while also reducing overfitting and exclusive feature bundling to handle categorical features without the need for one-hot encoding, further reducing the memory usage and training time. We evaluated both feature importance as well as an unpublished feature interaction detection method39, used in a Kaggle competition to predict customer transactions.

Epiblaster

Ref.21 is an algorithm that employs a two-stage approach to detect epistasis and generate a ranked list of SNPs with associated scores and adjusted p-values. The algorithm uses a combination of quasi-likelihood and linear models, such as linear regression or logistic regression depending on the output. In the first stage, an exhaustive filtering process is performed on all SNP pairs using the difference of Pearson’s correlation coefficient to rank them rapidly. In the second stage, only the top-k SNP pairs are selected, and a more accurate linear model with a real likelihood is used to compute the real p-value and test statistic. The p-value associated with the Beta is the measure of the association, and since multiple testing is performed, adjustment is needed. The retrieved p-value, adjusted for multiple testing, was used to rank the found SNP pairs.

MB-MDR

Ref.22 can identify genetic interactions in various SNP-SNP based epistasis models. The algorithm exhaustively explores the association between each SNP pair and the phenotype, using all available cases. It is a non-parametric method, in the sense that it makes no assumptions about the modes of interaction inheritance. The model-based part of MB-MDR refers to the ability to condition interaction testing on lower-order (main) SNP effects. For additional information and performance results, we refer to40,41; Such works report about the significance of interactions are corrected for multiple testing, using a step-down maxT inspired algorithm, controlling family-wise error rates (Type I errors). Exact permutation-based significance assessment is replaced by approximate such computations via the gammaMAXT algorithm as described in42. By default, approximations are invoked when the number of input SNPs, to interrogate for interactions, exceeds 10, 000.

Evaluation metrics

The Area Under the Receiver Operating Characteristic Curve (AUC-ROC) is a popular metric used to evaluate the performance of binary classifiers. The ROC curve is created by plotting the true positive rate (TPR) against the false positive rate (FPR) for different thresholds. The AUC is simply the area under the ROC curve, ranging from 0 to 1, with an AUC of 0.5 representing a model equal to random guessing. We use the AUC to evaluate the classification performance of the neural network.

The Area Under the Precision-Recall Curve (prAUC) is a useful metric to assess classifiers when there is a large imbalance between the classes. A high prAUC represents both high recall and high precision, where high precision relates to a low false positive rate, and high recall relates to a low false negative rate. The prAUC is used to evaluate epistasis detection.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Simulation results

We evaluated the performance and the consistency of interpretation methods for finding non-linear interactions with visible neural networks and compared these to more traditional approaches such as Epiblaster, MB-MDR and LGBM.

GAMETES

The heritability value used in generating the simulations and the ease of detection, the difficulty based on the penetrance tables, had a clear impact on the predictive performance in the expected directions (see Supplementary Fig. 2). To evaluate whether the post-hoc interpretation methods can extract the learned interactions in neural networks, we examined only simulations for which both types of neural networks found a predictive pattern, i.e., models with an AUC higher than an AUC of 0.5 in the test set (142/280).

Overall, the best interpretation method for the GenNet networks was DFIM with an average prAUC of 0.70 over all runs, followed by PathExplain (prAUC of 0.68) and NID (prAUC of 0.63) see (Fig. 2a). There were strong correlations (Pearson correlation coefficients between 0.62 and 0.64) between the predictive performance of the neural network (AUC of the test set) and the ability of the interpretation networks to capture epistasis (e.g., DFIM prAUC). Figure 2b further dissects the relation between predictive performance and the ability of the interpretation methods to detect epistasis. In this figure, the performance of the various methods (NID, DFIM and PathExplain), are reported separately if they were trained with or without the one hot encoding. Moreover, it can be observed (Fig. 2b) that for all networks with a prediction AUC of 0.6 or higher, DFIM and PathExplain achieved a prAUC of 0.98 and 0.95, respectively, with better results on the network without the one hot encoding. Interpreting the visible neural networks with NID resulted in a respectable prAUC of 0.89 for the same AUC threshold.

Fig. 2: GAMETES.
figure 2

In (a) the prAUC with the confidence interval of of the various epistasis interpretation methods. In (b) the average of the prAUC for methods for different thresholds of prediction AUC in the test set. There is a clear trend showing better prAUC given better prediction AUC. In (c) the correlation plot shows the correlation between the prAUC of various methods and the prediction AUC of the NN and LGBM (AUC NN; AUC NN OneHot; AUC LGBM).

Full size image

There were negligible differences between standard GenNet networks and networks with a one-hot encoding in terms of classification performance. The networks with one-hot encoding did perform slightly better (average AUC of 0.64 vs 0.63) but the performance of the interpretation methods was worse, most noticeable for DFIM, where the average prAUC was 5 percent points lower for networks with the one hot encoding compared to networks that did not have the encoding.

In addition, we performed simulations to investigate if these interpretation methods can find interaction between genes (gene-interaction). In these simulations the epistasis pairs are located in different genes. Classification performance was poor and dropped significantly compared to simulations where the interacting variants were in the same gene (see Supplementary Fig. 3).

Baseline methods performed very well on GAMETES. LGBM slightly outperformed the neural networks in classification performance and for epistasis detection MBMDR outperformed the neural network interpretation methods in most simulations. Epiblaster achieved an average prAUC of 0.80 over all the simulations. Figure 2c displays the correlation between the results of these methods. We find a strong correlation (Pearson) between the predictive AUC of GenNet (blue), with the prAUC of the DFIM; NID and PathExplain. The same is true between the AUC of prediction AUC and the epistasis prAUC of LBGM.

EpiGEN

The EpiGEN simulations were designed to investigate the behavior of the models for more realistic simulations with marginal effects and different interaction models. The interaction model strongly affects the classification performance of the GenNet models (see Supplementary Fig. 4). Networks performed best in simulations using a multiplicative model, followed by exponential and joint-dominant models. Joint-recessive interaction models were the hardest types of interactions to capture in these sparse neural networks. In comparison to the GAMETES simulations, the performance difference between simulations with interacting pairs in the same gene versus interacting variants in different genes, was less pronounced, possibly due to the presence of marginal effects (Supplementary Figs. 4, 5). The number of inputs and training-set size were clearly affecting predictive performance (Supplementary Fig. 6).

To investigate the performance of the epistasis methods, we considered the subset of trained networks that achieved an AUC of 0.5 or higher for both types of networks. Figure 3 shows the average performance for each interpretation method. Predictive performance and interpretation performance were generally better for neural networks with a one-hot encoding than their corresponding networks without one-hot encoding (see also Supplementary Figs. 5 and 7). Moreover, we investigated further if this is driven by the marginal effect, and we observed that the advantage of the one-hot encoded networks is stronger in EpiGen run with marginal effect than in networks without the one-hot encoding (Supplementary Section 10). We found a similar positive trend as in the GAMETES simulation between prAUC and the AUC of the prediction 3c for all the neural network interpretation methods. However, thanks to the marginal effect, the neural networks can achieve a higher AUC with a poorer prAUC. Inspecting fig. 3c shows that, for the same prediction AUC threshold, the prAUC is generally lower than in the GAMETES simulation (Fig. 2c).

Fig. 3: EPIGEN.
figure 3

In (a) the mean prAUC of the various methods are compared, with the confidence interval displayed. In (b) the mean prAUC of each method is displayed per type of interaction. In (c) each dot is the average of the prAUC for methods that have a prediction AUC equal or greater than the number on the x-axis.

Full size image

Inspecting the one-hot encoding (shown in detail in Supplementary Fig. 8) reveals that the networks encoded the interaction models differently. Supplementary Fig. 9 shows the deviations from linearity Rw per interaction model. The distribution deviates the most for the joint-dominant weights; causal joint-dominant pairs’ weights plateau for dosage input values 1 and 2, making them clearly separable from random or marginal weights (Supplementary Fig. 10). Multiplicative and exponential weights were stronger for all inputs, but this was indistinguishable from the weight distribution for the one-hot encoding for variants with marginal effects. The weights distribution for the joint-recessive variants was most similar to those of random variants without any effects.

The best performing algorithm was LGBM; LGBM detects epistatic pairs with high prAUC in simulations with exponential, joint-dominant, and multiplicative interactions models (Fig. 3b). All models struggle to detect epistatic pairs in simulations with an underlying joint-recessive model. For joint-recessive models LGBM is only second to MBMDR (MBMDR average prAUC for joint-recessive: 0.39). However, MBMDR and Epiblaster are unable to detect multiplicative pairs.

Application to the IBD dataset

To showcase the potential of our approaches in real-life data, we applied the methods to the IBD dataset with 66 280 observations and 38 825 SNPs after preprocessing. We divided the data into train (65%), validation (20%) and test (15%). As in Ellinghaus et al.33, we used the first 7 principal components to model population stratification.

Neural networks were created using GenNet command line functionality and both positional and functional annotations. As a result, a SNP can be linked to multiple genes. The covariates are inputs to the last hidden layer, before the final prediction. We built neural networks with and without one-hot encoding and achieved good predictive performance, with an AUC of 0.745 (0.715, for the one hot) in the validation set and 0.793 (0.761) in the test set. After training, we apply the epistasis detection methods on the trained models to extract the learned nonlinearities. We do this in a two-stage approach to improve the statistical power to detect epistasis. First, we reduce the search space by selecting only the most promising variant pairs. We evaluate the top 100 pairs of variants identified by that method. In the second stage, we test the significance of the interaction using logistic regression with an interaction term, using the validation and test set.

Interaction detection in visible neural networks

RLIPP provides insight into which parts of the network the largest non-linearities can be found. We found that the node representing the gene CCL11 had the highest relative improvement (see Supplementary Fig. 11). LYPLAL1-DT and SNX2P1 had the highest RLIPP values for the neural network trained with the one-hot embedding (see Supplementary Fig. 12).

NID, DFIM, and PathExplain

The top epistasic pair (hit) of NID, for both the network built with and without the one hot encoding, was rs2066844-rs2066845, both missense variants in the NOD2 gene and leading causal variants of Crohn’s disease and IBD in both DisGeNet and SNPedia databases (https://www.snpedia.com and https://www.disgenet.org). PathExplain, on the neural network with the one hot layer, had the SNP rs2066844 (NOD2) as part of the top epistasic pair together with rs5743293 (NOD2), a frameshift variant, related to both Crohn’s disease (vda score = 0.83) and IBD (vda score 0.02). rs5743293 is particularly important for PathExplain one hot, as it is a hub involved in all the top-100 interactions. DFIM (on the network with one hot), showed the same behaviour, having a SNP, rs12946510, involved in 99 out of the top 100 interactions. rs12946510 (IKZF3, GRB7) is an intergenic variant associated to Crohn’s disease, IBD and Ulcerative colitis, as per the GWAS catalog. DFIM’s, on the one-hot neural network, top epistasic pairs involve rs12946510 (IKZF3, GRB7) with rs2066844 and rs2066845, both previously described. A list of the top SNP-SNP interactions for NID can be found in Supplementary Table 3 for the network with the one hot encoding layer and in Supplementary Table 4 for the network without the one-hot layer.

The top interaction in DFIM, in the network without the one-hot encoding, was between rs80174646 (intron variant, IL23R) and rs11805303 (intron variant, C1orf141/IL23R); both previously reported in association with Crohn’s disease and IBD. (GWAS catalog). The second strongest interaction was between rs9988642 (IL23R) and rs11403745 (intergenic, LINC014675). The former is a downstream gene variant, mapped to the IL23R gene, a protein-coding gene associated with Inflammatory Bowel Disease. rs11403745 is an intergenic variants whose closest gene is LINC01475, a non-coding gene. Nearby is also SEC31B, which has been associated to IBD. rs11403745 (intergenic, LINC014675) is also the SNP most present, 24 times, in the DFIM’s top 100 interactions. The same variant (rs11403745) is also part of the second top association in NID (on the network trained with the one-hot layer), together with rs5743293 (NOD2), the hub SNP in PathExplain. Interestingly, a recent study highlighted rs11403745 in relation to IBD43. rs9988642 (IL23R) and rs80174646 (intron variant, IL23R), part of the top and second interaction in DFIM (without one hot encoding layer), are also the second-highest interaction of NID without one hot encoding.

PathExplain on the network with the one-hot encoding detected the strongest interaction between rs9296009 (intergenic, closest are PRRT1, FKBPL) and rs2413583 (intergenic, RPL3, PDGFB). While the former has not been reported in the literature, rs2413583 has been associated with Crohn’s disease, IBD, and ulcerative colitis, according to the GWAS catalog. Moreover, rs5743293 (NOD2) is the SNP most present, 26 times, in the top 100 interaction; it was part of all top 100 interactions of PathExplain with one hot layer and in the second position using NID on the network with the one-hot layer.

LGBM

There was no straightforward way to incorporate confounders into LGBM. Hence, we first regressed the phenotype with the 7 PCs with a linear model, subsequently using LGBM with the residuals as the outcome. LGBM provides both the feature importance and the interaction importance rankings for SNPs. Supplementary Tables 5 and 6 show the top-10 hits and the complete ranking can be found in Supplementary Table 5. Moreover, the most important feature according to feature importance, rs2066844 (NOD2), is known to be the leading causal variant of Crohn’s disease. The top 3 features per LGBM’s feature importance, rs2066844, rs5743293, and rs2066845, are all linked to gene NOD2 and all associated with both IBD and Crohn’s disease. Remarkably, out of the top-10 hits, 9 of them were already known in the literature to be associated with both Crohn’s and IBD. The only hit not present in DisGeNet, rs11403745 (intergenic, LINC014675) has been recently associated to IBD and has been extensively discussed in the previous subsection.

For the LGBM’s interactions score, the top two SNP-SNP pairs involved rs5743293 (NOD2), first with rs80174646 (IL23R); and then with rs2066844 (NOD2). All three SNPs are known in the literature and have been found and described by the various neural network interpretation methods above. Overall, out of the top-10 SNP-SNP interactions, all but one SNPs are present in DisGeNet, for either IBD or Crohn’s disease. The majority of them are mapped to either IL23R or NOD2. The single SNP that is not present in DisGeNet is rs11403745 (intergenic, LINC014675).

Rank aggregation and shared variants

Overall, we investigated the accordance and the peculiarities of each method on the IBD data for a broader picture of the agreement and disagreement of each interpretation method. We only calculated the interactions for the hundred most predictive variants for the DFIM and Pathfinder, restricting the search space, to reduce the computational burden.

First, we ranked every variant from NID, DFIM, PathExplain, both with and without one hot encoding layer, and LGBM, resulting in eight different rankings. For each method, the variant’s score is calculated as the sum of the interaction score (i.e., NID score, DFIM score, LGBM score,.) of every pair containing the variant. A comparative study from Li et al.,44 guides us toward using the geometric mean of the rankings. In this analysis, variants not present in a particular method, i.e., outside of the top-100 for DFIM and PathExplain, were assigned the lowest rank plus one. The geometric mean of the ranking of the eight methods highlights rs2066844, rs2066845, and rs5743293 (all NOD2 variants), as the top hits. Such variants were consistently present as top variants in each different method, with rs2066844 and rs2066845 ranked top-10 in 6/8 methods, with the only exceptions being 1) DFIM built without one hot layer and 2) the NID with the one hot layer.

Of the top-10 ranked hits, nine are already linked to either Crohn’s disease (9) or IBD (7) in DisGeNet. The other hit is rs11403745, recently related to IBD43. Another relevant SNP, in the top-100 in 7 out of 8 methods is rs9271588, a variant in the HLA region, that has been extensively studied in autoimmune disease and particularly Sjögren’s disease45,46. The full ranked table is available in the Supplementary Materials.

Furthermore, we plotted for each method the top 100 variants, the most promising candidates for epistasic effects, in an UpSet plot (Fig. 4a). To immediately visualize the adherence of our hits with the literature, we also included the list of SNPs associated with Crohn’s and IBD present in DisGeNet that are part of our 38,825 pool of input SNPs, respectively 314 and 228.

Fig. 4: UpSet plot showing the intersections of our eight interpretation approaches (7 Epistasis methods: NID; DFIM; Pathfinder with/without the one hot module, and LGBM’s feature interaction measure; plus LGBM feature importance) with the known variants from DisGeNet for IBD and Crohn’s disease.
figure 4

Each standing bar shows the number of overlapping pairs between the highlighted method(s). In (a) For each approach, the top-100 SNPs with the highest importance score were evaluated. The horizontal bar represents the number of SNPs included in each analysis, whereas the vertical bars show the overlap between each analysis; In (b) the top-100 SNPs were mapped to gene positionally (as explained in the method section), and the intersection is showed. Finally, in (c) the shared genes between at least one approach and one DisGeNet list are highlighted.

Full size image

From this UpSet plot it can be seen that the top-100 hits combining all methods have a high overlap with the known hits in DisGeNet. LGBM’s feature importance (LGBM 1d) and epistasis detection (LGBM 2d) had the biggest overlap with  > 40 out of the top-100 hits present in the DisGeNet hits for both Crohn’s disease and IBD, respectively 62 and 55 for Crohn’s and 52 and 45 for IBD. NID methods have around 20 hits, with, for NID with the regular embedding and the one-hot embedding, respectively 23 and 24 in Crohn’s disease and 17 and 21 in IBD. DFIM and Pathfinder have similar results, with the lowest number of hits belonging to DFIM without the one-hot embedding on the IBD list, with only 12 hits.

Out of the considered methods, DFIM and PathExplain on the one-hot encoded network were the ones with the most unique hits, with DFIM having almost half of the variants in the top-100 not being in the top-100 of any other method or a known SNP from DisGeNet. On the other side of the spectrum, PathExplain and LGBM’s feature importance had the lowest number of unique hits.

Three variants were in the top-100 of all the mentioned methods, respectively rs2836878 (intergenic, RPL23AP12 and LINC02940), rs3024505 (upstream of IL10; close to Y_RNA), and rs10781499 (CARD9), with known association to IBD and Crohn’s disease. The first is an intergenic variant, while the last is synonymous. Interestingly, in the GWAS catalog there are multiple studies linking rs10781499 to IBD disease, Ulcerative colitis and Crohn’s disease. rs2836878 has also been associated with IBD, Ulcerative colitis, and Crohn’s disease, as per the GWAS catalog. Finally, a study on a Danish cohort suggests a link between rs3024505 and the risk of Crohn’s disease47.

By mapping the top-100 SNPs to gene positionally (+/- 10 kb), we saw the overlap between methods and literature’s known hits (Fig. 4b). We found that eight relevant genes for both Crohn’s and IBD (Y_RNA; RPL23AP12; NOD2; LINC02943; IL23R; IL10; CARD9; C1orf141) have at least one SNP mapped to them in each method (Fig. 4c).

Association analysis for candidates pairs

We verified the findings from our previous methods with the most popular framework in epistasis detection, namely a logistic regression (LR). We grouped the top-100 SNP pairs from each of the seven epistasis methods. Hence, we ran a logistic regression to predict the phenotype using each pair of SNPs. The formula is, for a pair of SNPs SNPi and SNPj, as follows:

$$logit(Y)= \, {\beta }_{0}+{\beta }_{1}SN{P}_{i}+{\beta }_{2}SN{P}_{j}+\gamma SN{P}_{i}SN{P}_{j}\\ +{\alpha }_{1}P{C}_{1}+...+{\alpha }_{7}P{C}_{7}+\epsilon $$

Where the PCs are the seven principal components to model population stratification. Hence, the γ coefficient reflects the epistasis interaction between a pair of SNPs. To avoid inflating the results, we ran logistic regression on the validation and test set combined, excluding the training examples that the network has seen. This is a common approach to reduce the multiple testing burden (e.g. refs. 48,49. More formally, Pecanka and Jonker50, showed that if the two stages are independent, then only correcting for the number of tests in the second stage is sufficient.

Repeating the regression estimation for all pairs identified with the epistasis detection methods, we identified 7 significant SNP pairs after Bonferroni correction (Supplementary Table 7); out of those, two would stay significant under the usual GWAS threshold of 5*10−8. These epistasis pairs show different linear and non linear weights proportions (Supplementary Fig. 15), showing a prediction improvement, and with a different weight proportion from the zeroed-out weights of non-significant SNPs (Supplementary Fig. 16); Supplementary Fig. 17 shows the contribution of the interactions to the prediction.

Discussion

We adapted and applied various post-hoc interpretation methods to reveal the interactions learned by (visible) neural networks. Generally, we found that NID, DFIM and PathExplain are all suited to detect learned interactions from neural networks. There was a strong correlation between the predictive performance (AUC) and the ability of these interpretation methods to detect epistasis in the simulations (prAUC). That is, a neural network needed to have identified and learned the correct interactions before an interpretation method can extract it. There was no clear “best” interpretation method and the best interpretation method depends on the setting. In the GAMETES simulations, PathExplain performed best, while neural interaction detection (NID) was the best performing interpretation method for neural networks in most of the EpiGEN simulations. In the application to the inflammatory bowel disease, we found high agreement between the interaction interpretation methods. Interestingly, most variants identified by the interpretation methods were known variants earlier implicated in inflammatory bowel disease. From the candidate pairs identified with the interpretation methods on the neural networks and LGBM, 7 are significantly associated with IBD in the validation and test set.

In GAMETES, we empirically found that networks that achieved a classification AUC higher than 0.60 reliably detected interactions with most post-hoc analyses. Furthermore, the simulations revealed that interactions between variants located in different genes are hard to capture. The EpiGEN simulations confirmed both these findings and revealed that the ability to capture and detect epistasis pairs depends strongly on the underlying interaction model. Pairs based on a exponential model were consistently captured while pairs based on joint-recessive models were hard to model and detect. Increasing the depth of the neural networks, for example by adding pathway layers10, may help with providing the networks with the necessary capacity to model interacting variants in different genes and with more complex interaction models.

There are large methodological differences between the methods employed in the simulations. The machine learning methods (neural networks and LGBM) optimize towards finding a good classification boundary, whereas MBMDR and Epiblaster are primarily designed to test for interaction effects. This could be an advantage for the simulations, as these methods align more closely with the process used to simulate the data and outcome. Both Epiblaster and MBMDR can, however, be used in prediction models as part of a broader pipeline. For instance, prediction can be achieved via 1) separating into training/test, 2) identifying (on the training set) the hits, both main effect and SNP-SNP pairs, 3) creating, for each observation, a weighted average of the hits’ effect; notable examples in the literature are51, where MBMDR is used to build multilocus risk score (MRS) and MBMDRc22, where the average trait for each SNP combination is averaged to build the prediction. It involves a generic strategy that could also be applied to other epistasis detection tools that do not readily provide predictions (such as Epiblaster). Hence, a notable difference is that in ML approaches prediction precedes the interpretation, while in epistasis tools it is the contrary.

In the IBD case-control setting, we achieved good predictive performance with both GenNet and LGBM. Interpretation revealed many variants that have been implicated to have a role in biological mechanisms underlying inflammatory bowel disease. This is likely a consequence of the initial filtering, narrowing the interaction interpretation down to pairs with at least one predictive SNPs in DFIM and PathExplain. NID did not require a filtering step as it is computationally cheap but the method inherently focuses on the variants with the highest weight. The most significant epistatic pairs are mapped to NOD2 variants (rs2066844, rs2066845,rs5743293) and IL23R variants (rs80174646). We confirm the recent finding of SNP rs11403745 (intergenic, LINC014675) for IBD, and propose variant rs9271588 (HLA region), as a candidate for further validation, being in the top-100 of 7/8 methods.

Recently, Verplaetse et al.52 applied biologically meaningful sparse neural networks on whole exome sequencing data to predict IBD. The authors achieved similar predictive performance but did not find convincing proofs for epistasis when comparing their performance to that of linear models. Here, we showed that by applying interpretation methods to the visible neural network we can detect epistasis. The reduced candidate set compensates with a lower multiple testing burden and thus more power, even-though half of the data is allocated for training the network and is thus unavailable for association analysis. Missing heritability is still a relevant problem for IBD and Zuk et al.19 showed that up to 80% of the missing heritability could be due to genetic interactions. We detected 7 significant epistasis pairs in the real-life data but the simulations demonstrated that detecting epistasis pairs in different genes was difficult for the employed neural network architecture. Increasing the capacity of the neural networks to model these pairs could be a promising road for improving this strategy for epistasis detection.

In principle, the neural network detects interactions only between SNP-SNP both linked (either positionally or functionally) to the same gene, and specularly gene-gene interactions from genes connected to the same pathways. To enhance the detection of SNP-SNP interactions across different genes, we incorporated ConsensusPathDB (CPDB) to map SNPs to pathways rather than solely to individual genes. This adjustment allowed the network to identify epistatic interactions between SNPs linked to different genes within the same pathway, expanding its scope beyond positional or functional gene connections. The approach maintained predictive performance comparable to baseline, and key SNPs and interactions were identified using multiple methods. Several genes emerged as consistently significant across analyses, highlighting the potential of pathway-based mapping in capturing complex genetic interactions; more details are included in Supplementary Section 10.

While the proposed methods focus on detecting pairwise SNP interactions, higher-order interactions can be inferred when multiple significant pairs share common SNPs. For instance, if SNPi − SNPj, SNPi − SNPk, and SNPj − SNPk are all significant, they likely form a triplet interaction. We analyzed the top-100 interactions across methods and found that NID and NID on the one-hot network identified the most triplets (81 and 71, respectively), while LGBM detected 18 and PathExplain only 2 (Supplementary Fig. 18). Notably, SNPs rs2066844 and rs2066845 emerged as central in these higher-order structures, highlighting the potential for extending pairwise approaches to capture more complex interactions. We note that the number of triplets obtained with this approach is only a lower boundary of the number of existing higher-order interactions, since they do not consider cases where there is no 2-way epistasis but only 3-way epistasis. Supplementary Section 13 expands on the higher-order epistasis analysis.

We introduced several additions to the GenNet framework all of which, including the interpretation methods, are available from command line in the GenNet framework (https://github.com/ArnovanHilten/GenNet). We introduce multiple filters for visible neural networks, akin to channels in convolutional neural networks, and provide the option for an one-hot encoding for dosage input as a strategy to deal with the implicit bias to an additive model. With this encoding, the network is not forced to adhere to an additive model from the first layer and it is free to search for the encoding most suited for each single SNP. The one-hot encoding did result in minor performance gain in the EpiGen simulations and inspecting this layer revealed different weight distributions patters for the interaction models.

Here, we have demonstrated that interpretation methods for neural networks can identify non-linear interactions between genetic variants (epistasis pairs) in both simulated and real-life data. Most popular interpretation methods for neural networks provide a single importance (attribution) score per input, but this is inevitably a linear simplification of the true importance. Deep learning applications can model non-linear interactions and thereby provide a performance gain over linear models. In order to justify the use of these non-linear models it is thus necessary to use interpretation methods that can identify the non-linearities that lead to this performance gain. This does not only apply to epistasis; all tasks where neural networks are employed to leverage non-linear interactions can benefit from these interpretation methods.

Conclusion

We demonstrated that interpretable neural networks can learn and detect epistasis using both simulated and real-life data. Moreover, we provided a comprehensive tool set and a novel strategy to interpret genetic interactions with visible neural networks.