The neuroreceptors and transporters underlying spontaneous brain activity

Nakuci, Johan; Bansal, Kanika

doi:10.1038/s42003-025-08492-z

Download PDF

Article
Open access
Published: 30 July 2025

The neuroreceptors and transporters underlying spontaneous brain activity

Communications Biology volume 8, Article number: 1130 (2025) Cite this article

2095 Accesses
1 Citations
3 Altmetric
Metrics details

Subjects

Abstract

Determining the neuromodulators driving brain activity is critical for understanding cognition and neuropathology. Neuromodulators act through neuroreceptors in a coordinated manner, yet their interconnected dynamics are often overlooked. We show that a neuroreceptor-based modeling framework using cortical density maps of 19 neuroreceptors and transporters from Positron Emission Tomography (PET) can model BOLD-derived brain activity. This framework reconstructs activity across four datasets (N = 314) identifying two neuroreceptor modules linked to higher-order associative or somatomotor and visual networks. Applying the framework to independent datasets, we recover the binding profiles of LSD and Modafinil, demonstrating consistency with known pharmacological and neurobiological associations. Additionally, it uncovered associations between neuroreceptors, transporters, and altered brain activity in neuropsychiatric disorders. These findings demonstrate the framework’s potential to elucidate neuromodulatory mechanisms and advance our understanding of brain function across diverse states and conditions.

Neural variability in three major psychiatric disorders

Article 13 July 2023

Mapping neurotransmitter systems to the structural and functional organization of the human neocortex

Article Open access 27 October 2022

What can neuroimaging of neuromodulation reveal about the basis of circuit therapies for psychiatry?

Article 28 August 2024

Introduction

At any given moment, across the brain, a diverse array of neuromodulators bind to and unbind from neurons, driving activity and shaping large-scale brain dynamics. The complexity of this process becomes evident when considering that the human brain utilizes over 100 neuromodulators across approximately 10¹¹ neurons, each forming an average of 1000 unique connections¹. This intricate interplay presents an opportunity, albeit with a significant challenge, to understand how the interactions of specific neuromodulators drive large-scale brain activity in healthy brains and how these interactions change under specific pathological conditions.

Neuromodulators operate through diverse neuroreceptor subtypes with varying signaling cascades², spatial distributions³, and temporal dynamics⁴ to maintain the excitation/inhibition balance, enabling the brain’s vast computational capabilities⁵. These dynamic interactions underlie how molecular-level receptor activity translates to systems-level effects. For instance, tonic and bursting activity of the locus coeruleus, which releases norepinephrine, can shift network activity across the cortical hierarchy, modulating multiple brain states⁴. Moreover, the balance between excitatory and inhibitory inputs dynamically changes over time, reflecting different brain states⁶. These fluctuations have been linked to aging⁷, psychosis⁸, and can impact cognitive processes and behaviors across diverse domains, including social interactions⁹, economic decisions¹⁰, and even perception¹¹.

However, most studies investigate the relationship between one or two neuromodulators and brain activity at a time. Partly this is due to limitations of current methods, as they typically measure only a few neuromodulators at a time or are restricted to a subset of brain regions^12,13. Crucially, an understanding of the dynamic relationship among multiple neuromodulators that drive large-scale brain activity is lacking.

Building upon the burgeoning field of molecular-fMRI¹⁴, we present a neuroreceptor-based framework to unravel the dynamic relationship among multiple neuroreceptors and transporters underlying spontaneous brain activity. Previous work has investigated these questions utilizing spatial correlation through neuroreceptor-informed network control^15,16 or whole brain modeling¹⁷. Collectively, these approaches have the potential to unravel the link between molecular-level neuroreceptor activity and systems-level effects^18,19.

The concentration of neuroreceptors is an important factor in mediating the effects of neuromodulators on brain activity, as these serve as the primary sites for excitatory synaptic inputs²⁰, dynamically changing in response to neural activity, stimuli, and conditions²¹, and can shape long-term memory²². The concentration of neuroreceptors across the brain can be non-invasively estimated using PET tracer imaging^23,24. Moreover, recent work has shown that neuroreceptors shape brain-wide communication estimated from the BOLD signal^15,25,26. This association suggests that combining neuroreceptor density maps estimated from PET imaging with the BOLD signal could be a non-invasive method to uncover the neuromodulators that drive brain activity across the human cortex and unravel the complex mechanisms that underlie cognition, behavior, and neuropathology.

Here we show that a neuroreceptor-based framework can reconstruct the BOLD signal through a weighted summation of PET-derived neuroreceptor and transporter density maps. Leveraging this framework, we reveal that two distinct modules of neuroreceptors and transporters linked to higher-order associative or visual and somatomotor networks underlie the BOLD signal. Moreover, the framework can recover neuroreceptors and transporters—5-HT1a, 5-HT1b, 5-HT2a, and D2—known to bind lysergic acid diethylamide (LSD), and D2, 5-HT1a, 5-HT2a, and NET mediating the effects of Modafinil, demonstrating consistency with known pharmacological and neurobiological associations. Further, we demonstrate the framework’s utility by identifying associations linking neuroreceptors, transporters, and altered brain activity in schizophrenia, bipolar disorder, and ADHD.

Results

Reconstructing the BOLD signal and functional connectivity from neuroreceptor and transporter maps

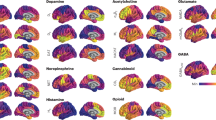
To determine if neuroreceptor and transporter density maps could non-invasively reveal the neuromodulators that drive spontaneous brain activity, we assessed whether a linear modeling framework could reconstruct the temporal dynamics of the BOLD signal. We utilize the most comprehensive neuroreceptors and transporters cortical density maps to date, as detailed in Hansen et al. 2022²⁷. In brief, PET tracer imaging from a combined 1238 healthy individuals was used to map the densities of 19 neuroreceptors and transporters from 9 neuromodulator systems: dopamine (D1, D2, DAT), norepinephrine (NET), serotonin (5-HT1A, 5-HT1B, 5-HT2A, 5-HT4, 5-HT6, 5-HTT), acetylcholine (α4β2, M1, VAChT), glutamate (mGluR5, NMDA), γ-aminobutyric acid (GABAa), histamine (H3), cannabinoid (CB1), and opioid neuroreceptor (MOR; Fig. S1). For each neuroreceptor and transporter, we estimated the average density within 200 brain regions based on the local-global parcellation of the human cerebral cortex estimated from resting-state fMRI by Schaefer et al., 2018, because voxel-wise estimates can be unstable and noisy²⁸.

Spontaneous brain activity was estimated from 15 min of resting-state fMRI (N = 48) part of the Human Connectome Project (HCP)²⁹. The extensive scanning duration of the HCP dataset allowed for an estimation of the relationship between neuroreceptors, transporters, and brain activity across a broader range of neural states. The voxelwise BOLD signal from each participant was averaged across the same brain regions defined by the Schaefer atlas, resulting in 200 × 1200 data points per participant and 200 × 57,600 data points across all participants. Independently, each of the 1200 time points of the BOLD signal were reconstructed from a weighted linear summation of the 19 neuroreceptor and transporter density maps (Fig. 1A). To quantify effectiveness of the neuroreceptor-based framework, Pearson correlation was used to estimate the accuracy between the reconstructed and the empirical brain maps for each of the 57,600 time points.

**Fig. 1: Neuroreceptor-based framework can reconstruct the BOLD signal and functional connectivity.**

Focusing on a representative participant, the BOLD signal at each moment in time was reconstructed with an average accuracy of R_{BOLD_subj24} = 0.53 ± 0.08 (mean ± std; Fig. 1B). Comparable accuracy was observed across all participants (R_BOLD = 0.51 ± 0.08; Fig. 1C). The observed reconstruction accuracy was significantly greater than that obtained from null models based on spatially permuted neuroreceptor and transporter maps (P_spatial < 0.001) and from a permutation that preserved the spatial auto-correlation, spin test (P_spin < 0.001; Fig. 1D)²⁵. Moreover, the accuracy in reconstruction was differentially distributed across the brain, with the visual network exhibiting, on average, higher accuracy (Fig. S2).

Further, given that spontaneous brain activity exhibits coordination, or functional connectivity (FC), among brain regions, we determined whether the reconstructed BOLD signal preserved this inherent property. Moreover, reconstructing the BOLD signal from neuroreceptor and transporter density does not inherently guarantee that the reconstruction will preserve FC at a comparable level. Thus, the ability to reconstruct the inherent FC would add to the reliability of the results. Conversely, if the reconstruction were dominated by random noise, the inherent FC would not be reproduced.

To assess whether the reconstructed BOLD signal preserved inherent functional connectivity, we concatenated the empirical and reconstructed BOLD signals across participants and used Pearson correlation to estimate the empirical and reconstructed functional connectivity networks, respectively. The reconstructed functional connectivity demonstrated comparable accuracy to that observed in the temporal BOLD signal (R_FC = 0.61; Fig. 1E) and was significantly greater than both null models (P_spatial < 0.001; P_spin < 0.001; Fig. 1F). Together, these findings highlight that a neuroreceptor-based framework can reconstruct spontaneous brain activity and its inherent functional connectivity.

Two distinct modules of neuroreceptors and transporters underlie dynamic brain activity

No neuroreceptor or transporter acts in isolation; their actions are inherently coordinated²⁶. However, most studies are limited to investigating only a few neuroreceptors and transporters at a time, and therefore, a comprehensive view is crucially lacking. To address this lack of knowledge, we investigated whether the neuroreceptor-based framework could unravel the coordinated interplay among neuroreceptors and transporters working together to drive brain activity.

As shown in Fig. 2A, these drive values (i.e. β-values) exhibit marked fluctuations over time within a participant. These observations may suggest that fluctuations in brain activity reflect coordination among multiple and distinct neuroreceptors and transporters (Fig. 2B). Understanding how neuromodulatory systems influence the emergent patterns of brain activity and cognitive processes requires quantifying the extent of temporal coordination among neuroreceptors and transporters.

**Fig. 2: Two neuroreceptor and transporter modules underlie spontaneous brain activity.**

To quantify the extent of coordination among neuroreceptors and transporters, the drive values were concatenated across participants and pairwise coordination was estimated using Pearson correlation. Positive correlations indicated coordinated changes, as observed between GABAa and M1 (R_GABAa:M1 = 0.68), while negative correlations suggested inverse relationships, such as between GABAa and H3 (R_GABAa:H3 = −0.29). Across all neuroreceptors and transporters, the correlations form a neuroreceptor drive network representing the overall coordination among all neuroreceptors and transporters.

The neuroreceptor drive network revealed distinct patterns of positive and negative correlations among drive values, consistent with those observed between GABAa, M1, and H3 (Fig. 2C, D). Moreover, clustering analysis identified two modules, NR1 and NR2, of neuroreceptors and transporters. Additionally, as shown in Fig. 2D, a subset of neuroreceptors within both the NR1 and NR2 modules exhibited strong coordination with other neuroreceptors in their respective modules (black outlined nodes), while another subset acted as connectors linking the NR1 and NR2 modules (red outlined nodes).

Neuroreceptors or transporters that showed strong coordination (i.e., positive correlations) within their module are referred to as provincial hubs, whereas those linking different modules are termed connector hubs (Fig. 2E). To quantify the role of a neuroreceptor or transporter as a provincial hub, we calculated the within-module degree, which measures the strength of coordination within the same module. The M1 neuroreceptor was identified as a candidate provincial hub in the NR1 module, while the D2 neuroreceptor was identified as a candidate provincial hub in the NR2 module (P_perm < 0.05; Fig. 2F). In contrast, the participation coefficient was used to quantify the role of neuroreceptors and transporters as connector hubs linking the NR1 and NR2 modules. The top candidate connector hubs identified were α4β2, 5-HT4, 5-HT6, CB1, and D1 (P_perm < 0.05; Fig. 2G).

Notably, the NR1 and NR2 modules were not defined by neuromodulatory families or by excitatory versus inhibitory properties. Instead, we observed distinct density distributions of these modules across the cortex (Fig. 3). The average density of neuroreceptors and transporters in both NR1 and NR2 was highest in the inferior prefrontal regions, insula, and temporal areas (Fig. 3A, B). Differences among the two modules indicated that the neuroreceptors and transporters associated with the NR2 module exhibited a higher density in the motor and visual network (P < 0.001), whereas the NR1 module exhibited a higher density in the limbic and default mode network (P < 0.001; Fig. 3C, D).

**Fig. 3: Cortical density differences between neuroreceptor modules.**

These spatial differences in density between modules were associated with different cognitive processes. For the NR2 module, the cognitive processes with large positive association were “movement”, “planning” and “coordination” (P < 0.05, FDR corrected; Fig. 3E). On the other hand, large negative associations were observed with “recognition”, “familiarity” and “emotion” (P < 0.05, FDR corrected; Fig. 3F).

Lastly, the neuroreceptor drive network retained the same organization (R = 0.93) even after accounting for spatial similarity (Fig. S3). Additionally, the neuroreceptor drive network was consistent (R = 0.96) after regularizing the β-values using ridge regression to control for collinearity (Fig. S4). Together, these findings indicate that coordinated interactions among diverse neuromodulators, neuroreceptors, and transporters shape the emergent patterns in brain activity.

Demonstrating consistency with known pharmacological and neurobiological associations

Merely demonstrating that the BOLD signal can be reconstructed from neuroreceptor and transporter density maps is insufficient to establish that the underlying relationship genuinely reflects neurobiological associations. This limitation highlights the necessity of providing confidence that the analysis reflects these associations. In humans, linking alterations in brain activity induced by neuropharmacological agents to known pharmacodynamics could provide such confidence. The critical aspect involves determining whether the analysis can successfully identify the neuroreceptors and transporters known to mediate the effects of a given neuropharmacological agent.

Toward this end, we utilized two datasets in which participants received LSD and Modafinil. In the first dataset, participants (N = 15) underwent 7 min of resting-state fMRI after receiving a Placebo and LSD³⁰. In the second dataset, participants (N = 13) underwent 5 min of resting-state fMRI scanning before and after receiving Modafinil³¹. Moreover, understanding the mechanism of action of these drugs is important because they have been shown to exhibit beneficial effects for the treatment of neurological and neuropsychiatric disorders^32,33.

Focusing on the LSD dataset, the BOLD signal and the functional connectivity were reconstructed in the same manner as was done in the HCP dataset. For the Placebo, the BOLD signal was reconstructed significantly greater than both null models (R_BOLD = 0.68 ± 0.02; P_spatial < 0.001; P_spin < 0.001) as well as the functional connectivity (R_FC = 0.64; P_spatial < 0.001; P_spin < 0.00; Fig. S5A–C). Similar results were obtained after the administration of LSD for the BOLD signal (R_BOLD = 0.66 ± 0.02) and functional connectivity (R_FC = 0.63; P_spatial < 0.001; P_spin < 0.001; Fig. S5D–F). However, the model reconstructed the temporal BOLD signal significantly better after administration of the Placebo compared to LSD (t = 2.82, P = 0.01), but the differences were minor (Fig. S5G). Moreover, the neuroreceptor-based framework reconstructed the empirical changes in functional connectivity between the LSD and the Placebo conditions estimated using edgewise paired sample t-test, significantly greater than both null models (R_LSD-Placebo = 0.38; P_spatial < 0.001; P_spin < 0.001; Fig. S5H, I).

The critical element in the analysis is to determine the neuroreceptor(s) and transporter(s) altering the neuroreceptor drive network and correspondingly the brain activity from the state before (D_pre) to the state after (D_post) administration of a neuropharmacological agent (Fig. 4A). The neuroreceptors and transporters inducing these changes are reflected in the modulation network. The modulation network can be estimated from the neuroreceptor drive networks D_pre and D_post, which correspond to the state before and after administration of LSD (Fig. 4B, C).

**Fig. 4: Neuroreceptor-based framework identifies the neuroreceptors and transporters mediating the effects of LSD and Modafinil.**

The neuroreceptor drive network exhibited only a small number of significant pairwise changes in response to LSD (P_FDR < 0.05; Fig. 4D). These alterations were part of broader shifts within and between modules indicating significant decreases in coordination among the neuroreceptors part of the NR1 module (t_ave = −0.60 ± 1.45; P = 0.01) and a shift toward enhanced coordination between modules (t_ave = 0.48 ± 1.71; P = 0.01; Fig. 4E).

As can be observed in Fig. 4F, the modulatory network indicated that LSD exerted a complex set of changes affecting most relationships across the neuroreceptor drive network. To determine the neuroreceptors primarily responsible for the modulations, principal component analysis (PCA) was used to identify the dominant constituents underlying the modulation network. The first principal component of the modulatory network accounted for 35.89% (P_perm < 0.001) of the variance, and all other components were not significant (P_perm > 0.05; Fig. S6A). The neuroreceptor primarily responsible for driving LSD induced changes in brain activity was 5-HT1b (P_perm = 7.2 × 10⁻⁴), followed by D2 (P_perm = 0.01), 5-HT1a (P_perm = 0.03), and 5-HT2a (P_perm = 0.07; Fig. 4G). These neuroreceptors are known to bind LSD, with 5-HT1b in particular having the highest affinity for LSD³⁴.

Extending the analysis to Modafinil, the model reconstructed the BOLD signal and functional connectivity pre (R_BOLD = 0.59 ± 0.03; R_FC = 0.62; P_spatial < 0.001; P_spin < 0.001) and post Modafinil (R_BOLD = 0.60 ± 0.03; R_FC = 0.66; P_spatial < 0.001; P_spin < 0.001; Fig. S7A–F). Additionally, we tested if there were statistically significant differences in the reconstruction of the BOLD signal before and after Modafinil. The analysis reconstructed equally well the brain activity pre and post Modafinil (t = −1.34, P = 0.20), and the reconstructed functional connectivity reflected the observed differences (R_Post–Pre = 0.37; P_spatial < 0.001; P_spin < 0.001; Fig. S7G–I). Further, significant pairwise differences in the neuroreceptor drive network were found (P < 0.05; Figs. 4H; S7J, K), but no significant differences were observed within and between the NR1 and NR2 modules (P > 0.05; Fig. 4I). Both the significant and non-significant pairwise differences deviate in direction within and between modules. However, these fluctuations result in an average within and between module differences not significantly deviating from zero.

The modulation network indicated that Modafinil-mediated effects were driven by a subset of neuroreceptors and transporters (Fig. S7L). The first PCA component, which accounted for 99.02% (P_perm < 0.001; Fig. S6B) of the variance in the modulation network, indicated that Modafinil-mediated effects were primarily driven by D2 (P_perm = 0.02), followed by 5-HT1a (P_perm = 0.03), 5-HT2b (P_perm = 0.05), and NET (P_perm = 0.07; Fig. 4J). The exact mechanism of action of Modafinil is not known, but these results align with prior work showing that Modafinil alters dopamine and serotonin levels in the brain^35,36,37,38. Taken together, these results provide confidence that the analysis reflects neurobiological associations.

Neuroreceptors associated with altered BOLD signal in neuropsychiatric illness

We then investigated whether this framework could be extended to uncover associations between neuroreceptors, transporters, and altered brain activity in neuropsychiatric disorders. Linking neuropsychiatric illnesses to specific neuroreceptors, transporters, or neuromodulators is critical since it could improve diagnosis and treatment. For this analysis, we used the UCLA Consortium for Neuropsychiatric Phenomics (UCLA5c) dataset, which includes individuals diagnosed with schizophrenia (N = 45), bipolar disorder (N = 36), and attention deficit/hyperactivity disorder (ADHD; N = 39), along with a healthy control group (N = 118)³⁹.

We reconstructed the temporal BOLD signal for each participant using the 19 neuroreceptor and transporter density maps. The reconstruction accuracy of the healthy control group (R_BOLD = 0.55 ± 0.01; mean ± SEM) was not significantly different from the schizophrenia (R_BOLD = 0.55 ± 0.01; P_{Diff_SCZ_to_HC} = 0.80), bipolar disorder (R_BOLD = 0.55 ± 0.02; P_{Diff_BD_to_HC} = 0.08), and ADHD groups (R_BOLD = 0.55 ± 0.01; P_{Diff_ADHD_to_HC} = 0.43; Fig. S8). Additionally, the neuroreceptor-based framework reconstructed differences in functional connectivity between neuropsychiatric groups and healthy controls significantly greater than null models for schizophrenia (R_{SCZ-HC_FC} = 0.56; P_spatial < 0.001; P_spin < 0.001), bipolar disorder (R_{BD-HC_FC} = 0.45; P_spatial < 0.001; P_spin < 0.001), and ADHD (R_{ADHD-HC_FC} = 0.35; P_spatial < 0.001; P_spin < 0.001; Fig. S9).

In the schizophrenia group, the neuroreceptor drive network exhibited a limited number of significant pairwise changes compared to healthy controls (P < 0.05), and these changes were part of a broader set of alterations within and between neuroreceptor drive network modules (P < 0.05; Fig. S10A). To determine the neuroreceptors and transporters driving these changes, we estimated the modulation network required to transition from the healthy to the schizophrenic brain state in the same manner as the analysis on LSD and Modafinil. The modulation network exhibited a complex pattern, with the first principal component accounting for 67.65% of the variance (P_perm < 0.001); all other components were not significant (P_perm > 0.05; Fig. S10B). The modulation analysis identified norepinephrine transporter (NET) as the primary driver (P_perm = 0.02; Fig. 5A). Other neuroreceptors mediating the effects included serotonin receptors 5-HT1a (P_perm = 0.03) and 5-HT4 (P_perm = 0.09), and additional associations with NMDA (P _perm = 0.02), α4β2 (P_perm = 0.07), and GABAa (P_perm = 0.09) were observed.

**Fig. 5: Neuroreceptors and transporters mediating the alterations in brain activity across neuropsychiatric disorders.**

For bipolar disorder and ADHD, the analysis similarly identified a small set of pairwise changes within and between neuroreceptor network modules (P < 0.05; Fig. S10C–F). In bipolar disorder, NET was the primary driver similar to schizophrenia (P_perm = 0.04; Fig. 5B). Overall, neuroreceptors mediating the effect of bipolar disorder included 5-HT1a (P_perm = 0.01), 5-HT4 (P_perm = 0.06), α4β2 (P_perm = 0.07), NMDA (P_perm = 0.08), and H3 histamine (P_perm = 0.09). In ADHD, changes were mediated by the dopamine, D1 (P_perm = 0.01), and acetylcholine, α4β2 (P_perm = 0.01; Fig. 5C). The analysis also implicated GABAa (P_perm = 0.04) and the 5-HT4 serotonin neuroreceptor (P_perm = 0.07). Taken together, these findings underscore the complexity of neuropsychiatric illness.

Consistent neuroreceptor drive networks across datasets

Further, we assessed the similarity of neuroreceptor drive networks across datasets. Strong similarity between these independent datasets would support the robustness of the results and framework. To quantify the extent of similarity, we compared the neuroreceptor drive networks derived from the LSD, Modafinil, and UCLA5c datasets to the network estimated from the HCP dataset. Neuroreceptor drive networks from each of the other datasets showed strong similarity with the HCP-derived network (R_ave = 0.92; Fig. S11). These results underscores the stable dynamical interplay between brain activity and the underlying neuromodulator, neuroreceptors, and transporters.

Reconstructing spontaneous brain activity: neuroreceptors vs. structural and geometric modes

Lastly, previous work has shown that spontaneous brain activity is shaped and constrained by anatomical factors— structural connectivity (SC)^40,41 and cortical folding geometry (GC)⁴². Models based on SC and GC suggest that spontaneous brain activity emerges from a weighted linear summation of modes (also called harmonics) of the SC or GC. However, it is an open question as to which model—neuroreceptor, structural, or geometric—can more parsimoniously reconstruct spontaneous brain activity.

To compare models, we utilized the BOLD signal from the HCP dataset due to its extensive scanning duration. PCA was applied to the concatenated BOLD signal to identify the dominant spatial patterns of activity. The analysis utilized components C1 through C10, which account for 40.85% of the variance in the BOLD signal. Specifically, we determined the number of SC- and GC-modes needed to match the accuracy obtained with the neuroreceptor maps. SC or GC-based reconstructions were deemed to be more parsimonious if fewer modes were required to achieve the same accuracy as the neuroreceptor maps. The model comparison revealed that reconstructing the BOLD signal using the neuroreceptor maps was more parsimonious for 8 out of the 10 BOLD components (see Supplemental for extended results and discussion; Figs. S12, S13). These results suggest that the neuroreceptor-based framework may provide a more direct and biologically meaningful basis for modeling brain activity compared to anatomical-based approaches.

Discussion

Neurotransmitters are the primary substrate by which neurons communicate⁴³. Like most aspects of the human brain, no individual neurotransmitter works alone to generate brain activity; instead, brain activity is generated from coordination among multiple neuromodulators acting through their corresponding neuroreceptors and transporters²⁷. Here, we present a neuroreceptor-based framework to identify the neuroreceptors and transporters working in congruence to drive spontaneous brain activity. Across four datasets, the neuroreceptor-based framework identified consistent associations between neuroreceptors and transporter density maps and fluctuations in the BOLD signal.

Spontaneous brain activity reflected a coordinated interplay among a diverse set of excitatory and inhibitory neuroreceptors and transporters, highlighting the complex neuromodulatory landscape of the cortex. This finding raises the hypothesis that the balance between excitation and inhibition is managed by two distinct modules—NR1 and NR2—reflecting visual and somatomotor networks or higher-order associative functions, respectively. The differences in density distribution between modules across cortical regions suggests that brain activity and function is locally shaped by specific neuromodulatory profiles. For instance, the higher density of NR1 module in the orbitofrontal, parietal, and temporal areas may facilitate the integration of sensory and associative information⁴⁴, whereas the NR2 module’s prominence in frontal, motor, and visual regions may align with the demand for rapid modulation of motor responses and visual processing^45,46. This spatial organization suggests that the brain dynamically allocates neuromodulatory resources in a region-specific manner, which may enhance its capacity to adapt to diverse cognitive and behavioral demands. Moreover, the modules may serve as a safeguard against excessive synchronization across cortical regions^47,48.

Why has the brain gone to such a great extent to maintain a rich tapestry of neuromodulators, neuroreceptors, and transporters to facilitate communication? One possible reason could be that utilizing multiple neuromodulators, neuroreceptors, and transporters could fine-tune the excitation–inhibition balance, enabling neurons to maintain responsiveness across a broad spectrum of inputs and to adapt to varying inputs without changing their fundamental properties^49,50. Furthermore, the interplay between different neuromodulators, neuroreceptors, and transporters may serve an important role in network-level flexibility. We speculate that the ability to respond to diverse neuromodulators enables a brain region to be part of multiple subnetworks depending on the context. This versatility may facilitate efficient communication across the brain and support diverse cognitive functions without necessitating dedicated, fixed circuitry for every task⁵¹. Such a flexible integration among multiple subnetworks could allow the brain to maximize computational power while minimizing metabolic costs⁵².

The analysis also provided insight into the mechanism of action of an administered neuropharmacological agent. Determining the mechanism of action has been challenging because neuropharmacological agents have direct and indirect effects on the activation propensity of neuroreceptors and neurons⁵³. The analysis identified the neuroreceptors that bind LSD and neuroreceptors thought to mediate the effects of Modafinil, providing support for known pharmacological and neurobiological associations. The analysis identified 5-HT1b as having high binding affinity for LSD in line with previous work³⁴ and suggesting the need for additional investigation of non-5HT2a-mediated mechanisms⁵⁴. However, there is a complex relationship between binding affinity and psychopharmacology. For instance, 5-HT2a is thought to be the primary functional mediator of psychedelic effects of LSD, suggesting that binding affinity may not directly translate to functional significance^55,56.

We extended our framework to investigate neuropsychiatric disorders—schizophrenia, bipolar disorder, and ADHD—to identify the neuroreceptors and transporters associated with alterations in brain activity for each condition. Specifically, in line with prior work, in schizophrenia the analysis identified significant associations with NET⁵⁷, 5-HT1a⁵⁸, NMDA^59,60,61 and trending associations with α4β2^62,63, 5-HT4, and GABAa⁶⁴. Interestingly, our results did not identify a significant association with dopamine neuroreceptors and transporters, aligning more closely with alternative hypotheses than the current dominant dopamine hypothesis in schizophrenia⁶⁵. The neuroreceptors associated with bipolar disorder were similar to the ones associated with schizophrenia, indicative of their close psychopathology⁶⁶. In the ADHD group, consistent with previous work, alterations in brain activity were associated with the D1^67,68,69, α4β2^70,71,72,73, GABAa^74,75, and 5-HT4⁷⁶ neuroreceptors. However, unlike prior work, we did not find an association with the norepinephrine system⁷⁷ (note see Supplemental for extended discussion).

Together, the results suggest that these disorders may involve dysregulation across multiple neuromodulators and/or neuroreceptor and transporter systems rather than a single system. This dysfunction affecting multiple neuroreceptor systems could arise from an initial impairment in one system, with compensatory adjustments in others to maintain homeostasis⁷⁸ or it could be indicative of a common underlying factor disrupting multiple systems⁷⁹. Alternatively, the observed dysfunction may reflect underlying abnormalities in the neurons responsible for releasing neurotransmitters such as norepinephrine or dopamine, with downstream effects manifesting in the associated neuroreceptors and transporters. The pattern of dysfunction spanning multiple systems highlights the complexity of neuropsychiatric conditions, underscoring the need for integrative approaches that consider the interplay among diverse neuromodulators. Toward this end, multimodal imaging can deepen our understanding of the coordinated roles of neuroreceptors and transporters in maintaining healthy brain function⁸⁰ and how their dysregulation can lead to pathological states^81,82.

Moreover, the framework could be utilized to provide insight into the mechanism of action of other neuropharmacological agents and narrow the search for therapeutic treatments for substance abuse^83,84 and neuropsychiatric illness^85,86. For instance, the findings in the psychiatric group could be used to identify compounds and/or optimal combinations of existing medications to improve efficacy. Overall, caution is warranted when interpreting these results, given the small sample size and that there is no ground truth in the molecular factors underlying these disorders.

The current work has several limitations. First, a causal relationship cannot be drawn from the analysis because the analysis is correlational. Investigating the spatial pattern of a neuroreceptor is insufficient to draw conclusions on the mechanism of action of neuropharmacological agents or neuropsychiatric illness. Specifically, the mechanism of action can be affected by multiple factors such as affinity, expression levels on different neuronal layers, or downstream effects. Moreover, the assumption that a certain neurotransmitter affects the BOLD signal in the exact same region may not hold, considering the complex projection of neurotransmitter systems. Future studies can utilize simultaneous PET/fMRI imaging to establish causal relationships. Second, despite the neuroreceptor frameworks’ ability to reconstruct the BOLD signal greater than both null models, this still leaves a large portion of spatial variance unexplained. This could in part be due to the small number of neuroreceptors used in the analysis. On the one hand, the 19 neuroreceptor and transporter density maps used in the analysis are the most comprehensive maps to date; on the other hand, these represent only a fraction of the total number in the brain. Therefore, future studies can test if the inclusion of additional neuroreceptors increases the variance explained in the BOLD signal. Third, the neuroreceptor and transporter maps have different spatial resolutions, smoothing levels, extent of autocorrelation, and scanner of origin, which could bias their correlation with the BOLD signal. Further, the spatial and spin null models used in the analysis may account for some aspect of these differences. Specifically, the spin null model may account for the autocorrelation in the neuroreceptor maps; nonetheless, it is an open question to what extent these null models account for these underlying factors. Future studies could account for this by using neuroreceptor maps from a single source or harmonizing the pre-processing of PET images to mitigate such concerns. Lastly, the analysis focused on cortical regions, which limits the biological interpretation, especially given that many key neuroreceptors have high density in subcortical structures. These subcortical regions may be critical in mediating alterations in brain activity due to psychiatric illness, medication, or psychedelics⁸⁷. This could explain the lack of association between neurotransmitter systems like dopamine in schizophrenia. Therefore, future studies can incorporate neuroreceptor maps from subcortical regions to provide a holistic relationship between molecular factors, brain activity, and neuropsychiatric illness.

In summary, identifying the neuromodulators that drive brain activity is crucial due to their central role in communication, cognition, and pathology. Here, we demonstrated that using cortical density maps of neuroreceptors and transporters from PET imaging can reveal the neuroreceptors and transporters underlying spontaneous brain activity. In the process, the framework revealed a complex network of neuroreceptors and transporters associated with brain activity. Further, this neuroreceptor-based framework can improve our ability to identify neuromodulators driving brain activity and opens new avenues for exploring dynamical brain activity, identifying neuropharmacological mechanisms of action, and markers of neuropsychiatric disorders. Future studies can build on these findings to unravel the complex mechanisms that underlie cognition and generate targeted diagnostics and therapies.

Methods

Neuroreceptor density maps

The analysis used data originally published in Hansen et al. 2022²⁷. In brief, PET tracer imaging was used to map the density of 19 neuroreceptors and transporters. The neuroreceptors include 9 neurotransmitter systems: dopamine (D1, D2, DAT), norepinephrine (NET), serotonin (5-HT1A, 5-HT1B, 5-HT2A, 5-HT4, 5-HT6, 5-HTT), acetylcholine (α4β2, M1, VAChT), glutamate (mGluR5, NMDA), γ-aminobutyric acid (GABAa), histamine (H3), cannabinoid (CB1), and μ-opioid neuroreceptor (MOR). PET images were acquired only from healthy participants (n = 1238; 718 males and 520 females). The images are used to estimate the binding potential and tracer distribution volume, which are referred to as receptor densities. PET-based estimation methods provide a direct measure of the neuroreceptor and transporter concentration across the cortex than estimates based on transcriptomics⁷⁴. PET images were all registered to the MNI-ICBM 152 non-linear 2009 template and parcellated into the 200 regions according to the Schaefer atlas²⁸. Finally, each map corresponding to individual neuroreceptors and transporters was z-score normalized. Moreover, the neuroreceptor maps are treated as maps of the relative spatial distribution of neuroreceptor/transporter density. Note that the ranking across regions is the same, whether an absolute estimate (e.g. distribution volume) or a relative estimate (e.g., distribution volume ratio). What may change the ranking of regions is the presence of flow effects or non-specific binding (e.g., when using a semiquantitative SUVR instead of specific volume or binding potential).

Functional MRI data

HCP resting-state fMRI dataset

We used pre-processed resting-state functional MRI (fMRI) data from 48 healthy human participants from the Human Connectome Project (HCP)²⁹. We downloaded 50 participants, but two were missing data. In brief, participants underwent four sessions of 15-min resting-state scanning sessions. fMRI volumes were recorded using a customized 3 T Siemens Connectome Skyra scanner with an EPI sequence (TR = 0.72 s, TE = 33.1 ms, 72 slices, 2.0 mm isotropic, field of view (FOV) = 208 × 180 mm). In addition to the pre-processing steps part of the HCP pipeline, we additionally regressed out the global signal, white matter, and cerebrospinal fluid. The global signal was removed in order to reconstruct the aspect of the BOLD signal that more closely reflects neuronal activity, since the global signal is associated with motion and/or physiological noise⁸⁸. The application of global signal regression (GSR) to the fMRI data is an ongoing debate, and different associations might be observed with the receptor templates if GSR is not applied⁸⁹. The data was mapped onto the Schaefer atlas to derive brain activity for 200 regions of interest because voxel-wise estimates can be unstable and noisy. Group-level functional connectivity (FC) was estimated using the Pearson correlation on the pooled data.

Lysergic acid diethylamide (LSD) resting-state fMRI dataset

The analysis was based on data detailed in Carhart-Harris et al. 2016^30,90. In brief, the analysis utilized pre-processed fMRI data from 15 participants who underwent 7 min of resting-state fMRI after a placebo and LSD. fMRI data were acquired using a gradient echo planar imaging sequence, TR/TE = 2000/35 ms, field-of-view = 220 mm, 64 × 64 acquisition matrix, parallel acceleration factor = 2, 90° flip angle, and 35 oblique axial slices and 3.4 mm³ voxel size.

Pre-processing steps are detailed in Carhart-Harris et al. 2016. fMRI data pre-processing involved de-spiking, slice time correction, motion correction, and non-linear registration to 2 mm MNI brain. Additionally, fMRI volumes with frame displacement >0.4 mm were removed. The functional data were spatially smoothed with a 6 mm full-width half max kernel and band-pass filtering between 0.01 and 0.08 Hz. Finally, 9 nuisance regressors (6 motion-related and 3 anatomically related) and linear and quadratic trends were removed. As in the HCP dataset, we additionally regressed out the global signal. Subject-level functional connectivity was estimated using the Pearson correlation.

Modafinil resting-state fMRI dataset

The analysis was based on data detailed in Cera et al. 2014^31,91. In brief, the study recruited 26 young male right-handed (as assessed by the Edinburgh Handedness inventory) adults (age range: 25–35 y.o.). Participants received, in a double-blind fashion, either a single dose of Modafinil or a placebo pill identical to the drug. The present analysis focused only on 13 participants who received Modafinil.

Resting-state-fMRI BOLD data were separated into three runs lasting four minutes each, followed by high-resolution T1 anatomical images. BOLD functional imaging was performed with a Philips Achieva 3 T Scanner (Philips Medical Systems, Best, The Netherlands), using T2*-weighted echo planar imaging (EPI) free induction decay (FID) sequences and applying the following parameters: TE 35 ms, matrix size 64 × 64, FOV 256 mm, in-plane voxel size 4 × 4 mm, flip angle 75°, slice thickness 4 mm and no gaps. 140 functional volumes consisting of 30 transaxial slices were acquired per run with a volume TR of 1671 ms. High resolution structural images were acquired at the end of the three rs-fMRI runs through a 3D MPRAGE sequence employing the following parameters: sagittal, matrix 256 × 256, FOV 256 mm, slice thickness 1 mm, no gaps, in-plane voxel size 1 mm × 1 mm, flip angle 12°, TR = 9.7 ms and TE = 4 ms.

MRI data were preprocessed with the CONN Toolbox⁹². Preprocessing involved the following steps: de-spiking, slice-timing correction, realignment, segmentation, coregistration, normalization, and spatial smoothing with 8 mm full width half maximum (FWHM). The preprocessing of the T1-weighted structural images involved skull-removal, normalization into MNI anatomical standard space, and segmentation into gray matter, white matter, cerebral spinal fluid, soft tissues, air, and background. In functional images, all volumes with frame displacement >0.3 mm were censored and followed by regression of the global signal.

UCLA Consortium for Neuropsychiatric Phenomics dataset

The Consortium for Neuropsychiatric Phenomics includes imaging of healthy individuals (N = 118 out of 122), individuals diagnosed with schizophrenia (N = 45 out of 50), bipolar disorder (N = 35 out of 37), and attention deficit hyperactivity disorder (N = 39 out of 40)³⁹. Resting-state functional MRI scans were obtained while participants kept their eyes open for 5 min in the scanner. Neuroimaging data were acquired on a 3 T Siemens Trio scanner. T1-weighted high-resolution anatomical scans (MPRAGE) were collected with a slice thickness = 1 mm, 176 slices, TR = 1.9 s, TE = 2.26 ms, matrix = 256 × 256, FOV = 250 mm. Resting-state MRI data were collected with a T2*-weighted EPI sequence with slice thickness = 4 mm, 34 slices, TR = 2 s, TE = 30 ms, flip angle = 90°, matrix = 64 × 64, FOV = 192 mm.

The analysis was based on minimally preprocessed data using FMRIPREP version 0.4.4 (http://fmriprep.readthedocs.io). T1-weighted volume was corrected for bias field using ANTs N4BiasFieldCorrection v2.1.0 skullstripped and coregistered ICBM 152 Nonlinear Asymmetrical template. Resting-state data were motion corrected using MCFLIRT v5.0.9. Functional data was skullstripped and coregistered to the corresponding T1-weighted volume using boundary-based registration. Motion correcting transformations, transformation to T1-weighted space, and MNI template warp were applied in a single step using antsApplyTransformations. Framewise displacement and dvars were calculated using the Nipype implementation. In addition to those regressors, the global signal and mean white matter signal were also calculated and removed. Additionally, analysis was conducted only on participants with an average frame displacement of <0.5 mm. In total, the analysis was based on 118 out of 130 healthy controls, 45 out of 50 participants diagnosed with schizophrenia, 35 out of 49 participants diagnosed with bipolar disorder, and 39 out of 43 participants diagnosed with ADHD. Moreover, in the remaining participants, all individual fMRI volumes with frame displacement >0.3 mm were removed. This dataset was chosen because it encompasses a diverse range of neuropsychiatric disorders while minimizing the potential measurement discrepancies that can occur when combining data from multiple sources.

Reconstructing BOLD time series, components and functional connectivity from neuroreceptor density maps

Reconstruction of the BOLD signal was conducted on both the timeseries and principal components of the BOLD signal. Specifically, each of 1200 fMRI volumes (time points) per participant was reconstructed from a weighted linear summation of the 19 neuroreceptor and transporter density maps. Formally, each volume of the BOLD signal is reconstructed as

$${B}_{i}={\beta }_{o}+ {\sum}_{j=1}^{19}{\beta }_{j}\times {R}_{j}$$

(1)

where B_i is the ith BOLD volume. Further, R_j is the spatial density map associated with the jth neuroreceptor and transporter, β_o is the intercept and β_j is the estimated beta-values for each neuroreceptor map in the model. Model fitting was performed using fitlm.m in Matlab 2021b.

Reconstruction accuracy of the BOLD signal was estimated using the Pearson correlation between empirical and reconstructed maps. We limited our analysis to the cortex because there are additional challenges associated with estimating the subcortical BOLD signal. For instance, subcortical BOLD signal tends to have a lower signal-to-noise ratio⁹³.

Accurate estimation of the beta values from a linear regression relies on the independence of the model terms. However, when terms exhibit collinearity, the least-squares estimate can be unstable. To test the extent this issue affected our results, we used ridge regression to regularize the beta coefficients. For the analysis, we compared the estimated neuroreceptor drive network without regularization and with ridge regression normalized.

Additionally, we determined if the neuroreceptor-based reconstruction of the BOLD timeseries preserved the inherent functional connectivity present in resting-state fMRI. To determine the accuracy in the functional connectivity of the reconstructed BOLD signal, the empirical and reconstructed BOLD signal was concatenated across participants, and Pearson’s correlation was used to estimate the functional connectivity, respectively.

The same framework was applied to the top ten BOLD spatial components in the HCP dataset. For the component analysis, the BOLD data from all participants were pooled together, resulting in 200 × 57,600 data points. Principal components of the BOLD signal were identified using pca.m in Matlab 2021b. Consistent with the terminology used by Pang et al. 2023, we refer to this process as “reconstruction” to describe the estimation of BOLD activity from the model⁴².

Pre-processing choices can bias fMRI results⁹⁴. We found that the average reconstruction accuracy was comparatively similar across the four datasets (r = 0.5-to-0.6). Moreover, as shown in Fig. S11, the similarity in neuroreceptor drive networks derived from the LSD, Modafinil, and UCLA5c datasets exhibited a strong similarity with the HCP-derived network (R_ave = 0.92). Together these results suggest that reconstructing the BOLD signal from neuroreceptor maps was robust to pre-processing choices.

BOLD reconstruction null models

Spatial permutation null model

Reconstruction accuracy was compared to the spatial permutation null model. Specifically, each of the 19 neuroreceptor and transporter density maps were spatially permuted, and the BOLD component and time series signal were reconstructed from the permuted maps. Additionally, we estimated the functional connectivity from the reconstructed BOLD signal from the spatial null model by first concatenating the reconstructed BOLD signal estimated from the spatially permuted null model across participants, and Pearson’s correlation was used to estimate the functional connectivity. A total of 1000 permutations were performed, and observed accuracy values greater than the spatial null model at a P_spatial < 0.05 were considered statistically significant.

Spin null model

Additionally, reconstruction accuracy was compared to the spin permuted null model^95,96. Spin permutation randomizes each of the 19 neuroreceptor and transporter density maps but preserves the distance dependencies between brain regions. Similar to the spatial permutation null model, BOLD component and time series signal were reconstructed from the spin-permuted maps. In the same manner as the spatial permutation null model, we estimated the functional connectivity from the reconstructed BOLD signal from the spin null model. A total of 1000 permutations were performed, and observed accuracy values greater than the spin null model at a P_spin < 0.05 were considered statistically significant.

Neuroreceptor drive network estimation and network properties

Estimating neuroreceptor drive network

Neuroreceptor drive network was estimated by correlating the beta-values from the time series model. The neuroreceptor drive network was estimated from the pooled data across participants. Clustering of the neuroreceptor drive network was conducted using modularity-maximization⁹⁷. Modularity-maximization does not require the number of clusters to be specified, and the resolution of the clusters was controlled with the resolution parameter, γ = 1. Modularity-maximization was implemented with the Generalized Louvain algorithm, part of the Brain Connectivity Toolbox⁹⁸. Clustering results from the Generalized Louvain algorithm can be dependent on the initial seeding. Therefore, clustering was repeated 100×, and final clustering results were based on the consensus across iterations⁹⁹. Specifically, consensus clustering identifies a single representative partition from the set of 100 iterations. This process involves the creation of a thresholded nodal association matrix, which describes how often nodes were placed in the same cluster. The representative partition is then obtained by using a Generalized Louvain algorithm to identify clusters within the thresholded nodal association matrix.

Provincial hubs

Provincial hubs are nodes in a network that have strong connections within a module⁹⁸. A provincial hub score for each node was estimated using the within-module degree, which quantifies the strength of the connections a node exhibits with other nodes within a module. This involved first thresholding the network to remove all negative connections. Brain connectivity toolbox was used to estimate provincial hub scores⁹⁸. Within-module z-score can be estimated as

$${Z}_{i}=\frac{{k}_{i}({m}_{i})-\underline{k}({m}_{i})}{{\sigma }^{k({m}_{i})}}$$

(2)

where m_i is the module containing node i, k_i(m_i) is the within-module degree of i, and $\underline{k}$(m_i) and ${\sigma }^{k({m}_{i})}$ are the mean and standard deviation.

Connector hubs

Connector hubs are nodes that link modules. A connector hub score was estimated for each node using participation coefficient (PC) as

$${{{{\rm{P}}}}{{{\rm{C}}}}}_{i}=1-{\sum}_{m\in M}{(\frac{{k}_{i}(m)}{{k}_{i}})}^{2}$$

(3)

where M is the set of modules, and k_i (m) is the strength of connection between i and all nodes in module m. As with the provincial hubs, the neuroreceptor network was first thresholded to remove all negative connections. Provincial hubs may act as coordinators within a module, whereas connector hubs modulate the contributions between modules and brain activity. Brain Connectivity Toolbox was used to estimate the participation coefficient, and values were z-score normalized⁹⁸.

Statistical testing of hub properties

Statistical significance for both provincial and connector hub scores was based on comparison to a null model. Specifically, a degree-persevering permutation was utilized to randomize the neuroreceptor network prior to estimating the provincial and connector hub scores from the null model. A total of 1000 permutations were performed, and empirical hub scores that were greater than the null model at a P_perm < 0.05 were considered statistically significant.

Neurosynth associated cognitive processes

Association between brain activity and cognitive processes was obtained from Neurosynth¹⁰⁰. Neurosynth contains more than 2000 terms associated with a cognitive process. We limited our analysis to the top 100 terms of interest, reflecting cognitive and behavioral terms. Specifically, the brain map representing differences in density between neuroreceptor modules were correlated with spatial maps representing the 100 cognitive terms. The analysis was performed using NIMARE¹⁰¹.

Neuroreceptors underlying LSD, Modafinil and neuropsychiatric illness induced changes

To identify the neuroreceptors and transporters contributing to changes in brain activity following LSD, Modafinil, and underlying neuropsychiatric conditions, we determined the neuroreceptors and transporters mediating these effects. The key analytical step involved identifying a modulatory network, M, that transforms the neuroreceptor drive network from state p to state q. The relationship can be expressed mathematically as

$${D}_{q}={D}_{p}{{\cdot }}M$$

(4)

Critically, all diagonal elements in D are set to zero, ensuring that the neuroreceptor and transporter do not activate themselves in the framework. $M$ can be determined by solving:

$$M={inv}\left({D}_{p}\right){{{\cdot }}D}_{q}$$

(5)

The neuroreceptors driving the modulations can be identified by decomposing $M$ using PCA. Conceptually, the PC1 of the modulation network can be thought of as reflecting the neuroreceptors driving the alterations in the BOLD signal due to LSD, Modafinil, or psychiatric illness.

Statistical significance was based on randomizing M, generating a random modulatory network, M_rand, in a degree-preserving manner. Randomizing the empirically derived M ensures that inherent properties such as the mean and standard deviation of M are preserved in M_rand. Once M_rand is estimated, it is decomposed using PCA, and the variance explained by each component is compared to M. The modulation values associated with each neuroreceptor and transporter are compared. A total of 1000 permutations are performed, and the principal component and neuroreceptors and transporters in the empirically derived M that deviate from M_rand at a probability of P_perm < 0.05 are considered to be statistically significant.

Model comparison: structural and cortical geometric eigenmodes

Structural connectivity and structural eigenmodes

Preprocessed diffusion-weighted images for each of the 48 participants part of the HCP were used to construct structural connectomes. Specifically, fiber tracking was done using DSI Studio with a modified FACT algorithm¹⁰². Data were reconstructed using generalized q-sampling imaging (GQI) in MNI space. Fiber tracking was performed until 250,000 streamlines were reconstructed with default parameters. For each participant, an undirected weighted structural connectivity matrix, A, was constructed from the connection strength based on the number of streamlines connecting two regions. Connectivity matrix was normalized by dividing the number of streamlines (T) between region i and j, by the combined volumes (v) of region i and j:

$${A}_{{ij}}=\frac{{T}_{{ij}}}{{v}_{i}\,+\,{v}_{j}\,}$$

(6)

Group structural connectivity was estimated by averaging all the individual structural connectivity networks together.

In accordance with Naze et al. 2021, structural eigenmodes were estimated from the normalized graph Laplacian of the structural network as:

$$L=\frac{1}{2}[(D-A)+{(D-A)}^{{{{\rm{T}}}}}]$$

(7)

where A is the adjacency matrix of the group-level structural connectome and D is the degree matrix¹⁰³. The graph Laplacian L is then decomposed into a finite number of eigenvalues λ_k and eigenvectors, ${\psi }_{k}$:

$$L{\psi }_{k}=\lambda {\psi }_{k}$$

(8)

Cortical geometric eigenmodes

Cortical eigenmodes capture how the anatomy constrains brain dynamics. The analysis relies on cortical modes derived in Pang et al. 2023⁴². In brief, cortical eigenmodes are estimated from the midthickness surface mesh part of the FreeSurfer’s fsaverage population-averaged template. Local vertex-to-vertex spatial relations and curvature are modeled using the Laplace–Beltrami operator from the surface mesh, from which the eigenmodes are estimated. Each eigenmode comprises spatial patterns with a specific wavelength.

Comparing reconstruction models

To compare the reconstruction models, we use the first 10 principal components of the BOLD signal. Specifically, each component is reconstructed using structural and geometric eigenmodes by sequentially adding modes to the model until the reconstruction accuracy of the model equals the accuracy obtained with the neuroreceptor-based model. Structural- or cortical geometric-based reconstructions were deemed to be more parsimonious if fewer modes were required to achieve the same accuracy as the neuroreceptor-based framework.

We can only compare the explained variance for a given set of input variables instead of the maximally explained variance by a model, because the number of neuroreceptor maps is limited by the number of available PET-imaging data on neuroreceptors; in this case, 19. Whereas the modes are limited by the dimensionality of the data. For instance, 200 in the case of structural connectivity. Therefore, adding more modes to a model could inherently increase the explainable variance of the BOLD signal. Nonetheless, there is still value in conducting the comparison since the preferred model would be the one that can explain the same amount of variance with the fewest parameters.

We opted to do the analysis on the components of the BOLD signal because this balanced the number of comparisons (i.e. components) and interpretability. Specifically, using the components C1-to-C10, we were able to account for 40.85% of the BOLD signal while preserving interpretability since there are only ten spatial maps. On the other hand, using the timeseries of the BOLD signal would have increased the temporal resolution, but it would have come at the cost and challenge of interpreting the spatial patterning, which anatomical modes are more parsimoniously able to reconstruct the BOLD signal. Additionally, since PCA is a linear decomposition of the spatial–temporal BOLD signal, it preserves the global structure of the data. Specifically, the linear mapping preserves the underlying distances in lower-dimensional space compared to non-linear methods such as uniform manifold approximation (UMAP) or t-SNE, in which the distances in the lower-dimensional space are distorted.

Statistics and reproducibility

All statistical testing was conducted using Matlab 2021b unless otherwise stated. Linear modeling was conducted using fitlm.m in Matlab. All neuroreceptor drive networks were estimated using Pearson correlations of the β-coefficients estimated using fitlm.m. Spatial permutations and spin-permutated maps were generated in Matlab (see the section “BOLD reconstruction null models” for details). Differences were assessed using Student’s t-test and FDR corrected for multiple comparisons. Detailed statistical information, including exact n values and test types, is provided in the respective figure legends. Statistical parameters, including mean and standard error of the mean, are provided. Neuroreceptor drive network consistency was estimated by correlating the estimated drive networks from the HCP, LSD, Modafinil, and UCLA5c datasets.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Code availability

The analysis was based on a combination of publicly available toolboxes and custom scripts. Network properties were estimated using the Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/). Brain Space Toolbox was used to generate spin-permuted neuroreceptor maps (https://brainspace.readthedocs.io/en/latest/). Custom scripts for data analyses are available at osf.io/58vxd/ (10.17605/OSF.IO/58VXD).

Data availability

Source data are provided with this paper as Supplementary Data 1. The anonymized data are available in online data repositories. Minimally pre-processed Human Connectome Project data can be downloaded from https://www.humanconnectome.org/. Neuroreceptor composition data can be obtained at https://github.com/netneurolab/hansen_receptors. LSD dataset can be obtained at https://openneuro.org/datasets/ds003059/versions/1.0.0. Modafinil dataset can be obtained at https://openneuro.org/datasets/ds000133/versions/00001. UCLA Consortium for Neuropsychiatric Phenomics Dataset can be downloaded at https://openfmri.org/dataset/ds000030/. The brain connectivity toolbox can be downloaded at https://sites.google.com/site/bctnet/. Cortical geometric eigenmode data can be obtained at https://osf.io/xczmp/.

References

Hyman, S. E. Neurotransmitters. Curr. Biol. 15, R154–R158 (2005).
Article CAS Google Scholar
Reiner, A. & Levitz, J. Glutamatergic signaling in the central nervous system: ionotropic and metabotropic receptors in concert. Neuron 98, 1080–1098 (2018).
Article CAS Google Scholar
Palomero-Gallagher, N. & Zilles, K. Cortical layers: cyto-, myelo-, receptor- and synaptic architecture in human cortical areas. NeuroImage 197, 716–741 (2019).
Article Google Scholar
Grimm, C. et al. Tonic and burst-like locus coeruleus stimulation distinctly shift network activity across the cortical hierarchy. Nat. Neurosci. 27, 2167–2177 (2024).
Article CAS Google Scholar
Luo, L. Architectures of neuronal circuits. Science 373, 7285 (2021).
Article Google Scholar
Deco, G. et al. How local excitation–inhibition ratio impacts the whole brain dynamics. J. Neurosci. 34, 7886 (2014).
Article CAS Google Scholar
D’Esposito, M., Deouell, L. Y. & Gazzaley, A. Alterations in the BOLD fMRI signal with ageing and disease: a challenge for neuroimaging. Nat. Rev. Neurosci. 4, 863–872 (2003).
Article Google Scholar
Reinen, J. M. et al. The human cortex possesses a reconfigurable dynamic network architecture that is disrupted in psychosis. Nat. Commun. 9, 1157 (2018).
Article Google Scholar
Durlauf, S. N. A framework for the study of individual behavior and social interactions. Sociol. Methodol. 31, 47–87 (2001).
Article Google Scholar
Kable, J. W. & Glimcher, P. W. The neural correlates of subjective value during intertemporal choice. Nat. Neurosci. 10, 1625–1633 (2007).
Article CAS Google Scholar
Afraz, A., Pashkam, M. V. & Cavanagh, P. Spatial heterogeneity in the perception of face and form attributes. Curr. Biol. 20, 2112–2116 (2010).
Article CAS Google Scholar
Posse, S., Otazo, R., Dager, S. R. & Alger, J. MR spectroscopic imaging: principles and recent advances. J. Magn. Reson. Imaging 37, 1301–1325 (2013).
Article Google Scholar
Stagg, C. J., Bachtiar, V. & Johansen-Berg, H. What are we measuring with GABA magnetic resonance spectroscopy?. Commun. Integr. Biol. 4, 573–575 (2011).
Article CAS Google Scholar
Bartelle, B. B., Barandov, A. & Jasanoff, A. Molecular fMRI. J. Neurosci. 36, 4139 (2016).
Article CAS Google Scholar
Dipasquale, O. et al. Receptor-Enriched Analysis of functional connectivity by targets (REACT): a novel, multimodal analytical approach informed by PET to study the pharmacodynamic response of the brain under MDMA. NeuroImage 195, 252–260 (2019).
Article CAS Google Scholar
Singleton, S. P. et al. Receptor-informed network control theory links LSD and psilocybin to a flattening of the brain’s control energy landscape. Nat. Commun. 13, 5812 (2022).
Article CAS Google Scholar
Deco, G. et al. Whole-brain multimodal neuroimaging model using serotonin receptor maps explains non-linear functional effects of LSD. Curr. Biol. 28, 3065–3074.e6 (2018).
Article CAS Google Scholar
Lawn, T. et al. From neurotransmitters to networks: transcending organisational hierarchies with molecular-informed functional imaging. Neurosci. Biobehav. Rev. 150, 105193 (2023).
Article CAS Google Scholar
Severino, M. et al. Molecular connectivity studies in neurotransmission: a scoping review. Imaging Neurosci. 3, imag_a_00530 (2025).
Article Google Scholar
Rose, C. R. & Konnerth, A. NMDA receptor-mediated Na⁺ signals in spines and dendrites. J. Neurosci. 21, 4207 (2001).
Article CAS Google Scholar
Yuste, R. & Denk, W. Dendritic spines as basic functional units of neuronal integration. Nature 375, 682–684 (1995).
Article CAS Google Scholar
Hou, Z.-H. & Yu, X. Activity-regulated somatostatin expression reduces dendritic spine density and lowers excitatory synaptic transmission via postsynaptic somatostatin receptor 4. J. Biol. Chem. 288, 2501–2509 (2013).
Article CAS Google Scholar
Sander, C. Y., Hansen, H. D. & Wey, H.-Y. Advances in simultaneous PET/MR for imaging neuroreceptor function. J. Cereb. Blood Flow Metab. 40, 1148–1166 (2020).
Article Google Scholar
Sander, C. Y. et al. Neurovascular coupling to D2/D3 dopamine receptor occupancy using simultaneous PET/functional MRI. Proc. Natl Acad. Sci. USA 110, 11169–11174 (2013).
Article CAS Google Scholar
Salvan, P. et al. Serotonin regulation of behavior via large-scale neuromodulation of serotonin receptor networks. Nat. Neurosci. 26, 53–63 (2023).
Article CAS Google Scholar
Shine, J. M. Neuromodulatory control of complex adaptive dynamics in the brain. Interface Focus 13, 20220079 (2023).
Article Google Scholar
Hansen, J. Y. et al. Mapping neurotransmitter systems to the structural and functional organization of the human neocortex. Nat. Neurosci. 25, 1569–1581 (2022).
Article CAS Google Scholar
Schaefer, A. et al. Local–global parcellation of the human cerebral cortex from intrinsic functional connectivity MRI. Cereb. Cortex 28, 3095–3114 (2018).
Article Google Scholar
Van Essen, D. C. et al. The Wu–Minn Human Connectome Project: an overview. NeuroImage 80, 62–79 (2013).
Article Google Scholar
Carhart-Harris, R. L. et al. Neural correlates of the LSD experience revealed by multimodal neuroimaging. Proc. Natl Acad. Sci. USA 113, 4853–4858 (2016).
Article CAS Google Scholar
Cera, N., Tartaro, A. & Sensi, S. L. Modafinil alters intrinsic functional connectivity of the right posterior insula: a pharmacological resting state fMRI study. PLoS ONE 9, e107145 (2014).
Article Google Scholar
Erritzoe, D. et al. Exploring mechanisms of psychedelic action using neuroimaging. Nat. Ment. Health 2, 141–153 (2024).
Article Google Scholar
Ko, K., Kopra, E. I., Cleare, A. J. & Rucker, J. J. Psychedelic therapy for depressive symptoms: a systematic review and meta-analysis. J. Affect. Disord. 322, 194–204 (2023).
Article Google Scholar
Ray, T. S. Psychedelics and the human receptorome. PLoS ONE 5, e9019 (2010).
Article Google Scholar
Madras, B. K. et al. Modafinil occupies dopamine and norepinephrine transporters in vivo and modulates the transporters and trace amine activity in vitro. J. Pharm. Exp. Ther. 319, 561 (2006).
Article CAS Google Scholar
Minzenberg, M. J. & Carter, C. S. Modafinil: a review of neurochemical actions and effects on cognition. Neuropsychopharmacology 33, 1477–1502 (2008).
Article CAS Google Scholar
Qu, W.-M., Huang, Z.-L., Xu, X.-H., Matsumoto, N. & Urade, Y. Dopaminergic D₁ and D₂ receptors are essential for the arousal effect of Modafinil. J. Neurosci. 28, 8462 (2008).
Article CAS Google Scholar
Volkow, N. D. et al. Effects of Modafinil on dopamine and dopamine transporters in the male human brain: clinical implications. JAMA 301, 1148–1154 (2009).
Article CAS Google Scholar
Poldrack, R. A. et al. A phenome-wide examination of neural and cognitive function. Sci. Data 3, 160110 (2016).
Article CAS Google Scholar
Atasoy, S., Deco, G., Kringelbach, M. L. & Pearson, J. Harmonic brain modes: a unifying framework for linking space and time in brain dynamics. Neuroscientist 24, 277–293 (2018).
Article Google Scholar
Atasoy, S., Donnelly, I. & Pearson, J. Human brain networks function in connectome-specific harmonic waves. Nat. Commun. 7, 10340 (2016).
Article CAS Google Scholar
Pang, J. C. et al. Geometric constraints on human brain function. Nature 618, 566–574 (2023).
Article CAS Google Scholar
Nadim, F. & Bucher, D. Neuromodulation of neurons and synapses. Curr. Opin. Neurobiol. 29, 48–56 (2014).
Article CAS Google Scholar
Dahl, C. D., Logothetis, N. K. & Kayser, C. Spatial organization of multisensory responses in temporal association cortex. J. Neurosci. 29, 11924 (2009).
Article CAS Google Scholar
Narayanan, N. S. & Laubach, M. Top-down control of motor cortex ensembles by dorsomedial prefrontal cortex. Neuron 52, 921–931 (2006).
Article CAS Google Scholar
Zanto, T. P., Rubens, M. T., Thangavel, A. & Gazzaley, A. Causal role of the prefrontal cortex in top-down modulation of visual processing and working memory. Nat. Neurosci. 14, 656–661 (2011).
Article CAS Google Scholar
Dasgupta, R., Seibt, F. & Beierlein, M. Synaptic release of acetylcholine rapidly suppresses cortical activity by recruiting muscarinic receptors in layer 4. J. Neurosci. 38, 5338 (2018).
Article CAS Google Scholar
Lee, S., Kruglikov, I., Huang, Z. J., Fishell, G. & Rudy, B. A disinhibitory circuit mediates motor integration in the somatosensory cortex. Nat. Neurosci. 16, 1662–1670 (2013).
Article CAS Google Scholar
Bharioke, A. & Chklovskii, D. B. Automatic adaptation to fast input changes in a time-invariant neural circuit. PLoS Comput. Biol. 11, e1004315 (2015).
Article Google Scholar
Sweeney, Y., Hellgren Kotaleski, J. & Hennig, M. H. A diffusive homeostatic signal maintains neural heterogeneity and responsiveness in cortical networks. PLoS Comput. Biol. 11, e1004389 (2015).
Article Google Scholar
Cole, M. W. et al. Multi-task connectivity reveals flexible hubs for adaptive task control. Nat. Neurosci. 16, 1348–1355 (2013).
Article CAS Google Scholar
Bullmore, E. & Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349 (2012).
Article CAS Google Scholar
Zhao, S. & Iyengar, R. Systems pharmacology: network analysis to identify multiscale mechanisms of drug action. Annu. Rev. Pharmacol. Toxicol. 52, 505–521 (2012).
Article CAS Google Scholar
Lawn, T. et al. Differential contributions of serotonergic and dopaminergic functional connectivity to the phenomenology of LSD. Psychopharmacology 239, 1797–1808 (2022).
Article CAS Google Scholar
Nichols, D. E. Psychedelics. Pharmacol. Rev. 68, 264–355 (2016).
Article CAS Google Scholar
Preller, K. H. et al. Changes in global and thalamic brain connectivity in LSD-induced altered states of consciousness are attributable to the 5-HT2A receptor. eLife 7, e35082 (2018).
Article Google Scholar
Mäki-Marttunen, V., Andreassen, O. A. & Espeseth, T. The role of norepinephrine in the pathophysiology of schizophrenia. Neurosci. Biobehav. Rev. 118, 298–314 (2020).
Article Google Scholar
Eggers, A. E. A serotonin hypothesis of schizophrenia. Med. Hypotheses 80, 791–794 (2013).
Article CAS Google Scholar
Patel, K. R., Cherian, J., Gohil, K. & Atkinson, D. Schizophrenia: overview and treatment options. Pharm. Ther. 39, 638 (2014).
Google Scholar
Frohlich, J. & Van Horn, J. D. Reviewing the ketamine model for schizophrenia. J. Psychopharmacol. 28, 287–302 (2014).
Article CAS Google Scholar
Fromer, M. et al. De novo mutations in schizophrenia implicate synaptic networks. Nature 506, 179–184 (2014).
Article CAS Google Scholar
Jones, C. K., Byun, N. & Bubser, M. Muscarinic and nicotinic acetylcholine receptor agonists and allosteric modulators for the treatment of schizophrenia. Neuropsychopharmacology 37, 16–42 (2012).
Article CAS Google Scholar
Cipriani, A., Agunbiade, A. & Salanti, G. Muscarinic drug shows efficacy in schizophrenia but much is left to be discovered. Lancet 403, 120–122 (2024).
Article CAS Google Scholar
Egerton, A., Modinos, G., Ferrera, D. & McGuire, P. Neuroimaging studies of GABA in schizophrenia: a systematic review with meta-analysis. Transl. Psychiatry 7, e1147–e1147 (2017).
Article CAS Google Scholar
Howes, O. D. & Kapur, S. The Dopamine Hypothesis of Schizophrenia: Version III—the final common pathway. Schizophrenia Bull. 35, 549–562 (2009).
Article Google Scholar
Moller, H.-J. Bipolar disorder and schizophrenia: distinct illnesses or a continuum?. J. Clin. Psychiatry 64, 23–27 (2003).
Google Scholar
Gold, M. S., Blum, K., Oscar–Berman, M. & Braverman, E. R. Low dopamine function in attention deficit/hyperactivity disorder: should genotyping signify early diagnosis in children?. Postgrad. Med. 126, 153–177 (2014).
Article Google Scholar
Volkow, N. D., Wang, G.-J., Fowler, J. S. & Ding, Y.-S. Imaging the effects of methylphenidate on brain dopamine: new model on its therapeutic actions for attention-deficit/hyperactivity disorder. Biol. Psychiatry 57, 1410–1415 (2005).
Article CAS Google Scholar
Volkow, N. D. et al. Therapeutic doses of oral methylphenidate significantly increase extracellular dopamine in the human brain. J. Neurosci. 21, RC121 (2001).
Gehricke, J.-G., Hong, N., Whalen, C. K., Steinhoff, K. & Wigal, T. L. Effects of transdermal nicotine on symptoms, moods, and cardiovascular activity in the everyday lives of smokers and nonsmokers with attention-deficit/hyperactivity disorder. Psychol. Addictive Behav. 23, 644 (2009).
Article Google Scholar
Levin, E. D. et al. Nicotine effects on adults with attention-deficit/hyperactivity disorder. Psychopharmacology 123, 55–63 (1996).
Article CAS Google Scholar
Potter, A. S., Schaubhut, G. & Shipman, M. Targeting the nicotinic cholinergic system to treat attention-deficit/hyperactivity disorder: rationale and progress to date. CNS Drugs 28, 1103–1113 (2014).
Article CAS Google Scholar
Wilens, T. E. & Decker, M. W. Neuronal nicotinic receptor agonists for the treatment of attention-deficit/hyperactivity disorder: focus on cognition. Biochem. Pharmacol. 74, 1212–1223 (2007).
Article CAS Google Scholar
Bollmann, S. et al. Developmental changes in gamma-aminobutyric acid levels in attention-deficit/hyperactivity disorder. Transl. Psychiatry 5, e589 (2015).
Edden, R. A. E., Crocetti, D., Zhu, H., Gilbert, D. L. & Mostofsky, S. H. Reduced GABA concentration in attention-deficit/hyperactivity disorder. Arch. Gen. Psychiatry 69, 750–753 (2012).
Article CAS Google Scholar
Banerjee, E. & Nandagopal, K. Does serotonin deficit mediate susceptibility to ADHD?. Neurochem. Int. 82, 52–68 (2015).
Article CAS Google Scholar
Rosa-Neto, P. et al. Methylphenidate-evoked changes in striatal dopamine correlate with inattention and impulsivity in adolescents with attention deficit hyperactivity disorder. Neuroimage 25, 868–876 (2005).
Article Google Scholar
Davis, G. W. Homeostatic signaling and the stabilization of neural function. Neuron 80, 718–728 (2013).
Article CAS Google Scholar
Borcuk, C. et al. Network-wide risk convergence in gene co-expression identifies reproducible genetic hubs of schizophrenia risk. Neuron 112, 3551–3566 (2024).
Article CAS Google Scholar
Steel, A., Mikkelsen, M., Edden, R. A. E. & Robertson, C. E. Regional balance between glutamate+glutamine and GABA+ in the resting human brain. NeuroImage 220, 117112 (2020).
Article CAS Google Scholar
Vattikuti, S. & Chow, C. C. A computational model for cerebral cortical dysfunction in autism spectrum disorders. Biol. Psychiatry 67, 672–678 (2010).
Article Google Scholar
Wei, S., Xie, Y. & Rahnev, D. Inferring serial correlation with dynamic backgrounds. In Proc. 38th International Conference on Machine Learning Vol. 139 (eds. Meila, M. & Zhang, T.) 11047–11057 (PMLR, 2021).
Khodosevich, K., Dragicevic, K. & Howes, O. Drug targeting in psychiatric disorders—how to overcome the loss in translation?. Nat. Rev. Drug Discov. 23, 218–231 (2024).
Article CAS Google Scholar
Tricklebank, M. D., Robbins, T. W., Simmons, C. & Wong, E. H. F. Time to re-engage psychiatric drug discovery by strengthening confidence in preclinical psychopharmacology. Psychopharmacology 238, 1417–1436 (2021).
Article CAS Google Scholar
Marder, S. R., Laughren, T. & Romano, S. J. Why are innovative drugs failing in Phase III?. AJP 174, 829–831 (2017).
Article Google Scholar
Spark, D. L., Fornito, A., Langmead, C. J. & Stewart, G. D. Beyond antipsychotics: a twenty-first century update for preclinical development of schizophrenia therapeutics. Transl. Psychiatry 12, 147 (2022).
Article CAS Google Scholar
Doss, M. K. et al. Models of psychedelic drug action: modulation of cortical–subcortical circuits. Brain 145, 441–456 (2022).
Article Google Scholar
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L. & Petersen, S. E. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage 59, 2142–2154 (2012).
Liu, T. T., Nalci, A. & Falahpour, M. The global signal in fMRI: nuisance or Information?. NeuroImage 150, 213–229 (2017).
Article Google Scholar
Carhart-Harris, R. L. et al. Neural Correlates of the LSD Experience Revealed by Multimodal Neuroimaging https://doi.org/10.18112/openneuro.ds003059.v1.0.0 (2020).
Cera, N., Tartaro, A. & Sensi, S. L. Modafinil alters intrinsic functional connectivity of the right posterior insula: a pharmacological resting state fMRI study. PLoS One, 9, e107145 (2014).
Whitfield-Gabrieli, S. & Nieto-Castanon, A. Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2, 125–141 (2012).
Article Google Scholar
de Hollander, G., Keuken, M. C., van der Zwaag, W., Forstmann, B. U. & Trampel, R. Comparing functional MRI protocols for small, iron-rich basal ganglia nuclei such as the subthalamic nucleus at 7 T and 3 T. Hum. Brain Mapp. 38, 3226–3248 (2017).
Article Google Scholar
Botvinik-Nezer, R. et al. Variability in the analysis of a single neuroimaging dataset by many teams. Nature 582, 84–88 (2020).
Article CAS Google Scholar
Alexander-Bloch, A. F. et al. On testing for spatial correspondence between maps of human brain structure and function. NeuroImage 178, 540–551 (2018).
Article Google Scholar
Vos de Wael, R. et al. BrainSpace: a toolbox for the analysis of macroscale gradients in neuroimaging and connectomics datasets. Commun. Biol. 3, 103 (2020).
Article Google Scholar
Mucha, P. J., Richardson, T., Macon, K., Porter, M. A. & Onnela, J. P. Community structure in time-dependent, multiscale, and multiplex networks. Science 328, 876–878 (2010).
Article CAS Google Scholar
Rubinov, M. & Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 52, 1059–1069 (2010).
Article Google Scholar
Bassett, D. S. et al. Robust detection of dynamic community structure in networks. Chaos 23, 013142 (2013).
Yarkoni, T., Poldrack, R. A., Nichols, T. E., Van Essen, D. C. & Wager, T. D. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods 8, 665–670 (2011).
Article CAS Google Scholar
Salo, T. et al. NiMARE: neuroimaging meta-analysis research environment. NeuroLibre 1, 7 (2022).
Article Google Scholar
Yeh, F. C., Verstynen, T. D., Wang, Y., Fernández-Miranda, J. C. & Tseng, W. Y. I. Deterministic diffusion fiber tracking improved by quantitative anisotropy. PLoS ONE 8, 1–16 (2013).
Article Google Scholar
Naze, S., Proix, T., Atasoy, S. & Kozloski, J. R. Robustness of connectome harmonics to local gray matter and long-range white matter connectivity changes. NeuroImage 224, 117364 (2021).
Article Google Scholar

Download references

Acknowledgements

We would like to thank Javier Garcia, Jessie J. Polanco, and Italo’Ivo Lima Dias Pinto for their thoughtful comments. This research was supported by the U.S. Army DEVCOM Army Research Laboratory through the Army Educational Outreach Program (W911SR-15-2-0001). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the U.S. Army DEVCOM Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes, notwithstanding any copyright notation herein.

Author information

Authors and Affiliations

U.S. ARMY DEVCOM Army Research Laboratory, Aberdeen Proving Ground, Aberdeen, MD, USA
Johan Nakuci & Kanika Bansal
Computer Science and Electrical Engineering, University of Maryland Baltimore County, Baltimore, MD, USA
Kanika Bansal

Authors

Johan Nakuci
View author publications
Search author on:PubMed Google Scholar
Kanika Bansal
View author publications
Search author on:PubMed Google Scholar

Contributions

Conceptualization: J.N.; Methodology: J.N.; Data curation: J.N.; Visualization: J.N.; Funding acquisition: J.N. and K.B.; Supervision: K.B.; Writing—original draft: J.N. and K.B.; Writing—review and editing: J.N. and K.B.

Corresponding author

Correspondence to Johan Nakuci.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Communications Biology thanks Timothy Lawn, Tommaso Volpi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Jasmine Pan. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Transparent Peer Review file

Supplemental Information

Description of Additional Supplementary Files

Supplementary Data 1

Reporting Summary

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Nakuci, J., Bansal, K. The neuroreceptors and transporters underlying spontaneous brain activity. Commun Biol 8, 1130 (2025). https://doi.org/10.1038/s42003-025-08492-z

Download citation

Received: 04 February 2025
Accepted: 07 July 2025
Published: 30 July 2025
DOI: https://doi.org/10.1038/s42003-025-08492-z