Introduction

Physiological temperature is critical for thermometric applications because it plays a role in thermoregulation, the body’s ability to maintain a stable internal temperature despite environmental changes. Thermoregulatory physiology keeps the core temperature around 37 °C, which is essential for normal cellular function. Disruptions in thermoregulation can lead to conditions like hypothermia (below 35 °C) or hyperthermia (above 40.5 °C), both of which can have serious health consequences. Thus, precise temperature monitoring is essential for detecting impairments in thermoregulatory pathways, such as in conditions affecting the autonomic nervous system, and for preventing life-threatening outcomes1. Accurate temperature measurement within the physiological range is vital for early detection and intervention in these potentially dangerous states, supporting the importance of new thermometric technologies in medical diagnostics and treatment.

The lanthanides have revolutionized materials science due to their proven applications in different areas, such as magnetism2,3,4, catalysis5, and optoelectronics6,7. Such distinctive properties arise from their electronic configuration, where the valence electrons lie in the well-shielded 4f orbitals8. The trivalent lanthanide ions are known for their narrow emission bands that span the ultraviolet (UV), visible, and near-infrared (NIR) regions, associated with long lifetimes of the emitting states. These optical properties are exploited for many applications in optoelectronics, lighting, LEDs, among others, particularly from cations emitting in the visible region, such as EuIII, TbIII, and DyIII 9.

Pioneering work in this area was developed in the visible range. However, other applications in telecommunications and biology, utilize NIR emissive cations, such as NdIII, ErIII, or YbIII, among others10,11. For the latter, NIR emission (and excitation) is vital since many biological species can fluoresce under high-energy (UV or visible) excitation, causing unwanted autofluorescence12. Moreover, NIR radiation within biological windows (BW) (BW-I: 650–950 nm; BW-II: 1000–1350 nm, and BW-III: 1550–1870 nm) offers deeper tissue penetration, enhanced image contrast, and reduced phototoxicity, making it a rapidly expanding field of study13. In this regard, lanthanide-based materials present key advantages, since some of their absorption and emission bands lie in these regions.

Among the lanthanide ions, NdIII is most advantageous since it can be directly excited in the first BW with 804 nm radiation, inducing emission in the second BW with bands centered at 908, 1065, and 1340 nm, arising from transitions between the 4F3/2 excited state to the lower 4I9/2, 4I11/2, and 4I13/2 states, respectively14,15. Furthermore, the energy gap between some of the NdIII excited states, such as the 4F7/2 and 4F5/2 states as well as the 4F5/2 and 4F3/2 states, have an energy gap close to 1000 cm−1, which are known as thermally coupled levels, that are useful for luminescence thermometry as the intensity of these two bands changes as a function of temperature (known as luminescence intensity ratio (LIR) thermometry)16. It is important to mention that in NdIII-based systems, it is also possible to evaluate thermometric performance by analyzing the behavior of a single band using the LIR of the individual Stark levels17.

Emissive transitions from the 4F7/2 and 4F5/2 states give emission bands that lie in the first BW, while from 4F3/2 it is also possible to obtain valuable information in the second BW, being an advantageous factor in avoiding excitation laser interference. This cation has been studied for luminescence thermometry in different luminescent materials, such as mononuclear complexes, nanoparticles, glasses, and some MOFs18,19,20,21. However, unlike inorganic nanomaterials, NdIII-based complexes are on size scales similar to those of biological molecules and thus can further extend the application of luminescence thermometry. Furthermore, it should be possible to incorporate ligands (L) interacting with biological systems, allowing us to investigate how temperature affects basic biological functions.

In lanthanide coordination compounds, modifications in the chemical environment influence the electronic structure of the cation giving rise to different Stark splitting22, which can be evidenced by optical spectroscopy and hence exploited for thermometry. Thus, molecular complexes are highly versatile platforms and can be easily tuned by modulating the crystal field of the cation, using different L, or synthesizing complexes with different nuclearities. Molecular thermometry has been explored by different researchers, where most of the work is focused on the visible range emitting cations23. In this area, remarkable results have been obtained, such as proper connectivity between emitting ions to modulate intermetallic energy transfer24,25, which have promoted improvements in thermal sensing. Despite all these interesting aspects, there are not many examples in the literature focused on the analysis of the thermometric performance of coordination compounds in the physiological temperature range operating in the BWs.

Anti-thermal quenching is a good approach to enhance the performance of luminescent materials, particularly in high-temperature applications26. This phenomenon arises because increased thermal energy can lead to non-radiative relaxation processes, which diminish the material’s luminescence efficiency. To avoid thermal quenching, strategies, such as incorporating energy reservoirs like Frenkel defects, optimizing host materials to resist thermal degradation, and employing controlled defect engineering have been developed27. These methods help to mitigate the loss of luminescence and maintain or even improve performance under elevated temperatures.

In this article, we have explored the NIR thermometric properties of three novel NdIII complexes within the physiological temperature range, by using 804 nm excitation that lies in the first BW. The influence of the first coordination sphere in the Stark splitting of the 4F3/2 → 4I11/2 transition was evidenced by the electronic structure obtained from theoretical calculations. Interestingly, the three compounds showed anti-thermal quenching effects, which allows an increase in the population of the 4F3/2 level, improving their thermometric performance. A thermal sensitivity of 2.4%K−1 at 293 K was obtained for the hexanuclear complex (6Nd) by using the LIR of two components of narrow 4F3/2 → 4I11/2 transition. Therefore, these results open the doors to using the anti-thermal quenching effect for boosting thermometric behavior in molecular systems and demonstrate the potential for NdIII-based systems in practical applications.

Methods

Experimental

The details of synthesis of the mononuclear ([Nd(L)(NO3)3], 1Nd)28,29,30,31, the dinuclear [(Nd(L)(NO3))2(µ-BDC)](NO3)2·H2O, 2Nd), and the hexameric ([(Nd(L))(µ-BTC)(H2O)]6·35H2O, 6Nd) complexes are in the Supporting Information. BDC and BTC correspond to the 1,4-bencenedicarboxilate and 1,3,5-bencenetricarboxilate, respectively.

FTIR spectra of the synthesized compounds were collected using a SpectrumTwo spectrophotometer from Perkin Elmer, coupled with an attenuated total reflectance accessory from PIKE Instruments. CHN analyses were performed on a Thermo Scientific Flash 2000 elemental analyzer. Thermal analysis was performed using an Iris TG209 from Netzsch. Data were collected from room temperature to 1273 K using a 10 K/min heating ratio in nitrogen atmosphere. Diffuse reflectance spectra were recorded on a UV-Vis PerkinElmer Spectrometer, model Lambda 35, coupled with an RSA-PE-20 integration sphere from LabSphere, while emission spectra were recorded using on a Horiba-Jobin Yvon spectrofluorimeter, Model Fluorolog-3 (FL3-221), using an 804 nm laser. Deconvolution of transition intensities I(λ) was done considering two peaks and using a Gaussian-type function: I(λ)=I0 + [A/(w√(π/2))]exp(-2[(λ-λ0)/w]2), where I0 represents the baseline intensity, A is the amplitude of the peak, λ0 is the barycenter, and w is the full width at half maximum of the Gaussian peak.

X-ray diffraction datasets for 1Nd, 2Nd, and 6Nd were collected on a SMART-APEX II CCD diffractometer at room temperature. Data were reduced using SAINT32, while the structure was resolved by direct methods, and subsequently completed by difference fourier synthesis and then refined by least-squares using SHELXL33. Multi-scan or numerical absorption corrections were applied using SADABS32. The hydrogen atoms were calculated at idealized positions after each cycle with SHELXL using a riding model, with C–H distance of 0.93 and 0.96 Å for aromatic and alkyl hydrogen atoms, respectively. Uiso(H) values were set equal to 1.2Ueq of the parent atoms. During the last stages of structure completion of 2Nd, it was evident that the structure should contain counterbalancing nitrate anions and solvent molecules in the inter-cationic space, but efforts to refine them as disordered positions failed. Considering this failure, we chose to use SQUEEZE34,35, a well-known and documented method for the modeling of ill-defined electron density, to consider the effect of the disordered anions and solvents. During the final refinement stages, the effect of the solvent and anions were considered by this means. It is important to note that the use of SQUEEZE has practically no effect on any structural parameters of the molecule. The formula was established based on elemental analysis and thermogravimetric analysis. Table S1 shows the main data collection and refinement details for each compound, which were prepared with the help of public CIF36. Table S2 presents selected bond lengths and angles for the molecules studied.

Theoretical

Electronic structure calculations were carried out by means of the ORCA 5.0.4 program37, CASSCF(3,12)38 calculations considered an active space composed by the 4f and 5d shells, in which 35 quartets were requested. Scalar relativistic effects were described by the DKH Hamiltonian39. The basis set for light elements was def2-TZVP40 and the basis for Nd was SARC2-DKH-QZVP41. CASSCF calculations are expected to overestimate interelectronic repulsion, while spin-orbit and L field effects are better described under this methodology42. To correct this shortcoming while maintaining the SOC and L field description of CASSCF, calculations were performed for the NdIII free ion, which allowed us to construct an effective Hamiltonian where the calculated Racah parameters are replaced with reference spectroscopic data43.

Comparing the CASSCF calculations of 1Nd, 2Nd, and 6Nd and the corrected and uncorrected results for the free ion allows to derive the energetic correction due to the change in the Racah parameters. The luminescence spectrum was approximated assuming I∝E4 (μ2 + m2 + Q2), following refs. 44,45, and the populations of the two doublets associated with the 4F3/2 multiplet were weighted according to a Boltzmann distribution.

The mononuclear models for 2Nd and 6Nd were constructed from their crystallographic structure. In the case of 2Nd, the L coordinated to one of the NdIII ions were retained intact. In the case of 6Nd, the environment of NdIII consisted of the belt macrocycle, one water L, and two BTC L, where the hydrogen positions were optimized using the BP density functional46,47. To avoid convergence problems in hydrogen optimization, the NdIII center was replaced by YIII described with electron core potentials48 and the Def2-TZVP basis set40.

Results and discussion

Structural description and characterization

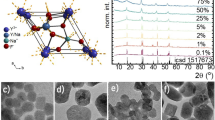
The three coordination compounds were characterized by single-crystal X-ray diffraction. The crystallographic data summarized in Table S1 reveals that these complexes crystallize in the monoclinic C2/c (1Nd), orthorhombic Fddd (2Nd), and trigonal R3 ̅ (6Nd) space groups. For the three complexes, the macrocyclic L is coordinated to the NdIII ions through the six donor nitrogen atoms as is shown in Fig. 1a. 1Nd is a mononuclear complex with a NdIII ion dodecacoordinated featuring a N6O6 coordination environment, where in addition to the macrocyclic L, three bidentate nitrate anions are coordinated to the metal center, where two of them are above and one below the macrocycle plane (Fig. 1b). For 2Nd, the data reveals a dinuclear complex where both NdIII ions are decacoordinated with an N6O4 coordination sphere (Fig. 1c). Each NdIII ion is coordinated to a macrocycle L and both centers are connected by the BDC anion through two oxygen atoms of the carboxylate moiety. Perpendicular to this bridging L, a bidentate nitrate anion completes the first coordination sphere, and two non-coordinated nitrate anions neutralize the positive charge of this complex. The 2,5-pyridilen moieties on the macrocyclic rings define stack interactions in the solid as depicted in Fig. S1 (ipd: 3.355(2) Å and CCD: 3.583(2)).

Fig. 1: Crystallographic structure for all presented complexes.
figure 1

a Coordination of the macrocyclic ligand (L) and b the molecular structures for 1Nd. The molecular structure of the c dimeric 2Nd and d the hexameric 6Nd compounds. Hydrogen atoms were omitted for clarity.

Full size image

For the hexameric 6Nd, six units of (NdL)3+ are linked by six BTC3− bridging L through two of the three carboxylate groups (Fig. 1d). As the repetitive units have the same charge, 6Nd corresponds to a neutral compound. Each of the six NdIII centers is decacoordinated exhibiting an N6O4 coordination sphere, where aside from the macrocyclic L, a bidentate, and a monodentate carboxylate groups of BTC3−, and a water molecule are coordinated to the metal ion. For major clarity, the repetitive unity is depicted in Fig. S2c.

To evaluate the coordination geometry of the NdIII center, continuous symmetry measurement (CShM) values were calculated using the SHAPE 2.1 program49 (Tables S3–S5). The lowest CShM value for 1Nd (2.054), 2Nd (1.811), and 6Nd (1.470), indicates that these complexes can be described as an icosahedron when twelve coordinated as in 1Nd and a tetradecahedron (2:6:2) for complexes 2Nd and 6Nd, where both compounds present the NdIII center with a ten-coordinated environment.

With regards to the characterization of 1Nd performed by FTIR spectroscopy (Fig. S3), it is important to highlight the vibration band due to the imine group at 1654 cm−1, which proves the successful condensation reaction. The bands observed at 2915 and 1590 cm−1 are due to the ethylene and pyridine moieties, respectively. Vibration bands due to nitrate ions are observed at 1450, 1300, and 1030 cm−1. These bands are associated with nitrate L with a bidentate coordination mode, in agreement with the structure obtained by X-ray diffraction.

A broad band above 3000 cm−1 is observed in the FTIR spectra of the 2Nd due to the presence of water molecules. Aside from the vibration bands due to the macrocyclic L at 1657 and 1559 cm−1 due to imine and pyridine groups, additional bands were detected at 1533 and 1506 cm−1, which are assigned to the carboxylate units and aromatic ring of the BDC bridging L. The band at 835 cm−1 is characteristic of the para substitution of the benzyl ring of the linker50. The spectrum also shows a band at 1383 cm−1 attributed to the anionic nitrate ions.

For compound 6Nd, vibrations due to the macrocyclic L are found at 1657 and 1607 cm−1, and bands due to BTC linker are present at 1550–1537 cm−1 due to carboxylate groups, while the band at 760 cm−1 is attributed to the ν(C-H) of 1,3,5-substituted benzene ring51. In this case, no bands due to nitrate ions are observed, consistent with the full replacement of these species, as described in the crystallography section.

From the thermal analysis (Fig. S4) it is important to mention that the obtained species are stable in the physiological temperature range, which was used to evaluate the thermometric properties in the present study. Compound 1Nd is anhydrous, as established by X-ray diffraction and confirmed by thermal analysis. This complex shows an abrupt mass loss near 563 K due to the decomposition of bidentate nitrate ions. This step represents a higher mass percentage than that calculated for only the three nitrate anions, which may be attributed to partial decomposition of the macrocyclic L since this is followed by a permanent mass loss until 1273 K. (Fig. S4)

On the other hand, complex 2Nd contains crystallization water molecules, evidenced by FTIR and by the mass loss below 373 K. A continuous mass loss is observed from 373 to 523 K, which may be attributed to the nitrate counterions present in the crystalline lattice. Another decomposition step takes place at 553 K, which should be attributed to the remaining bidentate nitrate ions, due to the similar decomposition temperature observed for 1Nd. Finally, above 573 K, a continuous weight loss is evidenced that should include the decomposition of the BDC linker and the macrocyclic L.

For compound 6Nd, three main decomposition stages can be distinguished. The first one corresponds to the loss of crystallization water molecules, similar to the profile observed for 2Nd. In this case, a much higher quantity of water content was found, which is explained by two factors: i) uncoordinated carboxylate groups, which are stabilized by water molecules, and ii) the cavity formed by the hexameric unit which should allow a higher hydration content as compared with 1Nd and 2Nd. A second decomposition is observed ca. 508 K, which is due to coordinated water molecules. Finally, a continuous mass loss is evidenced above 593 K that should include the decomposition of the bridging BTC and the macrocyclic L. It is important to remark that decomposition observed for 1Nd and 2Nd at 553 K assigned to nitrate ions is absent, in agreement with previous characterization techniques.

Optical properties

Solid-state diffuse reflectance spectra are depicted in Fig. S5. A broad band is observed below 350 nm ascribed to the absorption of the macrocyclic L. In the corresponding spectrum of the dimer 2Nd, a second broad absorption band is detected at 420 nm, which may be attributed to the BDC bridging L. Furthermore, in the hexameric unit 6Nd, this latter band expands to lower energies, almost overlapping the weak absorption band above 500 nm. Narrow bands were observed for the three complexes, due to the direct absorption transitions of the NdIII ion, originating from the 4I9/2 ground state to various 4f excited states (see Fig. S5 and Table S6)52. It should also be noted that the presence of the bands ca. 800 nm, due to the 4I9/2 → 4F5/2 + 2H9/2 transition, is of great importance since this wavelength is used to excite the NdIII center in the first biological window and is used to evaluate the thermometric performance.

Having analyzed the absorption spectra for all coordination compounds, the photoluminescence spectra of the studied species were recorded. By using an 804 nm laser, it was possible to detect the corresponding narrow emission bands in the second BW. Figure 2 shows the representative spectra for the three complexes at room temperature. The emissive pathway involves the direct excitation of the 4F5/2,2H9/2 mixed energy level, which consequently populates the lower-lying 4F3/2 level by non-radiative decay and thus leads to the observed emissions53.

Fig. 2: Emission spectra for the three complexes at 298 K, upon excitation with 804 nm laser.
figure 2

Dashed lines are guides for the barycenter of the two components of main transition 4F3/2 → 4I11/2, which will be further used in the analysis.

Full size image

The 4F3/2 → 4I11/2 band is convenient for luminescence thermometry since its profile and intensity can be modulated by the local environment, covering a narrow section of the spectra in the second BW54. Furthermore, its splitting has been associated with the energy span of the two doublets stemming from 4F3/215. The deconvolution of the main band was done by fitting the plot of intensity vs cm−1, as shown in Fig. S6, and the results of fittings are shown in Tables S7–S9.

Figure 3 shows the temperature-dependent emission spectra for the 6Nd complex within the physiological temperature range, while similar spectra for 1Nd and 2Nd are presented in Fig. S7. These figures highlight the temperature-dependent emission of the 4F5/2 → 4I11/2 transition. Notably, 6Nd is unique among the samples, as the 4F5/2 → 4I11/2 intensity decreases with increasing temperature, suggesting the presence of an additional feeding channel to the 4F3/2 level via multiphonon decay.

Fig. 3: Temperature dependent emission spectra of the hexanuclear complex [(Nd(L))(µ-BTC)(H2O)]6·35H2O (6Nd).
figure 3

a Displays the full emission spectrum, while b and c show the emissions corresponding to the 4F3/2 → 4I11/2 and 4F5/2 → 4I11/2 transitions, respectively. Spectra are presented from 293 to 333 K.

Full size image

As mentioned above, it is useful to have a narrow energy range to avoid instrumental error. Figure S8 presents the integrated areas of the two components of the 4F3/2 → 4I11/2 transition (named A1 for the higher energy component and A2 for the second component), and the total area as a function of temperature, where is possible to observe a general increase in intensity with increasing temperature, attributed to the anti-thermal quenching effect. This anti-thermal quenching may be due to the suppression of non-radiative pathways55.

As seen in Figure S8, the two components of compounds 1Nd and 2Nd have similar behavior, slightly increasing in intensity with the increase in temperature. However, the slight increase gives low Sr, ranging from 0.1 to 1.1%∙K−1. Interestingly, in 6Nd, while A2 slightly increases with temperature, from 8.6 to 11.0 (less than 0.3 times), A1 increases from 1.5 to 4.1 (more than 2.7 times). This increment in A1 yields a higher Sr of 3.9%∙K−1 at 293 K. Furthermore, as both components have different temperature dependencies, it is useful to analyze their LIR. Figure 4 shows the temperature dependencies of the LIR and corresponding Sr values (the corresponding values for LIR and the linear fit are presented in Table S10). For 1Nd and 2Nd, the LIR of the two components of the 4F3/2 → 4I11/2 transition is not a useful thermometric parameter.

Fig. 4: Temperature dependence of the LIR of the two components of the 4F3/2→4I11/2 transition for 6Nd and the respective relative thermal sensitivity values.
figure 4

The full red line is the linear fit to the LIR data. The dashed line is a guide to the eyes.

Full size image

From the LIR of the two components of 6Nd, it is possible to observe a linear behavior that is desirable to thermometry. This parameter achieves a thermal sensibility of 2.4% ∙ K−1 at 293 K, decreasing to 1.2% ∙ K−1 at 333 K.

The thermometric performance of the samples was also investigated by analyzing the (4F3/2→4I11/2)/(4F3/2→4I13/2) LIR. However, only complex 2Nd presents a linear temperature dependence, with a low relative thermal sensibility of 0.1%∙K−1. Table 1 compares the thermometric performance of the complexes studied with that reported for other NdIII coordination compounds.

Table 1 Summary of the thermometric performance and operating temperature range for NdIII-based coordination compounds
Full size table

Based on the data presented in Table 1, it can be concluded that 6Nd is the most sensitive NdIII compound reported to date, surpassing previous examples by at least one order of magnitude. This exceptional sensitivity suggests promising potential for future biological applications. Thus, this study underscores the significance of molecular complexes that may be effective molecular thermometers operating within the physiological temperature range. To further enhance the thermometric properties of NdIII complexes, future research should focus on developing species with varied nuclearities and alternative connectivities between metal centers.

Theoretical calculations

Electronic structure calculations were performed to grasp further details about the relation between the coordination environment and the shape of the 4F3/2→4I11/2 transition (see further technical details in the methods section). Figure 5 presents the calculated emission spectrum for 1Nd, 2Nd, and 6Nd. As expected from selection rules, calculations reveal that all emission bands associated with the 4F3/2 multiplet are dominated by the electric dipole mechanism, so magnetic dipole and electric quadrupole contributions can be safely neglected. Focusing on the 4F3/2→4I11/2 transition, we observe a trend that is qualitatively consistent with results from Fig. 2, as two maxima are discernible in 1Nd and 2Nd and appear merged in the case of 6Nd. The relative intensity of both maxima is not properly captured in all cases, as compound 2Nd shows its main peak at 1075 nm instead of a more intense signal at 1050 nm in comparison with the 1075 nm maximum.

Fig. 5: CASSCF(3,12) calculated emission profiles of NdIII complexes.
figure 5

Spectra are shown for 1Nd (bottom, black), 2Nd (middle, red), and 6Nd (top, blue) complexes.

Full size image

Figure 6 shows the Dieke diagram of 6Nd with the corresponding calculated spectra and the 4F3/2→4I11/2 transition decomposed in the intensity stemming from the lower and higher energy Kramers’ doublets of the emissive multiplet (identified as Γ and Γ′ in Fig. 6, respectively). Dieke diagrams for 1Nd and 2Nd are given in Figure S9. We observe the two-peak pattern for 1Nd and 2Nd, where the relative intensity of both maxima is dependent on the emissive state. In contrast, results for 6Nd show a single peak signal, irrespective of the emissive doublet. As the Γ doublet is at slightly lower energy, the band for this doublet (dashed line in Fig. S10a) is shifted to lower energy in comparison with the intensity associated with the Γ’ doublet (solid line in Fig. S10a). In any case, this splitting is significantly smaller than the energy difference of the two-peak pattern, suggesting that the origin of this separation is related to the splitting of the 4I11/2 multiplet instead of 4F3/2.

Fig. 6: Dieke diagram for 6Nd with the calculated emission spectrum, and the specific Stark splitting for the studied complexes.
figure 6

δ represents the calculated Stark splitting (in cm−1) between the two doublets \(\Gamma\) and \(\Gamma^{\prime}\) of the 4F3/2 level, used for the Boltzmann distribution. \({\sigma }_{1}\) and \({\sigma }_{2}\) denote the wavenumbers of the lower and higher energy bands, respectively, as determined from band deconvolutions in Fig. S6.

Full size image

To corroborate this point, the splitting of the 4I11/2 multiplet was analyzed in further detail. Interestingly, the Kramers’ doublets tend to cluster in two groups for all cases, with an energy separation between barycentres in the order of 100–150 cm−1, which is consistent with the observed splitting of the 4F3/2 → 4I11/2 signal (Fig. S10b). The number of doublets in each cluster is different for 1Nd, presenting two groups of three doublets each in comparison to 2Nd and 6Nd, where the lower cluster has two states and the upper has four (see the calculated splitting of 4I11/2 in Fig. 6). Thus, the emission to one of the clusters can be turned off to separate their contribution to the total emission. Figure S10b shows that both clusters are associated with only one peak, suggesting that the observed splitting in the 4F3/2 → 4I11/2 signal reflects the energy pattern of the 4I11/2 multiplet instead of 4F3/2.

While the shape of the 4F3/2 → 4I11/2 emission depends on the 4I11/2 splitting, the thermal behavior depends on the relative separation of the Γ and Γ′ doublets, which can be described by a Boltzmann distribution (Eq. S6).

Despite the clear evidence of anti-thermal quenching behavior in this series of compounds (Figs. 3 and S7), as evidenced by the sum of the A1 and A2 components in Fig. S8, the trend of these components in the 6Nd compound differs from the 1Nd and 2Nd samples. A plausible explanation is that the A2 (Fig. S8e) component predominantly originates from the emission of the higher Stark component of the 4F3/2 to upper Stark components of the 4I11/2 level, as shown by the σ2 line in Fig. 6. Conversely, the A1 (Fig. S8e) is primarily associated with the emission from the lower Stark component of the 4F3/2 (σ1 line in Fig. 6), exhibiting thermal behavior similar to that observed for the 5D4 → 7F5 emission in TbIII-based silsesquioxanes with acetylacetonate as antenna L54.

Furthermore, the anti-thermal quenching effect across all samples leads to an increase in the population of the 4F3/2 level. Without accounting for the increase in the 4F3/2 population (i.e., the population is maintained constant), the variation in the populations of the upper (Γ′) and lower (Γ) Stark levels of 4F3/2 with temperature can be estimated using Eq. S6 and is illustrated in Fig. 7 (empty symbols). Under this condition, the sum of the empty symbols equals 1 (normalized population). However, the anti-thermal quenching effect causes the 4F3/2 population to increase (full symbols in Fig. 6). Consequently, when the 4F3/2 population increases due to anti-thermal quenching, the total relative population grows such that η(\(\varGamma^{\prime}\)) + η(\(\varGamma\)) ≥ 1, reflecting the trend observed in Fig. S8e.

Fig. 7: Temperature-dependent Boltzmann populations.
figure 7

Boltzmann populations of the Kramer’s doublets of 4F3/2 (\(\Gamma\) and \(\Gamma^{\prime}\)) for 6Nd, showing the population distribution without considering the anti-thermal quenching effect (empty symbols) where the sum of populations is constant, and with the anti-thermal quenching effect, which causes an increase in the overall 4F3/2 population with temperature (full symbols). The trend is consistent with the observed in Fig. S8e.

Full size image

Regarding the thermal behavior of 1Nd and 2Nd compounds, it is reasonable that their emissions components originate from the same Stark components of 4F3/2 (\(\Gamma\) or \(\Gamma^{\prime}\), as illustrated in Fig. 6), which explains their similar trend with temperature and relative low thermometric performance in comparison with 6Nd.

Based on the theoretical framework for ratiometric single-ion thermometers by Suta and Meijerink56, and the calculated CASSCF energy gap between \(\Gamma\) and \(\Gamma^{\prime}\) for each compound, we can estimate the response function \(\rho \left(T\right)\), Fig. 8, normalized to the most responsive temperature56. This response function can be derived as:

$$\rho \left(T\right)=\frac{1}{4}{\left(\frac{\delta }{{k}_{B}\cdot T}\right)}^{2}{e}^{\left(2-\frac{\delta }{{k}_{B}\cdot T}\right)}$$
(1)

where \({k}_{B}\) and \(T\) are the Boltzmann constant and temperature.

Fig. 8: Thermal response profiles of compounds.
figure 8

Normalized response function \(\rho \left(T\right)\) for the compounds 1Nd (black), 2Nd (red), and 6Nd (blue).

Full size image

As expected for single-ion luminescent thermometers based on the ratio between two Stark components of lanthanide ions, all three compounds exhibit improved performance in the cryogenic temperature range54,56, as indicated by the \(\rho \left(T\right)\) trend in Fig. 8. However, these molecular thermometers may not achieve optimal sensitivity at cryogenic temperatures, as the anti-thermal quenching effect is not considered in the \(\rho \left(T\right)\) formulation, and this effect may not be evident at low temperatures. This is because at cryogenic temperatures, the population dynamics—specifically the thermal population of excited states—are less effective, resulting in a reduced anti-thermal quenching effect compared to higher temperatures. Nonetheless, the larger \(\delta\) calculated in 6Nd corroborates that this compound offers superior temperature response within the physiological temperature range compared to the others.

Concerning the anti-thermal quenching behavior, there are two reasons for the outperformance of 6Nd complex against 1Nd and 2Nd: L field effects and multiphonon decay. The stronger L field in 6Nd results in a greater splitting of the 4F3/2 energy level (Fig. 6), which extends the thermometer response function \(\rho \left(T\right)\) to higher temperature ranges compared to 1Nd and 2Nd (Fig. 8).

The energy gap between the 4F5/2 and 4F3/2 states is about 1000 cm−157, a value that can be easily bridged by phonons. Consequently, the 4F5/2⇝4F3/2 multiphonon process is more effective in 6Nd. This is probably due to the high number of vibrational modes available and confirmed by the decrease in the intensity of the 4F5/2 → 4I11/2 (this is also observed for the 4F5/2 → 4I13/2) transition with increasing temperature (Fig. 3c), suggesting that the population of the 4F5/2 state decreases via multiphonon relaxation, which leads to an increased population of the 4F3/2 state. This behavior, where the 4F5/2 population decreases with temperature, is not observed in 1Nd and 2Nd (Fig. S7).

Conclusion

Three distinct molecular complexes incorporating the NdIII cation and a macrocyclic L derived from 2,6-pyridinedicarbaldehide and ethylenediamine were synthesized. The introduction of bridging L, specifically 1,4-benzenedicarboxylate (BDC) and 1,3,5-benzenetricarboxylate (BTC) ions, facilitated the formation of novel polymetallic species. With BDC as the auxiliary L, a dinuclear complex was formed, wherein DBC bridged two mononuclear units, replacing two nitrate L with carboxylate groups. When BTC was employed as the linker, a hexanuclear cyclic compound was produced, featuring a complete substitution of nitrate L with BTC’s carboxylate groups. Direct excitation of the NdIII ion at 804 nm enabled the monitoring of its emission within the second biological window. Complex 6Nd emerged as the most sensitive with an LIR of the two Stark components of the 4F3/2 → 4I11/2 transition, achieving a sensitivity (Sr) of 2.4%∙K−1 at 293 K, surpassing that of complexes 1Nd and 2Nd. This indicates that optimizing the first coordination sphere and the nuclearity/connectivity of emitting systems can significantly enhance the thermometric performance of NdIII molecular complexes.

The comprehensive theoretical analysis of compounds 1Nd, 2Nd, and 6Nd provides an insightful understanding of their emission characteristics and thermal behavior. The calculated CASSCF emission spectra reveal a clear dependence on the coordination environment and electronic structure, with notable differences in the 4F3/2 → 4I11/2 transition.

For 1Nd and 2Nd, the observed two-peak emission pattern reflects the distinct contributions from lower and higher energy Kramers’ doublets of the 4F3/2 multiplet, aligned with the calculated splitting of the 4I11/2 multiplet. In contrast, 6Nd demonstrates a merged single peak, suggesting a different emission profile primarily influenced by the 4I11/2 multiplet’s splitting rather than the 4F3/2.

Thermal behavior analysis indicates an anti-thermal quenching effect across all samples, impacting the relative populations of the Kramers’ doublets. Notably, the compound 6Nd stands out with a larger 4F3/2 splitting, translating to superior sensitivity within the physiological temperature range. This highlights its potential for enhanced performance in temperature-sensitive applications.

Overall, the results underscore the significance of electronic structure and thermal effects in tuning the emission properties of NdIII-based compounds. Specifically, the 6Nd improved temperature response positioning it as a promising candidate for applications requiring precise thermal sensing, particularly in physiological contexts.