Introduction

Chemical reactions essentially consist of breaking and forming of molecular bonds. The mechanistic understanding of photoinduced bond breaking has been particularly shaped through femtosecond pump–probe spectroscopy1,2,3. Real-time tracking of the electronic and nuclear structure has provided insight into various processes accompanying photodissociation, such as curve crossings4,5, predissociation6 conical intersections7, or electronic relaxation8.

Photoassociation is used to form molecules in ultracold atomic clouds9,10, where the binding energy is dissipated into the light field11. In the time–domain, however, photoassociation has largely escaped observation so far, in particular for larger systems, due to difficulties in preparing the reactants in a well-defined initial geometry. This limitation could be overcome only in a few situations: In gas phase, where the broad distribution of impact parameters completely blurs the time resolution, bond formation could only be observed for selected dimer molecules through Franck–Condon filtering based on the resonance condition for laser excitation12,13,14. In a few cases, cold bimolecular van der Waals complexes15,16,17,18, and anionic clusters19, provide favorable initial conditions to study bond formation. In solution, a network of species separated by well-defined distances are readily achieved, however, inhomogeneous broadening prevents observation of individual states and structural dynamics can only be inferred by x-ray scattering20,21. Despite these versatile approaches, the formation of clusters larger than dimer molecules and bimolecular aggregates has not been experimentally realized so far.

The endeavor to combine the advantages of the previous approaches—homogeneous distances in solution, low environmental perturbation for well-defined resonances, and low temperatures in gas phase—leads us to the application of helium nanodroplets (HeN) as a cryogenic solvent. Helium nanodroplets have routinely been used for the synthesis and investigation of atomic and molecular aggregates, since they provide a high degree of control in the aggregation process, efficient cooling to 0.37 K, and enable measurements with low matrix effects compared to other noble gas environments22,23,24,25. Here, we show that the unique solvation properties of superfluid He can be used to prepare well-defined initial conditions for the time-resolved observation of bond formation of multiple reactants. This demonstration builds on recent observations that atoms solvated in HeN can arrange in metastable configurations at nanometer distance, enabled by the ultracold He solvent26,27,28,29,30,31,32. For two Mg atoms inside a HeN, density functional theory simulations predict such a metastable configuration at 9.5 Å interatomic distance, instead of the formation of a Mg2 molecule33. This dilute configuration is enabled through the accumulation of helium density between two Mg atoms, and referred to as “foam”33 or “quantum gel”34,35. We note that this prediction has been subject to discussion, since path integral Monte Carlo simulations of two and three Mg atoms inside HeN find no evidence for stabilization in a metastable configuration, but only equilibration to the strongly bound dimer and trimer36.

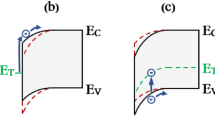
Here, we present an investigation of the dynamical response of Mgn aggregates inside HeN to photoexcitation with femtosecond photoelectron and -ion spectroscopy2,3. This approach has recently proven successful inside HeN for the observation of electronic37,38 and nuclear dynamics39,40. We obtain time-resolved photoelectron spectra (TRPES) containing two different dynamic signatures, indicating that Mgn aggregates exist in two different configurations inside HeN. An immediate signal rise followed by a fast τ1 = (380 ± 70) fs decay is characteristic for van der Waals clusters, where primary processes are electronic dynamics (Fig. 1b). In addition to this swiftly responding compact clusters, the TRPES also contains a PE band with delayed signal rise peaking 1.2 ps after photoexcitation and a much slower τ2 = (4.0 ± 0.9) ps decay. We interpret this slower response to photoexcitation as a signature for nuclear dynamics involved in the transition leading from the predicted foam-like Mgn configuration to a dense cluster (Fig. 1c). This transient signal reveals insight into the energy flow and nuclear dynamics during cluster formation.

Fig. 1: Sketch of the photoinduced dynamics of single Mg atoms, compact Mgn cluster and metastable Mgn foam inside HeN.
figure 1

The corresponding energy level diagrams depict pump (blue)-probe (green) photoionization and different ionization pathways are labeled with (1) to (4), correspondingly to the photoelectron bands in Fig. 2. a Three-photon ionization channels of Mg atoms. b Formation of compact Mgn cluster through collision of an energetic Mg atom with the foam-like aggregate during the pickup process43 and subsequent pump-probe photoionization. c Photoexcitation of Mg atoms within the Mgn foam triggers the transition to a compact cluster. Energy pooling (magenta arrows) leads to population of highly excited Mg levels and fragmentation.

Full size image

Results

The time-resolved photoelectron spectrum is shown in Fig. 2, depicted as a function of the electron binding energy Ebind (Ebind = hνprobe − Eel.kin, where Eel.kin is the measured electron kinetic energy). We first allocate the observed photoelectron bands to pump–probe ionization pathways based on energetic considerations of the 282 nm (4.40 eV photon energy) pump pulse and the 404 nm (3.07 eV) probe pulse. The temporal development of these bands, obtained from a global fitting analysis, reveals population transfers dynamics triggered by photoexcitation. Examination of the time-resolved ion yields and, in particular, the correlation of ion fragments to the photoelelctron bands gives information about the accompanying nuclear dynamics.

Fig. 2: Time-resolved photoelectron spectrum and global fitting analysis of Mgn aggregates embedded in HeN.
figure 2

a Pseudocolor plot showing the transient electron yield as function of binding energy. Four distinct bands are marked (1) to (4). b Comparison of energy-integrated PE transients (see legend) to decay functions N1,2,3 from global fitting. c Decay associated spectra DAS1,2,3 obtained from global fitting. Note that below 2 ps, the spectra feature a higher temporal resolution.

Full size image

Assignment of photoelectron bands

Inspection of Fig. 2a reveals four distinct bands. Band (1) between 2 and 3 eV rises instantaneously and shows a fast decay (Fig. 2b, yellow circles). Band (2) between 1 and 2 eV shows initially a cross correlation feature, followed by a moderate signal rise peaking at 1.2 ps and a slower decay than band (1) (Fig. 2b, purple circles). The assignment of bands (1) and (2) in Fig. 2 is difficult due to their overlap in time and energy. Both bands are related to states with binding energies lower than that of the photoexcited bare-atom 31P1 state (3.30 eV binding energy), given the lower probe photon energy of only 3.07 eV. Bands (3) and (4) can be assigned to two-photon ionization of the excited 31P1 Mg state (see Fig. 1a). Band (3) extends from −0.17 eV to 0.5 eV with a fast rise and slower decay, followed by a second slow rise after 10 ps (see Fig. 2b). This band represents the transient population of 31P1 Mg state, ionized by two probe photons. Note that the increased peak width is common for photoionization of atoms inside He droplets37. The brief appearance of band (4) around t0 is characteristic for a cross-correlation peak: With a binding energy slightly below –1 eV we assign this band to 31P1 ionization with one pump and one probe photon.

Global fitting analysis to retrieve population transfer dynamics

The spectral and temporal overlap of bands (1) and (2) in the time-resolved photoelectron spectrum (Fig. 2) poses a challenge for a quantitative analysis. In order to decode the different contributions, the spectrum is analyzed by applying a global fitting procedure41,42, i.e., species with different transient behavior contributing to the spectrum are identified by extracting the respective decay associated spectra, DAS(E), and the associated transient decay functions, N(t). Since the photoelectron bands in Fig. 2 differ in their signal rise behavior, we use two different types of decay functions: An instantaneous signal rise is modeled by a directly excited state followed by population decay (a Gaussian function convoluted with an exponential decay, as described in detail in Supplementary B). A delayed signal rise is modeled by assuming sequential population transfer from an initially excited state (which is not necessarily detected) into the state yielding the photoelectron signal of the observed band. This function accounts for an exponential signal rise followed by an exponential decay, with two different characteristic time constants.

Taking into account photoelectron-band assignments already made, one can simplify the fit process: Since band (3) originates from a different ionization process than bands (1) and (2) and since there is no overlap of band (3) with bands (1) and (2), one can split the time-resolved PE data into two energy domains at 0.42 eV binding energy. The low binding energy region, containing the 31P1 atom band (3), is modeled by DAS3 (Fig. 2c, green line). The 31P1 population appears instantly (Fig. 2b, green line), suggesting direct excitation by the pump pulse, and then decays with a time constant of τ3 = (1.1 ± 0.1) ps.

Relevant parameters of the decay functions are listed in Table 1 for better comparability. From this transient signal, one can deduce the temporal pump-probe overlap (time zero, t0) and the temporal instrument response function duration σ. Inspection of the low binding energy region in Fig. 2 shows that the signal rises towards long delay times, which is not represented by the fit function. We account for this deviation by introducing an additional background, as described in Supplementary B. Furthermore, the pump–probe cross-correlation signal of band (4) is determined to be (45 ± 3) fs in a separate measurement of the total electron yield around time zero. This cross-correlation signal, together with t0 and σ, is kept constant in the remaining global fitting process.

Table 1 Decay parameters
Full size table

In the high binding-energy domain two distinct populations, represented by different decay associated spectra and different decay functions, can be expected. In agreement with this assumption, DAS1 with a peak at 2.5 eV (Fig. 2c, yellow line) and the broader DAS2 peaking at 2 eV (purple line) can be identified, together with two corresponding decay functions. The transient population N1 rises quickly to a maximum at  ~250 fs, followed by a rapid decay with a characteristic time of τ1 = (380 ± 70) fs (Fig. 2b, yellow line). Note that the integrated 2.0–3.0 eV signal (yellow circles) deviates from the N1 transient (yellow line) because there is a significant contribution from the slower N2 (DAS2) signal in this energy interval. N2 features a delayed onset with respect to N1 with a rise time of \({\tau }_{2}^{{{{\rm{rise}}}}}=(450\pm 180)\) fs leading to a maximum at 1.2 ps and also a slower decay time constant of τ2 = (4.0 ± 0.9) ps (Fig. 2b, purple line).

Interpretation of DAS populations

Although the similarity of the band (1) decay time and the band (2) rise time might suggest sequential population transfer from states correponding to band (1) to states corresponding to band (2), we do not consider this option because band (2) appears at lower binding energy (energetically higher states) than band (1). For this conclusion it is important that the ionization process leading to bands (1) and (2) proceeds with the same number of probe photons, which we have verified through intensity dependence measurements. The different transient behavior of bands (1) and (2) thus indicates the presence of two different species. The sudden appearance of band (1) represents direct electronic excitation, presumably of compact Mgn clusters. These compact clusters, which are formed through collision of an energetic Mg atom with the foam-like aggregate during the pickup process, have a reduced electron binding energy compared to Mg atoms43 and can thus be ionized by the probe pulse immediately after excitation (see Fig. 1b).

The picosecond delay in the onset of band (2), in contrast, suggests that nuclear dynamics are involved, which are caused by the population of an undetected excited state. A possible origin would be the presence of a previously suggested foam-like Mgn configuration, in combination with a transition to a compact Mgn cluster triggered through 31P1 ← 31S0 photoexcitaiton by the pump pulse (see Fig. 1c)30,32,33. Given the 31P1 excited state binding energy of 3.30 eV, it is remarkable that DAS2 indicates transient population within the whole detection window given by the 3.07 eV photon energy of the probe pulse. In this scenario, the occupation of these highly excited states is caused by the transition of Mgn aggregates from a dilute to a compact configuration.

Testing the hypothetical assignment of band (1) to a compact Mgn cluster and band (2) to a forming Mgn cluster, the dependence of the photoelectron signal on the Mg doping level (see Supplementary Fig. A.1) was investigated. At high doping, band (2) decreases and band (1) increases in relative strength, consistent with earlier studies of the spontaneous collapse of the dilute Mg aggregate at high Mg doping concentrations43.

Direct photoexcitation of Mg atoms to states with such low binding energy, can be excluded since two-photon excitation leads to ionization (4.4 eV photon energy, 7.65 eV ionization energy44). Also, combined excitation with one pump and one probe photon can be excluded since this can only occur when pump and probe pulse overlap.

Transient photoion signal

A more direct insight into the nuclear dynamics and in particular the fragmentation behavior can be gained from the ion signals. Ions expelled from the droplet show up at time delays larger than Δt ≥ 1 ps. Figure 3 shows pump-probe ion spectra recorded at selected time-delays. The spectra consist of peaks corresponding to \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}\) (n = 1–8) clusters and \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\) snowballs.

Fig. 3: Ion mass spectra for different pump–probe time delays.
figure 3

The mass spectra represent the transient fragment distribution of \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}\) cluster ions formed after photoexcitation and probe ionization. The spectra are area normalized and vertically offset according to the time-delay, indicated for each spectrum on the right side. Both isolated \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}\) clusters and \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}\)-Hem snowballs are present in the mass spectra. The spectra were obtained by averaging the ion mass spectra in 2 ps time intervals and the mean cluster size is indicated as a black dot.

Full size image

The pump-probe spectra show ion signals only up to \({{{{\rm{Mg}}}}}_{8}^{+}\), while in the probe-only signal, masses as high as \({{{{\rm{Mg}}}}}_{12}^{+}\) appear. The average cluster size, taken as a measure and indicated by a black dot in Fig. 3 for each spectrum, decreases from 3.7 to 2.8 with increasing delay. Neglecting that the ionization probability may change with cluster size, this down-shift reflects the general trend that an increasing amount of energy is transferred to nuclear degrees of freedom with time.

Correlated electron–ion detection to identify fragmentation dynamics

To further test the assignment of TRPES band (1) to compact Mgn clusters and band (2) to foam-like aggregates, we examine correlations between photoelectrons and ions through covariance detection45,46,47. The assignment of ion fragments to each of the bands is of particular interest. This detection method has been applied to gas-phase molecules, where it allows to distinguish between different photochemical reaction pathways based on the ionic products48,49,50. For photoionization inside a helium droplet, the electrostrictive attraction prevents ion detachment from the droplet, except for situations where the ions gain sufficient kinetic energy through photodissociation51,52, or Coulomb explosion40,53. In our case, we will see that the processes behind photoelectron band (1) and (2) differ significantly in the probability to yield \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}\) ion ejection from the droplet.

Figure 4 shows the time-resolved PE spectra detected in covariance with \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}\) (n = 1 − 12). In contrast to the transient PE spectrum of all electrons in Fig. 2, only two bands show up: A broad band (α) that extends from 0.5 to 3 eV with a slow rise and fall time, and the cross-correlation band (β) originating from three-photon ionization of gas-phase Mg atoms [corresponding to band (4) in Fig. 2]. We compare covariance band (α) to the global fit results of TRPES band (2), separately in the spectral domain (Fig. 4c) and in the temporal domain (Fig. 4b). This comparison reveals good agreement in both domains, which is a strong indicator that both observables reflect the same underlying photoinduced process, especially under consideration of the difference of the experimental methods. The fact that only band (2) of the TRPES is apparent in the covariance spectrum, while band (1) is missing, shows that only the photoexcitation process represented by band (2) leads to ejection of Mg+ ions. In contrast to the dilute aggregate, photoexcitation of compact Mgn clusters (DAS1) leads to immediate promotion of electrons into the detection window for one-photon ionization of the probe pulse [band (1) in Fig. 2]. Fragmentation caused by energy conversion to nuclear motion appears much less pronounced for the compact clusters so that ion ejection from the droplet is prevented, eliminating band (1) from the covariance spectrum (Fig. 4). This finding further supports our hypothetical assignment that the two bands correspond to different species with different photoexcitation dynamics: compact Mgn clusters associated with DAS1 and the foam-like configuration associated with DAS2 and covariance band (α).

Fig. 4: Time-resolved photoelectron-photoion covariance spectrum of Mgn aggregates inside HeN.
figure 4

a Pseudocolor plot of TRPES correlated to ion masses between 16 and 300 u. Two energy bands (α) and (β) are marked. b Comparison of energy-integrated covariance band (α) to the time-dependent decay function N2 of DAS2. c Comparison of the time-integrated covariance band (α) to DAS2. Red vertical lines indicate highly excited Mg atom states44.

Full size image

An assignment of the electron signal shown in Fig. 4 to specific cluster sizes provides additional insight into the fragmentation process. To this end, Fig. 5 shows time-integrated (0.1–5 ps) electron spectra correlated to the ion complexes \({{{{\rm{Mg}}}}}_{2,3}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\), \({{{{\rm{Mg}}}}}_{4,5}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\) and \({{{{\rm{Mg}}}}}_{6,7,8}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\), with m = 0–5. The most likely energy, marked by vertical lines in Fig. 5, decreases from 2.2 eV for \({{{{\rm{Mg}}}}}_{2,3}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\) to 1.5 eV for \({{{{\rm{Mg}}}}}_{6,7,8}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\). This development shows that electronic relaxation to energetically lower states yields smaller fragments, as more electronic energy is converted to nuclear kinetic energy.

Fig. 5: Time-integrated photoelectron spectra correlated with different \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\) ion complexes.
figure 5

The photoelectron spectra were integrated in a time-window of 0.1 ps to 5 ps. The sizes of \({{{{\rm{Mg}}}}}_{{{{\rm{n}}}}}^{+}{{{{\rm{He}}}}}_{{{{\rm{m}}}}}\) complexes are indicated in the legend. For the presentation, a moving mean with a width of 0.4 eV is applied.

Full size image

Discussion

The combination of global fitting analysis of PE spectra and electron-ion covariance detection provides evidence that He droplets enable the formation of two Mgn configurations. These two configurations, represented by bands (1) and (2) in Fig. 2, show distinctively different photoexcitation responses, which is identified through the transient population of states with binding energies below 3.07 eV, corresponding to the one-photon detection window of the probe-pulse. We now discuss the energetics of the excitation processes leading to the population of these low-binding-energy states. Concerning band (1), compact Mgn clusters have a lower ionization potential than the single Mg atoms and since calculated absorption spectra of small Mgn clusters54,55 overlap with our pump photon energy, efficient pump-probe photoionization can be expected (Fig. 1c). The energetics leading to band (2) are less obvious: The transition from foam-like aggregate to compact cluster is triggered by the 31P1 atom excitation, which has a binding energy of 3.30 eV and thus lies outside the one-photon detection window. The highly excited state population of band (2) in the 0–3 eV binding energy range appears delayed, with a rise time of \({\tau }_{2}^{{{{\rm{rise}}}}}=(450\pm 180)\) fs (see Fig. 2 and band (α) in Fig. 4). This raises the question about the processes leading to population of these low-binding-energy states up to the ionization continuum. A further question that will be discussed in the following is the different fragmentation behavior of the two Mgn configurations in terms of ion ejection from the droplet.

Energy-pooling reaction

The observed population of excited states above the pump photon energy is reminiscent of energy pooling reactions, observed in mixtures of metal vapor and a noble gas56. For Mg, 457.1 nm excitation of two atoms from the 31S0 ground state to the 33P1 excited state at 4.94 eV binding energy in a He buffer gas environment leads to population of the higher states 31P1 and 43S1 at 3.30 eV and 2.54 eV binding energy, respectively57.

In our experiment, aggregates of cold Mg atoms are photoactivated in a dilute configuration with a Mg–Mg distance of 9.5 Å33. The excitation energy for the single–atom 31P1 ← 31S0 transition in this environment is slightly blue-shifted to 4.40 eV photon energy (282.5 nm), relative to the bare-atom transition at 4.35 eV (285.5 nm)44. The dynamics in the He solvation shell in response to the photoexcitation process37 leads to collapse of the dilute configuration and formation of a compact Mgn cluster. Interaction of ground-state and electronically excited Mg atoms leads to population of various states above the initially excited 31P1 state, as shown by the photoelectron signal in Fig. 4c. While population of these states cannot result from a two-photon excitation process (see above), energy transfer through collisions of two excited 31P1 atoms can populate all Mg states up to the ionization potential. We thus propose a similar energy pooling reaction, based on the excited-state potential energy curves of Mg258,59. The reaction starts with the He-mediated formation of excited \({{{{\rm{Mg}}}}}_{2}^{* }\) molecules (see also Fig. 1c):

$${{{{\mathrm{Mg}}}}}(3^1{{{{\mathrm{P}}}}}_1) + {{{{\mathrm{Mg}}}}}(3^1{{{{\mathrm{S}}}}}_0) + {{{{\mathrm{He}}}}} \rightarrow {{{{\mathrm{Mg}}}}}_2^*({\scriptstyle{1}\atop} \!{{{\Sigma}}}^+_{{{{\mathrm{u}}}}}, {\scriptstyle{1}\atop} \!{{{\Pi}}}_{{{{\mathrm{g}}}}}) + {{{{\mathrm{He}}}}}$$

Collision of \({{{{\rm{Mg}}}}}_{2}^{* }\) with another excited Mg* atom leads to population of the highly-excited states:

$${{{{\mathrm{Mg}}}}}_2^*({\scriptstyle{1}\atop} \!{{{\Sigma}}}^+_{{{{\mathrm{u}}}}}, {\scriptstyle{1}\atop} \!{{{\Pi}}}_{{{{\mathrm{g}}}}}) + {{{{\mathrm{Mg}}}}}(3^1{{{{\mathrm{P}}}}}_1) \rightarrow {{{{\mathrm{Mg}}}}}(4^3{{{{\mathrm{S}}}}}, 4^1{{{{\mathrm{S}}}}}, 3^1{{{{\mathrm{D}}}}}, ...) + 2 {{{{\mathrm{Mg}}}}}(3^1{{{{\mathrm{S}}}}}_{0})$$

In the covariance spectrum shown in Fig. 4, the photoelectron band spanning from 0 to 3 eV binding energy reveals the corresponding transient population distribution. On top of Fig. 4c, electronically excited states of Mg atoms are indicated for comparison. Since Mgn clusters up to n ~20 atoms exhibit non-metallic van der Waals-type bonding60, we refer to atomic states, which are, however, not resolved in the PE spectrum due to environmental broadening and laser bandwidth.

The proposed energy pooling reaction requires at least two excited Mg atoms in the foam-like aggregate. One can estimate the excitation probability of one Mg atom to be p1 = 0.81 ± 0.15, based on the photon absorption cross section and photon density, including experimental uncertainties (see Supplementary C). Excitation of at least two Mg atoms is therefore quite likely.

Cluster formation and fragmentation dynamics

The characteristic rise time of the transient photoelectron signal represents the highly-excited state population [N2 in Fig. 2b and band (α) in Fig. 4b]. This assignment is based on the correlated detection of electrons and ions: Only ions originating from ionization processes yielding band (α) [band (2)] electrons obtain sufficient kinetic energy to escape from the attractive solvation potential of the He droplet. Therefore, the rise of the ion-correlated photoelectron spectrum represents the transition from a foam-like Mg aggregate to a compact cluster. From parameters of the global fit population N2, a time constant of \({\tau }_{2}^{{{{\rm{rise}}}}}=(450\pm 180)\) fs for cluster formation is determined. This value agrees with the characteristic time-constant of 350 fs obtained by pump–probe strong-field ionization, which was proposed to represent the collapse of the dilute foam-like configuration30.

Concerning nuclear dynamics, including fragmentation of the Mg aggregate and acceleration of the fragments, it is important to realize that electronic energy can be converted into kinetic energy in each step of the energy pooling reaction. Initially, He atoms carry away some of the 4.4 eV photon energy stored in Mg* in order to form the \({{{{\rm{Mg}}}}}_{2}^{* }\) bond. In step two, the \({{{{\rm{Mg}}}}}_{2}^{* }\)–Mg* collision can lead to the population of various higher excited Mg* states (43S, 41S, 31D, ...). The difference in excitation energies of reactants (8.7 eV) and products is thus converted into Mg kinetic energy, ranging from ≤3.6 eV for population of the 43S state to ≤1.9 eV for population of states close to the IP (the ”≤” accounts for the kinetic energy of the He atoms)44. The released kinetic energy will increase the cluster temperature and, since the amount of energy is comparable to the binding energy of small Mgn clusters61, fragmentation and ejection from the droplets are expected. Figure 5 supports this assumption by showing that the population of lower electronic states is correlated with smaller clusters. This is in line with previous observations, where liberation of ions from the droplet (overcoming the solvation energy) is only possible through a release of kinetic energy51. Note, however, that the ionization potentials decreases with cluster size43.

The covariance measurements also reveal that the ion–to–electron ratio decreases from 52% for gas-phase Mg atoms (a characteristic value of our covariance spectrometer) to  ~15% for Mgn–HeN. This shows that the energy release is only in one out of three cases sufficient for liberation of the fragment ion from the solvation energy of the He droplet.

Relaxation of excited clusters through electron–phonon interaction

The decaying character of the TRPES signal in Fig. 2, observed for both compact [band (1)] and foam-like aggregates [band (2) in Fig. 2 and (α) in Fig. 4], indicate on fast electronic relaxation. The characteristic decay time constant of the compact Mgn cluster is τ1 = (380 ± 70) fs. Electronically excited metal clusters typically relax via electron–electron interaction on a time scale of less than  ~100 fs2,62,63. Our observation of a slower decay thus supports the assumption of a non-metallic complex64, in line with recent studies showing small magnesium clusters (n ≤ 18) are not metallic65,66. The electronic relaxation in van der Waals clusters proceeds through non-adiabatic transitions to lower electronic states with vibrational excitation. Electron–phonon coupling thus leads to electronically relaxed but vibrationally hot clusters.

For the Mgn clusters formed from the foam-like configuration, the photoelectron signal decay reveals a ten times longer time constant of τ2 = (4.0 ± 0.9) ps, compared to the compact clusters. This further points at the non-conductive van der Waals nature of Mgn clusters. The significantly slower decay might be rooted in the excitation of higher electronic states due to energy pooling, or a reduced electron–to–phonon energy transfer because the formed clusters are hot and potentially reduced in size due to fragmentation. Also, clusters (fragments) ejected from the droplet loose contact to the thermal bath, keeping them vibrationally excited for longer times. The transformation of electronic to vibrational energy within  ~10 ps leads to a reduction of the cluster fragment size, as depicted in the time-resolved mass spectra in Fig. 3. Electronic relaxation of the formed cluster also manifests as increase of the 31P1 population with a characteristic time of \({\tau }_{BG}^{low}=3.3\,{{{\rm{ps}}}}\) (see band (3) in Fig. 2 and Supplementary B). The increasing 31P1 population establishes agreement with the steady-state photoelectron spectra reported for dilute Mgn ensembles in HeN27. In photoemission experiments using nanosecond laser pulses, a strong signal from 31P1 and a relatively weak signal in the region above at 1–2 eV binding energy is observed. Considering that excitation and ionization occurs with two photons within a 10 ns time window, in combination with the picosecond lifetime of higher excited states and the increasing 31P1 population, our time-domain observations are in agreement with the steady state results.

Conclusions

Femtosecond time-resolved photoelectron and -ion spectroscopy and a subsequent global fitting analysis has been used to study the photo-induced dynamics of small magnesium clusters with emphasis on foam-like complexes. Photoexcitation of this metastable Mgn configuration leads to the contraction of the aggregate on a picosecond timescale. This contraction initiates the transient population of highly excited Mg states through energy pooling, as well as pronounced nuclear dynamics, which can clearly be resolved and distinguished from the compact Mg cluster response by inspecting the transient photoelectron signals.

The crucial prerequisite for this observation is the stabilization of Mg atoms at nanometer interatomic distance inside superfluid helium. First attempts to simulate these exceptional solvation properties of Mg atoms in HeN have led to contradictory results: While static DFT simulations predicted stable separation of two Mg atoms at 9.5 Å distance in He33, path integral Monte Carlo simulations found only equilibration to strongly bound Mg2 and Mg3 molecules36. Clarification of this discrepancy with frequency-domain spectroscopy might be challenging because the absorption spectra of small Mgn clusters are predicted to show a small dependence on the cluster size54,55, with many of them absorbing at the 4.4 eV transition of the metastable configuration32. A very recent beam depletion study of Mg clusters in He droplets only shows a weak depletion signal at the foam excitation wavelength of 282 nm (4.40 eV energy), and only for low amounts of Mg doping67. We note however, that the beam depletion method relies on energy transfer from the photoexcited chromophore to the He droplet and is thus insensitive to species that are swiftly ejected upon photoexcitation, such as the Mg monomer, which is not present in the depletion spectra67. Taking into account that \({{{{\rm{Mg}}}}}_{n}^{+}\) cluster ions are ejected from the droplet for excitation of foam aggregates, but not for excitation of compact clusters (Fig. 4), might explain the low depletion signal observed for foam excitation. Furthermore, according to our global fit analysis the foam aggregate signal is 27% weaker than the dense cluster signal, which is in agreement with the weak beam depletion signal.

Our time-domain analysis provides additional insight by revealing the photodynamical response: Photoexcitation of the foam-like Mgn configuration triggers nuclear dynamics leading to the contraction of the aggregate. This nanometer motion of Mg atoms is represented by significantly slower transient photoelectron signals, compared to the predominantly electronic dynamics of a compact van der Waals cluster. This difference in the transient response of the two Mgn configurations is the essential ingredient for distinguishing the overlapping spectra through global fitting analysis. Purely based on frequency-domain information, this distinction cannot be made. The observation that both configurations are simultaneously present within the observed MgnHeN ensemble is of relevance for cluster formation inside He droplets24. While the foam-like configuration is predicted to be favorable under steady-state conditions at the droplet temperature33, this weakly-bound aggregate can collapse during the pickup phase either by a hot (insufficiently cooled) Mg atom or when the dilute aggregate exceeds a critical size43. Cluster aggregation inside HeN, in particular the formation of foam-like configurations, is thus governed by an interplay of kinetics and thermalization. Recent time-dependent simulations, following TD-DFT68,69,70,71, particle-based69,70, or hybrid72 approaches are able to account for such kinematic effects. These simulations reveal that the growth of compact clusters can be hindered by freezing in metastable configurations, with a certain probability depending on kinematic parameters.

Metastable separation through formation of a He barrier has been predicted, in addition to Mg33, for rare-gas34,68,69,70,71,72 and halogen35 atoms, as well as larger molecules73. Experimental evidence for the existence of a metastable configuration was reported in early deflection and mass spectrometric experiments of Ar, Kr, Xe, H2O and SF6, which find that the cross section for pickup is larger than that for coagulation74. Electronic spectroscopy of anthracene–Ar clusters in HeN revealed indications for the shielding of an attached Ar atom by a helium layer75,76. Very recently, electron diffraction also found evidence for large Xe-Xe distances with He located in between71. In experiments with bulk liquid He, a very similar stabilization of atoms was reported77. Cold impurity atoms introduced into the He solvent through a supersonic jet expansion are found to condensate in an ”impurity–helium solid”, characterized by a pronounced spatial separation of the impurities78. Such structures, investigated by means of optical spectroscopy, electron spin resonance and thermometry, were recently also observed for H2O clusters79,80.

While the ability of HeN to freeze aggregates in non-equilibrium structures has long been appreciated81, stable and well-defined large-distance separation of reactants through a solvent layer barrier provides fundamentally new perspectives for bond-formation studies. Helium droplets furthermore enable stable separation of surface-located and solvated species28,31 and the possibility to switch between the two locations through electronic excitation29 or through ionization, which recently enabled the real-time observation of the primary steps of ion solvation in helium26. Taking into account the formation of exciplexes, consisting of excited atoms and He82,83,84,85, shows that helium nanodroplet isolation holds great promise to study bond formation dynamics in various species. Such studies will provide insight into elementary processes accompanying the photoinduced formation of chemical bonds, such as the transient population of highly excited states above the excitation photon energy, as observed here for the formation of Mg clusters. The proposed energy pooling process relies on merging the energy of two or more excited Mg atoms to populate highly excited states. The ability of photon upconversion to trigger photoinduced processes that lie outside the available spectrum has implications in various fields, including photomedicine86,87. Efficient upconversion requires close distances of the involved particles, as recently demonstrated with solid-state organic chromophore blends88, whereas gas-phase configurations suffer from prohibitory low yields due to large interparticle distance56,57. The nanometer confinement provided by He droplets, together with flexible opportunities for generating tailor-made aggregates, thus provides a new and promising route to characterize the underlying energy and charge-transfer dynamics.

Methods

Following a previous approach37, helium nanodroplets with a mean radius of 5.3 nm (13500 He atoms per droplet) are loaded with about ten Mg atoms (see Supplementary A for further details). Using an amplified Ti:sapphire laser (800 nm center wave length, 25 fs pulse duration), short pulses are generated and split into a pump and probe arm. The cross-correlation signal of the pump and probe pulse has a duration of (45 ± 3) fs. The pump pulse is tuned to 282 nm (4.40 eV photon energy) by an optical parametric amplifier, in order to trigger the collapse of the foam-like Mgn aggregate through Mg 31P1 ← 31S0 excitation, which appears slightly blue-shifted in the aggregate32 relative to the bare atom transition44 (see Fig. 1a). The probe pulse at 404 nm (3.07 eV), obtained through frequency doubling, ionizes the system and photoelectron spectra are recorded with a magnetic bottle time-of-flight spectrometer. The time-resolved variation of these photoelectron spectra, recorded through variation of the pump–probe time delay, provides insight into the evolution of excited state populations. Applying a high voltage pulse to the repeller electrode about 100 ns after the laser pulses accelerates the remaining ions towards the detector and thus allows for a simultaneous detection of electrons and ions in each laser shot89. This procedure enables a statistical analysis of covariances between electron energy and ion species45,46,47.