An open-source family of large encoder-decoder foundation models for chemistry

Abstract

The use of foundation models has extended from natural language processing to molecular modeling. In this context, large-scale pre-training strategies have been applied to chemical language models to enable representation learning across diverse tasks. Here we introduce a family of encoder-decoder chemical foundation models pre-trained on a curated dataset of 91 million molecular sequences from PubChem. These models support a range of applications, including property estimation and reaction outcome prediction. We evaluate two model variants across several benchmark datasets and show that they match or exceed existing approaches. We also assess the structure of the learned representations and find that the embedding space supports few-shot learning and separates molecules based on chemically relevant features. This structure appears to result from the decoder-based reconstruction objective used during pre-training. These findings suggest that the proposed models can serve as general-purpose tools for molecular analysis and reasoning with minimal supervision.

Introduction

Understanding molecular properties is crucial for accelerating discoveries in different fields, including drug development and materials science¹. Traditional methods rely on labor-intensive trial-and-error experiments, which are both costly and time-consuming². However, recent advances in deep learning have enabled the use of foundation models to predict molecular properties and generate molecule candidates^3,4,5,6,7,8, marking significant progress in scientific exploration.

The introduction of large-scale pre-training methodologies for chemical language models (LMs) represents a significant advancement in cheminformatics^9,10,11. These methodologies have demonstrated impressive results in challenging molecular tasks such as predicting properties and generating molecules¹². The success of these models can be attributed to their ability to learn contextualized representations of input tokens through self-supervised learning on large unlabeled corpora¹³. This methodological approach typically involves two phases: pre-training on unlabeled data followed by fine-tuning on specific downstream task¹⁴. By reducing the reliance on annotated datasets, this approach has broadened our understanding of chemical language representations¹⁵.

Simplified Molecular-Input Line Entry System, SMILES, provide natural graphs that encode the connectivity information from the line annotations of molecular structures¹⁶. SMILES defines a character string representation of a molecule by performing a depth-first pre-order spanning tree traversal of the molecular graph, generating symbols for each atom, bond, tree-traversal decision, and broken cycles¹⁷. Therefore, the resulting character string corresponds to a flattening of a spanning tree of the molecular graph. SMILES is widely adopted for molecular property prediction as SMILES is generally more compact than other methods of representing structure, including graphs¹⁸. There are billions of SMILES available on different open-sources repositories¹⁹. However, most SMILES sequences do not belong to well-defined molecules²⁰. Alternative string-based representations exist, such as SELFIES. However, focusing on molecular optimization tasks on the learned representation space, suggested no obvious shortcoming of SMILES with respect to SELFIES in terms of optimization ability and sample efficiency²¹. The quality of the pre-training data plays a more important role on the outcome of the foundation model^7,22.

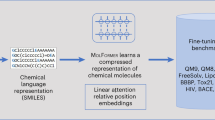
Towards this direction, we present a novel family of molecular encoder-decoder foundation models, denoted as SMI-TED_289M. Our SMI-TED_289M encoder-decoder foundation model was obtained using a transformer-based molecular tokens encoder model aligned with an encoder-decoder mechanism trained on a large corpus of 91 million carefully curated molecules from PubChem²³, SMI-TED_289M introduces novel pooling function that differs from standard max or mean pooling techniques, and allows SMILES reconstruction preserving its properties. Figure 1 illustrates the general architecture of SMI-TED_289M. Our main contributions are:

• We pre-train a large-scale family of encoder-decoder molecular open-source foundation models, denoted as SMI-TED_289M, on over 91 million molecules carefully curated from PubChem²³.

• Our SMI-TED_289M family of foundation models encompasses two distinct configurations: base, which has 289 million parameters; and the Mixture-of-O_SMI-Experts, MoE-O_SMI, characterized by a composition of 8 × 289M parameters.

• We perform extensive experimentation on several classification and regression tasks from 11 benchmark datasets, covering quantum mechanical, physical, biophysical, and physiological property prediction of small molecules. We also evaluate the reconstruction capacity of our SMI-TED_289M considering the MOSES benchmarking dataset²⁴. We also conducted high-throughput experiments on Pd-catalyzed Buchwald–Hartwig C-N cross-coupling reactions, predicting reaction yields. Furthermore, a study investigating the embedding created by SMI-TED_289M and few-shot learning is also provided, indicating compositionality of the learned molecular representations. We also provide a structure–property relationship study over the generated embedding space.

Fig. 1: Overview of the SMI-TED_289M model architecture.

This figure illustrates the general architecture of the base SMI-TED_289M model.

Our results section demonstrates state-of-the-art performance of SMI-TED_289M on different tasks, molecular properties prediction, molecule reconstruction, and an efficient metric for molecular latent space. Compositionality of the latent space suggests strong potential for chemical reasoning tasks. The SMI-TED_289M family consists of two main variants (289M, and 8 × 289M), offering flexibility and scalability for different scientific applications.

Benchmarking overview

To assess the performance and generalization of SMI-TED, we designed a suite of benchmarks that each target specific hypotheses regarding our model’s capabilities. In this section, we introduce all the benchmarks in one place, explain the rationale behind their selection, and describe what aspect of our model they are intended to validate.

Benchmark selection and validation hypotheses

Our evaluation framework is built upon four key benchmarks:

• MoleculeNet Datasets: We employ 11 datasets from MoleculeNet²⁵-6 for classification tasks and 5 for regression tasks-to assess the model’s predictive accuracy and generalization across diverse molecular properties. By using the same train/validation/test splits as the original benchmark, we ensure consistency and unbiased evaluation.

• MOSES Benchmarking Dataset: To test the reconstruction and generative abilities of SMI-TED, we use the MOSES dataset²⁴. This benchmark, with its unique scaffold test set, validates the hypothesis that our model can generate novel molecular scaffolds not seen during training.

• Pd-Catalyzed Buchwald–Hartwig Reaction Experiments: High-throughput experiments on these reactions²⁶ evaluate the model’s capacity to predict reaction yields over a complex combinatorial space. This benchmark confirms the model’s effectiveness in handling high-dimensional experimental data.

• Latent Space Evaluation: By analyzing structure–property relationships-such as the electron-donating effects of nitrogen substituents on HOMO energy-we validate the ability of our model to generate a meaningful and interpretable latent space that captures subtle chemical phenomena.

Results

Experiments

To evaluate the effectiveness of our proposed methodology, we conducted experiments using a set of 11 datasets sourced from MoleculeNet²⁵ as detailed in the Supplementary Table 1. Specifically, we evaluated 6 datasets for classification task and 5 datasets for regression tasks. To ensure an unbiased assessment, we maintained consistency with the original benchmark by adopting identical train/validation/test splits for all tasks²⁵. We conducted the experiments considering 10 different seeds in other to guarantee the robustness of the approach.

To assess the reconstruction/decoder capacity of SMI-TED_289M we considered the MOSES benchmarking dataset²⁴. The MOSES dataset contains 1,936,962 molecular structures. For experiments, we consider the split proposed by²⁴, where the dataset was divided into a training, test and scaffold test sets containing around 1.6M, 176k, and 176k molecules respectively. The scaffold test set contains unique Bemis-Murcko scaffolds that were not present in the training and test sets. We use this set to assess how well the model can generate previously unobserved scaffolds.

We also conducted high-throughput experiments on Pd-catalyzed Buchwald–Hartwig C-N cross-coupling reactions, measuring the yields for each reaction as described in²⁶. The experiments utilized three 1536-well plates, covering a matrix of 15 aryl and heteroaryl halides, four Buchwald ligands, three bases, and 23 isoxazole additives, resulting in a total of 3955 reactions. We employed the same data splits as in²⁶ to assess our model’s performance with training sets of varying sizes. An evaluation of the embedding space of SMI-TED_289M is also provided, it uses the compositional molecules to evaluate the capability of the model to generate metric latent spaces. An experiment over structure–property relationships in molecular latent space represention is also conducted. In this analysis, we examined the electron-donating effects of nitrogen substituents on HOMO energy, and the ability of the generated latent space to capture such phenomena.

Comparison with SOTA on MoleculeNet benchmarking tasks

Results for classification tasks

The analysis investigates the comparative efficacy of SMI-TED_289M in its fine-tuned and pre-trained states versus state-of-the-art algorithms for molecular properties classification, as demonstrated in Table 1.

Table 1 displays the performance of different advanced methods on different benchmarking datasets used for molecule classification tasks. SMI-TED_289M consistently shows superior performance in four out of six datasets. Interestingly, using SMI-TED_289M with its initial settings provided comparable results to SOTA methods available. However, fine-tuning SMI-TED_289M further enhances its performance across all datasets. This indicates SMI-TED_289M’ potential for accurate molecule classification, with potential for further optimization through fine-tuning.

Table 1 Methods and performance for the classification tasks of MoleculeNet benchmark datasets

Results for regression tasks

Next, we applied SMI-TED_289M for prediction of chemical properties. The performance results across five challenging regression benchmarks, namely QM9, QM8, ESOL, FreeSolv, and Lipophilicity, are summarized in Table 2.

Table 2 Methods and performance for the regression tasks of MoleculeNet benchmark datasets

Results presented in Table 2 indicates that SMI-TED_289M presents superior results when compared to the state-of-the-art, outperforming its competitors in all the 5 datasets considered. To fine-tune SMI-TED_289M is important to achieve state-of-the-art results in regression datasets, due to the complexity of such tasks. Table 2 elucidates the superiority of SMI-TED_289M over the QM9 dataset. The QM9 dataset is composed by 12 tasks regarding to the quantum properties of molecules. A detailed overview over the results for QM9 are depicted in the Supplementary Table 9.

Mixture-of-O_SMI-Experts perform studies

This study compare the results of MoE-O_SMI against single SMI-TED_289M models (pre-trained and fine-tuned). MoE-O_SMI is composed by 8 × 289M fine-tuned models for each specific task, we set k = 2, which means that 2 models are activated every step. The results for this study are detailed in the Supplementary Table 10.

The results from the study indicate that MoE-O_SMI consistently achieves higher performance metrics compared to single SMI-TED_289M models (Pre-trained and Fine-Tuned) models across different tasks, especially in regression tasks where it improved results in all scenarios. These findings suggest that the MoE approach effectively leverages specialized sub-models to capture diverse patterns in the data, leading to improved accuracy in molecular property predictions. The mixture-of-experts approach serves as an efficient solution to scale single models and enhance performance for various tasks due to its ability to allocate specific tasks to different experts, optimizing single model’s overall predictive capabilities.

Decoder evaluation over MOSES benchmarking dataset

Next, we compared SMI-TED_289M with different baseline models, such as the character-level recurrent neural network (CharRNN)²⁴, SMILES variational autoencoder (VAE)²⁴, junction tree VAE (JT-VAE)²⁷, latent inceptionism on molecules (LIMO)²⁸, MolGen-7b²⁹, and GP-MoLFormer³⁰. All baseline performances are reported on their corresponding test set consisting of 176k molecules. Standard metrics for evaluating model-generated molecules are reported in the Supplementary Table 11.

When compared to baselines, SMI-TED_289M is equally performant in generating unique, valid, and novel molecules that share high cosine similarity with the corresponding reference molecules at the fragment (Frag) level, consistent with low Fréchet ChemNet Distance (FCD). At the same time, SMI-TED_289M generates molecules with high internal diversity (IntDiv), i.e., average pairwise dissimilarity. The scaffold cosine similarity (Scaf) and similarity to the nearest neighbor in the test set (SNN) of SMI-TED_289M is superior to the baselines demonstrating that SMI-TED_289M is effective in generating molecules of varying structures and quality compared to baseline methods.

Reaction-yield prediction

Previously, we were able to show that the proposed SMI-TED_289M model was able to perform compared to single tasks transformer-based methods. Chemical reactions in organic chemistry are described by writing the structural formula of reactants and products separated by an arrow, representing the chemical transformation by specifying how the atoms rearrange between one or several reactant molecules and one or several product molecules. Machine learning methods are used to infer chemical reaction outcomes, such as yield, from data generated through high-throughput screening experiments.

We assessed this architecture against state-of-the-art methods using a high-throughput dataset of Buchwald–Hartwig cross-coupling reactions, focusing on predicting reaction yields²⁶. This involves estimating the percentage of reactants converted into products. Our evaluation adhered to the schema and data divisions outlined in²⁶. Table 3 presents the results for the SMI-TED_289M model and compares its performance with existing state-of-the-art approaches.

Table 3 Performance of SMI-TED_289M compared with the state of the art in reaction-yield prediction on experimentally determined yields of Buchwald–Hartwig reactions through HTEs

The results presented in Table 3 demonstrate the superiority of the proposed SMI-TED_289M foundation model when benchmarked against state-of-the-art methods, including gradient-boosting and fingerprint-based approaches (DRFP)³¹, a DFT-based random forest model (DFT)³¹, and transformer-based models like Yield-BERT³² and its augmented variant, Yield-BERT(aug.)³², and MSR2-RXN³³. The performance of the Mamba-based model can be attributed to its pre-training on an expansive dataset of 91 million curated molecules, which provides a robust foundation of chemical knowledge that significantly enhances its predictive capabilities. This pre-training enables the model to achieve high accuracy even with limited training data, as evidenced by its sustained performance when trained on just 2.5% of the available samples-a scenario where task-specific models experience a marked decline in accuracy. To ensure the robustness of our model, we conducted each experiment with 10 different random seeds.

Latent space study

Molecular compositionality

We conducted an experiment to investigate the structure of the latent space created by Large Language Models in the context of Chemistry. Molecular structures are composable from fragments, motifs, and functional groups. The composability of structure often translates into compositionality of structure–property relations, which is exemplified by powerful group contribution methods in chemical sciences. Compositionality of the learnt representation, however, does not follow automatically from the structure of the data and requires some combination of the learning architecture and learning constraints to emerge. Our approach was to utilize simple chemical structures that can be easily understood by humans, allowing us to anticipate relationships between elements, and examine the latent space for similar patterns. We constructed a dataset consisting of six families of carbon chains: ${{\mathcal{F}}}=\{CC,CO,CN,CS,CF,CP\}$. For each family, we generated a sequence of molecules by incrementally adding carbon atoms to the end of the SMILES string, up to a maximum of ten carbon atoms. For example, the family CO consists of {CO, CCO, ⋯  , CCCCCCCCCCO}. According to the domain expert’s intuition consistent with the theory of chemical structure, in a metric space, such sequences should exhibit a hierarchical distance structure, where the distance between consecutive elements is smaller than the distance between elements with a larger difference in carbon count, i.e., $| \overline{{C}_{n}{{{\mathcal{F}}}}_{i}}-\overline{{C}_{n+1}{{{\mathcal{F}}}}_{i}}| < | \overline{{C}_{n}{{{\mathcal{F}}}}_{i}}-\overline{{C}_{n+2}{{{\mathcal{F}}}}_{i}}|$. Here, n represents the number of carbon atoms, and $\overline{\,{\mbox{SMILES}}\,}$ denotes the projection of the SMILES string onto the embedding space.

First, we generated the embeddings for two different encoders, the MoLFormer and SMI-TED_289M, and used the t-SNE³⁴ projection technique to generate figures (Fig. 2) for visually inspecting the spaces. It is worth noting that the SMI-TED_289M generated an embedding space that creates a nice separation of each family and respects the hierarchical distance structure, almost creating a linear relationship between each family. To quantify this relationship, we created a dataset of triples of SMILES, ${{\mathcal{T}}}=\{({C}_{n}{{{\mathcal{F}}}}_{CC},{C}_{k}{{{\mathcal{F}}}}_{i},{C}_{n+k}{{{\mathcal{F}}}}_{i})\ | \ 0 < n\le 4,0 < k\le 5\}$, for the six families ${{{\mathcal{F}}}}_{i}$, resulting in six sub-datasets with 20 elements each, e.g., (CC, CCO, CCCCO) is one element of the subset of type CO where n = 1, k = 2. Then, we randomly selected one triple from each subset to feed a linear regression calculating α, β, and B₀ such that $\alpha \cdot \overline{{C}_{n}{{{\mathcal{F}}}}_{CC}}+\beta \cdot \overline{{C}_{k}{{{\mathcal{F}}}}_{i}}+{B}_{0}=\overline{{C}_{n+k}{{{\mathcal{F}}}}_{i}}$. We validated the linearity using the remaining 114 elements. The linear regression on the MoLFormer embeddings resulted in R² = 0.55 and MSE = 0.237, while on our model embeddings, it resulted in R² = 0.99 and MSE = 0.002.

Fig. 2: Comparison of small molecule embedding projections using t-SNE.

The figure shows the t-SNE projection of 60 small molecule embeddings. Color distinguishes between families, and point size represents the number of carbon atoms in the chain. a MoLFormer embeddings; b SMI-TED_289M embeddings.

We evaluated our encoder-decoder model using a few-shot learning process, where we input a few examples of triples, such as those mentioned earlier, to calculate α, β, and B₀. We then use these parameters to generate embeddings for subsequent SMILES pairs and recreate the SMILES strings. To validate our approach, we tested the process on the same dataset of triples. We calculated the molecule similarity between the expected and generated results using the Tanimoto score (TS)³⁵. We repeated this test with different combinations of input triples, yielding similar results.

For example, when using the input triples [CC + CCCS = CCCCCS, CCCCC + CCCS = CCCCCCCCS] and querying all pairs in our subsets, we obtained a mean TS of 0.52. It is interesting to note that the top two similar results were CC + CCCCCS = CCCCCS with TS = 0.92 and CC + CCCCCO = CCCCCO with TS = 0.92. For more detailed results see our Supplementary Information section.

Historically, group contribution was introduced in supervised learning context of structure–property relations. Our simple tests indicate that SMI-TED_289M derived an equivalent of group contribution method purely from self-supervised learning of molecular structure. Signs of the emergence of compositionality of the learned molecular representations suggest strong potential of SMI-TED_289M for reasoning applications. Further studies consistent with methodologies of compositionality analysis in natural languages are required to make stronger statements.

Structure–property relationship

Accurate representation of structure–property relationships in molecular data remains a significant challenge in computational chemistry. In particular, it is important to assess whether latent spaces generated by unsupervised pre-training can reflect chemical phenomena without subsequent task-specific fine-tuning. To address this issue, we compared two models: SMI-TED, an encoder–decoder architecture, and MoLFormer, an encoder-only model, using the QM9 test dataset.

Our analysis shows that nitrogen-containing molecules comprise 9.10% of the overall dataset, yet they account for 32.81% of the top 10% of molecules ranked by HOMO energy. This enrichment is consistent with classical chemical theory and indicates that the latent space encodes the electron-donating effects of nitrogen substituents. Figure 3 presents t-SNE projections of the latent spaces: in the SMI-TED model, nitrogen-containing compounds form clusters in regions associated with elevated HOMO values, whereas the latent space of MoLFormer displays a different organization. Quantitative evaluation using the Davies–Bouldin index yields a value of 2.82 for SMI-TED compared to 4.28 for MoLFormer, indicating that the SMI-TED latent space exhibits lower intra-cluster variance and higher inter-cluster separation when partitioned by the presence of nitrogen-containing groups.

Fig. 3: Visualization of HOMO energy embeddings for the top 10% ranked molecules.

The figure shows the t-SNE projection of the top 10% of molecules ranked by HOMO energy embeddings. Color distinguishes HOMO energy values, and the different markers represent the presence or absence of nitrogen atoms. a MoLFormer embeddings; b SMI-TED_289M embeddings.

A possible interpretation is that the inclusion of a decoder in SMI-TED introduces a reconstruction objective during pre-training, which enforces the encoding of a more comprehensive set of structural features. This additional constraint appears to promote the formation of a latent space that more effectively links molecular structure to properties such as HOMO energy. In contrast, the encoder-only architecture of MoLFormer may not impose the same constraints, resulting in a less organized latent representation with respect to functional group clustering.

In summary, the pre-trained SMI-TED model captures relevant structure–property relationships from SMILES data. The combination of quantitative metrics and t-SNE visualizations supports the conclusion that an encoder–decoder architecture, by incorporating a reconstruction process, yields a latent space with improved organization.

Discussion

This paper introduces the SMI-TED_289M family of chemical foundation models, which are pre-trained on a curated dataset of 91 million SMILES samples from PubChem. The SMI-TED_289M family includes two configurations: the base model with 289 million parameters and the MoE-O_SMI model, which consists of 8 × 289M parameters.

The performance of these models was evaluated through an extensive experimentation on different tasks, including molecular properties classification and prediction. Our approach achieved state-of-the-art results in most tasks, particularly in predicting molecular quantum mechanics, where it achieved the best or second-best results in 11 out of 12 tasks of the QM9 dataset.

One key observation is the model’s robustness across various data splits for reaction-yield prediction, particularly in low-resource settings where only a small fraction of the dataset is used for training. This resilience underscores the importance of leveraging large-scale pre-training to encode generalized chemical knowledge, which can then be fine-tuned for specific tasks like reaction yield prediction. In contrast, models that are tailored specifically for a given task tend to overfit to the nuances of the training data and struggle to generalize when the training set size is reduced, highlighting a critical limitation in their design.

The comparative analysis between the SMI-TED_289M model and other state-of-the-art methods for reaction-yield prediction also sheds light on the limitations of traditional approaches like DFT-based models, which, despite their theoretical grounding in quantum chemistry, may not capture the full complexity of reaction mechanisms in practical scenarios. Similarly, while transformer-based models like Yield-BERT and its augmented variant exhibit strong performance, they fall short of the SMI-TED_289M model, particularly in low-data regimes, indicating that the sheer scale and diversity of the pre-training data play a pivotal role in achieving superior results.

We also investigated the structure of the latent space created by these language-based foundation models, using simple chemical structures for clarity. SMI-TED_289M generated an embedding space that creates a nice separation of each family and respects the hierarchical distance structure, almost creating a linear relationship between each family. The encoder-decoder model’s capabilities in few-shot learning were assessed by generating embeddings from a few example triples and using them to recreate SMILES strings, achieving a Tanimoto score of 0.92 in the best case.

In addition to this, our investigation of the latent space structure further supports the model’s capability to capture relevant chemical information. Analysis of the QM9 dataset demonstrates that although nitrogen-containing molecules account for only 9.10% of the overall dataset, they constitute 32.81% of the top decile when molecules are ranked by HOMO energy. t-SNE projections indicate that, in the SMI-TED latent space, nitrogen-containing compounds cluster distinctly in regions associated with elevated HOMO values. Quantitatively, the Davies–Bouldin index is 2.82 for SMI-TED compared to 4.28 for MoLFormer, an encoder-only model, indicating that the latent space of SMI-TED exhibits lower intra-cluster variability and greater inter-cluster separation based on the presence of nitrogen-containing groups.

A plausible interpretation of these findings is that the inclusion of a decoder in the SMI-TED architecture imposes a reconstruction objective during pre-training, which enforces the encoding of a more comprehensive set of structural features. This additional constraint likely yields a latent representation that more effectively correlates molecular structure with properties such as HOMO energy. In contrast, an encoder-only architecture may not capture these details as effectively, resulting in a less organized latent space.

Collectively, these results suggest that the pre-trained SMI-TED model effectively captures relevant structure–property relationships from SMILES data. The integration of quantitative metrics and t-SNE visualizations supports the hypothesis that an encoder-decoder architecture, through the incorporation of a reconstruction objective, produces a more organized latent space. This enhanced organization has significant implications for the development of computational tools in molecular design, as models that combine both encoding and reconstruction processes may offer improved performance in downstream tasks such as property prediction and clustering in chemical space.

Recent developments in autonomous scientific discovery have emphasized the role of foundation models as components in multi-agent and graph-reasoning systems. In this context, the SMI-TED_289M model has been integrated into the dZiner agent, a language model-based system for inverse molecular design³⁶. dZiner generates candidate molecular structures conditioned on desired property profiles and employs SMI-TED to infer molecular properties from SMILES representations in real time. The agent supports both closed-loop and human-in-the-loop workflows, enabling iterative screening under property and feasibility constraints.

Methods

This section presents an overview of the proposed SMI-TED_289M foundation model for small molecules. Here, we outline the process of collecting, curating, and pre-processing the pre-train data. Additionally, we describe the token encoder process and the SMILES encoder-decoder process. Finally, we explain the Mixture-of-O_SMI-Experts approach used to scale the base model.

Pre-training data

The pretraining data originated from the PubChem data repository, a public database containing information on chemical substances and their biological activities²³. Initially, 113 million SMILES strings were collected from PubChem. These molecular strings underwent deduplication and canonicalization processes to ensure uniqueness³⁷. Subsequently, a molecular transformation was conducted to verify the validity of the molecules derived from the unique SMILES strings, resulting in a set of 91 million unique and valid molecules.

To construct the vocabulary, we employed the molecular tokenizer proposed by³⁸. All 91 million molecules curated from PubChem were utilized in the tokenization process, resulting in a set of 4 billion molecular tokens. The unique tokens extracted from the resulting output provided a vocabulary of 2988 tokens plus 5 special tokens. In comparison, MoLFormer, trained on 1 billion samples with minimal curation, presented a vocabulary of 2362 tokens using the same tokenization process¹². This suggests an improvement in the vocabulary model due to our curation process.

Model architecture

We conduct training for SMI-TED_289M model employing a deep-bidirectional-transformers-based encoder³⁹ for tokens and an encoder-decoder architecture to compose SMILES. The hyper-parameters of SMI-TED_289M base model are detailed in Table 4.

Table 4 SMI-TED_289M base architecture specificity

To optimize the relative encoding through position-dependent rotations R_m of the query and keys at position m, the SMI-TED_289M uses a modified version of the RoFormer⁴⁰ attention mechanism. These rotations can be implemented as pointwise multiplications and do not significantly increase computational complexity as shown in Eq. (1).

$$Attentio{n}_{m}(Q,K,V)=\frac{{\sum }_{n = 1}^{N}\left\langle \varphi ({R}_{m}{q}_{m}),\varphi ({R}_{n}{k}_{n})\right\rangle {v}_{n}}{\mathop{\sum }_{n = 1}^{N}\left\langle \varphi ({R}_{m}{q}_{m}),\varphi ({R}_{n}{k}_{n})\right\rangle }$$

(1)

where Q, K, V are the query, key, and value respectively, and φ is a random feature map.

We start with a sequence of tokens extracted from SMILES, each embedded in a 768-dimensional space. The encoder-decoder layer is designed to process molecular token embeddings, represented as ${{\bf{x}}}\,\in {{\mathbb{R}}}^{D\times L}$, where D denotes the maximum number of tokens and L represents the embedding space dimension. We limited D at 202 tokens, as 99.4% of molecules in the PubChem dataset contain fewer tokens than this threshold.

In encoder-only models, a mean pooling layer is typically employed to represent tokens as SMILES in the latent space. However, this approach is limited by the lack of a natural inversion process for the mean pooling operation. To overcome this limitation, we aim to construct a latent space representation for SMILES by submersing the x in a latent space, denoted as z, as described in Eq. (2).

$${{\bf{z}}}=\left(\,{\mbox{LayerNorm}}\,\left(\,{\mbox{GELU}}\,\left({{\bf{x}}}{{{\bf{W}}}}_{1}+{{{\bf{b}}}}_{1}\right)\right)\right){{{\bf{W}}}}_{2},$$

(2)

where ${{\bf{z}}}\in {{\mathbb{R}}}^{L}$, ${{{\bf{W}}}}_{1}\in {{\mathbb{R}}}^{D\times L}$, ${{{\bf{b}}}}_{1}\in {{\mathbb{R}}}^{L}$, ${{{\bf{W}}}}_{2}\in {{\mathbb{R}}}^{L\times L}$, with L denoting the latent space size (specifically, L = 768) and D representing the original feature space size (namely, D = 202). Subsequently, we can immerse z back by calculating Eq. (3).

$$\hat{{{\bf{x}}}}=\left(\,{\mbox{LayerNorm}}\,\left(\,{\mbox{GELU}}\,\left({{\bf{z}}}{{{\bf{W}}}}_{3}+{{{\bf{b}}}}_{3}\right)\right)\right){{{\bf{W}}}}_{4}$$

(3)

where $\hat{{{\bf{x}}}}\in {{\mathbb{R}}}^{D\times L}$, ${{{\bf{W}}}}_{3}\in {{\mathbb{R}}}^{L\times L}$, ${{{\bf{b}}}}_{3}\in {{\mathbb{R}}}^{L}$, ${{{\bf{W}}}}_{4}\in {{\mathbb{R}}}^{L\times D}$.

A language layer (decoder) is used to process $\hat{{{\bf{x}}}}$, where it applies non-linearity and normalization, and projects the resulting vector into a set of logits over the vocabulary, which can then be used to predict the next token in the molecular⁴¹.

Pre-training strategies

Pre-training of SMI-TED_289M was performed for 40 epochs through the entire curated PubChem dataset with a fixed learning rate of 1.6e−4 and a batch size of 288 molecules on a total of 24 NVIDIA V100 (16G) GPUs parallelized into 4 nodes using DDP and torch run. It involves two distinct phases: i) Learning of token embeddings through a masking process; ii) Subsequently, the token embeddings are mapped into a common latent space that encapsulates the entire SMILES string. This latent space not only facilitates the representation of the SMILES but also enables the reconstruction of both individual tokens and complete SMILES strings. Consequently, the pre-training process involves two separate loss functions: one for the token embeddings, which is based on the masking process, and another for the encoder-decoder layer, which focuses on the reconstruction of tokens. Two pre-training strategies are employed:

• In phase 1, the token encoder is initially pre-trained using 95% of the available samples, while the remaining 5% is reserved for training the encoder-decoder layer. This partitioning is necessary as the token embeddings may encounter convergence difficulties in the initial epochs, which could adversely affect the training of the encoder-decoder layer.

• In phase 2, once the token embeddings layer has achieved convergence, the pre-training process is expanded to utilize 100% of the available samples for both phases. This approach leads to an enhancement in the performance of the encoder-decoder layer, particularly in terms of token reconstruction.

For encoder pre-training we use the masked language model method defined in³⁹. Initially 15% of the tokens are selected for possible learning. From that selection, 80% of the tokens are randomly selected and replaced with the [MASK] token, 10% of the tokens are randomly selected to be replaced with a random token, while the remaining 10% of the tokens will be unchanged.

The adoption of different pre-training strategies has proven instrumental in enhancing the efficiency of our model, as evidenced by improvements observed in the loss functions.

Mixture-of-O_SMI-Experts

The Mixture-of-O_SMI-Experts, MoE-O_SMI comprises a set of n “expert networks” labeled as E₁, E₂, …, E_n, augmented through a gating network denoted as G, tasked with generating a sparse n-dimensional embedding space optimized for a downstream task as illustrated by Fig. 4.

Fig. 4: Architecture of the Mixture-of-O_SMI-Experts model.

Mixture-of-O_SMI-Experts for downstream tasks.

Here, we map each SMILES into tokens and then convert the input tokens to the latent space. A mean pooling method is applied to all token embeddings in order to produce a meaningful embedding of the molecule. The architecture is equipped with a router module responsible for determining the n experts that will be activated, refining the adaptability and specialization of the system. Let G(x) and ${E}_{i}(\hat{x})$ denote the output of the gating network and the output of the i-th expert network, respectively, for a given input $\hat{x}$ of SMILES and x, which is the embeddings space, following a similar notation as proposed in ref. ⁴². The resulting output y is defined as Eq. (4):

$$y=\mathop{\sum }_{i=1}^{n}G{(x)}_{i}{E}_{i}(\hat{x})$$

(4)

The resulting embedding space y is used to train a task-specific feed-forward network, where the loss function is chosen according to the studied downstream task. The optimization process refines the parameters of G(x). If the gating vector is sparse, we can use softmax over the Top-K logits of a linear layer⁴² defined as Eq. (5).

$$G(x):=Softmax(TopK(x\cdot Wg))$$

(5)

where (TopK(ℓ))_i ≔ ℓ_i if ℓ_i is among the TopK coordinates of logits $\ell \in {{\mathbb{R}}}^{n}$ and (TopK(ℓ))_i ≔ ∞ otherwise. The router layer retains only the top k values, setting the remaining values to  − ∞ (which effectively assigns corresponding gate values as 0). This sparsity-inducing step serves to optimize computational efficiency⁴³. Here, we define MoE-O_SMI as n = 8 and k = 2, which means that MoE-O_SMI is composed by 8 × SMI-TED_289M models, which 2 models are activated through the router each round.