Introduction

The seminal 1935 paper of Einstein–Podolsky–Rosen1 (EPR) is without question one of the most important and controversial papers in quantum mechanics, given the variety and intensity of discussions on foundational aspects that it triggered. Interestingly, while hidden variable theories2 and quantum nonlocality3,4 are perhaps the topics that historically have most commonly been associated with the EPR paper these two aspects are not explicitly addressed in the paper itself. Rather, EPR intended to question the completeness of quantum theory by proposing that, within what they claim is a reasonable criterion of reality, one can make predictions with certainty about the values of two non-commuting observables in any one of two subsystems described by a continuous variable version of what is now called the EPR state.

In terms of Bohm’s spin-1/2 variant5, the EPR argument goes like this: consider the predictions made by two space-like separated observers, Alice and Bob, about the outcomes of measurements carried out on the bipartite EPR-Bohm-singlet state: when Alice measures the Pauli operator \({\hat{\sigma }}_{z}\) on particle one with the result \({s}_{z}^{(1)}\) and Bob measures \({\hat{\sigma }}_{z}\) on particle two with the result \({s}_{z}^{(2)}\), Alice and Bob can predict with certainty the outcome of the other’s measurement since in this case \({s}_{z}^{(1)}=-{s}_{z}^{(2)}\). Similarly, since the singlet state exhibits the same correlations in any measurement basis, if the Pauli operator \({\hat{\sigma }}_{x}\) is measured by both observers, with results \({s}_{x}^{(1)}\) and \({s}_{x}^{(2)}\), Alice and Bob can predict with certainty the outcome of the others measurement using \({s}_{x}^{(2)}=-{s}_{x}^{(1)}\). Given the above facts, now consider the situation in which say, Alice measures \({\hat{\sigma }}_{x}\) on particle one, and Bob measures \({\hat{\sigma }}_{z}\) on particle two; then, the EPR claim is that Bob’s prediction about \({s}_{z}^{(1)}\) and Alice’s predictions about \({s}_{x}^{(2)}\), namely,

$${s}_{z}^{(1)}=-{s}_{z}^{(2)},$$
(1)
$${s}_{x}^{(2)}=-{s}_{x}^{(1)},$$
(2)

should still be valid simultaneously given the space-like separation of the measurements. In other words, the EPR argument states that knowledge of the outcomes \({s}_{x}^{(1)}\) and \({s}_{z}^{(2)}\) allows us to assign elements of reality to the values \({s}_{x}^{(2)}\) and \({s}_{z}^{(1)}\), respectively, and therefore to the simultaneous values of two non-commuting observables, \({\hat{\sigma }}_{x}\) and \({\hat{\sigma }}_{z}\), of each particle.

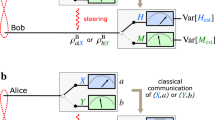
As stated in the original EPR paper, the verification of the predictions in Eqs. (1) and (2) is beyond experimental reach given their interpretation of the measurement process involved. Indeed, in order to test the simultaneous validity of Eqs. (1) and (2), the observers would need to perform simultaneous or sequential measurements of non-commuting observables using for example the scheme shown in Fig. 1a. This scheme is forbidden in the standard approach to quantum mechanics, in which the measurements are understood as projective measurements, which involve a strong coupling between system and measurement device, and therefore drastically perturb the state. However, these objections can be overcome if the measurements are understood to be weak measurements (WM)6,7, which minimally disturb the system. These kinds of measurements have proven to be a useful tool for explaining certain counter-intuitive and paradoxical behaviors predicted by the quantum theory. For example, WMs have been applied to experimentally prove and explain the three-box8 and Hardy’s9,10,11 paradoxes, to reconstruct Bohmian-like trajectories12, to measure anomalous probabilities in Bell-like tests13, to perform sequential or simultaneous measurements on the same particle14,15, to test measurement disturbance and complementary relations16, and more recently, to construct ontological models for quantum theory17. Given this broad scope of applications for the WM scheme, it is therefore interesting to explore whether the EPR predictions can be verified using weak rather than projective measurements.

Fig. 1: Schematic scenarios for testing the simultaneous validity of Eqs. (1) and (2).
figure 1

a Projective measurements of non-commuting operators are applied successively to each particle. b Scenario for measuring the weak value of \({\hat{\sigma }}_{z}\) acting locally on particle 1 whereas the projective measurement of \({\hat{\sigma }}_{z}\) is applied to particle 2. c Scenario for measuring the weak value of \({\hat{\sigma }}_{x}\) acting locally on particle 2 whereas the projective measurement of \({\hat{\sigma }}_{x}\) is applied to particle 1. d Scenario proposed in this work for performing successive measurements. Cases (b) and (c) are intended only for conceptual clarity.

Full size image

In this paper, we take advantage of WMs to propose and experimentally prove the joint validity of a pair of equations that can be interpreted as the predictions represented by Eqs. (1) and (2), except that they are formulated in terms of weak values in a post-selected ensemble defined by Alice and Bob’s projective measurements. The confirmation that the weak value predictions we propose are jointly valid provides positive evidence in favor of interpreting the joint weak values as EPR elements of reality in each member of the ensemble, and therefore suggests, in the spirit of the EPR argument, that simultaneous elements of reality can be associated to two physical quantities represented by two non-commuting operators.

Results

Theoretical discussion

In order to propose a pair of equations that can be considered analogous to the simultaneous predictions represented by the left hand sides of Eqs. (1) and (2) consider Fig. 1b, c. These scenarios correspond to a typical setup designed to measure local weak values of the form \({\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle }_{{\rm{w}}}\) and \({\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}\), in which a weak measurement is performed, appropriately preceded by a pre-selection and followed by a post-selection18,19. The weak value formula for an operator \(\hat{{\mathcal{O}}}\) is

$${\langle \hat{{\mathcal{O}}}\rangle }_{{\rm{w}}}=\frac{\langle {\psi }_{{\rm{fin}}}| \hat{{\mathcal{O}}}| {\psi }_{{\rm{ini}}}\rangle }{\left\langle {\psi }_{{\rm{fin}}}| {\psi }_{{\rm{ini}}}\right\rangle }.$$
(3)

When the initial state is the singlet, \(\left|{\psi }_{\text{ini}}\right\rangle =\left|{\psi }^{-}\right\rangle =\frac{1}{\sqrt{2}}\left|{+1}_{z},{-1}_{z}\right\rangle -\frac{1}{\sqrt{2}}\left|{-1}_{z},{+1}_{z}\right\rangle\), and the final state is \(\left|{\psi }_{\text{fin}}\right\rangle ={\left|{s}_{x}\right\rangle }_{1}{\left|{s}_{z}\right\rangle }_{2}\), with \({\left|{s}_{\eta }\right\rangle }_{\mu }\) satisfying \({\hat{\sigma }}_{\eta }^{(\mu )}{\left|{s}_{\eta }\right\rangle }_{\mu }={s}_{\eta }^{(\mu )}{\left|{s}_{\eta }\right\rangle }_{\mu }\), for particle μ ∈ {1, 2} and direction η ∈ {x, y, z}, the weak values of \({\hat{\sigma }}_{z}\) and \({\hat{\sigma }}_{x}\), in the situations depicted in Fig. 1b and c are respectively,

$${\langle {\hat{\sigma }}_{z}^{(1)}\rangle }_{{\rm{w}}}=-{s}_{z}^{(2)},$$
(4)
$${\langle {\hat{\sigma }}_{x}^{(2)}\rangle }_{{\rm{w}}}=-{s}_{x}^{(1)}.$$
(5)

Equations (4) and (5) state a relationship between weak values and the outcomes of the corresponding post-selections. Due to the formal similarity with Eqs. (1) and (2), we interpret (4) and (5) as the EPR predictions. However, as these equations involve experimentally-accessible weak values, they allow us to design an experiment through which we can verify their joint validity. Such an experimental scheme is shown in Fig. 1d where it is possible to jointly measure the weak values, \({\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle }_{{\rm{w}}}\) and \({\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}\), and compare them with the outcomes of the corresponding projective measurements.

The outcome of the projective measurements \({s}_{x}^{(1)}\) and \({s}_{z}^{(2)}\) are defined by the post-selected state and the weak values are obtained from a statistical analysis of the readout of the measuring devices associated with the weak measurements. There are four possible combinations of post-selected states, defined by \({s}_{\eta }^{(\mu )}\in \{-1,+1\}\), which can be used for testing Eqs.(4) and (5). These four states are listed in Table 1 together with the outcome of the projective final measurements.

Table 1 Possible combinations of post-selection states and expected weak values.
Full size table

For the scheme in Fig. 1d, the weak value is obtained from the joint probability distribution P(r1, r2) of finding the readout r1 in the weak measurement device for \({\hat{\sigma }}_{z}^{(1)}\) and readout r2 in the the weak measurement device for \({\hat{\sigma }}_{x}^{(2)}\), given the initial and final states. This joint probability is given by

$$P({r}_{1},{r}_{2})\propto | \left\langle {\psi }_{{\rm{fin}}};{r}_{1},{r}_{2}| \hat{U}| {\psi }_{{\rm{ini}}};{\phi }_{d}\right\rangle {| }^{2},$$
(6)

where \(\left|{\phi }_{d}\right\rangle\) and \(\left|{r}_{1},{r}_{2}\right\rangle\) denote the initial and final states of the meter, respectively, and \(\hat{U}\) is the unitary operator that describes the measurement process.

In general, a measurement can be modeled by the so-called von-Neumann scheme20 where an observable of interest \(\hat{A}\) is coupled to an observable associated with the measurement device \(\hat{{\mathcal{P}}}\), which is conjugate to the readout of the pointer observable. This coupling can be represented by a unitary operation \(\hat{U}=\exp (-i{\hat{H}}_{I}t/\hslash )\), with t the interaction time and \({\hat{H}}_{I}=g\hat{A}\otimes \hat{{\mathcal{P}}}\) the interaction Hamiltonian. The parameter g denotes the strength of the coupling. Before the measurement, the state of the meter can be considered as a Gaussian distribution centered at zero with width (standard deviation) Δ. As a result of the interaction between the system and the meter, such a distribution suffers a shift given by gt19. Depending on the ratio Δ/(gt), the regimes of strong measurement, when Δ/(gt) ≪ 1, and weak measurement, when Δ/(gt) ≫ 1, are defined.

For the situation in Fig. 1d, a local weak measurement is performed on each of the particles and the meters for each of the measurements are assumed to be initially independent. In this case, \({\hat{H}}_{I}\) can be written as

$${\hat{H}}_{I}={g}_{1}{\hat{\sigma }}_{z}^{(1)}\otimes {\hat{{\mathcal{P}}}}^{(1)}+{g}_{2}{\hat{\sigma }}_{x}^{(2)}\otimes {\hat{{\mathcal{P}}}}^{(2)}.$$
(7)

With this interaction Hamiltonian, P(r1, r2) in the weak regime can be approximated, at first order in gμt, as

$${P}_{{\rm{w}}}({r}_{1},{r}_{2})\approx {\mathcal{N}}\exp \left[-\frac{1}{2}\delta {{\bf{r}}}^{\top }{{\mathbf{\Sigma }}}^{-1}\delta {\bf{r}}\right],$$
(8)

where \({\mathcal{N}}\) is a normalization constant, \(\delta {r}_{\mu }={r}_{\mu }-{\bar{r}}_{\mu }\), and \({\mathbf{\Sigma }}={\rm{diag}}({\Delta }_{1}^{2},{\Delta }_{2}^{2})+{\mathcal{O}}({d}_{\mu }{d}_{\nu })\) is the co-variance matrix with dμ = gμt and Δμ (with μ = 1, 2) being the width of the Gaussian distribution associated with each meter. A detailed derivation can be seen in the Supplementary Note 1.

Given the distribution Pw(r1, r2), the weak values \(\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle_{\rm{w}}\) and \(\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle_{\rm{w}}\) required to prove the validity of Eqs. (4) and (5) are obtained operationally from the average shift of the respective meters according to

$${\rm{Re}}{\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle }_{{\rm{w}}}=\frac{{\bar{r}}_{1}}{{d}_{1}},\quad {\rm{Re}}{\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}=\frac{{\bar{r}}_{2}}{{d}_{2}},$$
(9)

where \({\bar{r}}_{1}\) and \({\bar{r}}_{2}\) are the expectation values of r1 and r2, obtained from Eq. (8), while d1 and d2 must be estimated independently. In addition, up to second order in the coupling constants, Pw(r1, r2) also provides information about the non-local weak value \({\big\langle {\hat{\sigma }}_{z}^{(1)}{\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}\)8,21, but this is out of the scope of the present work.

Experimental implementation

Figure 2 depicts the setup utilized for the implementation of the scheme shown in Fig. 1d. With the help of this setup we have performed a set of local weak measurements followed by strong measurements of the polarization for each photon in an EPR-singlet entangled pair, produced by spontaneous parametric down-conversion (SPDC).

Fig. 2: Experimental setup scheme.
figure 2

Each Weak-Measurement set (WM-Set) consists of two half wave plates (HWPs) and a calcite crystal. Other elements labeled in the scheme are: A continuous wave laser (CWL), a dual polarizer beam splitter (Dual-PBS), quarter wave plates (QWP), single mode fibers (SMF), multimode fibers (MMF), single-photon avalanche photo detector (APD) and the coincidence circuit (CC).

Full size image

The experimental setup consists of four stages. In the first one, \(\left|{\psi }_{{\rm{ini}}}\right\rangle\) and the initial state of the meters \(\left|{\phi }_{d}\right\rangle\), needed to perform the weak measurements, are prepared. \(\left|{\psi }_{{\rm{ini}}}\right\rangle\), which corresponds to photon pairs in a polarization-entangled singlet state, is produced by type II SPDC in a periodically-poled potassium titanyl phosphate (PPKTP) crystal placed within a Sagnac interferometer and pumped by a laser beam centered at 405 nm with a narrow linewidth of 200 kHz (MogLabs, DLC-405). For the meters, we used the transverse momentum distribution of the SPDC photons, i.e., the spatial biphoton, \(\Phi ({\vec{q}}_{1},{\vec{q}}_{2})\), in the transverse momentum variables, \(\{\vec{q}_{1},\vec{q}_{2}\}\). We render the function \(\Phi (\vec{q}_{1},\vec{q}_{2})\) factorable by coupling each photon to a single-mode fiber and thus accomplishing projection of each photon to a single transverse mode22,23. A local weak measurement is thus performed on each photon, relying on initially independent measurement devices.

In the second stage, two sets of optical elements, WM-Set1 and WM-Set2, were used in order to perform the weak measurements associated with the operators \({\hat{\sigma }}_{z}\) on particle 1 and \({\hat{\sigma }}_{x}\) on particle 2. These sets consist each of a 2-mm-long calcite crystal preceded and followed by a half waveplate (HWP). For the implementation of \({\hat{\sigma }}_{z}\) and \({\hat{\sigma }}_{x}\) the orientation of both HWPs in WM-Set1 and WM-Set2 were nominally set to 0 and 22.5°, respectively. The birefringence in the calcite crystals mediates the coupling between the transverse momentum distribution of the photon and its polarization, leading to the measurement process. The spatial separation dμ between outgoing orthogonally-polarized beams produced by each calcite determines gμt, as gμt = dμ (with μ ∈ {1, 2}). The length of the two calcite crystals was chosen so as to produce the same lateral displacement with a nominal value of d1 = d2 = 212 μm at 810 nm, i.e., the wavelength at which the SPDC photons are centered.

In the third stage, post-selection to any of four particular states \(\left|{\psi }_{{\rm{fin}}}\right\rangle\) was accomplished by means of a polarizer and a motorized HWP through which each of the two photons is transmitted. These four polarization states are listed in the third column of Table 1, where D1 (A1) refers to diagonal (antidiagonal) polarization for particle one.

Finally, in the fourth stage, we obtained experimentally the distribution Pw(r1, r2) and retrieved the values of the centroid coordinates \(({\bar{r}}_{1},{\bar{r}}_{2})\). Specifically, in our experiment \({\bar{r}}_{1}\) (\({\bar{r}}_{2}\)) corresponds to a displacement x1 (x2), parallel to the optical table so that the distribution Pw(x1, x2) can be obtained by spatially-resolved photon counting, i.e., as a function of x1 and x2. In our experiment the raster scanning was accomplished by translating, with the help of computer controlled motors, the tips of two multimode fibers (each with a 200 μm core diameter), each leading to an avalanche photo detector. The electronic signals from the two detectors were sent to an AND gate with a 7 nm coincidence window so as to record the number of coincidence counts per unit time.

We prepared a photon pair with its polarization state \(\left|{\psi }_{{\rm{ini}}}\right\rangle\) in the entangled EPR-singlet state \(\left|{\psi }^{-}\right\rangle =\left(\left|{H}_{1},{V}_{2}\right\rangle -\left|{V}_{1},{H}_{2}\right\rangle \right)/\sqrt{2}\), with fidelity 0.883 ± 0.007, where \(\left|H\right\rangle\) (\(\left|V\right\rangle\)) denotes horizontal (vertical) polarization. Additionally, our photon pairs were prepared so that they were factorable in the transverse spatial degree of freedom; this is evident from the experimental measurement of the initial joint distribution of the readout of the meters P0(x1, x2) as shown in Fig. 3. The circular shape confirms the absence of spatial correlations once the signal and idler photons are projected onto the collection modes of single mode fibers, which, in the case of a transform-limited biphoton, translates into the absence of momentum correlations; i.e., \(\Phi (\vec{q}_{1},\vec{q}_{2})\) is separable, implying that the weak measurements carried out on both photons are independent. By fitting to Gaussian functions for the directions x1 and x2, the widths of the distribution were found to be Δ1 = 343 ± 73 μm and Δ2 = 367 ± 36 μm.

Fig. 3: Initial joint distribution of the readout of the meters P0(x1, x2).
figure 3

No weak measurements and no post-selections were applied. CC denotes coincidence counts.

Full size image

The displacement produced by each calcite crystal, dμ, which is needed in Eq. (9), was measured in an alternative setup, and we obtained \({d}_{1}^{\exp }=228\pm 5\,{\rm{\mu}} {\rm{m}}\) and \({d}_{2}^{\exp }=232\pm 5\, {\rm{\mu}} {\rm{m}}\). These measurements together with the ones of Δμ lead to Δ1/(g1t) = 1.51 and Δ2/(g2t) ≈ 1.50. Although these values are strictly not much larger than unity, it is fair to consider that both measurements are performed in an approximately weak regime where Eq. (9) is valid. To see this, let us consider the expectation values \({\bar{r}}_{1}\) and \({\bar{r}}_{2}\) obtained from the probability P(r1, r2) in Eq. (6) which are valid for general values of the ratio Δμ/(gμt). At \({\mathcal{O}}\big({\Delta }_{\mu }/({g}_{\mu }t)\big)\), P(r1, r2) becomes Pw(r1, r2) that defines the weak values by means of Eq. (9). If one expands these expectation values up to terms of \({\mathcal{O}}\big({\Delta }_{\mu }^{2}/{({g}_{\mu }t)}^{2}\big)\), the leading correction that appears on the weak values according to Eq. (9) is around 3%, when Δμ/(gμt) ≈ 1.5, indicating that for our experimental conditions it is appropriate to use Eq. (9) for obtaining the respective weak values.

For each of the post-selected states listed in the third column of Table 1, we measured the experimental distribution Pw(x1, x2), from which we extracted the values for the centroid coordinates. Using Eq. (9) and the independently measured values of d1 and d2, we calculated the corresponding weak values. These data are shown graphically in Fig. 4, in a coordinate axis formed by \({\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle }_{{\rm{w}}}\) and \({\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}\) and with its origin placed at the center of mass of the measured functions Pw(x1, x2), for each of the four post selections. Four quadrants, I, II, III and IV can be then recognized and the centroid for each post-selected state appears in one of them, depending on the post-selection used. In quadrant III, there are two points because the measurement for the post-selection \(\left|{\psi }_{{\rm{fin}}}\right\rangle =\left|{D}_{1},{H}_{2}\right\rangle\) was carried out twice so as to demonstrate that the weak measurements were indeed producing a systematic effect.

Fig. 4: Experimental weak values for each post-selection.
figure 4

Relationship between the weak values \({\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle }_{{\rm{w}}}\) and \({\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}\), and the outcomes of the post-selections \(\big|{s}_{x}^{(1)},{s}_{z}^{(2)}\big\rangle\) here labeled by H, V, D, and A that represent the projections in the horizontal, vertical, diagonal and antidiagonal polarization directions respectively. The error bars were calculated from the standard error of the mean. The four quadrants of the plane are labeled by Roman numbers.

Full size image

In order to understand our results, let us frame the discussion in terms of the coordinate pair \(\big({\big\langle {\hat{\sigma }}_{z}^{(1)}\big\rangle }_{{\rm{w}}},{\big\langle {\hat{\sigma }}_{x}^{(2)}\big\rangle }_{{\rm{w}}}\big)\), for which the expected values are shown in the last column of Table 1. Comparing the experimental results in Fig. 4 with the fourth column of Table 1, there is clearly an agreement between the quadrant on which the experimental centroid of the distribution Pw(x1, x2) is located and its expected location as governed by the chosen post-selection. This agreement reveals that the weak values are correlated with the outcomes of the strong measurements according to Eqs. (4) and (5), thus proving their joint validity. The discrepancy between experimental and theoretical values is due to systematic errors including the non-ideal fidelity of the two-photon state, a temporal delay introduced by the calcite crystals in the WM-Sets and possible misalignment of the angles of the HWPs. So as to understand the role of non-ideal fidelity of the two-photon state one may consider it to be in the form of a Werner state \({\hat{\rho }}_{\rm{W}}=p\left|{\psi }^{-}\right\rangle \left\langle {\psi }^{-}\right|+\left(\frac{1-p}{4}\right)I\). In this case, the fidelity between the reconstructed state and \(\left|{\psi }^{-}\right\rangle\) gives an estimate of p which in our case corresponds to 0.844. By calculating the weak values with the initial polarization state \({\hat{\rho }}_{{\rm{W}}}\) instead of \(\left|{\psi }^{-}\right\rangle\), one obtains that the measured weak values have to be corrected by a factor of p as you can see in Supplementary Note 2. Additionally, the temporal delays due to the calcite crystals produce a deformation of the square structure (with a lobe at each vertex), leading instead to the observed rhomboid shape.

Another way to visualize our experimental results is by plotting the difference between Pw(x1, x2) and the product of the distributions P1(x1)P2(x2), where Pμ(xμ) is the probability of obtaining a detection at the position xμ in the path of particle μ not conditioned to a detection of the other particle. These results are shown in Fig. 5 for the four post-selected states shown in Table 1. The panels correspond, clockwise from the top left, to \(\left|{A}_{1},{H}_{2}\right\rangle\), \(\left|{A}_{1},{V}_{2}\right\rangle\), \(\left|{D}_{1},{V}_{2}\right\rangle\), and \(\left|{D}_{1},{H}_{2}\right\rangle\). It is possible to recognize in all four panels a bright spot, as well as a dark spot. The observation of these two spots is an indication of the shifts suffered by the measuring devices, with respect to their initial distributions. Placing a Cartesian coordinate system with its origin at the center of mass of the bright and dark spots, one observes that the bright spot appears in a specific quadrant, with the same as pattern as in Fig. 4. The visualization of the experimental data in Fig. 5 further clarifies the relationship between weak values and the outcome of the post-selections, in agreement with the theoretical predictions in Eq. (4) and (5), thus proving their joint validity.

Fig. 5: Alternative visualization of the experimental data to illustrate the relation between weak values and the outcome of the post-selections.
figure 5

Cartesian coordinate system centered at the center of mass defined by the position of the centroids of the bright and dark spots.

Full size image

An interpretation of our results is that a complete post-selection on one of the particles effectively determines an updated initial state of the other particle, at least with respect to the weak values of that particle’s observables. Thus, for instance, if the two particles are initially prepared in a singlet state and the first particle is post-selected in the state corresponding to \({s}_{x}^{(1)}=+1\), then the weak values of the second particle are consistent with those of an updated initial state corresponding to \({s}_{x}^{(2)}=-1\). The conjunction of the two post-selections performed on the two particles (i.e., \({s}_{x}^{(1)}=+1\), \({s}_{z}^{(2)}=+1\)) therefore allows us to interpret the weak values of two additional complementary observables (\({s}_{x}^{(2)}=-1\), \({s}_{z}^{(1)}=-1\)) as witnesses to the "strong” values that would have been obtained if for the corresponding particle the post-selection had instead been a verification measurement of that particle’s updated initial state. Although the discussion has pertained to the observables \({\hat{\sigma }}_{x}\) and \({\hat{\sigma }}_{z}\), the results here presented could be extended to any arbitrary observables of two-level systems.

Discussion

We have shown that using joint weak measurements, it is possible to experimentally test the type of assertions about the simultaneous values of non-commuting observables that served as the basis for the EPR critique of the completeness of the quantum-mechanical description afforded by the wave-function. The fact that our results are in correspondence with the EPR predictions allows us to suggest that joint weak measurements, together with post-selection, can be used to assign simultaneous elements of reality to two non-commuting observables in the EPR setting. We acknowledge that this suggestion touches on subtle issues such as the question of what constitutes an element of reality24,25,26,27,28,29, and whether the weak values, which are obtained from an ensemble, can furthermore be attributed to each member of that ensemble30,31. While a thorough epistemological discussion of these points lies beyond the scope of this work, we nevertheless believe that our suggestion is justified. On the one hand, since weak values are measurable quantities that can be predicted with certainty at the ensemble level, they can be interpreted according to the criterion of the EPR paper, as elements of reality of the corresponding ensemble. On the other hand, the fact that the weak values are obtained from an ensemble does not preclude us from making plausible inferences about each pair in the ensemble. Indeed, the fact that our experimental results arise from weak measurements that are performed simultaneously on each trial, together with the more than a reasonable assumption that the trials are statistically independent, constitutes positive evidence in favor of interpreting a statistical property of an ensemble as reflecting a corresponding property of each of its members, i.e. if we let A be the proposition that the effect is present in each element of the ensemble, B the proposition that the effect is measurable as an ensemble average, and C the reasonable implication A ⇒ B under the assumption of statistical independence, then B is evidence in favor of A given C in the sense that P(A∣BC)≥P(A∣C)32.

Finally, concerning the EPR controversy on the completeness of the quantum mechanical description, it is worth noting that the effects we report can only be retrieved from the weak measurement statistics of an ensemble conditioned by both the initial preparation of the entangled pair and the post-selections performed on each particle. As has been pointed out elsewhere18,33, such conditional statistics cannot be predicted using only the single state vector describing the preselected state, but rather require two state vectors that describe the pre- and post selections. In this sense, it is reasonable to suggest that while the single state vector that only describes an initial preparation of a system indeed fails to provide a complete description of the testable physical properties of a quantum system at a given time, the standard framework of quantum mechanics nonetheless furnishes the necessary elements to complete the description with an additional state vector describing a post-selection.