A Majorana perspective on understanding and identifying axion insulators

Abstract

An axion insulator is theoretically introduced to harbor unique surface states with half-integer Chern number ${{{{{{{\mathcal{C}}}}}}}}$. Recently, experimental progress has been made in different candidate systems, while a unique Hall response to directly reflect the half-integer Chern number is still lacking to distinguish an axion state from other possible insulators. Here we show that the ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$ axion state corresponds to a topological state with Chern number ${{{{{{{\mathcal{N}}}}}}}}=1$ in the Majorana basis. In proximity to an s − wave superconductor, a topological phase transition to an ${{{{{{{\mathcal{N}}}}}}}}=0$ phase takes place at critical superconducting pairing strength. Our theoretical analysis shows that a chiral Majorana hinge mode emerges at the boundary of ${{{{{{{\mathcal{N}}}}}}}}=1$ and ${{{{{{{\mathcal{N}}}}}}}}=0$ regions on the surface of an axion insulator. Furthermore, we propose a half-integer quantized thermal Hall conductance via a thermal transport measurement, which is a signature of the gapless chiral Majorana mode and thus confirms the ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$ (${{{{{{{\mathcal{N}}}}}}}}=1$) topological nature of an axion state. Our proposals help to theoretically comprehend and experimentally identify the axion insulator and may benefit the research of topological quantum computation.

Introduction

Topological states of matter are described in terms of topological invariant quantities, which usually indicate quantized transport response in two-dimensional (2D) systems^1,2,3,4. As the combination of topology and magnetism, axion insulators have drawn broad interest in recent years^5,6,7,8,9. An axion insulator is theoretically proposed to harbor unique surface states with half-integer Chern number ${{{{{{{\mathcal{C}}}}}}}}$^3,10,11,12. It is an attractive question to figure out the origin of the Chern number ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$ of an axion state and whether there is a corresponding half-quantized transport response. Several works suggest the electric transport outcome as the signature of the axion state^13,14,15. At this stage, experiments recognize axion insulators by the transport evidence, a large longitudinal resistance together with a zero Hall plateau, in doped or intrinsic magnetic topological insulators^16,17,18. However, a similar signature can also be observed in a normal insulator^19,20. The half-quantized Hall conductance and the half-integer Chern number of axion insulators have not been accurately shown.

Chiral Majorana fermions can arise as 1D self-conjugate quasiparticles in the topological superconducting system characterized by Chern number ${{{{{{{\mathcal{N}}}}}}}}$^{21,22,23,24,25}. The Majorana basis provides a new perspective on revealing the topology of a material. As one of the precursors, the quantum anomalous Hall insulator (QAHI), identified with integer Chern number ${{{{{{{\mathcal{C}}}}}}}}$, has been experimentally verified with the dissipationless edge mode^{26,27,28,29,30,31}. From the topology view, the ${{{{{{{\mathcal{C}}}}}}}}=1$ QAHI can be considered as an ${{{{{{{\mathcal{N}}}}}}}}=2$ phase in the Majorana basis^32,33, where the Majorana fermion can be treated as an elementary excitation. Therefore, it is promising to unveil the unique half-integer Chern number ${{{{{{{\mathcal{C}}}}}}}}$ of an axion state and the related topological properties from the Majorana perspective.

In this paper, we propose that a ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$ axion state corresponds to an ${{{{{{{\mathcal{N}}}}}}}}=1$ phase in the Majorana basis. In proximity with an s − wave superconductor, a topological phase transition from an axion insulating ${{{{{{{\mathcal{N}}}}}}}}=1$ phase to an ${{{{{{{\mathcal{N}}}}}}}}=0$ phase takes place at a critical superconducting pairing strength. At the corresponding boundary between the ${{{{{{{\mathcal{N}}}}}}}}=1$ and ${{{{{{{\mathcal{N}}}}}}}}=0$ regions forms a complete Majorana edge mode, which is expected to be observed in transport measurements. More interestingly, our theoretical calculations and analysis show that the emerging Majorana edge mode along the boundary of an axion insulating region carries half-integer quantized thermal Hall conductance. It provides a unique quantized measurement of the ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$ axion state.

Results and discussion

Phase of the axion surface state in the Majorana basis

An axion insulator possesses special surface states with half-quantized topological numbers ${{{{{{{\mathcal{C}}}}}}}}=\pm \!1/2$ depending on the magnetization orientation on the surface³. To explore the electronic property of the half-quantized topological number, we would adopt the Majorana basis to construct the integer-quantized phase diagram of the axion surface state in this subsection.

We first concentrate on one surface of an axion insulator, see the top surface of the device in Fig. 1a. The low-energy effective model Hamiltonian comes from the gapped surface of a 3D topological insulator, expressed as H_surf(k) = A(k_xσ_x + k_yσ_y) + mσ_z³, where σ_x,y,z is Pauli matrix in spin space, A is related to the Fermi velocity, and m is the mass term induced by magnetic exchanging interaction. When m ≠ 0, the H_surf(k) is a two-band massive Dirac Hamiltonian, which describes the surface of an axion insulator with a half-integer Chern number ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}{{{{{{{\rm{sgn}}}}}}}}(m)$ in the electron basis (see the Supplementary Note 1). The corresponding Hall conductance is robust as ±e²/2h since the correction from large momenta vanishes. The difference of Chern numbers between two adjacent regions is either 0 or ±1 with no edge modes or one gapless QAHI mode in Fig. 1b, where the half-integer Chern number ${{{{{{{\mathcal{C}}}}}}}}$ of the axion surface state does not show up directly³.

Fig. 1: Analysis of axion insulators in the Majorana basis.

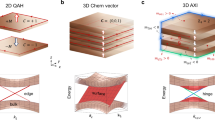
a Schematic diagram of an axion insulator with outward magnetization on surfaces of a 3D topological insulator and covered by s − wave superconductors on the top and bottom. Four lines with arrows represents the chiral Majorana hinge modes. b Phase diagram of one 2D surface of an axion insulator with homogenous magnetic doping m and covered by an s-wave superconductor with pairing potential Δ. c and d Band structures E − k_x of the axion-insulator-based device in a. c Four surfaces are in the ${{{{{{{\mathcal{N}}}}}}}}=1$ phase with no topological boundary for Δ < ∣m∣. d Top and bottom surfaces are driven into the ${{{{{{{\mathcal{N}}}}}}}}=0$ phase for Δ > ∣m∣, leading to two-fold degenerate gapless modes which are marked with solid and dashed lines, corresponding to chiral Majorana hinge modes in a.

When one covers an s-wave superconductor on the surface of an axion insulator, the superconducting pairing potential can penetrate into the magnetic layers at low temperature^34,35,36,37. Considering an induced superconducting pairing potential on the surface, introducing the Bogoliubov-de Gennes (BdG) Hamiltonian³², and doing basis transformation, one gets the block diagonalized Hamiltonian, ${H}_{{{{{{{{\rm{BdG}}}}}}}}}=\frac{1}{2}{\sum }_{{{{{{{{\bf{k}}}}}}}}}{{{\Psi }}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }{{{{{{{\mathcal{H}}}}}}}}({{{{{{{\bf{k}}}}}}}}){{{\Psi }}}_{{{{{{{{\bf{k}}}}}}}}}$, where the Majorana basis ${{{\Psi }}}_{{{{{{{{\bf{k}}}}}}}}}=\frac{1}{\sqrt{2}}{({c}_{{{{{{{{\bf{k}}}}}}}}\uparrow }+{c}_{-{{{{{{{\bf{k}}}}}}}}\downarrow }^{{{{\dagger}}} },{c}_{{{{{{{{\bf{k}}}}}}}}\downarrow }+{c}_{-{{{{{{{\bf{k}}}}}}}}\uparrow }^{{{{\dagger}}} },-{c}_{{{{{{{{\bf{k}}}}}}}}\downarrow }+{c}_{-{{{{{{{\bf{k}}}}}}}}\uparrow }^{{{{\dagger}}} },-{c}_{{{{{{{{\bf{k}}}}}}}}\uparrow }+{c}_{-{{{{{{{\bf{k}}}}}}}}\downarrow }^{{{{\dagger}}} })}^{T}$ with c_k↑/↓ (${c}_{{{{{{{{\bf{k}}}}}}}}\uparrow /\downarrow }^{{{{\dagger}}} }$) the annihilation (creation) operators of electrons. ${{{{{{{\mathcal{H}}}}}}}}({{{{{{{\bf{k}}}}}}}})$ is block diagonalized with ${{{{{{{{\mathcal{H}}}}}}}}}_{\pm }=A({k}_{x}{\sigma }_{x}\pm {k}_{y}{\sigma }_{y})+(\pm m+{{\Delta }}){\sigma }_{z}$ and the superconducting pairing potential Δ. Chern number of each block is calculated as (see the Supplementary Note 2).

$${{{{{{{{\mathcal{N}}}}}}}}}_{\pm }=\frac{1}{2}{{{{{{{\rm{sgn}}}}}}}}(m\pm {{\Delta }}),$$

(1)

$${{{{{{{\mathcal{N}}}}}}}}={{{{{{{{\mathcal{N}}}}}}}}}_{+}+{{{{{{{{\mathcal{N}}}}}}}}}_{-},$$

(2)

where ${{{{{{{\mathcal{N}}}}}}}}$ denotes the Chern number of one surface of an axion insulator in the Majorana basis. Thus, the surface state of an axion insulator (m ≠ 0, Δ = 0) can be characterized by ${{{{{{{\mathcal{N}}}}}}}}=\pm \!1$. The sign of ${{{{{{{\mathcal{N}}}}}}}}$, dependent on the direction of the magnetization, represents the chirality of Majorana fermions on the surface. Here, the half-integer ${{{{{{{\mathcal{C}}}}}}}}=\pm \!\frac{1}{2}$ axion insulating phases can be treated as the integer ${{{{{{{\mathcal{N}}}}}}}}=\pm \!1$ axion insulating phases.

Next, we focus on the phase diagram of an axion insulator covered by an s − wave superconductor with a nonzero superconducting pairing potential Δ (see the Supplementary Note 1). Δ plays the role as a revision of the mass term but with opposite signs to the ${{{{{{{{\mathcal{N}}}}}}}}}_{+}$ and ${{{{{{{{\mathcal{N}}}}}}}}}_{-}$ blocks [see Eq. (1)]. The Chern number ${{{{{{{\mathcal{N}}}}}}}}$ in Eq. (2) still remains well-defined but adds a new ${{{{{{{\mathcal{N}}}}}}}}=0$ phase between + 1 and − 1 with the phase boundary ∣Δ ± m∣ = 0 [see Fig. 1b where only the Δ > 0 part is shown]. In the limit Δ → 0, the phase diagram reduces to two ${{{{{{{\mathcal{N}}}}}}}}=\pm \!1$ axion insulating phases with a critical point at m = 0.

Away from m = 0, a small superconducting pair potential (Δ < ∣m∣) keeps the system in the ${{{{{{{\mathcal{N}}}}}}}}=1$ or −1 phase in Fig. 1c. When Δ > ∣m∣, the system enters the ${{{{{{{\mathcal{N}}}}}}}}=0$ phase which refers to a normal superconducting phase. To be clear, the $| {{{{{{{\mathcal{N}}}}}}}}| =1$ topological phase originates from the axion surface state with finite magnetization and the superconducting pairing potential can drive the phase into a new ${{{{{{{\mathcal{N}}}}}}}}=0$ phase. With the appearance of the new ${{{{{{{\mathcal{N}}}}}}}}=0$ phase, we are allowed to construct the boundary between the $| {{{{{{{\mathcal{N}}}}}}}}| =1$ phase and the ${{{{{{{\mathcal{N}}}}}}}}=0$ phase. At this well-designed boundary, the axion surface state is expected to carry a chiral Majorana fermion as the topological boundary state in Fig. 1d.

Chern number of a quasi-2D system

Above, we have claimed that one surface state of an axion insulator with homogenous magnetization can be characterized by the Chern number $| {{{{{{{\mathcal{N}}}}}}}}| =1$. However, such an axion surface state cannot solely exist as a purely 2D system with an open boundary conditions. In reality, an axion insulator is a 3D bulk material that owns a non-trivial topology on its surface. So we numerically calculate the Chern number of axion insulators within a quasi-2D structure where the x and y directions are in periodic boundary conditions but the z-direction is with finite thickness L_z (see the Supplementary Note 5).

The bulk Hamiltonian describes an axion insulator in the form as ${H}_{{{{{{{{\rm{ax}}}}}}}}}={H}_{{{{{{{{\rm{bulk}}}}}}}}}+{H}_{{{{{{{{\mathcal{M}}}}}}}}}$, where ${H}_{{{{{{{{\rm{bulk}}}}}}}}}=\mathop{\sum }\nolimits_{i = 1}^{4}{d}_{i}{{{\Gamma }}}_{i}$ is the four-band effective Hamiltonian of a 3D topological insulator and ${H}_{{{{{{{{\mathcal{M}}}}}}}}}$ represents the magnetization on the surface of the 3D topological insulator^38,39,40. Here, d₁ = A₂k_x, d₂ = A₂k_y, d₃ = A₁k_z and ${d}_{4}=M-{B}_{1}{k}_{z}^{2}-{B}_{2}({k}_{x}^{2}+{k}_{y}^{2})$, where A_i and B_i are material parameters and M determines the bulk gap. Γ_i = σ_i ⊗ τ_x for i = 1, 2, 3 and Γ₄ = σ₀ ⊗ τ_z where σ_i and τ_i are Pauli matrices for the spin and orbital degrees of freedom. In the calculation, we set A_1,2 = 0.55, B_1,2 = 0.25, M = 0.3. For the numerical Chern number model, ${H}_{{{{{{{{\mathcal{M}}}}}}}}}$ is expressed as ${{{{{{{{\mathcal{M}}}}}}}}}_{3}(z){\sigma }_{z}\otimes {\tau }_{0}$, where τ₀ is an identity matrix in the orbital space. ${{{{{{{{\mathcal{M}}}}}}}}}_{3}(z)$ picks ±m on the top and bottom surface, respectively, and keeps zero otherwise. In proximity to a superconductor, H_Δ denotes the s − wave pairing potential Δ added on the top and bottom surfaces. Thus, the full Hamiltonian is H = H_ax + H_Δ (see the Supplementary Note 4).

We calculate the non-commutative Chern number of H in the real space with^{41,42,43,44,45}

$${\mathfrak{N}}(Z)=2\pi {{{{{{{\rm{i}}}}}}}}{{{{{{{\rm{Tr}}}}}}}}{\left\{P\left[-{{{{{{{\rm{i}}}}}}}}\left[\hat{x},P\right],-{{{{{{{\rm{i}}}}}}}}\left[\hat{y},P\right]\right]\right\}}_{Z},$$

(3)

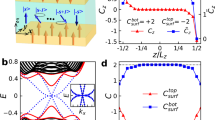
where P projects onto the occupied states below the Fermi energy E_f and ${{{{{{{\rm{Tr}}}}}}}}$ means trace over the Z − th layer. $\left[\hat{x}/\hat{y},P\right]$ represents the ${\partial }_{{k}_{x/y}}{P}_{{{{{{{{\bf{k}}}}}}}}}$ mapped on the real space lattice with $\hat{x}$ and $\hat{y}$ being position operators. For example, $\left[\hat{x},P\right]={{{{{{{\rm{i}}}}}}}}\mathop{\sum }\nolimits_{j = 1}^{Q}{c}_{j}\left({e}^{-{{{{{{{\rm{i}}}}}}}}j\hat{x}{\delta }_{{L}_{x}}}P{e}^{{{{{{{{\rm{i}}}}}}}}j\hat{x}{\delta }_{{L}_{x}}}-{e}^{{{{{{{{\rm{i}}}}}}}}j\hat{x}{\delta }_{{L}_{x}}}P{e}^{-{{{{{{{\rm{i}}}}}}}}j\hat{x}{\delta }_{{L}_{x}}}\right)$ with δ_Lx = 2π/L_x and the coefficient c_j is chosen for the exponential convergence^41,42. ${\mathfrak{N}}(Z)$ represents the Chern number of the Z − th layer of a quasi-2D axion insulator. In Fig. 2a, the total Chern number ${{{{{{{{\mathcal{N}}}}}}}}}_{{{{{{{{\rm{tot}}}}}}}}}=\mathop{\sum }\nolimits_{Z = 1}^{{L}_{z}}{\mathfrak{N}}(Z)$ reveals the topological feature of axion insulators that the whole system is an insulator and gives a zero Hall conductance plateau together with a huge longitudinal resistance in experiments^16,18. As a comparison, the total Chern number of QAHI comes to be $| {{{{{{{\mathcal{N}}}}}}}}| =2$ (see Supplementary Note 6), implying two chiral Majorana modes along the boundary. The local Chern marker of the top layers and bottom layers are denoted as ${{{{{{{{\mathcal{N}}}}}}}}}_{t}=\mathop{\sum }\nolimits_{Z = {L}_{z}-2}^{{L}_{z}}{\mathfrak{N}}(Z)$ and ${{{{{{{{\mathcal{N}}}}}}}}}_{b}=\mathop{\sum }\nolimits_{Z = 1}^{3}{\mathfrak{N}}(Z)$, respectively. When the Fermi energy locates within the gap, the local Chern marker ${{{{{{{{\mathcal{N}}}}}}}}}_{t}$ (${{{{{{{{\mathcal{N}}}}}}}}}_{b}$) is quantized as 1 (−1) shown in Fig. 2a. For the case with E_f = 0, we plot the ${\mathfrak{N}}(Z)$ which presents the localization at the boundary along the z-direction (see the Supplementary Note 7). This indicates that the Majorana excitation emerges around the top/bottom surface but with different chirality, which distinguishes an axion insulator from a normal insulator in principle. Besides, taking the hint from the phase diagram Fig. 1b, when covered by superconductors with a large pairing potential, the top and bottom surfaces of an axion insulator can be driven into a topologically trivial phase with ${{{{{{{{\mathcal{N}}}}}}}}}_{t}={{{{{{{{\mathcal{N}}}}}}}}}_{b}=0$ [see Fig. 2b]. Moreover, the integer-quantized Chern number is not sensitive to the specific amplitude of the magnetization and pairing potential, see the same results calculated with decaying parameters in Supplementary Note 8. These numerical results not only recognize the top and bottom surfaces of an axion insulator but also establish the connection between them, which further confirms the ${{{{{{{\mathcal{N}}}}}}}}=1$ nature of axion states and the effective regulation via superconducting pairing potential.

Fig. 2: Non-commutative Chern number ${{{{{{{\mathcal{N}}}}}}}}$ in the Majorana basis as a function of Fermi energy E_f.

a The total Chern number of a bare axion insulator is ${{{{{{{{\mathcal{N}}}}}}}}}_{{{{{{{{\rm{tot}}}}}}}}}=0$ but the local Chern markers are integer-quantized as ${{{{{{{{\mathcal{N}}}}}}}}}_{t}=1$ and ${{{{{{{{\mathcal{N}}}}}}}}}_{b}=-1$, revealing the topological nontriviality of the top and bottom surfaces. Here, m = 0.2, Δ = 0, and L_z = 10. b Top and bottom surfaces can be driven into the ${{{{{{{{\mathcal{N}}}}}}}}}_{t/b}=0$ phase in proximity with superconductors. Here, m = 0.2, Δ = 0.4, and L_z = 10.

Hinge state distribution

For the surface of axion insulators with the superconducting proximity effect, there are three possible phases characterized by the integer Chern number ${{{{{{{\mathcal{N}}}}}}}}=\pm \!1,0$ in the Majorana basis. Based on the bulk-boundary correspondence relation, such phases can be used to construct a proper boundary where the Majorana excitation emerges. So we plot the band structure and the state distribution to visualize the complete chiral Majorana mode on the surface of the axion insulator in this subsection.

The band structure E − k_x of the axion system is calculated along the x direction [see Fig. 1a]. We place outward magnetization on surfaces of an axion insulator with ${H}_{{{{{{{{\mathcal{M}}}}}}}}}=({{{{{{{{\mathcal{M}}}}}}}}}_{3}(z){\sigma }_{z}+{{{{{{{{\mathcal{M}}}}}}}}}_{2}(y){\sigma }_{y})\otimes {\tau }_{0}$, where ${{{{{{{{\mathcal{M}}}}}}}}}_{2}(y)$ picks the value of ± m on the front and back surfaces, respectively, and keeps zero otherwise (see the Supplementary Note 3 and 4). The nonzero ∣m∣ breaks the time-reversal symmetry and opens a hard gap of about 2∣m∣ on the surface [see Fig. 1c]. Though one surface of an axion insulator is characterized with nontrivial topology ${{{{{{{\mathcal{N}}}}}}}}=1$, the whole system is insulating if there is no special boundary for the surface. Things change when ${{{{{{{\mathcal{N}}}}}}}}=0$ regions form on the surface by means of the superconducting pairing potential Δ. With Δ = 0.4, the top and bottom surfaces are tuned into the ${{{{{{{\mathcal{N}}}}}}}}=0$ phase, topologically inequivalent with the front and back surfaces of the axion insulator with ${{{{{{{\mathcal{N}}}}}}}}=1$. The boundary forms at hinges. Thus, four gapless states with the linear dispersion relation emerge within the gap, see Fig. 1d.

To illustrate the distribution of the gapless states, we plot ∣Ψ∣² as functions of lattice position (Y, Z) at energy E = 0.085. There are two pairs of states corresponding to k_x = ±0.05π, marked by black arrows in Fig. 1d. As shown in Fig. 3, all four states are localized at the corners of the y-z plane, which are actually chiral hinge modes along the x-axis. The panels (Fig. 3a and b) correspond to k_x = −0.05π, states with negative group velocity; the panels (Fig. 3c and d) correspond to k_x = 0.05π, states with the positive group velocity. The chiral hinge states and their distribution shown in Fig. 3 are the corresponding topological boundary states of an axion state with a nontrivial Chern number ${{{{{{{\mathcal{N}}}}}}}}=1$. More specifically, here the counter-propagating chiral Majorana modes emerge at hinges [see Fig. 1a], reflecting the chiral Majorana excitations at the boundary of ${{{{{{{\mathcal{N}}}}}}}}=1$ and ${{{{{{{\mathcal{N}}}}}}}}=0$ regions on the surface of an axion insulator.

Fig. 3: Illustration of the spatial probability ∣ψ∣² distribution of hinge states in Y-Z plane.

ψ denotes the wavefunction of the state in each panel. Four states form two pairs of counter-propagating states localizing at hinges. a The hinge localized state with k_x = −0.05π propagates in −x direction and the chirality is clockwise. b The hinge localized state with k_x = −0.05π propagates in −x direction and the chirality is counterclockwise. c The hinge localized state with k_x = 0.05π propagates in + x direction and the chirality is counterclockwise. d The hinge localized state with k_x = 0.05π propagates in + x direction and the chirality is clockwise.

Quantized transport signature

After identifying topological excitation of an axion insulator with $| {{{{{{{\mathcal{N}}}}}}}}| =1$, we face the question that how to measure such edge modes in experiments. Given the Majorana mode at the boundary in Fig. 3, we design the transport scheme to detect this Majorana excitation and thus present the quantized signature of axion insulators. As to the transport property, the electric measurement of a Majorana mode will be easily affected due to the high conductivity of the superconductor^23,24,33,46, and more details of this explanation are provided in Supplementary Note 9. Since Cooper pairs in superconductors do not carry heat, thermal measurement turns out to be a proper way to identify a chiral Majorana mode^47,48,49,50.

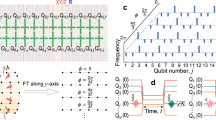
We calculate the thermal transport via the multi-probe Landauer-Büttiker formula^51,52,53. At low temperature, the electronic thermal conductivity dominates while the phononic thermal conductivity is overshadowed^54,55 so we focus on the thermal conductivity contributed by electrons. More details of this calculation are provided in the section “Method”. The cubic axion insulator device in Fig. 4a is connected with six leads on the top and the bottom surfaces. Here, ${H}_{{{{{{{{\mathcal{M}}}}}}}}}=({{{{{{{{\mathcal{M}}}}}}}}}_{3}(z){\sigma }_{z}+{{{{{{{{\mathcal{M}}}}}}}}}_{2}(y){\sigma }_{y}+{{{{{{{{\mathcal{M}}}}}}}}}_{1}(x){\sigma }_{x})\otimes {\tau }_{0}$, where ${{{{{{{{\mathcal{M}}}}}}}}}_{1}(x)$ picks the value of ± m on the left and right surfaces, respectively, and remains zero otherwise. The top and bottom surfaces of the axion insulator are covered by s − wave superconductors with the pairing potential Δ. Since the six surfaces are all gapped by magnetization, within the gap, the top and bottom surfaces are separated by the insulating side surfaces.

We first concentrate on the top surface of an axion insulator covered by a superconductor at a low background temperature ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$. When Δ < ∣m∣, the whole system remains ${{{{{{{\mathcal{N}}}}}}}}=1$ with a hard gap [see Fig. 1c] with no edge mode carrying heat. In this case, only the local Andreev reflection process occurs and it does not carry heat due to the particle conservation⁵² and see the Supplementary Note 9. So the normalized thermal Hall conductance ${\kappa }_{xy}^{{{{{{{{\rm{TH}}}}}}}}}$ tends to zero and the normalized thermal longitudinal resistance ${R}_{xx}^{{{{{{{{\rm{T}}}}}}}}}$ remains large [see Fig. 4b and c]. This case is similar to a normal insulator. Things change when Δ > ∣m∣. From our analysis above, one chiral Majorana mode will propagate at the hinge of the top surface of an axion insulator when Δ > ∣m∣. The chiral Majorana fermion is expected to act as an effective heat carrier, equivalent to half of a normal electron. The thermal Hall conductance is half-quantized in the unit of $\,\frac{{\pi }^{2}{k}_{{{{{{{{\rm{B}}}}}}}}}^{2}}{3h}$ and the thermal longitudinal resistance drops to zero. Note that Cooper pairs in the superconductor do not contribute to heat transfer. Here we propose that the half-integer quantized thermal Hall conductance of the chiral Majorana mode can serve as an observable quantity that characterizes the ${{{{{{{\mathcal{N}}}}}}}}=1$ (${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$) nature of axion states.

Considering the bottom surface, the normalized thermal Hall conductance satisfies ${\kappa }_{xy}^{b}=-{\kappa }_{xy}^{t}$ [see Fig. 4d], due to the different magnetization orientation. When Δ > ∣m∣, the opposite sign presents the counter-propagating chiral Majorana hinge modes on the top and bottom surfaces. Beyond the zero-temperature limit, ${\kappa }_{xy}^{t}$ and ${\kappa }_{xy}^{b}$ are robustly half-quantized within a range of background temperature ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$, [see Fig. 4d]. As to the candidate material of axion insulators, the surface gap of magnetic doped Bi₂Se₃ can be adjusted by controlling the doping concentration^5,16 and the experimentally reported magnetic exchanging gap on the surface of MnBi₂Te₄ can be 0.64 meV (7.4 K)³⁰. If the s − wave superconducting pairing potential is estimated to be about several Kelvins (K), Δ ~ 10 K, the background temperature is preferred to be an order of magnitude smaller, ${{{{{{{{\mathcal{T}}}}}}}}}_{0} \, < \,$1K. Such a requirement of thermal measurement under (10 mK, 1 K) is within the laboratory conditions^19,56,57. Besides, the schematic transport device in Fig. 4a is proposed with twelve leads for theoretical analysis. In experiments, there may only be the top and bottom surfaces with perpendicular magnetization in some potential axion insulating materials. Such a magnetic surface of an axion insulator can be partially covered by superconductors and performed the transport measurement along the boundary with six leads. If only the Hall response is concerned, four leads are enough to observe the precisely half-quantized thermal Hall plateau in the axion insulator.

Fig. 4: Quantized thermal transport signature to identify the axion insulator.

a Schematic diagram for a cubic axion insulator device with six metallic leads on the top or bottom, respectively. Magnetization of all the surfaces points outwards and top and bottom surfaces are covered by s − wave superconductors. b and c The normalized thermal Hall conductance ${\kappa }_{xy}^{{{{{{{{\rm{TH}}}}}}}}}$ and longitudinal resistance ${R}_{xx}^{{{{{{{{\rm{T}}}}}}}}}$ as functions of pairing potential Δ with m = 0.15, 0.2, and 0.25. For Δ > ∣m∣, ${\kappa }_{xy}^{{{{{{{{\rm{TH}}}}}}}}}$ exhibits precise half-quantized value in the unit of ${\pi }^{2}{k}_{{{{{{{{\rm{B}}}}}}}}}^{2}/3h$ and ${R}_{xx}^{{{{{{{{\rm{T}}}}}}}}}$ remains zero. d Thermal transport properties as a function of the background temperature ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$ with Δ = 0 and Δ = 0.4. Here, m = 0.2. Solid or dashed lines represent the top (t) or bottom (b) surfaces. The size of the cubic is L_x = 50, L_y = 30, L_z = 20, and other parameters can be found in Supplementary Note 10.

Conclusion

We have proposed a picture of axion insulators from a Majorana perspective. The unique surface of an axion insulator can be described with Chern number ${{{{{{{\mathcal{N}}}}}}}}=\pm 1$ in the Majorana basis. We introduce the superconducting pairing potential to enrich the phase diagram and make possible an ${{{{{{{\mathcal{N}}}}}}}}=0$ phase to appear between the ${{{{{{{\mathcal{N}}}}}}}}=1$ and ${{{{{{{\mathcal{N}}}}}}}}=-1$ phases. Thus, a chiral Majorana hinge mode emerging at the boundary of the ${{{{{{{\mathcal{N}}}}}}}}=1$ and ${{{{{{{\mathcal{N}}}}}}}}=0$ regions is clearly shown. With a multi-terminal Hall device, we obtain the precise half-integer quantized thermal Hall plateau. This thermal measurement can confirm the appearance of the chiral Majorana hinge modes and serve as a transport indicator of the ${{{{{{{\mathcal{C}}}}}}}}=\frac{1}{2}$ axion states.

Method

Here, we describe the non-equilibrium Green’s function methods for calculating the thermal transport.

We first focus on the transport on the top. The temperature and heat current of leads are labeled as ${{{{{{{{\mathcal{T}}}}}}}}}_{i}$ and Q_i with i = 1, 2, 3, 4, 5, 6. The Lead-1 and the Lead-4 are heat current probes with temperature difference $\delta {{{{{{{\mathcal{T}}}}}}}}$. The other four leads on the upper and lower edges are the temperature probes with zero heat current (${{{{{{{{\mathcal{Q}}}}}}}}}_{i}=0$, i = 2, 3, 5, 6). We set Q = Q₁ = − Q₄ to describe the heat current flowing from Lead-1 to Lead-4. With the heat current Q calculated via the multi-probe Landauer-Büttiker formula^51,52,53, we define the thermal Hall resistance between Lead-6 and Lead-2 as ${R}_{6,2}^{{{{{{{{\rm{TH}}}}}}}}}=({{{{{{{{\mathcal{T}}}}}}}}}_{6}-{{{{{{{{\mathcal{T}}}}}}}}}_{2})/Q$ and the thermal longitudinal resistance between Lead-6 and Lead-5 as ${R}_{6,5}^{{{{{{{{\rm{T}}}}}}}}}=({{{{{{{{\mathcal{T}}}}}}}}}_{6}-{{{{{{{{\mathcal{T}}}}}}}}}_{5})/Q$. Set ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$ to be the background temperature. To observe the quantized thermal transport, the resistances are usually normalized with respect to ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$, i.e., ${R}_{6,2}^{{{{{{{{\rm{TH}}}}}}}}}{{{{{{{{\mathcal{T}}}}}}}}}_{0}={R}_{xy}^{{{{{{{{\rm{TH}}}}}}}}}$ is the normalized thermal Hall resistance and ${R}_{6,5}^{{{{{{{{\rm{T}}}}}}}}}{{{{{{{{\mathcal{T}}}}}}}}}_{0}={R}_{xx}^{{{{{{{{\rm{T}}}}}}}}}$ is the normalized thermal longitudinal resistance. Both ${R}_{xy}^{{{{{{{{\rm{TH}}}}}}}}}$ and ${R}_{xx}^{{{{{{{{\rm{T}}}}}}}}}$ are in unit of $\frac{3h}{{\pi }^{2}{k}_{{{{{{{{\rm{B}}}}}}}}}^{2}}$. The normalized thermal Hall conductance is expressed as ${\kappa }_{xy}^{{{{{{{{\rm{TH}}}}}}}}}=\frac{{R}_{xy}^{{{{{{{{\rm{TH}}}}}}}}}}{{({R}_{xy}^{{{{{{{{\rm{TH}}}}}}}}})}^{2}+{({R}_{xx}^{{{{{{{{\rm{T}}}}}}}}})}^{2}}$ in the unit of $\frac{{\pi }^{2}{k}_{{{{{{{{\rm{B}}}}}}}}}^{2}}{3h}$.

Besides, to present the different chirality of Majorana hinge modes, we also calculate the thermal transport on the bottom surface with six leads labeled from Lead-7 to Lead-12 [see Fig. 4a]. The thermal longitudinal transport is measured between Lead-12 and Lead-11 and the thermal Hall transport is measured between Lead-12 and Lead-8.

For simplicity, the normalized thermal transport coefficients are notated as ${R}_{xx}^{t/b}$, ${R}_{xy}^{t/b}$, and ${\kappa }_{xy}^{t/b}$, with t/b for the top/bottom surface, as shown in Fig. 4.

The heat current flowing into Lead-n is expressed as^52,53,

$${Q}_{n}= \,\frac{1}{h}\mathop{\sum}\limits_{m}\,\int (E-e{V}_{n})\left\{{T}_{nm}(E)\left[{f}_{n}^{e}(E)-{f}_{m}^{e}(E)\right]+{T}_{n}^{{{{{{{{\rm{LAR}}}}}}}}}(E)\left[{f}_{n}^{e}(E)-{f}_{n}^{h}(E)\right]\right.\\ \left.+{T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E)\left[{f}_{n}^{e}(E)-{f}_{m}^{h}(E)\right]\right\}dE,$$

(4)

where ${f}_{i}^{e}(E)$ and ${f}_{i}^{h}(E)$ are the Fermi-Dirac distribution for electrons and holes, respectively, in Lead-i. To be specific, ${f}_{i}^{e}(E)=1/\left[{e}^{(E-e{V}_{i})/{k}_{{{{{{{{\rm{B}}}}}}}}}{{{{{{{{\mathcal{T}}}}}}}}}_{i}}+1\right]$ and ${f}_{i}^{h}(E)=1-{f}_{i}^{e}(-E)=1/\left[{e}^{(E+e{V}_{i})/{k}_{{{{{{{{\rm{B}}}}}}}}}{{{{{{{{\mathcal{T}}}}}}}}}_{i}}+1\right]$. Due to the particle-hole symmetry, the term including ${T}_{n}^{{{{{{{{\rm{LAR}}}}}}}}}$ disappears when the bias voltage of all leads are to be zero eV_i = 0. So Eq. (4) is simplified as

$${Q}_{n}=\frac{1}{h}\mathop{\sum}\limits_{m}\,\int \,E\left[{T}_{nm}(E)+{T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E)\right]\left[{f}_{n}^{e}(E)-{f}_{m}^{e}(E)\right]dE.$$

(5)

In the linear regime ($\delta {{{{{{{\mathcal{T}}}}}}}}\to 0$), expand the Fermi function around the Fermi energy E = 0 and background temperature ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$ as ${f}_{n}^{e}(E)={f}_{0}(E)+\frac{\partial {f}_{0}}{\partial {{{{{{{{\mathcal{T}}}}}}}}}_{0}}({{{{{{{{\mathcal{T}}}}}}}}}_{i}-{{{{{{{{\mathcal{T}}}}}}}}}_{0})$ where ${f}_{0}(E)=1/\left[{e}^{E/{k}_{{{{{{{{\rm{B}}}}}}}}}{{{{{{{{\mathcal{T}}}}}}}}}_{0}}+1\right]$ is the Fermi distribution with neither voltage bias nor thermal gradient.

As long as ${{{{{{{{\mathcal{T}}}}}}}}}_{i}-{{{{{{{{\mathcal{T}}}}}}}}}_{0}$ is small, Q_n displays the linear form as

$${Q}_{n}=\mathop{\sum}\limits_{m}\left({{{{{{{{\mathcal{T}}}}}}}}}_{n}-{{{{{{{{\mathcal{T}}}}}}}}}_{m}\right){C}_{nm},$$

(6)

$${C}_{nm}=\frac{1}{h}\int \left[{T}_{nm}(E)+{T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E)\right]\frac{{E}^{2}}{{k}_{{{{{{{{\rm{B}}}}}}}}}{{{{{{{{\mathcal{T}}}}}}}}}_{0}^{2}}{f}_{0}(1-{f}_{0})dE.$$

(7)

At the low background temperature ${{{{{{{{\mathcal{T}}}}}}}}}_{0}$ limit, T_nm(E) and ${T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E)$ can be viewed as constant, then the heat current is reduced into

$${Q}_{n}=\mathop{\sum}\limits_{m}\left[{T}_{nm}(E=0)+{T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E=0)\right]\left({{{{{{{{\mathcal{T}}}}}}}}}_{n}-{{{{{{{{\mathcal{T}}}}}}}}}_{m}\right)\frac{{\pi }^{2}{k}_{{{{{{{{\rm{B}}}}}}}}}^{2}}{3h}{{{{{{{{\mathcal{T}}}}}}}}}_{0}$$

(8)

Above, T_nm(E) denotes the transmission coefficient of electron with energy E from Lead-m to Lead-n, ${T}_{n}^{{{{{{{{\rm{LAR}}}}}}}}}(E)$ denotes the local Andreev reflection coefficient at Lead-n, and ${T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E)$ denotes the cross Andreev reflection coefficient from Lead-m to Lead-n. All these transport coefficients are calculated as⁵¹, ${T}_{nm}(E)={{{{{{{\rm{Tr}}}}}}}}\left[{{{\Gamma }}}_{n}^{e}{{{{{{{{\bf{G}}}}}}}}}^{r}{{{\Gamma }}}_{m}^{e}{{{{{{{{\bf{G}}}}}}}}}^{a}\right]$,${T}_{n}^{{{{{{{{\rm{LAR}}}}}}}}}(E)={{{{{{{\rm{Tr}}}}}}}}\left[{{{\Gamma }}}_{n}^{e}{{{{{{{{\bf{G}}}}}}}}}^{r}{{{\Gamma }}}_{n}^{h}{{{{{{{{\bf{G}}}}}}}}}^{a}\right]$, and ${T}_{nm}^{{{{{{{{\rm{CAR}}}}}}}}}(E)={{{{{{{\rm{Tr}}}}}}}}\left[{{{\Gamma }}}_{n}^{e}{{{{{{{{\bf{G}}}}}}}}}^{r}{{{\Gamma }}}_{m}^{h}{{{{{{{{\bf{G}}}}}}}}}^{a}\right]$, where ${{{{{{{{\bf{G}}}}}}}}}^{r}(E)={\left[{{{{{{{{\bf{G}}}}}}}}}^{a}\right]}^{{{{\dagger}}} }={\left[(E+{{{{{{{\bf{i}}}}}}}}\eta ){{{{{{{\bf{I}}}}}}}}-{{{{{{{\bf{H}}}}}}}}-{\sum }_{n}{{{\Sigma }}}_{n}^{r}\right]}^{-1}$. Here, H is the whole Hamiltonian of the axion-insulator-based device in Fig. 4a. Γ_n is the line-width function and remains constant as Γ in the wide-band limit. The self-energy term is ${{{\Sigma }}}_{n}^{r}=-\frac{{{{{{{{\bf{i}}}}}}}}}{2}{{{\Gamma }}}_{n}$. η is the infinitesimal energy relaxation rate describing the damping of quasiparticles inside leads. In the calculation, we set Γ = 2, η = 10⁻⁹. And details of the device and leads for the numerical calculation can be found in Supplementary Note 10.