Introduction

In the past two decades, laser-driven proton acceleration has been widely studied for its significance in applications such as probing high energy density states1, treating cancer therapy2, fast ignition fusion3, laboratory astrophysics4, and so on. These applications impose certain requirements for the energy and current intensity of proton beams. By optimizing the laser conditions and thickness of planar targets, protons could be accelerated up to 85 MeV via the robust target normal sheath acceleration (TNSA) mechanism5,6,7. A higher cutoff energy of 94 MeV has been reported via hybrid scheme of radiation pressure-sheath acceleration in an ultrathin planar foil8. These sub-100MeV protons are obtained by relatively long laser pulses of 100’s J energies. For femtosecond lasers, typical cutoff energy of protons lies in 30–70 MeV using planar targets9,10,11, since the pulse energy is usually much less than picosecond lasers.

Realizing the above-mentioned applications of laser-driven proton sources strongly relies on maximizing the laser-proton energy conversion efficiency. In laser-foil interaction, reducing target thickness12 is usually adopted to improve laser-to-proton energy conversion efficiency. In general, plasma targets irradiated by picosecond lasers behave differently from a femtosecond laser because the instability of the plasma and self-generated electromagnetic fields expand over time13,14. Consequently, high laser-to-proton energy conversion efficiency up to 10–15%5,15 tends to appear in TNSA when using large energy picosecond laser pulses. The efficiency of 3–4%11,16 is achieved on femtosecond lasers of much lower pulse energy, which is still below the theoretical value ~8% predicted by Sentoku et al.17.

For ultra-short laser pulses, optimizing the target condition to enhance the laser absorption efficiency has become a promising solution. Employing carbon nanotube foam on a planar diamondlike carbon foil has realized triple energy gain for protons18,19. An alternative method is to introduce periodic/aperiodic nano/micro-structures in front of planar targets20,21,22,23,24,25,26,27,28. Experimental data indicate that microstructure can greatly raise the temperature of hot electrons beyond that of the ponderomotive acceleration29,30. In the case of picosecond relativistic lasers irradiating microstructure targets at large angles, the yield of electron and X-ray could be increased31,32, but the proton energy from TNSA remains unchanged27 or even becomes less33. The main reason is that the rising edge of picosecond lasers is long enough to ionize the surface structure so that the plasma infill could shutter the laser from further interaction. Considerable energy enhancement for protons has been observed by using defocused picosecond lasers with normal incidence (1017–1018 W cm−2)25. The effect of pre-plasma infill is suppressed when employing ultrashort femtosecond relativistic lasers28. Judging from the reported results, when using fine surface structures to improve proton acceleration in TNSA, high contrast femtosecond lasers with an incidence angle as small as possible is more favorable.

We notice that the fast development of three-dimensional (3D) nano-printing technique allows for well-controlled fabrication of fine solid structures. The two-photon polymerization method can readily achieve lateral resolution ~100 nm and vertical resolution ~500 nm34. Compared to other approaches such as Si semiconductor-based technique33 and electrochemical deposition method28, 3D nano-printing can accurately print various complex structures as desired in experiments at micro or sub-micro scale. It is therefore timely to apply this advanced technique to laser-plasma physics such as to manipulate ultrafast laser-plasma interaction22, generation of high bright X/gamma-ray35, high power coherent Terahertz36, and positrons37.

In this paper, we use the Nanoscribe 3D printer38 to fabricate microwire array (MWA) onto SiN flat foils and investigate laser-driven proton acceleration at various spacing conditions of the array. The MWA structure boosts the laser-to-proton energy conversion efficiency to 8.7% (total number 1.2 × 1012 for proton energies more than 1 MeV), about three times more than that of flat foils of optimal thickness. It reaches 25 MeV (MWA targets) at on-target laser intensity of about 2.2 × 1020 W cm−2, which is 30% more than that of the optimized flat foil (1 µm-thickness). We change the spacing of MWA precisely via 3D nano-printing and find out how it influences the proton acceleration process. Our 2D hydrodynamic simulations point out that the pre-plasma condition of MWA targets induced by the pre-pulse is significantly different from the flat target case where the density length scale is almost uniform in the latter. The micro-structures can induce strong diffraction of the incident pre-pulse, resulting in featured pre-plasma distributions depending on the surface profile. After bringing the pre-expansion plasma conditions into 2D particle-in-cell (PIC) simulations, we reproduce the experimental results and find the optimal MWA parameters for proton acceleration.

Results and discussion

Experimental set-up

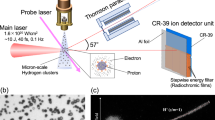
The experiments were carried out in a petawatt-class Ti:sapphire laser system with central wavelength λ = 800 nm, which delivers around 15 ± 2 J on-target energy within 35 fs duration (full width at half maximum, FWHM) in the current run. About 40% of the laser energy is enclosed in a focal spot of 10 μm diameter (FWHM), yielding a peak intensity of about (2.2 ± 0.3) × 1020 W cm−2. The laser contrast of amplified spontaneous emission pedestal is ~1011 (1010) at 30 (6) ps prior to the main pulse39, which could induce pre-plasmas with typical scale length of several hundreds of nanometers40. The sketch of the experimental setup is shown in Fig. 1a. The p-polarized laser pulse is focused by a f/4 off-axis parabolic mirror onto the target at an incident angle of 5.5°, which is the smallest angle one can set to avoid light backscattering to the laser chain. A stack of radiochromic films (RCFs) with a 3 mm-diameter hole in the center are enwrapped with 15 μm-thickness Al foil to shield the stack from debris. It is located at L1 = 5.3 cm to measure the proton energy spectrum and profile. Several EBT3-type RCFs of high sensitivity are placed behind the HD-V2s in stack to guarantee the accuracy near the spectral cut-off. The ion transport code SRIM41 was used to model the range of proton energies stopped in each layer. Following that a Thomson parabola spectrometer (TPS) equipped with a BAS-TR image plate is set at L2 = 46 cm. Both of RCF stacks and TPS are aiming at the target normal direction.

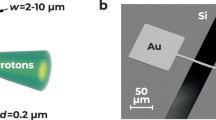
Fig. 1: Experimental arrangement and preparation of microwire array (MWA) targets.
figure 1

a Sketch of the experimental setup. b Schematic diagram of laser direct writing that prepares the MWA structure: the laser pulses with wavelength of 780 nm and duration of 100 fs are controlled via the galvanometer system to scan space voxel in the photoresin after the objective lens and the laser pulse energy is modulated by the acousto optic modulator. c, d Show the scanning electron microscope images of MWA with periods of 1.3 and 3.3 μm, respectively.

Full size image

We fix the diameter and height of the micro-wires of MWA targets at d = 0.4 μm and h = 2.5 μm and vary the period, i.e., p = 1.3, 1.8, 2.3, and 3.3 μm. The diagram of laser direct writing (see “Methods”) employed in our experiment is sketched in Fig. 1b. Figure 1c, d shows the scanning electron microscope images of two typical printed MWA structures with p = 1.3 and 3.3 μm, respectively. The MWAs are printed onto 1 μm-thickness (the optimal thickness of flat foils for TNSA under the current laser condition) SiN foil, covering an area of about 400 μm × 400 μm. This is much greater than the laser focal spot such that the laser beam could hit the MWA considering the beam jitter. The printed material is polymer with a mass density of 1.17 g cm−3. In addition, ultra violet treatment is employed before they are dried to maintain the stability of the structures42.

Enhancing proton acceleration

At given pre-pulse condition there exists an optimal thickness of planar targets for TNSA43. To identify the enhancement brought by the micro-structure, it is very important to exclude the effect of target thickening due to the additional structure. Therefore, before doing comparison we first find out the optimal foil thickness that gives highest proton energy. This was omitted in previous reports26,27,28, where the structure target is compared to the planar target with the same thickness of only the substrate, or the structure (substrate thickness is ignored). We scan over the thickness of planar SiN layers from 0.2 to 4.0 μm and summarize the measured results in Fig. 2a (black square). It can be clearly seen that with the target thickness increasing, the cut-off energy of protons increases first and then declines. For 1 μm-thickness flat foils, the proton energy reaches maximum of 18–19 MeV.

Fig. 2: Results of experiment and interpreting simulations.
figure 2

Cut-off proton energy (a) and energy conversion efficiency (b) as a function of the thickness of planar SiN foils (black) and the spatial period of microwire array (MWA) targets (red), from experiments (solid dots) and simulations (solid lines). The conversion efficiency from laser to protons (kinetic energy > 1 MeV) is obtained from the radiochromic film (RCF). Here the high conversion efficiency for 0.2 μm results from more complicated mechanisms thus is excluded from comparison. The error bars are defined by standard deviation from the mean of different shots. It should be noted that the calculation of conversion efficiency takes into account the laser energy measured in each shot. The light-gray shadings represent the scope of cutoff energy or conversion efficiency that planar targets involve. c Proton spectra obtained from RCF stacks (scattered points) and Thomson parabola spectrometer (TPS, dashed lines) for 1 μm SiN foils, and MWA targets with three periods of 1.3, 2.3, and 3.3 μm, respectively. The horizontal error bar marked for p = 3.3 μm as the last sheet of RCF stack changed color in this shot. The inset of (c) is the simulated proton spectra.

Full size image

For the case of MWA targets, the substrate thickness remains unchanged at 1 μm. Figure 2a also shows the measured cutoff energy of protons as a function of the microwire period of MWA targets (red circle). It should be noted that the cut-off energy for all period conditions of MWA targets are above the highest obtained with flat foils. As the array period increases from 1.3 to 3.3 μm, the cut-off energy of protons rises from 20 to 25 MeV. The maximum energy gain of protons is experimentally observed for MWA targets of 3.3 μm period, which is 30% more than that with 1 μm SiN-foil. The combined substrate and structure correspond to an effective thickness of about 4 μm for flat SiN-foil. When comparing to the latter, the MWA energy enhancement is close to 70%.

Representative proton spectra obtained from RCF stacks over the whole proton beam and TPS for 1 μm SiN foils, and MWA targets with three periods of 1.3, 2.3, and 3.3 μm are shown in Fig. 2c. The absolute response of the RCF dosimeter was calibrated following the method introduced previously44,45. The experimental results of proton spectra from RCF stacks are consistent with that of TPS. The total number of protons for MWA targets of 3.3 μm period with energy more than 1 MeV is about 1.2 × 1012 according to RCF spectrum integral, approximately 2.5 times more than that of 1 μm SiN foils of 4.8 × 1011. Here, the Al layer with thickness of 15 μm could minimize possible dose contribution from other heavy ion species. The presence of this foil limited the minimum detectable proton energy to around 1 MeV.

Further, the laser-to-proton energy conversion efficiency (η) is summarized in Fig. 2b. As the foil thickness decreases from 4 μm to 200 nm, a clear increase in conversion efficiency is observed. The number of 4.5% obtained with 200 nm flat can be interpreted as the appearance of piston-like acceleration due to the initial density gradient of rear pre-plasma11,46. To exclude this complication, we limit our discussion in the TNSA-dominated regime (thickness ≥1 μm). In this case, the maximum η of planar SiN is about 2.9 ± 0.2% for 1 μm SiN foils. When equipping MWA on 1 μm SiN foils, the η is significantly enhanced. The efficiency exhibits similar variation tendency as the cutoff energy such that the η increases with larger array spacing. The maximum η of MWA target reaches to 8.7% for one shot at p = 3.3 μm, corresponding to a total of 1.1 J for protons with energy > 1 MeV. This is three times that of the average value for the 1 μm SiN foil thickness. This high conversion efficiency is at the top end of report values for TNSA driven by Ti:sapphire based 10’s J laser systems11,16, which exceeds the maximum conversion efficiency predicted theoretically [30]. It should be noted that even though the cut-off energy for 1.3 μm MWA targets is almost the same as that of the 1 μm SiN, the energy conversion efficiency is almost doubled for the former. Both the cut-off energy and conversion efficiency increase with larger spatial period, indicating that the acceleration does not reach maximum for the MWA periods chosen in the current run. We, therefore, perform further simulations to interpret the experimental observation and more importantly, to find out the optimal condition for laser-proton acceleration.

Simulations

To better understand the experimental results, we carry out hydrodynamic and PIC simulations. The pre-plasma distribution is determined by 2D hydrodynamic simulations in Cartesian coordinate system using the FLASH47 code. Limited by the available material in the code, the Al material data is used in numerical simulation. The 3D-printed-MWA parameters are inputted into FLASH. After the pre-pulse ablating MWA targets, it can be seen from Fig. 3b that the heads of the pillars expand more than their roots. The plasma forms large clouds around the tips, which narrows the gap between the wires. This type of plasma expansion is more severe for denser pillar arrays. It may even shutter the laser from further interaction as shown in Fig. 3a. Figure 3c, d shows the mass density distribution along three y-positions y = 17, 18, and 19 μm from Fig. 3a, b, corresponding to the inside, edge, and outside of the array respectively. Obvious blocking inside the array can be seen in Fig. 3c, while the structure remains open for arrays with larger gaps (p = 3.3 μm) in Fig. 3d.

Fig. 3: The characteristics of pre-plasma for microwire array (MWA) target.
figure 3

Expanded pre-plasma of MWA targets after loading the pre-pulse in FLASH simulations for p = 1.3 μm (a) and p = 3.3 μm (b). Mass density distribution along y = 17 μm (black), 18 μm (blue) and 19 μm (red) for p = 1.3 μm (c) and p = 3.3 μm (d) related to (a), (b), respectively. The diffracted pre-pulse field Ex within the MWA structure (e). The density distribution of pre-expanding MWA target based on the FLASH results (f), which is inputted into particle-in-cell simulations. The inset shows the pre-plasma scale lengths, where lh and lx are for the pillars, and lf for the substrate flat.

Full size image

We further show the laser field distribution when incident onto the MWA structure. As seen in Fig. 3e, the laser field is diffracted by the periodic structure such that it is locally intensified around the tips of the pillars. Modulated laser intensity produces pre-plasma of larger scale length in the light-intensified vicinity, leading to the featured plasma profile in Fig. 3a, b.

Based on the results of FLASH simulations, we set the density distribution of pre-expanding MWA targets in Fig. 3f. Each pillar is surrounded with modulated pre-plasma of two components. Around the tip the pre-plasma forms a semicircular density profile with \({n}_{{{{{\rm{pre1}}}}}}={n}_{e1}\exp (-\varDelta r/{l}_{h})\), where ne1, Δr, and lh are the pillar electron density, the distance to the tip center, and the corresponding density scale length, respectively. The pre-plasma density in the rest area takes the form \({n}_{pre2}={n}_{e{1}}\exp \left(\right.{-}(\varDelta y/{l}_{h}+\varDelta x/{l}_{x})+{n}_{e{2}}\exp (-\varDelta x{\prime} /{l}_{f})\), where ne2, \(\varDelta (x,x{\prime} ,y)\), lx,f, are the foil electron density, the distance to initial target boundary, and the related scale lengths, respectively.

We take the above-modulated pre-plasma distribution in the following 2D PIC simulations using the code EPOCH48. The simulation box size was Wx × Wy = 65 μm × 30 μm with the cell size of dx = 4 and dy = 8 nm. Particle-per-cell is set to 9. The p-polarized Gaussian laser pulse is incident at 5.5° from the left side with a central wavelength of 800 nm of pulse duration of 35 fs (FWHM). Its peak intensity reaches 2.2 × 1020 W cm−2 after being focused to 10 μm spot size. Those parameters are the same as experimental conditions. The targets are fully ionized as cold plasma, which is initially neutral. The flat targets consist of Si14+ and N7+ with the same density of 12 nc (total electron density is ne = 252 nc, nc = meω2/4πe2 is the critical density). A thin CH contaminant layer of 20 nm and electron density 45 nc is attached to the rear side of the foil. The front surface of flat target is located at x = 0, with pre-plasma of scale length lf = 100 nm. We vary the foil thickness between 0.2, 1, 2, and 4 μm. In particular, for the ultrathin 0.2 μm foil a rear pre-plasma with the same scale length is also added11. The related simulation results of cut-off energy and spectra of protons are summarized in Fig. 2a and the inset of Fig. 2c, which are in reasonable agreement with the experimental results.

The pre-plasma parameters for MWA targets employed in 2D PIC simulations are based on the hydrodynamic results as shown in Fig. 3f. For spatial period of 2.3 and 3.3 μm, we set lh = 350 nm and lx = 1 μm while the one of the flat foil is lf = 100 nm, according to the modulated pre-pulse intensity by the periodic structure. At small period of 1.3 μm, lh is set to 100 nm according to the distribution in Fig. 3a. Here the wires are defined as fully ionized CH and the electron density is 210 nc (mass density ~1.17 g cm−3).

From the electron energy spectra in Fig. 4a it is seen that the MWA generates much higher temperature probably due to the direct laser acceleration (DLA) mechanism49. Here the highest temperature appears at p = 5.3 μm, which was not tested in the current experimental run. The corresponding temporal evolution of the longitudinal electric field Ex are plotted in Fig. 4b. We see that the peak field strength is largely enhanced due to the MWA. For the spatial period shown here (3.3 μm), one finds higher peak value for the situation without pre-plasma while a slow decrease with pre-plasma, indicating stronger proton acceleration for the former. As pointed out in previous studies27,29,30,50, enhancement of the sheath field results from the higher population of energetic electrons generated in micro-structures.

Fig. 4: Parametric simulation results for proton acceleration.
figure 4

a The electron spectra and temperature under pre-plasma conditions. The dashed lines are fits to the data. b The temporal evolution of Ex which is averaged in an area of 2 μm (x) × 8 μm (y) behind the substrate. c Proton maximum energy as a function of lh and lx scale length. d Proton maximum energy versus wire period with and without pre-plasma, while the diameter and height of the wire are 0.4 and 2.5 μm, respectively. The conversion efficiencies from the simulations in d are calibrated with the average value measured in experiment for p = 3.3 μm which gives a fixed ratio for all simulation data.

Full size image

The scale lengths of lh and lx have different influence on the proton maximum energy, as illustrated in Fig. 4c, where lf is fixed to 100 nm. When changing lx from 0.5 to 5 μm with lh = 350 nm, the proton cut-off energy remains at 27–28 MeV. The scale length of lf has similar effects when changing within several hundred nanometers range. However, the maximum energies drop from 35 to 22 MeV when slightly increasing lh from 250 to 450 nm with lf = 1 μm. It suggests that proton cut-off energy is more sensitive to the scale length of the wire tip lh, which is closely related to the modulated plasma expansion resulting from pulse diffraction.

In other words, the laser contrast has a significant impact on proton acceleration when using MWA targets. Figure 4d shows proton maximum energy as a function of the wire period with and without pre-plasma. When the pre-plasma is absent, proton energy is maximized to 42 MeV at optimal period around 2.3 μm. However, when introducing the modulated pre-plasma, the energy distribution shows slightly lower peak value of 37 MeV at much larger spatial period 5.3–6.3 μm. This trend agrees well with the electron temperature in Fig. 4a and more importantly, with the experimental observation, for the spacings we investigated here. The trend as a function of parameters beyond the current scope will be further explored. Because of the modulated pre-plasma in MWA, the optimal period for proton acceleration is modified such that one should increase the spatial period as compared to the case when no pre-plasma is considered. However, there is also tradeoff of using MWA with larger spacing. For finite laser spot size, decrease of wire number covered by the laser beam may lead to energy drop for protons28. In our case, optimized laser-proton acceleration is achieved when the laser spot size covers 0.7–1.5 unit. In the current experimental run, we had best results at p = 3.3 μm.

In addition, the energy conversion efficiency from simulations is plotted in Fig. 4d after including the pre-plasma condition. Since the simulations are 2D, we calibrate the efficiency with the average value of 6.9% measured in experiment for p = 3.3 μm, which gives a fixed ratio for all simulation data. The efficiency shows similar trend as the cut-off proton energy. The highest efficiency appears for p = 5.3 μm. When using the maximum calibration factor (8.7% for p = 3.3 μm measured in experiment), the η could boost to 10.7% with p = 5.3 μm.

Snapshots of phase space distribution of electrons at t = 100 fs from simulations are shown in Fig. 5a–c respectively in three cases. It can be seen that, for MWA target, the momentum of electrons moving towards target rear direction are higher than planar target. These highly directional electrons efficiently enhance the sheath filed. However, the pre-plasma of MWA could impair the DLA effect, therefore the proton energy is lower than that of clean structures. Longitudinal electric field Ex at t = 100 fs are shown in Fig. 5d–f. It is observed that the field strength and length scale are both evidently larger for MWA targets. When introducing pre-expanding plasma, much of the main laser pulse is reflected while only part of the laser pulse could propagate into structure, as shown in Fig. 5e. In this case, DLA of electrons becomes less effective. Comparing to the case without pre-plasma (Fig. 5f), the peak acceleration field is smaller in Fig. 5e which can also be seen in Fig. 4b. These distributions agree with the comparison in Fig. 4d for p = 3.3 μm. We notice the periodic structure induces diffraction for the main laser pulse in both cases. The reflected laser field is diffracted along large divergence angles while the sheath field is also modulated with significant periodic and divergent patterns. The difference between each case is also imprinted onto the proton acceleration process, as shown in Fig. 5g–i, where the one without pre-plasma generates several streams of protons following each unit of micro-wire. We did not see the streamed profile in the current experimental run due to the pre-pulse condition here. This feature could be further measured as an identification of the clean micro-structures during interaction, with higher beam contrasts enabled by plasma mirrors.

Fig. 5: The Comparison of proton acceleration processes under different target conditions.
figure 5

The phase space distribution of electrons for 1 μm planar target (a) and p = 3.3 μm microwire array (MWA) target with pre-plasma (b) and without pre-plasma (c). d–f The distribution of longitudinal electric field Ex. The fields are normalized to the incident laser electric field E0 = 4.1 × 1013 V m−1. g–i Proton energy (MeV) distribution at t = 300 fs.

Full size image

Conclusions

In conclusion, using a 3D-nano printer to fabricate MWA structures onto the front surface of flat foils, we have experimentally demonstrated simultaneous increase of the proton maximum energy and laser-proton energy conversion efficiency. We identified the effect of pre-plasma modulation caused by the diffraction of laser pre-pulse in MWA structure, which successfully interprets the experimental results. This is the first time to reveal the role of the scale length lh of the tip of wire structures, which depends on the wire gap and laser pre-pulse. Adjusting the wire number in the laser focal spot and the wire gap could further improve proton cutoff energy.

Methods

MWA fabrication

The 3D printing machine we employed is based on two-photon polymerization technique34. A brief schematic diagram is shown in Fig. 1b. A femto-fiber laser system delivers pulses at a center wavelength of 780 nm with a repetition rate of 80 MHz. The light pulses typically exhibit a duration of 100 fs with an average power of more than 350 mW. The laser is guided into the objective lens with a magnification of 63 × (NA1.4) and focused on the sample surface. The photo-resin is partial exposed following the designed structure model. To remove unexposed photo-resist, the structures are developed in the developer liquid followed by careful rinsing with isopropanol. After ultra violet treatment42 and natural drying in air, solid structures are obtained. The structure is a polymer C14H18O7 with a mass density of ~1.17 g cm−3. We use the commercial 3D printer of Nanoscribe Photonic Professional GT138 to fabricate MWAs onto the 1 μm SiN substrates within an area of 400 μm × 400 μm. The diameter and height of microwires were fixed at d = 0.4 μm (the minimum value we can get) and h = 2.5 μm (the largest length for the input diameter to maintain the structure stability), while their period varied from p = 1.3 μm to p = 3.3 μm. Spacing beyond 3.3 μm was not tested due to the limited beam time.

Simulations

The hydrodynamics simulations were performed using the 2D FLASH code47 in Cartesian coordinate system. A flat-top laser with a steep rising edge irradiated the Al MWA at an incident angle of 5.5°. The material initial temperature was set to 290 K. The laser intensity is 5 × 109 W cm−2 and ablation time was 500 ps for Fig. 3a, b. The PIC simulation was performed using the 2D EPOCH code48. The simulation box was 65 μm × 30 μm with mesh cell size equal to 4 nm × 8 nm. The incoming laser pulse temporal and spatial profiles were both Gaussian, with FWHM equal to 35 fs and 10 μm, respectively. The peak intensity was 2.2 × 1020 W cm−2. Open boundary condition was used in all simulations. The flat targets were initialized as a uniform mixture of Si14+ and N7+, both at 12 nc. The flats coupled with CH contaminant layers at the rear of the film with thickness of 20 nm and electron density of 45 nc. For MWA targets, the wires were defined as fully ionized CH and the electron density were 210 nc (mass density ~1.17 g cm−3). Each pillar is surrounded with modulated pre-plasma of two components. Around the tip the pre-plasma forms a semicircular with \({n}_{{{{{\rm{pre1}}}}}}={n}_{e1}\exp (-\varDelta r/{l}_{h})\), where ne1, \(\varDelta r\), and lh are the pillar electron density, the distance to the tip center, and the corresponding density scale length, respectively. The pre-plasma density in the rest area takes the form \({n}_{{{{{\rm{pre2}}}}}}={n}_{e{1}}\exp \left(\right.-(\varDelta y/{l}_{h}+\varDelta x/{l}_{x})+{n}_{e{2}}\exp (-\varDelta x{\prime} /{l}_{f})\), where ne2, \(\varDelta (x,x{\prime} ,y)\), lx,f, is the foil electron density, the distance to initial target boundary, and the related scale lengths, respectively. The substrate was the same as the flat situation.