Abstract
PdCoO2 layered delafossite is the most conductive compound among metallic oxides, with a room-temperature resistivity of nearly \(2\,\mu \Omega \,{{{{{\rm{cm}}}}}}\), corresponding to a mean free path of about 600 Å. These values represent a record considering that the charge density of PdCoO2 is three times lower than copper. Although its notable electronic transport properties, PdCoO2 collective charge density modes (i.e. surface plasmons) have never been investigated, at least to our knowledge. In this paper, we study surface plasmons in high-quality PdCoO2 thin films, patterned in the form of micro-ribbon arrays. By changing their width W and period 2W, we select suitable values of the plasmon wavevector q, experimentally sampling the surface plasmon dispersion in the mid-infrared electromagnetic region. Near the ribbon edge, we observe a strong field enhancement due to the plasmon confinement, indicating PdCoO2 as a promising infrared plasmonic material.
Similar content being viewed by others
Introduction
Surface plasmons, the collective oscillations of electrons in metals and doped semiconductors, show outstanding electromagnetic (EM) properties spanning from a reduced wavelength in comparison to that of an exciting electromagnetic field, an extreme local electric field enhancement several orders of magnitude larger than the incident em field, to several nonlinear effects like harmonic generation and optical rectification1. Those properties are the basis of nano-infrared and surface-enhanced Raman spectroscopies, currently applied in many bio-sensing techniques1,2,3,4. Although conventional metals, like gold and silver, are usually used in plasmonics1, non-conventional conductors like graphene5,6,7, transparent oxides8, high-Tc superconductors9,10, strongly-correlated oxides11,12,13, and topological materials14,15,16 are now on the scientific edge, providing additional properties like plasmon tunability due to their extreme sensitivity, to external parameters like doping, temperature, and electric and magnetic fields17. Among metallic oxides, PdCoO2 layered delafossite is the most conductive, having a room-temperature resistivity of nearly \(2\,\mu \Omega \,{{{{{{\rm{cm}}}}}}}\), corresponding to a mean free path of about 600 Å 18,19. These values are comparable to those of the best three-dimensional (3D) metallic conductors such as Al, Au, Cu, and Ag, although the charge density of PdCoO2 is ~30% the copper one. PdCoO2 has a nearly two-dimensional (2D) layered structure composed of Pd triangular layers and CoO2 slabs18. Theories20,21,22,23 and experiment24 show that the electronic density of states at the Fermi level is dominated by Palladium indicating that the electronic states are nearly 2D. Its single-particle electrodynamics has been measured on single crystals25 and it is dominated at Infrared (IR) and Terahertz (THz) frequencies by intraband excitations, well described by the Drude model, while interband transitions appear above 8000 cm−1 (1 eV). Although the very long mean free path at room temperature, and the nearly perfect separation between intra- and interband electronic transitions provide an ideal framework for investigating the collective electronic excitations (surface plasmons) of PdCoO2 layered delafossite, these modes have never been measured to our knowledge.
Here, we report experimental evidence of surface plasmonic excitations in thin films of PdCoO2 on sapphire substrates. In particular, we have fabricated parallel ribbons array structures of PdCoO2 and investigated their optical properties from THz to Visible (VIS) for light polarization parallel and perpendicular to the ribbons. When the polarization is perpendicular to the ribbon array, one excites plasmon modes at the surface of the PdCoO2 film. Through the measurements of several ribbon arrays, we have sampled the plasmon frequency vs. wavevector, being able to experimentally determine the energy/momentum dispersion of surface plasmons in PdCoO2.
Results and discussion
Five 100 nm films of palladium-cobalt delafossite were grown by molecular beam epitaxy (MBE) on 500 μm thick Al2O3 substrates26 (see Methods). The reflectance R(ω) of an as-grown film was measured across the THz to ultraviolet (UV) spectral range with a Fourier-transform Michelson interferometer (THz-IR) and a near-infrared (NIR)-UV spectrophotometer. R(ω) spectrum (Fig. 1a), shows a Drude-like behavior at THz and Mid-IR (MIR) frequencies, while hosting interband features in the NIR-UV range, in agreement with the previous bulk characterization of this material25. R(ω) spectra have been analyzed through the RefFit program27, taking into account the optical properties of the sapphire substrate measured in the same experimental conditions. The bare PdCoO2 reflectance (as extracted from RefFit fitting) is represented in the inset of Fig. 1a, showing a value around 1 from THz to MIR. Using the f-sum rule (see “Methods”), we obtain a plasma frequency of \(16800\pm 300\,{{{{{{\rm{cm}}}}}}}^{-1}\). This value is nearly two times lower than the bulk one25 in agreement with the decrease of the material conductivity in thin films26.
a Reflectance of the as-grown, unpatterned film of PdCoO2. The inset in the right upper side shows the bare reflectance of PdCoO2 extracted through RefFit program. b Scanning electron microscope (SEM) image of the W = 1 μm patterned film. The bar-size is 5 μm. c Reflectance of the four patterned films, with the radiation electric field parallel to the ribbons (left column) and perpendicular to the ribbons (right column). Arrows indicate approximately the frequency location of surface plasmon excitations. d Optical microscope images of the four patterned films with different widths W and periods 2 W. All the images have the same dimensions. Brighter parts are related to the oxide film, while darker regions are associated to the sapphire substrate.
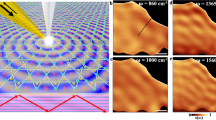
Micro-ribbon arrays (Fig. 1b) of different widths W and periods 2W have been fabricated through electron lithography (see Methods), to select suitable values of the plasmon wavevector q, so that a series of discrete values of \(q=\pi /W\) were obtained. In Fig. 1b we show a Scanning Electron Microscope (SEM) image for the \(W=1\,\mu {{{{{\rm{m}}}}}}\) patterned film, while in Fig. 1d, the optical images of all patterned films are reported. Plasmon excitations have been studied by measuring the reflectance of patterned samples for light polarization perpendicular to the ribbons (Fig. 1c) and comparing them to those with opposite polarization (Fig. 1c). When the electric field is parallel to the ribbons, one measures the Drude response of the film+substrate renormalized by the patterning. This is particularly evident for the \(W=5\,\mu {{{{{\rm{m}}}}}}\) pattern, where one clearly observes the main sapphire phonon located around 600 cm−1. This phonon is progressively shielded by the metallic response of the film for decreasing W. At W= 500 nm, a reflectance resembling that of the unpatterned film is finally reached. Plasmonic excitations are generated at the interface between a metal and a dielectric1 and, for the metallic films here considered, two different surface plasmons are expected: one at the interface between the PdCoO2 metal and sapphire substrate, and a second between metal and air (or vacuum)28. These modes can be excited when the electric field is perpendicular to the ribbons, appearing in the reflectance as a dip in an otherwise flat metallic response28,29. In our case, one indeed observes two peaks separated by a dip (see black arrows in Fig. 1c) in all patterned films, followed by a broader minimum. Although the second spectral feature is broader and then less visible in the experimental reflectances than the first one, both shift to higher frequencies as expected for an increasing plasmon wavevector \(q=\pi /W\). In order to better highlight the plasmonic absorption, we subtract from the reflectances in Fig. 1c, both the sapphire phonon contribution below \(\sim 1000\) cm−1 and the high-frequency background above ~7000 cm−1. This background is practically independent of patterning and polarization coming by high-frequency intrinsic electronic interband transitions of PdCoO2. The results are finally shown in Fig. 2, where we plot all plasmon excitations at different W. From this figure, the plasmon absorptions in patterned PdCoO2 as well as and their hardening vs. \(q=\pi /W\) are fully evident. A comparison among plasmonic experimental data, electromagnetic simulations and an analytical model allows us to assign the low-frequency dips to plasmons living at the PdCoO2–sapphire interface, while the high-frequency broad minima to plasmons at the PdCoO2–air interface. These assignments have been obtained by two different methods. In the former we simulate reflectance curves of patterned films through the COMSOL electromagnetic simulation program (see Methods), using as input the experimental conductivity of PdCoO2 unpatterned film. Simulated R(ω) for light polarization perpendicular to the ribbon array are represented (red lines) in Fig. 3a for the \(W=2\,\mu {{{{{\rm{m}}}}}}\) sample and in Fig. 3b for the \(W=1\,\mu {{{{{\rm{m}}}}}}\), respectively. They are in very good agreement with experimental data (blue lines). Simulations have been performed also for a patterned self-standing PdCoO2 film (PdCoO2–air interface), showing that the broad feature, observed in Fig. 3 at a higher frequency with respect to the dip, is related to plasmons at the same interface (see Supplementary Methods II). In the second approach, we model the Fresnel reflection coefficient of the PdCoO2 film on sapphire through a thin film approximation
where \({\varepsilon }_{s}(\omega )\) and \({\sigma }_{f}(\omega )\) are the dielectric function of sapphire or air, and the optical conductivity of the PdCoO2 film, respectively. d is the thickness of the film (\(d=100\,{{{{{\rm{nm}}}}}}\) in our case), \({Z}_{0}=377\,\Omega\) is the impedance of free space, and q⊥ and \({q^{\prime} }_{\perp }\) are the incident and transmitted (inside the film) wavevectors of the light, perpendicular to the film surface.
Model and simulated reflectances are shifted along the y-axis with an offset of 0.1 and 0.3 (a), and 0.2 and 0.4 (b), respectively. The dip in the reflectance spectra is related to plasmon excitations at the PdCoO2–sapphire interface, the broad minima at a higher frequency to the PdCoO2–air interface.
Since the light polarization is perpendicular to the ribbon array, the transmitted light wavevector acquires an additional longitudinal wavevector \({q{\prime} }_{\parallel }=\pi /W\) due to the pattern30. The normal incident light has thus a wavevector \({q}_{\perp }={q}_{0}=\omega /c\), while its transmitted component \({q{\prime} }_{\perp }=\sqrt{{\varepsilon }_{s}(\omega ){q}_{0}^{2}-{q{\prime} }_{\parallel }^{2}}\), with \({q{\prime} }_{\parallel }=\pi /W\). This model is valid as long as the incident light wavelength is higher than the film penetration depth, a condition satisfied in our PdCoO2 thin films. By remembering that we are in a half-filling condition, i.e., the array periodicity is \(p=2W\), where W is the ribbon width, the experimental reflectance of the ribbon-array patterned films can be obtained through the complex superposition of the ribbon covered and uncovered sapphire regions contributing to the Fresnel coefficient:
The calculated reflectances (black lines) for the \(W=1\,\mu {{{{{\rm{m}}}}}}\) and \(W=2\,\mu {{{{{\rm{m}}}}}}\) patterned films are represented in Fig. 3a, b, respectively in comparison to data (blue lines) and electromagnetic simulation (red lines, see above). In the calculation, we use both the experimental PdCoO2 conductivity \({\sigma }_{f}(\omega )\) and the experimental dielectric function of the sapphire substrate \({\varepsilon }_{s}(\omega )\). A similar calculation for the PdCoO2–air interface (\({\varepsilon }_{s}(\omega )\) = 1) is shown in Fig. S2 of Supplementary Methods II. Equation (2) describes the reflectance behavior of our patterned films, showing a well defined dip (see Fig. 3), corresponding to the plasmon excitation at the PdCoO2–sapphire interface. However, one can notice that the dip is much narrow with respect to the experimental one. Indeed, in the model equations, dissipation effects are only due to ohmic losses (contained in \({\sigma }_{f}(\omega )\)), while in the actual situation other dissipation mechanisms are working including radiative losses14, shifting and broadening the dip in the reflectance curves. The experimental plasmon frequency \({\omega }_{p}\) can be estimated from reflectance data through the zero-crossing of its second derivative (see Fig. S1 of Supplementary Methods I). In Fig. 4 we thus represent the dispersion \({\omega }_{p}\) vs. the plasmon wavevector \(q=\pi /W\) as determined by this method. Here, black points represent plasmon at the PdCoO2–sapphire interface. \({\omega }_{p}\) approximately grows linearly in the probed wavevector range indicating that we are in the plasmon-polariton region, with a slight deviation from the linear regime at \(W=2\,\mu {{{{{\rm{m}}}}}}\) and \(W=5\,\mu {{{{{\rm{m}}}}}}\) due to the variation of the sapphire dielectric function as induced by its phonon resonances. The calculation for the PdCoO2–air interface is represented in Fig. S3 of Supplementary Methods II (black points). In this case, the point related to the maximum wavevector (corresponding to W = \(0.5\,\mu {{{{{\rm{m}}}}}}\)) being out of the spectral region here measured has not been represented. Plasmon frequencies can be achieved from COMSOL simulation (using the same method developed for experimental data, see Supplementary Methods III), and they are represented in Fig. 4 as red stars at the PdCoO2–sapphire interface (for the PdCoO2–air interface, see Supplementary Methods II Fig. S3). These results show a very good agreement among data and COMSOL simulations. The plasmon frequency for a given ribbon width W (and periodicity 2W), can be obtained in the model, by the pole of the reflection coefficient of Eq. (1):
Black points correspond to experimental plasmon frequencies, red stars to COMSOL simulation and blue diamonds to the model (Eq. (3) main text). Experimental, simulation and modeling dispersion well coincide at each wavevectors here measured.In the right axis the field enhancement factor FE = |Ep/Ei| where Ep is the electric field at the plasmonic resonance and Ei the incident field, is plotted vs. the experimental wavevectors q. The strong field enhancement suggests a SEIRA device applications for PdCoO2-based ribbon arrays7.
Equation (3) applied for all \(q=\pi /W\) allows the calculation of the plasmon frequencies \({\omega }_{p}\), which are represented in Fig. 4 as blue diamonds for plasmons at the PdCoO2–sapphire interface. Moreover, the model well reproduces the experimental dispersion for both interfaces. The plasmon electric field spatial distribution in the ribbon arrays for the \(W=2\,\mu {{{{{\rm{m}}}}}}\) is represented in Fig. S4 of Supplementary Methods III. A strong electric field can be observed near the ribbon edges at the PdCoO2–sapphire interface, giving rise to a hot spot volume accessible for Surface Enhanced Infrared Spectroscopy (SEIRA) sensing applications7. From the field spatial distribution maps, one can calculate a parameter that cannot be easily measured experimentally, i.e., the plasmonic field enhancement (FE)31. \({FE}={{{{{\rm{|}}}}}}{E}_{p}/{E}_{i}{{{{{\rm{|}}}}}}\) is defined as the electric field at the plasmon resonance \({E}_{p}\) over the incident field \({E}_{i}\), both integrated over a circular area surrounding the ribbon section (see Fig. S4, Supplementary Methods III). Through electromagnetic simulation we obtain FE values (at the same experimental wavevectors of the dispersion curve) which are represented on the right axis of Fig. 4 by green circles. The strong field enhancement suggests a SEIRA device applications for PdCoO2-based ribbon arrays.
Conclusions
In conclusion, we measured and characterized the plasmonic excitations in the highly-conductive PdCoO2 metallic oxide. Four high-quality PdCoO2 films, grown on sapphire and patterned with micro-ribbon arrays with different width (W) and periodicity (2W), were fabricated by lithography methods and optically investigated from terahertz to ultraviolet. Plasmon excitations appear as a dip in the reflectance measured for light polarization perpendicular to the ribbons. By extracting the experimental plasmon frequency \({\omega }_{p}\) from reflectance measurements, we were able to estimate the plasmon dispersion \({\omega }_{p}\) vs. the wavevector q. Electromagnetic simulation and a thin-film analytical model reproduce very well this dispersion. Near the ribbon edges at the PdCoO2–sapphire interface, we calculate a strong field enhancement due to plasmonic confinement, suggesting the use of PdCoO2-based plasmonic structures for sensing and nonlinear spectroscopy applications in the mid-infrared and terahertz spectral regions.
Methods
Synthesis of PdCoO2 film
Metallic delaffosite PdCoO2 films were grown by Molecular Beam Epitaxy technique on Al2O3 substrates. Starting with sapphire substrates oriented along the (001) axis, the PdCoO2 film grows under plasma oxygen at a pressure of \(4\times 1{0}^{6}\,{{{{{{\rm{Torr}}}}}}}\). An annealing treatment in oxygen at 800 °C for 10 h allows us to improve the crystalline quality, decrease the resistivity and reduce the surface roughness26. Films here used have a thickness of 100 nm, with a room temperature resistivity of \(16\,\mu \Omega \,{{{{{{\rm{cm}}}}}}}\). Film quality was evaluated with different techniques (X-ray Diffraction, Rutherford Backscattering Spectroscopy, Atomic Force Microscopy, DC resistivity) as shown in Figs. S5 and S6 of Supplementary Methods IV.
Patterning of PdCoO2 film
The 100 nm thick PdCoO2 films on sapphire were treated with oxygen plasma cleaning (180 s, 100 W) to remove surface contaminants. Ribbons of 5, 2, and 1 μm in width were fabricated recurring to electron beam lithography (EBL) system (Raith 150-two). A resist layer made of Polymethyl methacrylate (MicroChem Corp. PMMA A4) was spin coated on top of the samples and soft baked at 180 °C for 7 minutes. Then the PMMA layer was patterned via EBL, developed in a solution of Methyl Isobutyl Ketone and Isopropyl Alcohol (MIBK/IPA 1:3) for 30 s and stopped in IPA for other 30 s. Once developed, the samples were coated with a 50 nm thick chromium film by using an electron beam evaporator. Then, by soaking the sample in acetone, a hard mask for the subsequent dry etching step was formed. Indeed the pattern obtained through lift-off was transferred to the PdCoO2 layer by means of a plasma-enhanced reactive ion etching system (Sentech SI500) with argon gas. The etched depth and the side walls verticality were optimized by carefully tuning the process parameters (Ar 40 sccm, RF power 60 W, ICP power 200 W, temperature −5 °C, etching rate 10 nm/min). Finally, the Cr-mask was removed in standard etchant solution (Chrome etch 18, Micro Resist Technology GmbH). A representative image of the final structures is shown in Fig. 1 Concurrently, 500 nm wide ribbons were fabricated via direct ion milling. A focused ion beam (FIB) system (FEI, dual-beam Helios Nanolab 650) working with Ga+ ions was operated for these purposes (current 200 pA, energy 30 keV). Prior to ion machining, a 200 nm thick Cr layer was deposited by electron beam evaporation. In this process the Cr film acted as a sacrificial mask, thus preventing charging effects and Ga+ implantation inside the PdCoO2 structures. The residual Cr layer was dissolved in the standard etchant solution previously described.
Optical measurements
Measures in the THz-IR range were carried out with a Bruker Vertex 70v spectrometer coupled with a Hyperion 1000 microscope, scanning from 100 cm−1 up to 8000 cm−1 with a resolution of 4 cm−1. In the IR-UV range the reflectance was measured with a JASCO V770 spectrometer, from 300 nm (3.3 × 104 cm−1) up to 3200 nm (3125 cm−1) with a resolution of 1 nm. A set of THz/IR and NIR/UV polarizers have been used to control the electric field direction with respect to the ribbon array pattern. Morphological characterization was performed with the optical microscope of the JASCO NRS5100 Raman micro spectrometer, using an ×100 magnification optic. Analysis of the SEM images shows a 6% uncertainty in the ribbon width W and 2% uncertainty in the periodicity 2 W. These uncertainties have been used to calculate the corresponing error in the wavevector \(q=\pi /W\). The PdCoO2 and Al2O3 reflectance spectra were analyzed with the RefFit software27, in order to extract the real and imaginary parts of both the dielectric function and the conductivity. On the real part of the optical conductivity we applied the f-sum rule30 in order to extract the plasma frequency \({\omega }_{{pl}}\) of PdCoO2 film. This results in a value of 16800 ± 300 cm−1. The optical conductivity can also be fitted using a Drude–Lorentz model with the RefFit software, obtaining a \({\omega }_{{{{{{{\rm{pl}}}}}}}}\) of 16000 ± 100 cm−1 in good agreement with that obtained by the f-sum rule.
Simulation
A finite-element method (FEM), implemented by means of COMSOL Multiphysics, was used to obtain the numerical simulations of the reflectance of films in the frequency range between 500 and 6500 cm−1. The ribbon arrays were simulated by applying periodic boundary conditions to a unit cell of period p = 2W, for a width of W = 500 nm, 1, 2, and 5 μm. As the input of the numerical simulation, we use the complex refractive indexes of PdCoO2 and Al2O3 as obtained from the RefFit data analysis of the non-patterned film and bare substrate, respectively.
Data availability
The datasets generated and analyzed during the current study are not publicly available due to Department policy but are available from the corresponding author on reasonable request.
References
Maier, S. A. Plasmonics: Fundamentals and Applications (Springer-Verlag, 2007).
Limaj, O., Lupi, S., Mattioli, F., Leoni, R. & Ortolani, M. Midinfrared surface plasmon sensor based on a substrateless metal mesh. Appl. Phys. Lett. 98, 091902 (2011).
Limaj, O. et al. Mid-Infrared surface plasmon polariton sensors resonant with the vibrational modes of phospholipid layers. J. Phys. Chem. C 117, 19119–19126 (2013).
Piccirilli, F. et al. Infrared Nanospectroscopy reveals DNA structural modifications upon immobilization onto clay nanotubes. Nanomat 11, 1103 (2021).
Koppens, F., Chang, D. & Garcia de Abajo, F. Graphene plasmonics: a platform for strong light-matter interactions. Nano Lett. 11, 3370–3377 (2011).
Low, T. & Avouris, P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 8, 1086–1101 (2014).
D’Apuzzo, F. et al. Terahertz and mid-infrared plasmons in three-dimensional nanoporous graphene. Nat. Commun. 8, 14885 (2017).
D’Apuzzo, F. et al. Mid-infrared plasmonic excitation in indium tin oxide microhole arrays. ACS Photonics 6, 2431–2436 (2018).
Limaj, O. et al. Superconductivity Induced transparency in terahertz metamaterials. ACS Photonics 1, 570–575 (2014).
Anlage, S. M. The physics and applications of superconducting metamaterials. J. Opt. 13, 0240001–0240010 (2011).
Liu, M. et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345 (2012).
Macis, S. et al. MoO3 films grown on polycrystalline Cu: morphological, structural, and electronic properties. J. Vac. Sci. Technol. A 37, 021513 (2019).
Macis, S. et al. Structural evolution of MoO3 thin films deposited on copper substrates upon annealing: an X-ray absorption spectroscopy study. Cond. Mat. 4, 41 (2019).
Di Pietro, P. et al. Observation of Dirac plasmons in a topological insulator. Nat. Nanotechnol. 8, 556–560 (2013).
Giorgianni, F. et al. Strong nonlinear Terahertz response induced by Dirac surface states in Bi2Se3 topological insulator. Nat. Commun. 7, 11421 (2016).
Di Pietro, P. et al. Terahertz tuning of Dirac plasmons in Bi2Se3 topological insulator. Phys. Rev. Lett. 124, 226403 (2020).
Cortie, M. B. et al. The quest for zero loss: unconventional materials for plasmonics. Adv. Mater. 32, 1904532 (2019).
Mackenzie, A. P. The properties of ultrapure delafossite metals. Rep. Prog. Phys. 80, 032501 (2017).
Banszerus, L. et al. Ballistic transport exceeding 28 μm in CVD grown Graphene. Nano Lett. 16, 1387–1391 (2016).
Seshadri, R., Felser, C., Thieme, K. & Tremel, W. Metal-metal bonding and metallic behavior in some ABO2 delafossites. Chem. Mater. 10, 2189 (1998).
Eyert, V., Frassard, R. & Maignan, A. On the metallic conductivity of the delafossites PdCoO2 and PtCoO2. Chem. Mater. 20, 2370 (2008).
Kim, K., Choi, H. C. & Min, B. I. Fermi surface and surface electronic structure of delafossite PdCoO2. Phys. Rev. B 80, 035116 (2009).
Ong, K. P., Zhang, J., Tse, J. S. & Wu, P. Origin of anisotropy and metallic behavior in delafossite PdCoO2. Phys. Rev. B 81, 115120 (2010).
Noh, H. J. et al. Anisotropic electric conductivity of delafossite PdCoO2 studied by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 102, 256404 (2009).
Homes, C. C. Perfect separation of intraband and interband excitations in PdCoO2. Phys. Rev. B 99, 195127 (2019).
Brahlek, M. et al. Growth of metallic delafossite PdCoO2 by molecular beam epitaxy. Phys. Rev. Mat. 3, 093401 (2019).
Kuzmenko, A. B. Kramers-Kronig constrained variational analysis of optical data. Rev. Sci. Instrum. 76, 083108 (2005).
Karabchevsky, A., Abdulhalim, I. & Auslender, M. Dual-surface plasmon excitation with thin metallic nanoslits. J. Nanophotonics 5, 051821 (2011).
Ye, M. & Crozier, K. B. Metasurface with metallic nanoantennas and Graphene nanoslits for sensing of protein monolayers and sub-monolayers. Opt. Express 28, 18479 (2020).
Dressel, M. and Gruner, G. Eletrodynamics of Solids: Optical Properties of Eletrons in Matter (Cambridge University Press, 2002).
D’Apuzzo, F. et al. Mid-infrared plasmonic excitation in indium tin oxide microhole arrays. ACS Photonics 5, 2431 (2018).
Acknowledgements
This work has received the financial support of the Bilateral Cooperation Agreement between Italy and China of the Italian Ministry of Foreign Affairs and of the International Cooperation (MAECI) and the National Natural Science Foundation of China (NSFC), in the framework of the project of major relevance 3-Dimensional Graphene: Applications in Catalysis, Photoacoustics and Plasmonics. Work at Rutgers University is supported by the National Science Foundation (NSF) Grant No. DMR2004125 and Army Research Oce (ARO) Grant No. W911NF2010108.
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to the work presented in this paper. S.M., L.T., and S.L. designed the experiment. S.L., S.M., and S.O. supervised the work. G.R. and S.O. prepared and characterized the films. A.T. and V.A. fabricated ribbon patterning. L.T. and S.M. developed the theoretical model. S.T. developed and performed the numerical simulations. S.M., A.T., F.P., and M.Z. took the optical, and SEM images. S.M. and L.T. performed the optical measurements and analyzed the data. S.M. L.T., and S.L. prepared the original draft. All authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Alexey Nikitin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Macis, S., Tomarchio, L., Tofani, S. et al. Infrared plasmons in ultrahigh conductive PdCoO2 metallic oxide. Commun Phys 5, 145 (2022). https://doi.org/10.1038/s42005-022-00924-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00924-0