Field-tuned quantum renormalization of spin dynamics in the honeycomb lattice Heisenberg antiferromagnet YbCl₃

Abstract

The basis for our understanding of quantum magnetism has been the study of elegantly simple model systems. However, even for the antiferromagnetic honeycomb lattice with isotropic spin interactions–one of the simplest model systems–a detailed understanding of quantum effects is still lacking. Here, using inelastic neutron scattering measurements of the honeycomb lattice material YbCl₃, we elucidate how quantum effects renormalize the single-magnon and multimagnon excitations and how this renormalization can be tuned and ultimately driven to the classical limit by applying a magnetic field. Additionally, our work reveals that the quantum effects tuned by the magnetic field not only renormalize the magnetic excitations but also induce a distinctive sharp feature inside the multimagnon continuum. From a more general perspective, this result demonstrates that structures within magnetic continua can occur over a wide experimental parameter space and can be used as a reliable means of identifying quantum phenomena.

Introduction

Understanding the exotic collective properties of quantum magnets is a continuously evolving challenge^1,2,3. Even within the context of seemingly well-controlled model systems, there are fundamental outstanding questions. For example, recent work on the triangular lattice material Ba₃CoSb₂O₉ shows that even sophisticated approaches to quantum magnetism fail for a frustrated lattice geometry^4,5,6. More broadly, the community is focused on identifying and understanding collective quantum properties across a wide range of materials and phenomena. A unifying theme of this endeavor is how to separate truly quantum behavior from extrinsic effects such as disorder^7,8,9 while moving beyond the limitations of linear spin-wave theory^10,11,12,13 in describing a system’s spin dynamics.

The aforementioned challenge of reliably identifying collective quantum behavior represents a major obstacle in the quest to harness and control quantum phenomena. Addressing this challenge requires systematically exploring and understanding well-controlled model systems, so that new ways can be developed to quantify quantum behavior. In this regard, the honeycomb lattice serves as a prototype geometry for studying the collective properties of quantum spins. Indeed, even in the absence of magnetic frustration, low dimensionality, and low connectivity both enhance quantum fluctuations. Since the honeycomb lattice has the minimum coordination number of three in two dimensions (2D), it is then a natural structural motif from which to explore quantum magnetism.

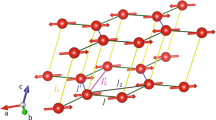
Recently, YbCl₃¹⁴ and YbBr₃¹⁵ have been shown to be exceptional realizations of 2D Heisenberg models on the honeycomb lattice. YbCl₃ has also been reported to host a quantum Bose gas near the critical field¹⁶. Here we focus on YbCl₃, which crystallizes in a monoclinic structure (space group C12/m1) with Yb atoms arranged in nearly ideal honeycomb layers separated by layers of Cl atoms, as shown in Fig. 1a^17,18,19. At zero field, we previously found the system is best described as a 2D antiferromagnet on the honeycomb lattice with a single nearest-neighbor Heisenberg interaction¹⁴. The dominance of Heisenberg interactions for an ion such as Yb³⁺ with strong spin-orbit coupling is somewhat surprising; however, for such ions, regions in a generalized phase diagram where the interactions are strongly Heisenberg have been predicted²⁰. The expected ground state for a honeycomb lattice system with only Heisenberg nearest-neighbor interactions is Néel type magnetic order which is the ground state found experimentally for YbCl₃^14,19,21. Zero-field inelastic neutron scattering measurements¹⁴ of the excitation spectrum have revealed a continuum of two-magnon excitations bounded by single-magnon spin-waves at low energies and a Van Hove singularity near the top of the continuum. This continuum scattering was able to be reproduced by including the longitudinal channel in a linear spin-wave theory with a single Heisenberg interaction on the honeycomb lattice¹⁴.

Fig. 1: Determination of exchange interactions in YbCl₃ from high-field neutron scattering data.

a The structure of a honeycomb layer in YbCl₃. In-plane first-neighbor (J₁), second-neighbor (J₂), and third-neighbor (J₃) Heisenberg interactions are indicated. b Energy of the spin-wave dispersion in the monoclinic (HK0) plane of YbCl₃ at zero field. Solid black lines indicate the Brillouin zone boundary. Solid red circles are Γ points, white squares, and open circles are K and M points used in the integration of data shown later, and blue dotted lines represent the path displayed in c–n. The dashed gray lines indicate the paths through reciprocal space discussed in “Quantum effects below the saturation field”. c–e and i–k Inelastic neutron scattering intensity of YbCl₃ as a function of energy transfer and wave-vector transfer for magnetic fields (μ₀H) of 8 T and 6 T, respectively, with μ₀H∥b. Data were acquired at T = 0.08 K with the CNCS instrument. A time-independent background subtraction and non-magnetic background subtraction as described in the Methods and Supplementary Note 4²² were subtracted from the data. Data in c–e and i–k were integrated over the L axis as described in the text and integrated over the orthogonal direction in the honeycomb lattice plane by ±0.05 reciprocal lattice units. Linear spin-wave theory calculations with a single first-neighbor Heisenberg interaction, J₁ = 0.344(6) meV, for μ₀H = 8 T (f–h) and μ₀H = 6 T (l–n) shown over the range of the acquired data and using partial transparency in the kinematically inaccessible regions. Red dashed lines in c–e and i–k are the refined dispersions for the honeycomb lattice Heisenberg model described in the text. As described in the text, data for energy transfers below the horizontal dashed white line were not included in fits, and the residual scattering visible there is due to unsubtracted background. High-symmetry points are indicated along the top horizontal axis.

In this article, we examine the spin excitation spectrum of the model quantum honeycomb magnet YbCl₃ as a function of the applied magnetic field. Starting from the completely saturated high-field regime where linear spin-wave theory is essentially exact, we reproduce the excitation spectrum using a single nearest-neighbor Heisenberg interaction, J = 0.344(6) meV, providing a highly accurate determination of the spin Hamiltonian and confirming that YbCl₃ is an ideal example of the honeycomb lattice Heisenberg model (HLHM). This value of the Heisenberg interaction is substantially smaller than the one extracted from linear spin-wave theory at zero field¹⁴, which reveals a significant renormalization of the zero-field spectrum as a result of quantum fluctuations. In the high-field regime, we observe a spectrum with gapless Dirac points that evolves linearly with applied magnetic field. For lower magnetic fields, linear spin-wave theory does not adequately reproduce the field-dependent spectrum since it overestimates the Heisenberg interaction by approximately 23% and does not account for a field-induced renormalization of both the spin-wave modes and the multimagnon continuum. However, if quantum corrections are included, this field-induced renormalization can be quantitatively explained using the Heisenberg interaction determined in the high-field regime. Additionally, distinctive sharp features inside the multimagnon continuum are also accurately reproduced, directly demonstrating the collective quantum behavior of the HLHM.

Results and discussion

Determining the spin Hamiltonian in the high-field regime

As a first step towards understanding the collective quantum behavior of YbCl₃ and the HLHM, we examine the high-field regime where quantum effects are suppressed and linear spin-wave theory is exact at zero temperature. Figure 1c–e, i–k provides an overview of the inelastic neutron scattering data at T = 80 mK for fields applied with μ₀H∥b at 8 T and 6 T, respectively. As in our zero-field measurements, we observe no dispersion along the L axis within the instrumental energy resolution and do not find evidence for strong stacking faults (see Supplementary Notes 2 and 5²²). Hence, we integrate our measured data over the entire range of L measured, from L = −1.2 to L = 1.2 reciprocal lattice units (RLU). We also combine the symmetry equivalent data in the +Q and −Q directions.

From previous estimates of the Heisenberg exchange interaction¹⁴ and the g factors¹⁸ as well as the magnetization data presented in ref. ¹⁹ and Supplementary Note 6²², we expect that 6 T and 8 T are inside the high-field regime where the spins are fully saturated along the direction of the applied field. This expectation is corroborated by (i) the presence of sharp spin-wave modes and concomitant absence of appreciable continuum features in both the 6 T and the 8 T data, and (ii) the fact that the spin-wave dispersions in the 6 T and 8 T data appear identical up to an overall energy shift. Additionally, the two spin-wave modes cross linearly at wave-vector $(\frac{2}{3}00)$, i.e., at the K point, which is consistent with the Dirac point reported for the honeycomb ferromagnet^{23,24,25,26,27}.

To determine the importance of any residual interactions in YbCl₃ beyond the dominant first-neighbor Heisenberg interaction, we carefully compare the spin-wave dispersions in the 8 T data with exact predictions from linear spin-wave theory. We first note that the lack of any dispersion along the L axis rules out sizeable interlayer interactions (See ref. ¹⁴ for data at zero field and Supplementary Note 5²² for data at 8 T). Focusing on the (HK0) plane, we then quantify the spin-wave dispersions by extracting peak locations from constant wave-vector cuts through the volumetric data at 238 individual wave-vectors within this plane. Finally, we fit the measured spin-wave dispersions with an exact closed-form expression given by linear spin-wave theory for a Heisenberg model with first-neighbor (J₁), second-neighbor (J₂), and third-neighbor (J₃) interactions [see Fig. 1a for an illustration] in a saturating field (see Supplementary Note 2²²). Since we obtain J₁ = 0.34(1) meV, J₂ = 0.002(4) meV, J₃ = − 0.010(8) meV, and an energy of the upper spin-wave mode at the Γ point of 0.34(4) meV, we conclude that further-neighbor Heisenberg interactions are negligible. Thus, we only keep the dominant nearest-neighbor Heisenberg interaction J ≡ J₁, and consider the simplified Hamiltonian

$${{{{{{{\mathcal{H}}}}}}}}=J\mathop{\sum}\limits_{\langle r,{r}^{{\prime} }\rangle }{{{{{{{{\boldsymbol{S}}}}}}}}}_{r}\cdot {{{{{{{{\boldsymbol{S}}}}}}}}}_{{r}^{{\prime} }}-{g}_{ab}{\mu }_{B}{H}_{b}\mathop{\sum}\limits_{r}{S}_{r}^{x}-{g}_{c}{\mu }_{B}{H}_{c}\mathop{\sum}\limits_{r}{S}_{r}^{z},$$

(1)

where H_b and H_c are fields parallel to the b and c directions, respectively, while g_ab and g_c are the corresponding in-plane and out-of-plane g factors.

To accurately extract the strength of the Heisenberg interaction J, we consider the entire measured 8 T scattering intensity along the high-symmetry path shown in Fig. 1b, and compare it to a linear spin-wave calculation based on Eq. (1) with H_b = 8 T and H_c = 0 T. The dynamical spin structure factor obtained from linear spin-wave theory (see Supplementary Note 7²²) is convolved with the instrumental energy resolution (See Supplementary Note 3²²). We refine the measured scattering intensity along the high-symmetry path for energy transfers greater than 0.22 meV, three energy resolution full width at half maxima from the elastically scattered neutrons. In addition to the refined values of J and g_ab, we include an overall constant to serve as a flat background for the scattering intensity and an overall multiplicative scaling factor to relate the measured and calculated intensities. This refinement for the 8 T data yields J = 0.344(6) meV for the Heisenberg interaction and g_ab = 2.93(1) for the in-plane g factor. Using the refined values of J and g_ab, the calculated linear spin-wave dispersions at 8 T and 6 T are then superimposed on Fig. 1c–e, i–k, respectively, and the corresponding linear spin-wave intensities are plotted in Fig. 1f–h, l–n. We remark that, in contrast to preliminary expectations, 6 T is slightly below the in-plane saturation field, which is found to be H_s,ab = 3J/(g_abμ_B) ≈ 6.1 T. Still, for practical purposes, linear spin-wave theory is highly reliable at both 6 T and 8 T, which explains the excellent agreement between the measured and calculated intensities in Fig. 1.

Importantly, an analogous fitting of the zero-field data with linear spin-wave theory gives a significantly larger value for the Heisenberg interaction: J = 0.421(5) meV¹⁴. Recalling that linear spin-wave theory is essentially exact in the high-field regime, we conclude that the true Heisenberg interaction in YbCl₃ is J = 0.344(6) meV and that the spin-wave energies at zero field are renormalized by ~23% with respect to linear spin-wave theory as a result of quantum fluctuations. We note that the refined value of J = 0.344(6) meV agrees with the one obtained from specific heat in ref. ¹⁴. Furthermore, a smaller value of J corresponds to a larger relative Néel temperature T_N/J and hence a larger, more reasonable interlayer interaction. To provide an additional check of this we performed quantum Monte Carlo simulations of the HLHM (see Supplementary Note 9²²) which demonstrate that T_N/J ≈ 0.15 (corresponding to T_N ≈ 0.6 K¹⁴ and J ≈ 4 K) can be reproduced from an interlayer interaction on the order of 10⁻³J.

Quantum effects below the saturation field

Below the saturation field, the spectrum is more complex, and quantum effects are readily observable. To study this low-field regime, we utilize fields applied with μ₀H∥c at 2 T and 4 T. Figure 2a–f shows the measured scattering intensity multiplied by the energy transfer as a function of energy transfer (vertical axis) and wave-vector transfer (horizontal axis) for both zero and finite fields. At zero field [see Fig. 2a, b], we observe the same spin-wave dispersion and continuum scattering as in our initial characterization¹⁴. As the field increases through μ₀H = 2 T [see Fig. 2c, d] and μ₀H = 4 T [see Fig. 2e, f], the degeneracy of the spin-wave modes is lifted around the Γ point with the upper mode acquiring a finite gap. At the same time, the spin-wave energies have an overall downward renormalization with the dispersion maximum at the K point decreasing from almost 0.7 meV at 0 T to <0.5 meV at 4 T. The continuum scattering also softens in energy as a function of the applied field, and the Van Hove singularity in the continuum becomes less distinct as the field increases. Remarkably, however, while the Van Hove singularity becomes less pronounced, the additional structure becomes evident in the continuum; at both 2 T and 4 T, we clearly observe a sharp feature inside the continuum that follows the upper spin-wave mode with an approximately constant energy offset for each field. This novel field-induced feature is one of the key findings of this manuscript, and we will return to it in greater detail below.

Fig. 2: Inelastic neutron scattering of YbCl₃ at low applied fields.

Measured (a–f) and calculated (g–i) scattering intensity times energy transfer (Iℏω) as a function of wave-vector transfer along the H10 and 1K0 directions [see dashed lines in Fig. 1b] with applied magnetic fields μ₀H∥c. The calculated intensities are obtained from the nonlinear spin-wave theory described in “Nonliner spin-wave theory”. Red points are the fitted peak positions of the transverse spin-waves as a function of energy and wave-vector transfer plotted in a reduced zone scheme. Solid blue lines are the fitted field-dependent linear spin-wave dispersions as described in the main text. a, b [g, h] are data measured [calculated] for μ₀H = 0, c, d [i, j] are data measured [calculated] for μ₀H = 2 T, and (e, f) [k, l] are data measured [calculated] for μ₀H = 4 T at the AMATERAS instrument. Data in a–f were integrated over the full range of the measured L wave-vector and over the orthogonal direction in the honeycomb lattice plane by ±0.05 RLU (reduced lattice units). Calculations include convolution with instrumental resolution (See Supplementary Note 3²²) and have been scaled based upon fits to constant wave-vector scans discussed in “Nonlinear spin-wave theory”. The only background subtracted from the data in a–f is a time-independent background.

To quantify the downward renormalization of the spin-wave energies, we perform a series of constant wave-vector scans throughout the (HK0) plane after integrating the wave-vector transfer over the (00L) direction from L = − 1.3 to L = 1.3 RLU. A Gaussian function with a constant background was used to quantify the energies of the spin-wave modes as a function of the wave-vector transfer. The resulting spin-wave energies at equivalent wave-vectors are then combined and overplotted as symbols in Fig. 2a–f. For each value of the field, we compare these spin-wave energies to linear spin-wave theory based on Eq. (1) with H_b = 0 T and H_c = 0, 2, and 4 T, allowing the Heisenberg interaction J and, for H_c > 0, the g_c factor to be refined values. The solid curves in Fig. 2a–f are the fitted linear spin-wave dispersions with the corresponding values of J shown in Fig. 3b as a function of field. Though linear spin-wave theory gives a reasonable match in each individual case, it fails to capture the downward renormalization of the spin-wave energies as it requires the fitted value of J to decrease by >23% between 0 T and 4 T. Therefore, we hypothesize that the downward renormalization of the spectrum is a quantum effect.

Fig. 3: Field-dependent parameters for YbCl₃.

a Field dependence of the mode at finite energy (ℏω_Γ) at the Γ point as a function of applied field for μ₀H∥c (red circles) and ∥b (blue squares). The g factors are extracted from the linear fits the data over the high-field range of measurement (solid lines). The dashed line is an extension of the fitted solid line over the range not included in the linear fit. The CAMEA instrument was used to determine the open red circle points as described in Supplementary Notes 1 and 2²². Values for CAMEA and AMATERAS were averaged over multiple peak locations based upon multiple measured Γ points. Values for CNCS are based upon peak location from integration over range of measured L as described in Supplementary Note 2²². Error bars correspond to the error in the mean of the fitted peak location added in quadrature with 10% of the fitted FWHM (full width at half maximum). b Field dependence of the nearest-neighbor Heisenberg interaction J as extracted by fitting the experimental data with linear spin-wave theory. The black circle and triangle are from the inelastic neutron scattering and heat capacity measurements in ref. ¹⁴, respectively. The error bar in the J values at finite field correspond to the standard deviation of the refined value.

Nonlinear spin-wave theory

We test our hypothesis by considering nonlinear spin-wave theory and determining whether quantum corrections to our linear spin-wave results can properly account for the downward renormalization of the spectrum. Adopting the formalism in refs. ^28,29, we compute the first 1/S corrections to the spin-wave energies and the scattering intensities in the on-shell approximation (see Supplementary Note 8²²). Note that our calculation differs from refs. ^28,29 in at least two ways. First, in the presence of the field, there is another correction to the spin-wave energies due to a renormalization of the spin canting angle³⁰. Second, we choose to consider the first 1/S corrections to both the single-magnon (i.e., spin-wave) and the two-magnon energies. This choice is important for treating the spin-wave modes and the continuum scattering on the same footing and is justified because, while they correspond to different intensities [O(S¹) and O(S⁰), respectively], the single-magnon and two-magnon energies are both O(S¹). We also note that our calculation generalizes ref. ¹² as it considers both the renormalization and the broadening of the spin-wave modes in the antiferromagnetic HLHM.

Our nonlinear spin-wave calculations are all based on the same Heisenberg interaction, J = 0.344(6) meV, determined as described at the beginning of this article by comparing the neutron scattering data to linear spin-wave theory above the saturation field. To obtain a similarly reliable value for the g factor g_c, we consider the energy of the upper spin-wave mode at the Γ point, ℏω_Γ, for fields applied with μ₀H∥c at 10.5 T and 11 T. Assuming that these fields are not significantly below the saturation field, we fit the linear spin-wave expression ℏω_Γ = μ_Bg_cH [see Fig. 3a] and readily obtain g_c = 1.509(6)³¹. The out-of-plane saturation field is then found to be H_s,c = 3J/(g_cμ_B) ≈ 11.8 T, which justifies our initial assumption and agrees with the magnetization data presented in ref. ¹⁹. We further note that an analogous fitting procedure for applied fields with μ₀H∥b at 6 T and 8 T gives g_ab = 2.90(1) [see Fig. 3a], which is very close to the previously obtained value of g_ab = 2.93(1). It is also interesting to remark that the extrapolations of these fits agree well with the measured values of ℏω_Γ all the way down to zero field.

The scattering intensities from the nonlinear spin-wave calculation are convolved with the instrumental energy resolution, multiplied by the energy transfer, and plotted in Fig. 2g–l for both zero and finite fields. We find that the first 1/S correction of nonlinear spin-wave theory provides a good match for the experimental data and, in particular, accurately captures the downward renormalization of the spectrum. Furthermore, the calculation reproduces the field-induced sharp feature inside the continuum, allowing us to identify this feature as the lower edge of a specific two-magnon continuum. Due to the two distinct magnon modes at finite field (lower and upper modes), there are three distinct two-magnon combinations (lower-lower, lower-upper, and upper-upper), translating into three distinct two-magnon continua. In two dimensions, the discontinuity of the two-magnon density of states is then expected to manifest as a sharp feature at the lower edge of each continuum. Due to the gapless Goldstone mode at the Γ point, the lower edges of the lower-lower and lower-upper continua coincide with the lower and upper magnon modes, respectively, which means that they cannot be experimentally observed. In contrast, the lower edge of the upper-upper continuum follows the upper magnon mode with a constant energy offset ℏω_Γ, which is consistent with the experimental data.

Figure 4 explicitly shows the measured and calculated scattering intensities at the K and M points for all three values of the applied field. We simultaneously compare all six calculations to the measurement with a single overall constant background (to account for residual background contributions) and a single multiplicative scaling for the calculated intensity, thus using only two fitting parameters. We utilize this fitting procedure for the nonlinear spin-wave calculation described above (solid line) as well as for a linear spin-wave calculation based on the same values of J and g_c that includes both the single-magnon modes and the two-magnon continua¹⁴ (dashed line). We observe that the first 1/S correction to the magnon energies is necessary to capture not only the downward renormalization of the single-magnon modes but also the field dependence of the two-magnon continuum. In turn, this observation highlights the importance of treating the single-magnon and two-magnon energies on the same footing.

Fig. 4: Neutron scattering intensities at high-symmetry points.

Constant wave-vector scans (symbols) at the K point (a–c) and at the M point (d–f) of the Brillouin zone for (a, d) μ₀H = 0, (b, e) μ₀H = 2 T, and (c, f) μ₀H = 4 T from the data shown in Fig. 2 with μ₀H∥c. Data were averaged over multiple K- and M-point wave-vectors measured throughout the Brillouin zone. Data were integrated over the full range of measured L wave-vector and over ± 0.05 RLU for the two wave-vectors in the (HK0) plane. Error bars correspond to error in scattering intensity from combined scans using Poisson statistics. The solid and dotted lines are the nonlinear and linear spin-wave calculations, respectively, for a nearest-neighbor Heisenberg interaction of J = 0.344(6) meV averaged over the same Brillouin zone points as the data. An overall constant background that accounts for residual background contributions and a single overall multiplicative scaling factor were used in comparing the model to the data.

Finally, we point out that, in contrast to the other cases in Fig. 4b–f, there is an observable discrepancy between the experimental data and nonlinear spin-wave theory at the K point for zero field [see Fig. 4a]. In particular, the experimental peak ~0.7 meV appears to be suppressed and broadened with respect to the theoretical one. This “K point anomaly” may be related to the “(π, 0) anomaly” previously observed on the square lattice¹⁰. If so, its explanation may require going beyond the 1/S expansion and accounting for nonperturbative effects³², which is an exciting direction for future work. There is also a discrepancy in the spin-wave intensities near the Γ point for finite fields, which is accentuated by the multiplicative factor of ℏω used in the intensity scale of Fig. 2. Data and calculations without this factor can be found in Supplementary Note 2²². This discrepancy may result from at least two sources. First, unlike in the high-field regime of Fig. 1, there is no analytical expression for the theoretical scattering intensity below the saturation field. Therefore, it is more challenging to obtain an accurate resolution convolution, which may impact the comparison with the experiment when modes of different slopes are present. Second, there may be small additional terms in the spin Hamiltonian of YbCl₃ that do not affect the dispersions but cause changes in the intensities. Such terms are expected to be quite small given the good description of the high-field dispersions in terms of a nearest-neighbor Heisenberg model. High-resolution magnetic field-dependent polarized inelastic measurements may serve to elucidate such terms in future experiments.

Nonetheless, our present work demonstrates and provides a comprehensive explanation of how quantum effects renormalize both the single- and multimagnon parts of the spin excitation spectrum and additionally produce sharp features in the continuum that attest to the collective quantum behavior inherent to the honeycomb lattice. The latter finding furnishes an additional bellwether for the experimental identification of collective quantum behavior.

Methods

Material synthesis

Single crystals of YbCl₃ were grown using the Bridgman technique in evacuated silica ampules using methods described in refs. ^14,33.

Inelastic neutron scattering measurements

Magnetic field-dependent inelastic neutron scattering measurements were performed with the cold neutron chopper spectrometer (CNCS)³⁴ at the Spallation Neutron Source at Oak Ridge National Laboratory [Fig. 1], the disk chopper spectrometer (AMATERAS)³⁵ at the Materials and Life Science Experimental Facility (MLF) of J-PARC [Fig. 2], and the Continuous Angle Multiple Energy Analysis (CAMEA) spectrometer^36,37 at the Paul Scherrer Institut (PSI) [See Supplementary Note 1²²].

CNCS measurements

The CNCS measurements were performed in a vertical field 8 T magnet coupled with a dilution refrigerator, employing a 0.625 g sample oriented with an (H0L) horizontal scattering plane. An incident energy (E_i) of 2.49 meV was used in the high flux configuration of the instrument. Data presented here were collected at T = 80 mK, with applied fields of μ₀H = 2, 4, 5, 6, and 8 T. The sample was rotated about its vertical axis by 180^∘ in one-degree steps to maximize the coverage of reciprocal space. Each individual sample rotation angle was measured for ~8 minutes. We employ a background subtraction based upon the understanding that magnetic scattering in the high-field regime is due only to the fully saturated spin-wave spectrum. The background for the CNCS measurement was determined by setting a mask of ±0.075 meV around the analytical dispersion for the μ₀H = 8 T measurement (see dashed red lines in Fig. 1c–e). The size of the energy transfer mask was selected based upon the CNCS energy resolution for the configuration of the measurement. All data outside of this mask were considered to be part of the background. This approximation is valid here due to the lack of magnetic diffuse scattering in the saturated phase. This background data set was then powder averaged according to the magnitude of wave-vector and energy transfer of each detected neutron. This results in a unique background intensity available for subtraction for individually measured wave-vector and energy transfers. This background subtraction procedure was separately applied to all the CAMEA measurements using a window of ±0.03 meV reflecting the energy resolution of the instrument. This procedure accounts for instrumental background, sample environment background, and multiple scattering components to the measured scattering intensity. Supplementary Note 4²² provides an example of this process for one of our measurements.

AMATERAS measurements

The AMATERAS experiment was performed in a vertical field magnet with a dilution refrigerator insert, employing a 0.6 g sample oriented with the (HK0) scattering plane horizontal and using E_i = 2.63 meV and E_i = 1.48 meV incident energies, in the high flux Repetition Rate Multiplication configuration of the instrument. To minimize the effects of the modest neutron absorption cross section of Yb and Cl the sample used at AMATERAS was constructed of a vertical stack of plates cut to basal dimensions of 3.2 mm by 3.4 mm with a total height of 25 mm. Data were collected at T = 80 mK, applying fields of H = 0, 2, and 4 T with the sample rotated by a total of 120^∘ in one-degree steps about its vertical axis. Each individual sample rotation angle was measured for ~15 minutes. Unless otherwise noted, a time-independent background was subtracted from the AMATERAS measurements. The AMATERAS measurements were integrated over the range of measured L from L = −0.8 to L = 0.8 RLU.

CAMEA measurements

The CAMEA^36,37 data set was collected in a vertical field 11 T magnet at T = 40 mK. Due to the nature of the multiplex analyser, runs collected at E_i = 3.5, 3.6, 4.48, and 4.6 meV were merged for four positions of the 60^∘-wide (in scattering angle) detector tank with the center scattering angle set to −38^∘, −42^∘, −54^∘, and −58^∘. This method results in 4 × 4 = 16 measurements where the sample is rotated by 210^∘ about its vertical axis ensuring detector coverage redundancy to eliminate artifacts due to the separation of the analyzers. The sample rotation range about its vertical axis of 210^∘ in steps of one-degree covers a large region of reciprocal space which includes three distinct K-points. This corresponds to approximately 45 hours of measurement time per magnetic field measured at μ₀H = 11, 8, and 6 T. Further information can be found in Supplementary Note 1²².