Cavity-renormalized quantum criticality in a honeycomb bilayer antiferromagnet

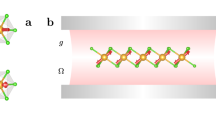
Abstract

Strong light-matter interactions as realized in an optical cavity provide a tantalizing opportunity to control the properties of condensed matter systems. Inspired by experimental advances in cavity quantum electrodynamics and the fabrication and control of two-dimensional magnets, we investigate the fate of a quantum critical antiferromagnet coupled to an optical cavity field. Using unbiased quantum Monte Carlo simulations, we compute the scaling behavior of the magnetic structure factor and other observables. While the position and universality class are not changed by a single cavity mode, the critical fluctuations themselves obtain a sizable enhancement, scaling with a fractional exponent that defies expectations based on simple perturbation theory. The scaling exponent can be understood using a generic scaling argument, based on which we predict that the effect may be even stronger in other universality classes. Our microscopic model is based on realistic parameters for two-dimensional magnetic quantum materials and the effect may be within the range of experimental detection.

Introduction

Recently, driving quantum systems with light has emerged as an intriguing route for material control. In the case of classical light this amounts to a non-equilibrium problem¹, and when the magnitude of the external drive is strong enough the field can have a profound impact on the matter degrees of freedom. This has led to many ground-breaking results in the field of polaritonic chemistry and beyond^2,3,4,5,6.

Advances in realizing ultra-strong light-matter coupling in optical cavities^7,8,9 have paved the way for an alternative approach, where the quantum fluctuations of light are harnessed in an equilibrium setting. In particular, the fluctuations of the electromagnetic modes can couple strongly to the matter and be used to control chemistry^{10,11,12,13,14,15,16,17,18} and material properties^8,9,19. In condensed matter systems, cavities hold the promise of circumventing the heating problems inherent to laser-driving^20,21,22 while achieving similar control over material properties^8,23. This includes proposals to realize quantum-light-induced topological phase transitions^24,25,26, ferro-electricity^27,28, excitonic insulators²⁹, magnetic phase transitions and quantum spin liquids^30,31, and superconductivity^{32,33,34,35,36,37}.

In addition, the effect of light on quantum phase transitions and their critical phenomena is of particular interest. Here, the ground state of the system becomes extremely susceptible to external influences³⁸, so that even a small light-matter coupling to the collective degrees of freedom could have a significant impact. The origin of this susceptibility is the divergence of quantum fluctuations with system size, which also makes quantum critical points prime examples of strongly correlated physics devoid of simple quasi-particle descriptions. The effects of such strongly correlated quantum fluctuations have so far only been scarcely explored in the cavity setting. Understanding them poses the combined challenge of treating quantum many-body systems and the intricacies that arise in low-energy formulations of quantum electrodynamics (QED) in a cavity^{17,39,40,41,42}.

The development of numerical methods to treat cavity systems has seen some recent progress, especially in the field of quantum chemistry where the quantum electrodynamical density functional theory^43,44 and coupled cluster theory^45,46,47 allows for an accurate ab initio treatment of molecules in a cavity. Established numerical methods for strongly correlated lattice models, capable of simulating a quantum critical systems, have on the other hand seen little development. Until now, mainly exact diagonalization^48,49 and density matrix renormalization group^50,51,52 studies have been performed, while higher-dimensional tensor-network methods have not yet been applied to the cavity problem. These approaches are either restricted to small systems, quasi-one-dimensional systems, or low entanglement, respectively. This leaves a blind spot for two-dimensional (2D) materials⁵³, which due to their tunability and richness in quantum critical phenomena may be useful platforms to investigate the effects of quantum light on quantum criticality.

In this work, we address this open issue by presenting a method capable of studying a 2D quantum critical magnet coupled to a single effective cavity mode. Inspired by recent advances in realizing magnetic van der Waals materials of atomic thickness^54,55, as evidenced in particular by the transition metal phosphoruos trichalcogenides MPX₃ (with M = Fe, Mn or Cr and X = S, Se or Te)^56,57,58, we consider a Heisenberg-type antiferromagnet (AFM) on a honeycomb bilayer (Fig. 1). This system is well known to have a quantum critical point (QCP) in the (2+1)D O(3) universality class at a given ratio of the intra- and interlayer exchange couplings^59,60,61,62 at the border between a Néel-ordered AFM state and a quantum-disordered interlayer dimer singlet state. This critical point can be reached by applying hydrostatic pressure, as recently demonstrated for a different magnetic phase transition in CrI₃⁶³. Furthermore, in cases where the magnetic point group breaks inversion symmetry, the AFM order parameter is accessible via the linear dichroism⁶⁴, reflectance anisotropy⁶⁵, and via Raman scattering⁶⁶.

Fig. 1: Magnetic phases of the 2D antiferromagnetic Heisenberg model on a bilayer honeycomb lattice.

Depending on the ratio between the interlayer coupling J_D (bold, red) and intralayer coupling J (thin, gray), the magnetic ground state either forms a Néel-type antiferromagnetic order or interlayer singlet dimers, breaking no symmetries. At the phase boundary there is a quantum critical point of the three-dimensional O(3) universality class. Here we consider ${J}_{{{{{{{{\rm{D}}}}}}}}}\approx {J}_{{{{{{{{\rm{D}}}}}}}}}^{c}$, the critical value corresponding to that critical point, and a coupling to a cavity mode described by the quantum vector potential $\hat{{{{{{{{\bf{A}}}}}}}}}$, linearly polarized along one of the in-plane bond directions.

Coupling the magnetic system to cavity photons will influence the spin exchange interactions along the direction of the photon polarization and potentially the quantum phase transition. Our numerical tool to address this question is quantum Monte Carlo (QMC) simulations, which so far have not seen much use in cavity-matter systems (although spin-boson models in general have been studied^67,68,69).

We find a relevant parameter region where the simulations are sign-problem free, and via simulations of large-size systems reveal that for a single cavity mode the QCP is not shifted. However, the magnetic fluctuations at the critical point experience an enhancement that can be understood as a finite-size correction to scaling, with a small universal fractional scaling exponent that is in stark contrast to the analytic scaling one would expect from simple perturbative arguments. The light-induced correction to scaling, while unable to change the universality class of the transition, manifests in an absolute enhancement of the AFM structure factor that remains in the thermodynamic limit, even though the energy content of the single cavity mode remains microscopic. This result may be interpreted as a light-induced change in the ground state of a quantum many-body system.

Results

Hamiltonian for a cavity-coupled antiferromagnet

While one possible starting point for modeling a cavity-coupled antiferromagnet is to write a phenomenologically motivated light-spin interaction, such an interaction may be missing higher-order terms that are important for the boundedness of the Hamiltonian^70,71. Therefore, we start instead from a lattice model that is manifestly gauge invariant, the Hubbard model with the Peierls substitution,

$$H = \mathop{\sum}\limits_{\langle ij\rangle \sigma }\left(-{t}_{ij}{e}^{i{\theta }_{ij}}{c}_{i\sigma }^{{{{\dagger}}} }{c}_{j\sigma }+\,{{\mbox{h.c.}}}\,\right)\\ +U\mathop{\sum}\limits_{i}{n}_{i,\downarrow }{n}_{i,\uparrow }+\Omega {a}^{{{{\dagger}}} }a,$$

(1)

where we assume a single relevant effective cavity mode at frequency Ω in the dipole approximation ${\theta }_{ij}=(e/\hslash )\int\nolimits_{i}^{j}d{{{{{{{\bf{r}}}}}}}}\cdot \hat{{{{{{{{\bf{A}}}}}}}}}\approx {\lambda }_{ij}({a}^{{{{\dagger}}} }+a)/\sqrt{N}$. In the large-U limit and at half filling, this model can be down-folded to a Heisenberg-like effective Hamiltonian using a perturbative expansion in t/U²³, resulting in

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\mathop{\sum}\limits_{\langle ij\rangle }{\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}({a}^{{{{\dagger}}} },a)\left({{{{{{{{\bf{S}}}}}}}}}_{i}\cdot {{{{{{{{\bf{S}}}}}}}}}_{j}-\frac{1}{4}\right)+\Omega {a}^{{{{\dagger}}} }a.$$

(2)

The most striking difference of this Hamiltonian to the regular Heisenberg model is the photon-dependent exchange coupling ${\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}({a}^{{{{\dagger}}} },a)$, which encodes the creation and annihilation of photons during the virtual hopping processes of the electrons mediated by the cavity mode.

The exact form of the downfolded Peierls coupling is quite complex and naive perturbative expansions in ${\lambda }_{ij}/\sqrt{N}$ can, like in the regular Peierls substitution, lead to unphysical consequences^70,71. Therefore, we will avoid further approximations and treat the full coupling, ${\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}$, exactly. Despite this, the perturbative downfolding itself is not gauge invariant since it hosts a spurious superradiant phase at sufficiently large λ (see Supplementary Note 1). Thus, to remain in the regime of validity of the downfolding, in the remainder of this work, we will restrict ourselves to values of λ where the photon occupation remains small and finite in the thermodynamic limit.

In the following, it is most convenient to express ${\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}$ in the occupation-number basis,

$$\langle n| {\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}| m\rangle \, = \, \frac{{J}_{ij}}{2}\mathop{\sum }\limits_{l=0}^{\infty }\,{{\mbox{Re}}}\,\,{D}_{nl}^{ij}{({D}_{lm}^{ij})}^{* }\\ \times \left(\frac{1}{1+\bar{\omega }(l-n)}+\frac{1}{1+\bar{\omega }(l-m)}\right),$$

(3)

in terms of the normal exchange coupling ${J}_{ij}=4{t}_{ij}^{2}/U$, the reduced frequency $\bar{\omega }=\Omega /U$ and the displacement operators

$${D}_{nm}^{ij} \, = \, \langle n| {e}^{i({\lambda }_{ij}/\sqrt{N})({a}^{{{{\dagger}}} }+a)}| m\rangle \\ \, = \, \sqrt{n!m!}{\left(\frac{i{\lambda }_{ij}}{\sqrt{N}}\right)}^{\delta }\mathop{\sum }\limits_{k=0}^{\mu }\frac{{e}^{-{\lambda }_{ij}^{2}/2N}{(-{\lambda }_{ij}^{2}/N)}^{k}}{k!(\mu -k)!(\delta +k)!},$$

(4)

with $\mu =\min \{n,m\}$ and δ = ∣m − n∣.

This expression for the coupling has two key features. First, the even and odd photon number sectors decouple, due to parity conservation. Second, singularities appear when $n\bar{\omega }=1$ that are associated with degeneracies between photon and doublon electronic excitations. At these singularities, our perturbation theory is expected to break down leading to a different effective model⁷². In Supplementary Note 2, we investigate this issue further by comparing our results for a small system to exact diagonalization results for the Hubbard model.

Considering the large U/J_ij regime, where higher-order terms are partly suppressed, one way to maximize the effect of the light-matter coupling is to tune $\bar{\omega }$ close but not too close to one of the singularities. There is, however, a trade-off as high cavity frequencies make cavity excitations less relevant in the ground state, and n-photon processes are suppressed by powers of ${({\lambda }_{ij}/\sqrt{N})}^{n}$ for n ≥ 2. We find that $\bar{\omega }=0.49$ is a good compromise.

Inspired by MnPSe₃, we consider the Hamiltonian of Eq. (2) on the AA-stacked honeycomb bilayer (Fig. 1). We assume antiferromagnetic exchange couplings both along the nearest-neighbor intralayer bonds, J, and the interlayer bonds, J_D, as well as U/J = 200. The polarization of the cavity mode is chosen so that it aligns with one of the J bonds, compatible with a vanishing in-plane momentum. In this way, it decouples from the J_D bonds, directly influencing the ratio J_D/J that is the relevant coupling at the critical point. Although the magnetic moments in MnPSe₃ are S = 5/2 and those in our model are S = 1/2, the Néel-dimer singlet QCP is expected to exist also at higher spin magnitudes⁶².

Quantum Monte Carlo

To achieve an accurate description of the physics close to the quantum critical point, it is crucial to solve the Hamiltonian of Eq. (2) taking all correlations into account. Without a cavity this is routinely accomplished for unfrustrated quantum magnets using large-scale quantum Monte Carlo simulations in the stochastic series expansion (SSE) formalism^73,74, which we outline in the context of our work in the “Quantum Monte Carlo” subsection of the Methods.

In this section, we present QMC results that shed light on the two main questions of our work: First, does the light-matter coupling change the critical ratio ${J}_{{{{{{{{\rm{D}}}}}}}}}^{c}/J$ and shift the position of the QCP? Second, does it change the nature of the QCP itself?

Position of the quantum critical point

To answer the first question we perform a finite-size crossing analysis, i.e., we look at the crossings of observables with known critical finite-size scaling to numerically determine the critical point ${J}_{{{{{{{{\rm{D}}}}}}}}}^{c}/J$. A convenient observable for this purpose is the Binder ratio $Q={\langle {m}_{s}^{2}\rangle }^{2}/\langle {m}_{s}^{4}\rangle$, where m_s is the staggered magnetization of the AFM order. At the critical point, the scaling of the numerator and the denominator cancel so that the Binder ratio becomes independent of system size. Thus, plotting the Binder ratio for different system sizes L leads to lines crossing at the point where the system displays critical behavior (Fig. 2).

Fig. 2: Numerical determination of the quantum critical point.

The critical coupling ratio ${J}_{{{{{{{{\rm{D}}}}}}}}}^{c}/J$ is determined using a finite-size crossing analysis. Shown are two bundles of curves of the Binder ratio Q for zero and finite light-matter coupling λ, respectively. Each bundle consists of the system sizes (light to dark shade) L = 12, 16, 20, 24, 32, 40, 48, 64, 80. The solid lines show cubic polynomial fits from which crossing points are extracted. The inset shows the crossings of the Q curves at L and L/2, in addition to those of the uniform magnetic susceptibility times system size, Lχ. From the convergence of the crossings, the position of the critical point ${J}_{{{{{{{{\rm{D}}}}}}}}}^{c}/J$ can be determined. J (J_D) is the intra- (inter)layer exchange coupling. The error bars represent the standard deviation of the data and are smaller than the symbols except when shown.

We extract the crossings between system sizes L and L/2 by fitting cubic polynomials to the data. The resulting crossing points still have a small system size dependence due to subleading corrections (inset of Fig. 2). To assess ground state physics with our finite-temperature method, we employ the standard approach of combined finite-temperature and finite-size scaling T = J/2L, so that the temperature scales like the finite-size gap of the system, assuming a dynamical exponent z = 1^62,75. In addition, the same analysis is carried out for another dimensionless quantity, the uniform magnetic susceptibility multiplied by the system size, Lχ. All extracted crossings appear within our resolution to converge to a common limit, ${J}_{{{{{{{{\rm{D}}}}}}}}}^{c}/J=1.6433(6)$, indicating that the $1/\sqrt{N}$ coupling to the cavity mode does not shift the position of the critical point, in agreement earlier scaling arguments^76,77,78.

Critical fluctuations

Next, we focus on the QCP itself. Even if the cavity vacuum fluctuations are not strong enough to shift its position, they may still change the nature of the quantum critical ground state in more subtle ways. The nature of a QCP is, in analogy to classical critical phenomena, usually classified by the universal scaling exponents of certain physical observables³⁸ that can be extracted from their finite-size scaling.

To investigate the influence of the cavity on the critical scaling, we calculate the energy per spin E as well as the AFM structure factor and susceptibility

$${S}^{{{{{{{{\rm{AFM}}}}}}}}}=\frac{1}{3{L}^{2}}\mathop{\sum}\limits_{ij}{(-1)}^{i+j}\langle {{{{{{{{\bf{S}}}}}}}}}_{i}\cdot {{{{{{{{\bf{S}}}}}}}}}_{j}\rangle ,$$

(5)

$${\chi }^{{{{{{{{\rm{AFM}}}}}}}}}=\frac{1}{3{L}^{2}}\mathop{\sum}\limits_{ij}{(-1)}^{i+j}\int\nolimits_{0}^{\beta }d\tau \langle {{{{{{{{\bf{S}}}}}}}}}_{i}(\tau )\cdot {{{{{{{{\bf{S}}}}}}}}}_{j}\rangle ,$$

(6)

where the signs in S^AFM are positive/negative on the different magnetic sublattices, and τ is imaginary time (Fig. 3). The AFM structure factor (S^AFM) is directly related to the critical fluctuations of the AFM order parameter, and shows an enhancement with increasing coupling to the cavity (Fig. 3a). The absolute difference from its λ = 0 value reveals that this enhancement remains in the thermodynamic limit and seems to grow with system size (Fig. 3b). A similar picture holds for χ^AFM, which additionally probes the low-lying excitations above the ground state (Fig. 3c). By contrast, the energy is only weakly enhanced with a vanishing effect for large system sizes. Away from the critical point, the effect of the cavity generally decreases with system size (Fig. 3d).

Fig. 3: Cavity effect on the critical scaling of the structure factor, susceptibility, and energy.

The absolute enhancement of the antiferromagnetic (AFM) structure factor and susceptibility, S^AFM and χ^AFM, as well as the energy per spin E, under the influence of the light-matter coupling λ and as a function of system size. a The critical scaling of S^AFM for different λ. b The absolute difference, $\Delta {S}^{{{{{{{{\rm{AFM}}}}}}}}}={S}^{{{{{{{{\rm{AFM}}}}}}}}}-{S}_{\lambda = 0}^{{{{{{{{\rm{AFM}}}}}}}}}$, for the data in panel (a). c Comparison of the absolute difference ΔA = A − A_λ=0 for different observables A = χ^AFM, S^AFM, E at the critical point. d Comparison of the absolute difference for different observables A = χ^AFM, S^AFM, E in the dimer-singlet phase. The interlayer exchange coupling is at the critical point ${J}_{D}={J}_{D}^{c}$. J is the intralayer exchange coupling. The error bars represent the standard deviation of the data and are smaller than the symbols except when shown.

In part, this behavior is simply due to the different magnitude of the observables itself and due to the fact that S^AFM and χ^AFM diverge with system size, whereas E converges to a constant. It is therefore instructive to consider the relative enhancement of these quantities as well (Fig. 4). For the relative enhancement, again, the energy shows the weakest effect, while both S^AFM and χ^AFM behave qualitatively different from the energy but similar among themselves. In all three cases, the relative enhancements decay in the thermodynamic limit, which means that the single-mode cavity does not change the leading scaling exponents and thus the universality class of the system. Instead it gives rise to what can be interpreted as a “correction to scaling”⁷⁹, analogously to the corrections to scaling that always appear because of microscopic (or macroscopic⁸⁰) details of the model.

Fig. 4: Cavity effect on the relative critical scaling of the structure factor, susceptibility, and energy.

The scaling of different observables normalized by their values for vanishing light-matter coupling, λ = 0. Shown are (a) the energy per spin, E, (b) the antiferromagnetic (AFM) structure factor S^AFM corresponding to the ordering pattern of the transition, and (c) the AFM susceptibility, χ^AFM. The black lines are fits based on a scaling argument in the “Field-theory picture” subsection of the Results. The error bars represent the standard deviation of the data and are smaller than the symbols except when shown.

For an effect perturbative in λ, we would expect such corrections to scale as λ⁴/L² as the leading order of our light-matter coupling is λ²/L² and the effect arises as a back-action from the ${{{{{{{\mathcal{O}}}}}}}}({\lambda }^{2})$ cavity vacuum fluctuations onto the matter system. The decay of the energy enhancement fits well with an L⁻² power-law with λ-dependent prefactor (Fig. 4). Choosing the prefactor proportional to λ⁴ is not entirely sufficient to fit the dependence on the light-matter coupling, which we attribute to a small ${{{{{{{\mathcal{O}}}}}}}}({\lambda }^{2}/N)$ direct renormalization of the exchange coupling in the $\langle 0| \hat{{{{{{{{\mathcal{J}}}}}}}}}| 0\rangle$ matrix element (see the subsection “Derivation of the continuum action in dimerized antiferromagnets” in the Methods).

However, in the presence of the singular behavior at a QCP, such simple perturbative arguments need not always hold true. This is illustrated here in the case of the magnetic fluctuations. Here, the power-law decay is better described by a much smaller exponent, compatible with 1/ν − d = −0.596(5) (based on ν = 0.7121(28) for the 3D O(3) class⁸¹), which we derive based on a scaling argument in the “Field-theory picture” subsection in the Results. In Supplementary Note 3, we show that the same exponent also appears in a different lattice featuring an AFM-dimer-singlet QCP.

At larger system sizes, this behavior may be modified due to the relevance of additional finite-q cavity modes. In Supplementary Note 4, we show within the field theory description to be discussed below that the inclusion of multiple modes leads to a finite shift of the QCP and a stronger non-local interaction term.

State of the cavity

So far, we have discussed observables of the matter system. The state of the cavity is also accessible to our QMC formulation via the occupation number distribution, $P({n}_{{{{{{{{\rm{ph}}}}}}}}})=\langle \vert {n}_{{{{{{{{\rm{ph}}}}}}}}}\rangle \langle {n}_{{{{{{{{\rm{ph}}}}}}}}}\vert \rangle$, (Fig. 5). Due to the downfolding, the photon states in our model do not exactly correspond to the physical photons, so that P(n_ph) = P_eff(n_ph) + ΔP(n_ph) is subject to a small correction term that we derive in Supplementary Note 2).

Fig. 5: Cavity mode occupation of the coupled spin-photon system.

Occupation number distribution P(n_ph) of the cavity photon at different values of the interlayer exchange coupling J_D at fixed light-matter coupling λ including the observable correction arising from the downfolding derived in Supplementary Note 2. The results for L = 32 shown here are converged to the thermodynamic limit as is visible in the inset, showing the average occupation 〈n_ph〉 as a function of the exchange coupling ratio J_D/J around the critical point ${J}_{D}^{c}$ (vertical line). J is the intralayer exchange coupling. P(5) and P(7) are finite but vanishingly small so that they do not show on the logarithmic axis. The error bars represent the standard deviation of the data.

In addition to numerical results for J_D = J and ${J}_{{{{{{{{\rm{D}}}}}}}}}={J}_{{{{{{{{\rm{D}}}}}}}}}^{c}$, we include analytical results obtained for the case J_D = ∞ where the spin state of the model becomes an exact singlet product.

Two contributions on the occupation number distribution can be separated. First, the light-matter coupling within our effective model leads a virtual occupation of the even-numbered photon sector. Second, an overall smaller contribution enters for all n_ph due to the correction ΔP(n_ph), dominating in the odd-numbered sector. Considering the parity symmetry, these odd-numbered states are likely a sign of light-matter entanglement similar to the ones recently found in a one-dimensional interacting model⁵². We find that the static occupation number distribution does not show a distinct signature at the critical point (inset of Fig. 5).

In principle, like for an impurity in a bulk system, the critical magnet should mediate long-time correlations that could be used as a cavity probe for critical behavior. Such correlations are, as we have shown, not visible in the static observables easily accessible in our QMC simulations. We do, however, expect them to appear in dynamical observables such as the second-order degree of coherence g⁽²⁾(t).

Field-theory picture

In the preceding section, we presented numerical results for the light-matter enhancement of different observables, which had several key properties: (i) The enhancement is strong for magnetic observables. (ii) The relative enhancement, when viewed as a correction to scaling, has an exponent that is similar for different observables and lattices. These properties suggest that the enhancement effect can be understood analytically through the lense of a field theory that has a more universal scope than our particular microscopic model.

The starting point of this idea is to perform the continuum limit of our lattice model, which is done in the framework of bond operator theory^82,83 in the Methods. For this limit, we assume from the start that the photon occupation is always low so that the higher-order terms of $\hat{{{{{{{{\mathcal{J}}}}}}}}}$ can be dropped. Furthermore, we drop higher-order magnetic interactions which are irrelevant (in the renormalization group sense) close to the critical point. These considerations lead to the action

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{s}}}}}}}}-{{{{{{{\rm{ph}}}}}}}}} = \int\,d\tau \left({a}^{* }{\partial }_{\tau }a+\Omega | a{| }^{2}+{\lambda }^{2}{\Gamma }_{0}\,{{\mbox{Re}}}\,\,{a}^{2}\right.\\ + \int\,{d}^{d}x\left[-\frac{1}{2}{{{{{{{\boldsymbol{\phi }}}}}}}}\cdot ({\nabla }^{2}-g){{{{{{{\boldsymbol{\phi }}}}}}}}+\frac{u}{4}{({{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2})}^{2}\right.\\ + \left.\left.\frac{{\lambda }^{2}}{{L}^{d}}\left({\Gamma }_{1}| a{| }^{2}+{\Gamma }_{2}\,{{\mbox{Re}}}\,\,{a}^{2}+{\Gamma }_{3}\right){{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2}\right]\right),$$

(7)

where d is the spatial dimension, τ is imaginary time, a is a complex field describing the cavity photon, and ϕ is a real vector field describing the coarse-grained AFM order parameter. In addition to the terms presented here, Ω is shifted by a term of ${{{{{{{\mathcal{O}}}}}}}}({\lambda }^{2})$, which does not affect our results at leading order in λ². While derived from our specific microscopic model in Eq. (2), we stress that this action is quite generic. It could in fact, based on symmetry considerations alone, have been written down phenomenologically for any O(N) critical point coupled quadratically to a single bosonic mode.

To understand the effect of the photon mode, it can be integrated out to leading order in λ (see Methods), yielding the standard O(N) model

$${{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{\rm{s}}}}}}}}} = \int\,d\tau {d}^{d}x\left[-\frac{1}{2}{{{{{{{\boldsymbol{\phi }}}}}}}}\cdot \left({\nabla }^{2}-g+\frac{\Sigma }{{L}^{d}}\right){{{{{{{\boldsymbol{\phi }}}}}}}}\right.\\ + \left.{{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2}\left(\frac{u}{4}{{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2}+\int\,d{\tau }^{{\prime} }{d}^{d}y\frac{V(\tau -{\tau }^{{\prime} })}{{L}^{2d}}{{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2}({\tau }^{{\prime} },y)\right)\right],$$

(8)

where both the mass and the interaction terms acquire corrections, Σ = λ²Γ₃ + λ⁴Γ₀Γ₂/Ω and $V=-2{\lambda }^{4}{\Gamma }_{2}^{2}/\Omega$. Intuitively, since at the critical point the mass term in the original (uncoupled) model is zero, Σ can have a strong effect even though it is suppressed by a volume factor 1/L^d. The modified interaction V, on the other hand, is always a small addition on top of the existing quartic interactions, although its non-local nature could have consequences as well.

In the following, let us consider an observable A close to the critical point. If A is singular (as e.g. the structure factor), it will assume a power-law form A ~ g^p with some observable dependent exponent p. For λ ≠ 0, g in this form is replaced by g + ΣL^−d. Further, g is related to the correlation length, which in turn is cut off by L for a finite system at the critical point, so that g ~ L^−1/ν. Then for any exponent p we get

$$\frac{A}{{A}_{\lambda = 0}} \sim \frac{{\left({L}^{-1/\nu }+\Sigma {L}^{-d}\right)}^{p}}{{L}^{-p/\nu }} \sim 1+{c}^{{\prime} }{L}^{1/\nu -d}.$$

(9)

For d = 2 and ν = 0.7121(28)⁸¹ in the (2 + 1)D O(3) universality class, the value of this correction exponent is 1/ν − d = −0.596(5) which fits well with our data (Fig. 4), while also explaining the similarity of the correction exponents for different observables. The absolute difference A − A_λ=0 ~ L^{(1−p)/ν−d} diverges or vanishes depending on the observable. In particular, for S^AFM, p = 2β − νd and (1 − p)ν − d ≈ 0.366(6) > 0.

The appearance of these exponents is actually quite unexpected and special to the strongly correlated nature of the system. In most situations, one would expect that a perturbative expansion in the light matter coupling, A ≈ A⁽⁰⁾ + A⁽¹⁾ΣL^−d exists so that the light-matter enhancement scales like L^−d. Such considerations form the basis of many arguments about the strength of a single mode in weakly correlated systems. Tuning the matter system to a QCP makes the λ → 0 limit singular, breaking simple perturbative arguments and giving rise to a stronger than expected non-analytic scaling. Finally, for observables either (i) dominated by their non-singular part such as the energy or (ii) far away from the critical point, the simple perturbative expansion works again and the L^−d scaling is recovered.

The exponent 1/ν − d of the relative enhancement further suggests that the effect is stronger in other universality classes. For example, in the (1+1)D Ising model, d = ν = 1 leading to a constant effect in the thermodynamic limit. For the (1+1)D three-state Potts universality class, ν = 5/6 < 1⁸⁴, so that the correction diverges with system size, signaling a shift of the critical coupling or a change in the leading critical exponents.

Conclusion

We have studied a quantum critical magnet coupled to a single-mode cavity in the dipole approximation using large-scale QMC simulations. Our results show that while the position and universality class of the quantum critical point are not changed, the single mode has an influence on observables related to the critical magnetic fluctuations in the magnet. Using a scaling argument, this influence can be viewed as a correction to the critical scaling with an exponent 1/ν − d that is independent on the microscopic details of the lattice. As a result, in our case, the relative enhancement of the fluctuations tends to zero in the thermodynamic limit. For certain observables such as the static AFM structure factor, the absolute enhancement, however, still diverges in the thermodynamic limit, which can be seen as a change in the ground state of the matter system, induced by a single cavity mode. On a fundamental level, the emergence of a fractional scaling exponent in the light-matter enhancement highlights that strong correlations coupled to light can induce qualitatively different behavior that falls beyond simple perturbative arguments applicable in weakly correlated systems.

A possible platform to realize our findings experimentally is the van der Waals magnet MnPSe₃, where the Néel AFM to dimer transition could be realized by applying hydrostatic pressure. Here, the renormalization of the AFM order parameter should be accessible by optical probes such as linear dichroism, reflectivity anisotropy, or Raman measurements. Further, while we show that the static photon number statistics are not sensitive to critical fluctuations, we expect the dynamical photon correlations to show a signal of the critical slowing down at the QCP.

In the true thermodynamic limit, additional finite-momentum modes should be taken into account. Including more modes in the QMC method, coupled via the downfolded Peierls coupling, comes with two challenges. First, it generally introduces a sign problem. Second, due to the structure of the coupling, all modes are coupled to each other in a complicated way that leads to an exponential scaling in memory for the current SSE formulation. Both problems may be tackled by a change of the computational basis or further controlled approximations of the coupling. However, including finite-momentum modes in the microscopically derived field theory is straight-forward and leads to a finite shift of the QCP.

Lastly, we stress that the field-theory picture of the physics here is quite robust to the microscopic details of the model and should apply also in other critical systems. While the exponent 1/ν − d is negative in the (2+1)D O(3) universality class we considered, this is not true for other phase transitions. In the (1+1)D Ising class, ν = 1⁸⁵ so that the exponent is exactly zero, leading to a constant relative enhancement of observables. In the (1+1)D Potts universality class, ν = 5/6⁸⁴ so that the exponent becomes positive and dominant over the original critical behavior.

Methods

Quantum Monte Carlo

We here extend the stochastic series expansion method to magnets coupled to cavity modes, as exemplified by the down-folded Peierls interaction presented in the Methods section. However, our method applies to any spin-photon Hamiltonian of the form

$${H}_{{{{{{{{\rm{s}}}}}}}}-{{{{{{{\rm{ph}}}}}}}}}=\mathop{\sum}\limits_{nm}\left({H}_{{{{{{{{\rm{s}}}}}}}},nm}+\Omega n{\delta }_{nm}\right),$$

(10)

where H_s,nm is a spin Hamiltonian whose parameters are determined by the photon number sector (nm). To apply the stochastic series expansion method, one needs two ingredients: a computational basis and a decomposition of the Hamiltonian into bond terms. Our computational basis is the exterior product of the photon occupation number ($\left\vert n\right\rangle$) and spin-S_z ($\vert \uparrow \rangle$ and $\vert \downarrow \rangle$) bases, where we truncate the photonic Hilbert space at a sufficiently large maximum occupation number, $n \, < \, {n}_{{{{{{{{\rm{ph}}}}}}}}}^{\max }$, to achieve converged results. Then, we decompose the Hamiltonian into “three-site” bond operators,

$$H=\mathop{\sum}\limits_{\langle ij\rangle }{h}_{0,ij},$$

(11)

$${h}_{0,ij}={\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}\left({{{{{{{{\bf{S}}}}}}}}}_{i}\cdot {{{{{{{{\bf{S}}}}}}}}}_{j}-\frac{1}{4}\right)+\frac{\Omega }{{N}_{b}}{a}^{{{{\dagger}}} }a,$$

(12)

all acting, apart from regular spin lattice sites i and j, on the same artificial “cavity site” denoted “0”, containing the photonic Hilbert space. The Ωa^†a term is split up evenly and distributed among all N_b bond terms.

In practice, a major obstacle to such extensions is that introducing new couplings to the Hamiltonian can cause the emergence of a sign problem⁸⁶, which arises when products of matrix elements of the operators h_0,ij become positive. The sign problem leads to an increase in statistical errors that typically fatally decreases the efficiency of the method. This also limits the application of the stochastic series expansion to most frustrated magnets and electronic systems. For the latter, other algorithms, such as auxiliary-field QMC methods⁸⁷, exist and may also be good candidates to study the light-matter problem.

Fortunately, while the addition of the down-folded Peierls coupling does in general cause a sign problem, the model can be made completely sign-problem-free for a large range of parameters using two basic unitary transformations. The first one is a π-rotation of the spins on one sublattice, mapping ${S}_{i}^{+}{S}_{j}^{-}\mapsto -{S}_{i}^{+}{S}_{j}^{-}$ for all bonds (ij). This transformation is routinely used to make bipartite AFMs sign-free in the S^z basis by making the off-diagonal spin interactions ferromagnetic. In the presence of the cavity, this step alone is not enough since each of the matrix elements of the cavity coupling ${\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}$ can add additional signs.

A sufficient (but not necessary) condition for sign-freeness is $\langle n| {\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}| m\rangle \ge 0$ for all $m,n \, < \, {n}_{{{{{{{{\rm{ph}}}}}}}}}^{\max }$. This condition can be fulfilled for a ${n}_{{{{{{{{\rm{ph}}}}}}}}}^{\max }$-dependent region in parameter space after performing a second, diagonal unitary transformation that maps a ↦ ia. Under this transformation, the matrix elements of the displacement operator, ${D}_{nm}^{ij}$, become positive, leaving only the signs from the denominators in Eq. (3). The sum over these denominators is positive in the blue-detuned region of $\bar{\omega }=1$ and the red-detuned regions of the other singularities $n\bar{\omega }=1$, as long as ${\lambda }_{ij}/\sqrt{N}$ is not too large (Fig. 6a). The resulting exactly sign-free regions shrink with increasing photon number cutoff ${n}_{{{{{{{{\rm{ph}}}}}}}}}^{\max }$ but grow with system size (due to the factor $1/\sqrt{N}$ in the coupling), so that simulations converged in both the cutoff and system size are possible in these regions and all simulations of this work are sign-problem free.

Fig. 6: The sign problem for a coupled spin-photon system.

Shown is the parameter space of light matter couplings normalized by system size $\lambda /\sqrt{N}$ and cavity frequencies Ω normalized by Hubbard repulsion U. Some parameter regions (depending on the photon number cutoff ${n}_{{{{{{{{\rm{ph}}}}}}}}}^{\max }$) give rise to signful quantum Monte Carlo (QMC) configurations, known as the sign problem. a Exactly sign-free regions according to a sufficient condition based on the matrix elements of the exchange coupling operator $\langle n| {\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{ij}| m\rangle \ge 0$ for all $n,m \, < \, {n}_{{{{{{{{\rm{ph}}}}}}}}}^{\max }$. b Actual average sign in a simulation at temperature T = J/2L. For an average sign 〈sign〉 = 1, i.e., outside of the white regions, efficient large-scale simulations are possible. J is the intralayer exchange coupling.

In our simulations, we find that even in the parameter regions outside of the ones in Fig. 6a, the average sign problem can be relatively benign at weak coupling $\lambda /\sqrt{N}$ or high Ω/U, where problematic negative matrix elements become very rare in the sampling (Fig. 6b).

With all ingredients of a sign-problem-free stochastic series expansion in place, we use the recently developed abstract loop update algorithm⁸⁸ to perform QMC sampling in the given basis and bond-operator decomposition without the need of engineering model specific loop update rules. To solve the linear-programming problem that appears when finding the optimal loop propagation probabilities^89,90, we employ the HiGHs package⁹¹.

At this point it is helpful to discuss parallels with the mathematically similar spin-phonon and one-dimensional electron-phonon models, where other stochastic series expansion methods have been developed. While earlier studies relied on rather inefficient local updates^67,92, recent advances in the sampling of retarded interactions allow efficient treatment of models where the phonons can be integrated out exactly^68,69.

Carrying over these advances into the photonic setting is in our case not straightforward due to the highly nonlinear nature of the downfolded Peierls coupling preventing the exact integration of the photons. On the other hand, we note that our method provides a global update for generic nonlinear spin-boson interactions and may in turn be useful in the phononic setting when generic nonlinear interactions have to be taken into account.

Derivation of the continuum action in dimerized antiferromagnets

To elucidate our numerical findings further, in this section, we will develop a complementary analytical approach based on a field theoretical scaling argument. Starting from the specific microscopic Hamiltonian (2), we derive a continuum action describing the physics of the magnetic quantum critical point coupled to a cavity photon. Upon integrating out the photon, we recover the well-known O(N) model with the addition of a cavity-induced mass term, which generally vanishes with increasing system sizes but becomes relevant close to the critical point.

The influence of the cavity-induced mass term will allow us to explain the scaling of the cavity-induced enhancements observed in our numerical results. While this approach starts from our specific model, the universal nature of the field-theory description allows us to anticipate under what conditions the same physics may be found also in other systems hosting a O(N) QCP.

The basic assumptions underlying this analysis is, first, that our model is close enough to the critical point to be described by a continuum theory of the lowest-energy excitations. Second, we assume (as we confirm in the numerical Results) that the photon occupation is low so that we can neglect higher order terms in the light-matter coupling.

To start, we consider the physics of our AFM close to the QCP separating the dimer-singlet and AFM phases. At this QCP, the relevant critical fluctuations are triplet excitations that break the dimer singlets of the disordered phase and condense to form AFM order. To describe these excitations in a bosonic language, we use the bond-operator formalism^82,83, which can be considered a version of spin-wave theory for dimer-singlet ground states.

The eigenbasis of a single dimer, consisting one singlet and three triplet states, can be written as

$$\left\vert s\right\rangle = \left(\left\vert \uparrow \downarrow \right\rangle -\left\vert \downarrow \uparrow \right\rangle \right)/\sqrt{2},\\ \left\vert {t}_{x}\right\rangle = \left(\left\vert \downarrow \downarrow \right\rangle -\left\vert \uparrow \uparrow \right\rangle \right)/\sqrt{2},\\ \left\vert {t}_{y}\right\rangle = i\left(\left\vert \downarrow \downarrow \right\rangle +\left\vert \uparrow \uparrow \right\rangle \right)/\sqrt{2},\\ \left\vert {t}_{z}\right\rangle = \left(\left\vert \uparrow \downarrow \right\rangle +\left\vert \downarrow \uparrow \right\rangle \right)/\sqrt{2}.$$

(13)

For these states, three bosonic bond operators are defined that create triplet states from the singlet “vacuum”

$${t}_{a}^{{{{\dagger}}} }\left\vert s\right\rangle =\left\vert {t}_{a}\right\rangle ,\quad a=x,y,z$$

(14)

and fulfill bosonic commutation relations.

To avoid unphysical states, the new bosonic Hilbert space has then to be constrained to the sector t^† ⋅ t ≤ 1. Where t is the vector of t_a operators, transforming like a vector under spin rotations.

In this language, the two spin operators belonging to the dimer can be expressed as

$${{{{{{{{\bf{S}}}}}}}}}_{1,2}=\frac{1}{2}(\pm {{{{{{{{\bf{t}}}}}}}}}^{{{{\dagger}}} }P\pm P{{{{{{{\bf{t}}}}}}}}-i{{{{{{{{\bf{t}}}}}}}}}^{{{{\dagger}}} }\times {{{{{{{\bf{t}}}}}}}}),$$

(15)

where P = 1 − t^† ⋅ t is a projector onto the physical subspace.

The dimerized magnet we are interested in is made up of J_D intradimer and J interdimer bonds. For each J_D bond b we introduce a set of bond operators t_b. Then, we express the Hamiltonian containing all bonds using Eq. (15). In a bilayer geometry⁹³, one gets $H={H}_{0}+{H}_{2}+{H}_{4}+{{{{{{{\mathcal{O}}}}}}}}({{{{{{{{\bf{t}}}}}}}}}^{6})$ with

$${H}_{0} \, = \, \Omega {a}^{{{{\dagger}}} }a-\frac{3N{J}_{{{{{{{{\rm{D}}}}}}}}}}{4}-\mathop{\sum}\limits_{\langle bd\rangle }\frac{{\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{bd}}{4},\\ {H}_{2} \, = \, {J}_{{{{{{{{\rm{D}}}}}}}}}\mathop{\sum}\limits_{b}{{{{{{{{\bf{t}}}}}}}}}_{b}^{{{{\dagger}}} }\cdot {{{{{{{{\bf{t}}}}}}}}}_{b}+\mathop{\sum}\limits_{\langle bd\rangle }\frac{{\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{bd}}{2}:({{{{{{{{\bf{t}}}}}}}}}_{b}^{{{{\dagger}}} }+{{{{{{{{\bf{t}}}}}}}}}_{b})\cdot ({{{{{{{{\bf{t}}}}}}}}}_{d}^{{{{\dagger}}} }+{{{{{{{{\bf{t}}}}}}}}}_{d}):\\ {H}_{4} \, = \, \mathop{\sum}\limits_{\langle bd\rangle }\frac{{\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{bd}}{2}\left(:({{{{{{{{\bf{t}}}}}}}}}_{b}^{{{{\dagger}}} }\cdot {{{{{{{{\bf{t}}}}}}}}}_{d})({{{{{{{{\bf{t}}}}}}}}}_{d}^{{{{\dagger}}} }\cdot {{{{{{{{\bf{t}}}}}}}}}_{b}):-({{{{{{{{\bf{t}}}}}}}}}_{b}^{{{{\dagger}}} }\cdot {{{{{{{{\bf{t}}}}}}}}}_{d}^{{{{\dagger}}} })\left.({{{{{{{{\bf{t}}}}}}}}}_{b}\cdot {{{{{{{{\bf{t}}}}}}}}}_{d})\right)\right.\\ - :\left.\left[({{{{{{{{\bf{t}}}}}}}}}_{b}^{{{{\dagger}}} }+{{{{{{{{\bf{t}}}}}}}}}_{b})\cdot ({{{{{{{{\bf{t}}}}}}}}}_{d}^{{{{\dagger}}} }+{{{{{{{{\bf{t}}}}}}}}}_{d})\right]({{{{{{{{\bf{t}}}}}}}}}_{b}^{{{{\dagger}}} }\cdot {{{{{{{{\bf{t}}}}}}}}}_{b}+{{{{{{{{\bf{t}}}}}}}}}_{d}^{{{{\dagger}}} }\cdot {{{{{{{{\bf{t}}}}}}}}}_{d}):\right)$$

(16)

where the sums count neighboring bonds and some terms contain normal ordering for brevity. The expansion also produces sixth-order terms in t, but we shall ignore them in the following analysis, where 〈t^† ⋅ t〉 is always assumed to be small. In a similar way, we drop terms ${{{{{{{\mathcal{O}}}}}}}}((\hat{{{{{{{{\mathcal{J}}}}}}}}}-J){{{{{{{{\bf{t}}}}}}}}}^{4})$ that are suppressed by low cavity occupation.

$$Z=\int\,{{{{{{{\mathcal{D}}}}}}}}{{{{{{{{\bf{t}}}}}}}}}_{b}^{* }{{{{{{{\mathcal{D}}}}}}}}{{{{{{{{\bf{t}}}}}}}}}_{b}{{{{{{{\mathcal{D}}}}}}}}{a}^{* }{{{{{{{\mathcal{D}}}}}}}}a\,{e}^{-{{{{{{{\mathcal{S}}}}}}}}[{{{{{{{{\bf{t}}}}}}}}}_{b}^{* },{{{{{{{{\bf{t}}}}}}}}}_{b},{a}^{* },a]}$$

(17)

with ${{{{{{{\mathcal{S}}}}}}}}=\int\nolimits_{0}^{\beta }d\tau \,{a}^{* }{\partial }_{\tau }a+{\sum }_{b}{{{{{{{{\bf{t}}}}}}}}}_{b}^{* }\cdot {\partial }_{\tau }{{{{{{{{\bf{t}}}}}}}}}_{b}+H[{{{{{{{{\bf{t}}}}}}}}}_{b}^{* },{{{{{{{{\bf{t}}}}}}}}}_{b},{a}^{* },a]={{{{{{{{\mathcal{S}}}}}}}}}_{0}+{{{{{{{{\mathcal{S}}}}}}}}}_{2}+{{{{{{{{\mathcal{S}}}}}}}}}_{4}$.

Due to the bipartiteness of our bilayer, the purely bilinear part of ${{{{{{{{\mathcal{S}}}}}}}}}_{2}$ is minimized by configurations following the sign structure of the AFM, t_b ∝ (−1)^b, where (−1)^b is negative on one sublattice and positive on the other. The low-energy theory including this mode and its low-energy excitations can be obtained by performing the continuum limit t_b ≈ (−1)^bt(r), where t(r) is a slowly varying function that can be expanded to second order in the bond length. Ignoring derivatives in both matter-matter and light-matter interaction terms, this leads to the action

$${{{{{{{{\mathcal{S}}}}}}}}}_{0} = \int\,d\tau \,{a}^{* }{\partial }_{\tau }a+\Omega | a{| }^{2}-\frac{zN}{8}\hat{{{{{{{{\mathcal{J}}}}}}}}}({a}^{* },a)+\,{{\mbox{const}}}\,,\\ {{{{{{{{\mathcal{S}}}}}}}}}_{2} = \int\,d\tau {d}^{d}x\,{{{{{{{{\bf{t}}}}}}}}}^{* }\cdot {\partial }_{\tau }{{{{{{{\bf{t}}}}}}}}\\ -({{{{{{{{\bf{t}}}}}}}}}^{* }+{{{{{{{\bf{t}}}}}}}})\cdot {\nabla }^{2}({{{{{{{{\bf{t}}}}}}}}}^{* }+{{{{{{{\bf{t}}}}}}}})\\ +{B}_{1}\left[{J}_{{{{{{{{\rm{D}}}}}}}}}| {{{{{{{\bf{t}}}}}}}}{| }^{2}-\frac{z\hat{{{{{{{{\mathcal{J}}}}}}}}}({a}^{* }, \, a)}{4}{({{{{{{{{\bf{t}}}}}}}}}^{* }+{{{{{{{\bf{t}}}}}}}})}^{2}\right],\\ {{{{{{{{\mathcal{S}}}}}}}}}_{4} = \int\,d\tau {d}^{d}x\,{B}_{2}\left[{(| {{{{{{{\bf{t}}}}}}}}{| }^{2})}^{2}-| {{{{{{{{\bf{t}}}}}}}}}^{2}{| }^{2}-2{({{{{{{{{\bf{t}}}}}}}}}^{* }+{{{{{{{\bf{t}}}}}}}})}^{2}| {{{{{{{\bf{t}}}}}}}}{| }^{2}\right].$$

(18)

Here, the isotropic form of the derivative term has been fixed by performing transformation of the coordinates and fields. This gives rise to the lattice dependent constants B₁ and B₂. The coupling $\hat{{{{{{{{\mathcal{J}}}}}}}}}$ arises from bond-averaging the lattice-dependent coupling,

$$\hat{{{{{{{{\mathcal{J}}}}}}}}}({a}^{* },a)=\frac{1}{z}\mathop{\sum}\limits_{\langle 0,d\rangle }{\hat{{{{{{{{\mathcal{J}}}}}}}}}}_{0d}({a}^{* },a),$$

(19)

where z is the number of nearest neighbor dimers.

Next, we express the the complex field t in terms of real fields t = ϕ + iπ, and noting that π is always gapped, we integrate it out, obtaining

$${{{{{{{\mathcal{S}}}}}}}} = \int\,d\tau {a}^{* }{\partial }_{\tau }a+\Omega | a{| }^{2}-\frac{zN}{8}\hat{{{{{{{{\mathcal{J}}}}}}}}}\\ + \int\,d\tau {d}^{d}x\,-\frac{1}{2}{{{{{{{\boldsymbol{\phi }}}}}}}}\cdot ({\partial }_{\tau }^{2}+{\nabla }^{2}+g){{{{{{{\boldsymbol{\phi }}}}}}}}\\ +{B}_{1}z(\hat{{{{{{{{\mathcal{J}}}}}}}}}-J){{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2}+\frac{u}{4}{({{{{{{{{\boldsymbol{\phi }}}}}}}}}^{2})}^{2}.$$

(20)

After approximating $\hat{{{{{{{{\mathcal{J}}}}}}}}}$ to quadratic order in λ, we arrive at the action from Eq. (7) in the Results section with

$${\Gamma }_{0} = -8{B}_{3}{\Gamma }_{2},\\ {\Gamma }_{1} = \, \alpha \left(\frac{4}{1-\bar{\omega }}-\frac{2}{1-4{\bar{\omega }}^{2}}-2\right),\\ {\Gamma }_{2} = \alpha \left(\frac{2}{1-\bar{\omega }}+\frac{1}{1-4{\bar{\omega }}^{2}}-1\right),\\ {\Gamma }_{3} = \, \alpha \left(\frac{2}{1+\bar{\omega }}-1\right),$$

(21)

where $\alpha ={B}_{1}J{\sum }_{\langle 0,d\rangle }{\hat{{{{{{{{\bf{r}}}}}}}}}}_{0,d}\cdot {{{{{{{\boldsymbol{\epsilon }}}}}}}}$ contains a sum over the polarization projected on the bond directions. B₃ is another geometrical factor. From there, the photons can be integrated out perturbatively up to order λ⁴/L^d. At this order and T = 0, only processes creating virtual photons (i.e. those not containing Γ₁) contribute (Fig. 7). This results in the O(N) model of Eq. (8).

Fig. 7: Perturbative diagrams from integrating out the photons.

The Feynman diagrams that contribute when integrating out the photons at temperature T = 0 up to order λ⁴ in the light-matter coupling. Wavy lines correspond to the photon field a, and solid lines to the order parameter field ϕ. The fields interact via the effective interactions Γ₁ and Γ₂ given in Eq. (7).